自动编码器的简介

自动编码器的应用

图片生成

在图1，你可以去说出那一个脸对是假的吗？事实上，两个都是由StyleGan2生成器生成的。虽然脸部细节非常逼真，但背景看起来很奇怪（左：模糊，右： 这是因为那个神经网络由脸部样本来训练。背景就是十分易变。这里的数据流型是50维，等于人脸图像的自由度。

图1: 生成的人脸

像素空間和潛在空間中插值的差異

图2: 狗和鸟

如果我们在狗和鸟的图像的像素空间之间进行线性插值，那我们就会在图3中看到有两幅图像淡入淡出。由上左方到下右方，狗的图像就消失，而鸟的图像就出现。

图3: 插值后的结果

如果我们对两个潜在空间表示进行插值并将其输入到解码器，我们将会在图4中获得从狗到鸟的转换。

图4: 如果我们对两个潜在空间表示进行插值并将其输入到解码器，我们将会在图4中获得从狗到鸟的转换。

明显然，潜在空间更适合取得图像的结构

转换实例

图5: 放大

图6: 移动

图7: 亮度

图8: 转动(注意旋转可以是3D)

图像超级分辨率

该模型目的是放大图片同时重建原始脸孔图片。在图9由左到右，第一列是16x16图片，而第2部份是从标准的双三次插值中得到的，而第二部份是神经网路输出的，而其右边的是真实图片。 (https://github.com/david-gpu/srez)

图9: 重建原来的脸孔

由输出的图片中，我们可以看到训练数据中是有偏见，那会令重建的脸孔不准确。比如，上左方的亚洲人面孔在输出中变得像欧洲人，那是因为训用来训练的图像例子中的占比数量不平衡，而左下角女人的重建后的脸看起来很奇怪，那是因为训练图像例子中没有足够的图像有奇数角。

图像修补

图10: 在脸上放上灰色的掩蔽

在脸上放上灰色的掩蔽如图10那样会令图片远离训练流形。而如图11那样重组是利用能量函数最小化在训练流形中找出最接近的样本图片。

图11: 图10的重建图像

由文字说明转成图片

图12: 由文字说明转成图片

在图12中，由文字描述翻译成图片是由提取图片中一些文字性的重要视觉信息，然后转换它们成图片。

什么是自动编码器?

自动编码器是由无监督方式来训练的人工神经网络，它目的是先学习我们数据的编码式表示，然后由学习了的编码式表示来生成输入数据(尽可接近地)。所以，自动编码器的输出是预测它自身的输入。

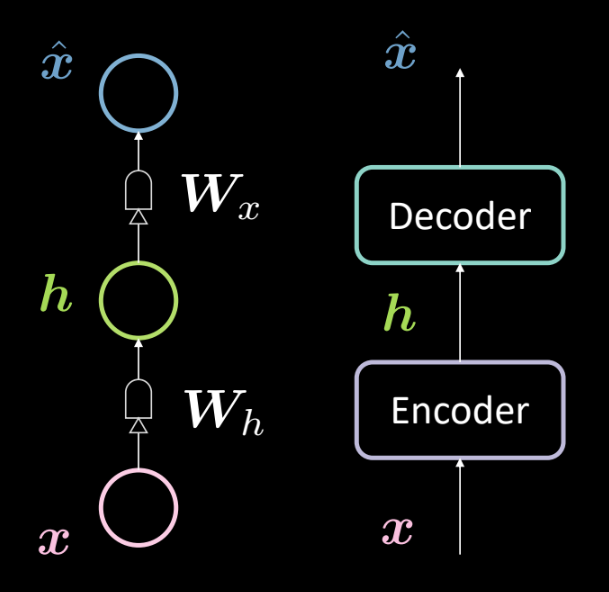
图13: 基本自动编码器的架构

图13显示出一个基本的自动编码器的架构。就如之前，我们由底部的输入 $\boldsymbol{x}$ 开始去输入到编码器( $\boldsymbol{W_h}$, followed by squashing). This results in the intermediate hidden layer $\boldsymbol{h}$. 定义的仿射变换，然后压缩)，然后结果在于中间隐藏层 $\boldsymbol{W_x}$定义的仿射变换，然后压缩)。这生成输出 $\boldsymbol{\hat{x}}$，也就是我们模型的预测或对输入的重建。按照我们的惯例，我们说这是3层神经网路。

我们可以使用以下方程式来数学上表示上方的网络：

以下是我们所使用的维度:

注意: 为了表示PCA，我们可以有一个很近的权重(或已经很近)，如以下表示 $\boldsymbol{W_x}\ \dot{=}\ \boldsymbol{W_h}^\top$

上方的点上等号意思是大约等于或很近﹑很接近。

为什么我们用自动编码器?

现在，你或很惊愕为什么要预测出输出和自动编码器的应用会是什么。

自动编码器的主要的应用是检测出异常或图像降噪。你知道自动编码器能够对在数据流形中的数据进行数据重建。换句话说，当给予了一个数据流形，我们就希望那个自动编码器仅能够重构该流形中存在的输入。所以我们去限制模型去重建那些在训练中模型看过的事物，而且这样的话，如果有任何变异存在新的输入中，那些变异都会被移除，因为模型对这类干扰不敏感。

另一个自动编码的应用是图像压缩器。如果有一个输入后的层的维度是 $d$ ，而且低低于输入的维度 $n$，那编码器可用作压缩器「隐藏的表示」（以编码方式表示的表示）将处理输入中的所有（或大部分）信息，但用更少的空间。

重建损失

让我们看一下我们一般使用的重建损失。数据集的总损失为每个样本损失的平均值，也就是

当输入是分类的时，我们可以使用交叉熵损失来计算每个样本的损失，下方所示

而且当输入是实值，我们或想使用「均方误差损失」，下方所示

完成过度

当隐藏层的维数$d$是小于输入$n$的维数，那我们说这是低于完成不足的隐藏层。而且类似地，当$d>n$，我们称这为过度完成的隐藏层。图14显示出左方是一个未完成的隐藏层，而右方是过度完成的隐藏层。

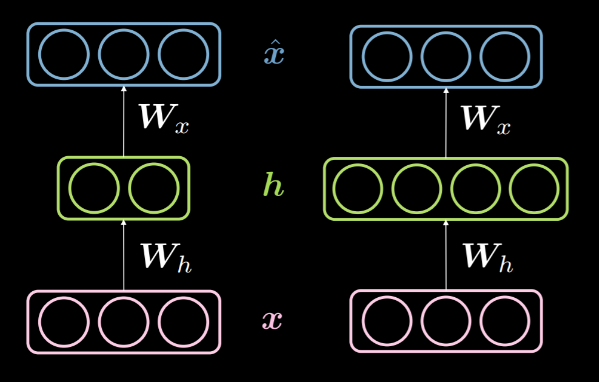
图14: 未完成与完全未完成的隐藏层

就如上方讨论过的，一个未完成的隐藏层可以被用在压缩用途，比如我们去把输入编码当中的信息编码到在更少的维度上。另外一面，在过度完成层中，那就会把输入编码到比输入更高的维度。

由于我们正在尝试对输入进行重建，模型倾向于复制所有输入的特性到隐藏层，然后将其作为输出输出来，所有这只不过是和恒等函数没分别。这虽要避免，因为这意味着你的模型无法学习任东西。所以，我们虽要用「信息瓶颈information bottleneck」来加上一些约束。我们去约束隐藏层可以采用的格局到仅适用于训练期间看到的那些配置。这样就可以进行选择性重建(被限于输入空间的一个子集)，而同时令模型更对所有不在流形中的东西更不敏感。

是可以看到的是「未完成层」是不能表现得如恒等函数一样，因为隐藏层的没有足够的维度来复制输入。所以「未完成隐藏层」和「过度完成隐藏层」比，它是不太会发生过度拟合问题，但它仍然可以发生过度拟合问题。比如，给予一个强大的编码器和一个解码器，模型简单地会将一个数字关联到每个数据点，同时这样地学会了映射。是有多个方法来避免过度拟合问题，比如正则化方法和架构法﹑其他方法。

Denoising autoencoder

图15 显示了降噪自动编码器的流形及由看下图直觉地看出其工作原理。

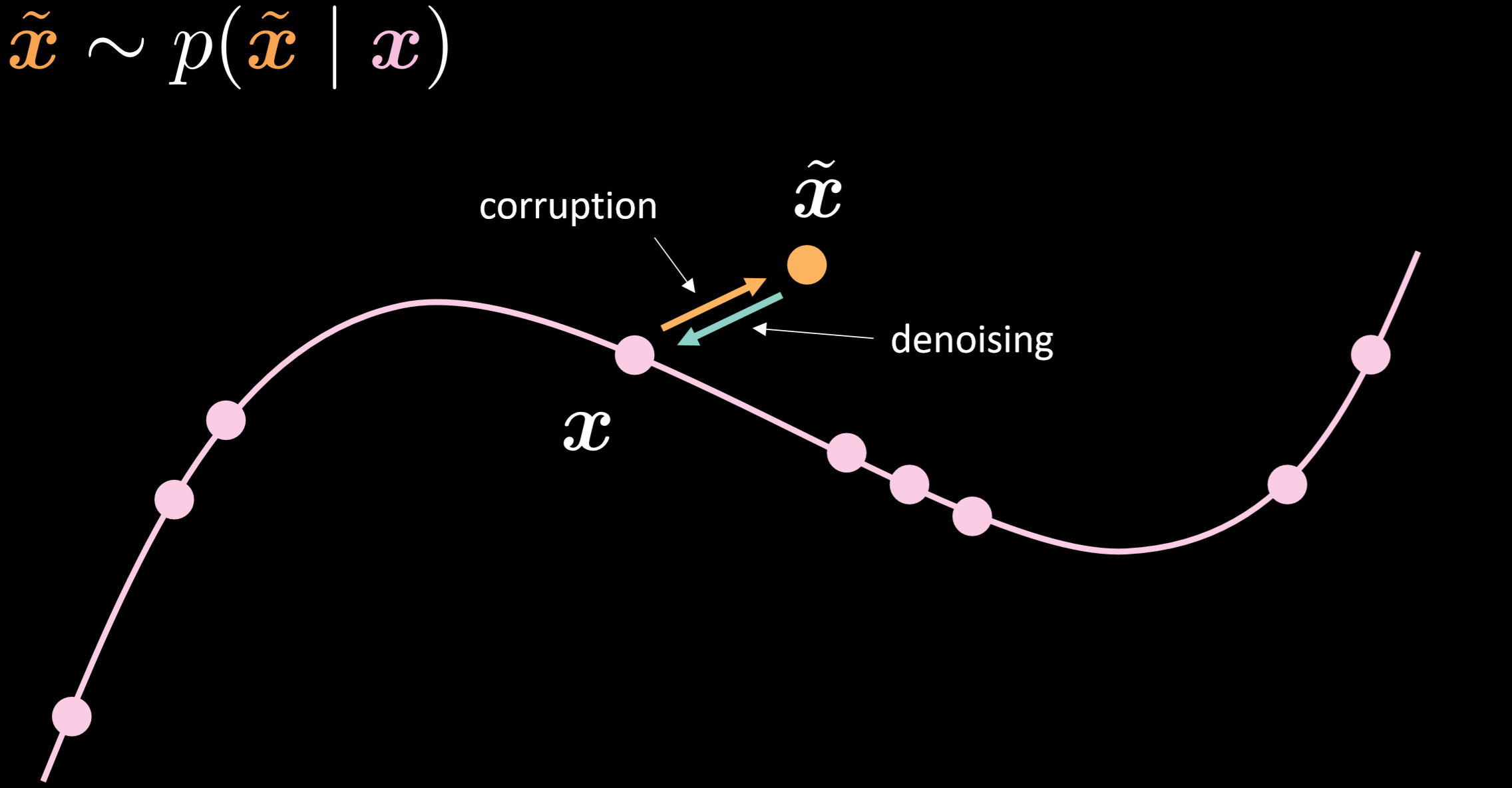
图15: 降噪自动编码器(Denoising autoencoder)

在这个模型，我们注入同样现实中我们将在现实中观察到的噪音分布(noisy distribution，就像一个数据点移开,如把正常声音弄成噪音一样，一个噪音分布或弄乱了的分布) ，所以我们可以学到如何稳健地恢复它。 由通过比较输入和输出，我们可以说出已经在流形中点没有移，而在点之外的移动了很多。

图16 给出了输入数据和输出数据之间的关系。

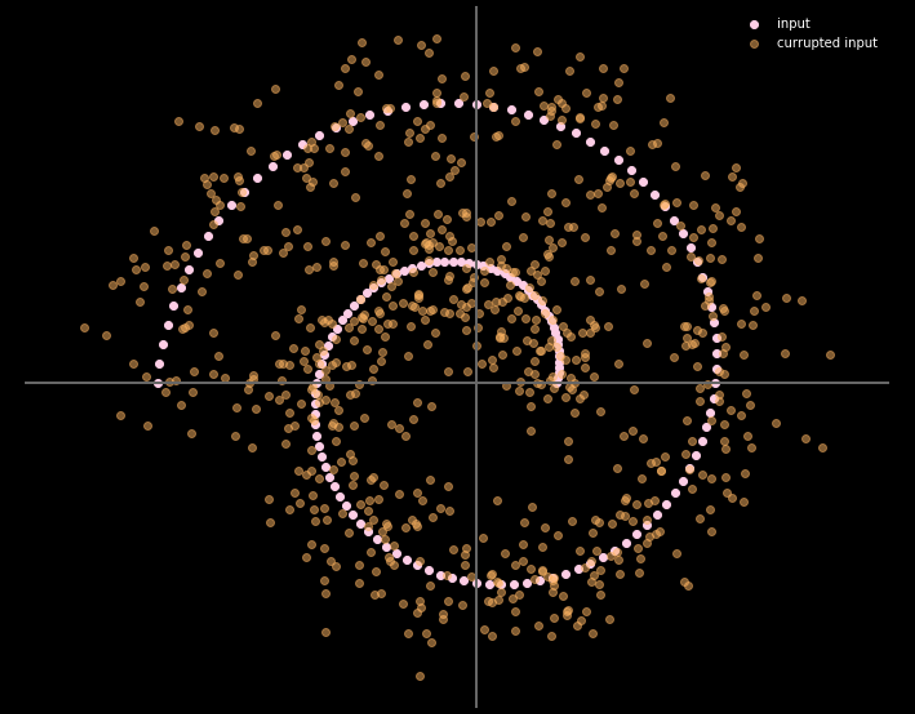
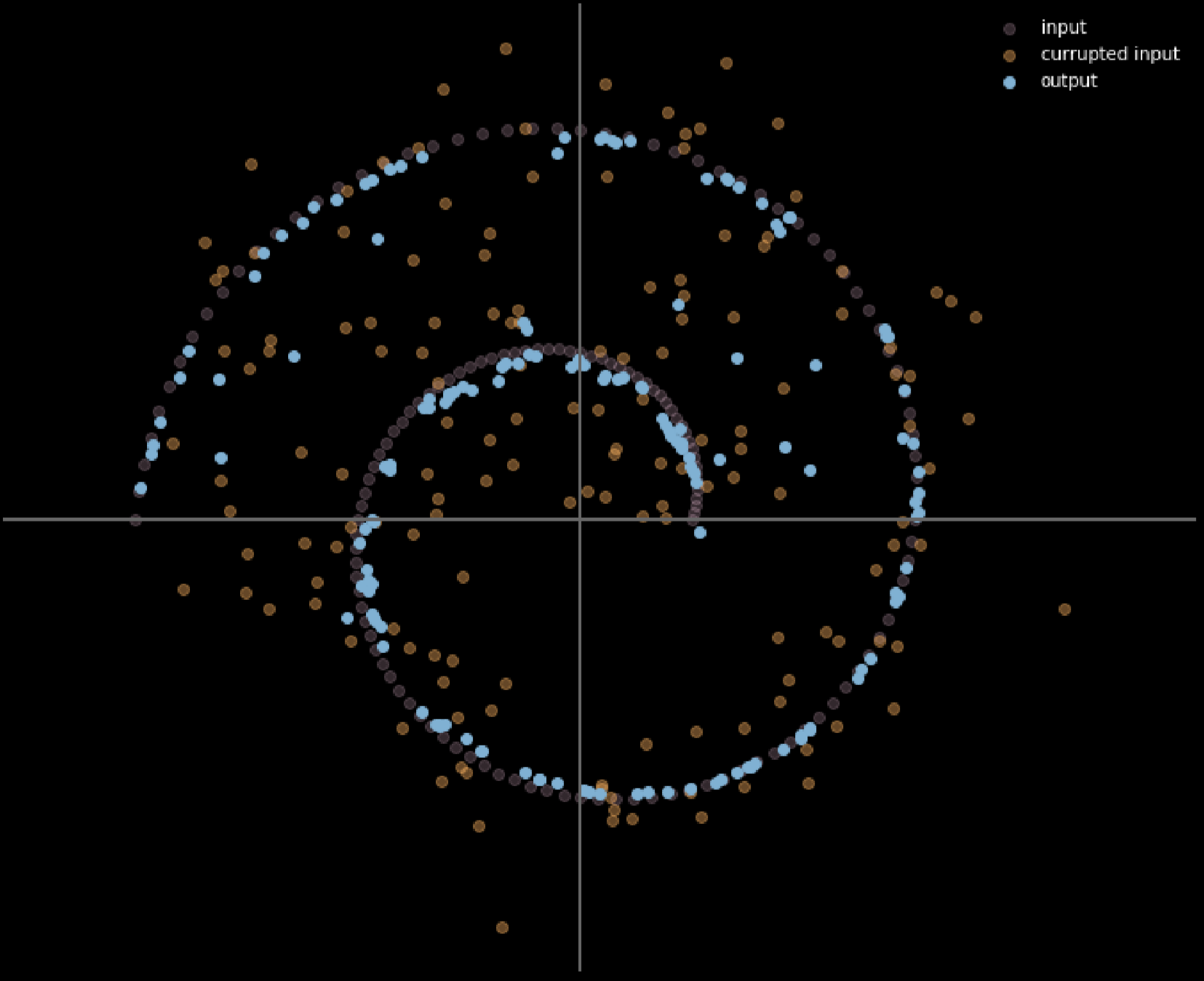
图16: 降噪自动编码器的输入和输出

我们也可以使用不同颜色去代表每一个点移动了的距离。图17显示了其图表。

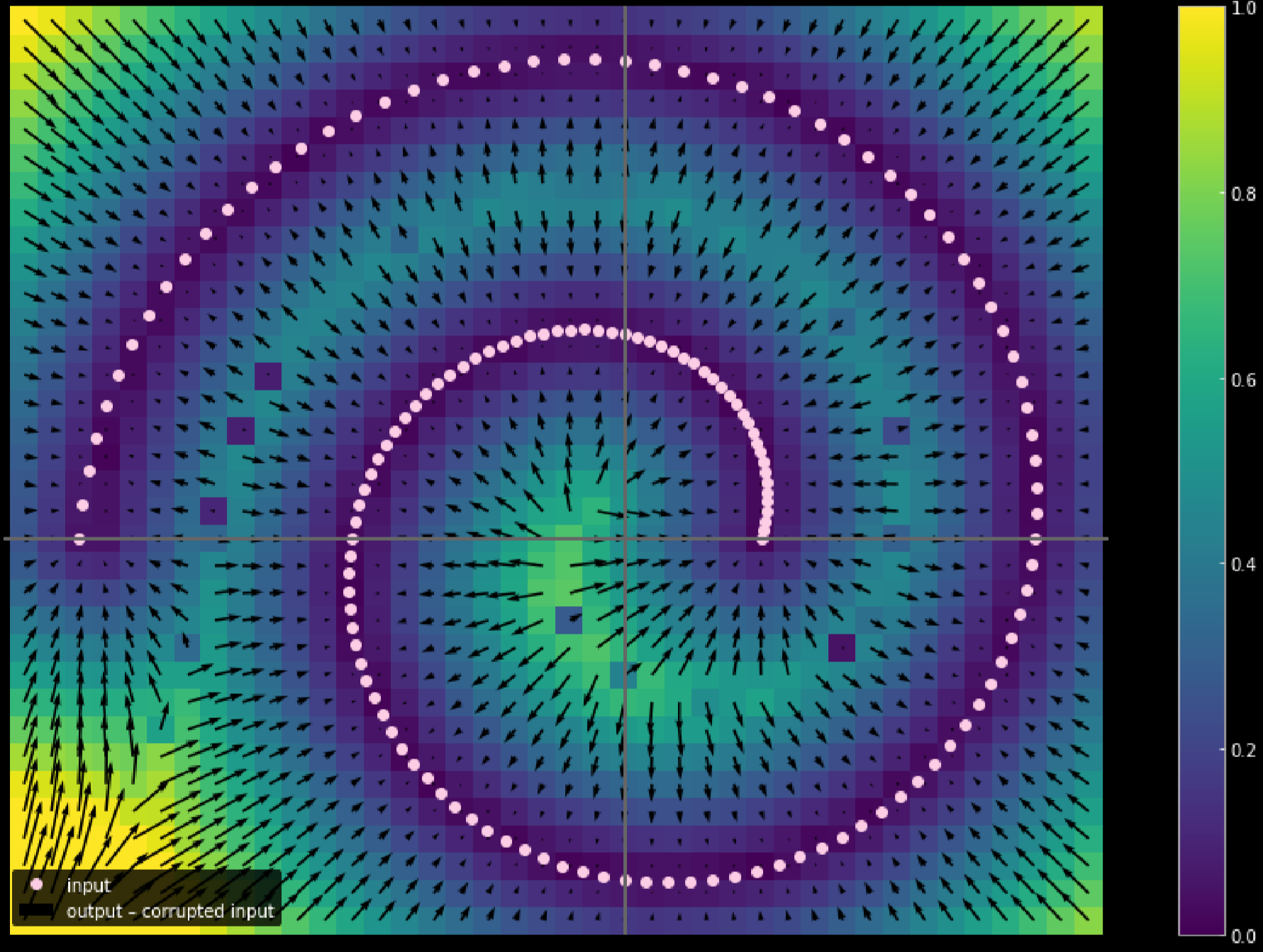
图17: 测量输入数据的移动距离

颜色越浅，移动了的距离就更远。由图表所看到的，我们可以说那些在角落的点移动了1个单位，而那些在两个分枝之间的没有移动过，那是因为它们在训练中被上方和下方的分支各自吸引着。

压缩式自动编码器

图18 显示出压缩式自动编码器的损失函数和其流形。

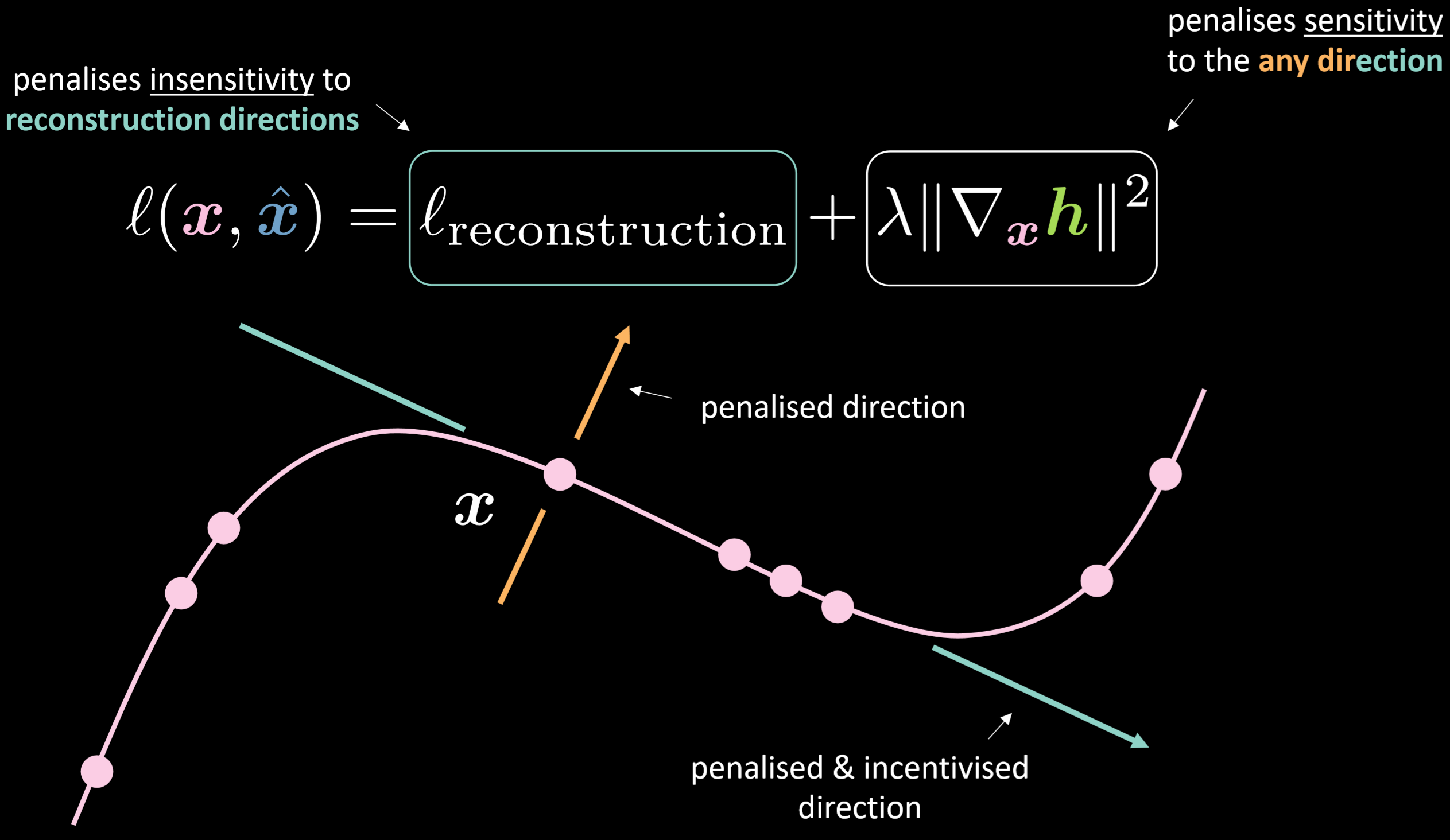
图18: 压缩式自动编码器

损失函数包含对「项」重行建进行，同时外加对应输入的隐藏表示的梯度的平方范数(squared norm of the gradient of the hidden representation with respect to the input)。因此，在输入变化的情况下，总损失将最小化隐藏层的变化。好处就是模型就会对重建目标而要走的方向感到敏感，同时不会对其化方向有敏感。图19显示了这些自动编码器的总体工作方式。

图19显示了这些自动编码器的总体工作方式。

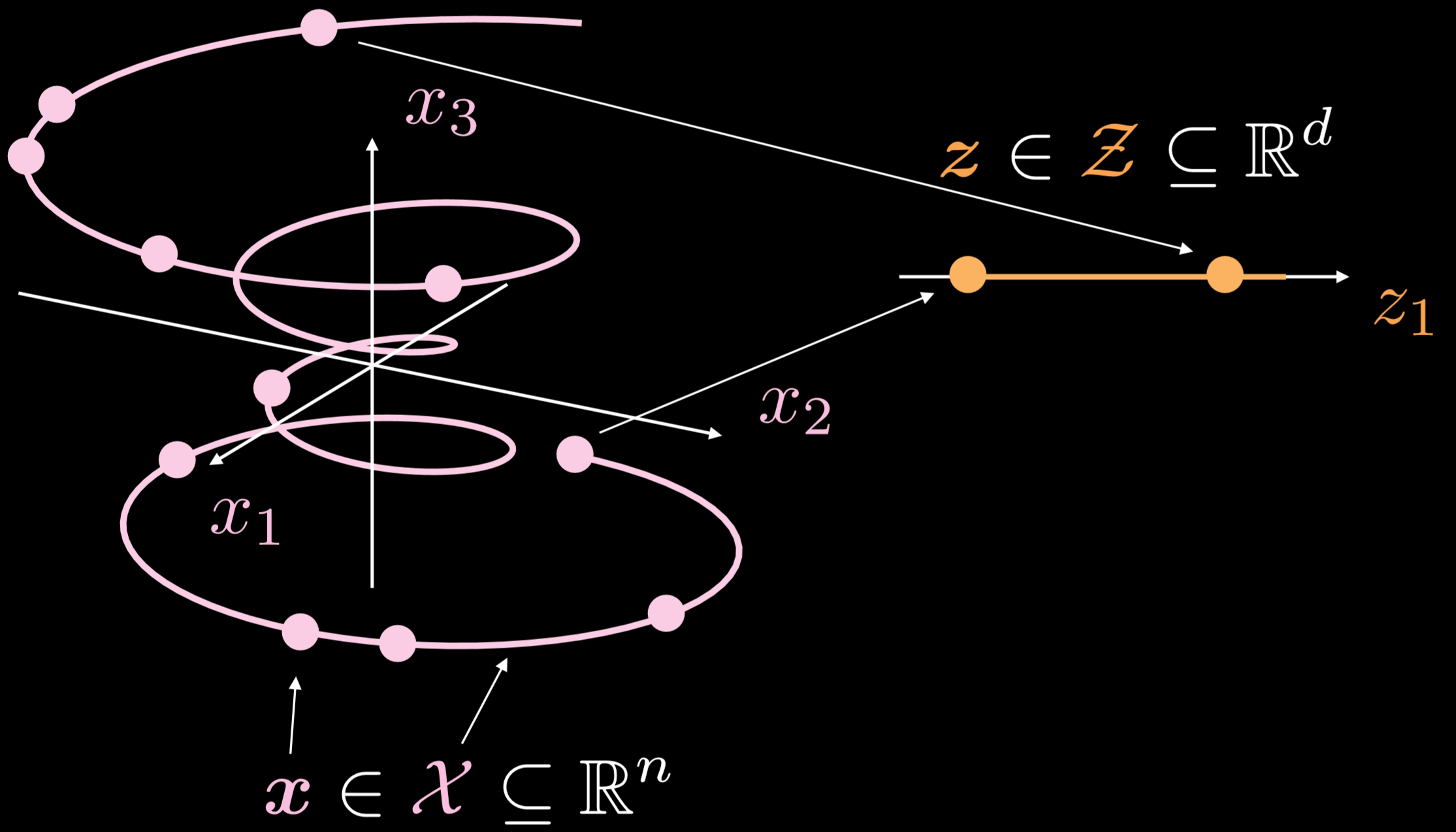
图19: 基本自动编码器

训练流形是一个单独有维度性的三维物体。而 $\boldsymbol{x}\in \boldsymbol{X}\subseteq\mathbb{R}^{n}$，自动编码器的目标是对卷曲线以一个方式来向下伸展或向内伸展，而$\boldsymbol{z}\in \boldsymbol{Z}\subseteq\mathbb{R}^{d}$。结果是，一个来自于输入层的点会被转成一个在潜在层的1点。现在，我们就有输入空间中的点和潜在空间中的点之间的对应性，但我们没有输入空间的区域和潜在空间的区域之间的对应性。之后，我们用解码器把潜在空间的一个点转换来生成一个有用的输出层。

实现自动编码器 - Notebook

Jupyter笔记本可以在这里找到。.

在这个笔记本中，我们将实现一个标准的自动编码器和降噪自动编码器，然后去比较它们的输出。

定义自动编码器模型架构和重建损失

使用大小为 $28 \times 28$ 图片，和30维的隐藏层。转换程序就会是由 $784\to30\to784$. 。如果使用双曲正切目标函数(hyperbolic tangent function )在编码器和解码器的转换程序之中，那我们就能够将输出范围限制为$(-1,1)$。均方误差损失(Mean Squared Error loss)会在模型中被作为损失函数来使用。

class Autoencoder(nn.Module):
    def __init__(self):
        super().__init__()
        self.encoder = nn.Sequential(
            nn.Linear(n, d),
            nn.Tanh(),
        )
        self.decoder = nn.Sequential(
            nn.Linear(d, n),
            nn.Tanh(),
        )

    def forward(self, x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x

model = Autoencoder().to(device)
criterion = nn.MSELoss()

训练标准的自动编码器

去使用PyTorch训练一个标准的自动编码器，你要用接下来五个方法在训练循环中:

向前:

1) 给模型输入图片，那就要用上这个: output = model(img) 。
2) 比较损失，就用这个: criterion(output, img.data)。

向后:

3) 清理梯度来确保我们没有积累其值，那就要用上这个: optimizer.zero_grad()。
4) 反向传播，用这个:loss.backward()
5) 向后退一步: optimizer.step()

图20 显示了标准自动编码器的输出。

图20: 标准的自动编码器的输出

训练降噪自动编码器

要对自动编码器进行降噪，您需要添加以下步骤：
1) 叫 nn.Dropout() 来随机关闭一些神经元。
2) 创建掩盖型噪音: do(torch.ones(img.shape))。
3) 把好图片乘「二进制掩盖码binary masks」来创建一个坏了的图片: img_bad = (img * noise).to(device)。

图21 示出了降噪自动编码器的输出。

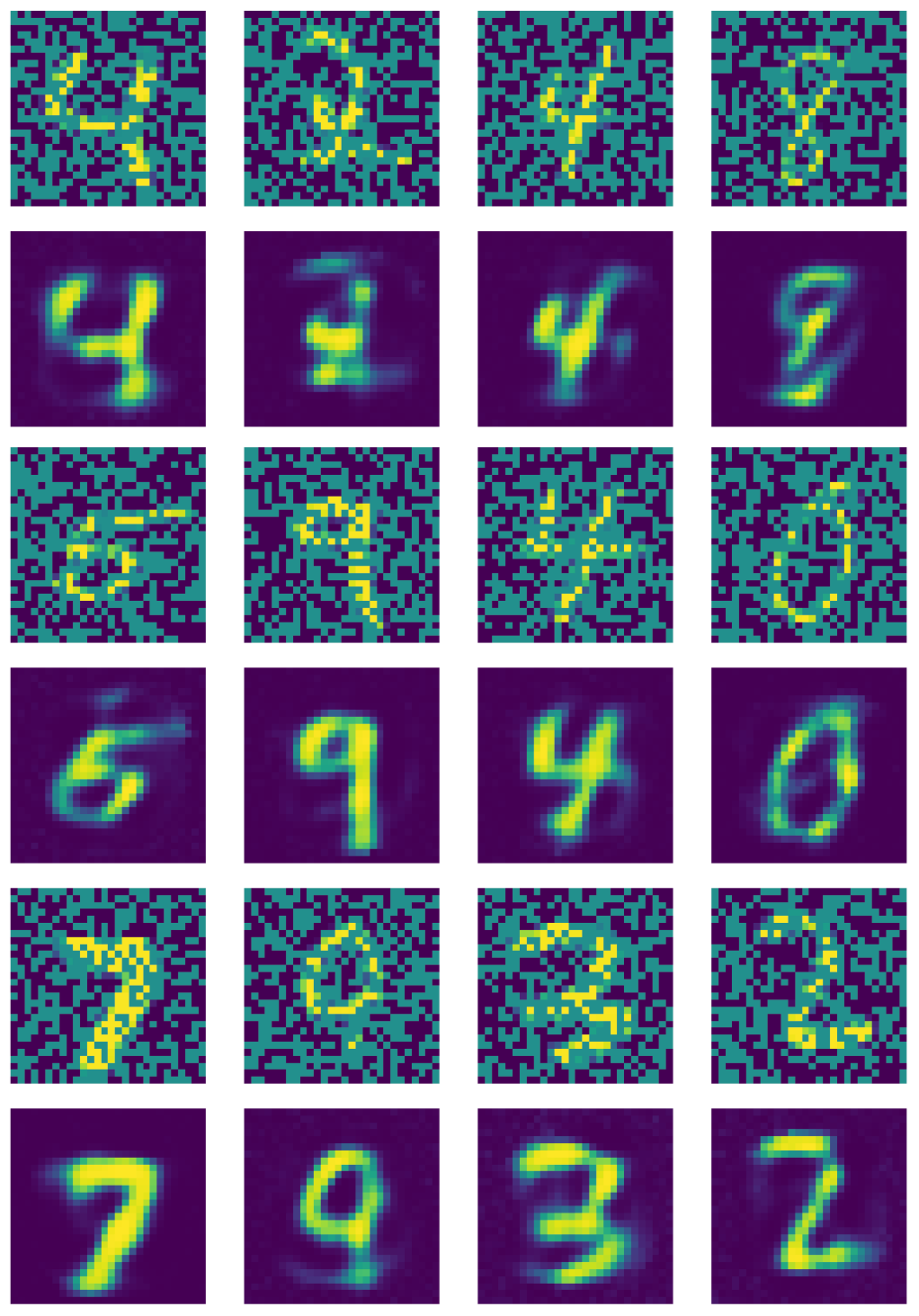
图21: 降噪自动编码器的输出

Kernels comparison

一个重要的注意是，即使事实上输入维度是 $28 \times 28 = 784$，但一个维度为 500的隐藏层也还是过度完成层，因为图片中的黑色像素。下方内核的例子用未完成层的标准自动编码器来训练。明显地，一些存在数字的区域中的像素说明了某种图案被检测到，同时地，这些区外的像素就基本上是随机的。这说明了一个标准自动编码器是不会理会数字存在的区域以外的区域。

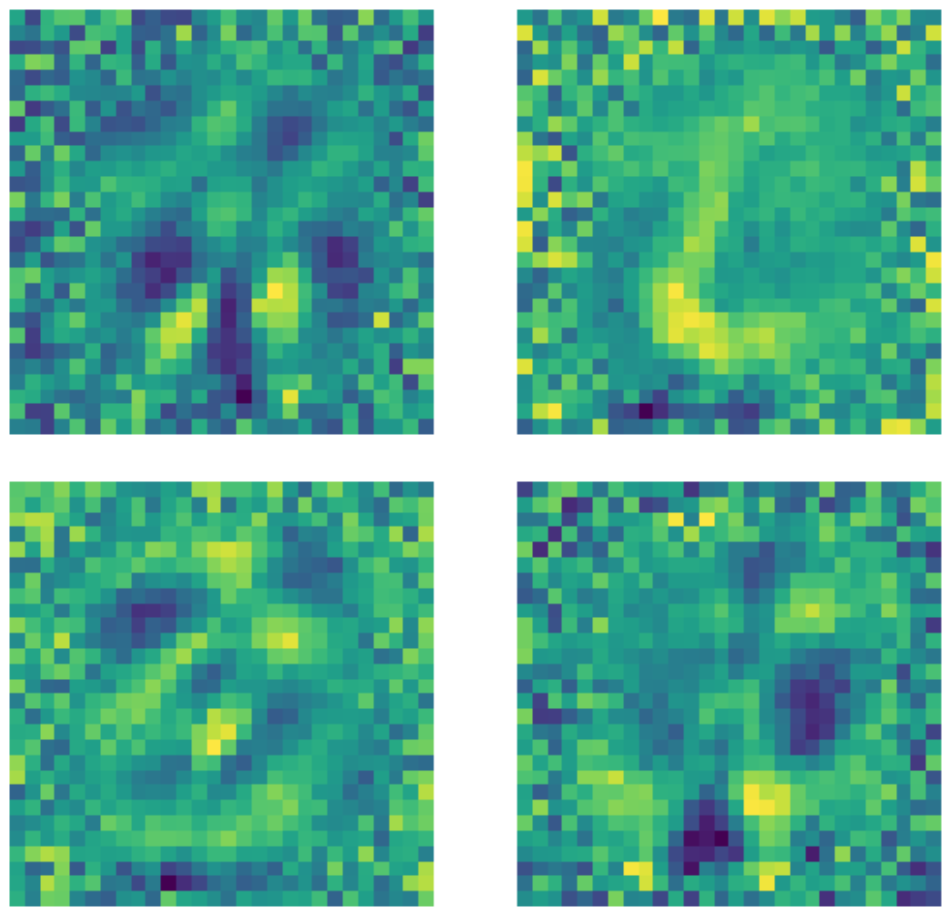
图22: 标准AE内核。

相反地，当同样的数据被传到降噪自动编码器中时，而在拟合(fitting)模型之前对每一张图都用了Dropout 掩膜（Dropout mask）时，一些不一样的东西就会发生了。每个学习存在数字之外的区域的结构的内核都会学到成一些恒定值，所以这个模型现在就会关心数字区域以外的像素，那是因为对图片实行了Dropout 掩膜（Dropout mask )。

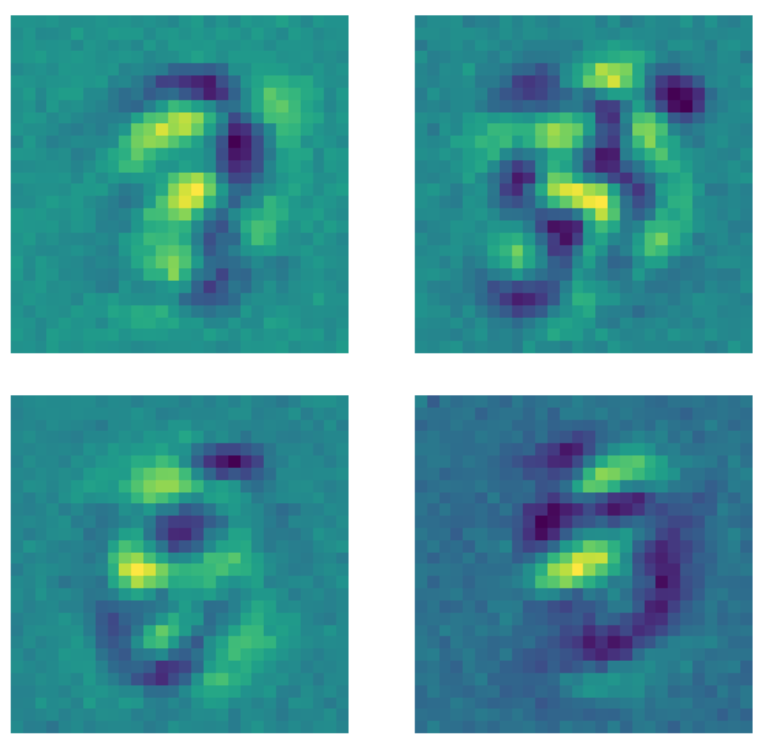
图23: 降噪AE内核。

比较一下那一个最强最厉害的话，那我们的自动编码器是做得更好!你可以在下方看到其结果。

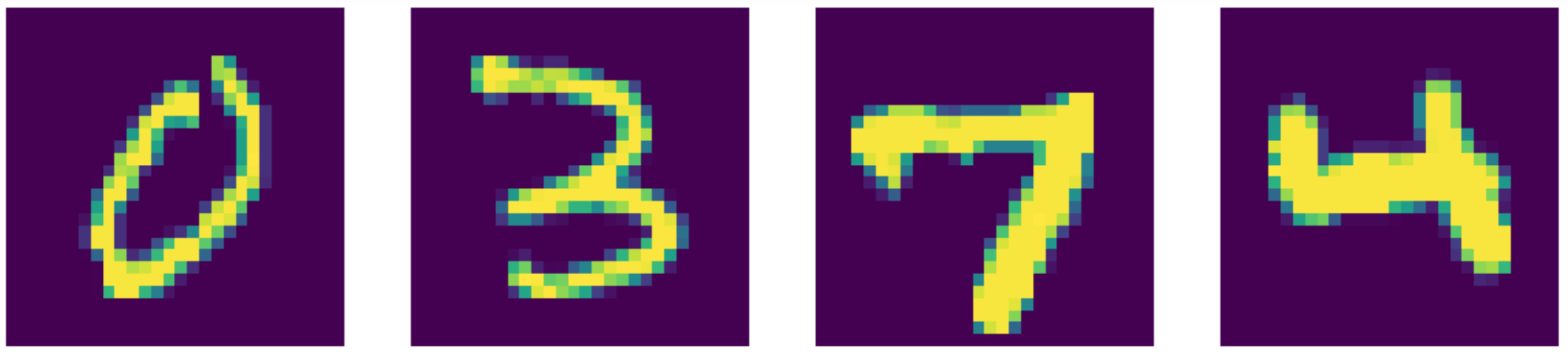
图24: 输入数据（MNIST数字版）。

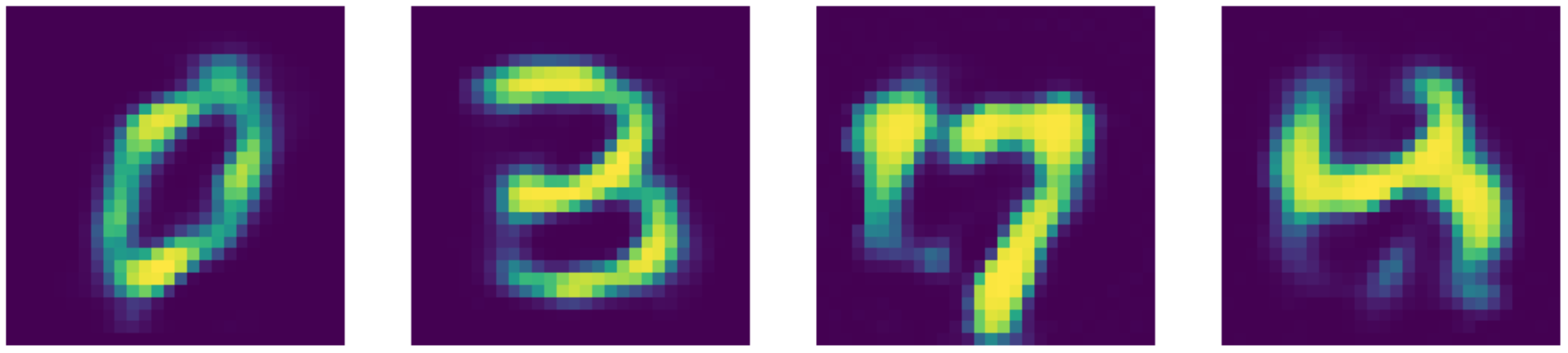
图25: 降噪AE重建。

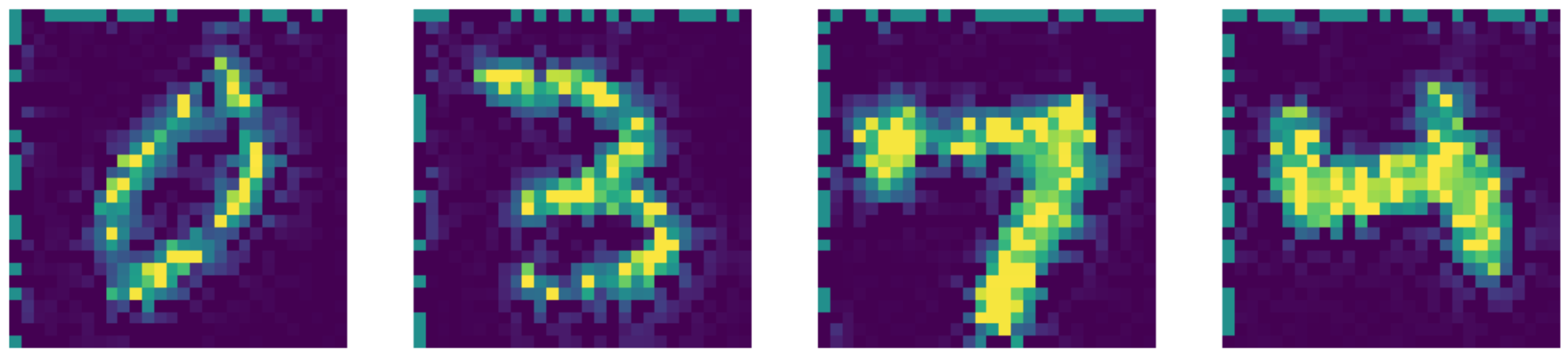
图26: Telea修复输出。

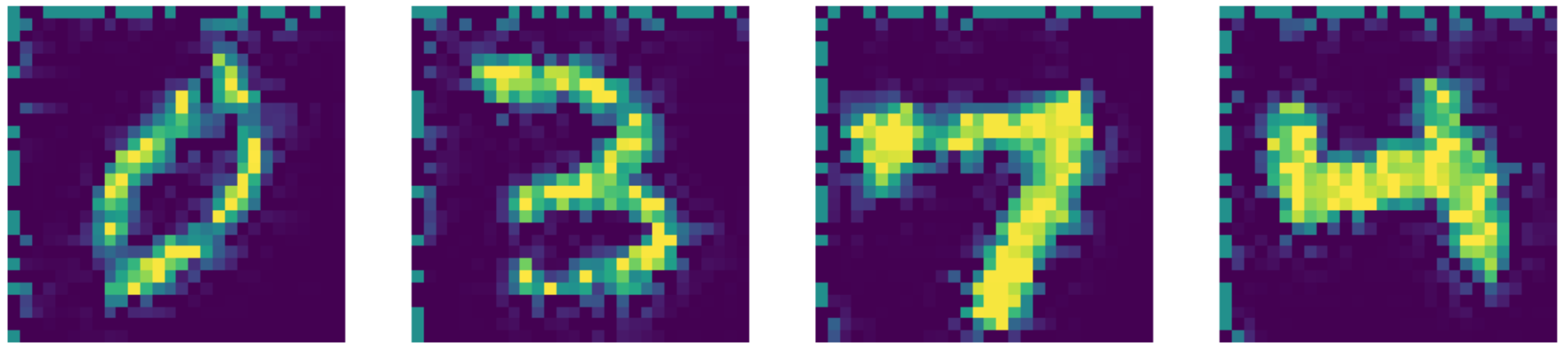
图27: Navier-Stokes修复输出。