自我监督学习(SSL)﹑能量基础模型(EBM)的细节和例子

自我监督学习(Self supervised learning)

自我监督学习(英文简称SSL)同时包含着有监督学习和无监督学习。自我监督学习(SSL)的预训练的目标就是为了学到一个能很好地代表输入的「表示」，那样之后它就能被用在监督任务。在自我监督学习(SSL)，模型是被训练到能只要给一部份数据，就能预测出另一部份的数据。比如，BERT是被训练为在使用自我监督学习(SSL)技巧和降噪自动编码器(Denoising Auto-Encoder (DAE) )来在自然语言处理（NLP）任务中达到出色的效果。

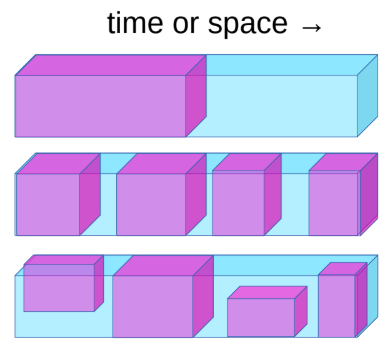
图1：自我監督學習任務可以定義如下

自我监督学习任务可以如以下定义:

• 用过去来预测未来。
• 从可见的部份预测蒙着的部份。
• 从所有提供了的部份中预测那些是被困在一个空间的。

例如，如果系统是被训练了当相机被移动时，然后预测下一帧，那系统就会明显地学到深浅和视差。这会强迫系统去学到物件是困在系统看到的空间中，而且物件没有消失，继续存在，而且学到区分那些东西是动或不动，最后也学到了那一个是背景，它也能学到直观中能学到的物理，比如引力。

能力出色的自然语言处理系统伯特（BERT）会预先在实行自我监督学习前训练一个巨大的神经网路。你会先在一个句子中移除一些文字，然后去给系统预测移除了的文字，而且在下面的图片中，你可以对一张图片，去掉图片的一部分，训练你的模型去预测去掉的部分。

图2: 计算机视觉中相应的结果

虽然这些模型能补上图片中消失的部份，但他们没有如自然语言处理系统有相同的成功水平。如果你用这些模型生成的「内容表示」来作为的计算机视觉系统的输入，是没法去击败一个用了ImageNet以监督方式进行了训练的模型。

一个智能系统(人工智能代理AI agent)为了能做出智能的决定，它需要能够在周围环境中和自身中去预测自己行为所带来的结果。因为世界是活的，而不能死定起来的，而且对机器和人脑来说，也没有足够的计算能力去计算每一个可能性，所以我们需要要教人工智能系统去在一个高维度之中，在存在着不确定性之中，去进行预测，能量基础模在这方面是非常有用的。

神经网路是用了最小平方法来预测视频的下一帧的话，结果就是图像模糊，因为模型不能准确预测出未来，所以它从训练数据中学到了平均了下一帧的所有可能性来降低损失。

用(潜在变量能量基础模型)来作为解决方法来预测出下一帧:

这与线性回归不一样，潜在变量能量基础模型取了任何我们对世界所知的，包括向我们提供有关现实情况的潜在变量。当两个信息组合起来用来造预测时，那预测出来的就会发生的一分接近。

这些模型可以被想像成一个评估相应度的系统，就是当使用潜在变量来降低和最小化一些系统的能量来预测时，评估输入$x$和实际输出$y$的相应度。你就是观察输入$x$，然后生成可能会发生的预测$\bar{y}$，就是为了把输入x和潜在变量z组合成不同的组合，同时选择一个组合来在系统中来降低和最小化系统中的能量和系统预测误差。

根据我们绘制的潜在变量，我我们可以得出所有可能发生的预测。而潜在变量会被想成一些对输出y来说是重要信息，同时是在输入x中没有。

标量值过的能量函数有两种版本:

1. 有条件性 $F(x, y)$ - 测量$x$和$y$之间的相应度
2. 无条件性 $F(y)$ - 测量$y$的组件之间的相应度

训练能量基础模型

以下两类学习模型可以训练基于能量的模型来参数化 $F(x, y)$.

1. 对比法: 推低$F(x[i], y[i])$部份，推高其他点$F(x[i], y’)$
2. 架构法: 在最小化中加入和使用 $F(x, y)$ 函数，那低能量部份的容量就会在正则化过程中被限制或被最小化

其实是有七种类方法去塑造能量函数。对比法和其他方法不同之处是它找一个点来推高它，同时最小化法是限制编码的信息容量。

其中一个对比法的例子是「最大似然学习」，而能量可以被解释为非归一化负对数的密度(unnormalised negative log density)。波兹曼分布(Gibbs distribution)给我们这个，而如果我们给予特定$x$的话，那波兹曼分布(Gibbs distribution)就会给予$y$的似然。

最大似然尝试令分子变大，而分母变细来最大化似然。这是跟最小化 $-\log(P(Y \mid W))$ 一样，也就是以下这样

对于一个样本 Y ，负对数似然损失的的梯度(Gradient of the negative log likelihood loss)是如下:

在上方的梯度，在数据点Y的梯度的第一项和梯度的第二项，它们给我们一个在所有$Y$上「能量的梯度」的预期值。所以，当我们运行梯度下降时，第一项就会尝试在给予的那些$Y$点上去降低能量，而第二项就会尝试在其他给予的那些$Y$上去提高能量。

能量函数的梯度通常地是十分复杂，而所以对常常令人棘手的它来说，计算或估计﹑近似它的积分是十分有意思的。

潜在变量基础模型

潜在变量的主要优势是它们容许令用潜在变量来进行多个预测。如果$z$在一个集合之中变化着，那$y$也在一个预测可能发生的流形中变化着。一些例子包括:

1. K均值(K-means)
2. 稀疏建模(Sparse modelling)
3. GLO

这些可以有两种类型：:

1. 條件性模型，$y$取決於$x$的
   1. \[F(x,y) = \text{min}_{z} E(x,y,z)\]
   2. \[F_\beta(x,y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(x,y,z)}\]
2. 無條件模型，是有標量值能量函數的，而$F(y)$測量$y$的組成部分中各部分的相應性。
   1. \[F(y) = \text{min}_{z} E(y,z)\]
   2. \[F_\beta(y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(y,z)}\]

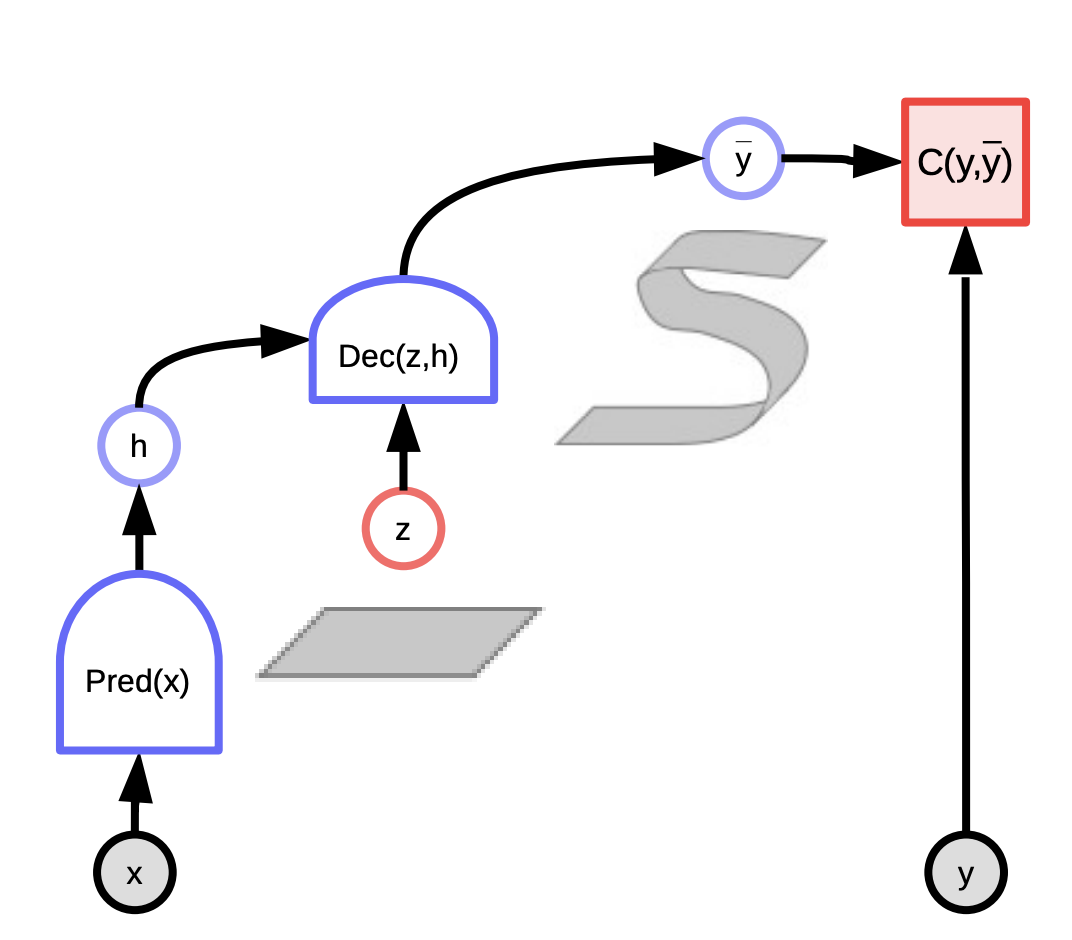
图3: 潜在变量能量基础模型(Latent Variable EBM)

潜在变量能量基础模型(EBM)例子: $K$均值

K均值是一个简单的聚类算法，当我们去尝试去建造一个$y$分布模型时，那能够被称为能量基础模型。能量函数是 $E(y,z) = \Vert y-Wz \Vert^2$ 而$z$ 是 a $1$-hot 向量。

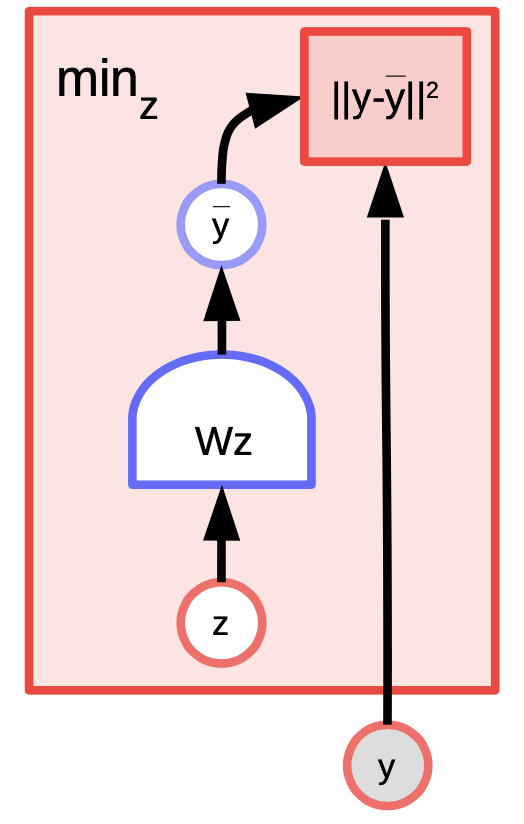
图4: K均值示例

给予y的值和$k$的值，我们就能通过弄清楚W中那k个列有可能可以最小化「重建误差」或「能量函数」来推理。训练算法的做法是这样，我们可以采用一种方法，方法是找出$z$，而这个$z$能够选出$W$中一那一列是最接近$y$，然后在不断的重复中用梯度来找出更接近的那一列。相反地，坐标梯度下降实际上比这个更好更快。

在下面的图中，我们可以看到数据点沿着一个粉色螺旋形。黑色斑点围着这条线，同时对应于周围二次的井形状，周围是每一个$W$的原型。

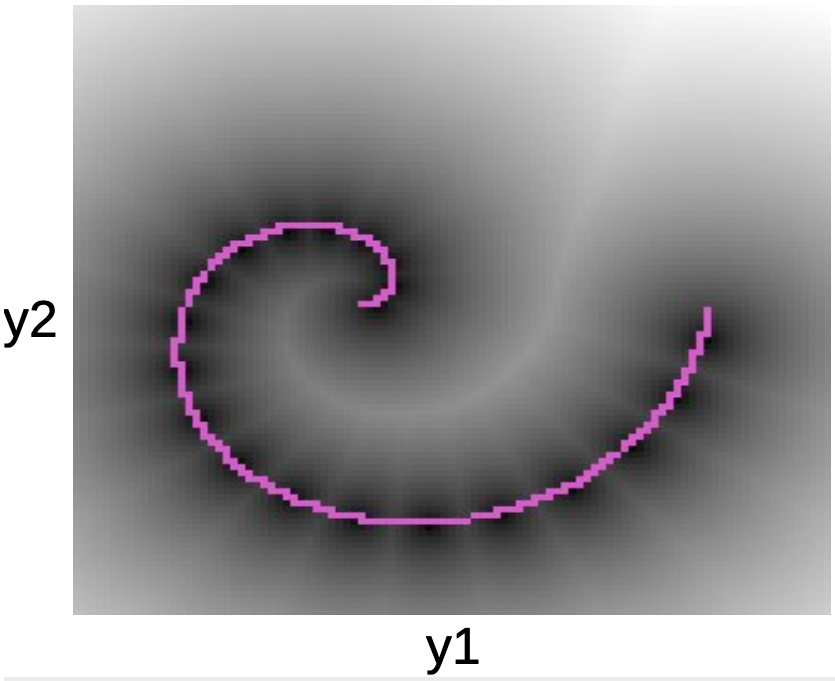
图5: 螺旋图

一旦我们学习了能量函数，我们可以开始解决以下问题:

1. 给予 $y_1$点, 我们能预测 $y_2$么?
2. 给予 $y$, 我们能找出最接近数据流型的点吗?

K均值属于最小化法(和对比法对立着)。所以我们不会推高能量，而我们做的只是在某些区域中推低能量。其中一个坏处是一但$k$的值是被决定了，那就会限定只有$k$个点是有$0$能量，而其他点就会有更高的能量，每向外走一步，就二次地升高。

对比法

根据杨立昆博士(Dr Yann LeCun)的说法，每个人都在某个时刻使用架构法，但在此刻，我们说适用于图像的对比法。看一下和想一下方的图像，它显示出数据点和能量表面的轮廓。理想的话，我们想在数据流形上的能量面(能量表面)有最低的能量。所以我们想做的是在训练例子附近降低能量(即$F(x,y)$)的值)，但单单只是这样做是不足够的。因此，为了$y$，我们也针对本应具有较高的能量但具有足够的能量的该地区的提升其能量。

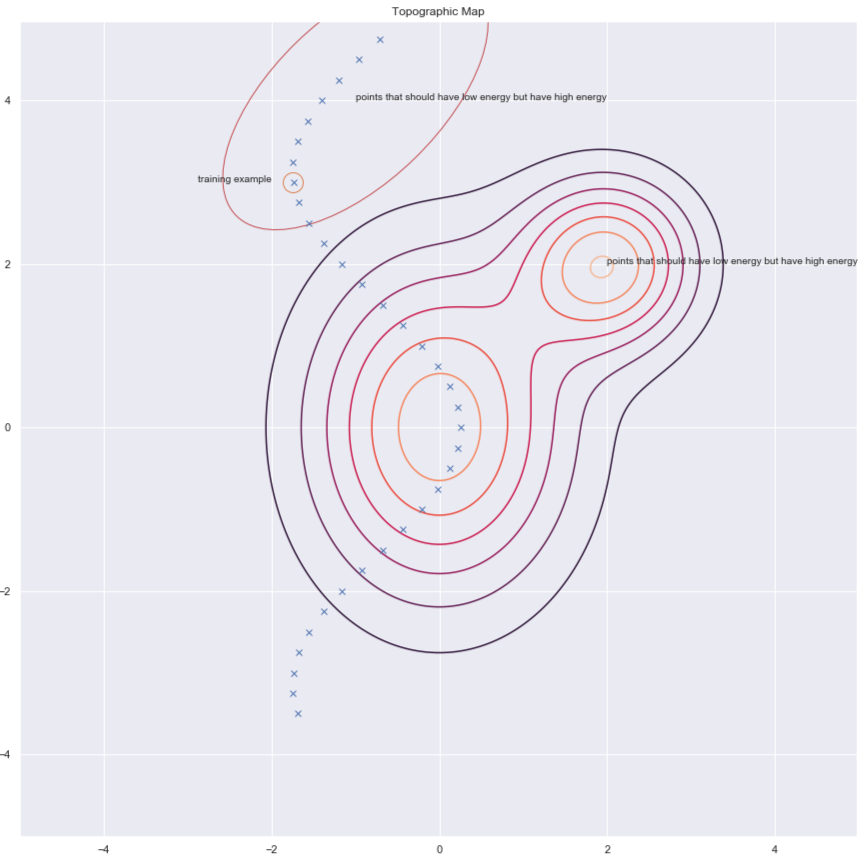
$F(x,y)$) 图6: 对比法

这里有数个方法去找出这些$y$来令我们能提高我们想提高的能量。一些例子包括:

1. 去噪自动编码器(Denoising Autoencoder)
2. 对比发散(Contrastive Divergence)
3. 蒙特卡洛(Monte Carlo)
4. 马尔可夫链式蒙特卡洛 Markov Chain Monte Carlo
5. 汉密尔顿式蒙特卡洛 Hamiltonian Monte Carlo

我们会简单地讨论一下去噪自动编码器和对比发散。

去噪自动编码器（Denoising autoencoder，简称 DAE）

其中一个找出这些$y$来提高能量的方法，那是随机扰动训练例子，下方图像中的1绿色箭头就是说这个。

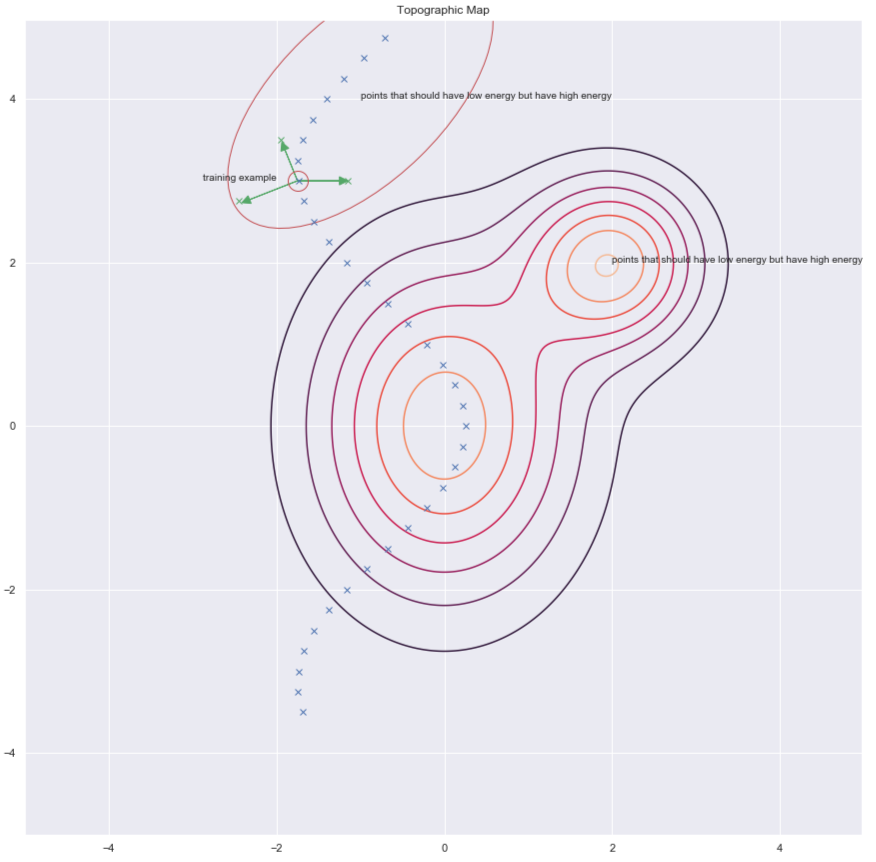
图7: 地形图

一旦我们有很多乱起来了的数据点，那我们能推这些能量上到这里来。如果我们对这些数据点推的次数是足够的话，那能量样本就会沿着训练例子卷起来。而下方的图就说明了训练是如何完成。

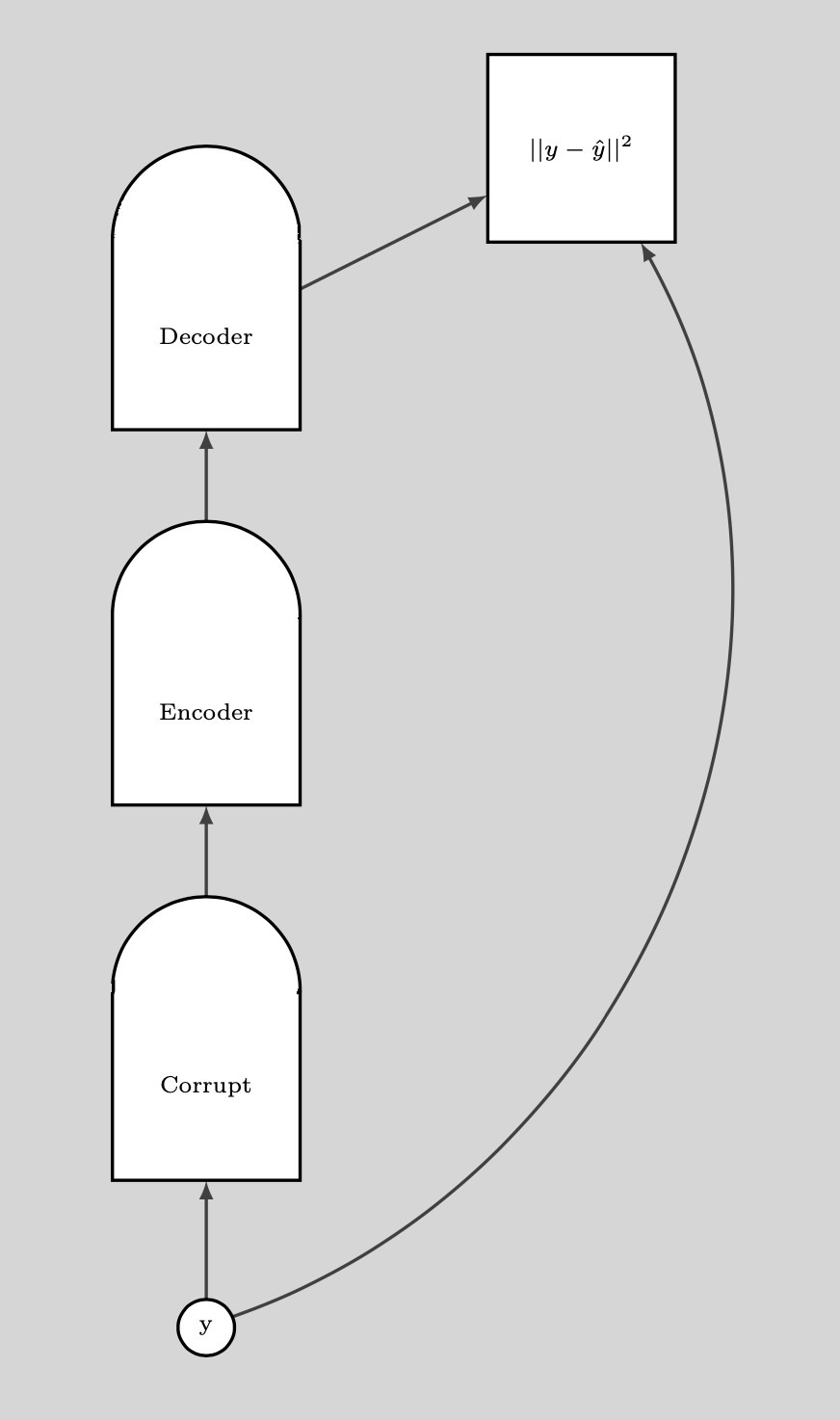
图. 8: 训练

训练步骤:

1. .选一个$y$点然后弄乱它
2. 训练编码器和解码器来重建弄乱了的数据点到原来的数据点

如果去噪自动编码器(DAE)是训练得正确的话，那当我们离开数据流体时，能量就二次地升高。

下方的图说明了我们如果使用去噪自动编码器(DAE)

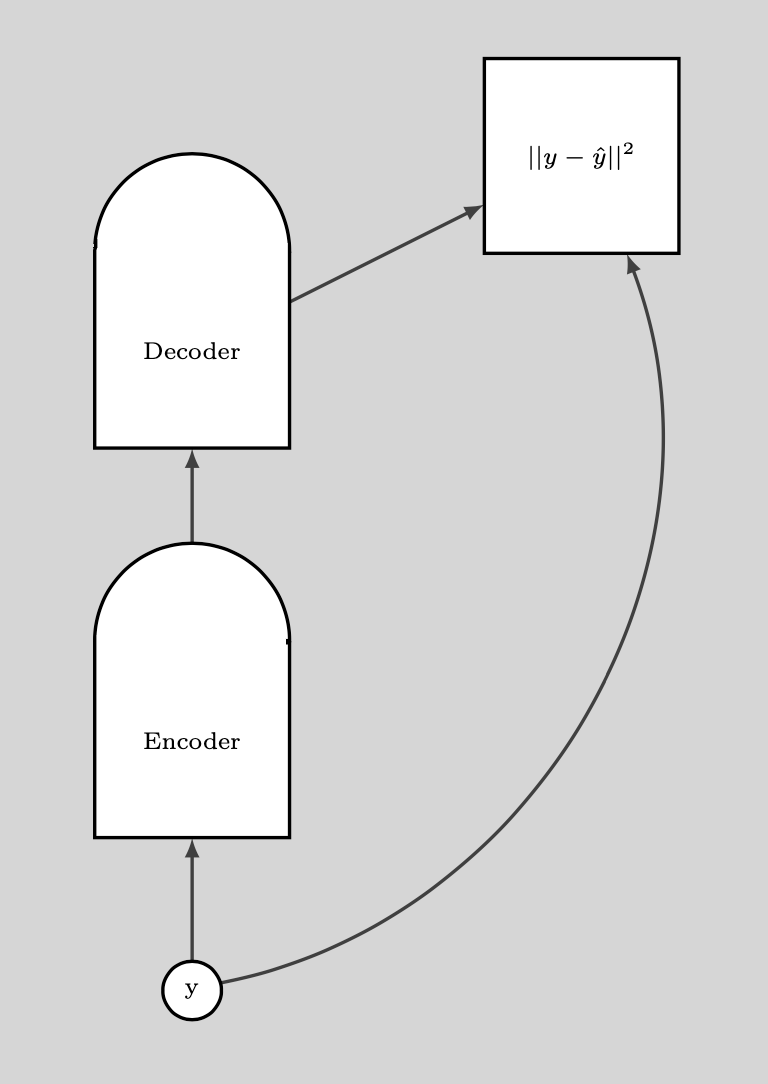
图9: 如何使用去噪自动编码器(DAE)

伯特模型(BERT)

跟训练伯特的方法是有点相似，除了当我们处理文字时，空间是离散的话，那就不太一样。 「弄乱」技巧是由掩盖一些文字做法组成的，而「重建」步骤是试图预测这些掩盖了的文字。因此，这也称为掩盖式自动编码器。

对比发散

对比发散向我们呈现了一个更聪明的方式去找出我们想要提高能量的$y$点。我们可以对训练点用「随机踢」，之后就会用梯度下降来令能量函数下移。在轨道最后的部份，我们对我们落在的点上提高能量。下图用绿线来说明了。

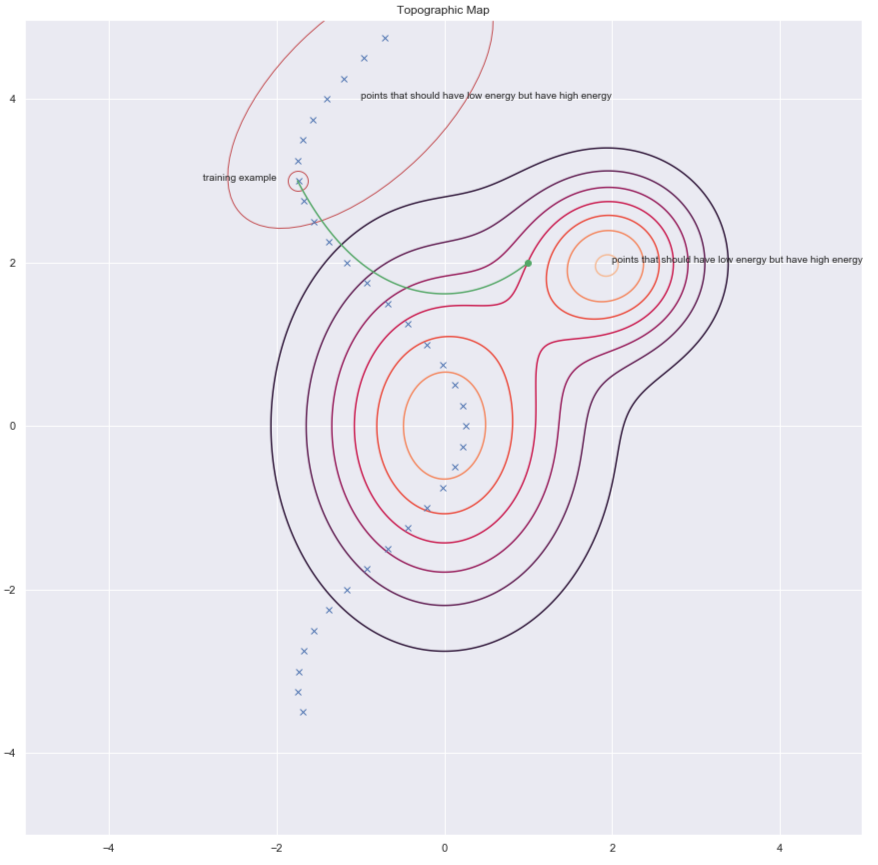
圖10: 对比发散