能量基础模型(Energy-Based Models)

總覽

我们现在介绍一个新框架来定义模型。它提供了一个统一和系列性的方式来定义「监督模型」，「无监督模型」和「自我监督模型」。能量基础模型根据一组变量$x$然后输出一组$y$。这里有两个主要问题：

1. 如果推理程序是比一层又一层的加权总和更复杂的计算?
2. 如果这里有多个可能输出,而同时只有一个输入?比如预测的视频未来的部份。特别地是在分类型神经网路中,我们训练神经网路去输出一个分数表示是那一个类。但是,这是不可能在高维度域中这样用的（我们不能对图像使用归一化softmax！）。即使输出是离散的,样本空间也是一分巨大。比如文字是构成性组合的，那会引起庞大的不同可能会出现的组合。能量基础模型提供一个更好的框架来对这些模型建立模型。

能量基础模型(EBM)方法

现在我们不做把数个$x$分类为数个$y$，而是我们想去预测特定的配对($x$, $y$)是否适合地放在一起。或转另一面来说,找出一个y那是对应x。我们也可以这样提出一个问题,找出一个$y$那是能令一些$F(x,y)$数值低下,比如:

• 那$y$是$x$的高画质版吗?
• 那文字A是B的良好翻译版吗?

定义

我们定义「能量函数」 $F: \mathcal{X} \times \mathcal{Y} \rightarrow \mathcal{R}$当$F(x,y)$是被描述成这配对$(x,y)$是中所有的依变度。 (注意这能量是用在推理上,而不是学习上。)推理是以下这个方程式: \(\check{y} = \displaystyle \text{argmin}_y \left \{ F(x,y)\right \}\)

解决方案：基于梯度的推理

我们想「能量函数」是畅滑而且是可微的,所以我们可以用它来运行一些基于梯度的用法来进行推理。为了进行推理，我们要用函数来以梯度方式来找出用来配起来的y。许多替代方法都可以通过梯度方法获得最小值。

同时: 图形化模型是「能量基础模型」的特例。 「能量函数」是所有能量部件的和。每一个能量部件都对应一个变量子集,而这些变量子集是我们正在处理的。如果它们是被组织成一些特定的结构，那就会是一個有效的推理算法去找出一个最小的值,这个值是所有能量部件加起来的值，而这个值「相對於respect」变量,而这些变量是我们有兴趣想想用来推理的。

有潜在变量的能量基础模型

输出$y$是根据$x$和另一个变量$z$(潜在变量)，但我们不知道它的值。这些潜在变量可以提供辅助信息。比如一个潜在变量可以根据一堆文字中各自的部份进行分区。这是在没有空隔的手写文字中十分有用。这是特别对十分难进行分区的言语中十分有用。外加上，有些语言有很微弱的文字区域性(比如法语)。所以在我们的模型中有这些潜在变量是在理解这类型输入时是十分有用的。

推理

去用「潜在变量EBM」做推理时，我们同时用能量函数找出最小值，能量函数「相對於respect」y和z。

而且这是等于重新定义能量函数: \(F_\infty(x,y) = \text{argmin}_{z}E(x,y,z)\), 也等于: \(F_\beta(x,y) = -\frac{1}{\beta}\log\int_z \exp(-\beta E(x,y,z))\)。 当 $\beta \rightarrow \infty$, 那 $\check{y} = \text{argmin}_{y}F(x,y)$.

另一个使用「潜在变量」的重大优点，也就是改动一个集合中「潜在变量」的值，那样我们就能令输出$y$随着多个不同可能性组成的流形影响着。(那个流形在下方的图显示着): $F(x,y) = \text{argmin}_{z} E(x,y,z)$.

这样一台机器就可以产生多个输出，而不仅仅是一个。

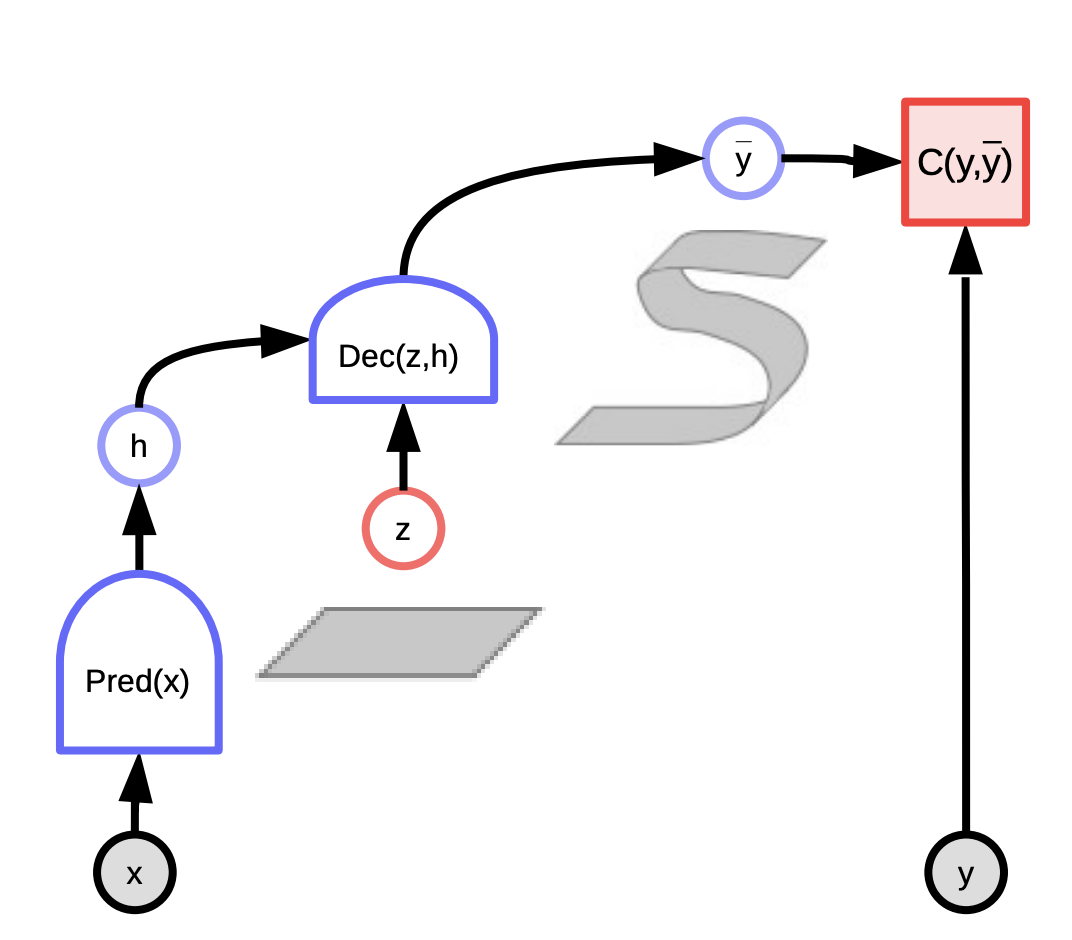
圖1：能量基础模型的计算图

例子

一个例子是视频预测。事实上已经有很多应用领域让我们使用视频预测，一个例子是制作视频压缩系统。另一个是使用自动驾驶汽车的视频去预测别的车下一步是做什么。

另一个例子是翻译。语言翻译一直以来都是一个很困难的问题，因为一小部份文字由一个语言到另一个语言的翻译，是没有一个正确的翻译。通常这里有很多不同的方式去表达同样的想法，人们很难说出为什么他们选这个方式,而不是另外一个。所以好一点的做法是参数化所有可能的翻译的方式，那系统就能根据输入的文字去表达对应的输出。比如我们说如果我们去翻译德文到英文，那就会有多个英文翻译方式都是对的，同时改变一些潜在变量,就会改变翻译结果。

能量基础模型和机率模型的对比

我们看到能量是非归一化的负对数机率(unnormalised negative log probabilities)，同时在归一化(normalization)后使用波兹曼分布(Gibbs-Boltzmann distribution)去由这个「能量」写成「可能性」是这样的:

那个 $\beta$ 是正恒量数同时需要根据你的模型来量身定做。大一点的 $\beta$ 给剧烈一点的模型，而细一点的 $\beta$ 给一点更畅滑的模型。 (在物理上，$\beta$是逆温度:$\beta$无限大,那温度就无限地接近零)。

现在如果边缘化 y: $P(y \mid x) = \int_z P(y,z \mid x)$, 我们就有:

所以,如果我们有潜在变量模型，同时想概率论上的正确做法那样的去掉潜在变量$z$的话，我们要重新定义能量函数 $F_\beta$ (自由能Free Energy)

自由能(Free Energy)

计算这个是很难的…事实上，大部份例子中，更可能很棘手。所以如果你有一个潜在变量，而你想要在模型中最小化这个变量，或你有一个潜在变量要边缘化(重新定义能量函数F来逹成这个做法)，和同时想对应着这个方程式中无限大$\beta$的极限来最小少这个潜在变量，那你就计算得到。

在上方 $F_\beta(x, y)$ 的定义, $P(y \mid x)$ 只是是玻尔兹曼分布公式(Gibbs-Boltzmann formula)的应用 ，而$z$ 被边缘化同时隐含地在公式中。物理学家称为「自由能」。这就是为什么我们将其称为$F$。$e$是能量，$F$是自由能。

问题:你能阐述能量基础模型的优点吗?在基于机率的模型，你也可以有可以被边缘化的潜在变量。

基于机率的模型和能量基础模型的分别，就是基于机率的模型上你基本上在用来最少化的目标函数上是别无选择，你必须保留机率框架的观念,因为你操作的每个东西都必须被归一化分布(你可以使用变异方法(variational methods)﹑等等去估计﹑或其他方法）。这里,我们说最终你想要用这些模型做的是做决定。如果你建立一个系统去驾驶汽车，然后系统对你说:「我想转左,转左机率为0.8，或转右，转右机率为0.2。」那你就转左。事实上机率为0.2和0.8机率都没关系…你想做的是做最好的决定，因为你会被强行要求做决定。所以如果你想做决定，机率是没用的。你想要结合自动化系统的输出和另一个东西(比如:人,其他系统)，而这些系统没有一起被训练，而是分开被训练,然后你想要的是校正这些分数,那样你就可以将两个系统的得分相结合，以便做出更好的决定。只有一条方法去校正这些分数，就是转换它们成机率，所有其他方式都是劣等或一样的，但是，如果您要端对端训练系统来做出决定，那你用什么计分函数都可以，只要它为最佳的決定提供最佳的分数即可。能量基础模型在对应模型时给你更多的选择，或可能可以选择更多不同的训练方式，和以及给你您更多选择选用什么目标函数。但你还是想坚持你的模型是概率化的话，那你必须要用最大似然，那你基本上要训练你的模型去给予一个你所看到过的「数据」有最大的可能性。问题即使这种模型能被证明可行的,但也只会是你的模型是「正确」–––而同时你的模型永远都不「正确」。有一位著名统计学家(乔治·鲍克斯Goerge Box)说过:「所有模型都是错的，但有些是有用。」所以概率模型，特别是那些高维度空间的，和那些组合空间的，比如文字,都是近似模型。它们都是在一些地方是错的，同时如果你尝试去归一化它们，你会令它们更错。所以你最好就不要归一化它们。

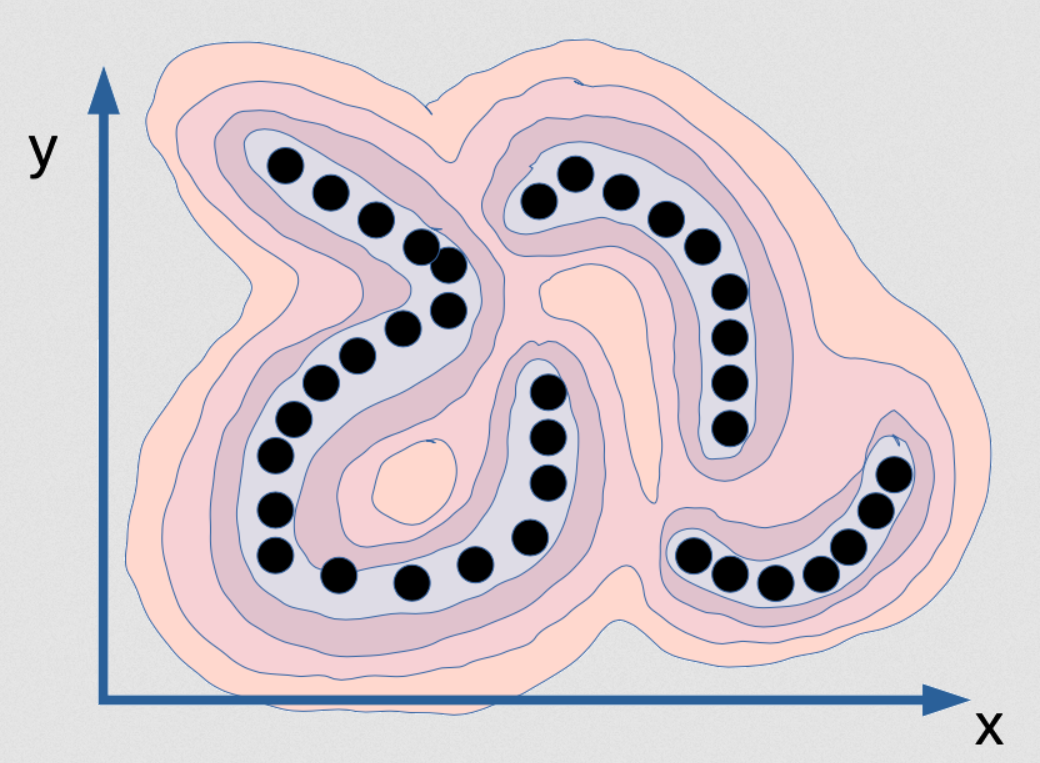
图2：图像化了的能量函数,当中的能量函数是用来得到x和y的依变度。

这就是能量函数,就是用来得到x和y的依变度。如果想像的话，就如山脉一样。黑点就是山谷的位置(这些点是数据点)，和到处都是山。现在，你就用这个来训练概率模型，想像那些点是在十分薄的流形中。所以黑点的数据分布实际上是一条线,这里有三条，它们都没有任何宽度，所以你用这个来训练概率模型的话，当你的位置在流形上，你的密度模型应该就会说给你听一样的话。在这个流形，密度是无限的，而且$\varepsilon$距离外面远离它的话，密度就是零的，那就是这种分布的正确模型。不单只密度是无限，而且在[X和Y]上的积分是1。这是十分难去在电脑上实行!不单只这样，也基本上没可能的。比如说你想用一些神经网来计算这个函数，那你的神经网就会有「无限权重」，而且它们会要被校正到积分在整个域上系统的输出为1。这是基本上没可能的。对于这种的数据例子，准确和正确的概率模型是不可能的。这就是最大似然想得到的，而且世界上没有任何电脑能计算出这个。事实上，这也不有趣。想像下你给这个例子有一个完美的密度模型，这模型就是在那片在(x,y)空间中的薄板…那你更无法做推理!如果我给你X的值，然后问你:「在y中最好的值是什么?」你不能找出来，因为对y来说,除了一些零可能性的集合外，可能有几个值的是有数量的。对于这些x值：

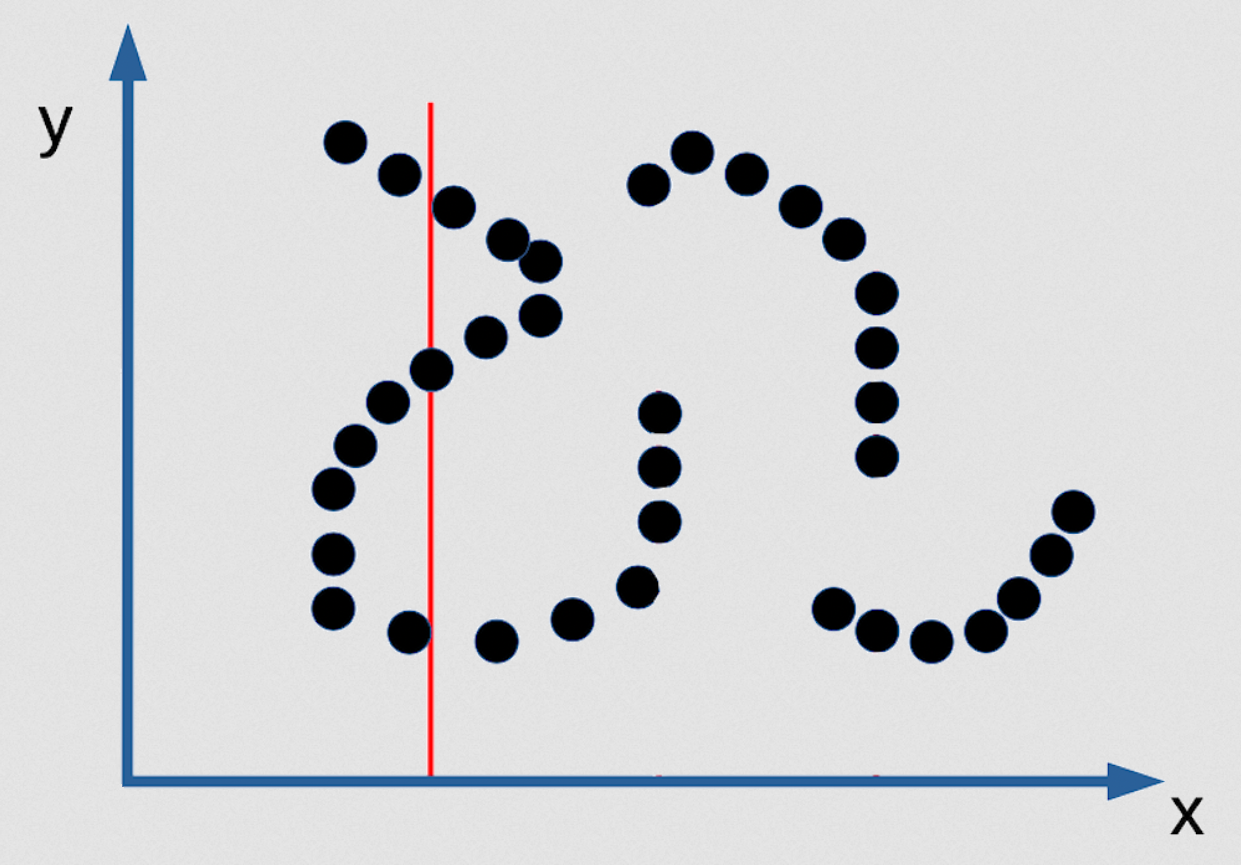
图3: 将EBM(能量基础模型)作为潛在函数进行多重预测的示例。

这里有三个Y的值是可能的，它们是无限地窄。所以你不能找到它们。这里没有推理算法能给你找出它们来的。唯一找出它们的方法是如果你令你的「对比函数(contrast function)」是畅滑同时可微分的，然后你就由任何一点开始去梯度找出一个不错和对应x值的y值，但如果是上方说过的第一种类数值分布，这不会给这种数值分布有一个好的概率模型。所以这里就是一个坚持想要好的概率模型例子，而下埸是十分糟糕。 「最大似然」很烂极了[在这个案例的话]!

所以如果你是一个真实的贝叶斯人(Bayesian)的话，你就会说：「喂！你可以用一个很强大的「先验概率（prior）」来修正这个问题，而把那个先验概率设定为说你的密度模型是畅滑的。」你可以想这个为先验概率（prior）。但你以贝叶斯术语来行事的话…在当中做对数，然后把忘归一化了吧…之后你就会得到能量基础模型。能量基础模型有自己的正则化部分，它是外加上去你的能量函数，这些有正则化的能量基础模型和那些用“似然（likelihood）”来作为能量的指数的贝叶斯模型是完全一样的，然后现在你得到的就是exp（能量）exp（正则化器regularizer），也得于exp（能量+正则化器regularizer）。而如果你去除自然底数，你有的就是能量基础模型外加一个正则化器。

因此，概率方法和贝叶斯方法之间存在着对应关系，但是对于坚持使用「最大似然」的你来说有时都只有坏的，特别地在高维度空间或组合空间中，你的概率模型就只是错得很离谱了。不是在离散分布中有错（没关系的）,而是有「连续不断性」的用例中就会错得很离谱了，而且不论什么模型，都会是错的。