循环神经网络与LSTM模型的架构

概述

循环神经网络（Recurrent Neural Networks, RNN）是一种可以用来处理数据序列的架构。在之前的CNN课程中，我们学到了信号可以是一维、二维、或者三维。其中维度取决于它的定义域（domain）。定义域是函数自变量的取值范围。因为序列数据的定义域是时间轴（temporal axis），所以处理序列数据是个1维的操作。不过，你也可以用RNN来处理双向的二维数据。

Vanilla vs. Recurrent NN

图1是一个三层的Vanilla神经网络图 （Vanilla NN)（注：“Vanilla”意指平淡的、普通的）。图中粉色泡泡代表的是输入向量x，中间绿色的是隐藏层，蓝色的是输出。以右侧的数字电路为例，它类似于组合逻辑电路 （combinational logic)，其每一时刻的输出仅仅取决于该时刻的输入变量的值。

图1: Vanilla基本网络架构

相对于Vanilla NN，RNN在每一时刻的输出不仅取决于该时刻的输入，还依赖于系统状态（如图2所示）。RNN好比是数字电路中的时序逻辑电路（sequential logic)，其输出还依赖于触发器（flip-flop）（注：数字电路中的基本记忆单元）。所以这两种神经网络的主要区别是RNN比Vanilla多依赖了整个场景的状态。

图2: RNN基本架构

图3: 基本神经网络架构

Yann在图示的网络神经之间添加了一些特殊图形，用来表示从一个张量到另一个张量的映射。如图3所示，输入向量x通过一个特殊图形映射到隐藏层h。这个特殊图形是一个仿射变换（affine transformation），包括旋转加畸变（rotation and distortion）。经过另一个变换后，我们从隐藏层得到了最终输出。同理，在RNN图里的网络神经之间亦可添加同样的小图形。

图4: Yann的RNN基本网络架构

RNN的4种架构与实例

• 向量至序列（vector to sequence)。输入是一个向量，然后转化为系统内部的状态（如图中绿色泡泡所示）。当系统转化时，在每一个时刻都会有一个具体的输出。

图5: Vec to Seq

例如，输入为一个图像（向量），输出是一组描述输入图的英文单词序列（一串符号的序列）。如图6所示，每个蓝色泡泡表示一个英文词典里的索引。比如输出为：“This is a yellow school bus”，你得到的是“This”的索引，然后是“is”的索引，以此类推。下图展示了部分由这个神经网络运算的结果。第一列最底部的图像的描述是：“A herd of elephants walking across a dry grass field（一群大象经过干旱的草场）”。这个结果是非常准确的。第二列第一张图的描述为：“Two dogs play in the grass（两只狗在草坪上玩耍）”。然而图中却有三只狗。最后一列都是错误较多的例子，比如“A yellow school bus parked in a parking lot (一辆黄色校车停在了停车场里）”。总之，这些结果显示了这个神经网络时而准确时而错误百出。这种网络结构称之为自回归网络(Autoregressive Network)。自回归网络是一种将之前的输出引入此刻的输入从而得到新的输出的一种网络。

图6: vec2seq Example: Image to Text

• 序列至向量（sequence to vector)。这种网络不断在末尾引入一串符号的序列最终得到结果。应用之一是用这种网络阐释Python语言。比如，这里的输入是每一行的Python代码。

图7: Seq to Vec

图8: Input lines of Python Codes

然后，神经网络会输出程序的正确结果。

另一个更复杂的程序如下所示：

图9: Input lines of Python Codes in a more Completed Case

得到的输出应为12184。通过这两个例子，我得知可以训练一个神经网络来实现这样的操作。我们只需要引入一串符号的序列并且强制最终输出为一个具体的值。

• 序列至向量至序列（sequence to vector to sequence）。如图10所示。这个架构曾是一个标准的机器翻译方法。输入为一个符号序列（如下图粉色泡泡所示）。然后压缩至隐藏层h，代表一个概念。比如我们可以用一句话表示输入，然后把它暂时挤压到一个向量中。这个向量表示句子的意思和发送的信息。得到意思后，神经网络把它展开到另一种语言。比如，“Today I’m very happy”是一个英文单词的序列，可以翻译成意大利语或中文。总之，神经网络将某种转码（encoding）的输入转换成一个密集的表示。我们最近见过这种网络，比如Transformers，它的表现甚至超过了这个机器翻译方法。我们在下节课会细讲。这种架构在两年前（2018年）堪称一绝。

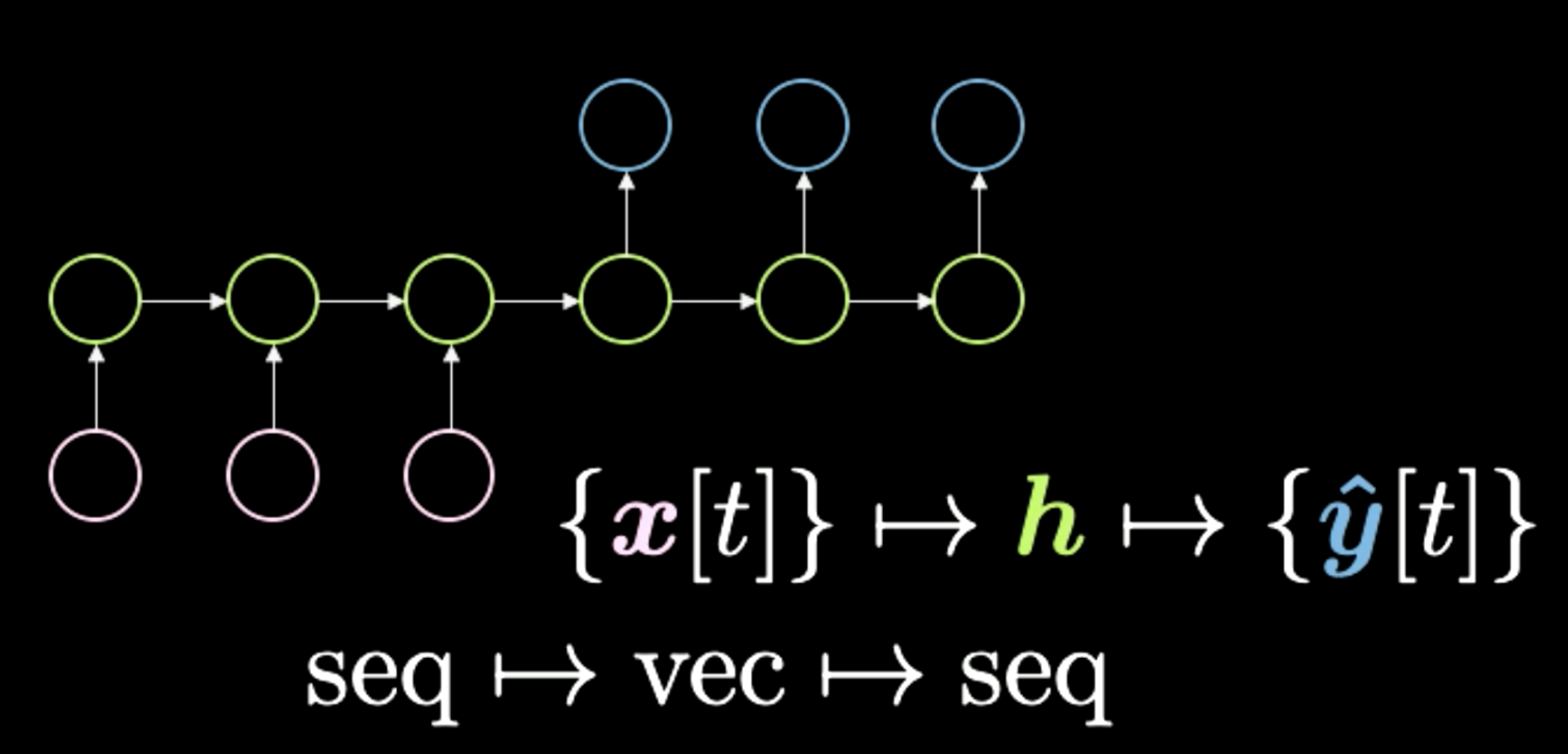
图10: Seq to Vec to Seq

如果你在潜空间（latent space）上使用主成分分析（PCA），你会得到一堆由语义组成的单词（如下图所示）。

图11: PCA训练后由语意分组的词汇

放大后我们看到在同一位置有不同的月份，比如January（一月）和November（十一月）。

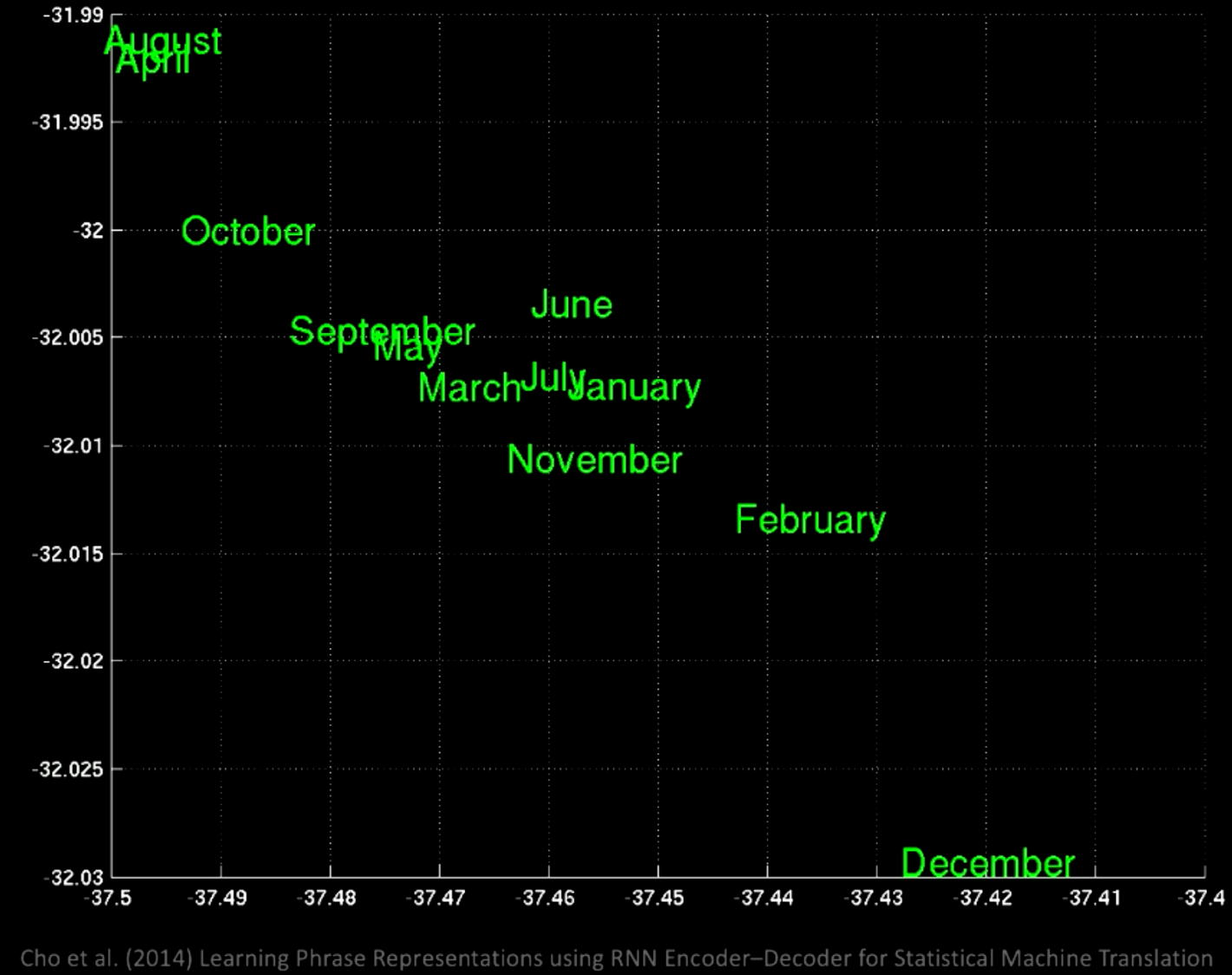
图12: 词组的局部放大图

如果你关注到不同的区域，你会得到“a few days ago（一天前）”、“the next few months（之后几个月）”之类的词组。

图13: 另一个区域的词组

由这些例子可得，在不同的位置会有一些相同的含义

图14展示了训练这类网络会挑拣一些语义特征。比如你看到有一个连接man和woman的向量，和一个连接king与queen的向量。这表示woman减去man等于queen减去king。在这类male-female的例子中，你会得到同样的距离。另一个例子是walking到walked，和swimming到swam。你始终可以应用这种由一个单词到另一个单词或一个国家到一个首都的线性变换。

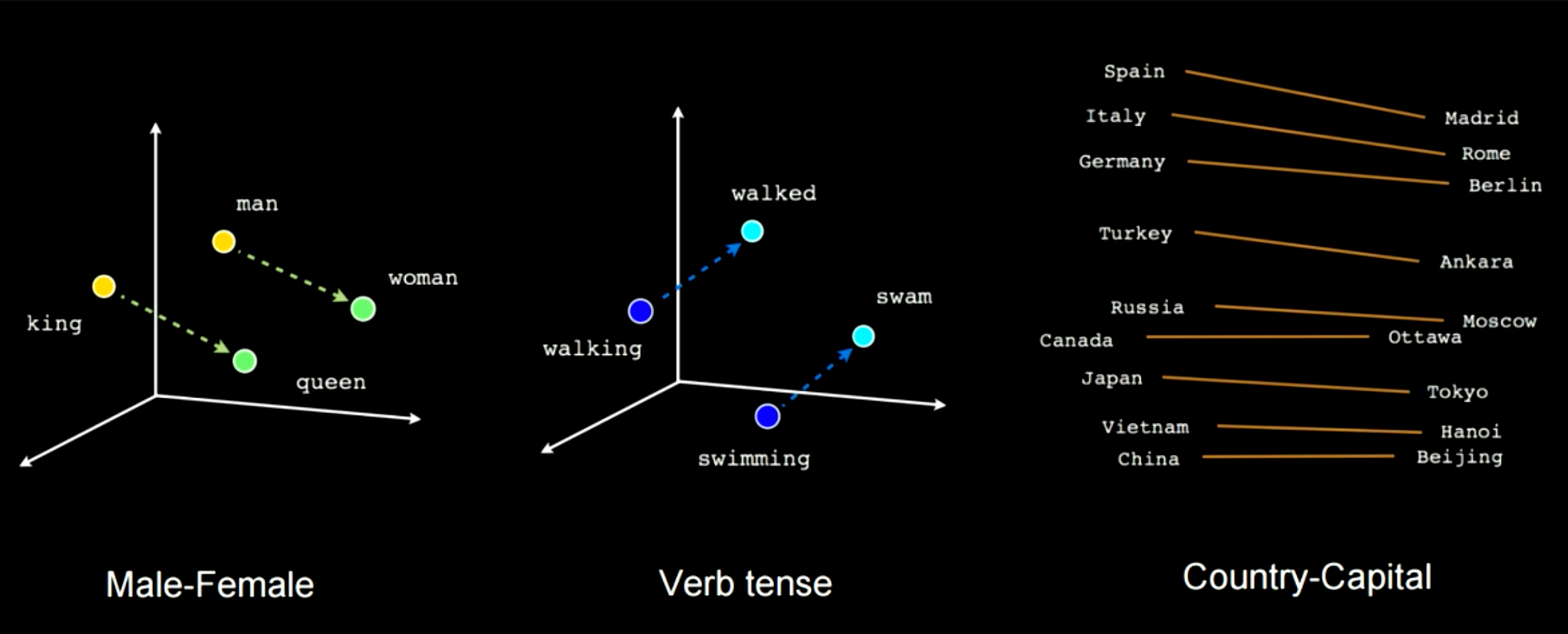
图14: 训练时挑出的语义特征

• 序列至序列（sequence to sequence）。在你引入输入的同时，网络就开始生成输出。例如，文字预测技术（T9）。如果你使用过诺基亚手机，每次打字的时候都会有文字建议。另一个例子是语音转文字。还有一个很酷的例子是这个RNN写字机。当你打了“the rings of Saturn glittered while（土星之环闪闪之时）”后，它会建议“two men looked at each other（两个男人面面相觑）”。这个网络是用几部科幻小说训练的，便于你用它来帮你写一本小说。再有一个例子如图16所示，你输入上面部分的简述，然后网络就会完成余下的部分。

图15: Seq to Seq

图16: Seq to Seq模型的文字自动完成的实例

基于时间的反向传播算法（Back Propagation through time）

模型架构

在训练RNN的时候，必须用到基于时间的反向传播算法（BPTT）。RNN的架构如图17所示。图左是未展开的循环表示，图右是将循环按照时间序列展开。同时中间的权值跨时共享，这点和CNN中的参数共享很相似。

图17: Back Propagation through time

隐藏层表达式为：

$h[t]$是一个非线性函数，将堆叠形式的输入进行旋转操作，其中加入了前一步的隐藏层。$h[0]$初始值设为1。$W_h$可简化为两个不同的矩阵$\left[ W_{hx}\ W_{hh}\right]$，变换后的公式可以写成

与堆叠形式的输入同理。

$y[t]$由最后一步的旋转计算得出，之后我们可以用链式法则来反向传递前一步的残差。

语言建模中的分批处理（Batch-Ification in Language Modeling ）

在处理符号序列时，我们可以将文字分批成不同的大小。比如，在处理图18中的序列时，先将它分批处理（Batch-Ification），它的时间定义域是垂直向。这个例子中的Batch的大小为4。

图18: Batch-Ification

如果将BPTT的周期$T$设为3， 那么第一组RNN的输入$x[1:T]$和输出$y[1:T]$为：

在运行RNN的第一组样本时，我们首先引入 $x[1] = [a\ g\ m\ s]$并强制输出为$y[1] = [b\ h\ n\ t]$。隐藏层表达式$h[1]$向前传递到下一步，帮助RNN从$x[2]$预测$y[2]$。当传递$h[T-1]$至最后一组$x[T]$和$y[T]$后，我们停止$h[T]$和$h[0]$的梯度传递步骤，使得梯度不会无限地传递（.detach() in Pytorch）。整个过程如图19所示。

图19: Batch-Ification

梯度消失与梯度爆炸（Vanishing and Exploding Gradient）

问题

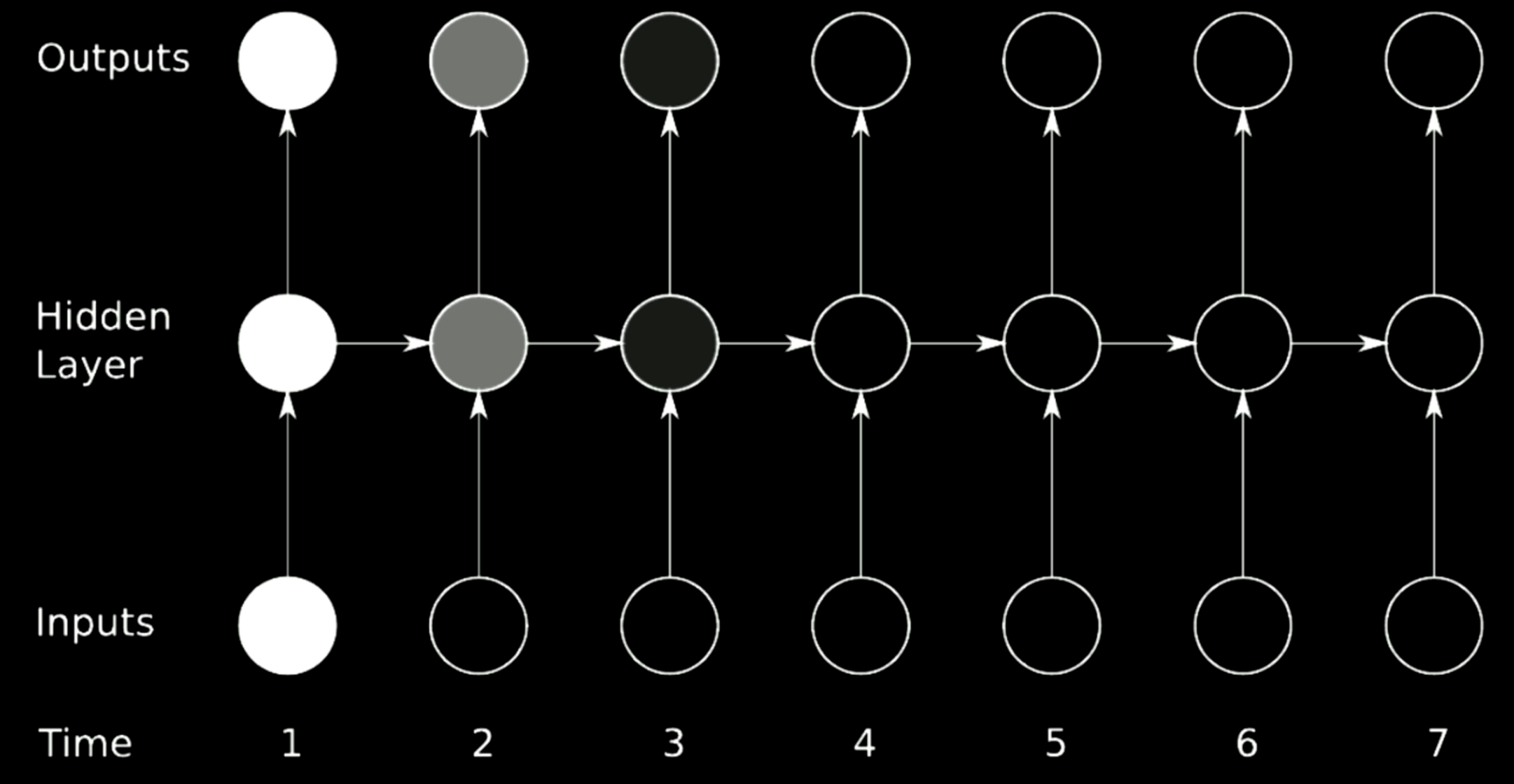
图20: 梯度消失问题

图20展示了一个经典RNN架构。我们用矩阵对RNN里的前一步进行旋转操作，在这个模型中用水平箭头表示。假设我们选择的行列式大于1，因为矩阵可以改变输出的大小，梯度会随时间增大并造成梯度爆炸。相对而言，如果我们选择的特征值小于0，则传播过程会收缩梯度并导致梯度消失。

在经典RNN中，梯度会通过所有可能的箭头来传播。这有很大的几率会使梯度爆炸或者消失。例如，梯度在时刻1的时候非常大（图中白色圆点）。当进行一个旋转后，梯度在时刻3收缩，即消失。

解决办法

理想的预防梯度爆炸或梯度消失的办法是跳过连接。我们可以通过相乘网络来实现。

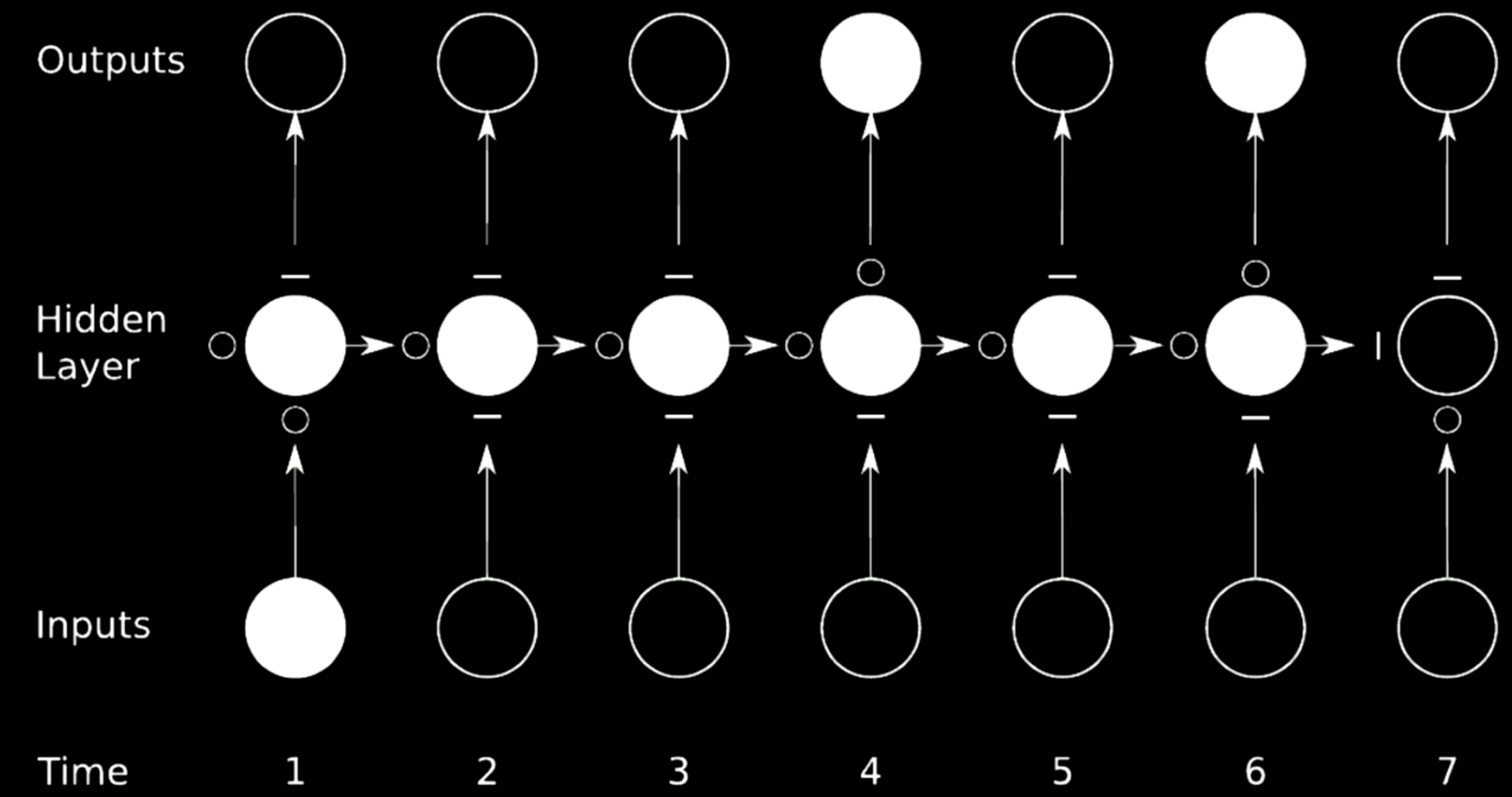
图21: 跳过连接

在图21的例子中，我们把原来的网络分成了4个网络。以第一个网络为例，从时刻1输入一个值，然后输出到第一个隐藏层的中间状态。这个状态有其他三个网络，$\circ$s可以使梯度通过，$-$则会阻止梯度传播。这种方法称为门控循环网络（Gated Recurrent Network)。

长期记忆网络（LSTM）是一个很普遍的门控循环神经网络，我们随即作它的详细介绍。

LSTM模型

模型架构

图22为LSTM的表达式。黄色方框中的是输入门，它是一个仿射变换。将这个输入变换乘以$c[t]$，我们得到候选门。

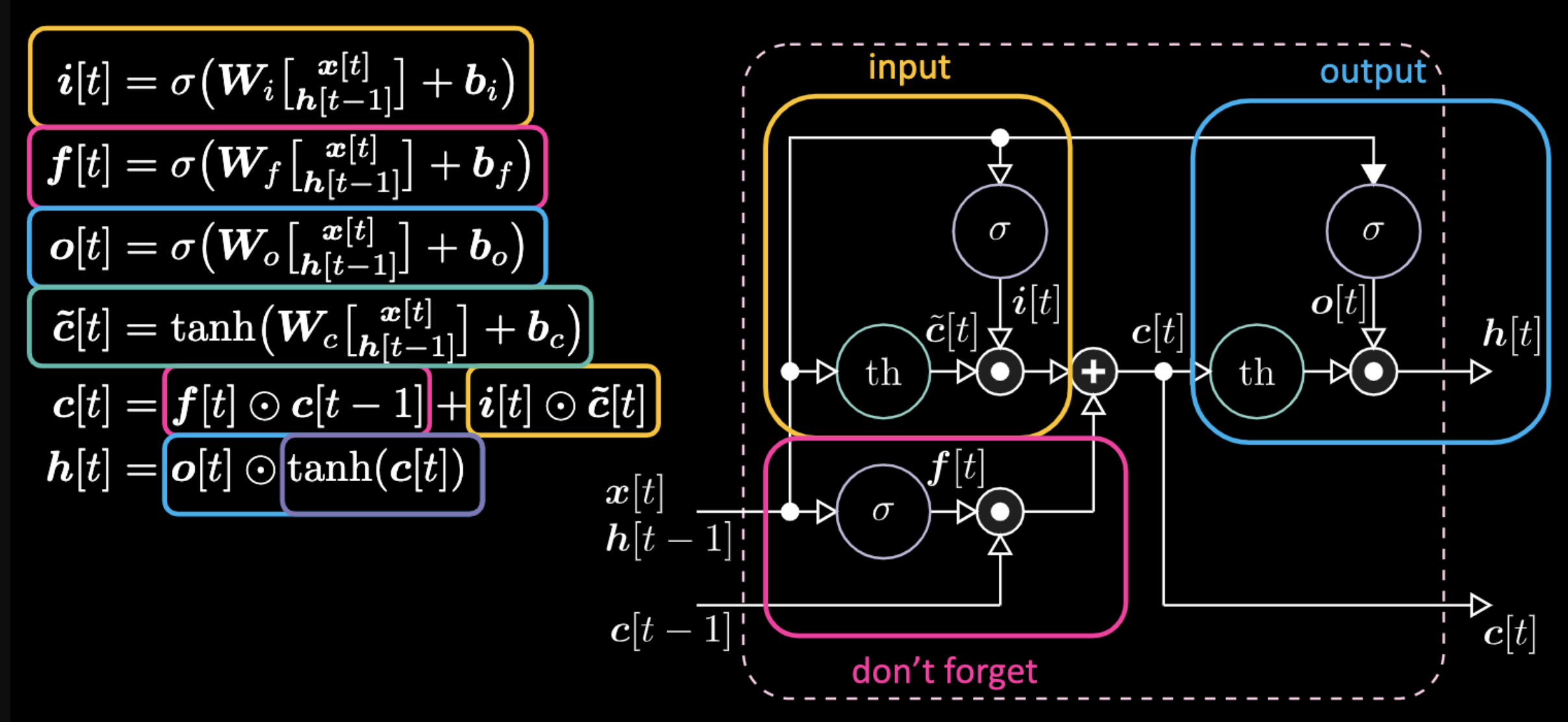
图22: LSTM架构

遗忘门与前一步的细胞记忆值$c[t-1]$相乘。总细胞值$c[t]$是遗忘门加输入门。最终隐藏表达式为输出门元素$o[t]$和双曲正切形式的细胞$c[t]$之间对应相乘，它们是有界的。候选门$\tilde{c}[t]$ 是一个循环网。我们用$o[t]$来调整输出，用$f[t]$调整遗忘门，并且用$i[t]$调整输入门。这些记忆和门之间都是相互相乘。$i[t]$、$f[t]$，和$o[t]$都是0和1之间的Sigmoid函数。因此，当乘以0时，我们得到一个关闭门。当乘以1时，我们得到一个开放门。

我们如何关闭输出？假设我们有一个紫色的内部表达式$th$，并且在输出门放置0。输出就会被乘以0，结果得0。如果在输出门放置1，我们会得到和紫色表达式同样的值。

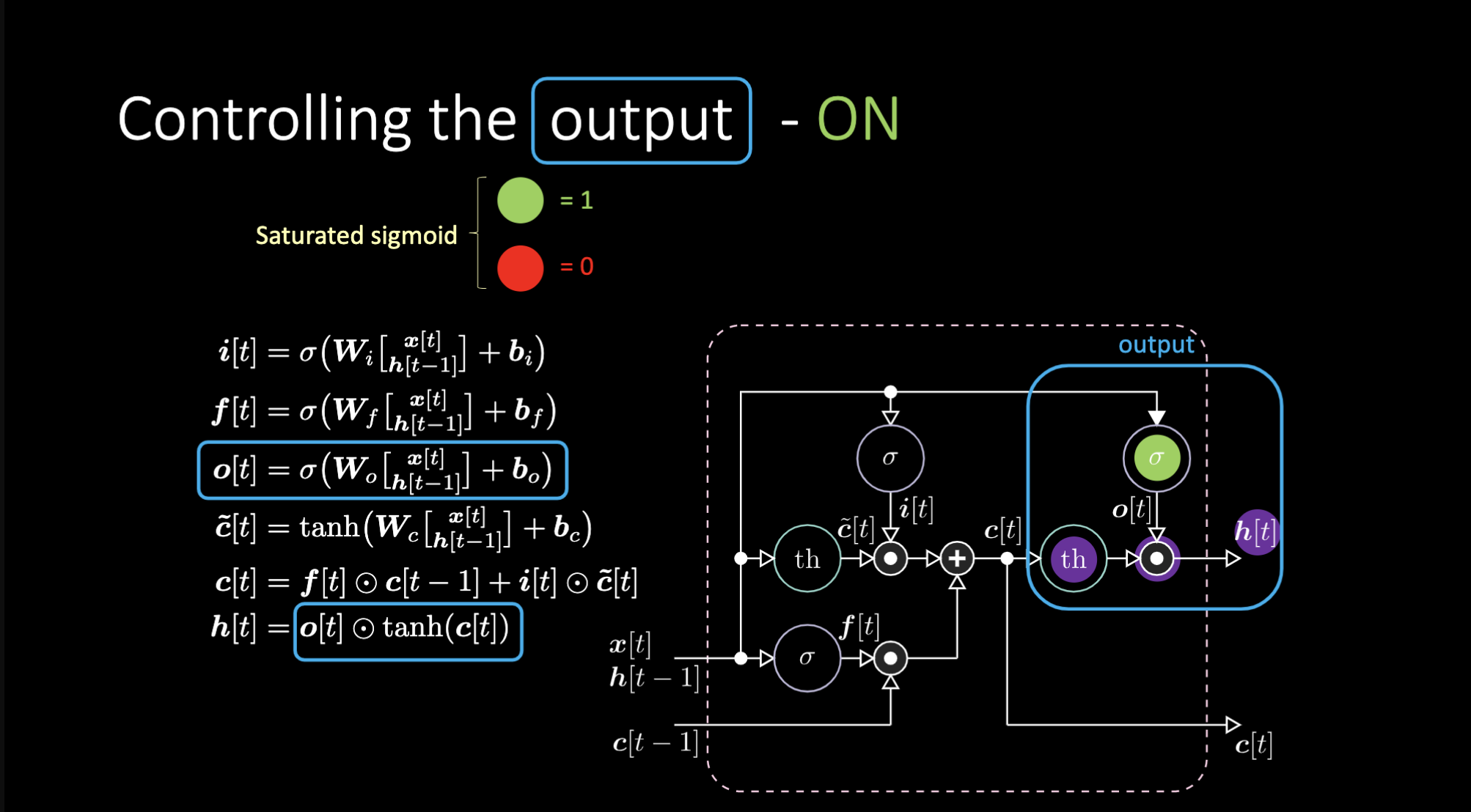
图23: LSTM架构——输出打开

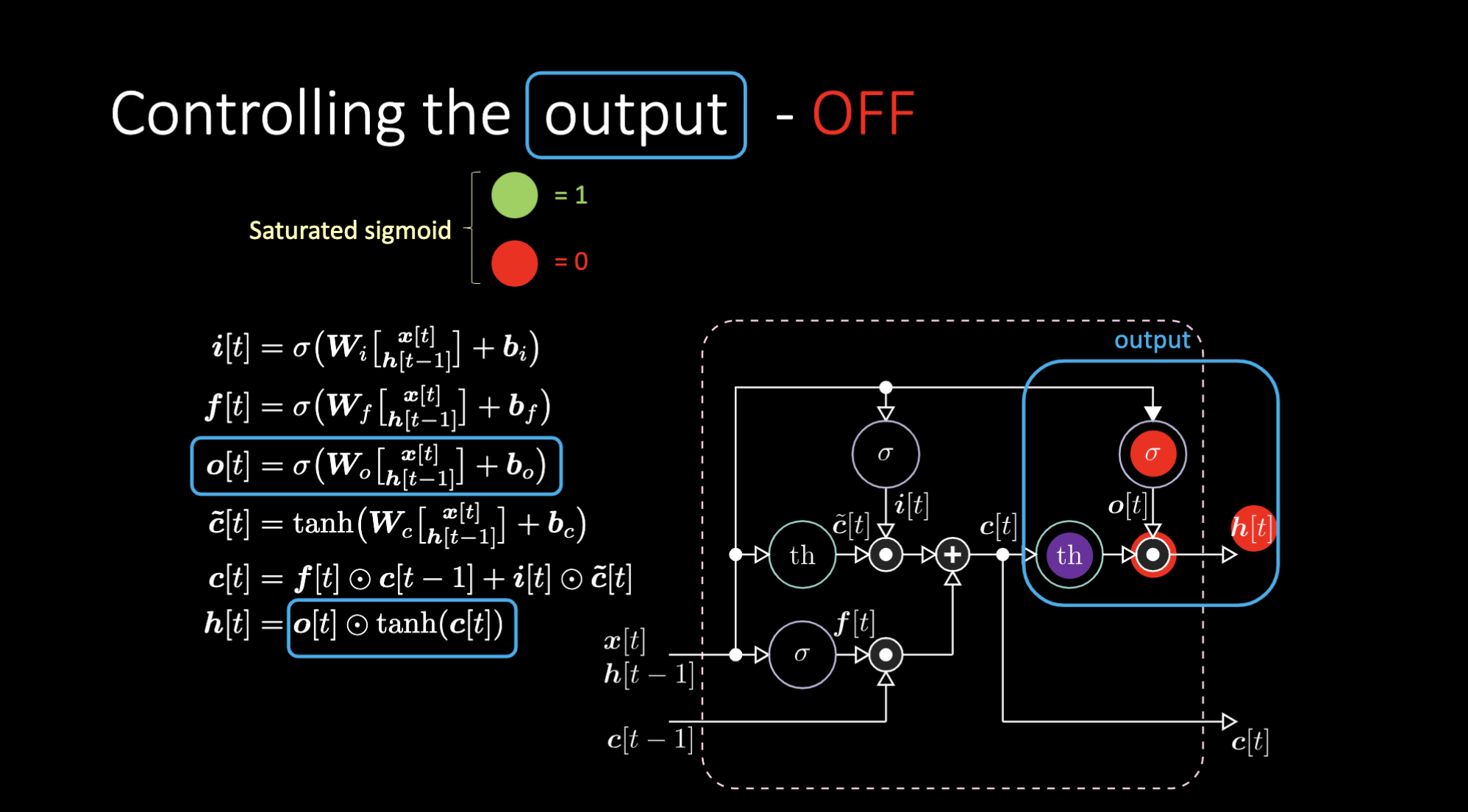
图24: LSTM架构——输出关闭

同样的道理，我们可以控制记忆。比如，我们可以把$f[t]$和$i[t]$重设为0。在相乘和相加之后，记忆里包含0。或者为了保留记忆，我们可以将内部表达式$th$清零，但在$f[t]$里保留1。因此，总和得到$c[t-1]$并且一直将它输送出去。最后，我们在输入门得到了1，相乘得到紫色表达式，然后在遗忘门里设置0，这样它就真的会“遗忘”。

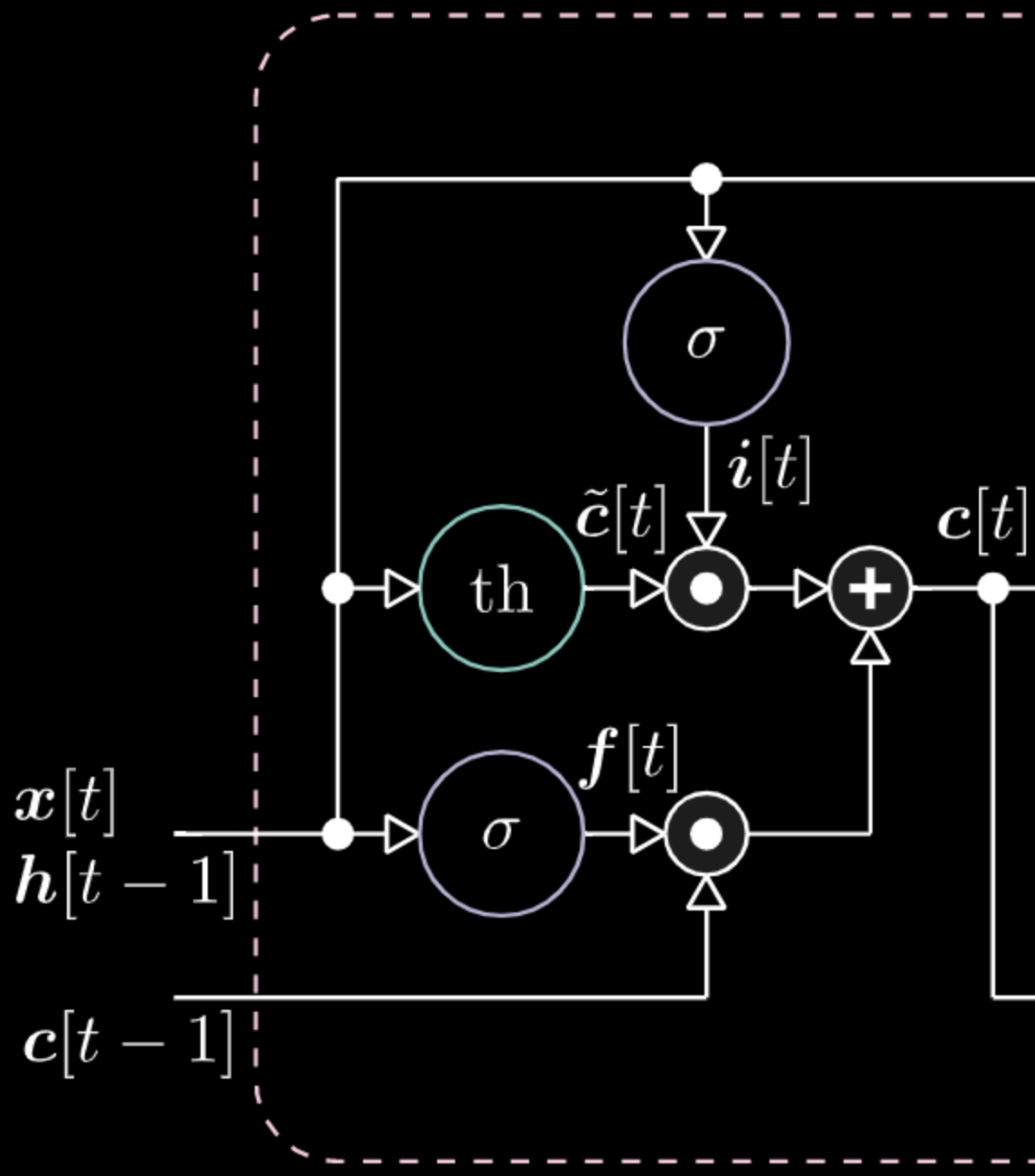
图25: 记忆细胞的可视化

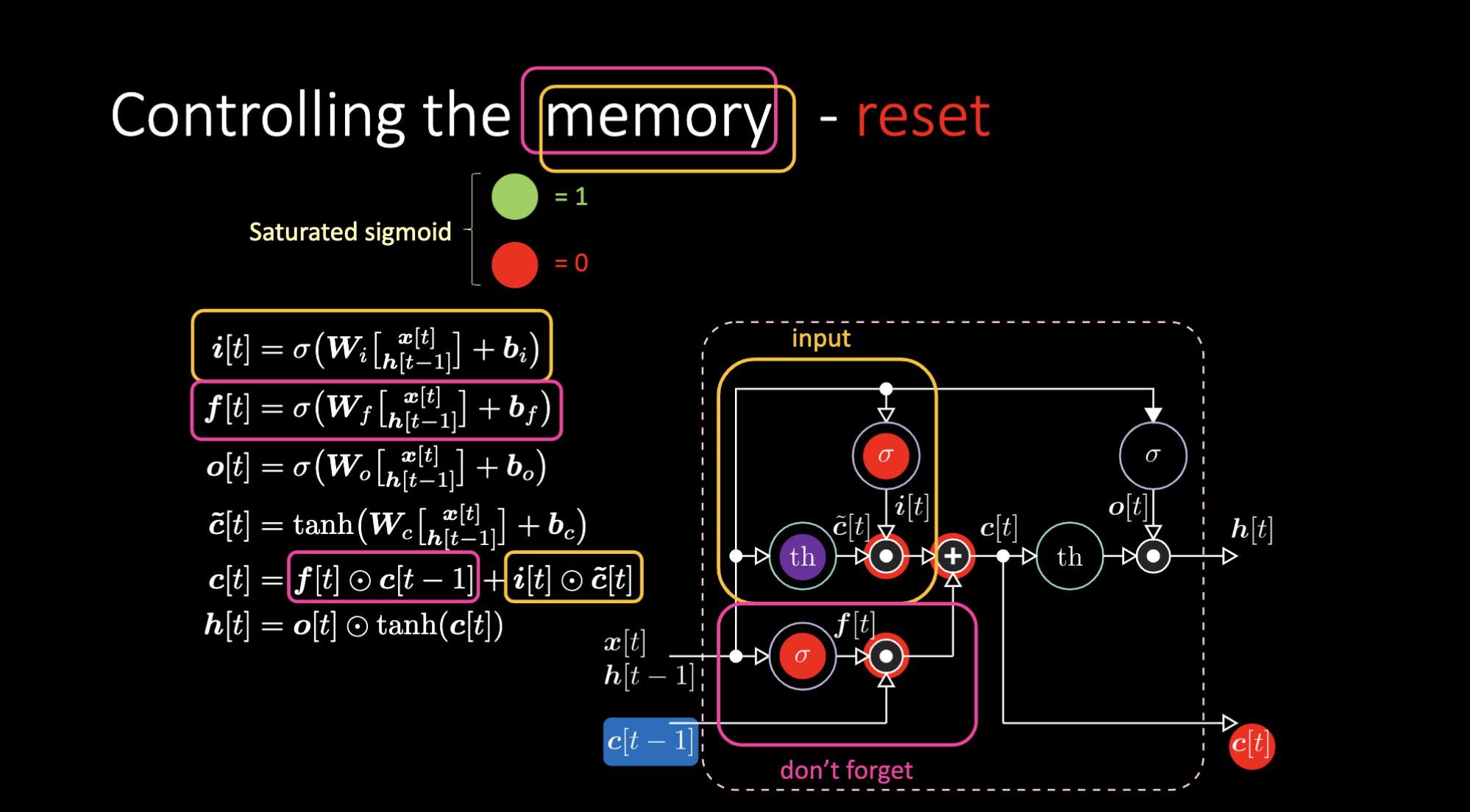
图26: LSTM架构——重设记忆

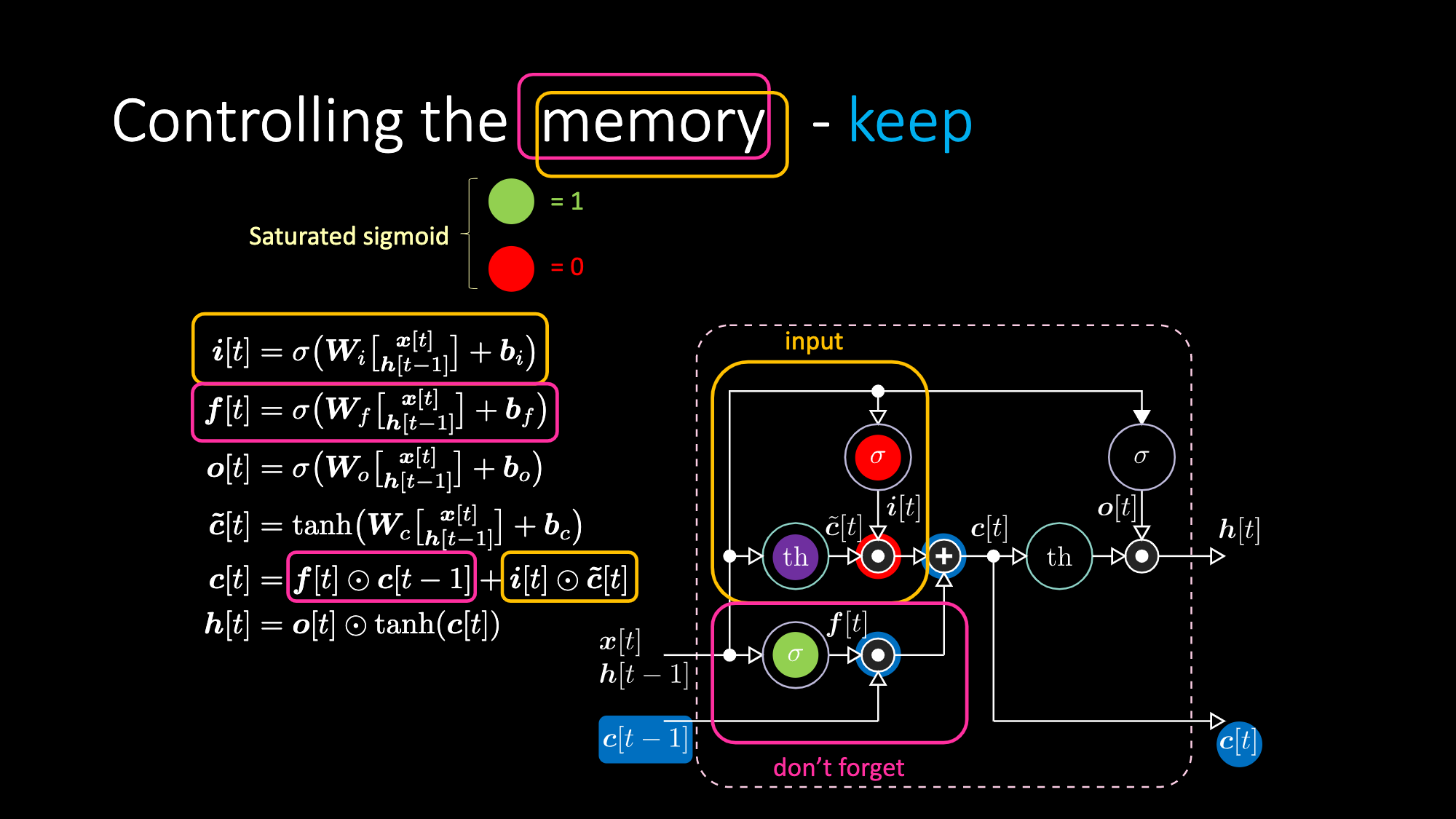
图27: LSTM架构——保留记忆

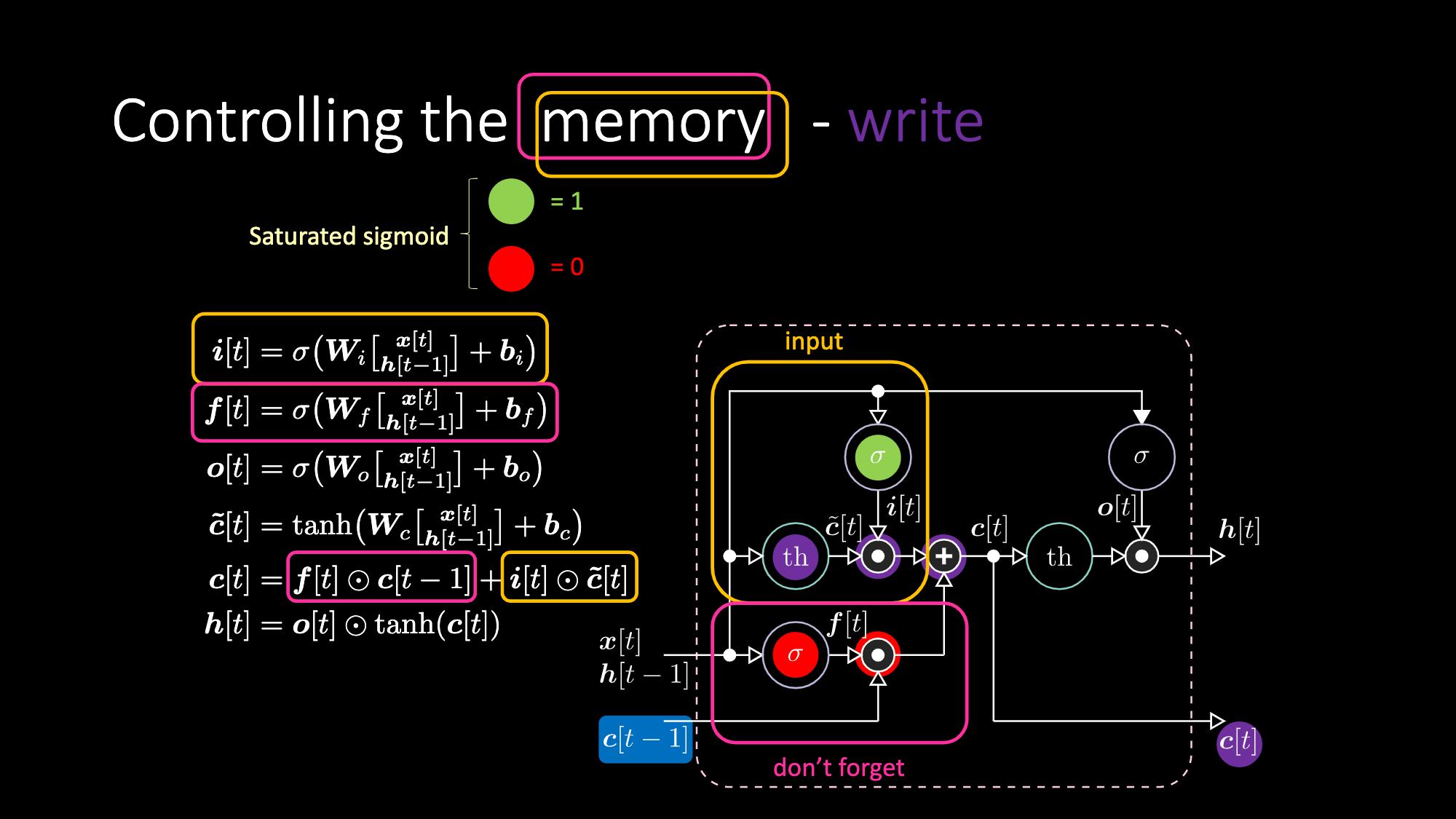
图28: LSTM架构——编写记忆

笔记里的示例

序列的分类（Sequence Classification）

我们的目标是给序列分类。元素和目标是局部的表现形式（只有一个非零比特的输入向量）。序列开头是B，结尾是E（触发符号）。其他的位置是由从{a, b, c, d}集里随机抽取的符号组成，除了在$t_1$和$t_2$位置只能由 X 或Y组成。在DifficultyLevel.HARD的例子中，序列长度是在100到110之间随机抽取、$t_1$是在10到20之间随机抽取，且$t_2$是在50到60之间随机抽取。一共有四个序列门类：Q、 R、 S，和 U，它们都依赖X和Y的时间顺序。其规则是：X, X -> Q；X, Y -> R； Y, X -> S； Y, Y -> U。

1). 探索数据集

数据生成器返回的数据类型时一个长度为2的Tuple。Tuple里的第一项是序列的Batch，其形状为$(32, 9, 8)$。这个数据会被输送进神经网络。每行里有8个不同的符号：(X, Y, a, b, c, d, B, E)。每一行是一个One-hot向量。一个行的序列代表一个符号的序列。第一个全零行叫做Padding。当序列长度小于Batch里的最大长度的时候，我们使用Padding。Tuple里的第二项是门类标签的对应Batch，其形状是$(32, 4)$。我们有四个门类：(Q, R, S, U)。第一个序列是BbXcXcbE，它解码后的门类标签是$[1, 0, 0, 0]$，表示Q。

图29: 输入向量示例

2). 定义并训练模型

让我们建立一个简单的RNN，一个LSTM，并且训练10次。在训练环节，我们应当始终寻找一下五点：

• 完成模型的向前传递

• 计算损失

• 梯度缓存清零

• 向后传播，计算损失函数的关于系数的偏分

• 进入梯度的相反方向

图30: 简单RNN vs LSTM - 10 Epochs

在简单模式下，训练了10次后的RNN有50%的准确率，而LSTM有100%的准确率。但是LSTM有比RNN大4倍的权重，而且有两个隐藏层。所以这样比较不是很公平。训练了100次后，RNN才有了100%的准确率，比LSTM花了更长的训练时间。

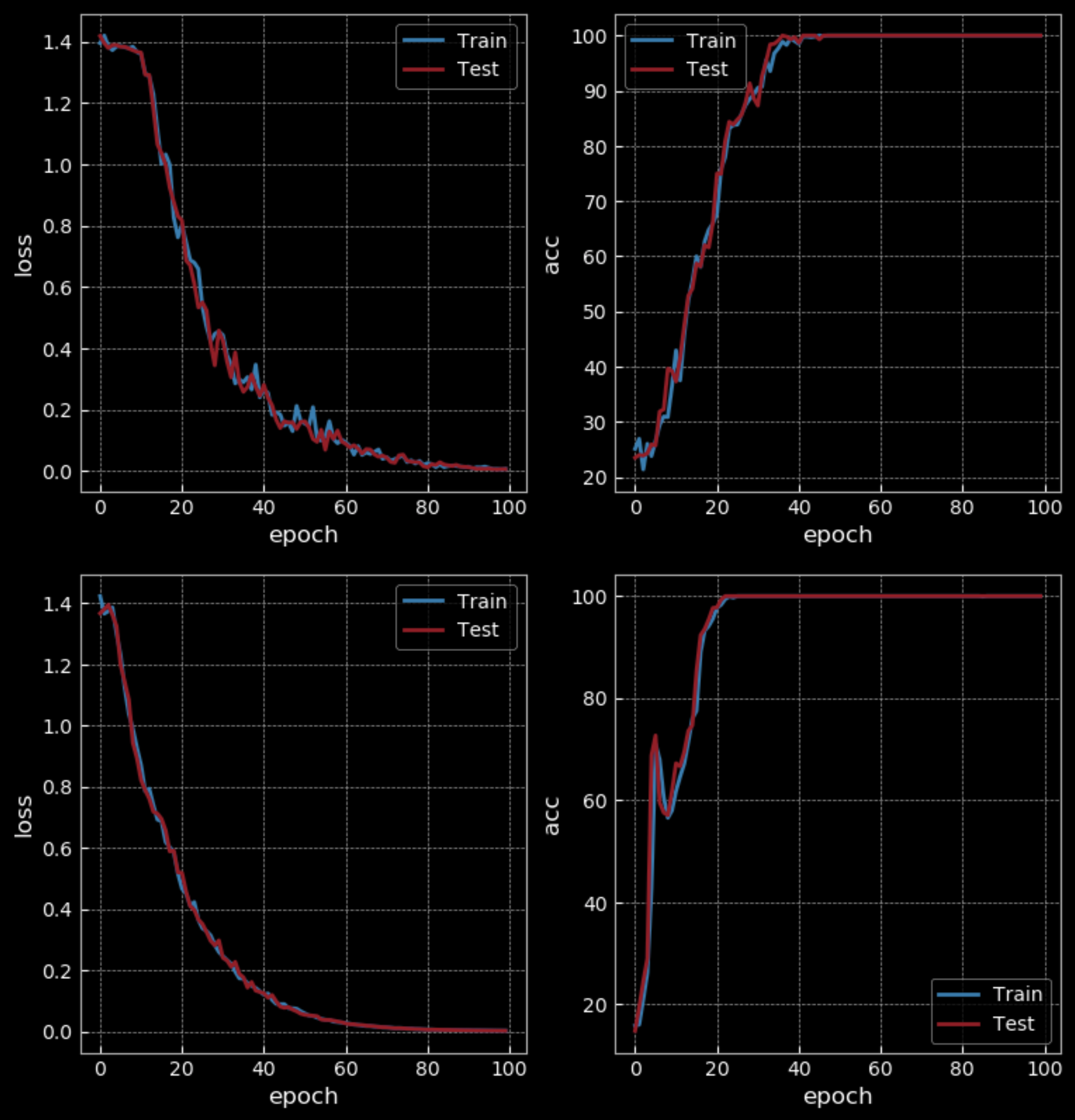
图31: 简单RNN vs LSTM - 100 Epochs

如果我们增加训练的难度（使用更长的序列），我们会看到RNN失败，而LSTM继续工作。

图32: 隐藏状态值的可视化

图23展示的是随时间变化的LSTM的隐藏状态。我们将输入送进一个双曲正切函数。这样当输入值小于$-2.5$时，会被映射到$-1$；当它大于$2.5$时，会被映射到$1$。这种情况下，隐藏层挑中X（图中第五行），然后变成红色，直到另一个X出现。所以第五个细胞的隐藏单元因观测到 X而被触发，然后在遇到另一个 X 后渐渐平息。这个过程让我们能辨认出序列的门类。

信号反射 (Signal Echoing)

反射信号是一个同步多对多形式（many-to-many）的例子。比如，第一个输入序列是"1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 1 1 1 ..."， 第一个目标序列是"0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 ..."。这种情况下，输出延迟了3步。所以我们需要短期工作记忆来保留之前的信息。然而在语言模型中，它要根据提示说出之前没说过的信息。这就是两者之间的区别。

在我们往神经网络里输送整个序列并迫使目标为某个值之前，我们需要将长序列切分成几个小块。当输送一个新的小块时，我们需要跟踪隐藏状态，并在加入下一小块时把它输入到内部状态。在LSTM中，只要你有足够的储存空间，保留多久的记忆都可以。在RNN中，达到了一定长度后，网络会忘记过去发生的事。