循环神经网络(RNNs)和门控循环单元(GRUs)﹑长短期记忆(LSTMs)﹑注意模组(Attention)﹑序列对序列(Seq2Seq)﹑记忆网络(Memory Networks)

深度学习架构

在深度学习中，有不同的模組 来实现不同的功能。深度学习的专业知识包括设计架构以完成特定任务。这是有点像过去使用算法编写的程序对计算机来发出指令，深度学习将复杂的功能简化为一些图形模組（也可以是动态的），这些功能的是由通过网络架构学习來建立的。

就像我们在卷积网络中看到的那样，网络模組架构是很重要。

循环神经网络(RNN)

在卷积神经网络中，模組 之间的图形或他們的連接是沒有循环的。 卷积神经网络的模組 中是有顺序,就好像有由输入到输出一樣。

Figure 1. 卷起來的循环神经网络

• $x(t)$ : 随时间变化的输入函数
• $\text{Enc}(x(t))$: 能生成代表输入数据的编码器
• $h(t)$: 代表输入数据的数据
• $w$: 可训练的参数
• $z(t-1)$: 先前的隐藏状态，也是上一步时间的输出
• $z(t)$: 当前的隐藏状态
• $g$: 可以是复杂神经网络的函数； 其中一个输入是 $z(t-1)$ ，它是上一步时间的输出
• $\text{Dec}(z(t))$: 生成输出的解码器

循环网络：摊开循环的网络的循环

摊开來的循环网络，他的输入是一个序列 $x_1, x_2, \cdots, x_T$.

"
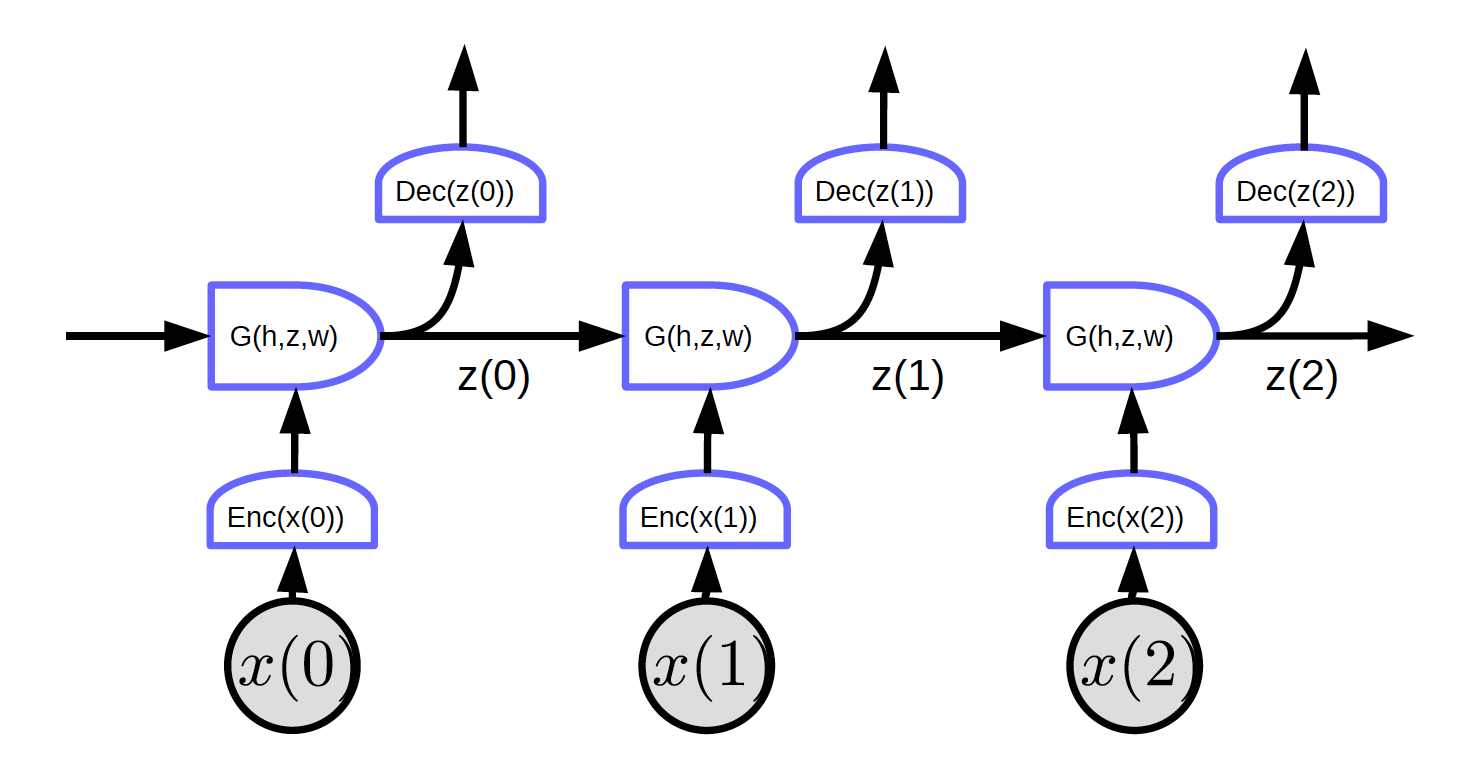
图2.摊开來的的循环网络

在图2中,输入是 $x_1, x_2, x_3$.

在时间点为零时(t=0), 输入 $x(0)$ 是被输入到编码器, $h(x(0)) = \text{Enc}(x(0))$ 。之后,将其输入到G以生成隐藏状态z。 $z(0) = G(h_0, z’, w)$. 在时间点为零时(t=0)， $t = 0$, 用来输入给 $G$ 的 $z’$ 可以被初始化为$0$ 或随机初始化。 $z(0)$ i是会被输入到解码器来生成输出和成為下一步时间其中一個输入。

这个网络没有循环,我们可以实施反向传播。

图2显示了一个的常规网络具有的特定特征：每个分段块共享相同的权重。三个编码器，三个解码器和G函数在不同的时间点上的权重是一样的。

随时间反向传播（BPTT）：随时间反向传播。很可惜，随时间反向传播（BPTT）在循环神经网络的原本形式效果不佳。

循环网络的问题：

1. 梯度消失
   • 在很长的序列中，渐变在每一个时间点中乘“权重矩阵（转置）”。权重矩阵中有很小值的值，渐变范数就越来越小，而且是指数地变小。
2. 梯度爆炸
   • 如果有权重矩阵是很大和非线性层是没有饱和，梯度就会爆炸。每次更新权重就变成一次又一次的划分。然后我们或许只能用学习率极低的学习率来解决问题。

使用循环神经网络的一个原因是因為它可以记住过去的信息。但是一个太过简单的循环神经网络可能因为记住很久的信息而失败。

一个消失梯度问题的例子:

输入是字符,是来自一个C程式。系统会说这个程式是否语法正确。语法正确的程式是会正确数量的有效数量的括号和括号。因此，网络应记住要检查的括号和花括号有多少个，以及是否括号包含另一些括号。网络必须如计数器一样在隐藏状态中存储此类信息。但是，由于梯度消失，它将无法在输出很较长的程式中保留此类信息。

循环神经网络的技巧

• 裁剪梯度: (避免梯度爆炸) 当梯度太大时，将其缩小。
• 初始化技巧 (在开始时就要避免梯度爆炸或梯度消失) 初始化权重矩阵以在一定程度上保留一些标准来对应问题。 例如，正交初始化将权重矩阵初始化为随机正交矩阵。

乘法模组

在乘法模组中,我们不单只计算输入的加权总和,我们也分别计算不同的输入的积,然后用它们来一起加权总和。

假设 $x \in {R}^{n\times1}$, $W \in {R}^{m \times n}$, $U \in {R}^{m \times n \times d}$ and $z \in {R}^{d\times1}$. 这里U是张量。

而 $s_i = w_{i}^\top x = \sum_j w_{ij}x_j$.

系统的输出是典型的是输入和权重的 加权总和。但权重本身也是权重和自己的输入的加权总和。

超网络体系结构：权重是由另外一个网络计算出来的。

注意模组

$x_1$ 和 $x_2$ 是向量, $w_1$ 和 $w_2$ 是归一化后的标量，而 $w_1 + w_2 = 1$, 而且 $w_1$ 和 $w_2$ 是各自在0 到1之间。

$w_1x_1 + w_2x_2$ 是 $x_1$ 和 $x_2$ 的加权总和,而 $w_1$ 和 $w_2$ 作为它們的系数来加权的。.

通過更改 $w_1$ 和 $w_2$相對的大小， 我們可以切換 $w_1x_1 + w_2x_2$ 的輸出為 $x_1$ 或 $x_2$ 或 $x_1$ 和 $x_2$ 的線性組合 .

输入可以具有多个 $x$ 向量 (可多于 $x_1$ 和 $x_2$).系统将选择适当的组合, 其选择由另一个变量z决定。注意模组允许神经网络将其注意力集中在特定的输入上，而忽略其他输入。

注意模組在自然语言处理 (NLP)的系统中变得越来越重要，在使用转换器体系结构或其他注意模组体系结构中重要。

权重是数据中独立的,因為Z是数据中独立的。

門控循環單元（GRU）

就如上方所说的一样,循环神经网络(RNN)因梯度消失或梯度爆炸而出现很多问题,同时它又不能记忆「状态」很长时间。门控循环单元(GRU) Cho, 2014,是一个试图解决这些问题的乘法模块的应用。它是一个能记忆的循环神经网络(另外一个是长短期记忆,英文名是LSTM)。门控循环单元的结构如下所示：

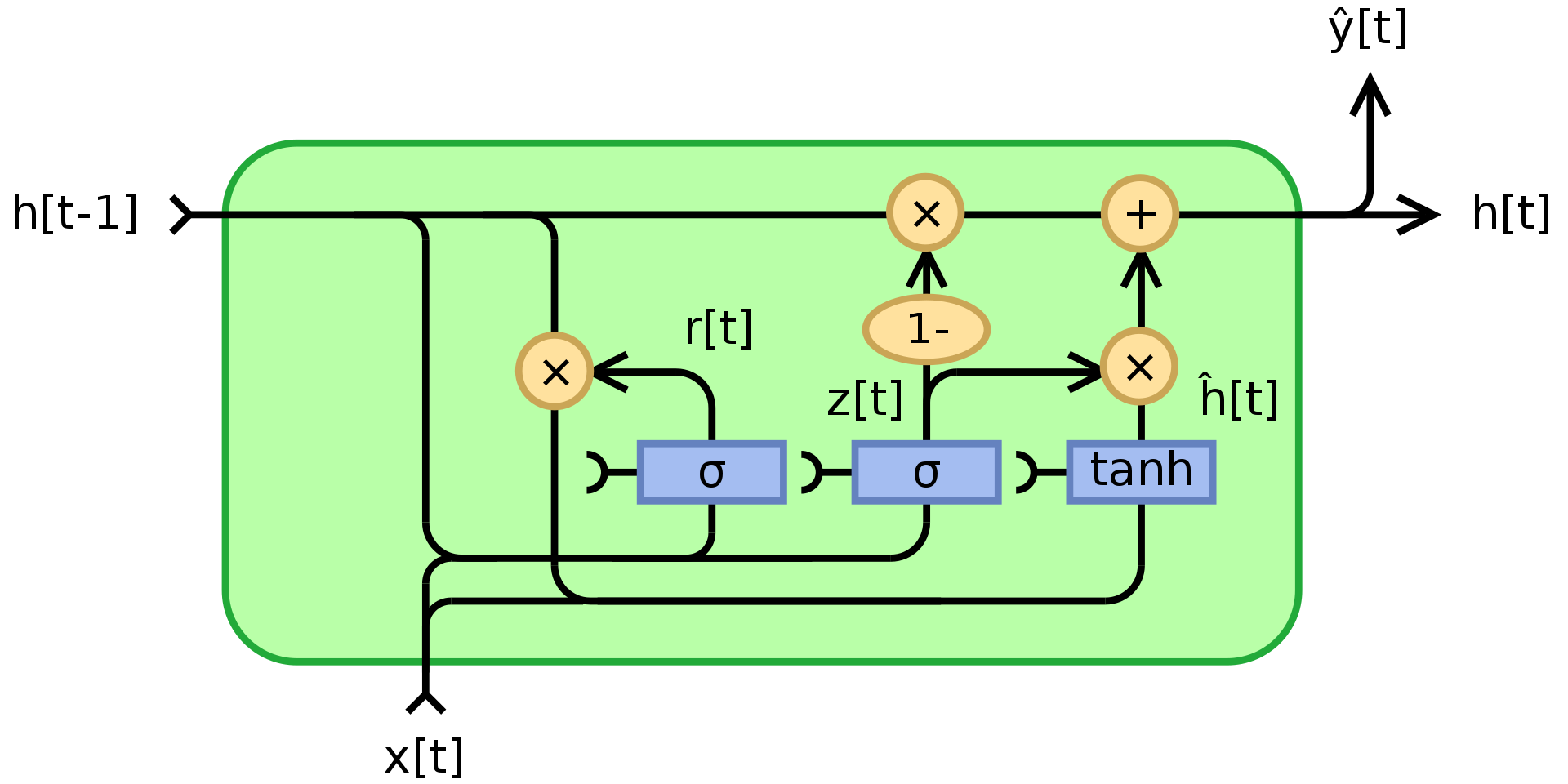
图3.门控循环单元

而 $\odot$ 是表明是逐元素乘法(阿达玛乘积)。 $x_t$ 是输入向量, $h_t$ 是输出向量， $z_t$ 是更新门的向量，$r_t$ 是重设门的向量, $\phi_h$ 是双曲正切(hyperbolic tanh) ，并且 $W$,$U$,$b$ 是可学习的参数。

具体来说， $z_t$ 是一个输出向量的门。它决定有多少过去的信息传递给未来。它先把两个线性层和一个偏置加起来,第一个线性层的输入是 $x_t$ ，而第二个线性层的输入是「先前状态状态」 $h_{t-1}$，最后加起来的数输入到一个S型函数(sigmoid function) 。 $z_t$ 在输入过S型函数后，它包含的系数是在0和1之间。后输出的「状态」 $h_t$ 是经由 $z_t$ 的 $h_{t-1}$ 和 $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$ 的凸组合。如果 $h_t$ 系数为1，当前部份的门控循环单元的输出只不过单纯是「先前状态」，并且同时忽略现在的输入（这是默认行为）。如果 $h_t$ 系数少于1， $h_t$ 就會输入现在的输入來输入新信息。

重设门 $r_t$ 是用来决定忘记多少过去的信息。 在用来输入新「记忆」的部份 $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$,，如果 $r_t$ 的系数为 0, ,那就没有保存任何过去的记忆。如果 $z_t$ 同时是0的话,那系统就完全重设。 ,因为 $h_t$ 只输入「现在的输入」。

長期短期記憶(Long Short-Term Memory,简称LSTM)

门控循环单元（GRU）是长短期记忆的简单版，长短期记忆是比门控循环单元早一点出的。 Hochreiter, Schmidhuber, 1997. 一样地,长短期记忆也加入了记忆元件,它可以保持过去的信息。长短期记忆也是解决循环神经网络(RNN)长时间后会记忆丧失的问题。 LSTM的结构如下所示：

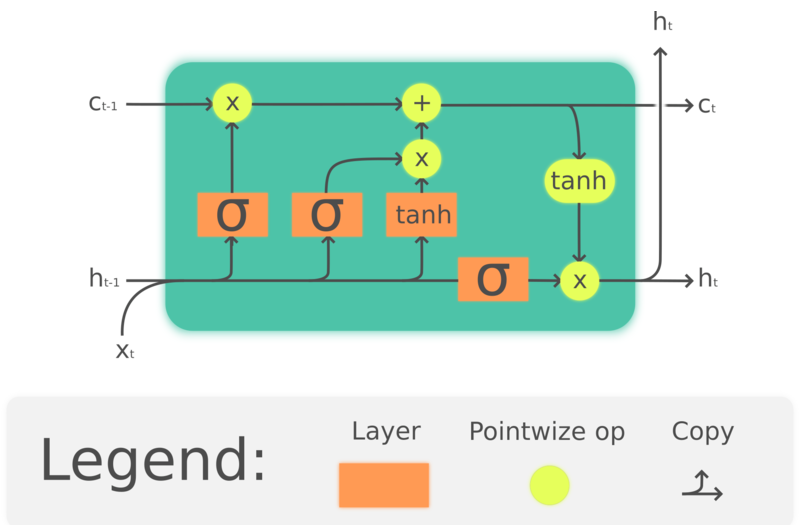
图4. 長期短期記憶(LSTM)

$\odot$ 表示逐元素乘法，$x_t\in\mathbb{R}^a$ 是输入到长期短期记忆单元的输入向量， $f_t\in\mathbb{R}^h$ 是忘记门的激活向量， $i_t\in\mathbb{R}^h$ 是输入门或更新门的激活向量, $o_t\in\mathbb{R}^h$ 是输出门的激活向量， $h_t\in\mathbb{R}^h$ 是「隐藏状态向量」（也是「输出」）， $c_t\in\mathbb{R}^h$ 是元件状态向量。

一个长期短期记忆(LSTM)单元用「元件状态」 ct向外来传达信息。它利用「元件状态」通过「门」的结构来监控信息保留或删除信。而忘记门 $f_t$ 根据当前输入和「先前的隐藏状态」来决定有多少来自「先前的元件状态」 $c_{t-1}$ 的信息要保留，然后就生成一个数是在0和1之间来作为 $c_{t-1}$ 的系数。 $\tanh(W_cx_t + U_ch_{t-1} + b_c)$ 是计算和选出新的选择来更新「元件状态」，就如忘记门一样，输入门 $i_t$ 决定要更新多少。最后，输出数 $h_t$ 会把元件状态 $c_t$ 来作为输出，但元件状态 $c_t$ 要先将通过 $\tanh$ ，然后输出门 $o_t$ ，才能作为输出数 $h_t$ 来输出。

虽然LSTM（长期短期记忆）在自然语言处理(NLP)中被广泛使用，但是它们的普及程度正在下降。例如，语音识别正朝着使用时间卷积网络(TCNN)的方向发展，而自然语言处理(NLP)正在朝着使用变型模型(Transformers)的方向发展。

序列到序列模型

提出的方法 Sutskever NIPS 2014 是第一个可以能和传统方法比较的神经机器翻译系统。它使用「编码器-解码器」体系结构，其中编码器和解码器均为多层LSTM。

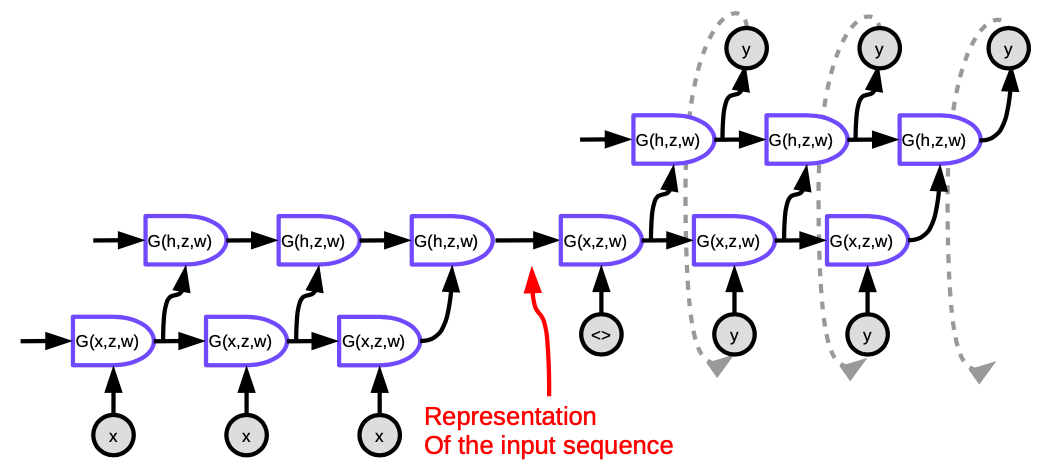
图 5. 序列到序列模型 (Seq2Seq)

图中的每个单元都是一个「长短期记忆」,简称(LSTM)。编码器（左侧的部分）的时间步总长等于要翻译的句子的长度。每时间步中，都有一堆长期短期记忆（论文中为四层），其中前一个「长短期记忆」的隐藏状态被馈送到下一个「长短期记忆」。最后一个时间步的最后一层输出的向量代表了整个句子含义，然后将其馈送到另一个多层「长短期记忆」（也就是解码器）中，该多层「长短期记忆」之后生成「目标语言」的单词。在解码器中，它生成序列形式的文字。每个时间步骤产生一个单词，每一个时间步生成一个单词,一个单词作为输入来输入到下一个时间步。

这种体系结构不能以两种方式令人满意：第一，必须将句子的整个含义压缩为编码器，然后进行隐藏状态，最后解码器。第二，「长短期记忆」实际上不会将信息保留超过20个单词。解决这些问题的方法称为「双向长短期记忆」,简称Bi-LSTM，它可以运行两个「长短期记忆」，一个向前,另一个相反方向,也就是向后。在「双向长短期记忆」中，「数据的含义」是被两个向量编码出來，一个向量是通过从左到右运行「长短期记忆」生成的，另一个就一樣从运行「长短期记忆」右到左运行生成的。这样可以使句子的长度加一倍，而不会丢失太多信息。

序列到序列加注意模型

上方成功的造法十分短命。另一篇论文(Bahdanau, Cho, Bengio)建议如果用一个庞大的网络挤压整个句子的意思成一个向量，不如每一个时间点注意句子中相应的位置,同时又保留同样的意思。比如注意机制。

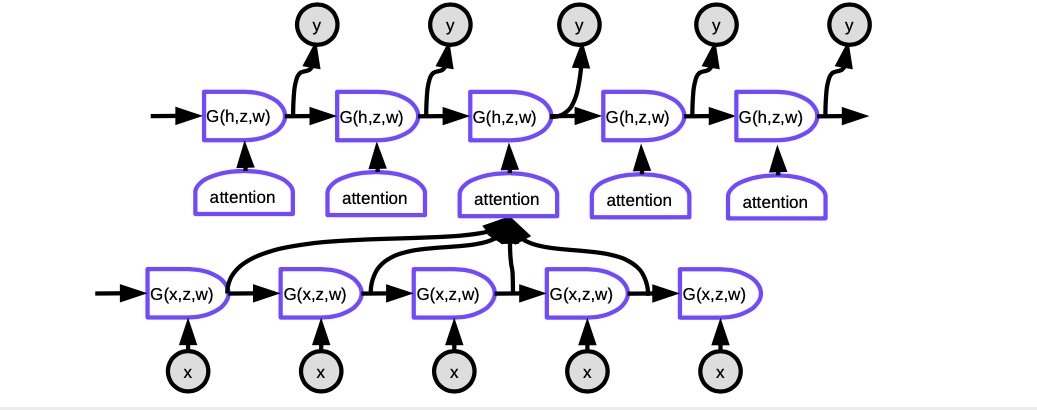
图6。序列到序列加注意模型

在注意模型中，要在每个时间步生成该时间点的单词，我们首先需要确定该代表词词的隐藏状态要集中注意。对准，网络将学习对每个编码化的输入与解码器当前 这些评分被归一化指数函数（softmax）进行归一化过，然后将其的系数用于计算编码器中隐藏状态在不同时间步的增加和。通过调整权重， 系统可以调整要注意的输入区域。这种机制的神奇之处在于，它可以通过反向传播来训练使用计算系数的网络。絕對不用親手去寫程式來建立它們。绝对不用亲手去写程式来建立它们!

注意机制完全改变了神经机器翻译。后来，谷歌发表了一篇论文《注意模型就是你所需要的一切》 Attention Is All You Need，他们提出了「向前转换器」，而神经元的每一层和每一组都是用注意模型来写。

记忆网络

记忆网络源于Facebook中的工作，由2014年 Antoine Bordes 和2015年 Sainbayar Sukhbaatar 发起的。

记忆网络的想法是来自两个在大脑中重要的部份:一是大脑皮层,那里是长期记忆的所在地，而有一大块的神经元叫海马体。它有有很多线连到皮层各处。海马体是被认为用作短期记忆,在较短的时间内记住事物。流行理论是，由于海马容量有限，因此当您睡觉时，有很多信息从海马体传递到皮质，从而在得以巩固为长期记忆。

对于记忆网络，网络有一个输入$x$ 将其视为内存地址），并将此 $x$ 与向量 $k_1, k_2, k_3, \cdots$ （“称呼为键”），用点积来进行比较，通过点积。让它们经过一个归一化(softmax)，然后就会得到一个数字数组，这些数字的总和为1。还有一组其他向量 $v_1, v_2, v_3, \cdots$ (“称呼为值”）。将这些向量与之前归一化后得出的标乘起来的缩放器相乘，最后加起所有向量（留意这和注意模型的相似）来得出结果。

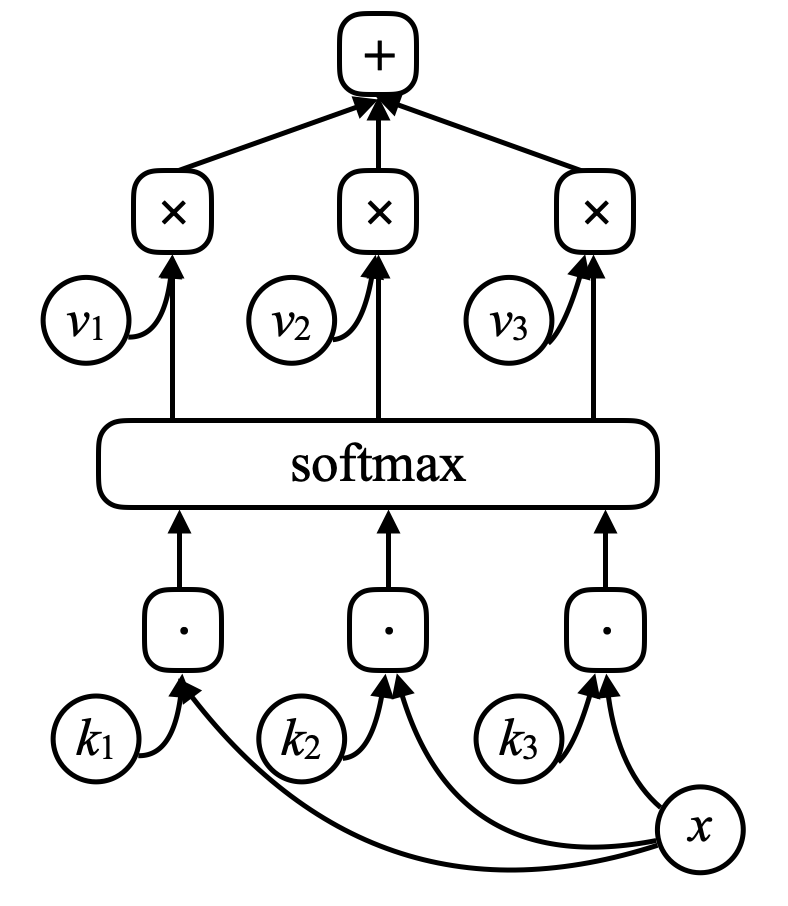
图7。记忆网络

如果其中一个键（例如, $k_i$) 完全匹配s $x$，那对应这个键的系数将非常接近1。那系统的输出本质上将是 $v_i$.

这就是 可地址化关联记忆。关联记忆是，如果您的输入与键匹配，则将获得该值。这只是它的一个简单可区分版本，它允许您反向传播和通过梯度下降更改向量。

作者所做的是通过给系统多个排序过的句子来讲述一个故事。使用未经过预训练的神经网络来对句子进行编码成向量，可以将这些句子编码为向量。那些句子都被用作返回一个记忆类的值。之后当您向系统提出问题时，您将对问题进行编码并输入到神经网络的，神经网络生成一个x输入到「记忆」，然后「记忆」会返回一个值。该值与网络的先前状态一起用于重新访问内存。然后，您将训练整个网络来回答您的问题。经过广泛的培训，该模型实际上学会了存储故事并回答问题。

这个值与网络的先前状态是一起被用于重新访问「记忆」。然后，您将训练整个网络来回答您的问题。经过多次的训练，该模型实际上学会了存储故事并回答问题。

在记忆网络中，有一个神经网络，它接受输入，然后为「记忆」生成地址，然后将该值返回给网络，继续运行，最后产生输出。这非常类似于计算机，因为有一个CPU和一个用于读写的外部记忆体。

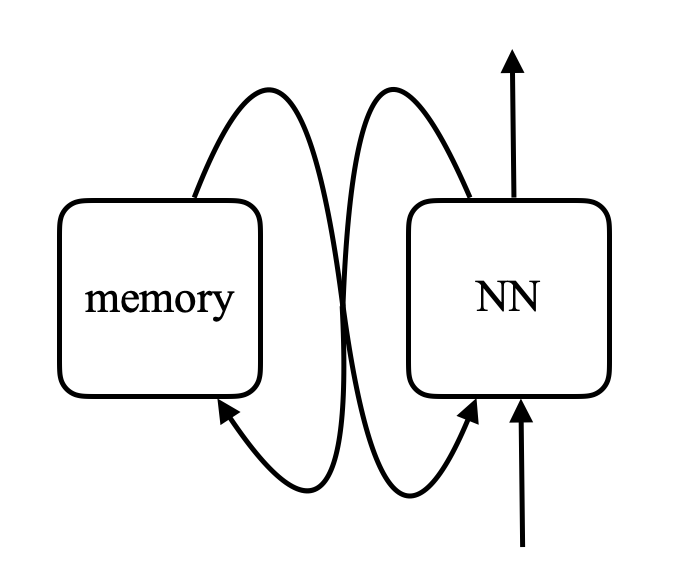
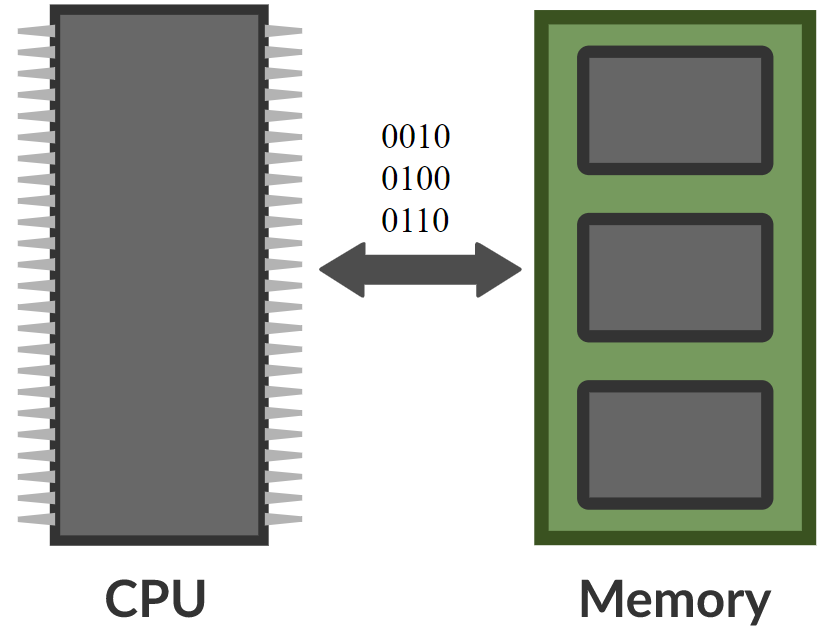
图8.内存网络与计算机之间的比较（Khan Acadamy摄影） (Photo by 可汗学院Khan Acadamy)

有些人认为您实际上可以基于此构建 可区分的计算机 ,英文為differentiable computers 。一个例子Neural Turing Machine是DeepMind的Neural Turing Machine，它是在Facebook论文在arXiv上发布三天后公开的。

想法是将输入与键进行比较，生成系数,然后生成出值-基本上就是转变器。转变器基本上是一个神经网络，其中每组神经元都是这些网络之一。