卷积网络的应用

邮政编码识别器

在之前的讲座中，我们示范了一个卷积层是如何去认知数字，相反，如果问题还存在，那模型是如何去选取每一个数字同时避免触及相邻的数字。而下一步就是去检测非重叠对象或重叠对象。而同时用非最大抑制(Non-Maximum Suppression, NMS)一般的做法。现在，给予一个假说，就是输入是一系列不重叠的数字，而秘诀就是去训练多个卷积神经网络，接着采用多数投票(majority vote)或用卷积层网络对每个数字生成分数，然后选出当中有最高的分数的数字。

使用CNN进行识别

这里我们呈现一个任务，就是识别五个没有重叠的邮政编码。系统没有被指示出如何去分开每个数字，但知道必定有五个数字。这个系统(图1)由4个不同大小的卷积网络组成，每一个生成一组输出。这个输出由矩阵表示。而那四个输出矩阵是由模型以最后一层不同宽度的核输出来的。而每一个输出，这里有10行，代表10个类，也就是0到9。而大一点的白色正方形代表着在所有类别中一个高一点分数的那一个类。在这四个输出块中，最后的核层的宽度大小分别为5和4、3、2。这个核的大小决定模型对输入看到的窗口的宽度大小，所以每个模型基于不同的窗口尺寸来预测数字。接着，模型利用多数投票(majority vote)并选择在那个窗口中对应最高分的那个类别。为了抽取有用信息，需要牢记的是，不是所有的字符组合都是可能的，因此，利用输入限制进行纠错，对于确保输出是正确的邮编是有用的。

Figure 1: 邮编识别的多分类器

现在来讨论字符的顺序。这里的技巧是使用一个最短路径算法。由于我们已知可能的字符的范围以及需要预测的数字的数量，我们可以通过计算产生数字以及数字间转换的最小消耗来解决这个问题。这个路径需要在图中从左下单元到右上单元连续，同时该路径被限制为只能包含从左到右、从下到上的移动。注意，如果相邻数字是相同的，那么算法应该能够辨别出存在重复数字，而不是预测单个数字。

人脸检测

卷积神经网络在检测任务上表现良好，对于人脸检测当然也不例外。为了完成人脸检测，我们需要收集一组包含人脸与不包含人脸的图像数据集。基于该数据集，我们训练一个具有 30 $\times$ 30 像素的检测窗口的卷积网络，该网络可以辨别窗口是否存在人脸。一旦训练完毕，我们可以将该模型运用于一张新的图像，如果图像中具有大概在 30 $\times$ 30 像素的窗口内的人脸，卷积网络将在对应的位置高亮提示该输出。不过，还是存在两个问题。

• 假阳性: 有很多非人脸物体的各种变体会出现在图像的像素块中。在训练阶段，模型可能无法见过所有可能(也即一个完整的非人脸像素块代表集合)。因此，在测试阶段模型可能出现很多假阳性的判断。比如，如果网络没有在包含手的图像上训练过， 由于模型可能会基于皮肤色调去检测人脸，因此它会错误地将包含手的像素块判断为人脸，因而引起假阳性。

• 不同人脸尺寸: 并不是所有的人脸都是 30 $\times$ 30 像素的尺寸，因此其它尺寸的人脸可能就无法检测到。一个解决办法是生成同一张图片的多尺度版本。原始检测器将检测 30 $\times$ 30 像素的人脸。如果在原图像上应用 $\sqrt 2$ 倍的缩放，那么模型将可以检测到小于原始图像的人脸，因为原来 30 $\times$ 30 的人脸现在大概是 20 $\times$ 20 像素。为了检测更大的人脸，我们可以缩小图像尺寸。这个过程代价很小，因为一半的代价来自原始的非缩放图像的处理。所有其它网络组合的总代价与原始的非缩放图像的处理基本相同。网络的尺寸是图像一侧尺寸的平方， 因此如果你按照 $\sqrt 2$ 倍缩放图像，你需要运行的网络就缩小2倍。因此总消耗为 $1+1/2+1/4+1/8+1/16…$，即2。 完成一个多尺度模型仅仅需要双倍的计算消耗。

一个多尺度人脸检测系统

Figure 2:人脸检测系统

图3中显示了人脸检测器的得分。该人脸检测器识别 20 $\times$ 20 像素尺寸的人脸。在小尺度(Scale 3)下， 有很多高分，但并不明确。当缩放因子提高(Scale 6)， 我们看到更多聚集的白色区域。那些白色区域表示检测到的人脸。接着我们应用非极大值抑制(non-maximum suppression)来获取人脸的最终位置。

Figure 3: 不同尺度因子的人脸检测得分

非极大值抑制

对每个高分区域，就有可能对应一个(潜在的)人脸。如果有更多的接近第一个的人脸被检测到，这就意味着应该只有一个被认为是正确的，而其它的都是错误的。利用非极大值抑制，我们选择重叠的边框中的最高值而移除其它。结果就是在最优位置的单个边框。

负样本挖掘

在上一节我们讨论了在测试阶段，由于存在许多非人脸对象容易混淆成人脸，模型可能会产生大量的假阳性。没有任何训练数据能够包含所有可能的类似人脸的非人脸对象。我们可以通过负样本挖掘减轻此类问题。在负样本挖掘中，我们利用非人脸像素块构建一个负样本数据集，而模型会(错误地)将它们检测为人脸。我们通过在已知不包含人脸的输入上运行模型从而收集这类数据。接着通过负样本重新训练检测器。我们可以通过重复该过程来增强模型对抗假阳性的鲁棒性。

语义分割

语义分割任务为输入图像中的每一个像素赋值一个类别。

长程自适应机器人视觉中的卷积神经网络

在这个项目中，目标是对输入图像进行区域标注，从而使得机器人可以区分道路和障碍。在图中，绿色区域是机器人可以行使的区域，红色区域是障碍，比如茂密的草丛。为了针对该项目进行网络训练，我们从图像上取一块区域并且手工将其标注为可穿越或不可穿越(绿色和红色)。之后我们通过使其预测像素块的颜色来在这样的像素块上进行卷积网络的训练。一旦系统训练得足够好，那么将其应用到整个图像上，模型就可以为图像上所有的区域标注绿色或红色。

Figure 4: 长程自适应机器人视觉中的卷积神经网络 (DARPA LAGR program 2005-2008)

这里有5类预测: 1) 翠绿, 2) 绿色, 3) 紫色：障碍物下沿线, 4) 红色障碍 5) 超高红色：绝对是一个障碍。

立体标签 (图4，第二列) 我们通过机器人上的四个摄像机捕获图像，这四个摄像机分为两组立体视觉对。使用立体视觉对的摄像机间的已知距离，三维空间中的每个像素的位置将通过测量立体视觉对的两个摄像机里的像素之间的相对距离被估测。这个过程与我们大脑估测我们看到的物体的方式一样。使用估测的位置信息，我们可以为地面拟合出一个平面，如果像素在地面附近，则标注为绿色，如果在地面上方，则标注为红色。

• 卷积神经网络的限制与推进: 立体视觉最多可在10米范围工作，而驱动一个机器人需要长程视觉的支持。但是如果训练得当，一个卷积神经网络能够在更远的距离上进行目标检测。

Figure 5: 距离规范化图像的缩放不变金字塔(Scale-invariant Pyramid)

• 作为模型输入: 重要的预处理包括构建一个距离规范化图像的缩放不变金字塔。(图5)。这与我们之前尝试检测多尺度人脸的做法很类似。

模型输出 (图4，列3) 模型给图像中直到地平线的每个像素都输出一个标签。这些是一个多尺度卷积网络的分类器输出。

• 模型如何是如何变得自适应的:机器人对于立体标签具有持续获取的权限，这允许网络被重训练从而适应新的环境。请注意，这里只有网络的最后一层会被重新训练。前一层已在实验室被训练好并且被固定。

系统性能

当尝试获取障碍另一边的GPS坐标时，机器人很远就“看到”障碍并规划一个路线去规避它。这得幸亏CNN预先检测到50-100米外的目标。

限制

回到2000年时，计算资源是受限的。机器人的处理速度在大概每秒1帧，这意味着它无法检测到一秒之内的行人并作出及时反应。对于这类限制的解决方案是低能耗视觉里程计模型。它并不基于神经网络，它具有大约2.5米的视觉，但是反应快速。

场景解析与标注

在这个任务中，模型为每个像素输出一个对象类别(楼房，汽车，天空等)。网络结构也是多尺度的(图6)。

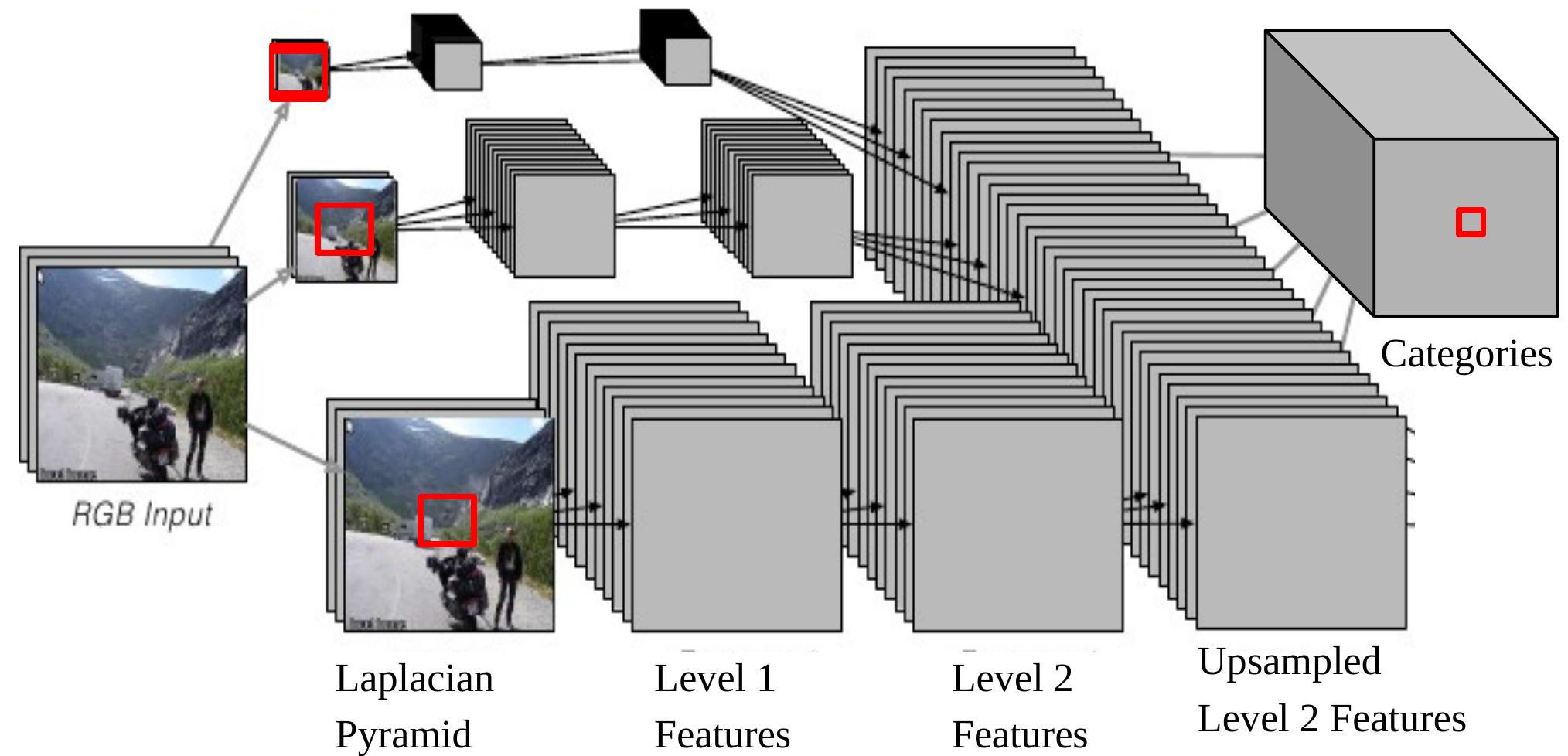
Figure 6: 用于场景解析的多尺度CNN

注意，如果我们将CNN的一个输出背靠一个输入，它对应着拉普拉斯金字塔底部的原始图像上的一个 $46\times46$像素的输入窗口。这意味着使用 $46\times46$ 像素的上下文去决定中心像素的类别。

尽管如此，有时候这个上下文尺寸并不足以决定更大物体的类别。

多尺度方法通过提供额外的重新标度图片作为输入能够提供更广阔的视觉。 步骤如下：

1. 选取同样的图像，分别缩减2倍和4倍。
2. 这两种额外重新标度的图像被送入相同的卷积网络(相同的权重，相同的核)，我们将得到另外两组2级特征(Level 2 Features)。
3. 上采样这些特征， 因此它们能够拥有与原始图像的2级特征(Level 2 Features)一样的尺寸。 堆叠这三组(上采样)特征，将其送入一个分类器。
4. 堆叠这三组(上采样)特征，将其送入一个分类器。

现在，来自 1/4 调整尺寸的图片的内容最大有效尺寸，是 $184\times 184\, (46\times 4=184)$。

性能: 没有后处理，逐帧运行，模型即使在标准硬件上也可以很快地运行。虽然它的训练数据很小(2k~3k)，但是结果仍然是破纪录的。