了解卷积和自动微分引擎

了解 1 维的卷积

这里我们要讨论卷积，因为我们想探索资料的稀疏性、平稳性与复合性。

我们使用的不是上周的 $A$ 矩阵，而是将其宽度改变为核的大小 $k$。因此，矩阵的每一列都是一个核。我们可以将核堆叠并滑动来使用（见图 1）。 如此我们会得到 $m$ 个高度为 $n-k+1$ 的层。

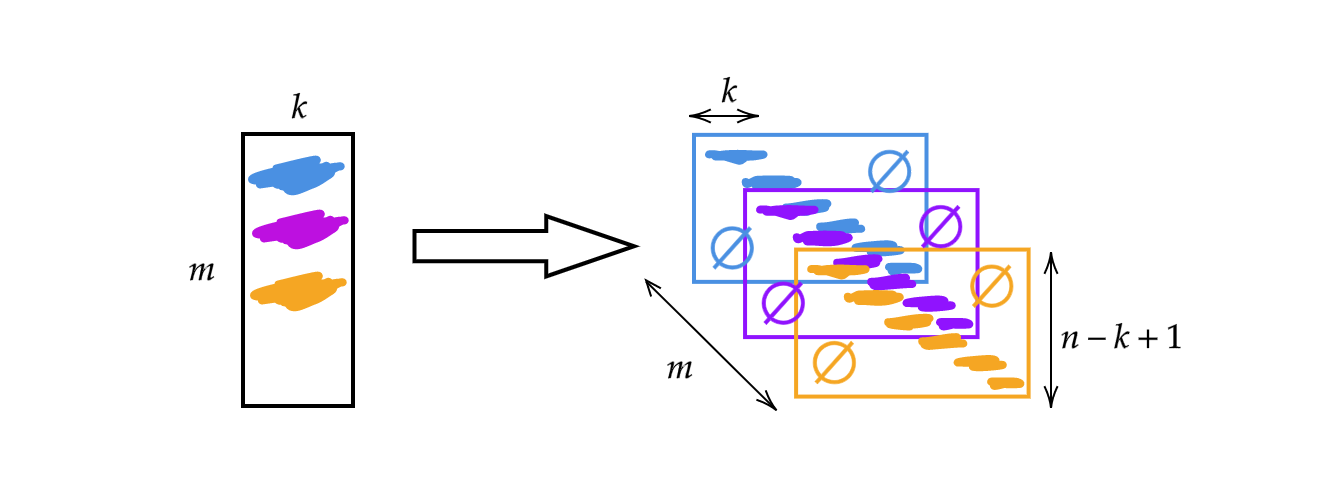
图 1: 一维卷积的插图

输出是 $m$（厚度） 个尺寸为 $n-k+1$ 的向量。

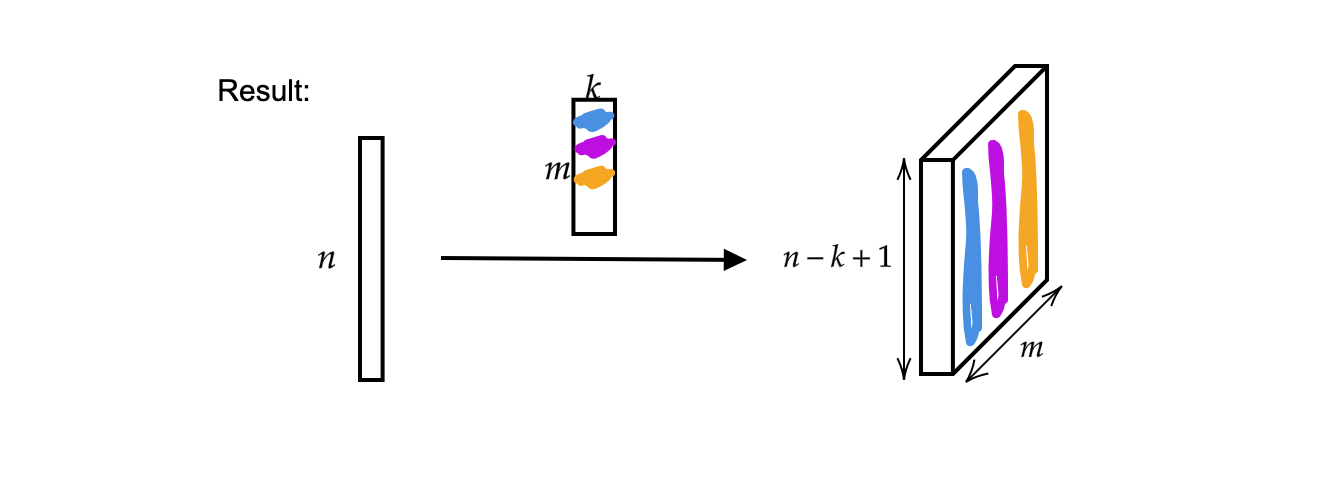
图 2: 一维卷积的结果

一个单独的输入向量可以视作一个单音讯号。

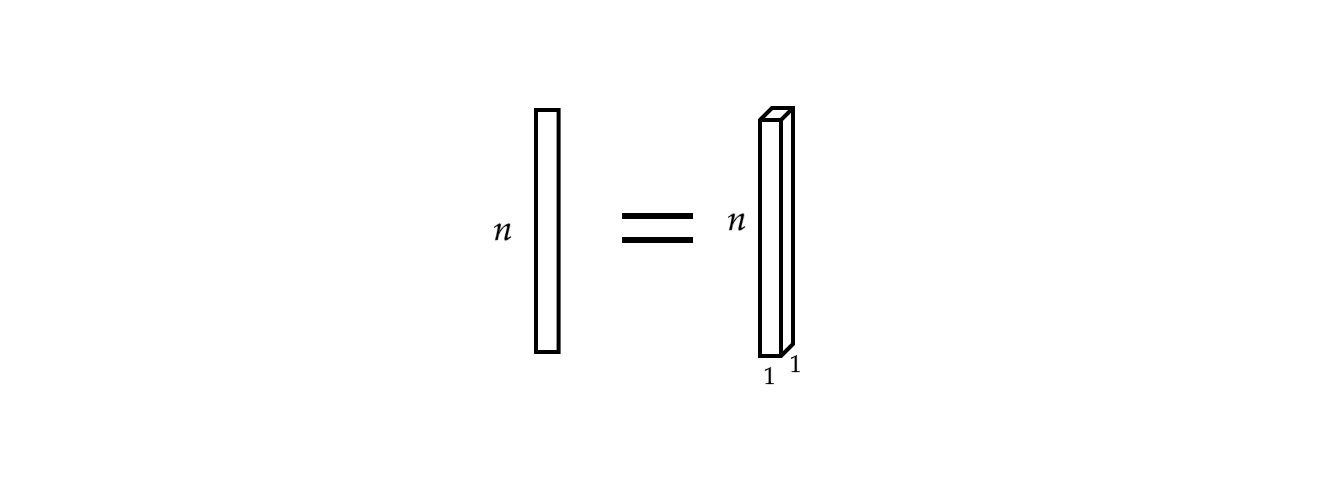
图 3: 单音讯号

现在，输入 $x$ 是一个映射：

其中 $\Omega = \lbrace 1, 2, 3, \cdots \rbrace \subset \mathbb{N}^1$（因为这是个一维讯号；它的定义域是一维的）且此情况中通道数 $c$ 是 $1$。2; 当 $c=2$ 这就成为了立体声的讯号。

对于一维的卷积，我们可以逐个核计算标量乘积（如图 4）。

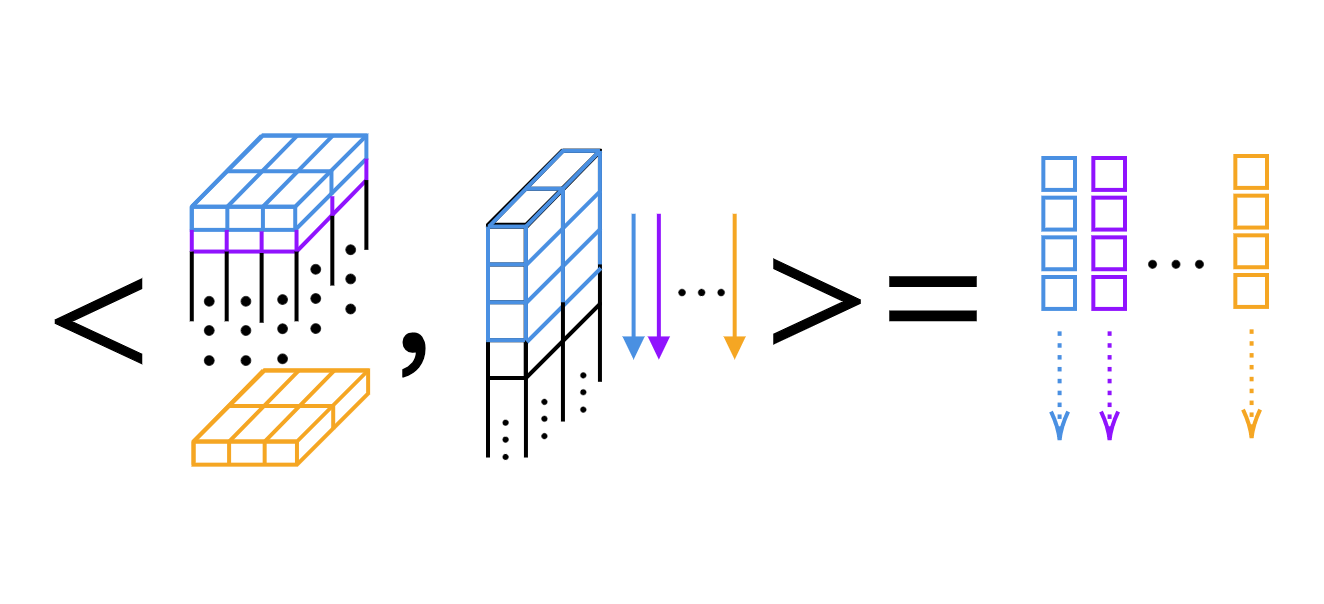
图 4: 在一维卷积逐层进行标量乘积

Pytorch 中核的维度与输出的宽度

技巧：我们可以在 Ipython 中使用 问号 来取得函数的文件。例如

Init signature:
nn.Conv1d(
    in_channels,           # number of channels in the input image
    out_channels,          # number of channels produced by the convolution
    kernel_size,           # size of the convolving kernel
    stride=1,              # stride of the convolution
    padding=0,             # zero-padding added to both sides of the input
    dilation=1,            # spacing between kernel elements
    groups=1,              # nb of blocked connections from input to output
    bias=True,             # if `True`, adds a learnable bias to the output
    padding_mode='zeros',  # accepted values `zeros` and `circular`
)

一维卷积

我们用大小为 $3$，步幅 $1$ 的一维卷积使通道从 $2$ 个（立体声讯号）变为 $16$ 个（$16$ 个核）。于是我们有 $16$ 个厚度为 $2$ 长度为 $3$ 的核。假设输入信号是一个大小 $1$ 通道 $2$ 个且有 $64$ 个样本的批次。生成的输出层会有 $1$ 个信号，具有 $16$ 个通道与长度 $62$ ($=64-3+1$)。并且，如果我们输出偏置的大小，会是 $16$ 因为我们每个权重都有一个偏置。

conv = nn.Conv1d(2, 16, 3)  # 2 channels (stereo signal), 16 kernels of size 3
conv.weight.size()          # output: torch.Size([16, 2, 3])
conv.bias.size()            # output: torch.Size([16])

x = torch.rand(1, 2, 64)    # batch of size 1, 2 channels, 64 samples
conv(x).size()              # output: torch.Size([1, 16, 62])

conv = nn.Conv1d(2, 16, 5)  # 2 channels, 16 kernels of size 5
conv(x).size()              # output: torch.Size([1, 16, 60])

二维卷积

首先我们定义输入资料有一个样本，$20$ 个通道（假设我们使用的是高光谱影像）高 $64$ 而 宽 $128$。二维的卷积有 $20$ 个来自输入的通道，与 $16$ 个 $3\times 3$ 大小的卷积核。卷积之后，输出的资料有一个样本，$16$ 个通道，高 $62$ $(=64-3+1)$ 且宽 $124$ $(=128-5+1)$。

x = torch.rand(1, 20, 64, 128)    # 1 sample, 20 channels, height 64, and width 128
conv = nn.Conv2d(20, 16, (3, 5))  # 20 channels, 16 kernels, kernel size is 3 x 5
conv.weight.size()                # output: torch.Size([16, 20, 3, 5])
conv(x).size()                    # output: torch.Size([1, 16, 62, 124])

如果我们想输出相同的维度，可以采用填充。以上方的代码为基础，我们可以于卷积函数添加新的参数：stride=1 和 padding=(1, 2)，表示 $y$ 方向填充 $1$（一上一下），$x$ 方向填充 $2$。如此，输出的信号就与输入信号有相同尺寸。储存二维卷积使用的卷积核共需要 $4$ 个维度。

# 20 channels, 16 kernels of size 3 x 5, stride is 1, padding of 1 and 2
conv = nn.Conv2d(20, 16, (3, 5), 1, (1, 2))
conv(x).size()  # output: torch.Size([1, 16, 64, 128])

自动梯度如何运作？

在这个部份，我们将使用 torch 来记录所有在张量上进行的运算，以计算偏导数。

• 建立一个 $2\times2$ 且能累积梯度的张量 $\boldsymbol{x}$；
• 从 $\boldsymbol{x}$ 的所有元素减去 $2$，取得 $\boldsymbol{y}$；（若我们印出 y.grad_fn 会得到 <SubBackward0 object at 0x12904b290> 代表 y 是从减法的模组 $\boldsymbol{x}-2$ 产生。我们也可以用 y.grad_fn.next_functions[0][0].variable 导出原始的张量。）
• 再度进行运算：$\boldsymbol{z} = 3\boldsymbol{y}^2$；
• 计算 $\boldsymbol{z}$ 的均值。

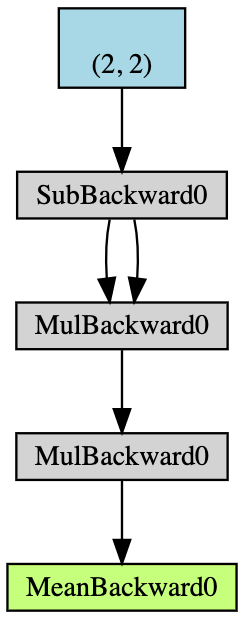
图 5：自动梯度范例的流程图

反向传播用于计算梯度。在这个例子里，反向传播的过程可视为计算梯度 $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$。如果手算 $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$ 作为验证，我们会发现执行 a.backward() 给我们的值等同于我们自己计算的 x.grad。

这里是手动进行反向传播的过程：

在 PyTorch 中，偏导数总是有与原资料相同的形状。不过雅各比矩阵其实应该是转置的。

从基础到更刺激的

考虑我们有 $1\times3$ 的向量 $x$，指定 $y$ 为 $x$ 的两倍并持续加倍直到范数不小于 $1000$。由于我们给 $x$ 的随机性，我们不能直接知道这个过程终止前经过多少次迭代。

x = torch.randn(3, requires_grad=True)

y = x * 2
i = 0
while y.data.norm() < 1000:
    y = y * 2
    i += 1

然而，靠着梯度就能简单的推测出来

gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)

print(x.grad)
tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])
print(i)
9

在推断的时后，我们可以如下地使用 requires_grad=True 来标记想要记录梯度的张量。如果我们省去 $x$ 或 $w$ 的 requires_grad=True，将造成执行时错误，由于没有梯度积累于 $x$ 或 $w$。

# Both x and w that allows gradient accumulation
x = torch.arange(1., n + 1, requires_grad=True)
w = torch.ones(n, requires_grad=True)
z = w @ x
z.backward()
print(x.grad, w.grad, sep='\n')

我们也可利用 with torch.no_grad() 来避免梯度积累：

x = torch.arange(1., n + 1)
w = torch.ones(n, requires_grad=True)

# All torch tensors will not have gradient accumulation
with torch.no_grad():
    z = w @ x

try:
    z.backward()  # PyTorch will throw an error here, since z has no grad accum.
except RuntimeError as e:
    print('RuntimeError!!! >:[')
    print(e)

更多东西－－自定梯度

此外，除了基础的数值运算，我们可以自定义模组、函数，并将其加入神经网络的图中。Jupyter Notebook 在这里。

为此，我们要继承 torch.autograd.Function 并覆盖 forward() 和 backward() 函数。举例而言，假如我们想训练网络，我们就必须取得前向传播，了解输入对输出的偏导数，如此我们才能在代码中的任何部份使用这个模组。接者，藉由反向传播（链式法则），我们可以在一连串的运算中的任何部份插入这个模组，因为我们知道了输入对输出的偏导数。

在这个案例，有三个 自定模组 在 notebook 中，分别是 add，split 和 max。例如自定的加法模组：

# Custom addition module
class MyAdd(torch.autograd.Function):

    @staticmethod
    def forward(ctx, x1, x2):
        # ctx is a context where we can save
        # computations for backward.
        ctx.save_for_backward(x1, x2)
        return x1 + x2

    @staticmethod
    def backward(ctx, grad_output):
        x1, x2 = ctx.saved_tensors
        grad_x1 = grad_output * torch.ones_like(x1)
        grad_x2 = grad_output * torch.ones_like(x2)
        # need to return grads in order
        # of inputs to forward (excluding ctx)
        return grad_x1, grad_x2

如果要将两数相加并输出，我们必须像这样覆盖 forward 函数。当我们进行反向传播，梯度会复制到两边，所以我们以复制来重写 backward 函数。

至于 split 和 max，参阅 notebook，看看我们如何覆盖 forward、backward 函数。当我们从一个东西 分割，计算梯度时要相加。对 argmax，因为它选择了最大值的索引，那个有着最大值的索引的梯度就是 $1$ 而其他是 $0$。记住，根据不同的自定模组，我们必须覆盖其前向传播与反向传播计算。