优化工具1
🎙️ Aaron Defazio梯度下降
我们以所有方法中最基本,最差的(原因后文叙述)的梯度下降法来开始我们对优化方法的学习。
问题:
\[\min_w f(w)\]迭代式:
\[w_{k+1} = w_k - \gamma_k \nabla f(w_k)\]其中,
- $w_{k+1}$ 是第$k$次迭代后的更新值,
- $w_k$是第$k$次迭代前的初始值,
- $\gamma_k$ 是步长,
- $\nabla f(w_k)$ 是$f$的梯度。
这里假设函数 $f$ 是连续且可导的。 我们的目标是找到优化方程的最低点(谷)。但是,实际到最低谷的方法是未知的。 我们只能局部地看, 因此梯度的负方向就是我们知道的最好的信息。 向那个方法移动一小步将向最小值靠近。我们每移动一小步便重新计算梯度并且再向其相反方向移动一小步,直到我们到达最低谷。因此本质上来讲,梯度下降法所作的一切就是沿着下降地最急剧的方向(负梯度)。
迭代更新式中的参数 $\gamma$ 叫做 步长。总的来说,我们不知道最佳的步长值; 所以我们必须尝试不同的值。 标准的方式是尝试一串呈对数比例的值然后使用最好的值。 这里可能会出现一些不同的情况。 上面这张图描绘了一元二次函数的情况。 如果学习率太小,那么我们将稳定地向最小值前进。 但是,这可能会比理想状态更费时。想得到一个步长值可以直接得到最小值是非常困难的(或者不可能的)。 一个比较理想的想法是得到一个比理想步长稍大一点的步长。 实际中,这样收敛最快。但是如果我们使用过大的学习率,那么将会迭代至离最小值很远导致不收敛。 在实际中,我们想使用稍小于不收敛的学习率。
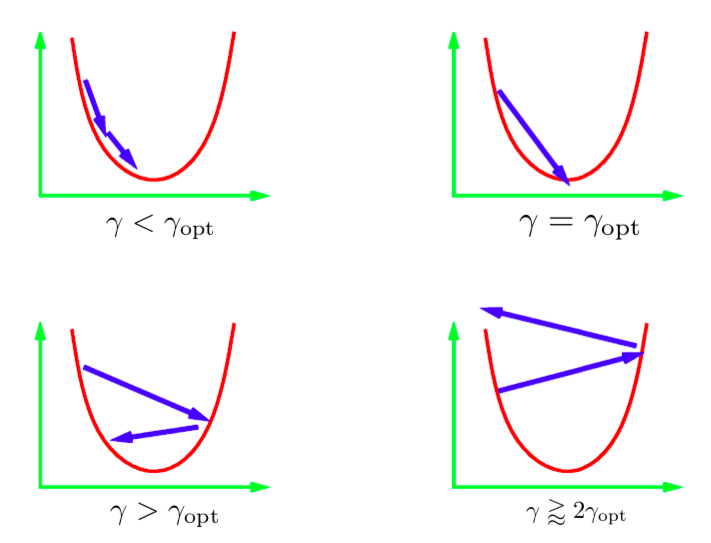
Figure 1: 一元二次函数的步长
随机梯度下降
在随机梯度下降中,我们用梯度向量的随机估计替换实际的梯度向量。 专门针对神经网络,随机估计是指单个数据点(单个实例)的损耗梯度。
令 $f_i$ 表示 第 $i$个实例的网络损失。
\[f_i = l(x_i, y_i, w)\]最终我们想最小化的函数是 $f$,表示所有实例的总损失。
\[f = \frac{1}{n}\sum_i^n f_i\]在SGD中,我们根据 $f_i$ 上的梯度(而不是总损失$ f $上的梯度)更新权重。
\[\begin{aligned} w_{k+1} &= w_k - \gamma_k \nabla f_i(w_k) & \quad\text{(i随机选择统一)} \end{aligned}\]如果 $i$ 是随机选择的, 那么 $f_i$ 是一个有噪声但无偏的$f$的估计量, 其表达式为:
\[\mathbb{E}[\nabla f_i(w_k)] = \nabla f(w_k)\]结果,SGD的预期第$k$步与完全梯度下降的第$k$步相同:
\[\mathbb{E}[w_{k+1}] = w_k - \gamma_k \mathbb{E}[\nabla f_i(w_k)] = w_k - \gamma_k \nabla f(w_k)\]因此,任何SGD更新都与预期的批次更新相同。 但是,SGD不仅具有噪声的更快的梯度下降。 除了更快之外,SGD还可以比全批次梯度下降获得更好的结果。 SGD中的噪声可以帮助我们避免浅的局部最小值,并找到更好的(较深)最小值。 这种现象称为 退火.
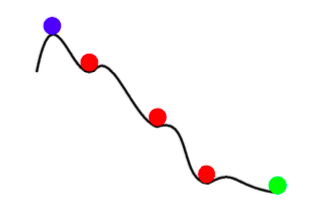
Figure 2: Annealing with SGD
总的来说,随机梯度下降的优点如下:
1.跨实例有很多冗余信息,SGD可以防止很多此类冗余计算。
- 在初期,与梯度中的信息相比,噪声较小。 因此,SGD的一步和GD的一步实际上一样好 .
- 退火 - SGD更新中的噪声可阻止收敛到坏的(浅)局部最小值。
- 随机梯度下降计算的成本大大降低(因为您无需遍历所有数据点)。
小批次处理
在小批次处理中,我们考虑多个随机选择的实例上的损失,而不是仅计算一个实例上的损失。 这样可以减少步进更新中的噪声。
\[w_{k+1} = w_k - \gamma_k \frac{1}{|B_i|} \sum_{j \in B_i}\nabla f_j(w_k)\]通常,我们可以通过使用小型批处理而不是单个实例来更好地利用我们的硬件。 例如,当我们使用单实例训练时,GPU使用率很低。 分布式网络训练技术将大型微型批处理在群集的机器之间进行分割,然后汇总生成的梯度。 Facebook最近使用分布式训练在一个小时内对ImageNet数据上的网络进行了训练。
重要的是要注意,梯度下降绝对不能用于全尺寸批次。 如果您想以完整的批次大小进行训练,请使用一种称为LBFGS的优化技术。 PyTorch和SciPy都提供了该技术的实现。
动量
在动量中, 我们有两个迭代($p$ 和 $w$),而不仅仅是一个。 更新式如下:
\[\begin{aligned} p_{k+1} &= \hat{\beta_k}p_k + \nabla f_i(w_k) \\ w_{k+1} &= w_k - \gamma_kp_{k+1} \\ \end{aligned}\]$p$ 称作 SGD 动量. 271/5000 在每个更新步骤中,我们将动量的旧值减去系数$\beta$(0到1之间的值),然后将其添加到动量的旧值。 可以将$ p $视为梯度的平均值。 最后,我们向新动量$p$的方向移动$w$。
替代形式:随机重球法
\[\begin{aligned} w_{k+1} &= w_k - \gamma_k\nabla f_i(w_k) + \beta_k(w_k - w_{k-1}) & 0 \leq \beta < 1 \end{aligned}\]该形式在数学上与先前的形式等价。 在这里,下一步是上一步的方向($ w_k-w_ {k-1} $)和新的负梯度的组合。
直观
SGD动量类似于物理学中的动量概念。优化过程就像一个沉重的球滚下山坡,动量使球保持与已经移动的方向相同的方向,梯度可以认为是沿其他方向推动球的力。

Figure 3: 动量的影响
Source: distill.pub
动量并没有使行进方向发生巨大变化(如左图所示),而是产生了适度的变化。 动量可减轻仅使用SGD时常见的振荡。
$\beta$参数称为阻尼因子。$\beta$必须大于零,因为如果它等于零,那么你只是在进行梯度下降; 它也必须小于1,否则一切都会崩溃。 $\beta$的值较小会导致方向更改更快。 对于较大的值,转向需要更长的时间。
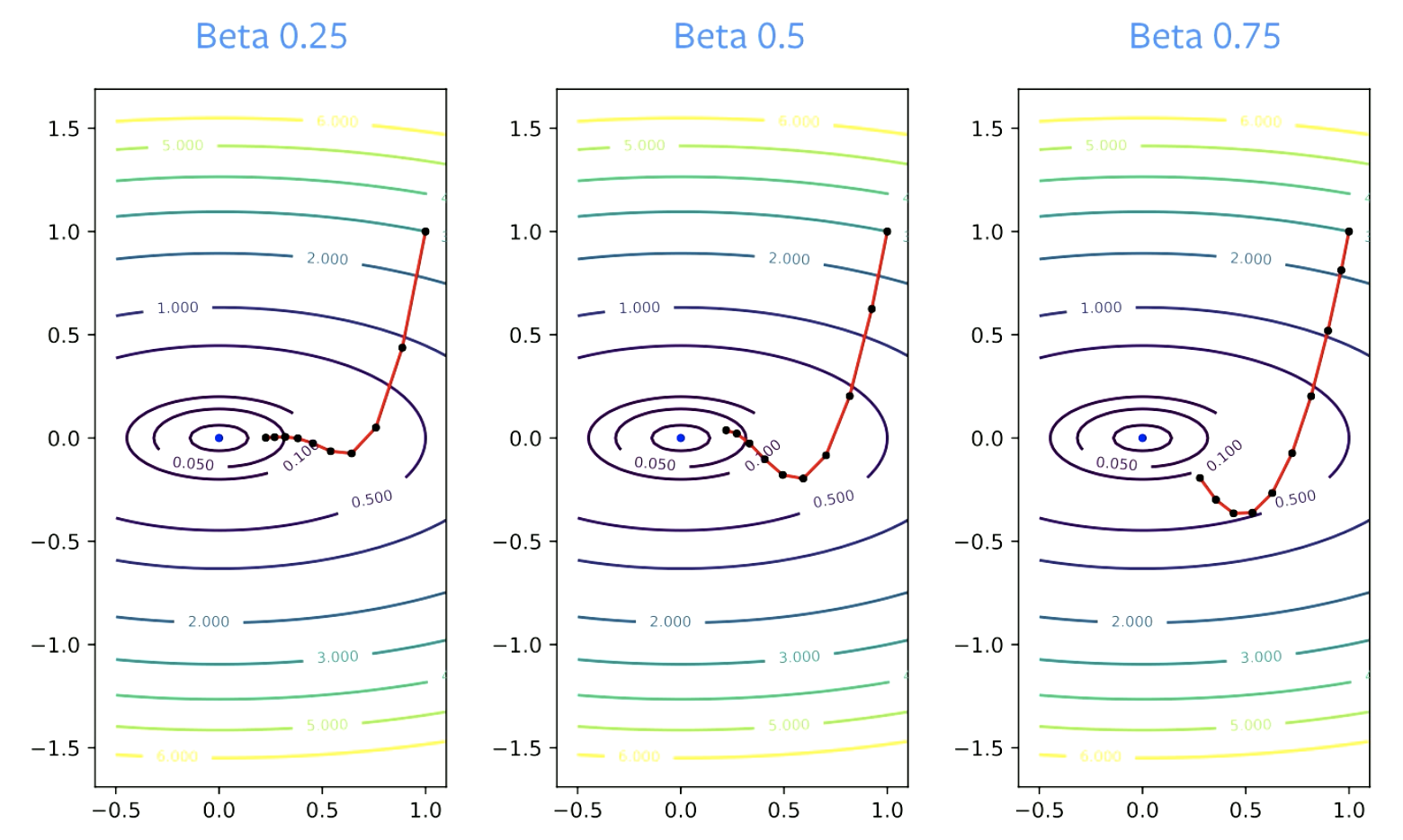
Figure 4: Beta对收敛的影响
实用指南
动量必须总是与随机梯度下降一起使用。 $\beta$ = 0.9或者0.99 基本上效果会很好。
当增加动量参数以保持收敛时,通常需要减小步长参数。 如果$\beta$从0.9变为0.99,则学习率必须降低10倍。
为什么动量有用?
加速
以下是涅斯捷罗夫动量的更新规则。
\[p_{k+1} = \hat{\beta_k}p_k + \nabla f_i(w_k) \\ w_{k+1} = w_k - \gamma_k(\nabla f_i(w_k) +\hat{\beta_k}p_{k+1})\]使用涅斯捷罗夫动量,如果你非常仔细地选择常数,则可以加快收敛速度。 但这仅适用于凸问题,不适用于神经网络。
许多人说,正常的动量也是一种加速的方法。 但实际上,它仅对二次方加速。 此外,由于SGD带有噪音,加速不适用于SGD,因此不适用于SGD。 因此,尽管Momentum SGD有一些加速作用,但仅凭它并不能很好地解释该技术的高性能。
噪声平滑
可能一个更实际和更可能动量效果很好的原因是噪声平滑。
动量平均梯度。 这是我们用于每个步骤更新的渐变的平均值。
从理论上讲,为了使SGD能够正常工作,我们应该对所有步骤进行平均。
\[\bar w_k = \frac{1}{K} \sum_{k=1}^K w_k\]SGD具有动量的优点在于,不再需要进行平均。 动量为优化过程增加了平滑度,从而使每次更新都很好地接近了解决方案。 使用SGD,你需要平均一堆更新,然后朝这个方向前进一步。
加速和噪声平滑都有助于提高动量性能。
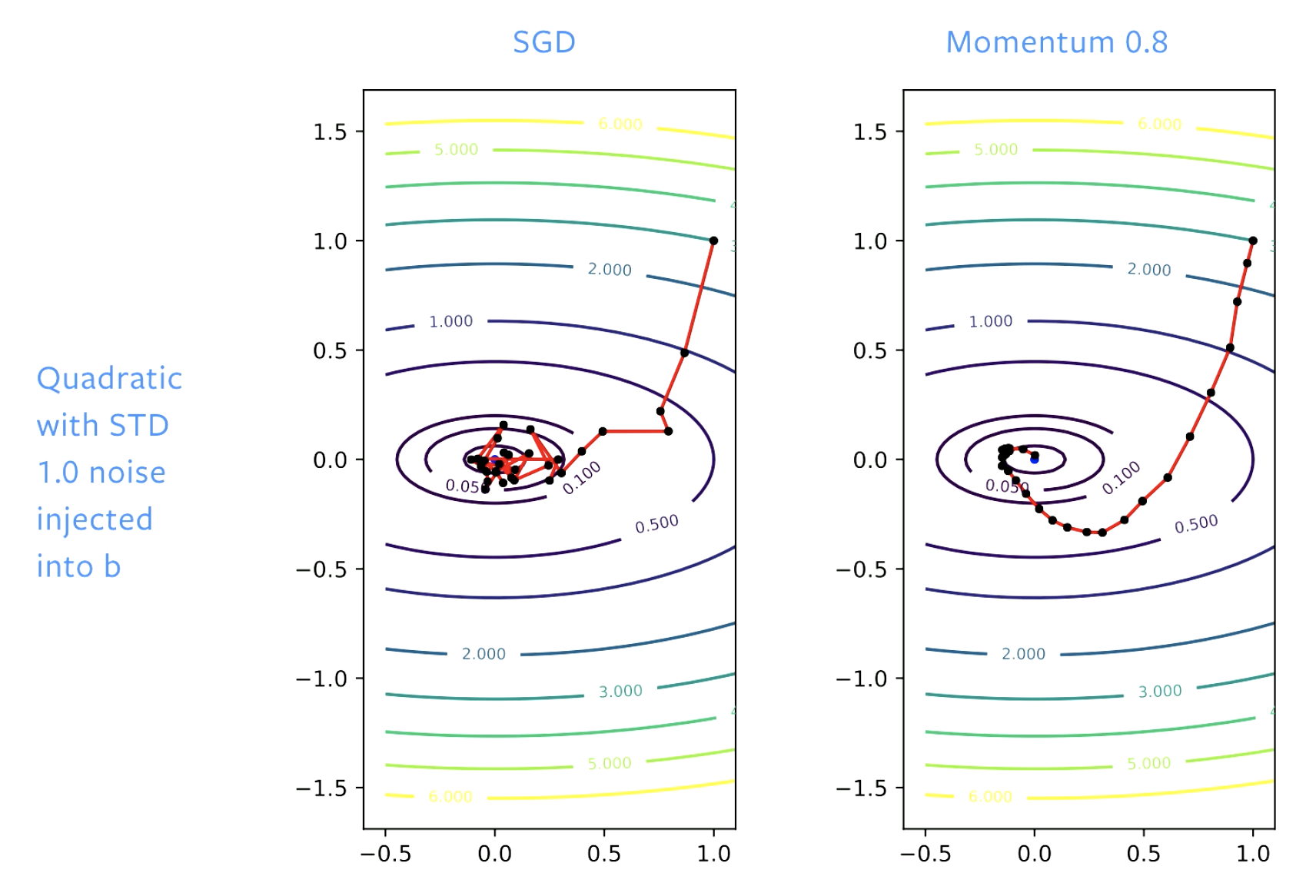
Figure 5: SGD vs. Momentum
使用SGD,我们最初在解决方案方面取得了良好的进展,但是当我们到达函数最低区域(谷底)时,我们会在此反弹。 如果我们调整学习率,我们的反弹速度将会变慢。 有了动量,我们就使步伐变得平稳,以至于没有反弹发生。
📝 Vaibhav Gupta, Himani Shah, Gowri Addepalli, Lakshmi Addepalli
Shengkun Tang
24 Feb 2020