神经信号的性质

神经信号的性质

所有的信号都可以被看作向量。例如音频信号是一个一维信号$\boldsymbol{x} = [x_1, x_2,…,x_T]$ 其中每个数值$x_t$代表了在时间点$t$上波形的振幅。为了理解某人在说什么，你的耳蜗首先会将空气压力的变化转化为信号，然后你的大脑使用一个语言模型将这个信号转化成一种语言也就是说大脑需要从信号中挑选最有可能的表达。对于音乐而言这种信号是环绕立体的，也就是拥有两个或更多的通道以此让你产生声音从不同方向传输而来的感觉。即使它拥有两个通道，它还是一个一维信号，因为信号仅随着时间变化。

一张图片是一个二维信号因为信息是空间性得被描绘的。需要注意的是，每个点自身都是一个向量。这意味着如果我们在图片中有$d$个通道，图片中的每一个点都是一个$d$维向量。对一张RGB形式的彩色图片，这意味着$d = 3$。对任何一个点$x_{i,j}$，向量的数值依次对应了红，绿和蓝的强度。

我们可以用上面的方法来表达语言。每一个词都对应一个one-hot向量，对应该单词在词典中的位置为1其余位置均为0。这意味着每个词都是一个词典大小的向量。

神经信号拥有以下一些性质:

1. 固定性: 某些序列在信号中重复出现。在音频信号中，我们观察到同样种类的模式在当前区域中反复出现。在图像中，这意味着我们可以预见相似的图案在不同维度上重复。

1. 区域性: 相互靠近的点相比远离的点更加相关了。对一维信号，这意味着如果我们观察到了一个波峰在点$t_i$，我们可以预期在该点周围的一个极小窗口中的点会拥有类似的值，而对于一个远离的点$t_j$两者的值关系不大。更正式的表述是，如果一个信号与其翻转版本完美重合，那么他们的卷积会存在一个波峰。两个一维信号的卷积(交叉相关)无外乎是二者的点乘，即描述二者如何相似或相近。所以信息是被保存在信号中特定的部分中。对于图像，这意味着两个点之间的相关性随着其距离的远离而降低。如果像素$x_{0,0}$是蓝色的，那么下一个像素($x_{1,0},x_{0,1}$)为蓝色的概率会比较高，而如果你看向图片的另一端($x_{-1,-1}$)，这个像素的值就与$x_{0,0}$的值无关。

2. 组合性: 小的部件组成大的部件，这个过程往复循环就形成了自然界中的万物。例如，字符可以形成字符串，而字符串形成了单词，单词的组合形成了句子。众多的句子形成了文章。这种组合性让世界是可解释的。

如果我们的数据展现了如上三种特性，我们就可以用稀疏的，参数共享的并由堆积层形成的网络来探索它。

探索自然信号的特性以建立不变性和同变性

区域性 $\Rightarrow$ 离散型

图1展现了一个5层全连接网络。每一个箭头代表了一个被输入乘上的权重。如我们所见，这个网络非常消耗算力。

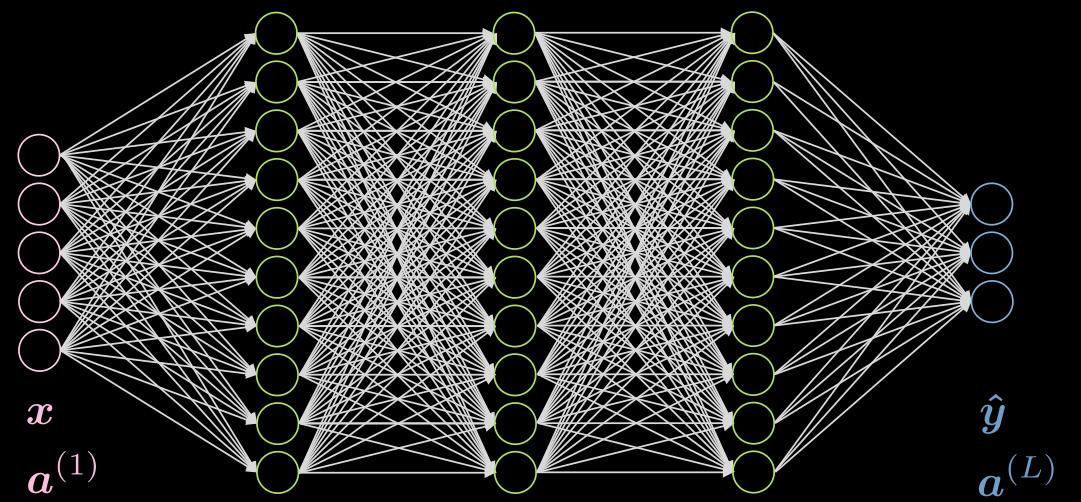
Figure 1: Fully Connected Network

如果我们的数据展现了区域性，每一个神经元只需要与附近的一些上一层的神经元相连。所以，如图二所示某一些连接是可以被去除的。图二a代表了一个全连接网络。利用数据的区域性，我们在图二b中丢弃一些较远的神经元之间的连接。尽管图二中的隐藏层中的绿色神经元没有覆盖整个输入，但是整个架构有能力解释所有的输入神经元。感受野(RF)的大小由前一层的神经元数目决定，也就是说每个特定层中的神经元都被考虑在内了。所以输出层对于隐藏层的感受野为3，隐藏层对于输入层的感受野是3，但是输出层对于输入层的感受野是5.

Figure 2(a): Before Applying Sparsity	Figure 2(b): After Applying Sparsity

固定性 $\Rightarrow$ 参数共享

如果我们的数据展现了固定性，我们可以在网络结构中多次使用参数中的一个小子集。例如在我们的稀疏网络图三a，我们能使用黄、橙、红三个共享参数的集合，那样参数的数目就会从9降到3！新的网络甚至可能会表现得更好，因为我们有更多数据来训练参数。具有区域性和固定性的权重参数就被称为卷积核。

Figure 3(a): Before Applying Parameter Sharing	Figure 3(b): After Applying Parameter Sharing

使用稀疏性和参数共享有如下优势:-

• 参数共享
  • 更快得收敛
  • 更好的泛化性
  • 不被输入大小限制
  • 卷积核独立 $\Rightarrow$ 高并行度
• 连接稀疏
  • 减少计算量

图四显示了一个在一维数据上的核的例子。其中核的尺寸为: 2(核的个数) * 7(前一层的厚度) * 3(唯一的连接/权重的数目)。

对于核尺寸的选择是经验性的。3 * 3大小的卷积似乎是应用在空间数据上的最小尺寸。大小为1的卷积可以被用来得到一个能被应用到更大的输入图像上的最后一层。尺寸为偶数的核可能会降低数据质量，所以我们通常会选择技术作为核的尺寸，通常为3或者5。

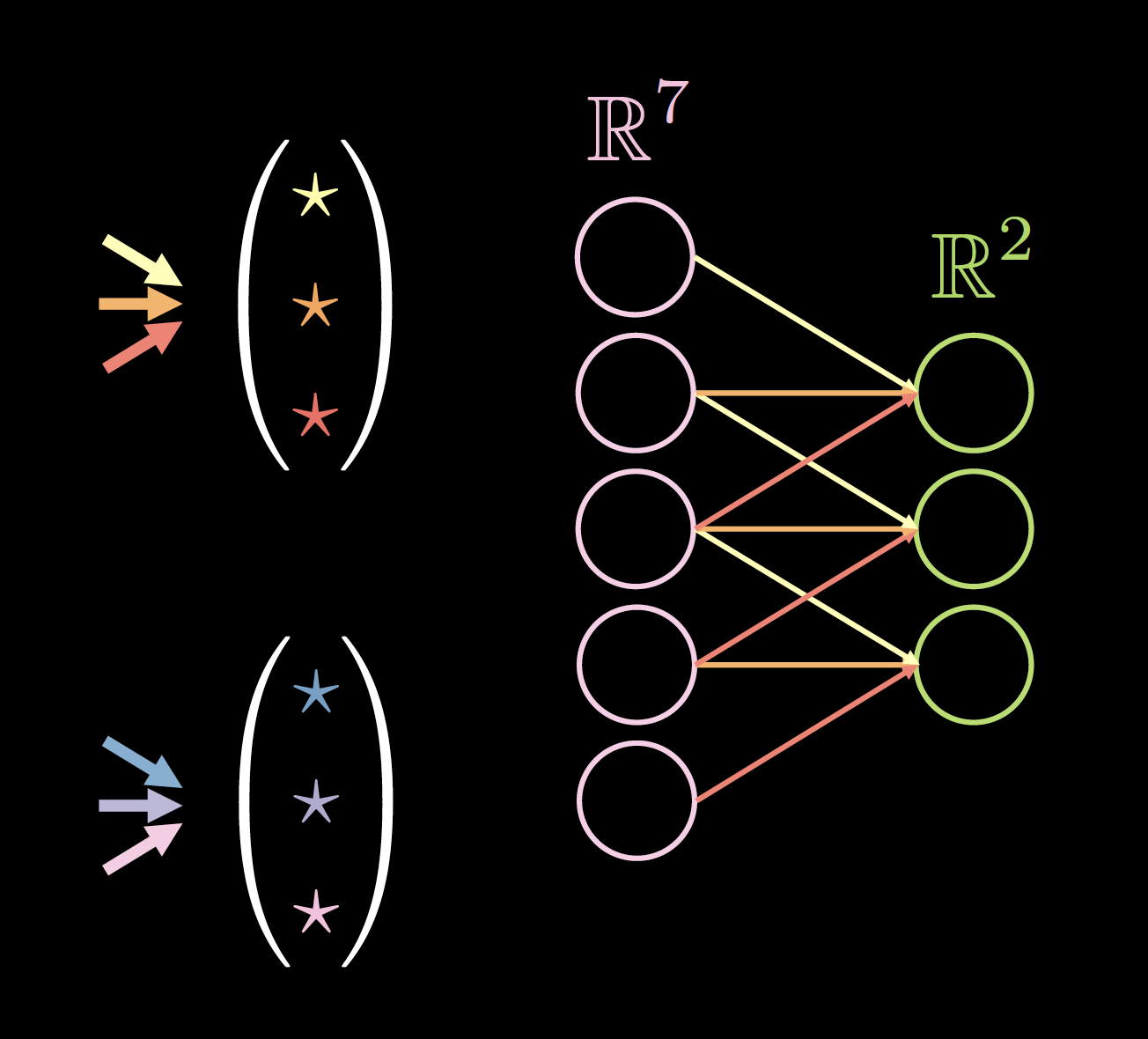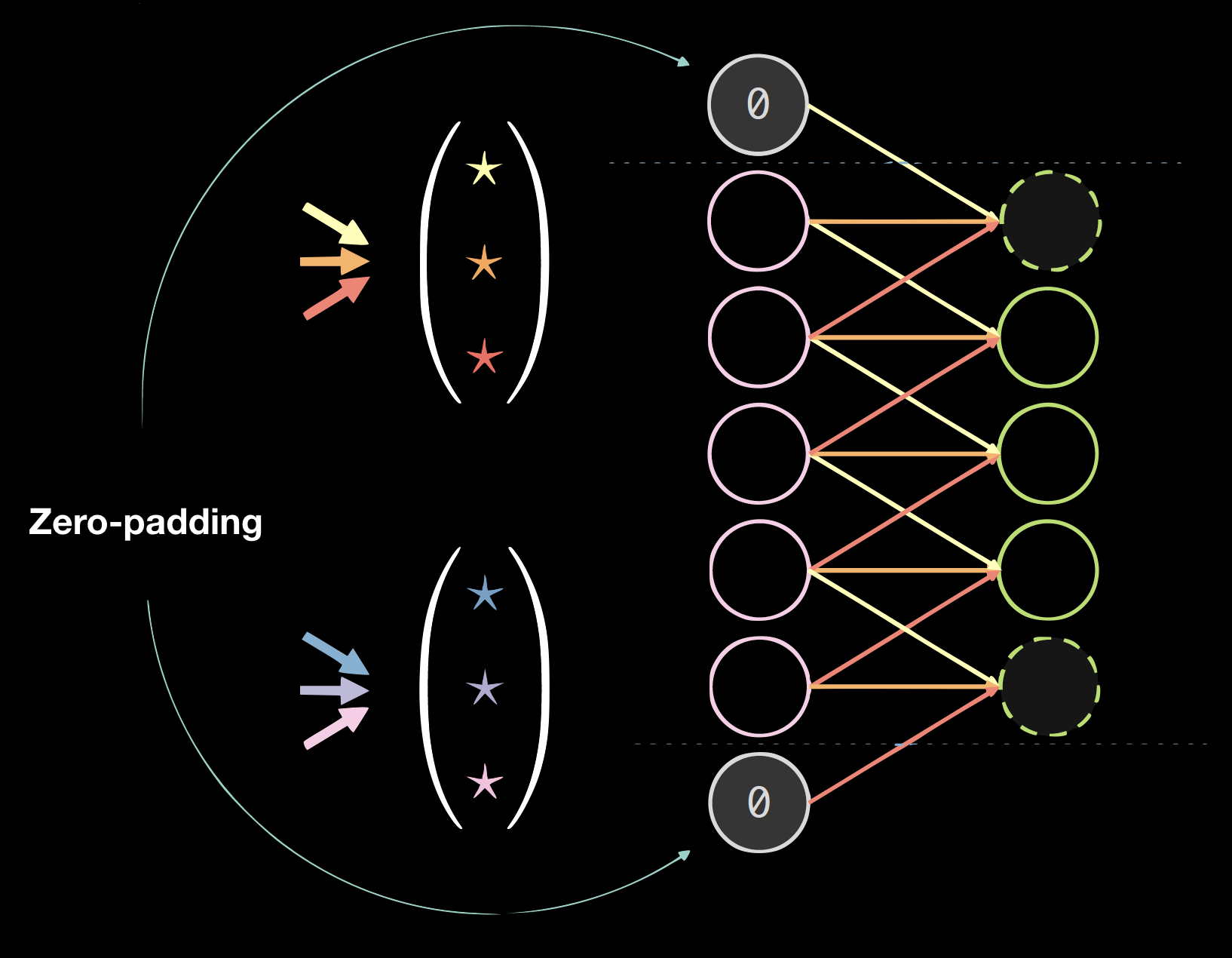Figure 4(a): Kernels on 1D Data	Figure 4(b): Data with Zero Padding

填充

填充通常会伤害最终结果，但是很编程便利。我们一般使用0值填充即: size = (kernel size - 1)/2。

Standard spatial CNN

标准的面向空间数据CNN

一个标准的面向空间数据的CNN有如下性质:

• 多种层
  • 卷积层
  • 非线性层 (ReLU and Leaky)
  • 汇合
  • 批量归一化
• 残差跨层的连接

批量归一化和残差跨层连接对网络训练是很有帮助的。 如果太多层堆叠，信号的一部分信息会在这个过程中丢失。所以通过残差绕过在层之间的额外连接能够保证从底部到顶部的路径，也就形成一个梯度从顶到底的传播路径。

在图五中，尽管输入图像主要包含横跨两个维度的空间信息(除了典型的信息，即每个像素包含的颜色信息)，输出层却是比较厚的。在网络中存在空间信息和典型信息直接的权衡使得表征变得稠密。所以当我们沿着层级结构向上的时候，我们会得到更加稠密的表征同时会市区空间信息。

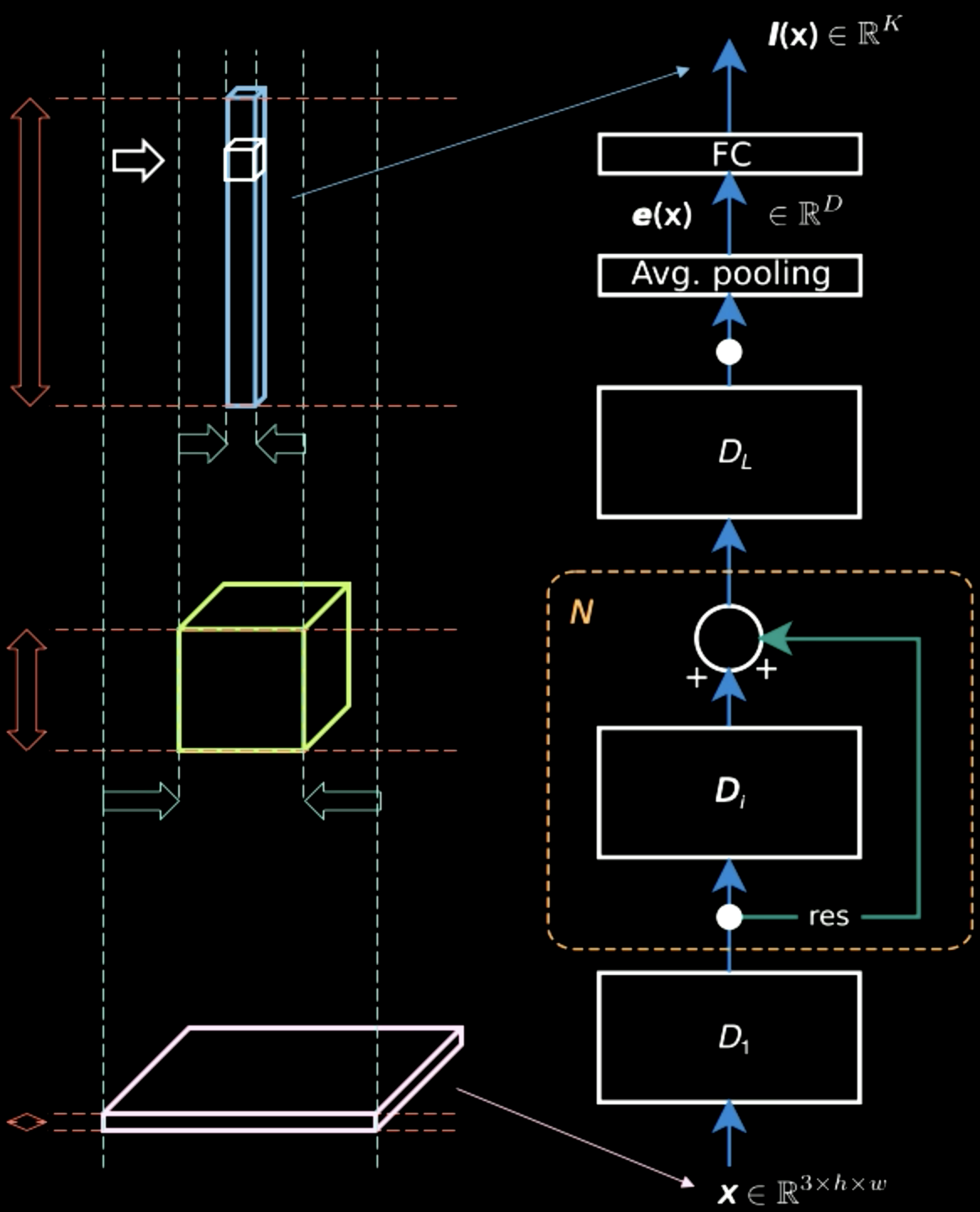
Figure 5: Information Representations Moving up the Hierachy

汇合

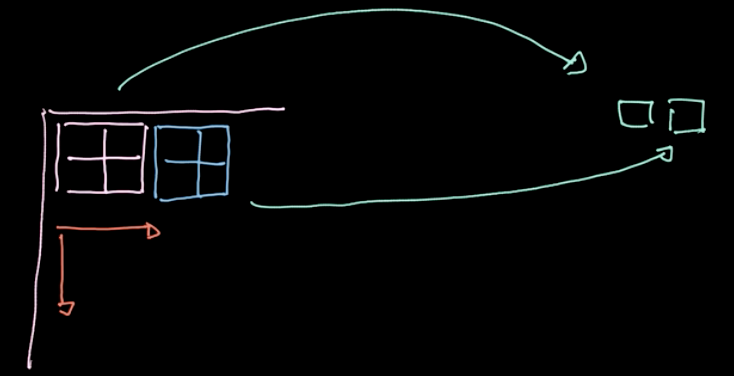
Figure 6: Illustration of Pooling

如图六所示，一个特定的算子,$L_p$-norm,被应用在不同的区域上。这个算子对每个区域只给出一个值(在我们的例子中，每四个像素产生一个值)。我们依次在每个区域数据上按照步进移动循环这个操作。如果我们有一个$m * n$大小$c$个通道的数据，我们最后会获得$\frac{m}{2} * \frac{n}{2}$ 大小$c$个通道的数据(见图七)。汇合不是一个参数化的操作；尽管如此，我们能选择不同的汇合的种类，例如最大值汇合，均值汇合等等。汇合的主要目的是减少数据量这样我们就可以在合理的时间中完成计算。

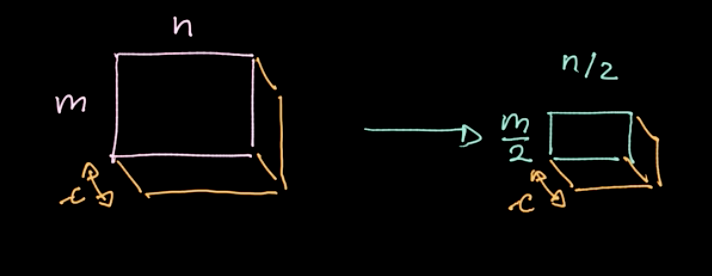
Figure 7: Pooling results

CNN - Jupyter Notebook

Jupyter notebook可以在链接中找到here. 运行notebook需要确保你已经安装 pDL 环境，具体内容参考README.md。

在这个notebook中，我们训练了一个多层感知器(全连接网络)和一个卷积神经网络(CNN)来完成在MNIST数据集上的分类任务。需要注意的是，两个网络都有相同数目的参。(图八)

Figure 8: Instances from the Original MNIST Dataset

在训练之前，我们标准化数据使得网络的初始化能够与数据分布吻合(重要！)。同时，保证下列的五个运算/步骤被包含在你的训练中:

1. 输入数据到模型。
2. 计算损失。
3. 使用zero_grad()清除累积的梯度的缓存。
4. 计算梯度。

5. 在优化器方法中执行一步操作。 <!– Before training, we normalize our data so that the initialization of the network will match our data distribution (very important!). Also, make sure that the following five operations/steps are present in your training:

6. Feeding data to the model
7. Computing the loss
8. Cleaning the cache of accumulated gradients with zero_grad()
9. Computing the gradients
10. Performing a step in the optimizer method –>

首先我们在标准化的MNIST数据上训练两个网络。全连接网络的精确度为$87\%$而CNN的精确度为$95\%$ 。在同样数目的参数条件下，CNN能够训练更多的过滤器。在全连接网络中，训练得到的过滤器试图获得远离的点和靠近的点之间的关系。这些过滤器是完全被浪费的。相反的，在卷积网络中，所有这些参数都专注于相邻像素的关系。

下一步，我们在整个数据集上的所有像素上执行一次随机组合。这讲图八转变为图九。然后我们在改动过的数据集上训练两个网络。

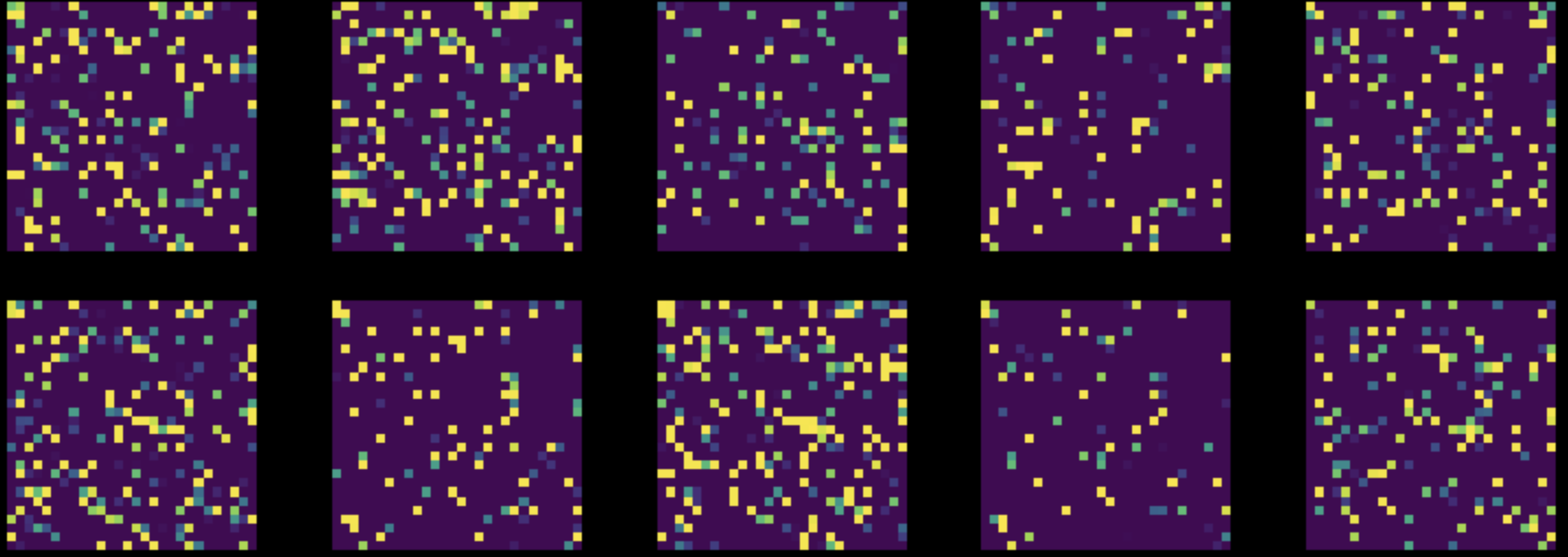
Figure 9: Instances from Permuted MNIST Dataset

全连接网络的表现保持不变($85\%$)，但是CNN的精确度下降到了$83\%$。这是因为，经过一次随机排列，图片再也不保持区域性，固定性和组合性这三个被CNN利用的性质。