神经网络参数变换可视化及卷积的基本概念

神经网络的可视化

在这一节，我们将展示神经网络的可视化以及线性变换和ReLU操作的效果

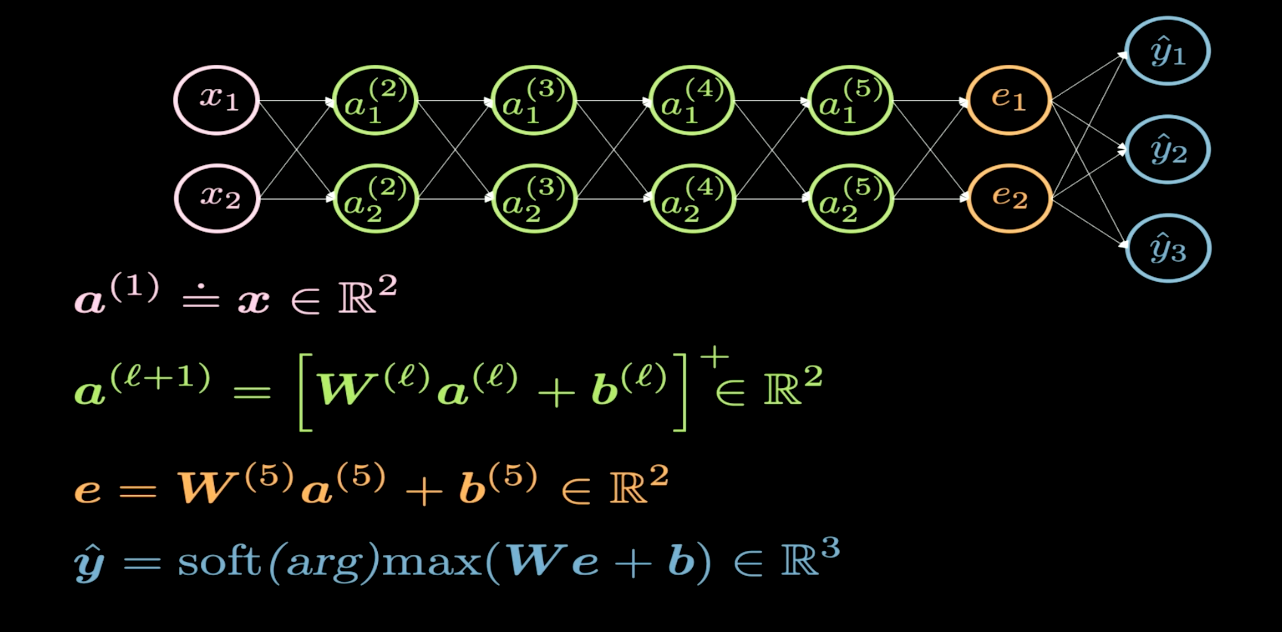
Fig. 1 网络结构

图1是一个神经网络的可视化表示。一般来说，神经网络的输入位于图的底部或者左侧，而输出位于图的顶部或者右侧。在图1中，粉色的神经元是输入，蓝色的神经元是输出。在这个网络中，我们有4个隐藏层，这意味着整个网络总共有6层（4个隐藏层 + 1个输入层+1个输出层）。我们使用$2\times2$矩阵作为权重矩阵$W$。这是因为我们希望将输入平面变换为另一个平面。而线性变换则包括切变、旋转、反射和缩放。

Fig. 2 折叠空间的可视化

每层的变换类似于将我们的平面折叠进如图2所示的一些特定区域。在实验中我们发现，如果每个隐藏层仅仅有两个神经元，则优化过程会变长；而如果在隐藏层中有更多神经元，则优化过程会变得容易。那么问题来了：为何较少的神经元数量会让训练变得困难？我们将在可视化$\texttt{ReLU}$之后回答这个问题。

(a)	(b)

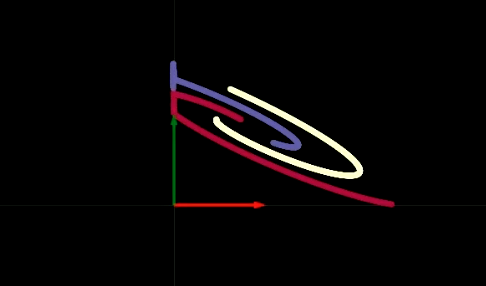
当我们分离每个隐藏层，我们会发现每一层都执行了线性变换中的某些步骤，然后再执行可将负值转化为零的ReLU操作。在图3(a)(b)中，我们可以观察到ReLU操作的可视化效果。ReLU操作为我们执行了非线性变换。经过一些变换之后，我们最终将得到如图4所示的线性可分的数据。

Fig. 4 输出的可视化

那么现在我们终于知道了两个神经元的隐藏层难以训练的原因。在我们的6层网络中，每个隐藏层都具有一个偏移。因此如果其中一个偏移将数据点移出右上象限，那么ReLU操作将使这些点变为零。之后，无论后续的层如何变换，那么该值将一直保持零。为了让神经网络更容易训练，我们可以通过在隐藏层中添加更多的神经元让网络变宽，也可以通过添加更多的隐藏层，亦或者使用两个方法的组合。在剩下的学期中，我们将深入探索网络的最佳架构是什么这个主题，请保持关注。

参数变换

一般的参数变换意味着我们的参数向量$w$是一个函数的输出。通过这个变换，我们可以将原始参数空间映射到另一个空间。在图5中，$w$是含参数$u$的$H$的输出。$G(x,w)$是一个网络，而$C(y,\bar y)$则是代价函数。反向传播公式也做了如下改变：

这些公式以矩阵形式应用。注意，右边的项的维度需要保持协调。$u$,$w$,$\frac{\partial H}{\partial u}^\top$,$\frac{\partial C}{\partial w}^\top$的维度分别是$[N_u \times 1]$,$[N_w \times 1]$,$[N_u \times N_w]$,$[N_w \times 1]$。因此反向传播公式的维度是协调一致的。

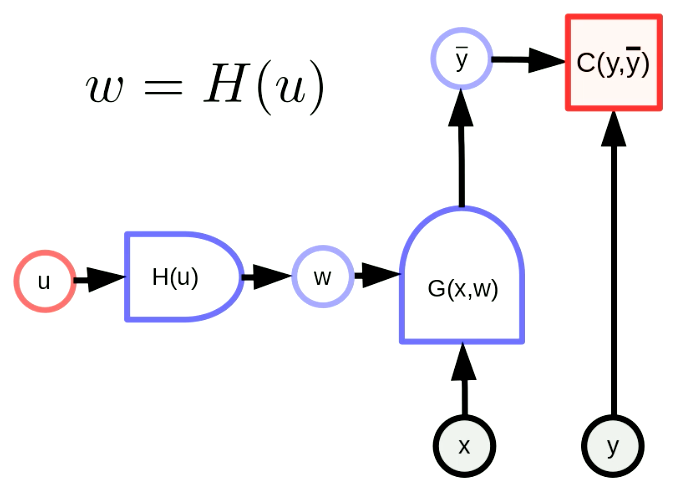
Fig. 5 参数变换的一般形式

一个简单的参数变换：权重共享

权重共享变换意味着$H(u)$只是将$u$的一个分量复制为$w$中的多个分量。 $H(u)$就像一个Y形分支，将$u_1$复制到$w_1$, $w_2$。我们可以将其表达为，

我们强制共享参数保持相等，因此关于共享参数的梯度将在反向传播中被求和。举个例子，代价函数$C(y, \bar y)$关于$u_1$的梯度是代价函数$C(y, \bar y)$关于$w_1$的梯度和代价函数$C(y, \bar y)$关于$w_2$的梯度之和。

超网络

超网络是指网络的其中一个网络权重是另一个网络的输出。图6显示了一个“超网络”的框架。其中，函数$H$作为一个网络具有参数向量$u$和输入$x$。因此$G(x,w)$的权重是通过网络$H(x,u)$动态配置的。这个想法虽然古老，但即使在现在也非常有效。

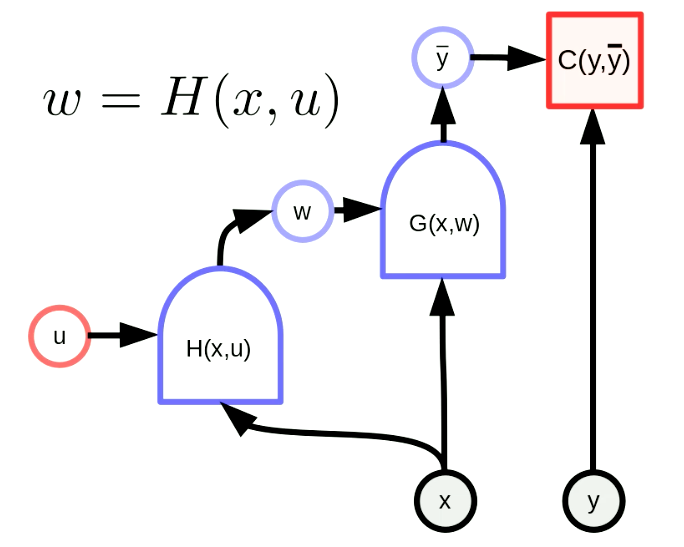
Fig. 6 "超网络"

序列数据中的主题检测

权重共享变换可被用于主题检测。主题检测表示在序列数据中找出某些主题，比如在语音或者文本数据中找出关键词。如图7所示，一种解决方案是在数据上使用滑动窗口，即通过移动权重共享函数来检测特定的主题（即语言信号中的一组特定声音），然后将输出（即评分）传给最大值函数。

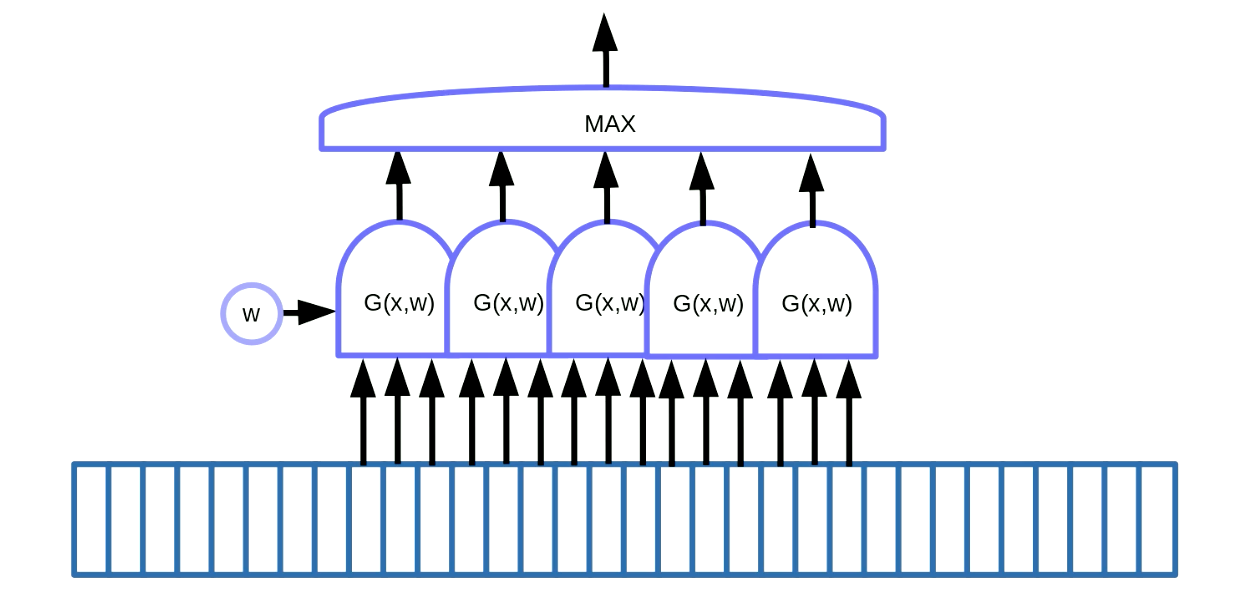
Fig. 7 序列数据的主题检测

在这个例子中，我们有5个这样的函数。这个方案的结果就是，我们对5个梯度求和并进行反向传播计算。我们不想要这些梯度隐式累加，因此我们需要使用PyTorch中的zero_grad()来初始化梯度。

图像中的图案检测

另一个有用的场景是图像中的图案检测。我们经常通过在图片上刷动我们的“检测模板”进行形状检测，而这并不依赖于形状的位置和形变。一个简单的例子如图8所示，即对字母”C”和”D”进行区分。”C”与”D”的区别在于”C”拥有两个端点，而”D”则有两个拐角。因此我们可以基于此设计“端点模板”和“拐角模板”。如果形状与模板相似，则会有阈值输出。然后我们可以通过对这些输出求和以区分字母。在图8中，该网络检测到两个端点和0个拐角，因此答案“C”被激活。

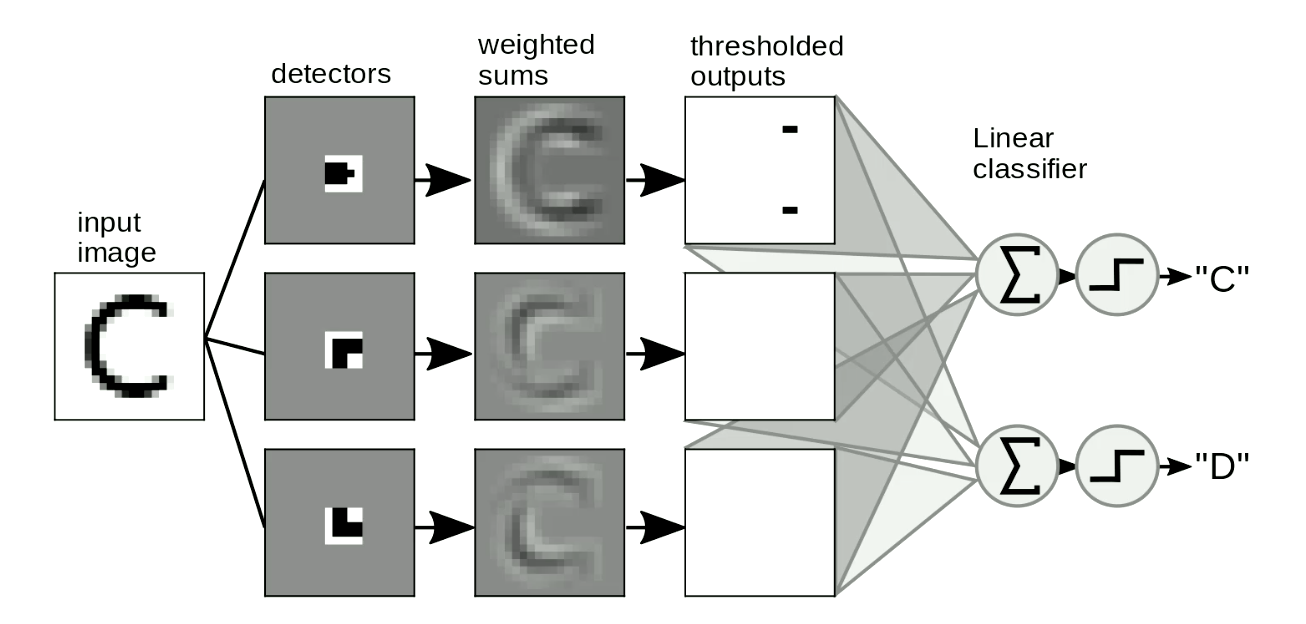
Fig. 8 图像中的图案检测

这里同样重要的是，我们的“模板匹配”应该是平移不变的 - 即当我们对输入进行移位，输出或者说被检测到的字母不应该改变。这在权重共享变换中被完美解决。如图9所示，当我们改变“D”的位置，我们依然可以检测到拐角图案，即使它们已经被移位。当我们对检出的图案进行求和，“D”的检测将被激活。

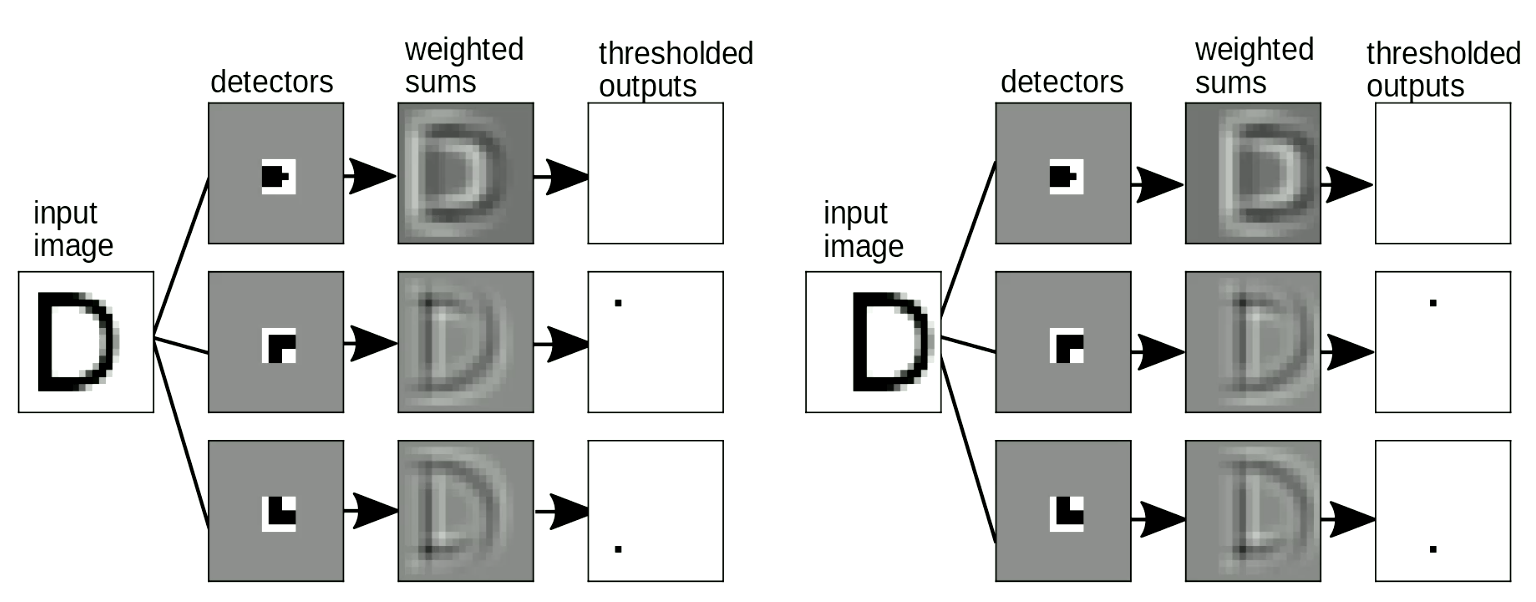
Fig. 9 平移不变性

使用局域检测器，然后对所有检测进行求和来检测图像中的字母，这是一种我们已经使用了多年的手工规则方法。而这就带来一个问题：我们如何能够自动设计这些“检测模板”呢？我们能够使用神经网络来学习这些“检测模板”吗？接下来我们将会介绍卷积，即我们用“检测模板”来匹配图片的操作。

离散卷积

卷积

1维情况下，输入$x$和$w$之间卷积的精确数学定义是：

也就是说，第$i$个输出是翻转的$w$和$x$上同样大小的滑窗之间的点积。为了计算完整的输出，我们从起始位置运行滑窗，每次移动该滑窗一个单元的位置，一直重复，直到滑遍$x$。

互相关

实际上，在PyTorch这样的深度学习框架中使用的卷积定义会有一点点不一样。PyTorch中的卷积实现上，$w$并没有进行翻转：

数学家称这个公式为“互相关”。这两个形式在这里只是约定不同而已。实际上，如果我们前向或者反向读取内存中的权重的时候，互相关和卷积是可以互换的。

但有的时候，比如当我们在数学文献中想要利用卷积/互相关的某些数学性质的时候，知道这个区别则是非常重要的。

高维卷积

对于像图像这样的二维输入，我们可以使用卷积的二维版本：

这个定义可以从二维，类似地扩展到三维、四维。这里，$w$被称为卷积核

在深度卷积神经网络(DCNN)中，卷积操作中可用的一般变化

1. 步幅: 前文提到，在$x$中的滑窗每次移动都是一个单位，但是其实我们也可以增大步长（比如每次两个、三个单位）。举例来说：假设输入$x$为1维，大小为100且$w$的尺寸为5。那么使用1或者2为步幅的输出尺寸如下表所示：

1. 填充: 在设计深度神经网络架构的时候，我们经常希望卷积的输出与输入保持相同尺寸。而这可以通过对输入填充一些零单元（通常情况下）完成，一般是两边都进行填充。填充一般是为了方便。它有时会影响一些性能，还会产生一些有趣的边界效应，但即便如此，当非线性变换为ReLU时，其实零单元填充是合理的。

深度卷积神经网络 (DCNNs)

正如前文所述，深度神经网络是由线性操作和逐点非线性层重复交替组成的。在卷积神经网络中，线性操作就是上面描述的卷积操作。需要注意的是，这里还有一种第三类层称之为汇合层（这是可选的层）。

之所以去堆叠这些层的原因是我们想要构建数据的一个层次化表征。 卷积网络不是只局限于处理图像，它们同样被成功地应用于语音和语言。技术上来看，它们适用于任意数组形式的数据类型。当然，这些数组需要满足一些特定的性质。

那么为什么我们需要获取世界的层次化表征呢？因为我们生活的世界是组合的。这个观点在前文中有提及。这样的层次化的特性可以从很多事实中观察到。比如，局域像素汇集形成如有向边这样的简单样式，而这些边又进一步汇集形成更加抽象的图样。这样的层次组合不断进行，直到我们在现实中看到的部分物体、整个物体最终形成。

Figure 10. 在ImageNet上训练的卷积网络的特征可视化，取自 [Zeiler & Fergus 2013]

这个在自然世界里观察到的组合的层次化特性，不只是因为我们视觉感知到如此，这在物理层面上也是事实。在物理学描述的最低层次，我们拥有基本粒子，这些基本粒子形成原子，原子形成分子，这个过程持续，最终构成各种材料，物体的局部，直到各种物理世界中的物体。

世界的这个组合的特性可能可以回答爱因斯坦关于人类如何理解他们生存的世界之经典感叹。

这个宇宙最不能被理解之处是它居然可以被理解。

幸亏这样的组合性质人们才能够理解世界，这个事实对Yann来说似乎仍然像一个共谋之事。如果世界没有组合性，那么也许理解我们这个世界将会需要更多的魔法。这里，我们引用伟大的数学家Stuart Geman的一句话：

要不这个世界就是组合而成的，要不则存在上帝。

来自生物学的灵感

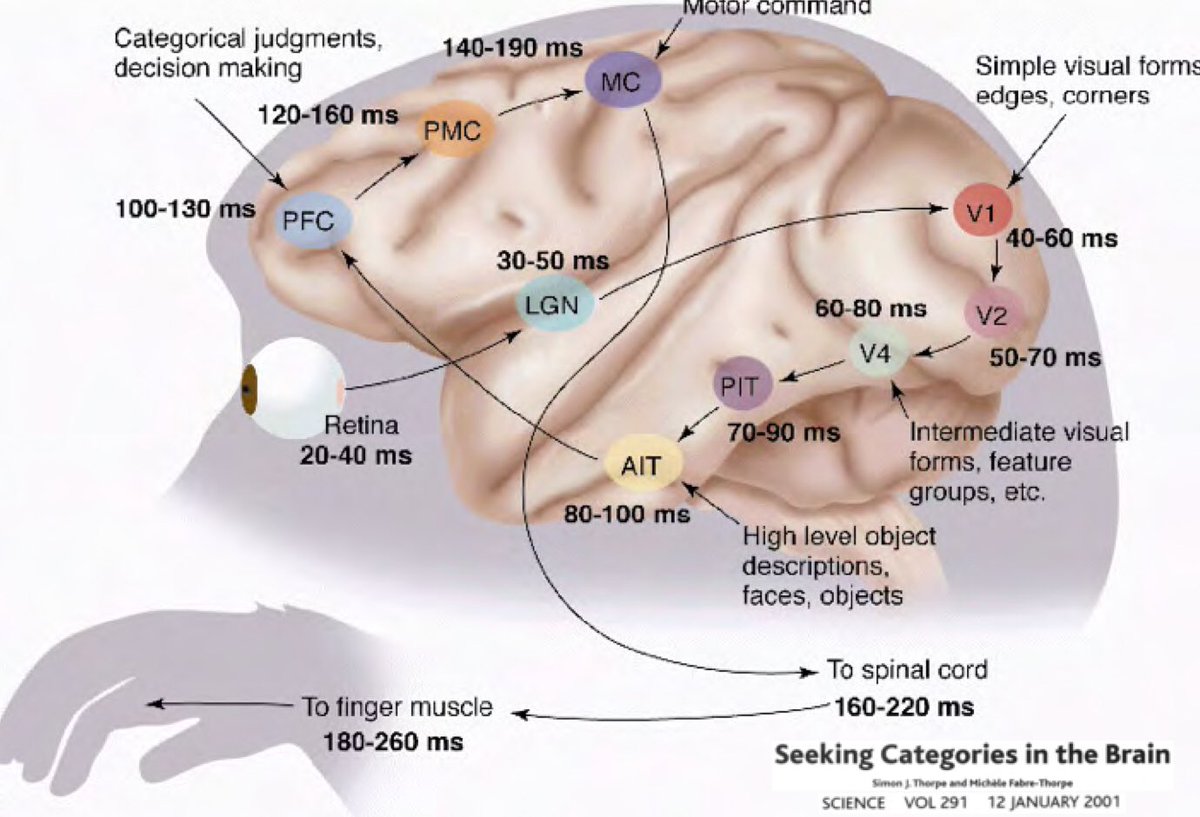
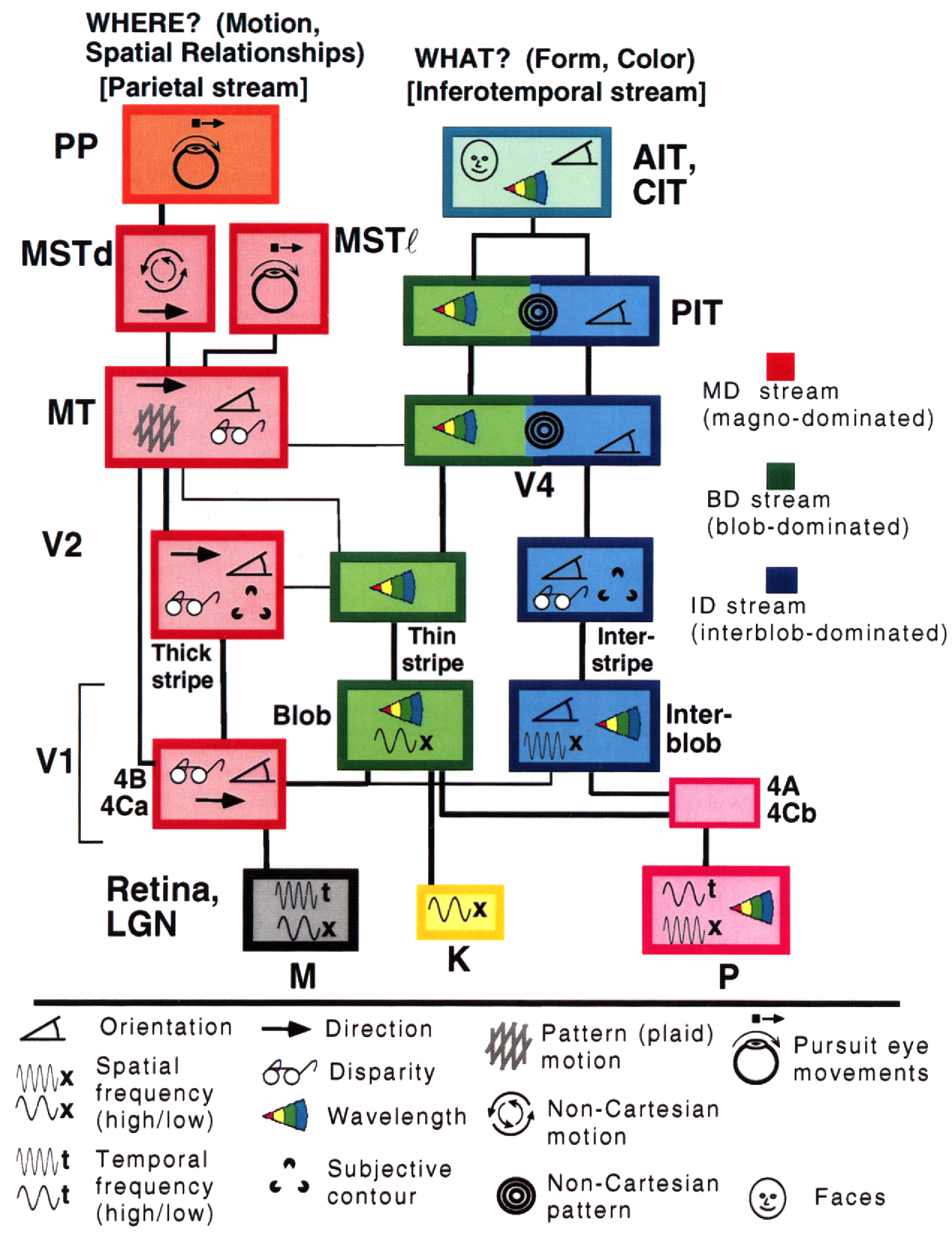
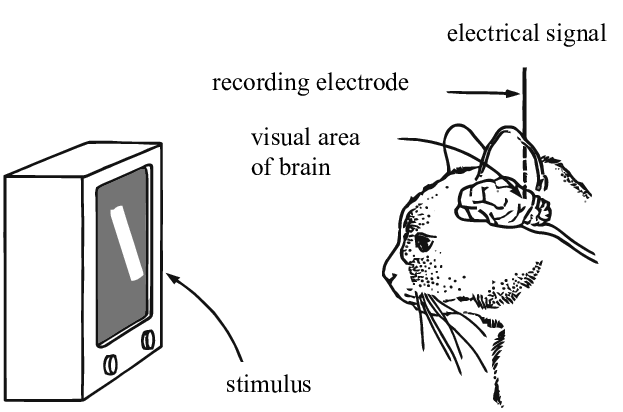
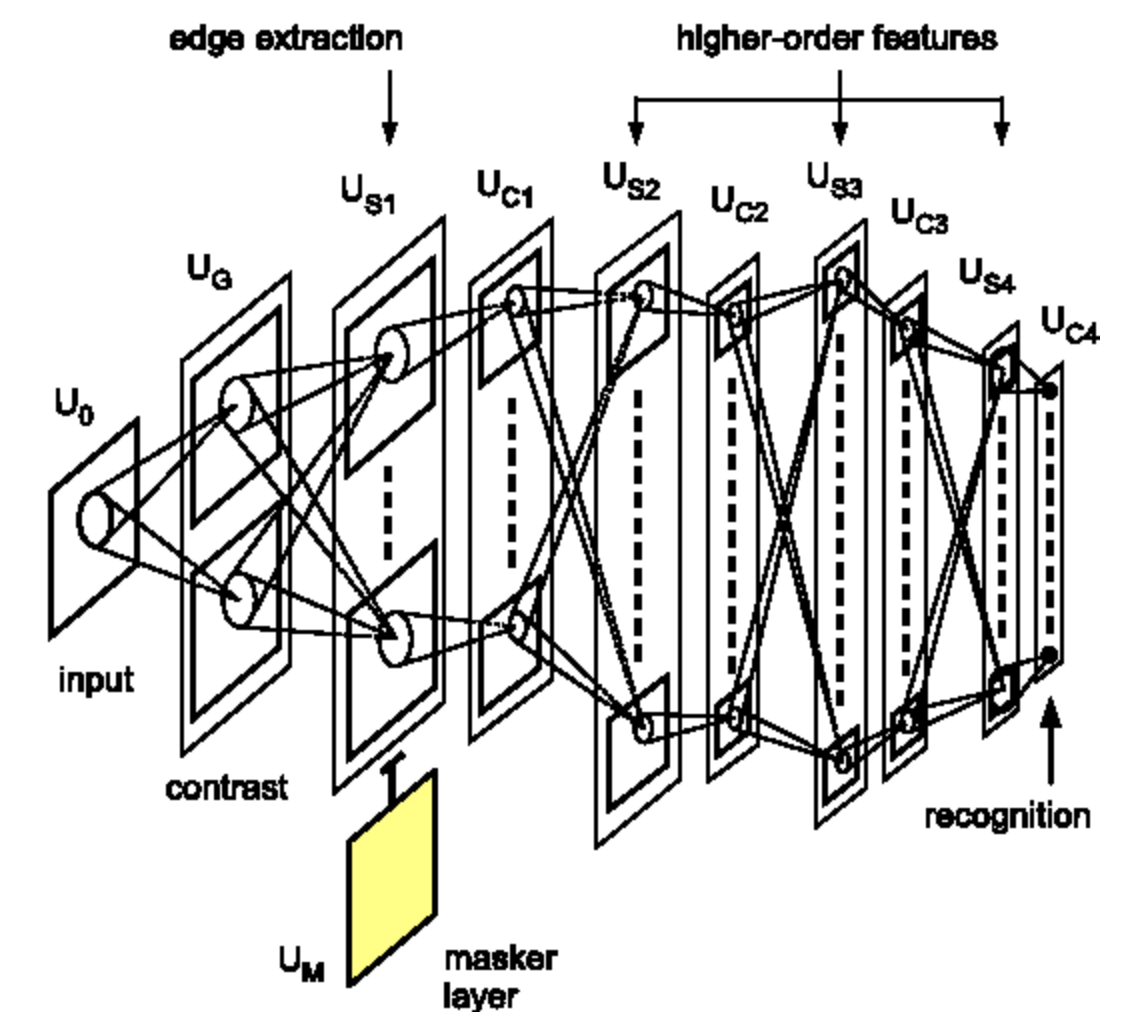
那么为何深度学习应该根植于我们的世界是可理解的并且有着组合化的性质这样的想法呢？Simon Thorpe所做的研究让我们对此有了更多的理解。他证明我们识别日常物体的方式是非常迅速的。他做了这样的实验，即每100毫秒快速出示一组图像，然后让被试识别这些他们能够识别的图片。这表明人类检测物体通常需要100毫秒。此外，下图描述了在大脑不同的部分中，神经元从一个区域传播到下一个区域所需的时间：

Figure 11. Simon Thorpe的脑部视觉信息流模型

从图中我们可以看到，信号从视网膜传递到LGN（用于对比增强、门控制，等等），然后传往V1初级视皮层，再到V2，V4，然后是下颞叶皮质(PIT)，类别在大脑的这个部分被定义。开放性大脑手术中的观察表明， 如果你为人类放映一部影片，PIT中的神经元只有在检测到某些特定的影像 -- 比如Jennifer Aniston或者某人的祖母的时候才会被激活 -- 其它的时候则不会。神经元活动不受像位置、尺寸、光照、您祖母的朝向、她的穿着等等的影响。 此外，人类能够在极短暂的反应时间内归类物体，这表明即使没有在复杂的循环计算上花费时间，这也是可能做到的。当然，这只是一个单一的前馈过程。 这些洞见启发我们开发出完全前馈的神经网络架构，而这样的架构仍然可以以一种不受输入的不相关变换影响的方式解决识别问题。 关于人类大脑的更进一步的洞见来自于Gallant 和Van Essen，他们关于人类大脑的模型描述了两个不同的通路：

Figure 12. Gallen 和 Van Essen关于脑部的背侧通路和腹侧通路的模型

右侧表示腹侧通路，它会告知你的所见；而左边代表背侧通路，它可以识别位置、几何和运动。他们在人类（还有灵长目动物）的视觉皮质（当然还有它们之间的相互作用）中看上去相当不同。 ### Hubel 和Weisel的贡献 (1962)

Figure 13. Hubel 与 Weisel关于猫脑部视觉刺激的实验

Hubel 和 Weisel 在实验中使用电极来测量猫脑部的神经活动针对视觉刺激的响应。他们发现在V1区域的神经元只对视野的某些区域（称为“感受野”）敏感，并且在那片区域可检测有向边。比如，如果你给猫看一个垂直的线条，然后开始转动线条，在转到某一个角度的时候，神经元开始激活。类似地，随着线条离开那个角度，神经元的激活也随之消失。对于这一类选择性激活神经元，由于它们能够检测局域特征，Hubel 和 Weisel 称之为“简单细胞”。 此外，他们还发现如果你将线条远离感受野，那个特定的神经元就不再激活，但另一个神经元将会被激活。对于视野中的所有区域，都有针对性的局域检测单元，因此，人类大脑处理视觉信息的过程可以看做是一系列的“卷积”。 另一类神经元，也就是他们称之为“复杂细胞”， 能够聚合一定区域里的多个简单细胞的输出。我们可以将这些操作看做使用类似求最大值、求和、平方和这样的函数，或者任何不依赖于顺序的函数去计算激活的聚合。不论那些刺激位于区域的哪个部分，这些复杂细胞都可以检测一个区域中的边与方向。换句话说，它们对于输入位置的微小变化是平移不变的。 ### Fukushima的贡献(1982)

Figure 14. Fukushima的CNN模型

Fukushima第一个利用计算机模型，使用手写数字数据集将多层简单细胞和复杂细胞的想法进行实现。其中的一些特征检测器是手工提取或者学习到的，虽然这里的学习用到的是非监督的聚类算法，而且由于反向传播还未被使用，这里是针对每一层分别训练。 Yann LeCun在几年后（1989,1998）对此进行研究并实现了同样的架构。但是这次，他是利用反向传播在监督学习的框架下进行训练。这通常被认为是现代的卷积神经网络的起源。（MIT的Riesenhuber在1999年也重新发现了这套架构，虽然他并没有使用反向传播。）