人工神经网络（ANNs）

🎙️ Alfredo Canziani

进行分类的监督学习

• 看看底下的 图 1(a) 。图中的点分布在这个螺旋的旋臂上，并且是在 \(\R^2\) 中。每个颜色代表一个类别标记。总共有 $K = 3$ 个不同的类别。数学上由 方程式 1(a) 表示。

• 图 1(b) 展现了一个类似的螺旋，加上高斯噪声。它的数学表示是 方程式 1(b) 。

  在两个例子中，这些点都不是线性可分的。

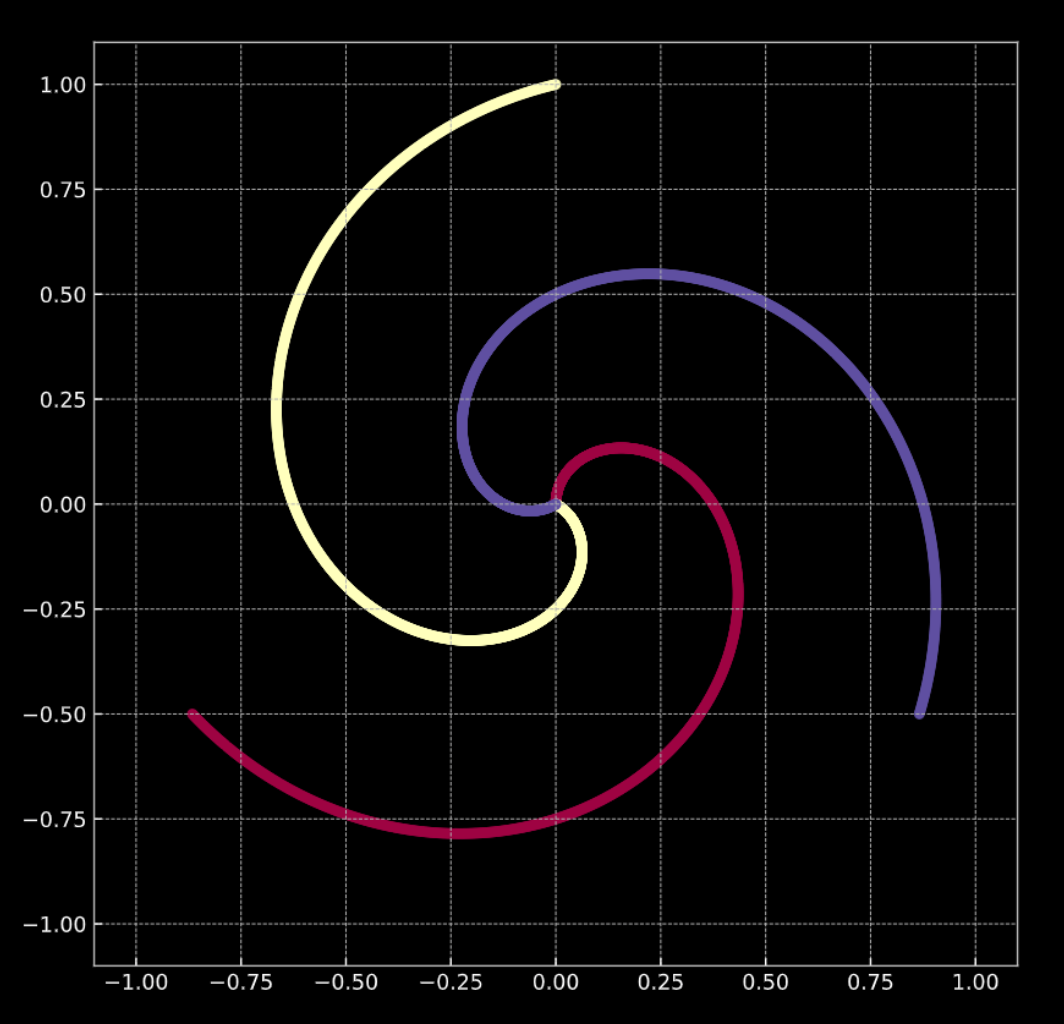
  图 1(a) "干净的" 2D 螺旋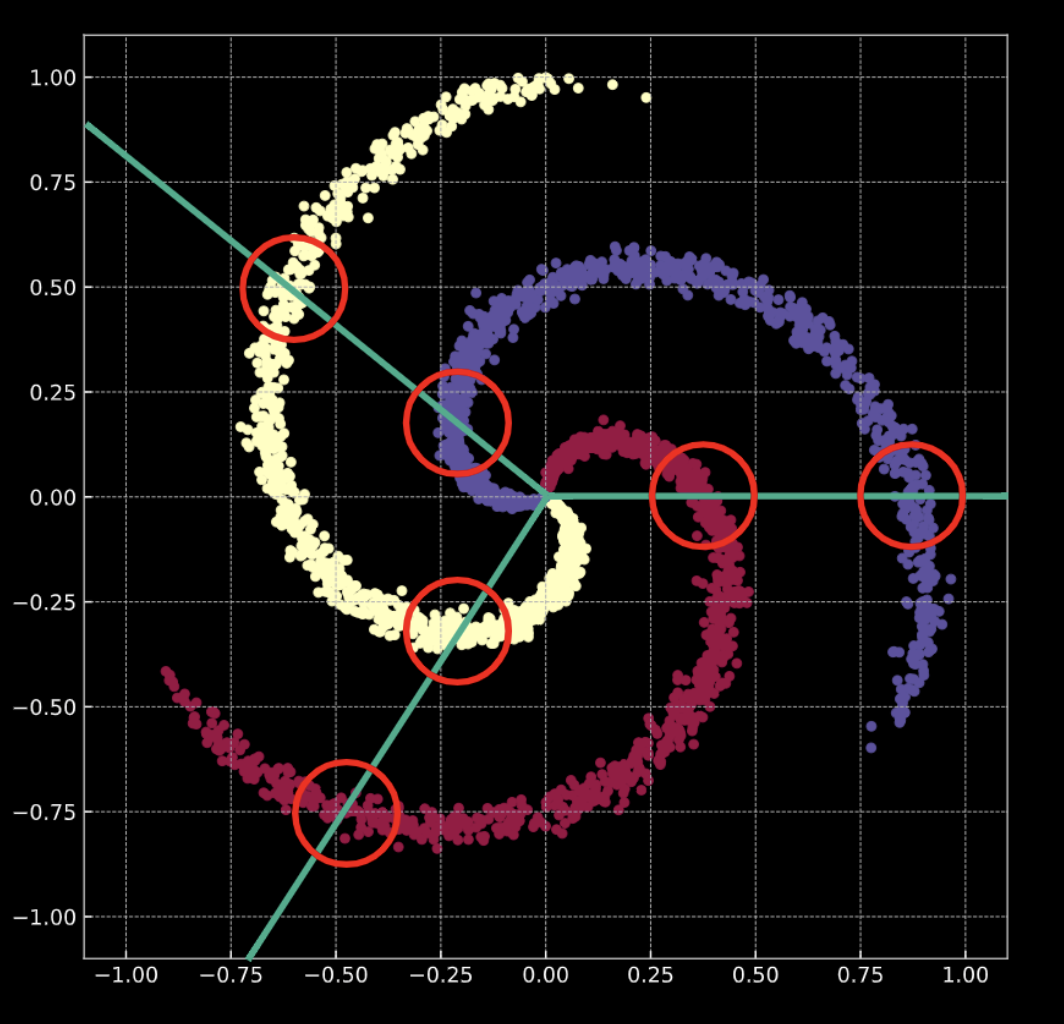

  图 1(b) "嘈杂的" 2D 螺旋

\[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1)\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1)\right]}\end{array}\right) \\ 0 \leq t \leq 1, \quad k=1, ..., K\] 方程式 1(a) \[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]}\end{array}\right)\\0 \leq t \leq 1, \quad k=1, ..., K\] 方程式 1(b)

进行 分类 是什么意思呢？请想想看 逻辑回归 (LR) 的情况。如果用逻辑回归来分类这个数据，它会创造一系列的 线性平面 （决策边界）以尝试分离数据到各自的类别。这种解法存在问题，那就是每个区域中，都有属于不同类别的点。因为螺旋的悬臂会跨越决策边界，这不是一个好的解法。

我们该如何解决这个问题？我们可以变换输入空间，使得数据变的线性可分。在训练一个神经网络的过程，它所习得的决策边界会试着符合训练数据的分布。

注意：一个神经总是用由下而上的方式来表示。第一层在最底下，最后一层在顶端。这是因为概念上，输入数据对神经网络处理的任务而言是低阶的特征。当资料向上遍历网络时，每一层会提取更高阶的特征。

训练数据

上周，我们看到刚初始化的神经网络会任意的变换它的输入。这个变换（起初）对完成眼下的任务没有功效。我们来探索如何用数据来使这个变换具有与手边的任务有关的含义。下列是用来训练的输入数据。

• $\boldsymbol X$ 代表输入数据，一个 $\mathbf m$ x $\mathbf n$ 的矩阵（$\mathbf m$ 是数据点的数量，$\mathbf n$ 是每个输入点的维度）。在图1(a) 和 1(b) 的例子 $\mathbf n = 2$.

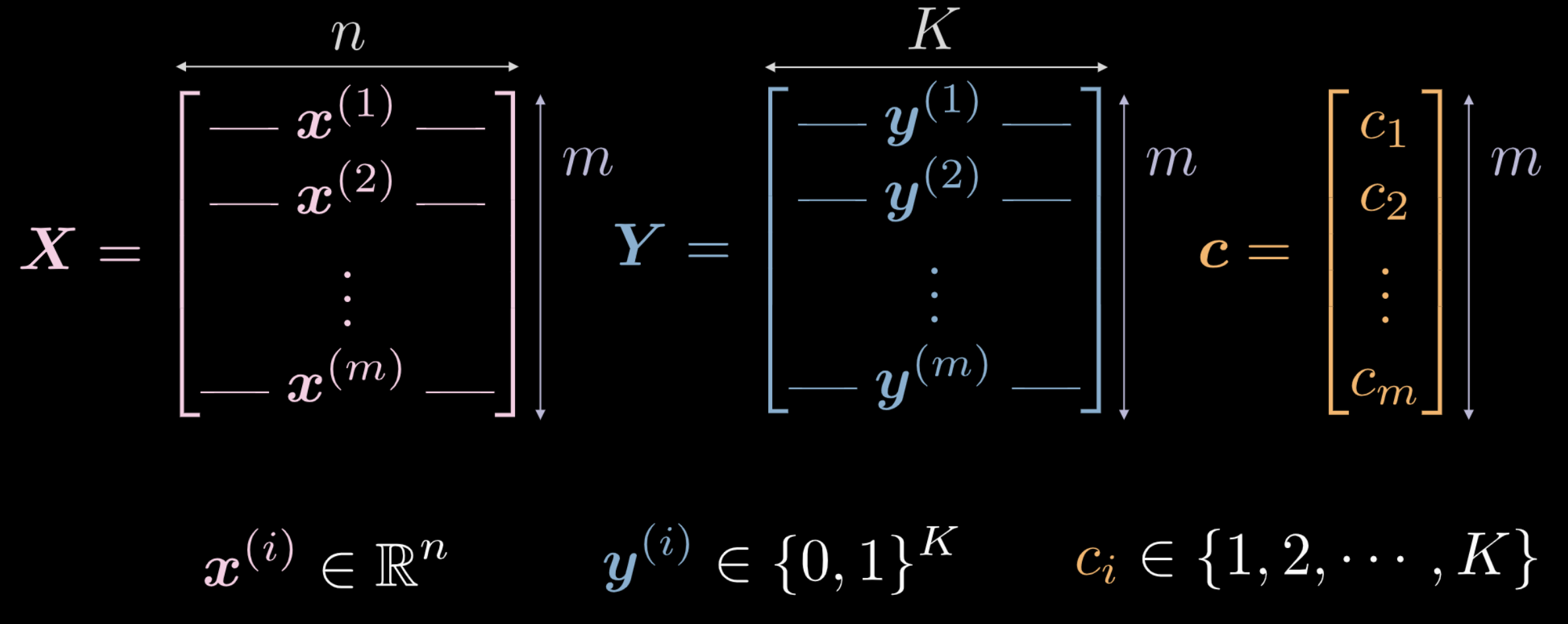
图 2 训练数据

• $\boldsymbol c$ 和 $\boldsymbol Y$ 都是代表这 \(\mathbf m\) 个数据点中每一个点属于的类别。在前述的例子中，共有 \(3\) 个不同的类别。

  • $c_i \in {1, 2, …, K}$ 和 $\boldsymbol c \in \R^{m \times 1}$。然而 \(\mathbf Y\) 并不 \(\in \R^{m \times 1}\)，亦即我们不用 \(\mathbf c\) 作为训练数据。如果我们使用这些不同的数字类别标记 $ c_i \in {1, 2, …, K}$，网络可能会推断出类别的顺序，而这是不能代表数据分布的。
  • 为了绕过这个问题，我们使用 one-hot 编码。我们为每个数据点建立一个 $K$ 维的向量 $\boldsymbol y^{(i)}$，其第 \(i\) 个元素设为 1（$i \in {1, 2, …, K}$ 是数据点们的类别标记，如图 3）。
  
  Fig. 3 One hot encoding

</center>

• 故 $\boldsymbol Y \in \R^{m \times K}$。这个矩阵也可以想成是有着完全集中在 $K$ 点其中一点的几率质量。

全连接层（fully connected (FC) layer）

我们将见到什么是一个全连接（FC）网络，以及它如何运作。

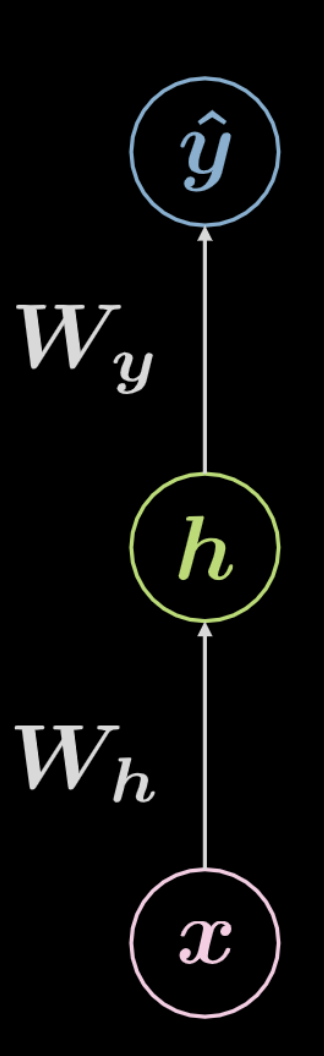
图 4 全连接神经网络

考虑图 4所描绘的网络。输入数据，$\boldsymbol x$，受到由 $\boldsymbol W_h$ 定义的仿射变换，再经过一个非线性变换。非线性变换的结果表示为 $\boldsymbol h$，代表一个隐藏的输出，也就是一个从网路外部看不见的输出。接下来又有另一个仿射变换（$\boldsymbol W_y$）以及非线性变换，于是产出最终的输出 $\boldsymbol{\hat{y}}$。这个网络可以用下方的方程式 2来表示，其中 \(f\) 和 \(g\) 都是非线性函数。

\[\begin{aligned} &\boldsymbol h=f\left(\boldsymbol{W}_{h} \boldsymbol x+ \boldsymbol b_{h}\right)\\ &\boldsymbol{\hat{y}}=g\left(\boldsymbol{W}_{y} \boldsymbol h+ \boldsymbol b_{y}\right) \end{aligned}\] 方程式 2 一个全连接网络背后的数学

之前看到的这样基础的神经网络只是一连串先仿射变换再非线性运算（挤压）的搭配。常用的非线性函数包含 ReLU、sigmoid、hyperbolic tangent 和 softmax。

上面展示的网络是一个 3 层的网络

\(1\) - 输入神经元

\(2\) - 隐藏神经元

\(3\) - 输出神经元

因此，一个 \(3\) 层的神经网络有 \(2\) 个仿射变换。这可以类推至 \(n\) 层的网络。

现在让我们看看更复杂的例子。

这个网络有 3 个隐藏层，每一层都是全连接的。图 5 描绘了这个网络。

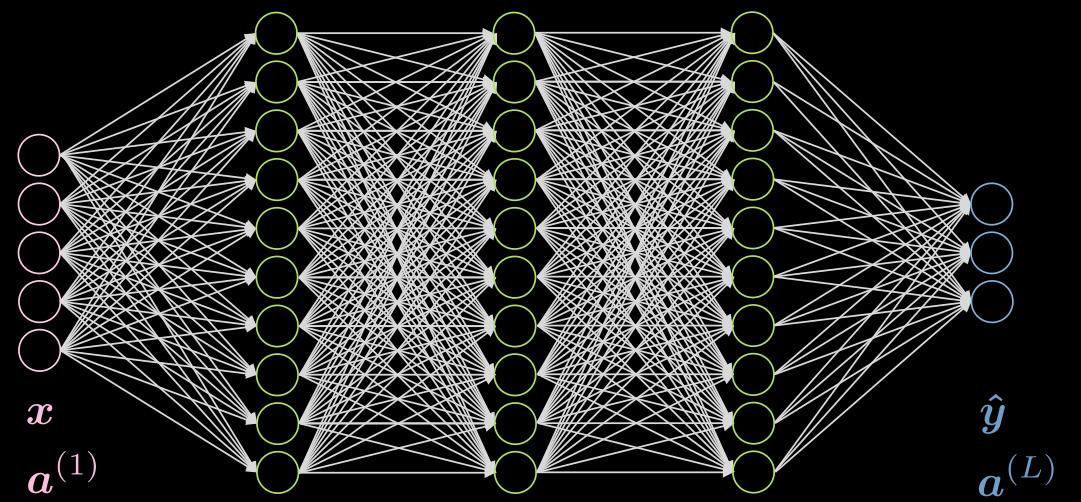
图 5 神经网络，3 个隐藏层

来考虑第二层的神经元 $j$。它的激活值是： \(a^{(2)}_j = f(\boldsymbol w^{(j)} \boldsymbol x + b_j) = f\Big( \big(\sum_{i=1}^n w_i^{(j)} x_i\big) +b_j ) \Big)\) 其中 $\boldsymbol w^{(j)}$ 是 $\boldsymbol W^{(1)}$ 的第 j 行。

注意在此例中输入层的激活函数只是恒等函数。隐藏层的激活函数可以是 ReLU、hyperbolic tangent、sigmoid、soft (arg)max 等等。

最后一层的激活函数通常取决于使用情况，这篇 Piazza post 提供了一个解释。

神经网络（推断 (inference)）

让我们再次考虑两层的神经网络（输入层，隐藏层，输出层），见图 6

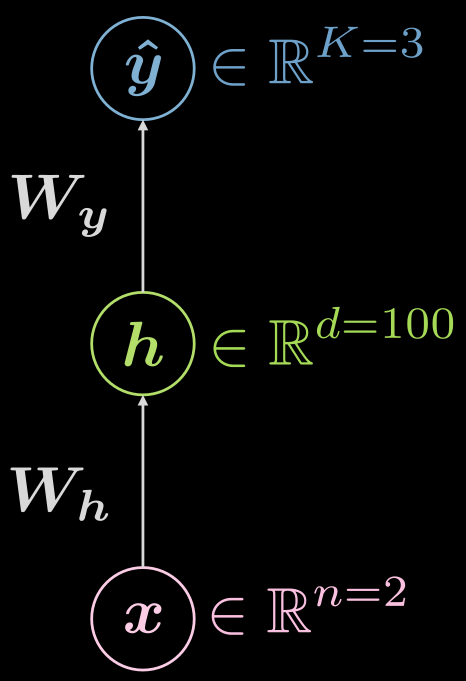
图 6 两层的神经网络

这个函数是什么样子的呢？

\[\boldsymbol {\hat{y}} = \boldsymbol{\hat{y}(x)}, \boldsymbol{\hat{y}}: \mathbb{R}^n \rightarrow \mathbb{R}^K, \boldsymbol{x} \mapsto \boldsymbol{\hat{y}}\]

不过，将视隐藏层视觉化会很有帮助，这样，这个映射关系就被扩展为：

\[\boldsymbol{\hat{y}}: \mathbb{R}^{n} \rightarrow \mathbb{R}^d \rightarrow \mathbb{R}^K, d \gg n, K\]

这个情况的范例构造长什么样子？在我们的例子里，输入的维度是二（$n=2$），有一个 1000 维（$d = 1000$）的隐藏层，以及三个类别（$C = 3$）。就实际而言，有很多好的理由不在一个隐藏层中放这么多神经元，所以我们可以把这一个隐藏层换成三个各具有 10 个神经元的隐藏层（$1000 \rightarrow 10 \times 10 \times 10$）。

神经网络（训练 I）

那么典型的训练是如何？我们最好用损失（losses）的标准术语来阐述这个过程。

首先，来重新介绍 soft (arg)max 并明确的说：它是一个最后一层经常使用的激活函数，用于搭配 negative log-likelihood loss 处理多类别预测。如同 LeCun 教授在讲座中所说，这是因为它提供比 sigmoid 与均方误差更好的梯度。而且，使用 soft (arg)max 时，你的最后一层已经被归一化（最后一层中所有神经元输出的和为 1），以一种对于梯度方法来说较显性归一化（除以范数）更好的方法。

soft (arg)max 会给你最后一层的 logit，如下：

\[\text{soft{(arg)}max}(\boldsymbol{l})[c] = \frac{ \exp(\boldsymbol{l}[c])} {\sum^K_{k=1} \exp(\boldsymbol{l}[k])} \in (0, 1)\]

必须注意这不是一个闭区间因为指数函数自然会产生正值。

给定预测值的集合 $\hat{Y}$，损失函数值是：

\[\mathcal{L}(\boldsymbol{\hat{Y}}, \boldsymbol{c}) = \frac{1}{m} \sum_{i=1}^m \ell(\boldsymbol{\hat{y}_i}, c_i), \quad \ell(\boldsymbol{\hat{y}_i}, c) = -\log(\boldsymbol{\hat{y}_i}[c])\]

这里 c 表示整数的标记而非 one-hot 编码的表示方法。

那么我们来做两个例子，其一的数据被正确分类的数据，另一个不是。

比方

\[\boldsymbol{x}, c = 1 \Rightarrow \boldsymbol{y} = {\footnotesize\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}}\]

每一笔数据的损失是多少呢？

如果是 接近完美的预测 （$\sim$ 的意思是 大约）：

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow 0^{+}\]

如果是 几乎完全错误：

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow +\infty\]

注意在上面的例子中，$\sim 0 \rightarrow 0^{+}$ and $\sim 1 \rightarrow 1^{-}$。为何如此，请稍为思考一下。

注意：当你使用CrossEntropyLoss，就同时具备了LogSoftMax和 negative loglikelihood NLLLoss，所以不要用了重复的功能。

神经网络 （训练 II）

做训练时，我们集结所有可以训练的参数－－权重矩阵和偏置－－于一个集合 $\mathbf{\Theta} = \lbrace\boldsymbol{W_h, b_h, W_y, b_y} \rbrace$。所以我们可以把目标函数，也就是损失，写成：

\[J \left( \Theta \right) = \mathcal{L} \left( \boldsymbol{\hat{Y}} \left( \Theta \right), \boldsymbol c \right) \in \mathbb{R}^{+}\]

这使得损失取决于网络的输出 $\boldsymbol {\hat{Y}} \left( \Theta \right)$，所以我们可以将其转换为一个优化问题。

在图 7当中你可以看到它如何进行，$J(\mathcal{v})$ 是我们想最小化的函数。

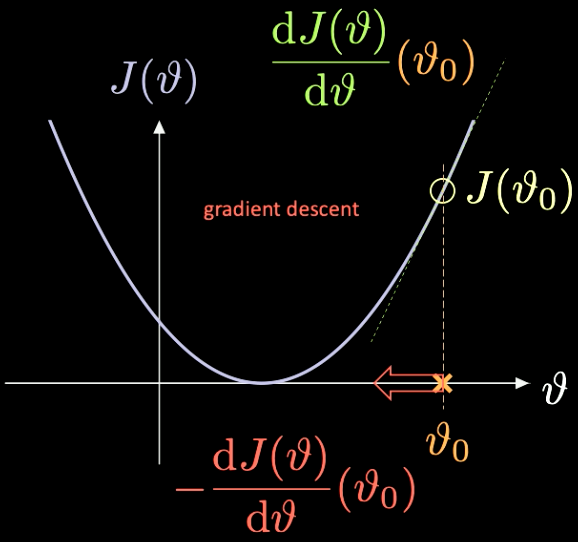
图 7 藉由梯度下降优化损失函数

我们挑选一个随机初始化的点 $\vartheta_0$ – 它对应的损失是 $J(\vartheta_0)$。我们可以计算在该点的导数 $J’(\vartheta_0) = \frac{\text{d} J(\vartheta)}{\text{d} \vartheta} (\vartheta_0)$。这个例子里，导数的斜率是正的。我们要向下降最陡的方向走一步。在此是 $-\frac{\text{d} J(\vartheta)}{\text{d} \vartheta}(\vartheta_0)$。

这个迭代重复的过程被称作梯度下降。梯度的方法是训练神经网络的主要工具。

为了计算必要的梯度，我们要使用反向传播。

\[\frac{\partial \, J(\mathcal{\Theta})}{\partial \, \boldsymbol{W_y}} = \frac{\partial \, J(\mathcal{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol{W_y}} \quad \quad \quad \frac{\partial \, J(\mathcal{\Theta})}{\partial \, \boldsymbol{W_h}} = \frac{\partial \, J(\mathcal{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol h} \;\frac{\partial \, \boldsymbol h}{\partial \, \boldsymbol{W_y}}\]

分类螺旋 - Jupyter notebook

Jupyter notebook 在这里。为了运行此 notebook，请确定你依照 README.md 里所说的安装好the dl-minicourse环境。

上礼拜的笔记有解说如何使用torch.device()。

像之前一样，我们操作的是 $\mathbb{R}^2$ 中的点，而其有三种不同的类别标记（红、黄、蓝），如图 8。

图 8 螺旋分类数据

nn.Sequential() 是一个容器，能够将模组按照加入的顺序送入建构子；nn.linear()的命名不太精确，因为它是对输入的数据进行仿射变换： $\boldsymbol y = \boldsymbol W \boldsymbol x + \boldsymbol b$。更多资料请参照 PyTorch 文件。

记住，仿射变换有五种：旋转、反射、平移、缩放和推移。

如 图 9，当尝试使用线性的决策边界来分隔螺旋的数据 - 只使用nn.linear()模组，而不在之间加上非线性 - 我们只能达到 50% 的正确度。

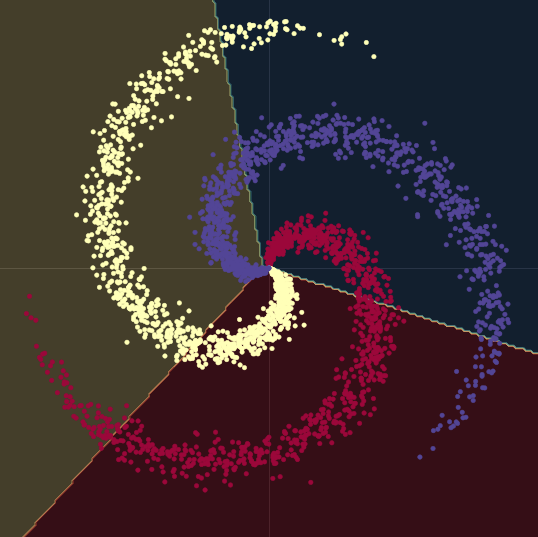
图 9 线性的决策边界

当我们从线性模型换成在两个 nn.linear() 模组再经过一个 nn.ReLU() 的模型，正确度增加到了 95%。这是因为边界变成非线性的并且更好的顺应资料的螺旋，像 图 10中所呈现的。

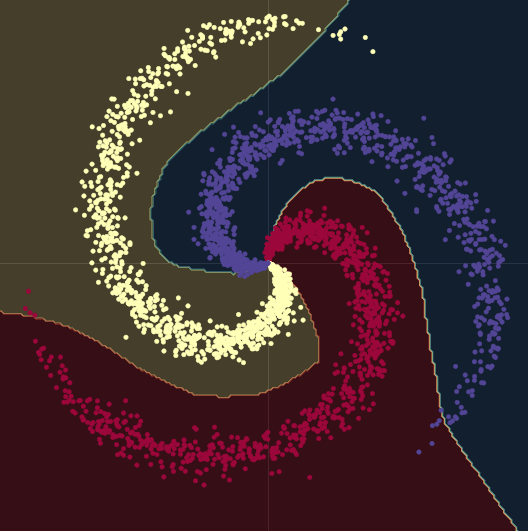
图 10 非线性的决策边界

这个 notebook和图 11表现了一个无法用线性回归完成，但可以用这个相同的网络解决的问题。图 11展现了 10 个不同的网络，其中五个使用 nn.ReLU()，另外五个是nn.Tanh()。前者是一个分段的线性函数，后者则是连续、平滑的回归。

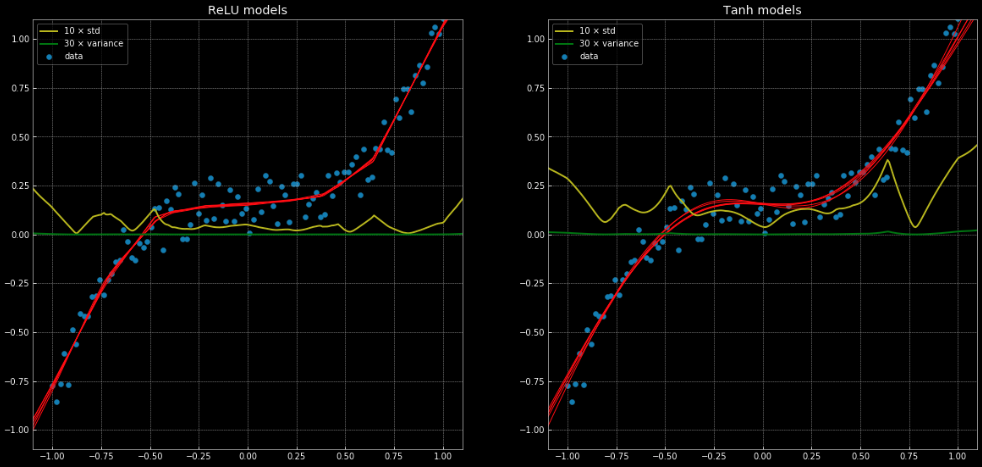
Fig. 11: 10 个神经网络与他们的方差、标准差
左：5 个 ReLU 网络；右：5 个 tanh 网络

黄色和绿色线分别表示网络的标准差和方差。这些可以有如同置信区间的效果 - 因为这些模型只会给出单一的预测。集成的方差预测帮助我们估计做出的预测的不确定性。这个方法的重要性显现于 图12，当我们将决策函数扩展到训练的范围外，这些数值都趋近 $+\infty, -\infty$。

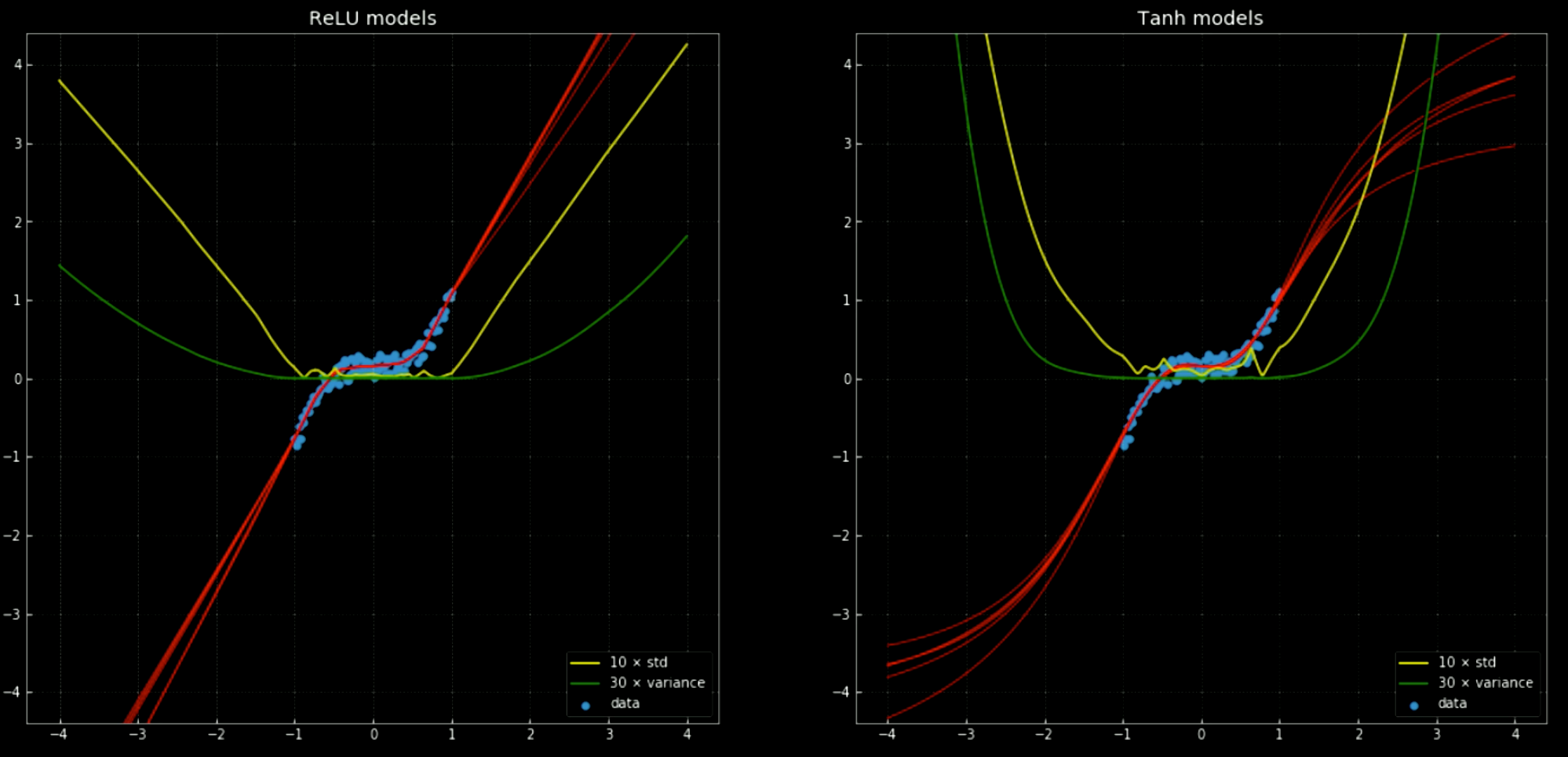
图 12 10 个神经网络与他们的方差、标准差，在训练的区间外
左：5 个 ReLU 网络；右：5 个 tanh 网络

要想用 Pytorch 训练任何神经网络，训练回圈包含 5 个基础步骤：

1. output = model(input) 是模型的前向传播，接收输入并生成输出。
2. J = loss(output, target <or> label) 接收模型的输出，并计算训练时对于真实目标的损失。
3. model.zero_grad() 清除计算的梯度，使它们不会积累到下次的传播。
4. J.backward() 进行反向传播和累加：它为每个我们指定了 requires_grad=True 的变数 $\texttt{x}$ 计算 $\nabla_texttt{x} J$。这些会累计到每个变数的梯度：$\texttt{x.grad} \gets \texttt{x.grad} + \nabla_\texttt{x} J$。
5. optimiser.step() 进行梯度下降的一步：$\vartheta \gets \vartheta - \eta\, \nabla_\vartheta J$。

当训练一个神经网络，很有可能你要依序进行这五个步骤。

---

📝 Yunya Wang, SunJoo Park, Mark Estudillo, Justin Mae
Titus Tzeng
4 Feb 2020