为神经网络的模组计算梯度，与反向传播的实用技巧

一个反向传播的具体例子还有介绍基础的神经网络模组

范例

接下来我们会考虑一个反向传播的例子，并使用图像来辅助。任意的函数 $G(w)$ 输入到损失函数 $C$ 中，这可以用一个图来表示。经由雅可比矩阵的乘法操作，我们能将这个图转换成一个反向计算梯度的图。（注意 Pytorch 和 Tensorflow 已经自动地为使用者完成这件事了，也就是说，向前的图自动的被「倒反」来创造导函数的图形以反向传播梯度。）

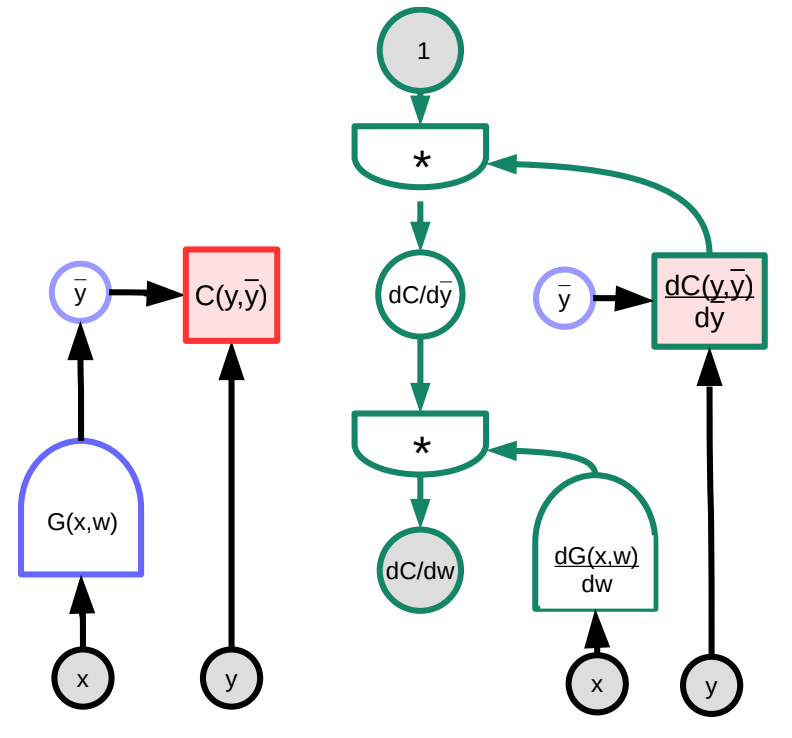
在这个范例中，右方的绿色图代表梯度的图。跟着图从最上方的节点开始的是：

从维度来说，$\frac{\partial C(y,\bar{y})}{\partial w}$ 是一个行向量，大小为 $1\times N$，其中 $N$ 是 $w$ 中成员的数量；$\frac{\partial C(y,\bar{y})}{\partial \bar{y}}$ 是个大小 $1\times M$ 的行向量，其中 $M$ 是输出的维度；$\frac{\partial \bar{y}}{\partial w}=\frac{\partial G(x,w)}{\partial w}$ 是个大小 $M\times N$ 的矩阵，其中 $M$ 是 $G$ 输出的数量，而 $N$ 是 $w$ 的维度。

注意当图的结构不固定而是依赖于数据时，情况可能更为复杂。比如，我们可以根据输入向量的长度来选择神经网络的模组。虽然这是可行的，当迭代数量过度增加，处理这个变化的难度会增加。

基本的神经网络模组

除了习惯的线性和 ReLU 模组，还有其他预先建立的模组。他们十分有用因为他们为了各自的功能被特别的优化过（而非只是用其他初阶模组拼凑而成）。

• 线性： $Y=W\cdot X$

• ReLU： $y=(x)^+$

  \[\frac{dC}{dX} = \begin{cases} 0 & x<0\\ \frac{dC}{dY} & \text{otherwise} \end{cases}\]

• 重复： $Y_1=X$, $Y_2=X$

  • 如同一个「分接线」，两个输出都与输入相同

  • 反向传播时，梯度相加

  • 可以类似的分配成 $n$ 个分支

    \[\frac{dC}{dX}=\frac{dC}{dY_1}+\frac{dC}{dY_2}\]

• 相加： $Y=X_1+X_2$

  • 当两个变数相加，其中一个若被改变，输出也会以相同幅度改变，即

    \[\frac{dC}{dX_1}=\frac{dC}{dY}\cdot1 \quad \text{and}\quad \frac{dC}{dX_2}=\frac{dC}{dY}\cdot1\]

• 最大值： $Y=\max(X_1,X_2)$

  • 因为这个函数也可以写作：

• 因此，根据链式法则

LogSoftMax vs SoftMax

SoftMax，另一个 Pytorch 模组，是一种方便的方式，可以将一组数字转换为 $0$ 到 $1$ 之间的数值，并使它们和为 $1$。这些数字可以理解为概率分布。因此，它经常用于分类问题。下方等式中的 $y_i$ 是一个记录着每一个类别概率的向量

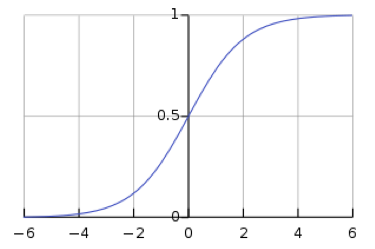
然而，使用 softmax 使网络容易面临梯度消失。梯度消失是一个问题，因为它会使得随后的权重无法被神经网络改动，进而停止神经网络进一步训练。Logistic sigmoid 函数，就是单一数值的 Softmax 函数，展现出当 $s$ 很大时，$h(s)$ 是 $1$，而当 $s$ 很小时，$h(s)$ 是 $0$。因为 sigmoid 函数在 $h(s) = 0$ 和 $h(s) = 1$ 处是平坦的，其梯度为 $0$，造成消失的梯度。

数学家想到可以用 logsoftmax 来解决 softmax 造成的梯度消失问题。LogSoftMax 是 Pytorch 当中的另一个基本模组。正如下方等式所示，LogSoftMax 组合了 softmax 和对数。

下方的等式提供同一个等式的另一种观点。下图显示函数中 $\log(1 + \exp(s))$ 的部份。当 $s$ 非常小，其值为 $0$，至于 $s$ 很大时，值是 $s$。如此一来，它不会造成饱和，就避免了梯度消失。

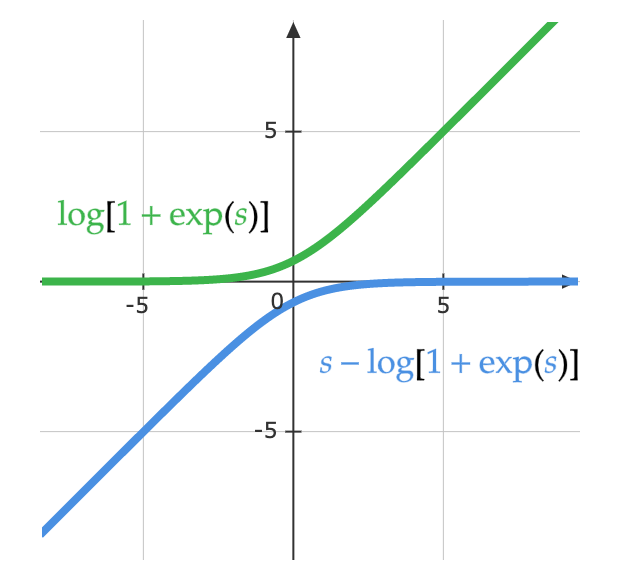
反向传播的实用技巧

用 ReLU 作为非线性函数

对于有很多层的网络，ReLU 的效果最好，甚至使其他函数如 sigmoid、hyperbolic tangent $\tanh(\cdot)$ 相形之下过时了。ReLU 很有效的原因可能是因为它具有的一个尖点使它具有缩放的等变性。

用交叉熵作为分类问题的损失函数

在讲座里前面提到的 Log softmax是交叉熵损失的特例。Pytorch 里，请保证传给交叉熵损失函数时要使用 Log softmax 为输入（而非一般 softmax）。

训练时使用小批量（minibatch）的随机梯度下降

如同之前所讨论的，小批量使你能更有效率的训练，因为数据中有重复；你不需要每一步对每个观察进行预测、计算损失以估计梯度。

训练时打乱样本顺序

顺序会造成影响。如果模型在一回的训练中只有来自同一类别的样本，它会去直接预测该类别而非学习为何要预测该类别。例如，如果你试着分类 MNIST 数据集的数字而没有打乱数据，那最后一层的偏置易开始总会预测零，接着改成总是预测一、二，依此类推。理想上，每个批量中都应该要有来自每个类别的样本。

不过是否要在每回（epoch）的训练都改变次序仍然存在争论。

将输入归一化使其具有零平均值与单位方差

训练之前，先归一化每个输入特征，让均值为零、标准差为一是很有用的。使用 RGB 图像数据时，经常会单独取每个通道的均值和标准差，以通道为单位进行归一化。举例而言，取数据集中所有蓝色通道的数值的均值 $m_b$ 和标准差 $\sigma_b$，接着归一化每个图像的蓝色通道数值如下：

其中 $\epsilon$ 是个任意小的数字，用于避免除以零。对绿色通道和红色通道进行同样操作。这个必要的操作使我们能从不同光线下的图像取得有用的信号；例如日光中的相片有很多红色，但水下的图片则几乎没有。

按照进度递减学习率

随着训练持续，学习率应该下降。实际上，大多进阶的模型是用 Adam/Momentum 这些能自我调整学习率的算法训练的，而非学习率固定的单纯 SGD。

使用 L1 和（或）L2 正则化进行权重衰减

你可以在损失函数中附上对巨大权重的损失。例如，使用 L2 正则化，我们定义损失为 $L$ 并且如下更新权重 $w$：

为了理解为何这称作权重衰减，我们可以将上方的方程式重写来展现我们在更新时把 $w_i$ 乘以一个小于一的常数。

L1 正则化（Lasso）是类似的，只不过我们使用 $\sum_i \vert w_i\vert$ 而不是 $\Vert w \Vert^2$。

本质上，正则化尝试告诉系统要以最短的权重向量来最小化损失函数。L1 正则化会将无用的权重缩减至 $0$。

权重初始化

权重要被随机的初始化，但它们不能太大或太小，因为输出得要有与输入差不多的方差。Pytorch 有诸多内建的初始化技巧。其中一个适合深层模型的是 Kaiming 初始化：权重的方差与输入数量的平方根成反比。

使用 dropout

Dropout 是另一种正则化。它可以当做神经网络的另一层：它接受输入，随机将 $n/2$ 的输入设为零，并且回传这个结果为输出。这迫使系统从所有输入单元获得信息而不是过度依赖少数的输入单元，从而能将资讯分配于一层中的所有单元。这个方法最初是由Hinton et al (2012)提出。

更多技巧参见 LeCun et al 1998.

最后，注意反向传播不只适用于层层堆叠的模型；它可用于任何有向无环图（DAG）只要模组间具有偏序关系，