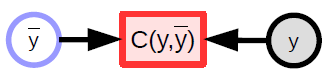梯度下降和反向传播算法导论

梯度下降优化算法

参数化模型

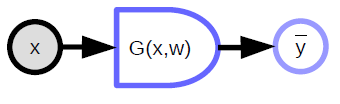
简单来讲，参数化模型就是依赖于输入和可训练参数的函数。 其中，可训练参数在不同训练样本中是共享的，而输入则因每个样本不同而不同。 在大多数深度学习框架中，参数是隐性的：当函数被调用时，参数不被传递。 如果把模型比作面向对象编程，这些参数相当于被“储存在函数中”。

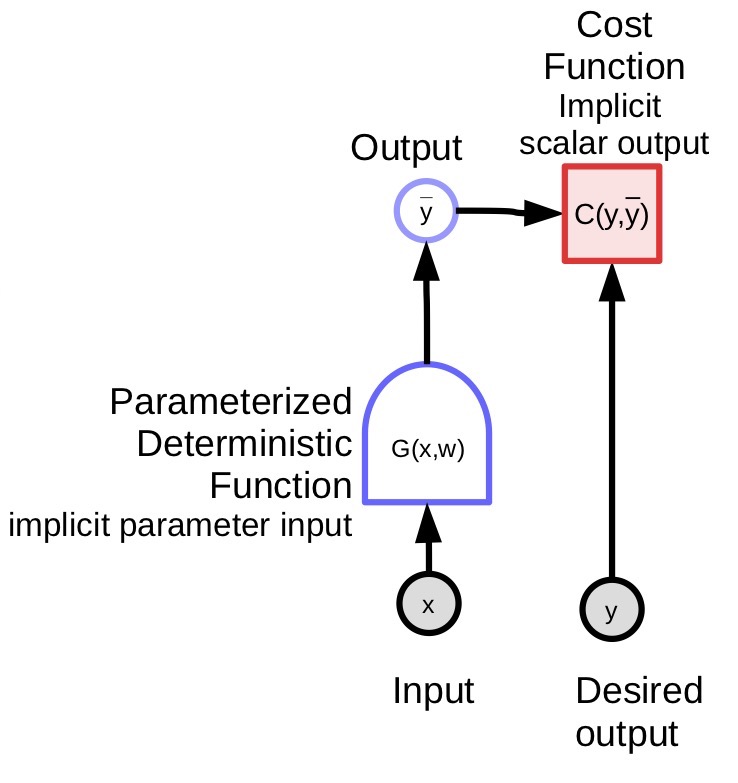
参数化模型（上文提到的函数）包含一个参数向量，这个模型可以将一个输入转化成输出。 在监督学习中，我们把模型的输出 ($\bar{y}$) 送入代价函数 ($C(y,\bar{y}$))，并将它与正确答案 (${y}$) 对比。 图1是这个过程的示意图。

图1: 参数化模型示意图

下列是几个参数化模型的例子。

• 线性模型 - 输入向量的加权和：

  \[\bar{y} = \sum_i w_i x_i, C(y,\bar{y}) = \Vert y - \bar{y}\Vert^2\]

• 近邻算法 - 给定一个输入 x 和一个权重矩阵 W，我们用 k 来表示 W 中的某一行。这个模型的输出是矩阵 W 中，与 x 最接近的那一行的编号 k。

  \[\bar{y} = \underset{k}{\arg\min} \Vert x - w_{k,.} \Vert^2\]

  复杂的函数也可以被用到参数化模型中。

用方块图表达参数模型的计算图

• 变量（张量，标量，连续变量，离散变量）
  • 是参数模型的输入
  • 是由函数计算出的变量，这个函数是确定，非随机的。

• 确定性函数

  

  • 可以有多个输入和多个输出
  • 包含一些隐性的参数变量 (${w}$)
  • 圆头表示了容易计算的方向。比如在上面的图里，从 ${x}$ 计算 ${\bar{y}}$ 更容易一些。

• 标量函数

  

  • 用来表示代价函数
  • 拥有一个隐性的标量输出
  • 用多个输入计算出一个值（通常情况下这个值是这几个输入之间的距离）

损失函数

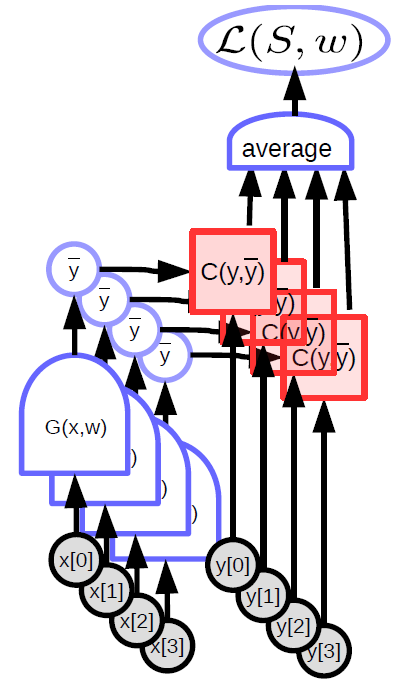
在训练过程中，我们最小化损失函数。 大体上存在两种损失函数：

1) 逐样本损失函数 - \(L(x,y,w) = C(y, G(x,w))\) 2) 平均损失函数 -

​ ​ 对于任意一个样本的集合 \(S = \lbrace(x[p],y[p]) \mid p \in \lbrace 0, \cdots, P-1 \rbrace \rbrace\)

​ ​ 在集合 $S$ 上的平均损失函数定义为： \(L(S,w) = \frac{1}{P} \sum_{(x,y)} L(x,y,w)\)

图2: 使用平均损失函数的模型的计算图

在标准的监督学习里，（逐样本）损失函数就是代价函数的输出。 机器学习在很大程度上就是寻找函数的最优解（经常情况下，是寻找某个函数的最小值）。 有的时候（比如在生成对抗网络里），我们学习寻找两个函数的纳什均衡。 我们用一系列和梯度相关的方法（包含但不总是梯度下降）寻找函数的最优解。

梯度下降

假设我们可以很容易地计算一个函数的梯度，我们可以用 梯度相关方法 去寻找这个函数的最小值。 这个方法建立在一个假设上，即，这个函数在大部分区间连续可微分（并不需要在所有地方连续可微分）。

梯度下降背后的逻辑直觉 - 想象在一个大雾弥漫的夜晚，我们在一座山里，想要回到山下的村庄。 因为视野非常有限，我们只能靠观察路面倾斜的角度来判断下山的方向，并且向着那个方向前进。

不同梯度下降的方法

• 对整批样本进行梯度下降时的参数更新法则： \(w \leftarrow w - \eta \frac{\partial L(S,w)}{\partial w}\)

• SGD (随机梯度下降)的参数更新法则：

  • 从 $\lbrace 0, \cdots, P-1 \rbrace$ 里选取一个 $p$ ，进行参数更新

    \[w \leftarrow w - \eta \frac{\partial L(x[p], y[p],w)}{\partial w}\]

其中， ${w}$ 表示要进行优化的参数。

在这里，\(\eta\) 是一个常数，但是在更高级的算法中，它可以是一个矩阵。

如果这是一个半正定矩阵，虽然我们确实是在往山下走，但是我们走的方向并不一定是向着最陡的方向走。 事实上，最陡的那个方向并不一定总是我们想要去的方向。

如果我们处理的函数不可微分，比如，函数曲线上有个洞，曲线是阶梯形状，或者干脆是平的，这时候梯度不能提供任何有用信息，我们必须借助其他方法 - 比如0阶方法，或者一些不需要梯度计算的方法。 深度学习说白了就是围绕着梯度相关方法展开的。

其实也存在例外，比如在RL（强化学习）中，我们不直接计算梯度，而是去估计梯度。 举个例子，我们教一个机器人学习骑车，它经常摔来摔去。 这时候我们可以让目标函数是自行车不摔倒的累计时长。 不幸的是，这种目标函数无法计算梯度。 我们的机器人需要自己探索，去找到适合它自己的骑车的方法。

虽然 RL 的代价函数在多数情况下不可微分，神经网络依然可以适用梯度相关的方法去学习。 这是监督学习和强化学习的主要区别之一。 在强化学习里，代价函数 $C$ 不可微分。 实际上它是完全未知的。 像一个黑箱子一样，你给它一些输入，它返回一些输出。 这也导致 RL 非常低效，尤其当参数向量维度很高的时候（换言之，算法需要在巨大的空间里探索，寻找解决方案）。

在RL里，有一种非常常用的方法叫做 Actor Critic（演员-评论家）。 其中，评论家模块有一个自己的代价函数C，这个模块是已知并且可训练的。 这个模块是可微分的，人们训练这个模块去近似真正的代价函数或者奖励（reward）函数。 这样以来，人们就可以用可微分的函数去近似代价函数，从而进行反向传播。

在传统神经网络中随机梯度下降和反向传播算法的优势

随机梯度下降的优势

在实际操作中，我们利用随机梯度下降算法来计算目标函数在参数上的梯度。 相比于在所有样本上计算目标函数的梯度，再进行平均，随机梯度下降算法每步只选取一个样本，计算损失 $L$，进而获取损失函数在训练参数上的梯度值。 之后，随机梯度下降算法在这个梯度的反方向上移动一步。

在这个公式中，我们用 $w$ 减去步长乘以上述的（基于每个样本 $x[p]$,$y[p]$ 的损失计算出的）梯度值，而得到新的 $w$。

因为基于每个样本进行计算，我们得到的轨迹存在非常大的干扰，如图3所示。 我们计算出的损失并不是直指山下，而是看起来非常随机。 每个样本都会把我们的损失拽向各不一样的方向。 不过平均来看，这些小的移动把我们带去了山谷。 虽然看起来有点低效，这种方法其实比起在整批样本上做梯度下降要快得多，尤其是当样本之间有很多重复信息的时候。

图3: 逐个样本更新时，随机梯度下降的轨迹

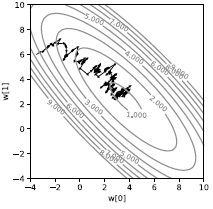在实际中，我们并不用单个样本做随机梯度下降，相反，我们每次更新用一小批的样本。 我们计算一小批样本的平均梯度，然后移动一小步。 我们这么做的唯一原因是因为这样可以更有效地优化算法，让它们更适应当前的硬件（比如GPU，多核GPU）。 批量运算是一种简单的并行化运算方法。

传统神经网络

传统的神经网络由互相穿插的线性运算和逐点非线性运算构成。 其中，线性运算就是矩阵-向量乘法，我们将（输入）向量与权值矩阵相乘。 之后，我们将相乘之后的加权和（向量）进行非线性运算（比如 $\texttt{ReLU}(\cdot)$, $\tanh(\cdot)$, …）

图4: 传统神经网络

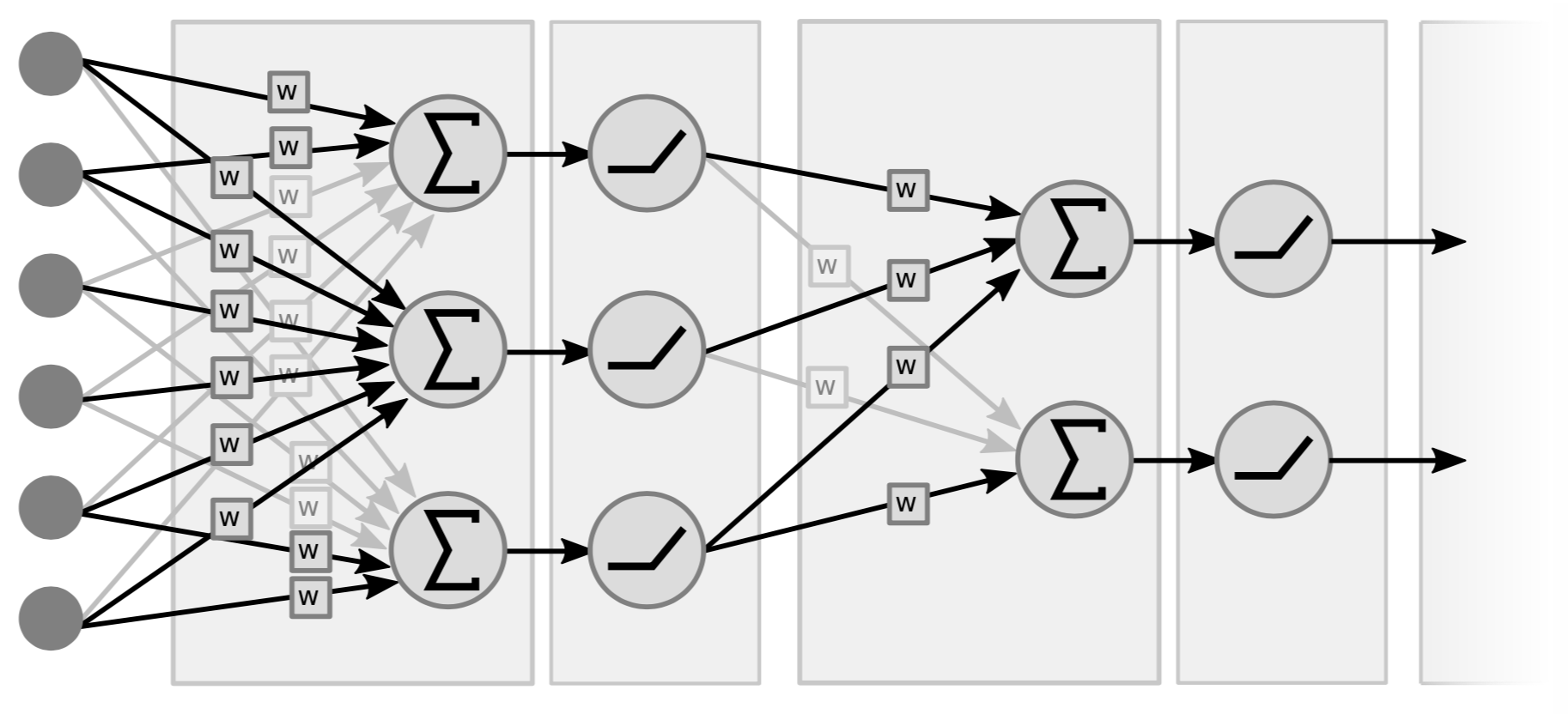图4所示是一个两层的神经网络，图中可以看到两对线性-非线性层。 也有人称这个网络为三层网络，因为他们包括了输入变量。 注意，当没有中间的非线性层时，这个网络有可能会转化成一个单层网络，因为两个线性函数的乘积依然是一个线性函数。

图5展示了神经网络里，线性和非线性模块是如何堆叠的：

图5: 一窥线性和非线性模块的内部构造

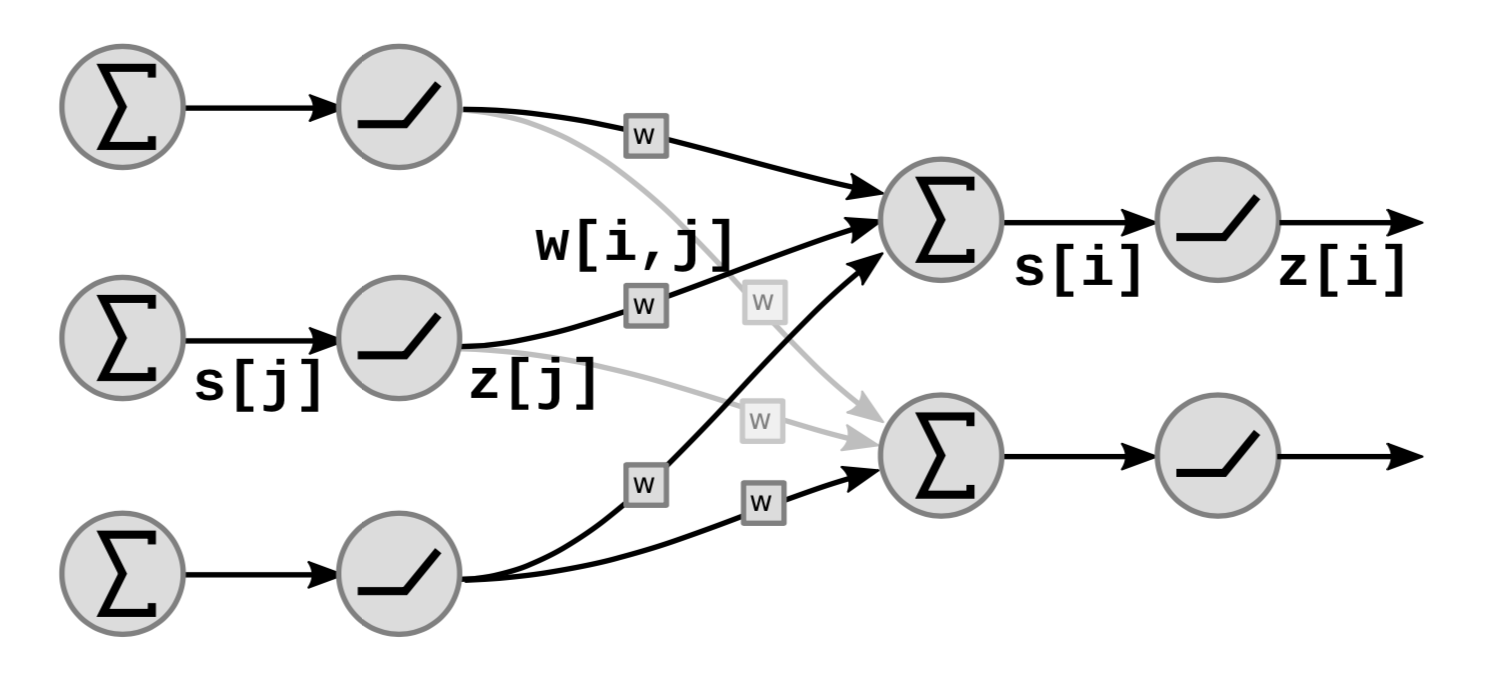在图中，$s[i]$ 代表了单位 ${i}$ 的加权和：

其中 $UP(i)$ 表示 $i$ 之前一层的单位， $z[j]$ 是之前一层的第 $j$ 个输出。

从而我们计算 $z[i]$ 用：

其中 $f$ 是非线性函数。

通过非线性函数进行反向传播

我们要介绍的第一种方法，是通过非线性函数进行的反向传播。 我们从神经网络里单拿出非线性函数 $h$，忽略黑盒子里的其他部分。

图6: 通过非线性函数进行反向传播

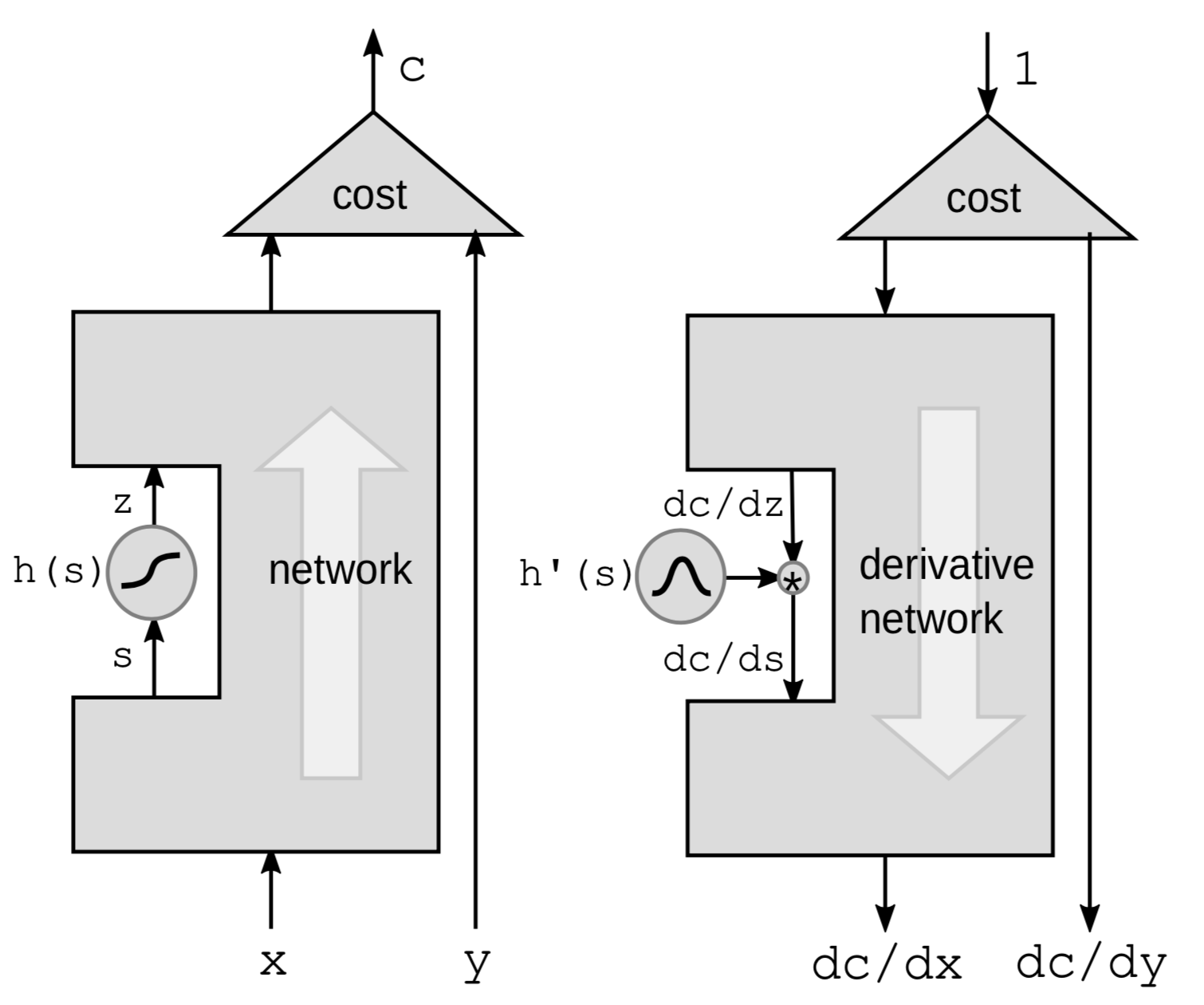这里我们利用链式法则来计算梯度：

其中， $h’(s)$ 是 $z$ 对 $s$ 的导数，即 $\frac{\mathrm{d}z}{\mathrm{d}s}$。 为了更清楚地表示这个导数，我们改写上面的公式为：

这样以来，我们只要可以用串联的一系列函数来表示一个神经网络，我们就可以逐层乘以每个${h}$ 函数的导数，从而进行反向传播。

我们也可以用扰动法的角度去想这个问题。 对 $s$ 添加 $\mathrm{d}s$ 的扰动，会相应地在 $z$ 上添加如下扰动：

从而，这也会在 $C$ 上添加如下扰动：

这样以来，我们得到了和之前一样的公式。

通过加权和进行反向传播

对于线性模块，我们通过加权和进行万象传播。 这次，我们关注变量 ${z}$ 和那一系列变量 $s$ 之间的连接，默认其他的部分是黑盒子。

图7: 通过加权和进行反向传播

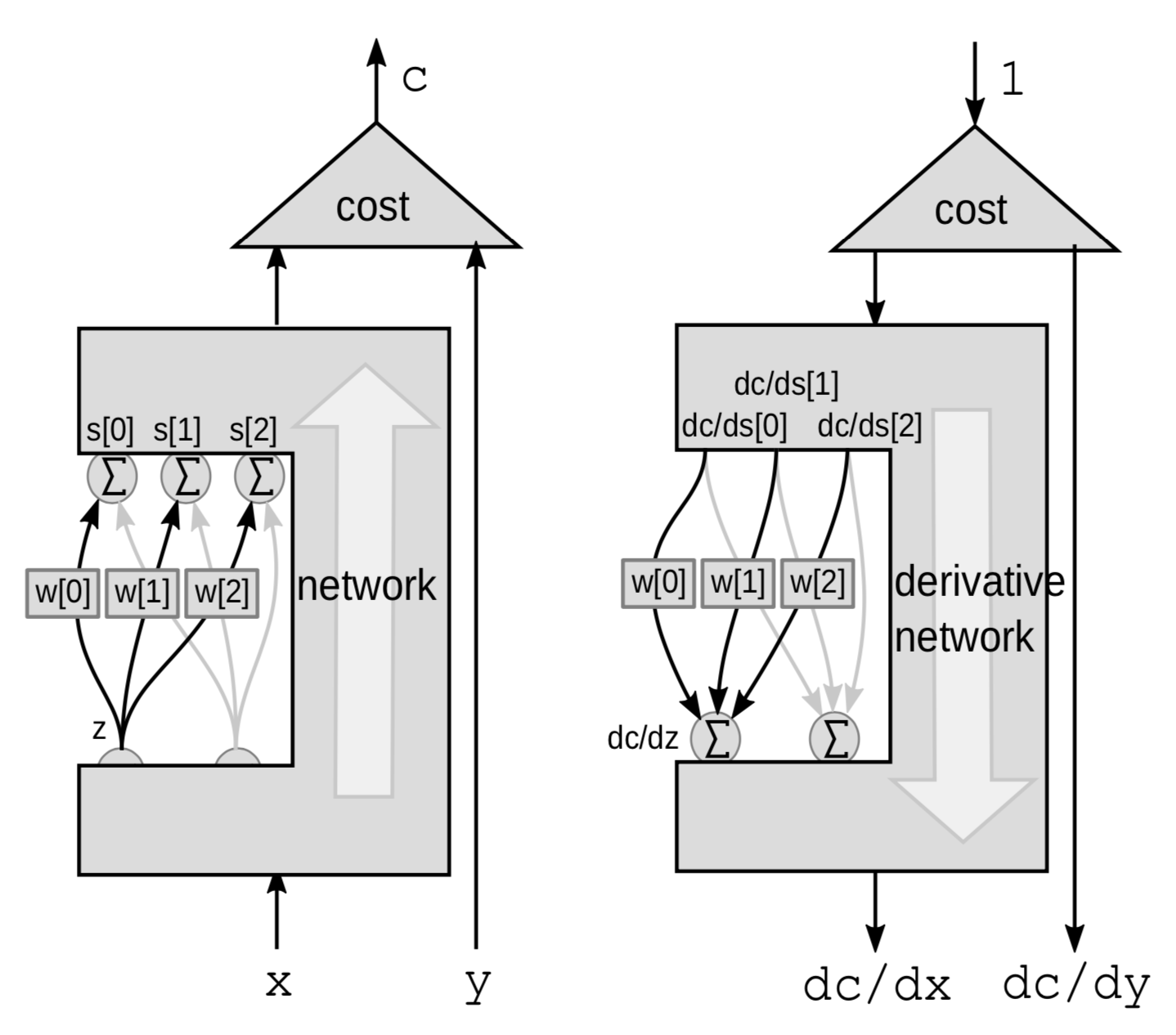这次，扰动是一个加权和。 $z$ 会对多个变量造成影响。 对 $z$ 施加扰动 $\mathrm{d}z$，对相应对 $s[0]$，$s[1]$ 和 $s[2]$ 施加如下扰动：

相似地，这会对 $C$ 施加如下扰动：

因此 $C$ 会受到三个变量的影响而改变。

一个神经网络和反向传播的PyTorch实现

一个传统神经网络的方块图表示

• 线性模块表示为 $s_{k+1}=w_kz_k$

• 非线性模块表示为 $z_k=h(s_k)$

  

$w_k$ 是矩阵； $z_k$ 是向量； $h$ 是一个函数，它对输入的每一个元素调用 ${h}$ 函数。 如图所示是一个三层神经网络，这个神经网络由一系列的线性-非线性函数对组成。 大多数现代神经网络并不像图中所示的例子一样具有这么清晰的结构，它们一般来说要更加复杂。

PyTorch实现

import torch
from torch import nn
image = torch.randn(3, 10, 20)
d0 = image.nelement()

class mynet(nn.Module):
    def __init__(self, d0, d1, d2, d3):
        super().__init__()
        self.m0 = nn.Linear(d0, d1)
        self.m1 = nn.Linear(d1, d2)
        self.m2 = nn.Linear(d2, d3)

    def forward(self,x):
        z0 = x.view(-1)  # flatten input tensor
        s1 = self.m0(z0)
        z1 = torch.relu(s1)
        s2 = self.m1(z1)
        z2 = torch.relu(s2)
        s3 = self.m2(z2)
        return s3
model = mynet(d0, 60, 40, 10)
out = model(image)

• 运用PyTorch，我们可以用面向对象的方法来实现神经网络。 首先，我们定义一个神经网络的类，在构造方法中，可以用PyTorch里用定义的 nn.Linear 类去初始化线性层。 我们需要分别为每一个线性层定义不同的对象，因为每个对象会包含自己的参数向量。 nn.Linear类还提供了偏置向量，它会被加到输出里。 接下来，我们定义一个前向传播函数，我们用 $\text{torch.relu}$ 作为非线性激活函数。 我们不用定义多个 ReLU 函数，因为它不包含参数，所以可以被共用。

• 我们不用自己自己算梯度，因为PyTorch会根据我们提供的前向传播函数，自己计算用于反向传播的梯度。

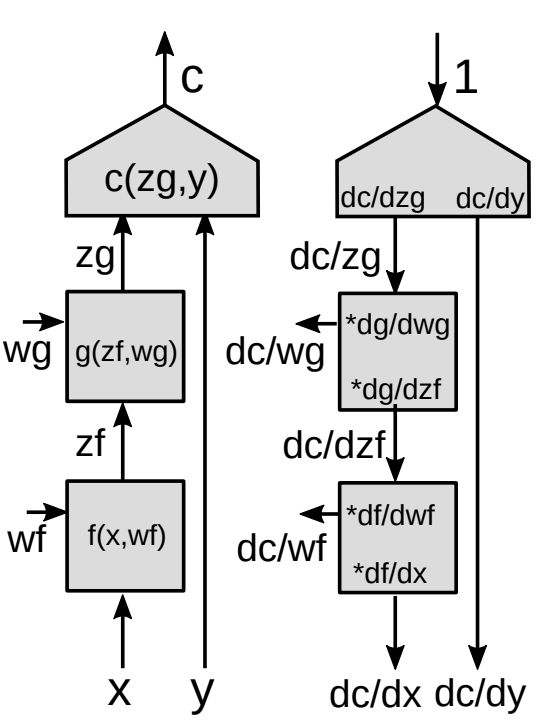
对于一个模块进行反向传播

下面我们展示一个反向传播的例子。

图8: 对模块进行反向传播

• 在向量函数中使用链式法则

  \[z_g : [d_g\times 1]\] \[z_f:[d_f\times 1]\] \[\frac{\partial c}{\partial{z_f}}=\frac{\partial c}{\partial{z_g}}\frac{\partial {z_g}}{\partial{z_f}}\] \[[1\times d_f]= [1\times d_g]\times[d_g\times d_f]\]

这是利用链式法则计算 $\frac{\partial c}{\partial{z_f}}$ 的基本公式。 值得注意的是，一个标量对于一个向量的梯度，是一个和这个向量同样形状的一个向量。 我们统一用行向量而非列向量去表示这些向量。

• 雅可比矩阵（一阶偏导数矩阵）

  \[\left(\frac{\partial{z_g}}{\partial {z_f}}\right)_{ij}=\frac{(\partial {z_g})_i}{(\partial {z_f})_j}\]

  利用 $\frac{\partial {z_g}}{\partial {z_f}}$ (雅可比矩阵的元)，通过已知代价函数对于$z_g$的梯度，我们可以计算代价函数对于 $z_f$ 的梯度。 每一个元 $ij$ 等于输出向量的第$i$个元素对于输入向量第$j$个元素的偏导数。

  当网络中有一系列串联的模块，我们可以在每一层用乘雅可比矩阵的方法一路向下，从而得到每个变量的梯度值。

对于多层结构的反向传播

设想一个由多个模块堆叠的神经网络，如图9所示。

图9: 对于多层结构的反向传播

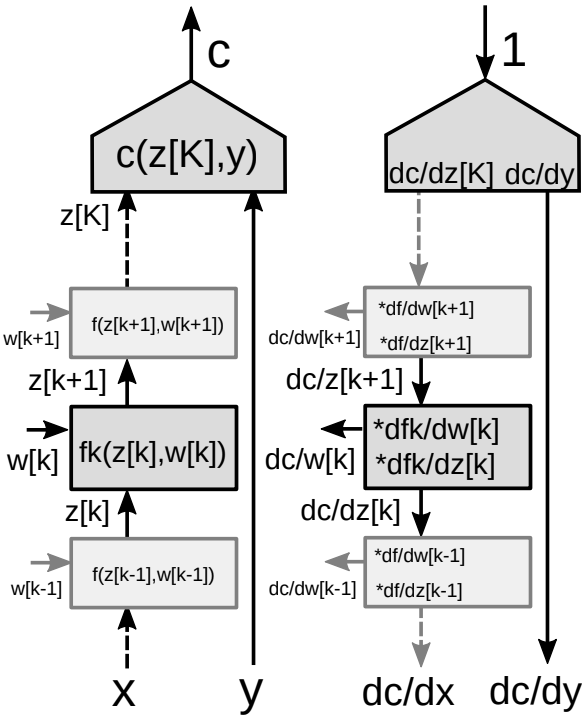在反向传播算法中，我们需要两套梯度：一套是对于状态（网络中的每一个模块）的梯度，另一套是对于权值（某一个模块中所有的参数）的梯度值。 因此，对于每个模块，我们需要两个雅可比矩阵。 这里我们再次利用链式法则完成反向传播。

• 对向量函数使用链式法则

  \[\frac{\partial c}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {z_k}}\] \[\frac{\partial c}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {w_k}}\]

• 模块中的两个雅可比矩阵
  • 对于 $z[k]$
  • 对于 $w[k]$