问题动机、线性代数与视觉化
资源
请在推特上跟随 Alfredo Canziani @alfcnz。影片、讲述线性代数与奇异值分解(SVD)相关细节的课本都可以在 Alfredo 的推特上找到,比如在搜索栏输入linear algebra (from:alfcnz)。
变换与其动机
让我们看看一个图像分类的例子。比方我们用一个一百万像素的相机拍一张照片,这张图片铅直、水平各有约 1000 个像素,而每个像素会有红绿蓝三个色彩的维度。每个图像因此就可以当作三百万维空间中的一点。在这样大的维度中,许多我们想分类的有趣图像——像是狗对上猫——必然会在空间中的相同区域中。
为了有效分离这谢图像,我们考虑对资料进行一些变换以移动这些资料点。请回想一下,在二维空间中,一个线性变换等同于矩阵乘法。例如下列这些线性变换:
- 旋转(当矩阵为正交矩阵)
- 缩放(当矩阵为对角矩阵)
- 反射(当行列式为负值)
- 错切
值得注意的是,平移不是一个线性变换,因为原点不会保留在原处,但它是仿射变换。再回到我们的图像例子,我们可以先平移使各点移动到 0 的周遭,再用对角矩阵缩放来放大那个区域,最后,我们就能寻找能分割空间将各点分到各自的类别的直线。亦即,藉由线性与非线性的转换,将资料点映射到一个使他们线性可分的空间。下个部份我们会更具体的说明这个想法。
资料视觉化 - 通过神经网路将不同颜色的点分离
我们的视觉化展现的是由五个股组成的螺旋,每个股对应不同颜色。这些点在一个二维平面中,可以用元组来代表;这些颜色代表第三个维度,或者当作是各点的类别。接着我们可以用一个网路来分开不同颜色的点。
 |
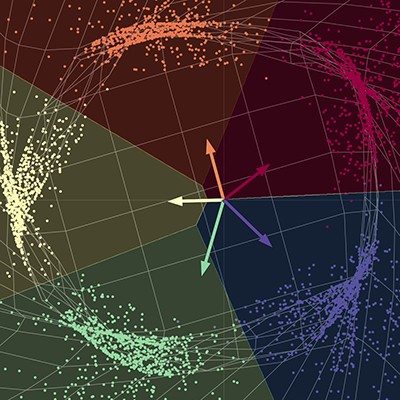 |
| (a) 输入各点,通过网路前 | (b) 输出各点,通过网路后 |
这个网路会拉伸空间以使各点能被分离. 当收敛时,网路会把每种颜色分开至最终流形中的不同子空间。也就是说,新的空间中的每个颜色,对于一对全的回归都是线性可分的。图中的这些向量可以用一个 5 x 2 的矩阵表示;这个矩阵乘上每个点产出属于五种不同颜色的分数,于是每个点可以再以它们的分数分为不同颜色。这里输出维度是五,每个颜色有一个;输入维度则是二,对应 x 与 y 坐标。总之,这个网路对空间进行变换,而这种变换可参数化为数个矩阵与非线性变换。
网路结构
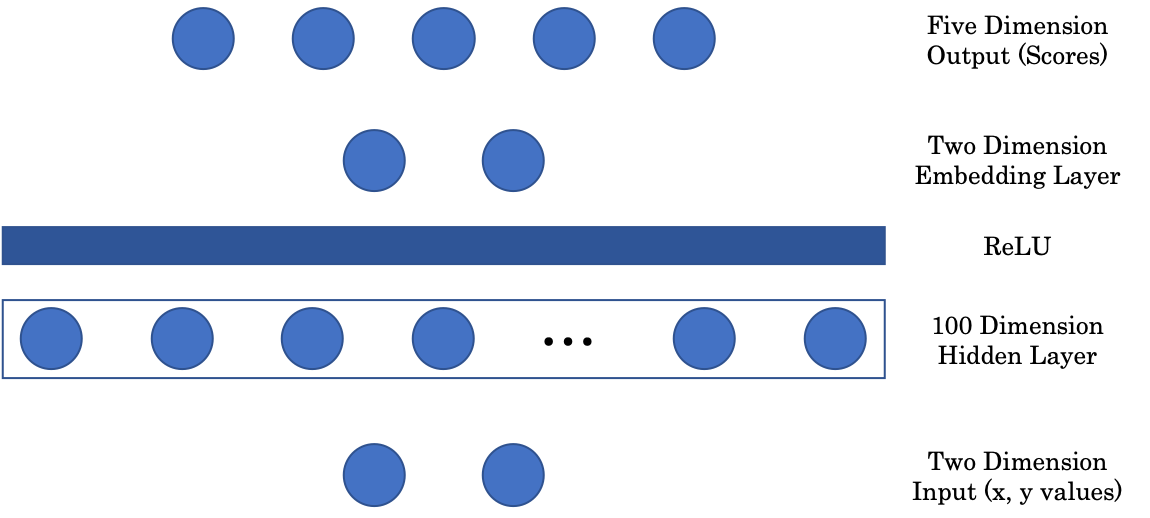
图 2: 网路结构
第一个矩阵将 2 维的输入映射到 100 维的隐藏层。接着加上一个非线性层:ReLU,即 Rectified Linear Unit,就是一个输出输入大于零部分的函数$(\cdot)^+$。接下来,为了用图片的方式显示图像,我们用一个嵌入层来将 100 维的隐藏层映射到 2 维的输出。最后,嵌入层被投影到 5 维的最后一层,每个维度代表各个颜色的分数。
随机投影 - Jupyter Notebook
你可以在这里找到这个 Jupyter Notebook。如果要运行这个 notebook,请先依照README.md指明地方法安装pDL环境。
PyTorch device
PyTorch 可以在 CPU 以及 GPU 上运行。CPU 擅长处理序列型的工作,GPU 则善于平行运行的工作。在想要的装置上执行前,我们要先把张量和模型转移到那个装置的记忆体中。下面两行的代码可以完成这个工作:
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
X = torch.randn(n_points, 2).to(device)
第一行创造一个名叫device的变数,并且如果有可用的 GPU 就置入其中;否则就使用 CPU。下一行中,我们建立了一个张量并且放入装置的记忆体中,藉由呼叫.to(device)。
Jupyter Notebook 小技巧
按Shift + Tab.以在 notebook cell 中查看函式的文件。
将线性变换视觉化
回想一下,一个线性变换可以用矩阵来表示。藉由奇异值分解,我们可以把这个矩阵分解成三个成分矩阵(component matrix),每个都代表一个不同的线性变换。
\[W = U\begin{bmatrix}s_1 & 0 \\ 0 & s_2 \end{bmatrix} V^\top\]在等式 (1), 矩阵 $U$ 和 $V^\top$ 是正交的,表示旋转和镜射变换。中间的矩阵则是一个对角的缩放矩阵。
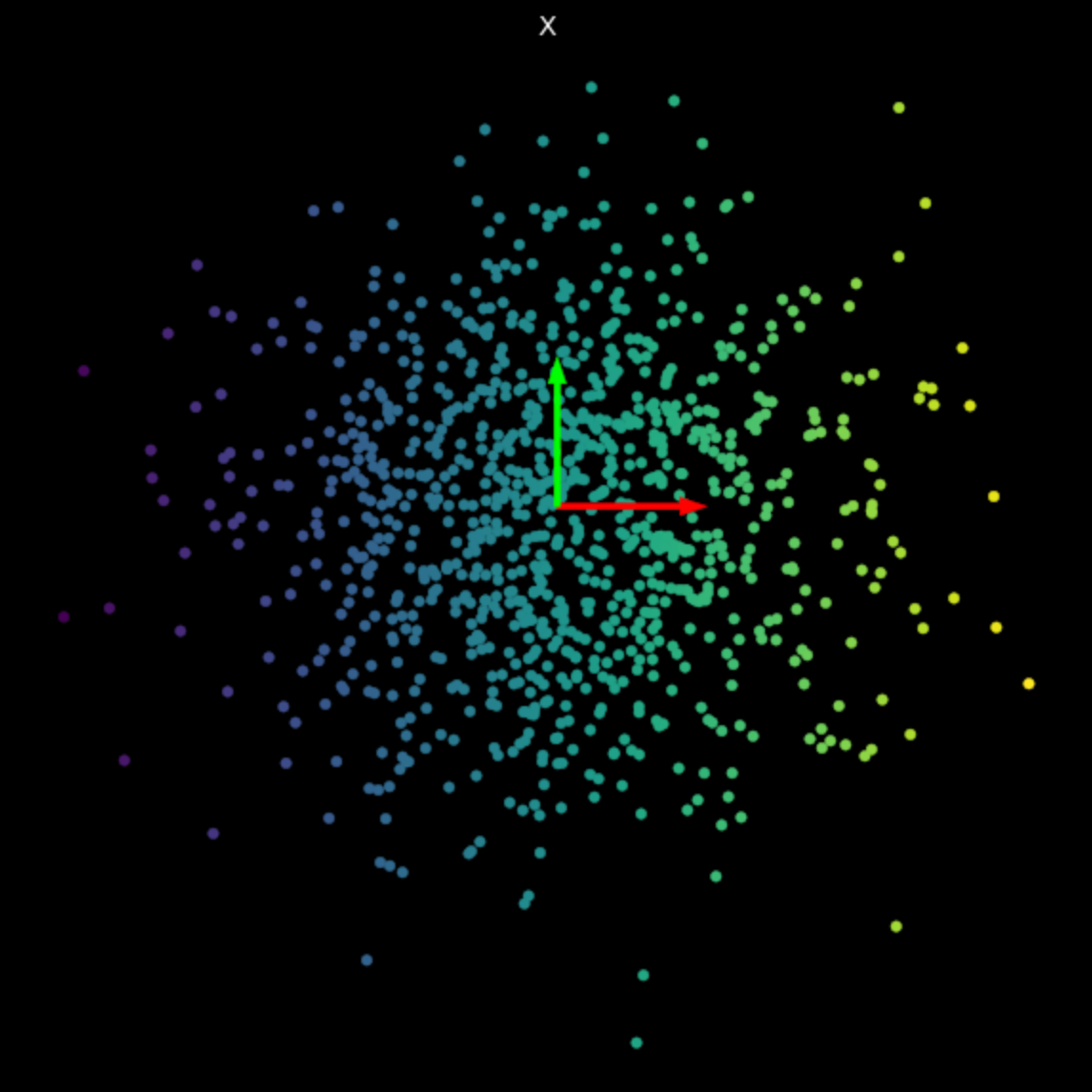
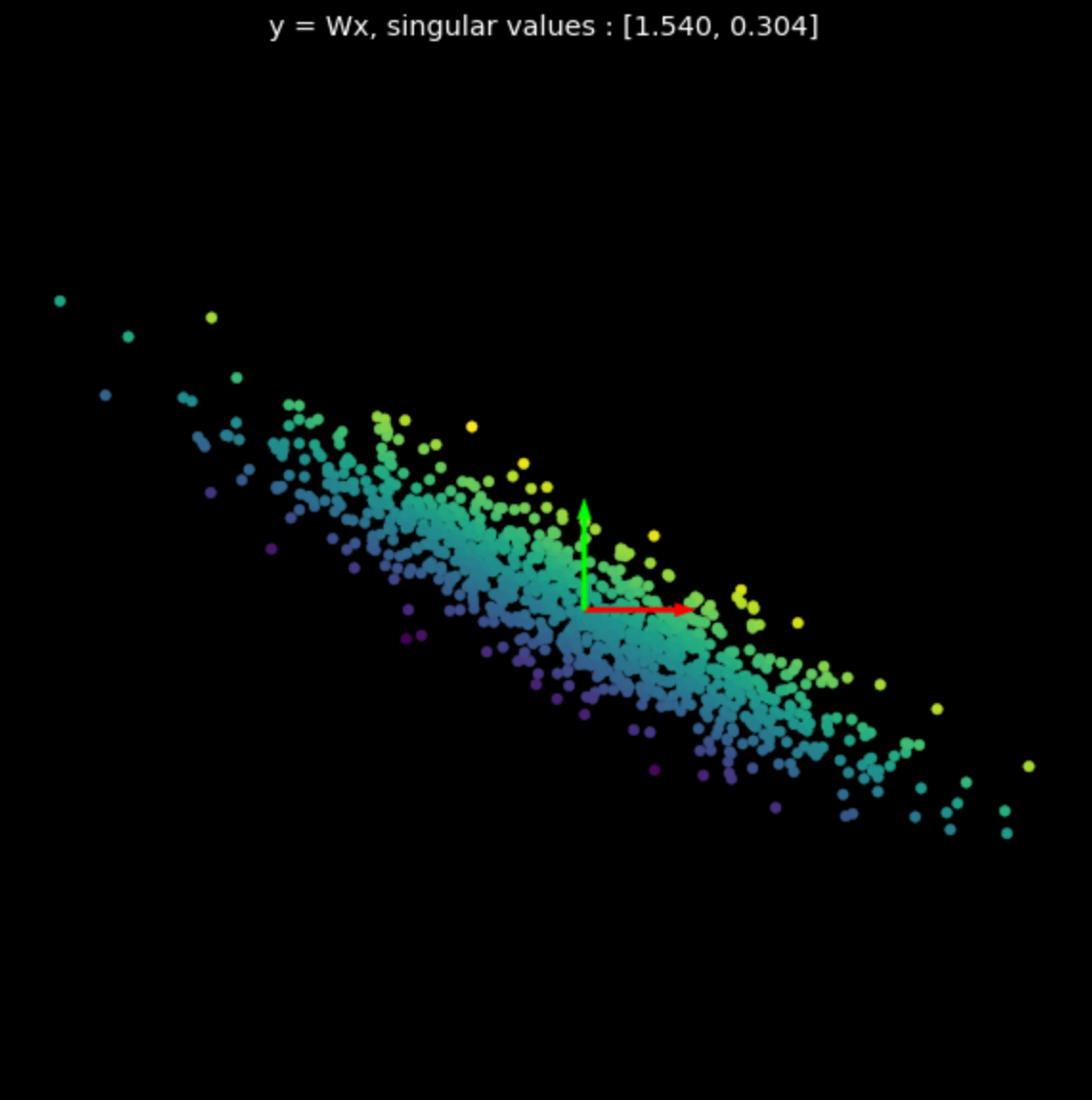
在图 3 中,我们视觉化数个随机矩阵进行的线性变换。请注意奇异值对于它对应的变换的影响。
这里我们用 Numpy 来产生这些矩阵;但我们也可以用 PyTorch 的nn.Linear 类别(设定bias = False)来建立线性变换。
 |
 |
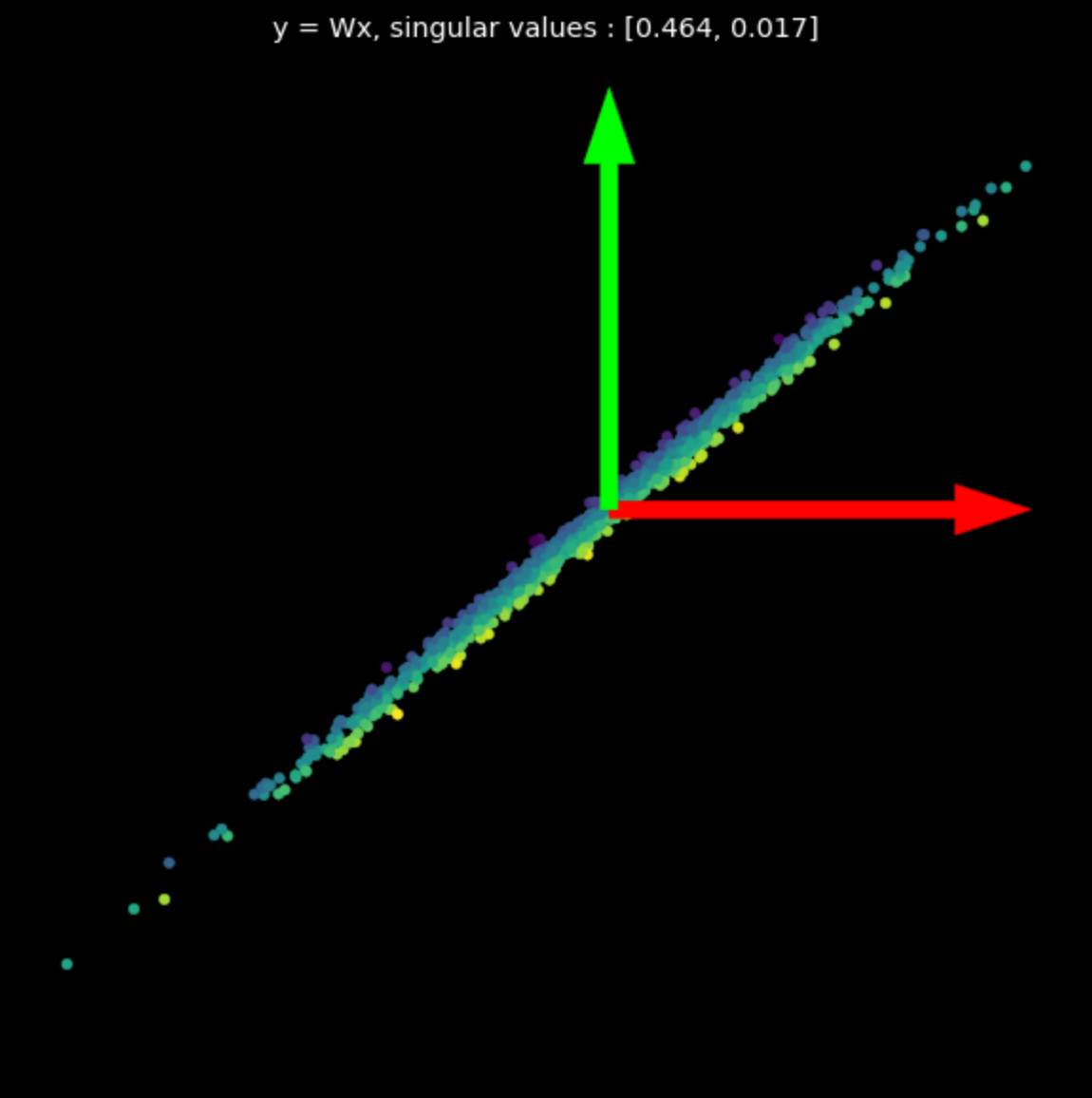 |
| (a) 原来的点 | (b) $s_1$ = 1.540, $s_2$ = 0.304 | (c) $s_1$ = 0.464, $s_2$ = 0.017 |
非线性变换
接下来我们要视觉化这个变换: \(f(\vx) = \tanh\bigg(\begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix} \vx \bigg)\) 请回忆 $\tanh(\cdot)$ 的图形(参考图 4)
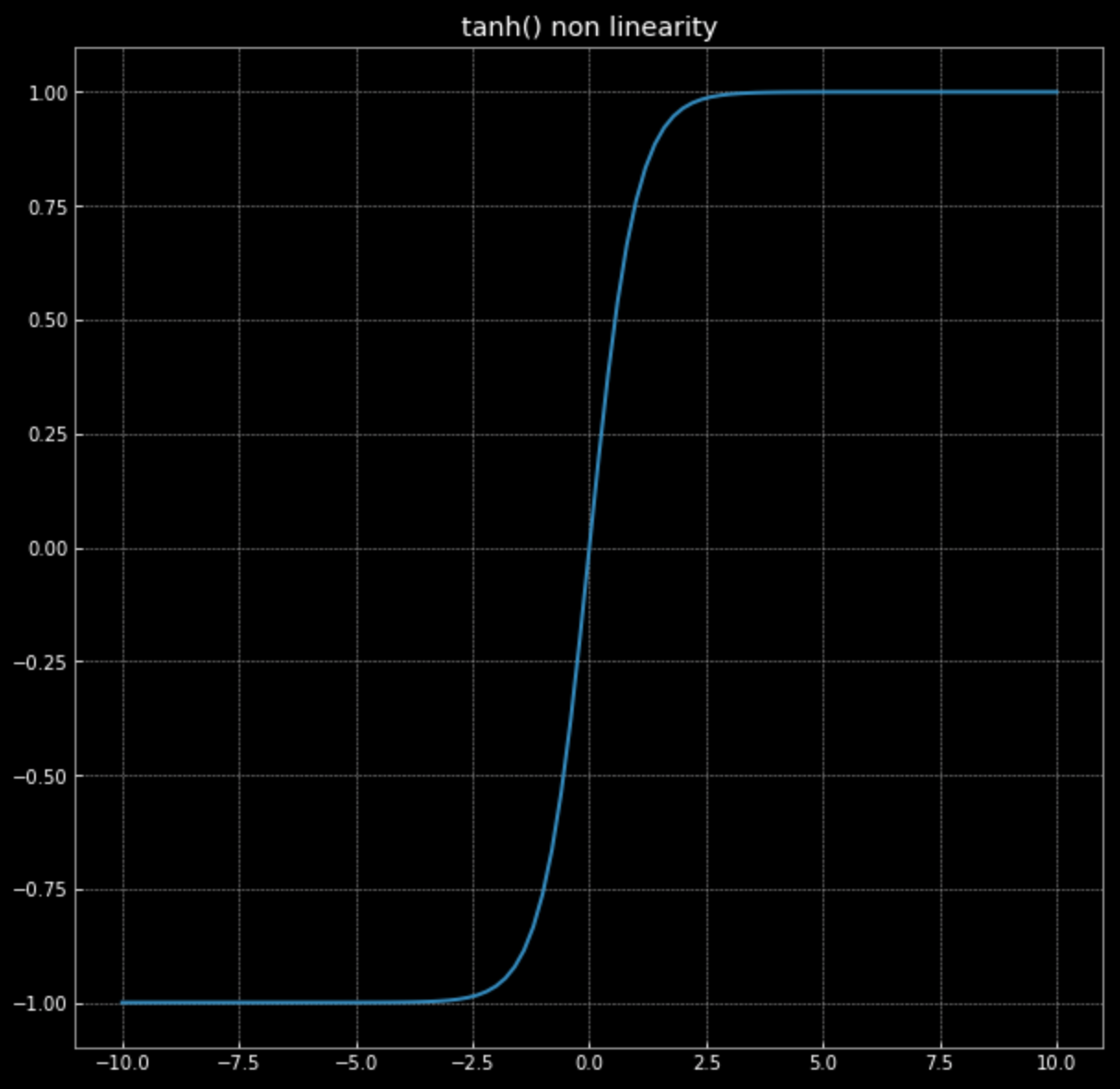
图 4:非线性函数--hyperbolic tangent
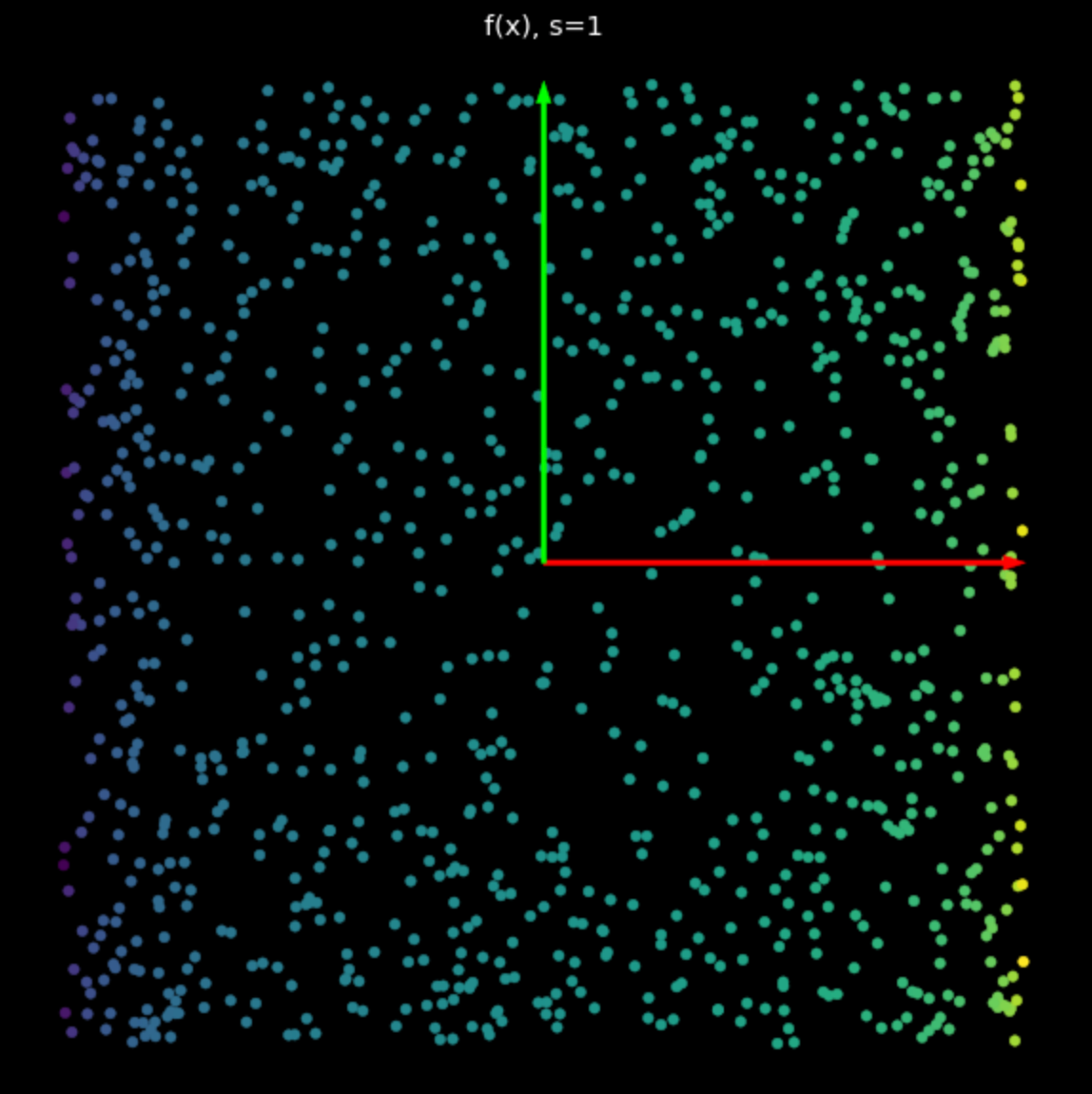
这个非线性的功能是将各点限制在 $-1$ 和 $+1$ 之间,形成一个方形。当方程式 (2) 中 $s$ 的值增加,愈来愈多的点会被推到方形的边上,我们可以在图 5 看到。藉由把更多的点推到边缘,我们把这些点更加的扩展开,能够接着来分类它们。
 |
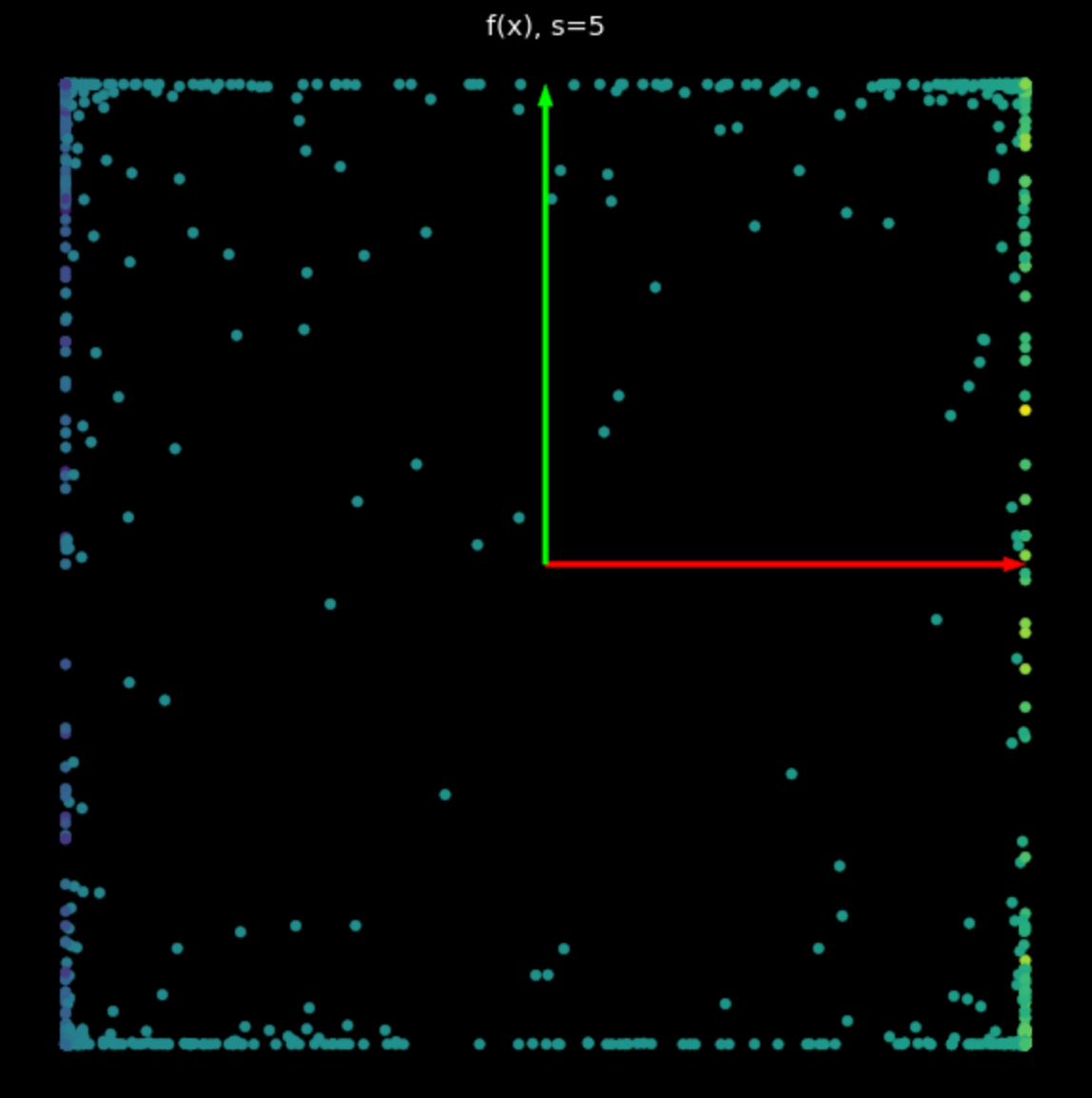 |
| (a) $s=1$ 时的非线性 | (b) $s=5$ 时的非线性 |
随机的神经网路
最后,就让我们来视觉化一个单纯、未训练的神经网路所进行的变换。这个网路包含一个线性层--进行仿射变换--一个 tanh 的非线性,以及另一个线性层。仔细看看图 6 中的变换,我们发现它不同于先前看见的线性和非线性变换。之后我们会看到如何让神经网路所进行的变换完成分类的目标。
图 6: 未训练的神经网路所进行的变换
Titus Tzeng
28 Jan 2020