Grafiksel Enerji-Bazlı Modeller
🎙️ Yann LeCunKayıp Fonksiyonlarının Karşılaştırılması
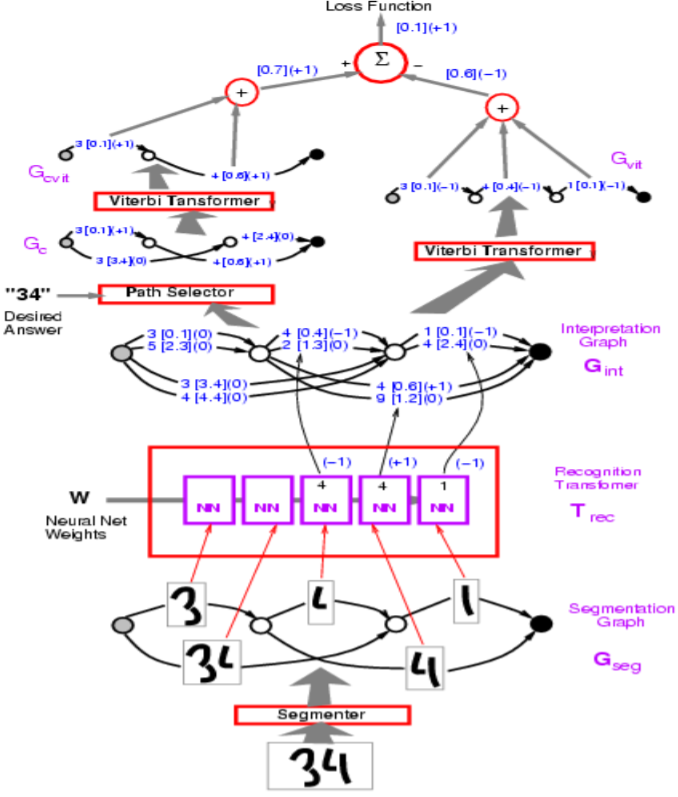
Figure 1: Ağ Mimarisi
Yukarıdaki figürde yanlış yollar -1 değerine sahiptir.
Profesör LeCun ilk olarak yukarıdaki Çizge Dönüştürücü Modelinde kullanılan algılayıcı (perceptron) kaybı ile başlıyor. Burada hedef, yanış cevapların enerjilerini büyütmek ve doğru cevapların enerjilerini küçültmektir.
Kodlarken, her bir oku bir vektör olarak düşünmelisiniz. Her bir kategori için ayrı bir oktan ziyade, tek bir vektör hem kategorileri hem de herbirk ategori için uygun skoru tutabilir.
Soru: Yukarıdaki modelde bölütleyici (segmenter) nasıl implement edilmiştir?
Cevap: Bölütleyici önceden tanımlanmıştır. Model bölütleyicinin bu tanımına rağmen uçtan uca eğitilebilir hale getirilebilir. Bu el yapımı yaklaşımın yerini, karakter tanıma için kayan pencere yaklaşımı almıştır.
Kayıp Fonksiyonlarına Genel bir Bakış
| Kayıp denklemi | Formül | Marjin |
|---|---|---|
| Enerji kaybı | $\text{E}(\text{W}, \text{Y}^i, \text{X}^i)$ | None |
| Algılayıcı | $\text{E}(\text{W}, \text{Y}^i, \text{X}^i)-\min\limits_{\text{Y}\in\mathcal{Y}}\text{E}(\text{W}, \text{Y}, \text{X}^i)$ | 0 |
| menteşe | $\max\big(0, m + \text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)$ | $m$ |
| Log | $\log\bigg(1+\exp\big(\text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)$ | >0 |
| LVQ2 | $\min\bigg(M, \max\big(0, \text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)$ | 0 |
| MCE | $\bigg(1+\exp\Big(-\big(\text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\Big)\bigg)^{-1}$ | >0 |
| Square-Square | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i)^2-\bigg(\max\big(0, m - \text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)^2$ | $m$ |
| Square-Exp | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i)^2 + \beta\exp\big(-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)$ | >0 |
| NNL/MMI | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i) + \frac{1}{\beta}\log\int_{y\in\mathcal{Y}}\exp\big(-\beta\text{E}(\text{W}, y,\text{X}^i)\big)$ | >0 |
| MEE | $1-\frac{\exp\big(-\beta E(W,Y^i,X^i)\big)}{\int_{y\in\mathcal{Y}}\exp\big(-\beta E(W,y,X^i)\big)}$ | >0 |
Algılayıcı hatasının marjini sıfırdır, ve bu da fonksiyonun çökme riskinin olduğunu göstermektedir.
- Menteşe kaybı da ien istenmeyen cevap ile doğru cevabın enerjileri arasındaki farkı hesaplar. Mantıken, m marjini ile menteşe kaybı, doğru cevabın enerjisi en rahatsız edici cevabın enerjisinden en az m daha düşük olduğundan 0 değerine ulaşacaktır.
- MCE kayıbı konuşma tanımada kullanılmakta olup, sigmoid e benzemektedir.
- NLL kaybı ise doğru cevabın enerjisini küçültürken, denklemi logaritmalı kısmının enerjisini de büyütmeye çalışır.
TANIM:
Bir çözücü (decoder) seslerin veya görüntülerin skorları/enerjileri ifade eden vektörler dizisini girdi olarak alır, ve olabilecek en iyi çıktıyı seçer. Soru: Çözücü kullanan problemlere örnek hangi problemler verilebilir ? Cevap: Dil modellemesi, makine tercümesi, ve dizi etiketleme. <!–
DEFINITION:
A decoder inputs a sequence of vectors that indicate the scores or energy of individual sounds or images, and picks out the best possible output. Q: What are some examples of problems that can use decoders? A: Language modelling, machine translation, and sequence tagging. –>
Çizge dönüştürücü ağlarında ileri algoritma
Çizge Bileşimi
çizge bileşimi, iki çizgeyi birleştirmemizi sağlar. Bu örnekte bir dil modeli sözlüğü, $trie$ (bir çizge) ve bir sinir ağı ile üretilen bir tanımlama çizgesi ile ifade edilmektedir.
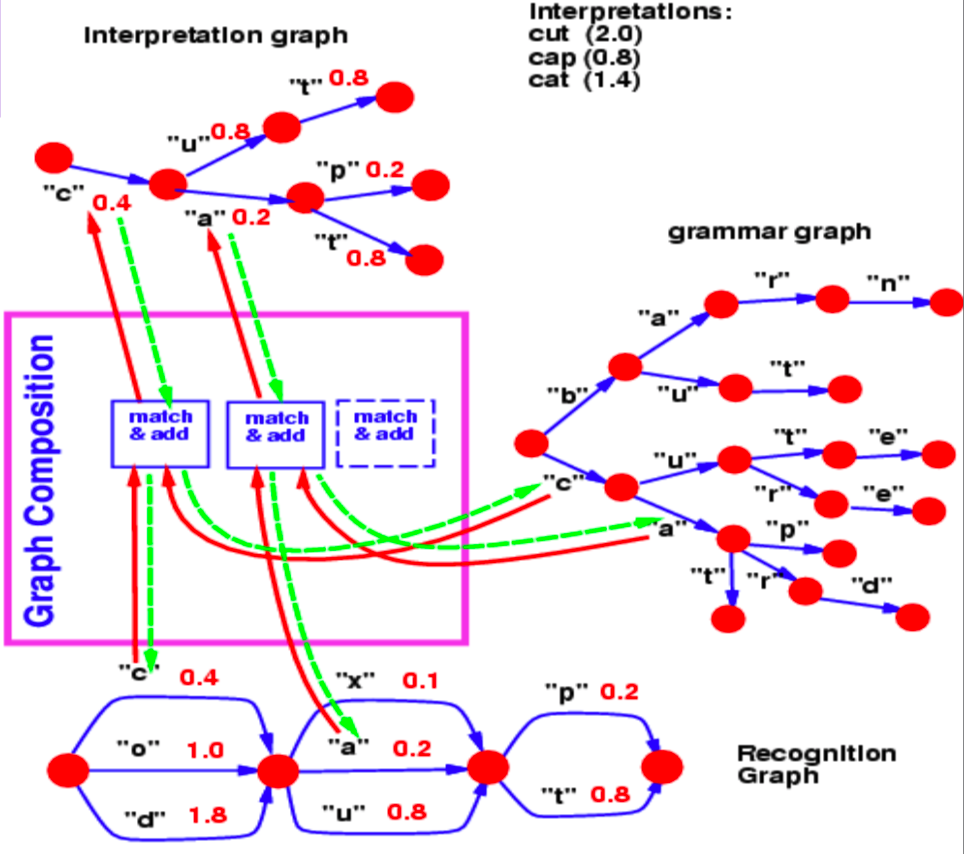
Şekil 2: Çizge Bileşimi
Tanımlama çizgesi, belli bir adımdaki karakterin ne kadar olası olduğunu fakrlı enerji değerleri ile ifade eder.
Bu örnek için, çizge bileşim işlemiyle cevaplamaya çalıştığımız soru, algılama çizgesinde sözlüğümüzle bağdaşan en iyi yol nedir?
Algılama çizgesi ile gramer arasında, birinci adımdan ikinci adıma giderkenki ortak sıçrama, $c$ karakteri e bu karakterin enerjisi 0.4. Bu yüzden, yorumlama çizgemiz, iki adım arasında $c$ karakterini temsil eden 1 tane ok bulundurur. Benzer bir biçimde, algılama çizgesinde 2. ve 3. adımlar arasındaki olası karakterler $x$, $u$ ve $a$. Gramer çizgesinde $c$ karakterini takip eden dallanmalar $u$ ve $a$’yı içerir. Yani çizge bileşimi, yorumlama çizgesinde $u$ ve $a$ nın bulunduğu okları seçer. Ayrıca tanıma grafiğinden kopyaladığı yayı enerji değerleri ile ilişkilendirir.
Eğer gramer oklara ait enerji değerlerini de içerseydi, çizge bileşimi bu enerji değerlerini eklerdi ve başka bir işlem aracılığıyla birleştirirdi.
Benzer bir biçimde, çizge bileşimi sinir ağlarıyla ifade edilen iki bilgi kaynağını da birleştirmemizi desağlayabilir. Yukarıdaki örnekte, gramer aslında sonraki karakteri tahmin etmekte kullanılan bir sinir ağı gibi düşünülebilir. Sinir ağının softmax çıktısı bize verilen bir noktadan diğer karaktere geçiş olasılıklarını vericektir.
Yan not olarak, bu örnekteki dil modeli bir yapay sinir ağıdır, ve yapısı üzerinden geri yayılım gerççekleştirebiliriz. Bu da döngüler , koşullar, özyinelemeler içeren programlar üzerinden geri yayılım yaapbildiğimiz türevlenebilen programlara bir örnektir.
90’ların ortasından kalma bir okuyucu <!–
The entire architecture of a check reader from the mid-90s is quite complex, but what we are primarily interested in, is the part starting from the character recogniser, which produces the recognition graph.
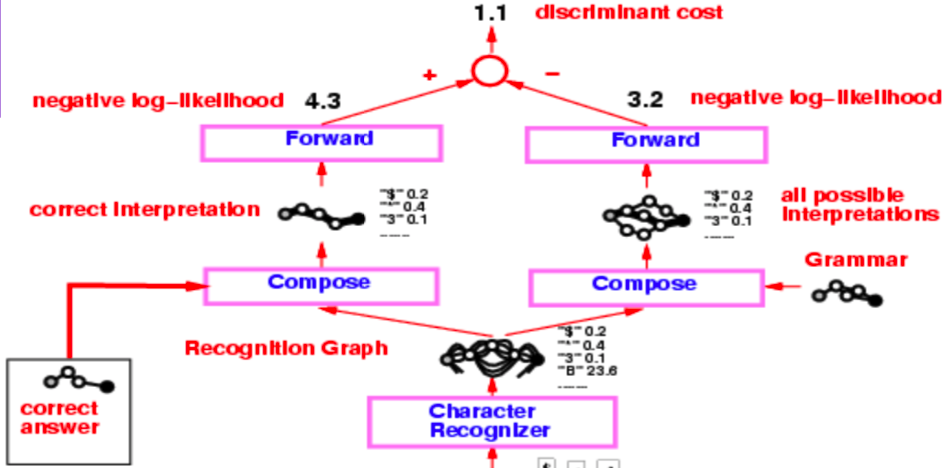
Figure 3: Check reader
This recognition graph undergoes two separate composition operations, one with the correct interpretation (or the ground truth) and second with the grammar which creates a graph of all possible interpretations. The entire system is trained via the Negative Log-Likelihood loss function. The negative log-likelihood says that each path in the interpretation graph is a possible interpretation and sum of energies along that path is the energy of that interpretation. Now, instead of using the Viterbi algorithm, we use the forward algorithm. The following sub-sections discuss the differences between the two approaches. –>
Bir okuyucunun 90’ların ortasından kalma mimarisi oldukça karmaşıki fakat bizi ilgilendiren kısım, algılama çizgesini oluşturan karakter algılayıcıdan başlayan kısım.

Figure 3: Okuyucu
Algılama çizgesi iki ayrı birleştirme işleminden geçer: biri doğru yorumlama( veya gerçek doğruluk) ile ve ikincisi ise tüm olası yorumlamaların çizgesini oluşturan gramer ile.
Tüm sistem, negative log-olabilirlik kayıp fonksiyonuyla eğitildi. Negatif log-olabilirlik, yorumlama çizgesindeki her bir yol aslında olası bir yorumlama olup o yoldaki enerjilerin toplamı açıklamanın enerjisini verir.
Viterbi algoritmasının yerine ileri algoritmayı kullanacağız. Sonraki ksıımlar, bu iki yöntemin farkını anlatmakta.
Viterbi algoritması
Viterbi algoritması, verilen bir çizgede en olası yolu(veya minimum emerjiye sahip yolu) bulmak için kullanlan bir dinamik programlama algoritmasıdır. Enerjiyi çizgede aldığımız yolu ifade eden saklı değişken z’ye göre minimize eder. \(F (x, y) = \min_{z} \; E(x, y, z)\)
İleri algoritma (The forward algorithm)
İleri algoritma, tüm yollardaki negatif enerjilerin log-toplam-exponansiyeli aşağıdaki gibi hesaplar:
\(F_{\beta} (x, y) = -\frac{1}{\beta} \; \log \; \sum_{z \, \in \, \text{paths}} \; \exp \, (- \beta \; E(x, y, z))\)
Diğer bir değişle, saklı değişken z üzerinden marjinalleştirme gerçekleştiriyor, bu işlem de algılama çizgesindeki yolları tanımlamamızı sağlıyor. Bu yöntem ile belli bir noktaya giden tüm yolların log-toplam-exponansiyelini hesaplar. Bu tüm olası yolların bedellerini narin bir şekilde toplamak gibi.
İleri algoritmanın implementasyonu basit ve viterbi algoritmasından daha verimlidir. Ayırca, çizgedeki ileri algoritmanın düğümü üzerinden geri yayılım gerçekleştirebiliriz.
İleri algoritmanın çalışmasını aşağıda tanımlanmış olan yorumlama çizgesinde görebiliriz.
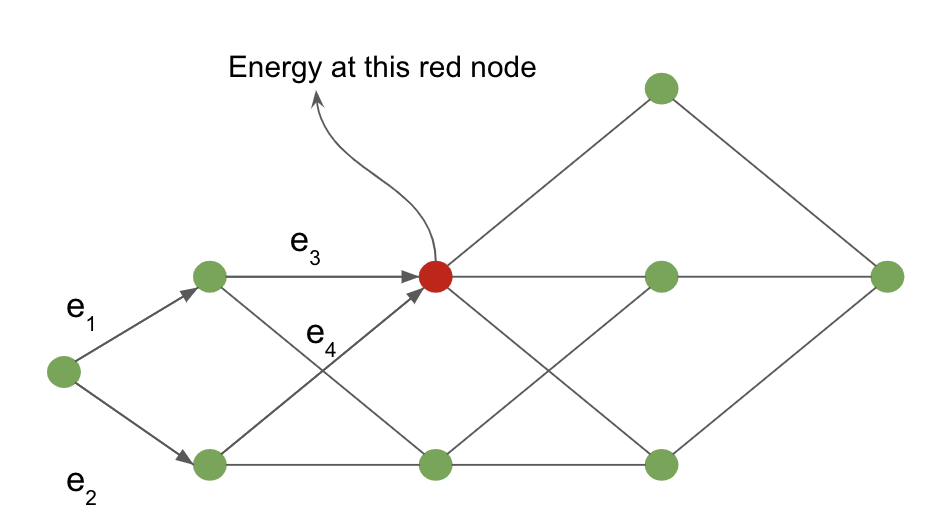
Şekil 4: Yorumlama çizgesi
Girdi noktasından kırmızı gölgeli noktaya olan hasar, kırmızı noktaya varan tüm yollar üzerinden marjinalleştirerek hesaplanır. Kırmızı noktaya giren tüm oklar, örneğimizdeki tüm olası yolları ifade eder.
Kırmızı nokta için enerji aşaıdaki gibidir: \(-\frac{1}{\beta} \; \log \; [ \, \exp \, (- \, \beta (e_1 \, + \, e_3)) \; + \; \exp \, (- \, \beta (e_2 \, + \, e_4)) \, ]\)
İleri algoritmanın Sinir Ağı Benzetmesi
Yapının altında yatan çizge zincir yapısına sahip ise, ileri algoritma aslında inanç yayılım (belief propagation) algoritmasının özel durumudur. Bu algoritma aslında ileri beslemeli sinir ağı gibi düşünülebilir: her bir noktada log-toplam-exponansiyel ve bir toplama işlemi var.
Yorumlama çizgesindeki her bir düğüm için bir $\alpha$ değişkeni tutuyoruz:
\[\alpha_{i} = - \; \log \; \biggl[ \sum_{k \, \in \, \text{parent} \, (i)} \; \exp \, (- \, \beta \; (\alpha_k \, + \, e_{ki})) \biggl]\]burada $e_{ki}$ $k$ noktasından $i$ noktasına giden okun enerjisidir..
$\alpha_i$, sinir ağındaki $i$ düğümünün aktivasyonunu oluştururken $e_{ki}$ ise $k$ ve $i$ düğümleri arasındaki ağırlığı ifade eder. Bu formülasyon cebirsel olarak sinir ağlarındaki ağırlıklı toplamaya denktir, ama logaritmik uzayda.
İleri algoritmayı uyguladığımız dinamik yorumlama ağı (örnekle değişmekte) üzerinden geriyayılım gerçekleştirebiliriz. $F(x,y)$’nin çizgenin son noktasından hesaplanan ve $e_{ki}$ ağrılıklarına göre gradyanlarını hesaplayabiliriz.

Şekil 5: Okuyucu
Okuyucu örneğinde ileri algoritmayı iki çizgenin bileşimini uygular ve son noktanın enerjisini log-toplam-exponansiyel işlemi uygulayarak ile elde edebiliriz. Enerji değerlerinin arasındaki fark bize negatif log-olabilirlik kaybını verir.
Çizge bileşimine uygulanan ileri algortima sonucu elde ettiğimiz değer, doğru cevabın log-toplam-exponansiyelidir. Hatta, çizge algılama çizgesi ile gramerin bileşiminin son noktasının log-toplamexponansiyeli aslında tüm olası yorumlamalar üzerinde marjinalize edilmiştir.
Geri yayılımın Lagrangian formülasyonu
Girdi $x# ve hedef çıktı $y$ için ağımızı fonksiyonların kolleksiyonu $f_k$ ve ağırlıklar $w_k$ ile ifade edebilir ve ağın çıktısı $z_k$’yı ardışık adımlar ile $z_{k+1} = f_k(z_k, w_k)$ modelleyebiliriz. Denetimli öğrenmede ağın amacı $C(z_n, y)$2i minimize etmek yani n’inci çıktının gerçek doğruya göre bedelini küçültmek. Bu problem, $C(z_n, y)$’yi sınırlamalarımız $z_{k+1} = f_k(z_k, w_k)$ ve $z_0 = x$’ye göre minimize etmeye denktir.
Lagrangian aşağıdaki gibi yazılabilir: \(\mathcal{L}(x, y, \lambda_i, z_i, w_i) = C(z_n, y) + \sum\limits_{k=0}^{n-1} \lambda^T_{k+1}(z_{k+1} - f_k(z_k, w_k))\)
burada $ \lambda $ Lagrange çarpanlarını ifade etmekte (Hatırlama amaçlı Paul’s online notes yardımcı olacaktır).
$\mathcal{L}$’yi minimize etmek için, $\mathcal{L}$’nin her bir argümanına göre olan kısmi türevlerini sıfıra eşitleyip çözmeliyiz.
- Lagrange çarpanı $\lambda$ için, sınırlamayı elde ederiz: $\frac{\partial{\mathcal{L}}}{\partial \lambda_{k+1}} = 0 \rightarrow z_{k+1} = f_k(z_k, w_k)$.
- $z_k$ için, $\frac{\partial \mathcal{L}}{\partial z_k} = 0 \rightarrow \lambda^T_k - \lambda^T_{k+1} \frac{\partial f_k(z_k, w)}{\partial z_k} \rightarrow \lambda_k = \frac{\partial f_k(z_k, w_k)^T}{\partial z_k}\lambda_{k+1}$, bu da bildiğmiiz geri yayılımın formülüdür.
Bu yöntem, klasik mekanikte Lagrange ve Hamilton tarafından bulunmuştur ve bu alanda sistemin enerjisini minimize etmeye çalışırken $\lambda$ terimleri sistemin fiziksel sınırlarını ifade etmek için (örneğin iki topun metal bir çubukla tutturulması nedeniyle birbirinden sabit bir mesafede kalmaya zorlanması) kullanılmakta. Eğer her bir zaman adaımında kaybımız $C$’yi minimize etmemiz gerekirse yeni Lagrangian’ımız aşağıdaki gibidir: \(\mathcal{L} = \sum_k \left(C_k(z_k, y_k) + \lambda^T_{k+1}(z_{k+1} - f_k(z_k, w_k)) \right)\). –>t
Neural Diferansiyal Denklemler
Geri yayılımın bu formülasyonu ile, yeni bir model üzerine konuşabiliriz. Neural Diferansiyel denklemler (Neural ODE)‘ler, yinelemeli sinir ağları olup, durumu $z$’nin $t$ zamanındaki $z$, at time $t$ is given by $ z_{t+\text{d}t} = z_t + f(z_t, W) dt $, burada $ W$ bazı sabit parametreleri temsil etmekte. Bu yapı, diferansiyel denklemler ile ifade edilebilir (parçalı türev yok ): $\frac{\text{d}z}{\text{d}t} = f(z_t, W)$.
Böyle bir ağı Lagrangian formülasyonu ile eğitmek oldukça kolay. Eğer hedefimiz $y$ varsa ve sistemin $T$ sürede hedefimize ulaştığı durumu istiyorsak yapmamız gereken tek şey $z_T$ ve $y$ arasındaki mesafeyi bedel fonksiyonu olarak tanımlamaktır. Bu ağların başşka bir amacı da ssitemin kararlı (stable) bir durumunu bulmak, yani belli bir noktadan sonra değişmeyen durumlar. Matematiksel olarak bu özelliğin sağlanması için $\frac{\text{d}z}{\text{d}t} = f(y, W) = 0$ koşulu sağanmalı. Denklemin çözümü $y$yi bulmak zaman üzerinden geriye yayılım yapmaktan çok daha kolaydır çünkü ağın tüm diziye göre gradyanı hatırlama ihtiyacı yokrı ve sadece $f$’i veya $\lvert f \rvert^2$’yi minimize etmemiz yeterli olucaktır. Neural ODE’lerin eğitimi için (Lecun88) yararlı bir kaynak.
Enerjiler Üzerinden Değişimsel Çıkarım
Giriş
Enerji fonksiyonu $E(x,y,z)$ için, eğer sadece $x$ ve $y$ üzerinden bir kayba yani z değişkeni üzerinden marjinalize etmemiz gerekiyorsa, hesaplamamız gereken fonksiyon
\[L(x,y) = -\frac{1}{\beta}\int_z \exp(-\beta E(x,y,z))\]Sonra $\frac{q(z)}{q(z)}$ ile çarparsak, $L(x,y)$ aşağıdaki gibi yeniden yazılabilir. \(L(x,y) = -\frac{1}{\beta}\int_z q(z) \frac{\exp({-\beta E(x,y,z)})}{q(z)}\)
Eğer $q(z)$ z üzerinde bir olasılık dağılımı ise, yeniden yazdığımı hata fonksiyonu integralini $\frac{\exp({-\beta E(x,y,z)})}{q(z)}$ dağılımına göre ortalama bir değer gibi görebiliriz.
Bu yaklaşımı, Jensen eşitsizliğini ve örnekleme bazlı yaklaşımları, hata fonksiyonumuzu dolaylı bir şekilde optimize etmek için kullanacağız.
Jensen Eşitsizliği
Jensen Eşitsizliği geometrik bir gözlem olup şu söylemi ifade eder: Eğer konveks bir fonksiyonumuz varsa, o fonksiyonun bir bölgedeki ortalamada daldığı değer fonksiyonun aynı bölgedeki averajından küçük olacaktır. Geometrik olarak düşünürsek:
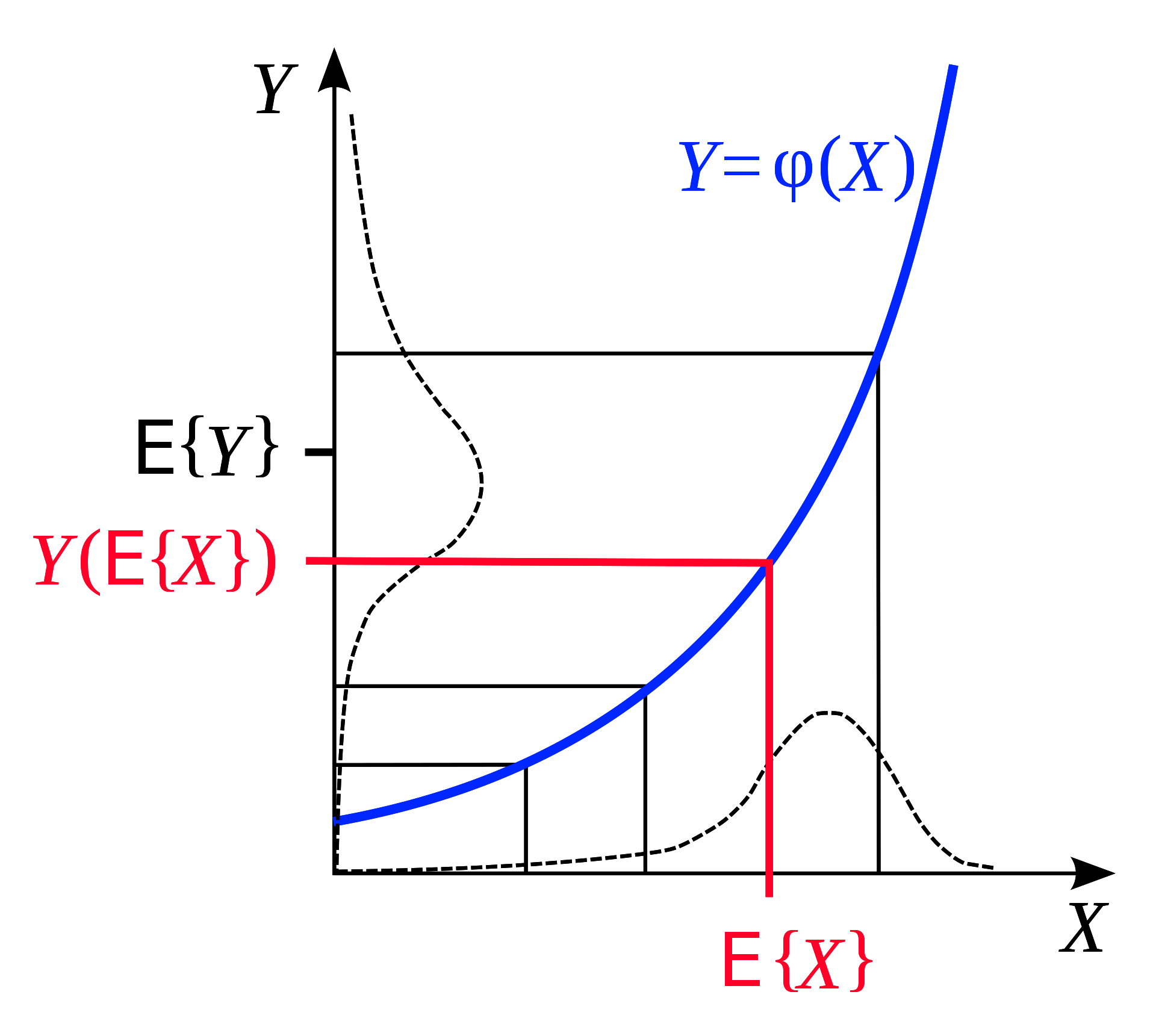
Figure 6: Jensen Eşitsizliği ( [Wikipedia](https://en.wikipedia.org/wiki/Jensen%27s_inequality)'dan alınmıştır)
Aynı şekilde, eğer $F$ sabit bit olaslılık dağılımı olan $q$ ‘ya göre konveks ise , $z$’nin aralığı için Jensen’in Eşitsizliğ’nden: \(F\Bigg(\int_z q(z)h(z)\Bigg) \leq \int_z q(z)F(h(z)) \tag{1}\) Şimdi, $\frac{q(z)}{q(z)}$ ile çarğtıktan sonra marjinalleştirilmiş $L(x,y)$’yi inceleyelim:
\[L(x,y) = -\frac{1}{\beta}\int_z q(z) \frac{\exp({-\beta E(x,y,z)})}{q(z)}\]Eğer $h(z) = -\frac{1}{\beta} \frac{\exp({-\beta E(x,y,z)})}{q(z)}$ ise, Jensen eşitsizliğinden \(F\Bigg(\int_z q(z)\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg) \leq \int_z q(z)F\Bigg(\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg)\) Şimdi, örnek olarak, konveks bir kayıp fonksiyonu $F(x) = -\log(x)$ ile çalışalım: \(-\log\Bigg(-\frac{1}{\beta}\int_z q(z)\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg) \leq \int_z q(z) * \frac{-1}{\beta}\log\Bigg(\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg)\) \(\leq \int_z q(z)[E(x,y,z) + \frac{1}{\beta}\log(q(z))]\) \(\leq \int_z q(z)E(x,y,z) + \frac{1}{\beta}\int_z q(z)\log(q(z))\)
Güzel! Artık elimizde hata fonksiyonumuz $L(x,y)$ için bir üst sınıra sahibiz ve bu sınır bildiğimiz iki terimden oluşmakta. İlk terim $\int_z q(z)E(x,y,z)$ ortalama enerjidir. İkinici terim $\frac{1}{\beta}\int_z\log(q(z))$ ise sadece faktör($-\frac{1}{\beta}$) ile dağılım $q$’nun entropisinin çarpımıdır.
Amaç?
Şimdi, karmaşık integrallerden kaçınabileceğimiz ve bunun yerine kendi seçtiğimiz bir dağılımdan ($q(z)$) örnekleyerek integralleri yaklaşık olarak tahmin edebileceğimiz bir şekilde bir üst sınır bulduk!
Üst sınır fonksiyonunun ilk teriminin değeri için, önce o dağılımdan örnek alıyor sonra bu örnek ile $L$’nin ortalama değerini hesaplıyoruç
İkinci terim (entropi faktörü) ise seçtiğimiz dağılım sonucu ortaya çıkmıştır, ve $q$’dan rastgele örnekler çekerek yakınsayabiliriz.
Son olarak, $L$’yi parametrelerine göre minimize etmek için $L$ yi yukarıdan sınırlayan fonksiyonu minimize etmemiz yeterli olucaktır. Bu işlem için iki değişkenimizi güncelliyporuz: (1) $q$’nun entropisi ve (2) model parametreleri $W$.
Özet
Burada değişimsel çıkarımın (variational inferece) “enerji” açısından ele aldık. Eğer exponensiyallerin toplamının logiatmasını hesaplamanız gerekiyorsa, foksiyonun ortalaması ile entropy terimini dikakte almamız yeterlidir. Bu bize bir üst sınır vericektir. Sonra, bu üst sınırı minimize ederek aslında istediğimiz fonksiyonu da minimize etmiş oluyoruz.
📝 Yada Pruksachatkun, Ananya Harsh Jha, Joseph Morag, Dan Jefferys-White, and Brian Kelly
emirceyani
4 May 2020