Yapılandırılmış Kestirim için Derin Öğrenme

Yapılandırılmış Kestirim (Structured Prediction)

Burada problemimiz, skaler, ayrık veya gerçek değerler yerine karşılıklı bağımlı ve sınırlandırılmış belirli bir x girdisi verildiğinde çıktı y’yi elde etmektir. Çıktı değişkeni tek bir kategoriye ait olmayıp üstel veya sonsuz sayıda olası değere sahiptir. Örnek olarak, konuşma/el yazısı tanımada veya doğal dil işlemede, çıktının gramer bakımından doğru olması gerekiyor ve çıktı olasılıklarının sayısını sınırlamamız mümkün değil. Modelin görevi, problemdeki sıralı, uzaysal veya kombinasyonel yapıyı öğrenebilmektir.

Yapılandırılmış kestirim üzerine ilk çalışmalar

Girdiyi ifade eden vektörümüzü Zaman Kayması Sinir Ağı’na (Time Delay Neural Network, TDNN) gönderip bir öznitelik vektörü elde ederiz ki bu vektörü sonra bir kategoriyi temsil eden softmax ile karşılaştırabilelim. Söylenen bir kelimeyi tanımlarken karşımıza çıkabilecek bir sorun ise aynı kelimeyi farklı kişilerin farklı şekillerde ve hızlarda söyleyebilmesidir. Bu sorunu çözmek için Dinamik Zaman Yamultması (Dynamic Time Warping) kullanılmıştır.

Buradaki ana fikir, sisteme, biri tarafından kaydedilmiş dizi veya öznitelik vektörlerine karşılık gelen önceden kaydedilmiş kalıpları vermek. Sinir ağı, kalıpla aynı anda eğitiliyor ki sistem kelimenin değişik telaffuzlarını öğrensin. Saklı değişken, öznitelik vektörünü, kalıpların uzunluğuyla eşleştirebilelim diye öznitelik vektörünün zamanını büzmemize (timewarp) olanak sağlar.

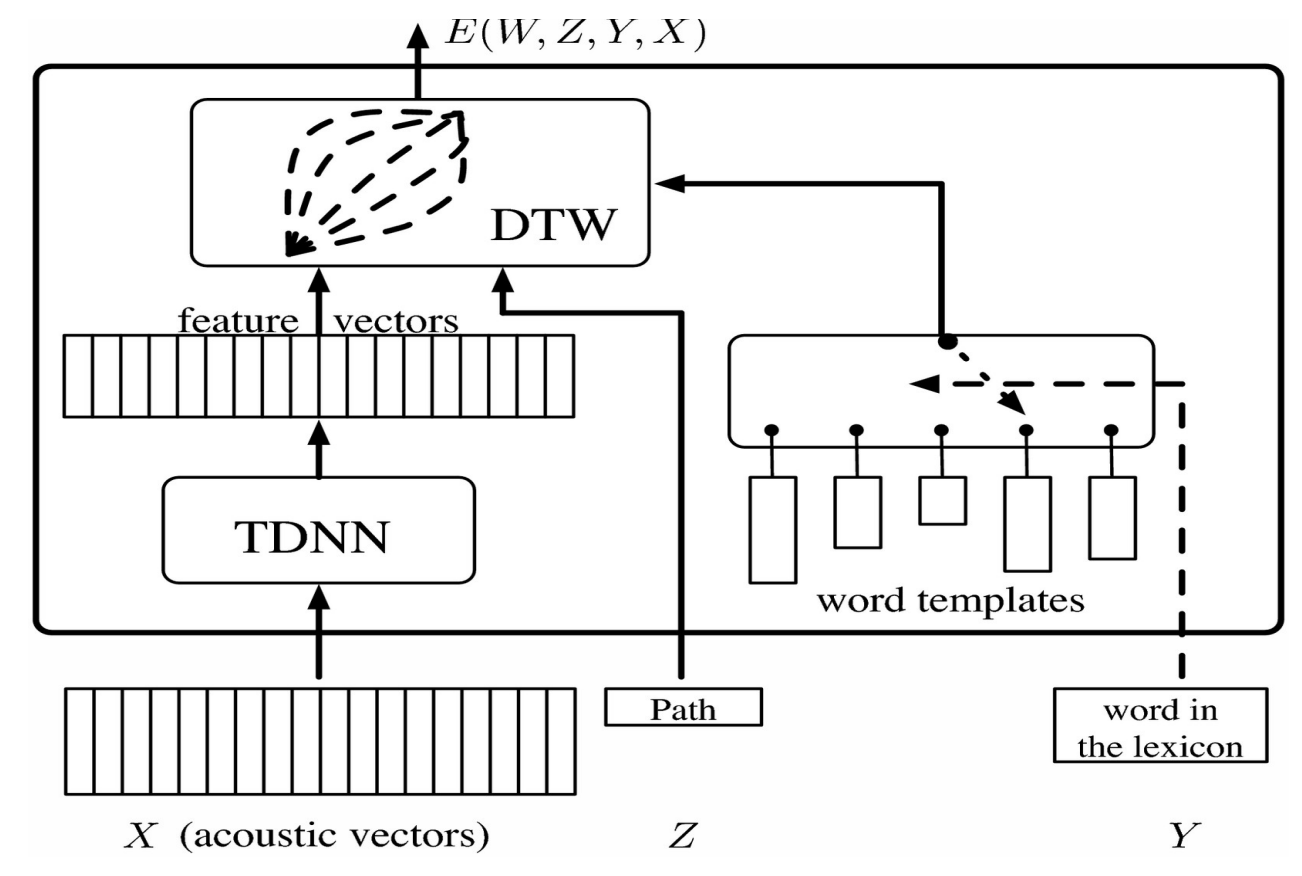
Şekil 1

Bu durumu, TDNN yapısından elde ettiğimiz öznitelik vektörlerini yatay olarak ve kelime kalıplarını dikey olarak yerleştirdiğimiz bir matris olarak görselleştirebiliriz. Bu matrisin her bir girdisi öznitelik vektörleri arasındaki mesafeye denktir. Bu matrisi de sol alt köşeden sağ üst köşeye giderken mesafeyi minimize ettiğimiz bir çizge (graf) problemi olarak düşünebiliriz.

Saklı değişken modelini eğitebilmek için, doğru cevapların enerjisini olabildiğince küçültmemiz ve tüm yanlış cevaplar için ise olabildiğince büyütmemiz gerekir. Bunun için, yanlış kelimelerin kalıplarını o anki öznitelik dizilerinden uzaklaştıran ve gradyanları geri yayan bir objektif fonksiyonu kullanmamız gerekir.

Enerji bazlı faktör çizgeleri (Energy based factor graphs)

Bu yapıların ardındaki ana fikir, enerjinin kısmi enerji terimlerinin toplamı veya olasılığın faktörlerin bir ürünü olduğu enerji bazlı bir model oluşturmaktır. Bu modellerin yararı ise verimli çıkarım algoritmaları kullanabilmemizdir.

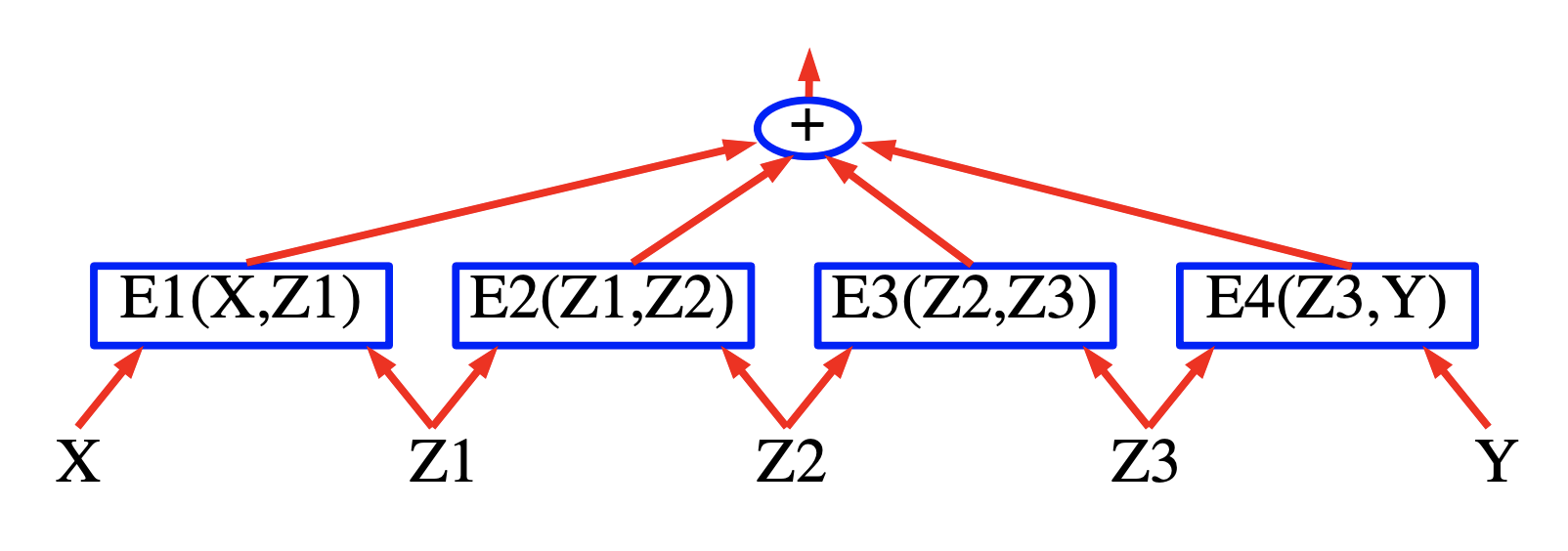
Şekil 2

Dizi Etiketleme (Sequence Labeling)

Model, konuşma sinyali X’i girdi olarak alır ve etiketleri Y’yi, toplam enerjiyi minimize edecek biçimde, çıktı olarak verir.

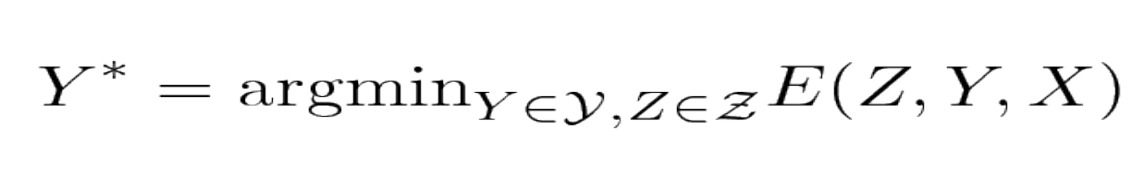
Şekil 3

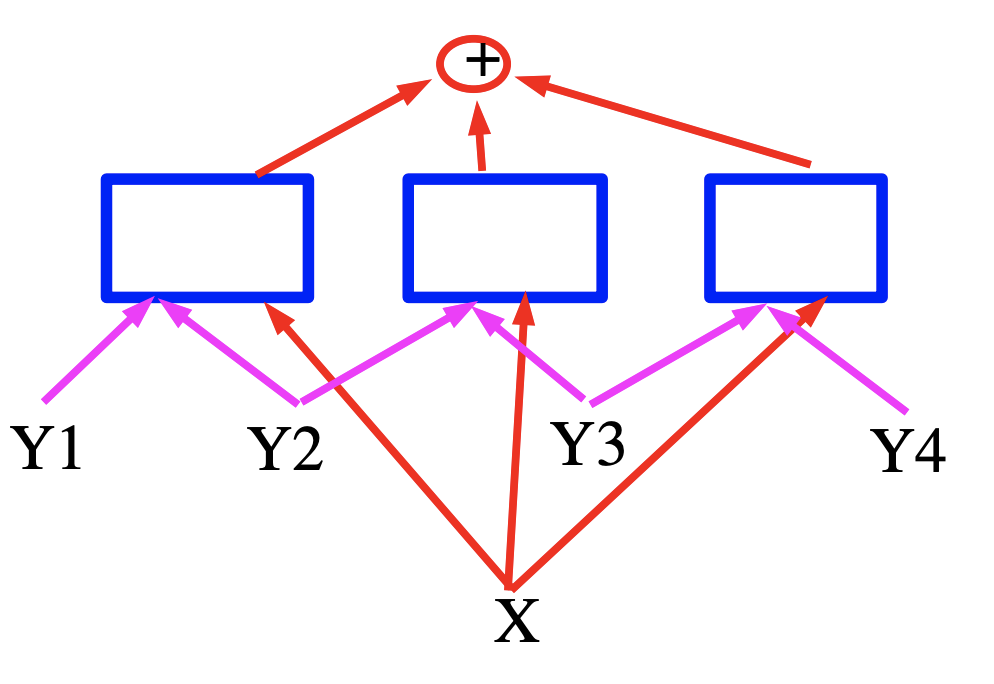
Şekil 4

Bu durumda, enerji mavi karelerle ifade edilen üç terimin toplamıdır ve mavi kareler girdi değişkenleri için öznitelik vektörleri üreten sinir ağlarıdır. Konuşma tanımada, X konuşma sinyali olarak düşünülürken kare kutular gramer sınırlamalarını ve Y ise üretilen etiket çıktılarını ifade etmektedir.

Enerji Bazlı Faktör Çizgelerinde Verimli Çıkarım

Enerji Bazlı Öğrenmeye Giriş (Yann LeCun, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, ve Fu Jie Huang, 2006):

Enerji bazlı modellerde öğrenme ve çıkarım, enerjinin cevaplar $\mathcal{y}$ ve saklı değişkenler kümesi $\mathcal{z}$ üzerinden minimizasyonuyla gerçekleşir. Kartezyen çarpım $\mathcal{y}\times \mathcal{z}$’nin kardinalitesi büyük ise, bu minimizasyon kontrol edilemez hale gelebilir. Bu probleme bir çözüm, enerji fonksiyonunun yapısını kullanarak minimizasyonu verimli bir şekilde gerçekleştirmektir. Yapının kullanılabildiği bir durum, enerjinin her biri Y ve Z’deki değişkenlerin farklı altkümelerine bağlı bireysel fonksiyonların (faktörler) toplamı olarak ifade edilebildiği zaman ortaya çıkar. Bu ihtiyaçlar en iyi şekilde faktör çizgesi (factor graph) ile ifade edilebilir. Faktör çizgeleri, grafik modellerinin genelleştirilmiş hali veya inanç ağlarıdır(belief networks).

Şekil 5

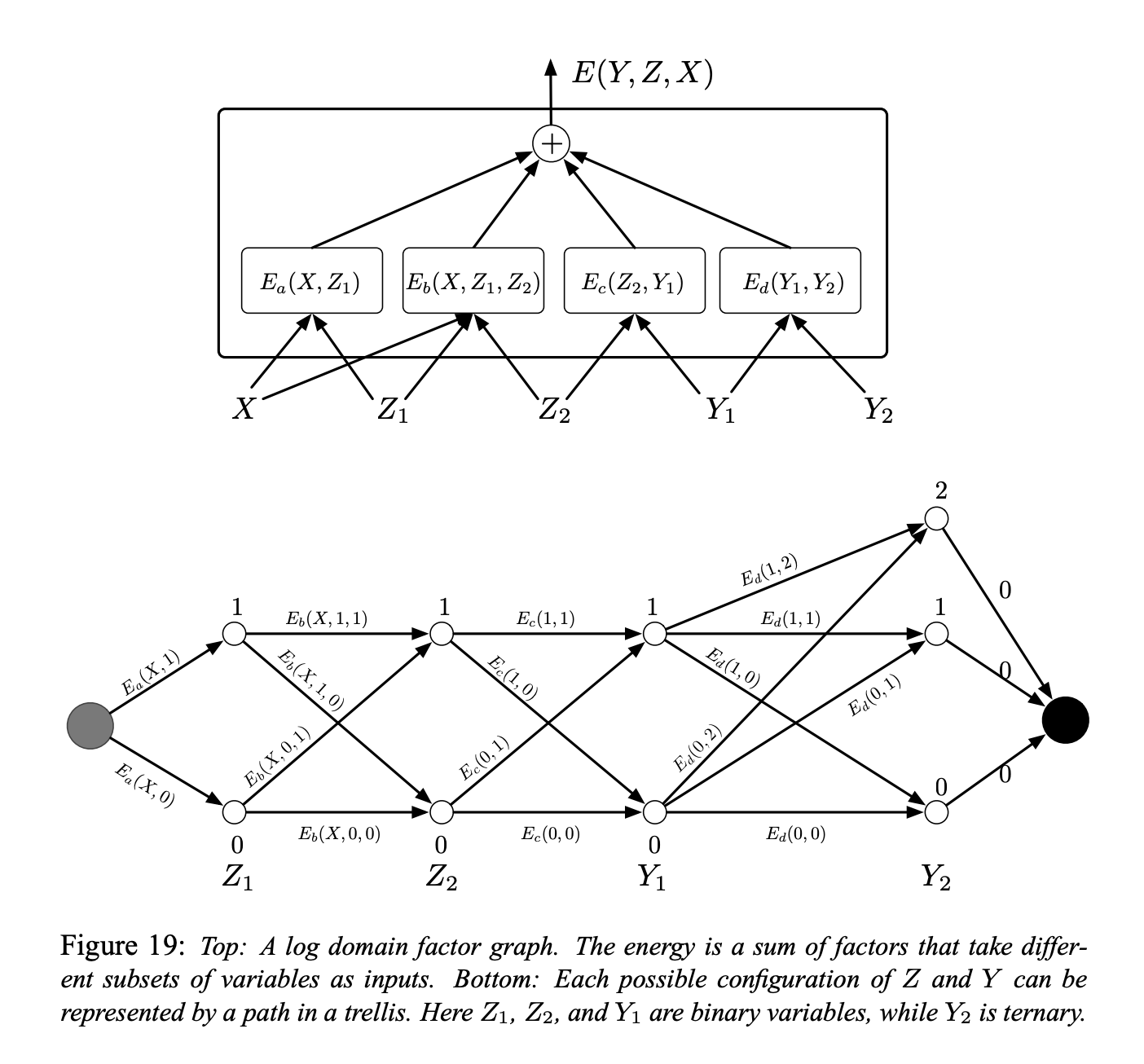
Şekil 5’te faktör çizgesi için bir örnek görebilirsiniz. Enerji fonksiyonu, 4 adet faktörün toplamı olarak ifade edilmektedir:

burada $Y = [Y_1, Y_2]$ çıktı değişkenleri ve $Z = [Z_1, Z_2]$ ise saklı değişkenleri ifade etmektedir. Her bir faktörü, girdi değişkenlerinin değerleri arasında tanımlı, hafif bir sınırlama olarak düşünebiliriz. Çıkarım problemini matematiksel olarak ifade etmek gerekirse:

$Z_1$, $Z_2$, ve $Y_1$ ayrık ikili değişkenler ve $Y_2$’yi de üçlü değişken olarak sayalım. $X$ kümesinin kardinalitesi önemsizdir çünkü X her zaman gözlemlenebilmektedir. X bilindiğinde $Z$ ve $Y$’nin olası konfigürasyonlarının sayısı $2 \times 2 \times 2 \times 3 = 24$’tür. Naif bir minizasyon algoritması, kapsamlı bir arama ile tüm enerji fonksiyonunu 24 kere (96 tane faktör hesaplaması) hesaplar.

Fakat, bize verilen $X$ ve $E_a$ sadece iki olası girdi konfigürasyonuna sahip: $Z_1 = 0$ ve $Z_1 = 1$. Aynı şekilde, $E_b$ ve $E_c$ sadece 4 ve $E_d$ sadece 6 olası girdi konfigürasyonuna sahiptir. Böylece, sadece $2 + 4 + 4 + 6 = 16$ faktör hesabı yeterli olacaktır.

Bu yüzden, önceden 16 faktör değerini hesaplayıp onları aşağıdaki Şekil 5’teki trellis diyagramındaki kavislerin üzerine yerleştirebiliriz.

Her bir sütundaki nokta (node), bir değişkenin olası değerlerini temsil eder. Her bir ayrıt (edge) ise faktörün girdisi olan değişkenlerin değerleri için açığa çıkan enerjiyle orantılıdır. Bu gösterim sayesinde, başlangıç noktasından bitiş noktasına olan bir yol, tüm değişkenlerin olası bir konfigürasyonunu temsil eder. Yol üzerindeki ağırlıkların toplamı, o konfigürasyonun toplam enerjisine eşittir. Böylelikle, çıkarım problemi, çizge üzerindeki en kısa yolu bulma problemine dönüşür. Bu problemi, bir dinamik programlama yöntemi olan Viterbi algoritmasını veya A* algoritmasını kullanarak çözebiliriz. Bedelimiz, yolların toplam sayısından oldukça küçük olan, ayrıtların sayısıyla (16) doğru orantılıdır.

$E(Y, X) = \min_{z\in Z} E(Y, z, X)$’yi hesaplamak için aynı prosedürü kullanacağız; fakat burada çizgemizi $Y$’nin önceden belirlenmiş değeriyle uyumlu olan kavislerin alt kümesiyle sınırlandırıyoruz.

Yukarıdaki prosedür bazen min-sum algoritması olarak da adlandırılır, ve grafik modelleri için kullanılan max-product algoritmasının logaritmik versiyonudur. Prosedür rahatlıkla faktörlerin girdi olarak ikiden fazla değişken aldığı aldığı faktör çizgelerine ve zincir yapısı yerine ağaç yapısına sahip olan faktör çizgelerine de genellenebilir.

Fakat, prosedür, sadece ikili ağaçlar (döngüleri olmayan) şeklinde olan faktör çizgelerine uygulanabilir. Eğer çizgede döngüler varsa, min-sum algoritması ya yaklaşık bir sonuç verir ya da sonuç veremez. Bu tarz bir durumda, benzetimli tavlama (simulated annealing) gibi bir iniş algoritması kullanılır.

Sığ Faktörler ile Basit Enerji Bazlı Faktör Çizgeleri

Şekil 6

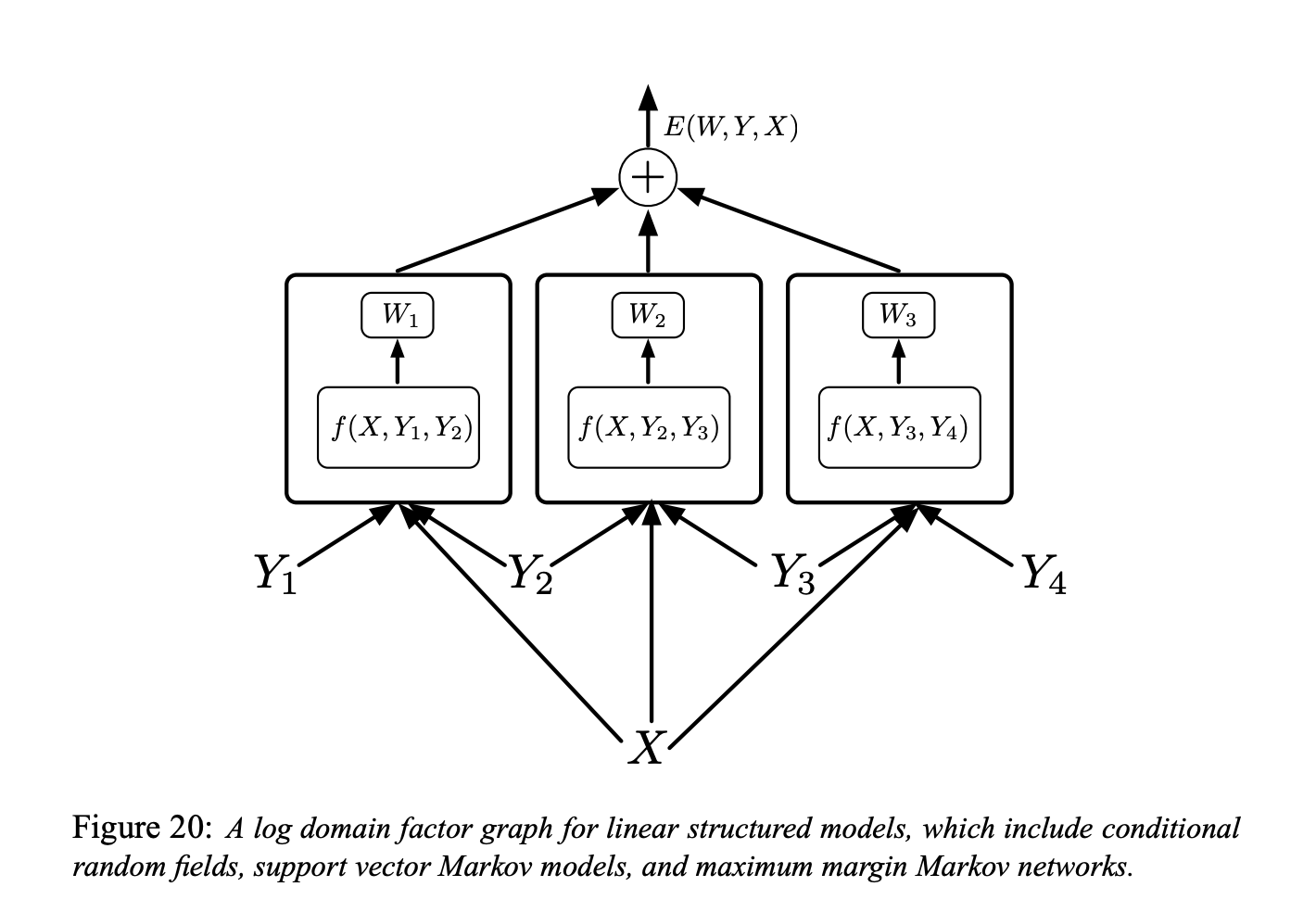
Yukarıdaki faktör çizgesi, linear yapılandırılmış modeller için logaritmik bir faktör çizgesini göstermektedir (basit enerji bazlı faktör çizgeleri).

Her bir faktör, eğitilebilen parametrelerde tanımlı bir doğrusal fonksiyondur. Faktörler, girdi $x$ ve ikili etiket çiftleri $(Y_m, Y_n)$’ne bağlıdır. Genelde, her bir faktör, ikiden fazla etikete bağlı olabilir; ancak notasyonu basitleştirmek için tartışmayı ikili faktörlerle sınırlayacağız:

Burada, $\mathcal{F}$ faktörlerin kümesini (birbirlerine doğrudan bağlı etiket ikililerinin kümesi), $W_{m n}$ faktör $(m, n)$ için tanımlı olan parametre vektörünü ve $f_{m n}\left(X, Y_{m}, Y_{n}\right)$ ise (sabit) öznitelik vektörünü temsil etmektedir. Global parametre vektörü $W$ ise tüm $W_{m n}$’lerin birleştirilmesiyle oluşturulur.

Sonrasında, farklı yitim fonksiyonları hakkında düşünebiliriz. Şimdi farklı değişik modellere değineceğiz.

Koşullu Rastgele Alanlar (Conditional Random Fields)

Negatif logaritmik olabilirlik yitim fonksiyonunu lineer yapılandırılmış bir model eğitirken kullanabiliriz. Buna da koşullu rastgele alanlar (conditional random fields) adını veriyoruz. Burada doğru cevabın enerjisinin düşük ve iyi olanın da dahil olduğu tüm cevapların üsselinin logaritmasının büyük olmasını istiyoruz.

Negatif logaritmik olabilirlik yitim fonksiyonun tanımı aşağıdaki gibidir:

Maksimum Marjin Markov Ağları ve Saklı SVM

Menteşe yitimi (Hinge loss) fonksiyonunu da optimizasyon için kullanabiliriz.

Bunun altında yatan fikir, doğru cevap için enerjinin düşük olmasını istememiz. Sonrasında, tüm yanlış cevapların olası konfigürasyonlarında yanlış veya kötü olanların arasında en düşük enerjiye sahip olanı arayacağız. Bundan sonra, bulduğumuz konfigürayonun enerjisini yükselteceğiz. Diğer kötü cevapların enerjisini zaten fazla olduğu için onların enerjilerini yükseltmemize gerek yok.

Maksimum Marjin Markov Ağları ve Saklı SVM’ler arkasındaki mantık budur. <!–

Max Margin Markov Nets and Latent SVM

We can also using the Hinge loss function for optimization. The intuition behind is that we want the energy of the correct answer to be low, and then among all possible configurations of incorrect answers, we are going to look for the one that has the lowest energy among all the wrong or the bad ones. And then we are going to push up the energy of this one. We don’t need to push up the energy for the other bad answers because they are larger anyway. This is the idea behind Max Margin Markov Nets and Latent SVM. –>

Yapılandırılmış Algılayıcı Modeli

Algılayıcı (perceptron) yitim fonksiyonunu kullanarak doğrusal yapılandırılmış bir model eğitebiliriz.

Collins [Collins, 2000; Collins, 2002] bu hata fonksiyonunun doğal dil işleme bağlamında doğrusal yapılandırılmış modellerde kullanımını savunmuştur:$$

\mathcal{L}{\text {perceptron }}(W)=\frac{1}{P} \sum{i=1}^{P} E\left(W, Y^{i}, X^{i}\right)-E\left(W, Y^{* i}, X^{i}\right) $$ burada $Y^{* i}=\operatorname{argmin}_{y \in \mathcal{Y}} E\left(W, y, X^{i}\right)$ sistem tarafından üretilen cevaptır.

Konuşma/el yazısı tanıma için ayrımcı eğitimde ilk denemeler

Minimum Empirik Hata Kaybı(Ljolje ve Rabiner, 1990): Diziler üzerinde eğitim yaparken, sisteme bu ses veya o yer gibi bilgileri söylemezler. Sisteme, girdi cümlesini ve kelimelere göre transkripsiyonunu verirler ve sistemden zamanı bükerek (time warping) bunu çözmesini isterler. Eskiden sinir ağlarını kullanmamışlardı ve konuşma sinyallerini ses kategorilerine dönüştürmenin başka yollar vardı.

Çizge Dönüştürücü Ağ (Graph Transformer Net)

Bu kısımda problemimiz, girdi olarak elimizde bir rakam dizisinin olması ve bunu nasıl bölütleyeceğimizi bilmememizdir. Yapabileceğimiz şey ise her bir yolun elimizdeki karakter dizisini ayırmanın bir yolu olduğu bir çizge oluşturmaktır ve bu çizgedeki en düşük enerjili yolu yani en kısa yolu bulacağız. Bu yöntemin nasıl çalıştığına dair somut bir örneği inceleyelim.

Elimizde girdi resmi 34 var. Bu resmi bölütleyiciden geçirip bir sürü alternatif bölütleme elde edelim. Bu bölütlemeler aslında elimizdeki parçaları gruplama yollardır. Bölütleme çizgesindeki her bir yol, elimizdeki mürekkep parçalarını birleştirebileceğimiz belirli bir yola karşılık gelmektedir.

Şekil 7

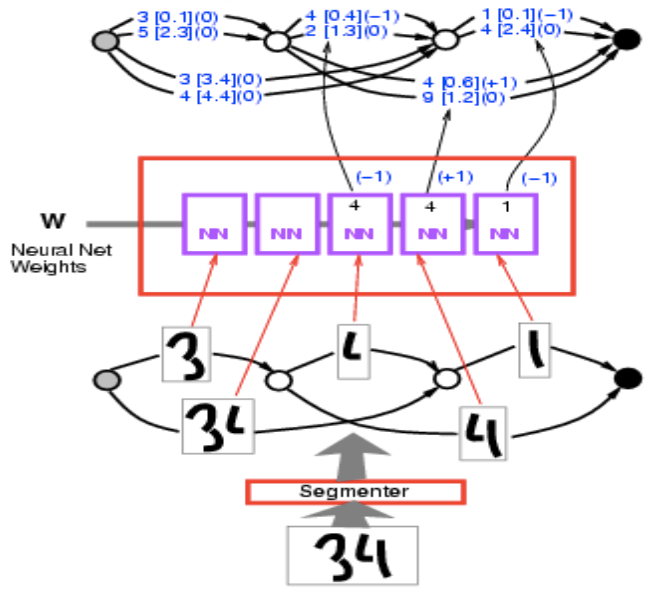
Her birini ConvNet’te aynı karakter tanımadan geçiririz ve 10 skordan oluşan bir liste elde ederiz (Burada iki tane olsa da normalde 10 kategoriyi gösteren 10 skor olmalıdır.). Örneğin, 1 [0.1] 1. kategori için enerjinni 0.1 olduğu anlamına gelir. Burada bir çizge elde ediyorum ve bu yapıyı tensörün garip bir formu olarak düşünebilirsiniz. Aslında bu yapı seyrek bir tensör. Bu tensör, bir değişkenin tüm olası konfigürasyonları için bu değişkenin bedelini bize söyleyen bir tensör. Bu, tensörler üzerinde bir dağılım veya log dağılımı çünkü enerji bazlı modeller hakkında konuşuyoruz.

Şekil 8

Bu çizgeyi ele alalım ve doğru cevabın enerjisini hesaplayalım. Size doğru cevabın 34 olduğunu söylüyorum. Yukarıdaki yollar arasından doğru cevabın 34 olduğu yolları bulun. İki tane var: birinin enerjisi 3.4 + 2.4 = 5.8, diğerinin ise 0.1 + 0.6 = 0.7. En düşük enerjili yolu seçin. Enerjisi 0.7 olan yolu seçtik.

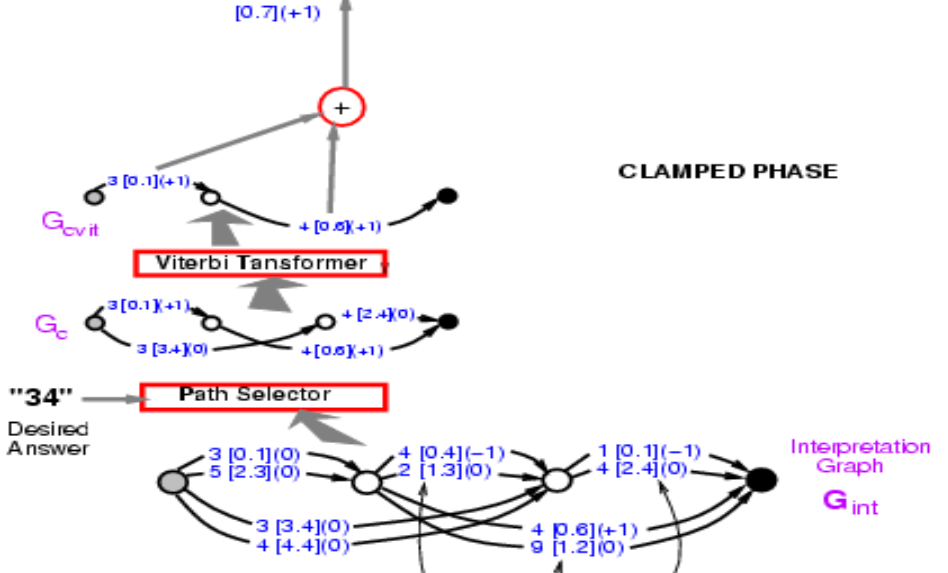
Şekil 9

Yolu bulmak, saklı değişkene, yani seçtiğimiz yola göre, göre minimize etmek gibi. Kavramsal olarak, saklı değişkenin bir yola denk geldiği bir enerji modeli.

Şimdi elmizide doğru olan yolun enerjisi var, 0.7. Şimdi yapmamız gereken bu yapı üzerinde gradyanları geri yaymak, böylece ConvNet ağırlıklarını son enerji düşecek şekilde değiştirebilelim. Göz korkutucu gözükse de imkansız değil çünkü tüm sistem bildiğimiz yapılardan oluşuyor. Sinir ağı sıradan ve Yol Seçici ve Viterbi Dönüştürücüsü ise aç kapa görevini üstlenir yani belli bir ayrıtı (veya yolu) seçip seçmemizi kontrol eder.

Peki geri yayılımı nasıl gerçekleştireceğiz? 0.7 noktası 0.1 ve 0.6’ nın toplamı. Yani 0.1 ve 0.6 noktalarının ikisinin de gradyeni +1 olacak ve köşeli parantezler ile göstereceğiz. Viterbi Dönüştürücüsü iki yoldan birini seçecek. Sonrasında, girdi çizgesinde bu yola karşılık gelen ayrıtın gradyenini kopyalamamız ve seçilmeyen diğer yolların gradyanlarını 0 olarak belirleyeceğiz. Tıpkı maksimum örnekleme (max pooling) ve ortalama örnekleme (mean pooling)‘de olduğu gibi. Örneklemelede ve burada da yol seçici aynı; yol seçici doğru cevabı seçen bir sistem sadece. Çizgedeki 30.1‘in bu aşamada 30.1 olması gerektiğine dikkat edin, buna daha sonra döneceğiz. Artık sinir ağı üzerinde gradyanı geri yayabilirsin. Böylelikle, doğru cevabın enerjisini küçültmüş olacağız.

Buradaki kritik kısım, yapının dinamik olması yani sisteme yeni bir girdi verdiğimizde, sinir ağındaki örnek sayısı bölütleme sayısı ile değişecektir ve üretilen çizgeler de değişecektir. Geri yayılımı, bu dinamik bir yapı üzerinde gerçekleştirmemiz gerekiyor. İşte bu tarz durumlarda PyTorch oldukça önemli hale geliyor.

Bu fazda, geri yayılım ile doğru cevabın enerjisini küçültüyoruz. İkinci fazda ise yanlış cevabın enerjisini büyütüyoruz. Bu durumda, sistemin istediği cevabı seçebilmesine izin veriyoruz. Bu işlemler ile algı kaybı (perception loss) fonksiyonu kullanan yapılandırılmış kestirim problemleri için ayrıştırıcı eğitimin basit bir hali olacak.

İkinci fazın ilk adımları, ilk fazınkiyle tamamen aynı. Viterbi Dönüştürücüsü yine en düşük enerjili yolu seçecek, seçilen yolun doğru veya yanlış olduğunu burada önemsemiyoruz. Burada elde ettiğimiz enerji, ilk fazda elde ettiğimiz enerjiden ya küçük ya da bu enerjiye eşit olacak çünkü bu fazda elde ettiğimiz enerji, tüm olası yollardaki enerjilerin en küçüğü.

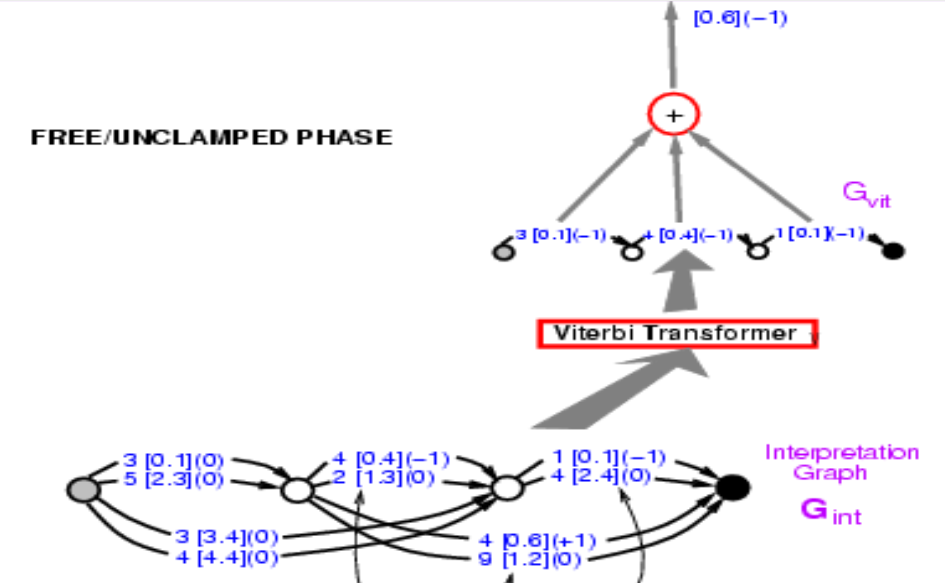
Şekil 10

Faz 1 ve Faz 2’yi birleştirelim. Yitim fonksiyonu enerji1 - enerji2 olmalı. Sol dal üzerinde geri yayılımı nasıl gerçekleştireceğimizi anlatmıştık, şimdi sırada tüm yapı üzerinde geri yayılımı gerçekleştirmekte. Sol taraftan herhangi bir yol +1 ve sağ taraftaki herhangi bir yol ise -1 gradyanına sahip. Bu yüzden, iki yolda da 3[0.1] var, bu nedenle 3[0.1]’in gradyanı 0 olmalı. Bunu yaparsak, sistem nihayetinde doğru cevabın enerjisi ile en iyi cevabın enerjisi arasındaki farkı minimize edecektir. Buradaki yitim fonksiyonu, algılayıcı yitim fonksiyonudur.

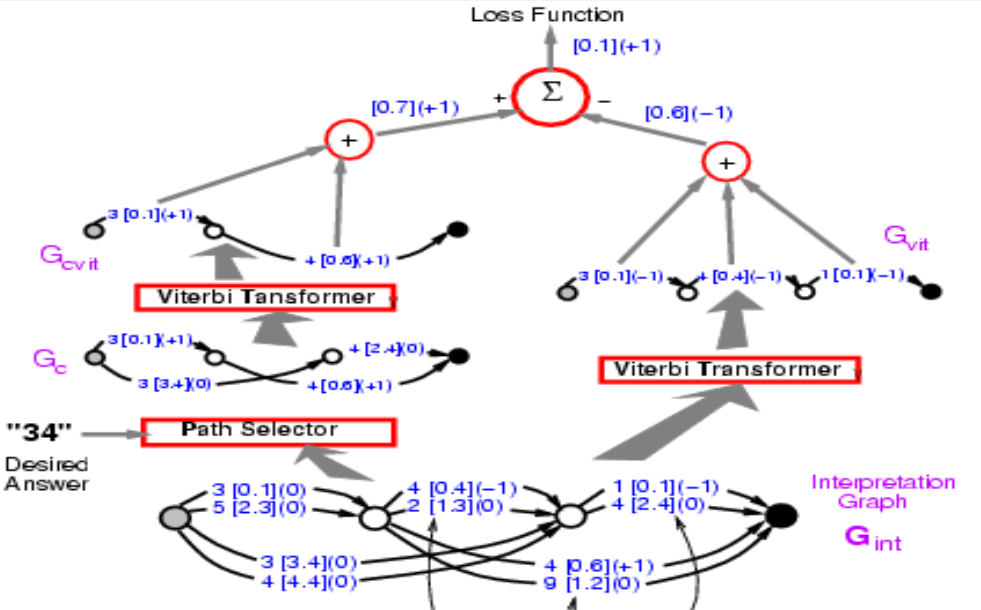
Şekil 11

Kavrama Soruları ve Cevapları

Soru 1: Neden enerji bazlı faktör çizgelerinde çıkarım kolaydır?

Saklı değişkenli enerji bazlı modellerde çıkarım, enerjiyi minimize etmek için gradyan inişini kullanmak gibi kapsamlı yöntemleri içermektedir; ancak, bu durumda, enerji, faktörlerin toplamı olduğu olduğu için gradyan inişi yerine dinamik programlama gibi teknikler kullanılabilir.

Soru 2: Faktör çizgelerindeki saklı değişkenler sürekli değişkenler olsaydı ne olurdu? Minimum toplam algoritmasını kullanmaya devam edebilir miydik?

Devam edemezdik çünkü şu anda tüm faktör değerleri için olası tüm kombinasyonları arayamıyoruz; ancak, bu durumda, enerjiler bize bir avantaj sağlıyor çünkü birbirinden bağımsız optimizasyon işlemleri yapabiliyoruz. Tıpkı Şekil 5’te $Z_1$ ve $Z_2$’nin kombinasyonunun sadece $E_b$’yi etkilediği gibi. Çıkarım için bağımsız optimizasyon ve dinamik programlama yapabiliriz.

Soru 3: Sinir ağı kutuları ayrı ConvNet’leri mi temsil ediyor?

Kutular paylaşılıyor yani kutular aslında aynı ConvNet’in kopyalarından ibaret. Bu sadece bir karakter tanıma ağı.