Dikkat ve Dönüştürücü

Dikkat

Dönüştürücü (Transformer) modelini anlatmadan önce dikkat konseptini anlatmıştık. İki çeşit dikkat vardır: öz dikkat vs. çapraz dikkat. Bu iki kategori kendi içinde, hard (keskin) ve soft (yumuşak) diye de ayrılır.

Daha sonra da göreceğimiz gibi, dönüştürücüler dikkat modüllerinden, yani diziler yerine kümeler arası eşleşmelerden oluşmuşlardır, bu da girdi/çıktılara bir sıralama empoze etmediğimiz anlamına gelir.

Öz Dikkat (I)

$t$ girdili $\boldsymbol{x}$ lerden oluşan bir küme düşünelim:

Her $\boldsymbol{x}_i$ bir $n$-boyutlu vektörü temsil eder. Kümenin, her biri $\mathbb{R}^n$ ‘ye ait $t$ tane elemanı olduğundan, bu kümeyi $\boldsymbol{X}\in\mathbb{R}^{n \times t}$ şeklindeki bir matris şeklinde ifade edebiliriz.

Öz dikkatte, gizli gösterim $h$, girdilerin bir lineer kombinasyonudur:

Yukarıda tanımlanan matris gösterimini kullanarak, gizli katmanı matris çarpımı olarak yazabiliriz:

Burada $\boldsymbol{a} \in \mathbb{R}^t$, bileşenleri $\alpha_i$ olan bir sütun vektörüdür.

Dikkat edin, bu daha önce gördüğümüz, girdilerin ağırlık matrisleriyle çarpıldığı gizli gösterimlerden farklı.

$\vect{a}$ denilen vektöre empoze ettiğimiz sınırlamalara bağlı olarak keskin ve yumuşak dikkati elde edebiliriz.

Keskin (Hard) Dikkat

Keskin dikkatte, alpha değerleri üzerinde şu sınırlamayı empoze ediyoruz: $\Vert\vect{a}\Vert_0 = 1$ . Bu da $\vect{a}$ ‘ın bir one-hot (her elementin, bir adet konumu belli 1 ve kalanının 0 olarak ifade edildiği vektör) vektörü olduğu anlamına gelir. Bu nedenle, girdilerin lineer kombinasyonunda bir tanesi hariç diğer bütün katsayılar sıfıra eşittir, ve gizli gösterim de $\boldsymbol{x}_i$ girdilerinin $\alpha_i=1$ elementlerine indirgenmiş hali olur.

Yumuşak (Soft) Dikkat

Yumuşak dikkatte, $\Vert\vect{a}\Vert_1 = 1$ olmasını isteriz. Gizli gösterimler girdilerin katsayılar toplamı 1 olacak şekilde yapılan lineer kombinasyonudur.

Öz Dikkat (II)

$\alpha_i$ nereden geliyor?

$\vect{a} \in \mathbb{R}^t$ vektörünü şu şekilde elde ediyoruz:

Burada $\beta$, $\text{soft(arg)max}(\cdot)$ ‘nın sıcaklık parametresinin ters halini gösteriyor. $\boldsymbol{X}^{\top}\in\mathbb{R}^{t \times n}$ ise $\lbrace\boldsymbol{x}_i \rbrace_{i=1}^t$ kümesinin transpoze matrisinin gösterimi ve $\boldsymbol{x}$ de kümeden genel bir $\boldsymbol{x}_i$ ‘ı temsil ediyor. Burada $X^{\top}$ ‘ın $j$’inci satırı $\boldsymbol{x}_j\in\mathbb{R}^n$ elemanına tekabül ediyor, yani $\boldsymbol{X}^{\top}\boldsymbol{x}$ matrisinin $j$’inci satırı, $\lbrace \boldsymbol{x}_i \rbrace_{i=1}^t$ ‘ın her bir $\boldsymbol{x}_i$ elemanının $\boldsymbol{x}_j$ ile iç çarpımı oluyor.

$\vect{a}$ vektörünün her bir elementine “skor” adı verilir çünkü iki vektör arasındaki iç çarpım bu iki vektörün ne kadar aynı doğrultuda ya da benzer olduğunu gösterir. Bu nedenle, $\vect{a}$ ‘nın elemanları, bütün kümenin belli bir $\boldsymbol{x}_i$ ile benzerliği hakkında bilgi vermiş olur.

Köşeli parantezler opsiyonel argümanları gösterir. Eğer $\arg\max(\cdot)$ kullanılırsa, alpha’lardan oluşan bir one-hot vektörü elde ederiz, yani keskin dikkat olmuş olur. Diğer yandan $\text{soft(arg)max}(\cdot)$ ‘ı kullanmak yumuşak dikkate tekabül eder. Her iki durumda da sonuçta oluşan $\vect{a}$ vektörünün elemenlerinin toplamı 1 olur.

$\vect{a}$ vektörünü bu şekilde yaratmak her biri $\boldsymbol{x}_i$ olan bir küme oluşturur. Hatta $\vect{a}_i \in \mathbb{R}^t$ sağlanır ve böylece alpha değerlerini $\boldsymbol{A}\in \mathbb{R}^{t \times t}$ matrisine yığabiliriz.

Her bir gizli durum $\boldsymbol{X}$ girdileri ve $\vect{a}$ vektörünün lineer kombinasyonu olduğundan, $t$ adet gizli durum elde etmiş oluruz ve bunları $\boldsymbol{H}\in \mathbb{R}^{n \times t}$ matrisine yığabiliriz.

Anahtar-değer depolama

Anahtar-değer depolama, depolamak (kaydetmek), erişmek (sorgulamak), ve birbiriyle ilişkili dizinleri yönetmek (sözlükler, anahtarlı tablolar) için dizayn edilmiş bir paradigmadır.

Örneğin, lazanya yapmak için bir tarif bulmak istiyoruz. Bir tarif kitabımız var ve “lazanya” için arama yapıyoruz-sorgumuz bu. Bu sorgu, veriserti içindeki bütün anahtarlarla karşılaştırılacak, bu durumda anahtarlar kitaptaki tüm tariflerin başlıkları oluyor. Sorgunun her başlıkla ne kadar “aynı yönde” olduğunu kontrol edip o sorgu ve tüm anahtarlar arasındaki en büyük uyuşma skorunu buluruz. Eğer çıktımız argmax fonksiyonu ise, en yüksek skorlu bir tarifi elde ederiz. Değilse, mesela soft argmax fonksiyonu kullanırsak, bir olasılık dağılımı elde edebiliriz ve bundan sıralı şekilde elimizdeki sorguya en benzer içeriği ve daha az alakalı tarifleri elde edebiliriz.

Kısacası, sorgu bizim sorduğumuz sorudur. Bir sorgu verildiğinde, bu sorguyu bütün anahtarlarla karşılaştırıp eşleşen tüm şeyleri elde ederiz.

Sorgular, anahtarlar ve değerler

\(\begin{aligned} \vect{q} &= \vect{W_q x} \\ \vect{k} &= \vect{W_k x} \\ \vect{v} &= \vect{W_v x} \end{aligned}\)

$\vect{q}, \vect{k}, \vect{v}$ vektörlerinin her biri, özel bir $\vect{x}$ girdisinin döndürülmüş halleri gibi düşünülebilir. Burada $\vect{q}$, $\vect{x}$’nin $\vect{W_q}$ ile, $\vect{k}$ ise $\vect{x}$’nin $\vect{W_k}$ ile döndürülmüş halidir, $\vect{v}$ için de benzer şekilde. Dikkat edilmelidir ki burada ilk defa “öğrenilebilir” parametrelerden bahsediyoruz. Ayrıca hiçbir lineer olmayan dönüşüm yok, çünkü dikkat tamamen oryantasyona bağlı.

Bir sorguyu tüm anahtarlarla karşılaştırabilmek için, $\vect{q}$ ve $\vect{k}$’nin aynı boyutlara sahip olması gerekir, yani $\vect{q}, \vect{k} \in \mathbb{R}^{d’}$.

Fakat $\vect{v}$ herhangi bir boyutta olabilir. Lazanya tarifi örneğimizden devam edersek, sorgunun anahtarlarla aynı boyutta olmasını istiyoruz, yani aradığımız tüm tariflerin başlıklarıyla. Elde ettiğimiz tariflerin boyutu ise, yani $\vect{v}$, herhangi bir uzunlukta olabilir. Bu nedenle $\vect{v} \in \mathbb{R}^{d’’}$ olmalıdır.

Daha kolay anlaşılır olması için, her şeyin $d$ boyutunda olduğu varsayımını yapacağız, yani:

Şu anda elimizde $\vect{x}$’ler, yani sorguların kümesi, anahtarlar kümesi ve değerler kümesi var. Bu kümeleri matrislere şu şekilde depolayabiliriz: her matrisin $t$ sütunu olacak $t$ adet vektör koyduğumuzdan, ve her vektörün boyu da $d$ olacak.

\(\{ \vect{x}_i \}_{i=1}^t \rightsquigarrow \{ \vect{q}_i \}_{i=1}^t, \, \{ \vect{k}_i \}_{i=1}^t, \, \, \{ \vect{v}_i \}_{i=1}^t \rightsquigarrow \vect{Q}, \vect{K}, \vect{V} \in \mathbb{R}^{d \times t}\) $\vect{q}$ sorgusunu $\vect{K}$ matrisindeki tüm anahtarlarla karşılaştırıyoruz: \(\vect{a} = \text{[soft](arg)max}_{\beta} (\vect{K}^{\top} \vect{q}) \in \mathbb{R}^t\) Gizli katman $\vect{V}$ matrisinin sütunlarının, $\vect{a}$ katsayılarıyla bir lineer kombinasyonu olacak: \(\vect{h} = \vect{V} \vect{a} \in \mathbb{R}^d\) $t$ adet sorgumuz olduğundan, $t$ adet $\vect{a}$ ağırlığında katsayı elde edeceğiz ve $\vect{A}$ matrisinin boyutları $t \times t$ olacak.

\(\{ \vect{q}_i \}_{i=1}^t \rightsquigarrow \{ \vect{a}_i \}_{i=1}^t, \rightsquigarrow \vect{A} \in \mathbb{R}^{t \times t}\) Böylece matris notasyonuyla şunu elde ederiz: \(\vect{H} = \vect{VA} \in \mathbb{R}^{d \times t}\) Öte yandan, genellikle $\beta$’ya şu değeri atarız:

Bunu yapmamızın sebebi, değişik $d$ boyutu seçimlerindeki sıcaklığı sabit tutmak istemektir, bu nedenle boyut $d$’nin kareköküne bölüyoruz.($\vect{1} \in \R^d$ vektörünün boyutunun ne olduğunu düşünün.)

Uygulamaya geçirirken hesapların daha az süre alması için $\vect{W}$’lerin hepsini uzun bir $\vect{W}$’ye depolayabilir ve tek seferde $\vect{q}, \vect{k}, \vect{v}$’yi şu şekilde hesaplayabiliriz:

\(\begin{bmatrix} \vect{q} \\ \vect{k} \\ \vect{v} \end{bmatrix} = \begin{bmatrix} \vect{W_q} \\ \vect{W_k} \\ \vect{W_v} \end{bmatrix} \vect{x} \in \mathbb{R}^{3d}\) Ayrıca bir de “baş” konsepti var. Yukarda gördüğümüz örnek tek başlı idi fakar birden fazla baş olabilir. Örneğin $h$ adet başımız olsun, elimizde $h$ adet $\vect{q}$, $h$ adet $\vect{k}$ ve $h$ adet $\vect{v}$ olacak ve sonunda $\mathbb{R}^{3hd}$ uzayında bir vektör oluşacak:

Fakat yine de çok başlı değerleri orijinal boyutları olan $\R^d$’ye $\vect{W_h} \in \mathbb{R}^{d \times hd}$ vektörünü kullanarak dönüştürebiliriz. Bu anahtar-değer depolamanın yollarından yalnızca biri.

Dönüştürücü

Dikkat ile alakalı öğrendiklerimzden yola çıkarak, dönüştürücünün temel yapı taşlarını yorumlayacağız şimdi. Özel olarak basit bir dönüştürücüden ileri geçiş yaptırdığımızda, RNN’lerin dizisel yapılarına kıyasla, dönüştürücüde dikkatin standart kodlayıcı-çözücü paradigmasında nasıl yer aldığını göreceğiz.

Kodlayıcı-Çözücü Yapısı

Bu terminolojye aşina olmalıyız. Bu yapı otokodlayıcı gösterimlerinde bariz bir şekilde karşımıza çıkmıştı, ve dersin burasına kadar bilmemiz gerekiyor bu kadarını. Özet geçmek gerekirse, bir girdi, verinin darboğaz olacağı şekilde kodlayıcı ve çözücüden geçiriliyor, böylece sadece en önemli bilgi aktarılmış oluyor. Bu bilgi, kodlayıcı bloğunun çıktısı olarak saklanır ve birden fazla değişik ve alakasız amaç için kullanılabilir.

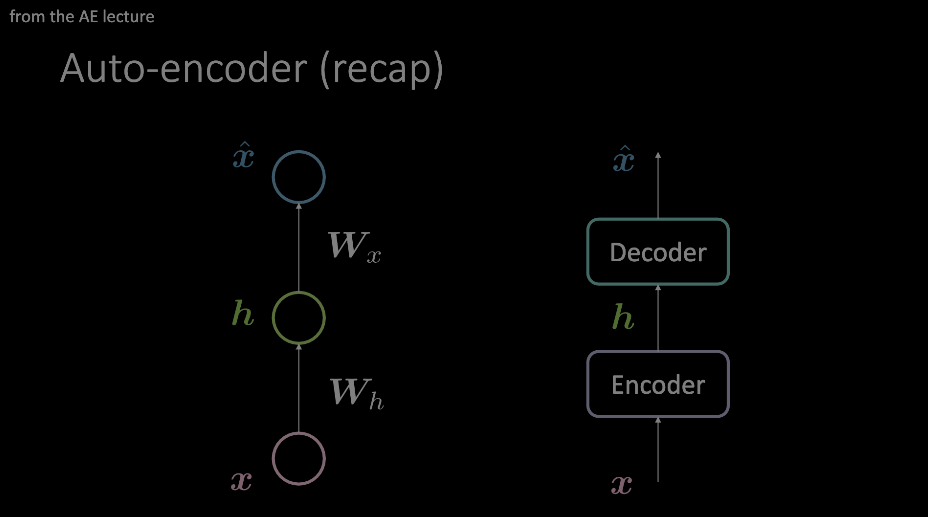
Figure 1: Otokodlayıcıya iki örnek şekil. Soldaki model iki ilgin *(affine)* dönüşüm ve aktivasyonlarla nasıl otokodlayıcı dizayn edilebileceğini gösteriyor. Sağdaki şekilde ise tek katmanın yerine nasıl rastgele bir işlem modulü kullanılabileceği gösteriliyor.

Biz “dikkatimizi” sağdaki modelde verilen otokodlayıcı şemasına verip içinde dönüştürücü bağlamında neler olduğuna bakacağız.

Kodlayıcı modülü

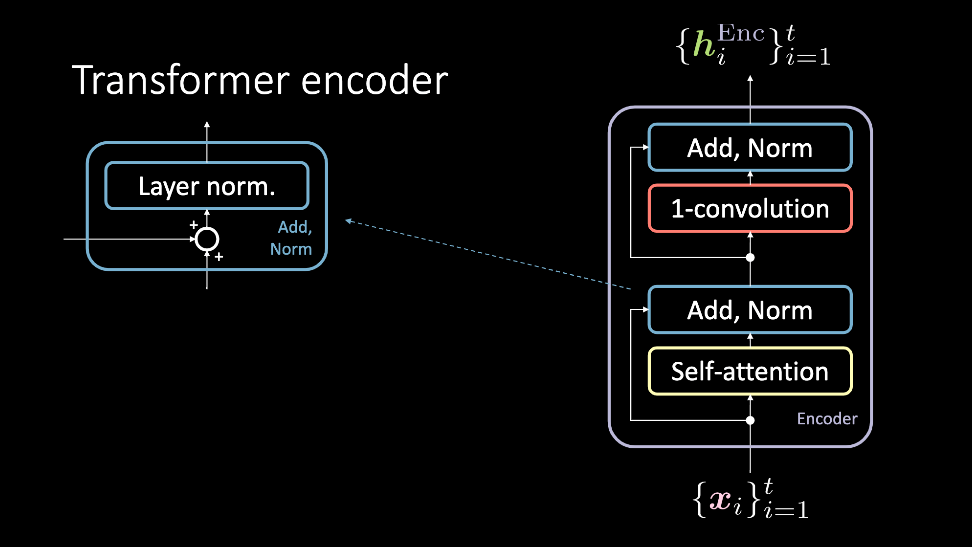
Figure 2: Dönüştürücünün kodlayıcısı, $\vect{x}$ girdilerini alıyor ve gizli gösterimler olan $\vect{h}^\text{Enc}$ 'ları çıktı olarak veriyor.

Kodlayıcı modülü bir girdi kümesi alır, ve bu girdilerin hepsi öz dikkat bloğuna aynı anda beslenir ve daha sonra Ekleme ve Normalizasyon(Add, Norm) bloğuna geçer. Ve sonrasında bunlar tekrar aynı anda 1D-evrişim operasyonundan ve başka bir Ekleme ve Normalizasyon bloğundan geçip gizli gösterimler kümesi olarak çıktılanırlar. Bu gizli gösterimler daha sonra ya gelişigüzel sayıdaki kodlayıcı modullerine yollanırlar (yani daha fazla katmana), ya da çözücüye giderler. Bu blokları şimdi daha ayrıntılı şekilde inceleyeceğiz.

Öz-dikkat

Öz-dikkat modeli normal bir dikkat modelinden ibarettir. Sorgu, anahtar ve değerler aynı birim olan dizisel girdiden üretilirler. Dizisel veriyi modellemeye çalışan işlerde, pozisyona bağlı kodlamalar, girdiye eklenir. Bu bloğun çıktısı da dikkat katsayılarıyla çarpılmış değerler olur. Öz-dikkat bloğu, $1, \cdots , t$ dan bir girdi kümesi alır ve $1, \cdots, t$ gibi dikkat katsayılı çıktılar verir, ve bunlar kodlayıcının geride kalan kısmına yollanırlar.

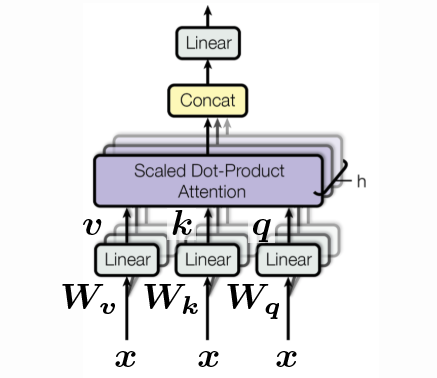
Figure 3: Öz-dikkat bloğu. Dizi halindeki girdiler, üçüncü boyut üzerindeki bir küme olarak gösterilmiş ve uç uca eklenmiş halleridir.

Ekleme, Normalizasyon

Ekleme normalizasyon bloğu iki bileşenden oluşur. Birincisi bir artık (residual) bağlantı olan ekleme bloğu, ve sonra katman normalizasyonudur.

1D-evrişim

Bu adımı takriben, tek boyutta evrişim (yani pozisyona bağlı ileri doğru ağ) uygulanır. Bu blok iki adet yoğun katmandan oluşur. Önceden belirlenen değerlere gçre, bu blok $\vect{h}^\text{Enc}$ çıktısının boyutlarını ayarlamaya yardımcı olur.

Çözücü modülü

Dönüştürücünün çözücüsü, kodlayıcıyla benzer mantıkta çalışır. Sadece ekstra bir altblok daha vardır. Ek olarak, bu modüle giren girdiler farklıdır.

Figure 4: Çözücünün daha arkadaş canlısı bir açıklaması.

Çapraz-dikkat

Çapraz dikkat, öz-dikkat bloklarında kullanılan sorgu, anahtar ve değer konseptiyle aynı şekilde çalışır. Fakat girdiler biraz daha karmaşıktır. Çözücüye giren girdi $\vect{y}_i$ adında bir veri noktasıdır, ve bu girdi öz dikkat ve ekleme-normalizasyon bloklarından geçer, sonunda çapraz dikkat bloğuna ulaşır. Bu çıktı, çapraz dikkat için bir sorgu niteliği taşır, $\vect{h}^\text{Enc}$ çıktısı anahtar ve değer çiftlerine tekabül eder ve bu çıktı daha önceki girdiler olan $\vect{x}_1, \cdots, \vect{x}_{t}$ ‘lar ile hesaplanır.

Özet

$\vect{x}_1$ to $\vect{x}_{t}$ kümesi kodlayıcıya girer. Öz dikkat ve birkaç tane daha blok kullanımı sonucunda, $\lbrace\vect{h}^\text{Enc}\rbrace_{i=1}^t$ şeklindeki çıktı gösterimi elde edilir ve bu çözücüye beslenir. Buna öz-dikkat uygulandıktan sonra bir de çapraz dikkat uygulanır. Bu blokta sorgu, hedef dil $\vect{y}_i$’deki bir sembolün gösterimine tekabül eder, anahtar ve değerler ise kaynak dilin cümlesinden gelirler ($\vect{x}_1$ den $\vect{x}_{t}$ ‘ye). Sezilebileceği üzere, çapraz dikkat girdi dizisi içindeki değerlerden $\vect{y}_t$ ‘yı oluşturmak için en alakalı olanları bulur ve bundan ötürü en yüksek dikkat katsayılarına ihtiyacı vardır. Bu çapraz dikkat sonucundaki çıktı ise bir adet daha 1D evrişim alt bloğundan geçer ve elimizde $\vect{h}^\text{Dec}$ olur. Önceden belirlenmiş bir hedef dil için, eğitmeyi nasıl yapabileceğimiz açık: $\lbrace\vect{h}^\text{Dec}\rbrace_{i=1}^t$ ile hedef veriyi karşılaştırarak.

Kelime Dil Modelleri

Dönüştürücünün en önemli modüllerini açıklamadan önce göz ardı ettiğimiz birkaç şey var, ama bunları şimdi dönüştürücülerin dil işlerinde şu anki en iyi sonuçlara nasıl ulaştığını anlamak için tartışacağız.

Pozisyona bağlı kodlama

Dikkat mekanizmaları yaptığımız operasyonları paralel olarak hesaplamaya izin vererek bir modelin eğitme süresini oldukça indirgeyebilir, ama aynı zamanda dizisel bilgiyi kaybetmiş olur. Pozisyona bağlı kodlama özelliği bu bağlamda o bilgiyi korumaya yarar.

Anlamsal Gösterimler

Dönüştürücünün eğitilmesi sırasında çok sayıda gizli gösterimler oluşur. Pytorch örneğinde kelime-dil modeli için kullanılan gibi bir gömme uzayı oluşturabilmek için, çapraz-dikkatin çıktısı $x_i$ kelimesinin anlamsal bir gösterimini oluşturcaktır, böylece bu veriseti üzerinde daha fazla şey denenebilir.

Kodun Özeti

Şimdi yukarıda bahsettiğimiz dönüştürücüleri daha anlaşılabilir bi şekilde göreceğiz: kod olarak!

Bakacağımız ilk kod modülü çok başlı dikkat bloğu. Giren sorguya, anahtara ve değerlere bağlı olarak bu blok öz ya da çapraz dikkat için kullanılabilir.

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads, p, d_input=None):
        super().__init__()
        self.num_heads = num_heads
        self.d_model = d_model
        if d_input is None:
            d_xq = d_xk = d_xv = d_model
        else:
            d_xq, d_xk, d_xv = d_input
        # Embedding dimension of model is a multiple of number of heads
        assert d_model % self.num_heads == 0
        self.d_k = d_model // self.num_heads
        # These are still of dimension d_model. To split into number of heads
        self.W_q = nn.Linear(d_xq, d_model, bias=False)
        self.W_k = nn.Linear(d_xk, d_model, bias=False)
        self.W_v = nn.Linear(d_xv, d_model, bias=False)
        # Outputs of all sub-layers need to be of dimension d_model
        self.W_h = nn.Linear(d_model, d_model)

Çok başlı dikkat class’ının ilk değerlerinin verilmesi. Eğer d_input girdisi verilmiş ise, bu bir çapraz dikkate dönüşür, yoksa öz dikkattir. Sorgu, anahtar, değer düzeni, d_model girdisinin bir lineer transformasyonu olarak oluşturulmuştur.

def scaled_dot_product_attention(self, Q, K, V):
    batch_size = Q.size(0)
    k_length = K.size(-2)

    # Scaling by d_k so that the soft(arg)max doesnt saturate
    Q = Q / np.sqrt(self.d_k)  # (bs, n_heads, q_length, dim_per_head)
    scores = torch.matmul(Q, K.transpose(2,3))  # (bs, n_heads, q_length, k_length)

    A = nn_Softargmax(dim=-1)(scores)  # (bs, n_heads, q_length, k_length)

    # Get the weighted average of the values
    H = torch.matmul(A, V)  # (bs, n_heads, q_length, dim_per_head)

    return H, A

Değerlerin kodlanmış haline tekabül eden saklı katmanı, dikkat vektörü ile çarpıldıktan sonra döndürür. Kayıt tutabilmek açısından (dizideki hangi değerler dikkat vektörü tarafından maskelenip atıldı?), fonksiyon A’yı da döndürüyor.

def split_heads(self, x, batch_size):
    return x.view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)

Son boyutu (baş × derinlik) (heads × depth) olarak ayırır. (grup boyutu × baş sayısı × dizi uzunluğu × d_k) (batch_size × num_heads × seq_length × d_k) boyutlarında olacak şekilde transpozunu alıp döndürür.

def group_heads(self, x, batch_size):
    return x.transpose(1, 2).contiguous().
        view(batch_size, -1, self.num_heads * self.d_k)

Dikkat başlarını, grup boyutu ve dizi uzunluğu ile uygun olacak şekilde bir araya getirir.

def forward(self, X_q, X_k, X_v):
    batch_size, seq_length, dim = X_q.size()
    # After transforming, split into num_heads
    Q = self.split_heads(self.W_q(X_q), batch_size)
    K = self.split_heads(self.W_k(X_k), batch_size)
    V = self.split_heads(self.W_v(X_v), batch_size)
    # Calculate the attention weights for each of the heads
    H_cat, A = self.scaled_dot_product_attention(Q, K, V)
    # Put all the heads back together by concat
    H_cat = self.group_heads(H_cat, batch_size)  # (bs, q_length, dim)
    # Final linear layer
    H = self.W_h(H_cat)  # (bs, q_length, dim)
    return H, A

Çok başlı dikkatin ileri doğru geçiş (forward) fonksiyonu.

Verilen girdi önce q, k ve v olarak ayrılır ve iç çarpımlı dikkat mekanizmasına beslenir, daha sonra birleştirilir ve son lineer katmana beslenir. Dikkat bloğunun son çıktısı bulunan dikkat ve geriye kalan bloklardan geçen gizli gösterimdir.

Dönüştürücünün kodlayıcısında gösterilen bir sonraki blok ekleme,normalizasyon olsa da, bu özellik zaten PyTorch’ta var. Böylece kod çok daha kolay hale geliyor ve bu blok kendine özel bir class oluşturulmasına gerek duymuyor. Bir sonraki ise 1D evrişim, daha fazla detay için önceki kısımlara bakabilirsiniz.

Bütün ana class’larımızı oluşturduğumuza (ya da bizim için oluşturulmuş olduklarına) göre, kodlayıcı modülüne geçebiliriz.

class EncoderLayer(nn.Module):
    def __init__(self, d_model, num_heads, conv_hidden_dim, p=0.1):
        self.mha = MultiHeadAttention(d_model, num_heads, p)
        self.layernorm1 = nn.LayerNorm(normalized_shape=d_model, eps=1e-6)
        self.layernorm2 = nn.LayerNorm(normalized_shape=d_model, eps=1e-6)

    def forward(self, x):
        attn_output, _ = self.mha(x, x, x)
        out1 = self.layernorm1(x + attn_output)
        cnn_output = self.cnn(out1)
        out2 = self.layernorm2(out1 + cnn_output)
        return out2

En güçlü dönüştürücülerde, bu kodlayıcılar (encoder) çok fazla sayıda art arda eklenmiş halde bulunur.

Öz dikkatin kendisinin yinemleme ya da evrişime sahip olmadığını, bu nedenle çok hızlı çalıştırılabildiğini hatırlayın. Pozisyona bağlı olabilmesi için pozisyona bağlı kodlamaları ekliyoruz ve bunlar şu şekilde hesaplanıyor:

Daha ince detaylı haliyle çok fazla yer kaplamamak için, sizi tüm kodu içeren https://github.com/Atcold/pytorch-Deep-Learning/blob/master/15-transformer.ipynb defterine yönlendiriyoruz.

Tüm haliyle, N ader kodlayıcı katmanıyla ve pozisyona bağlı gömmelerle oluşturulmuş kodlayıcı, şu şekilde yazılıyor:

class Encoder(nn.Module):
    def __init__(self, num_layers, d_model, num_heads, ff_hidden_dim,
            input_vocab_size, maximum_position_encoding, p=0.1):
        self.embedding = Embeddings(d_model, input_vocab_size,
                                    maximum_position_encoding, p)
        self.enc_layers = nn.ModuleList()
        for _ in range(num_layers):
            self.enc_layers.append(EncoderLayer(d_model, num_heads,
                                                ff_hidden_dim, p))
    def forward(self, x):
        x = self.embedding(x) # Transform to (batch_size, input_seq_length, d_model)
        for i in range(self.num_layers):
            x = self.enc_layers[i](x)
        return x  # (batch_size, input_seq_len, d_model)

Örnek Kullanım

Bir kodlayıcının çok fazla işlevi olabilir. Bu derse eşlik eden “notebook”ta, bir kodlayıcının duygu analizi konusunda nasıl kullanılabileceğini göreceğiz.

IMDB yorumları veri setini kullanarak, bir dizi yazının kodlayıcıyla nasıl gizli gösteriminin oluşturulabileceğini ve bu kodlayıcı sürecinin olumlu ve olumsuz film yorumuna tekabül eden ikili çapraz entropi ile nasıl eğitilebileceğini göreceğiz.

Sadede gelirsek, sizi notebook’a yönlendiriyoruz, ama aşağıda dönüştürücüde kullanılan en önemli yapısal birimleri görüyoruz, ve bu model normal bir şekilde eğitiliyor.

class TransformerClassifier(nn.Module):
    def forward(self, x):
        x = Encoder()(x)
        x = nn.Linear(d_model, num_answers)(x)
        return torch.max(x, dim=1)

model = TransformerClassifier(num_layers=1, d_model=32, num_heads=2,
                         conv_hidden_dim=128, input_vocab_size=50002, num_answers=2)