Belirsizlik Altında Tahmin ve Politika Öğrenimi (BATPÖ)

Giriş ve Problem Tanımı

Diyelim ki modelden bağımsız bir pekiştirmeli öğrenme yolu ile nasıl sürüleceğini öğrenmek istiyoruz. Modelin hata yapmasını ve hatalarından öğrenmesine izin vererek modelleri RL’de eğitiyoruz. Ancak hatalar bizi öğrenmenin hiçbir anlamı olmayan cennet/cehennem gibi koşullara götürebileceğinden bu en iyi yol değildir.

Öyleyse, araba kullanmayı öğrenmenin daha ‘insansı’ bir yolundan bahsedelim. Şerit değiştirme örneğini düşünün. Arabanın 100 km/s hızla gittiğini varsayarsak, bu kabaca 30 m/s’ye karşılık gelir, eğer önümüzdeki 30 mye bakarsak, kabaca 1s geleceğe bakabildiğimiz anlamına gelir.

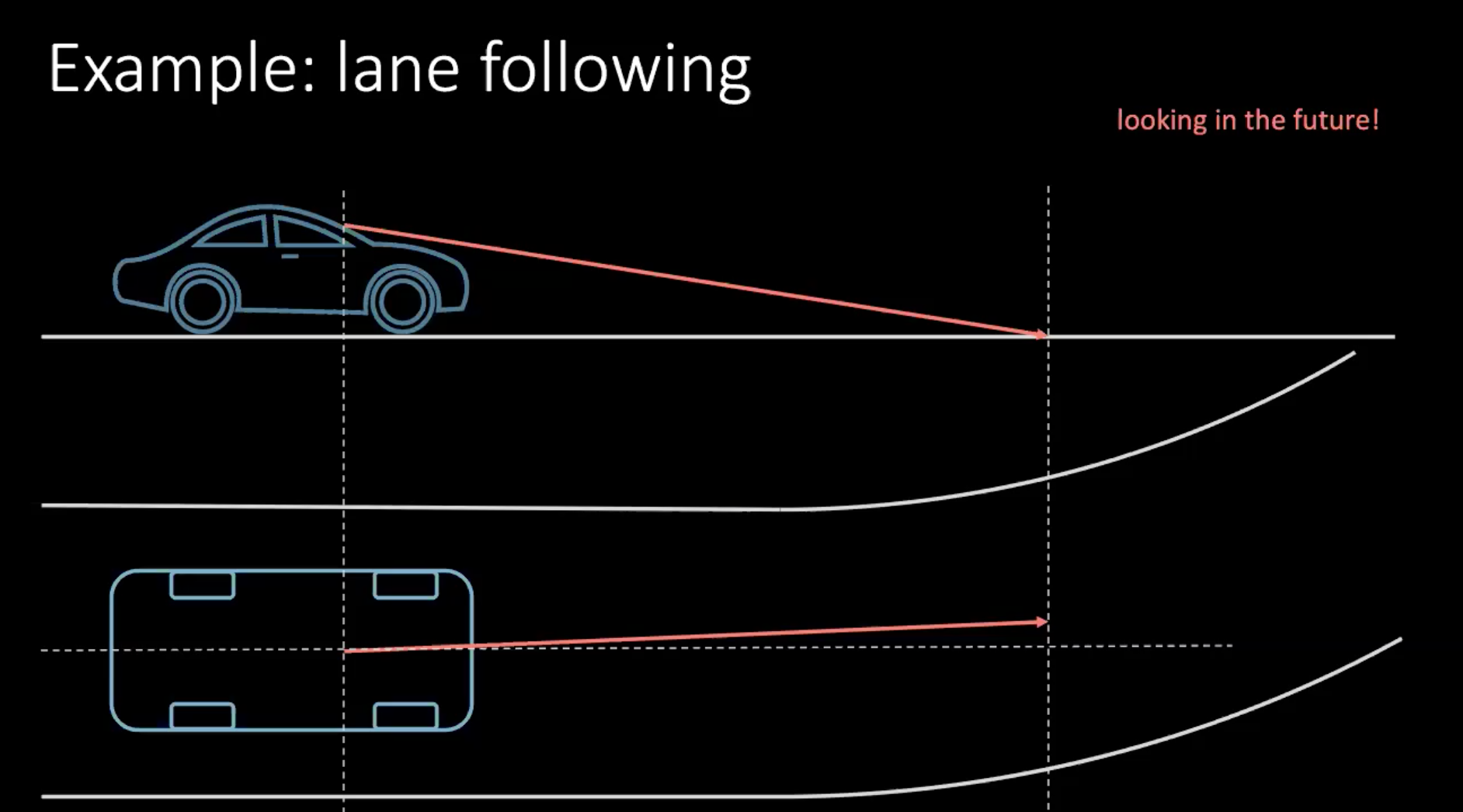
Şekil 1: Sürüş sırasında geleceğe bakmak

Dönüyorsak, yakın geleceğe göre bir karar vermemiz gerekiyor. Birkaç metre sonra bir dönüş yapmak için, şu an bir aksiyon alıyoruz. Bu bağlamda direksiyon simidini çeviren bir aksiyona girişiyoruz. Aldığımız kararlar sadece sizin sürüşünüze değil, aynı zamanda trafikte çevredeki araçlara da bağlıdır. Çevremizdeki herkes o kadar deterministik olmadığı için her olasılığı hesaba katmak çok zor.

Şimdi bu senaryoda neler olduğunu inceleyelim. Girdiyi alan bir ajanımız var (burada bir beyin ile temsil edilir) $s_t$ (pozisyon, hız ve resim) ve bir aksiyona karar veriyor $a_t$(direksiyon kontrolü, hızlanma ve frenleme). Çevre bizi yeni bir duruma götürür ve bir maliyet geri dönderir $c_t$.

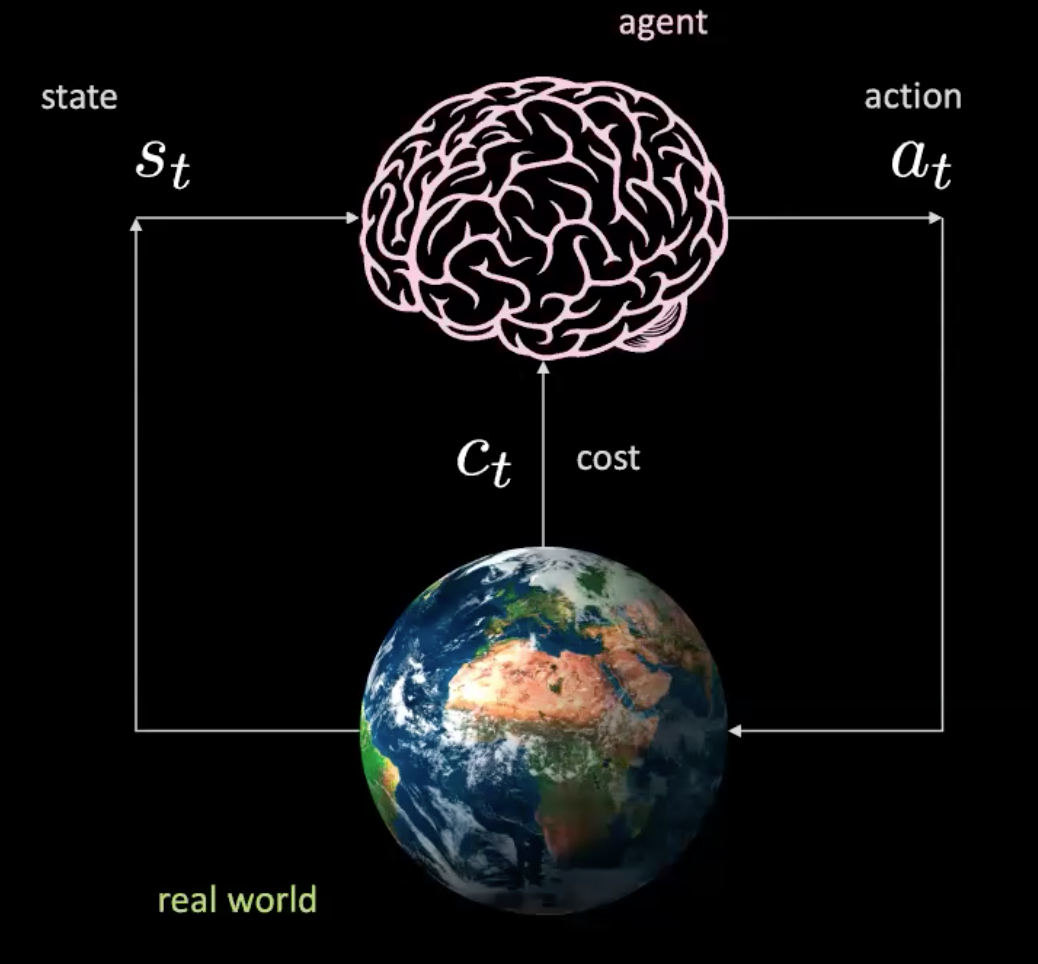
Şekil 2: Gerçek dünyadaki bir ajanın çizimi

Bu, belirli bir durumla ilgili eylemlerde bulunduğunuz ve dünyanın bize bir sonraki durumu ve bir sonraki sonucu verdiği basit bir ağ gibidir. Bu model içermez çünkü her eylemde gerçek dünya ile etkileşim halindeyiz. Ama gerçek dünyayla etkileşime girmeden bir ajan eğitebilir miyiz?

Evet yapabiliriz! Buna “dünya modeli öğrenme” bölümünde bakalım.

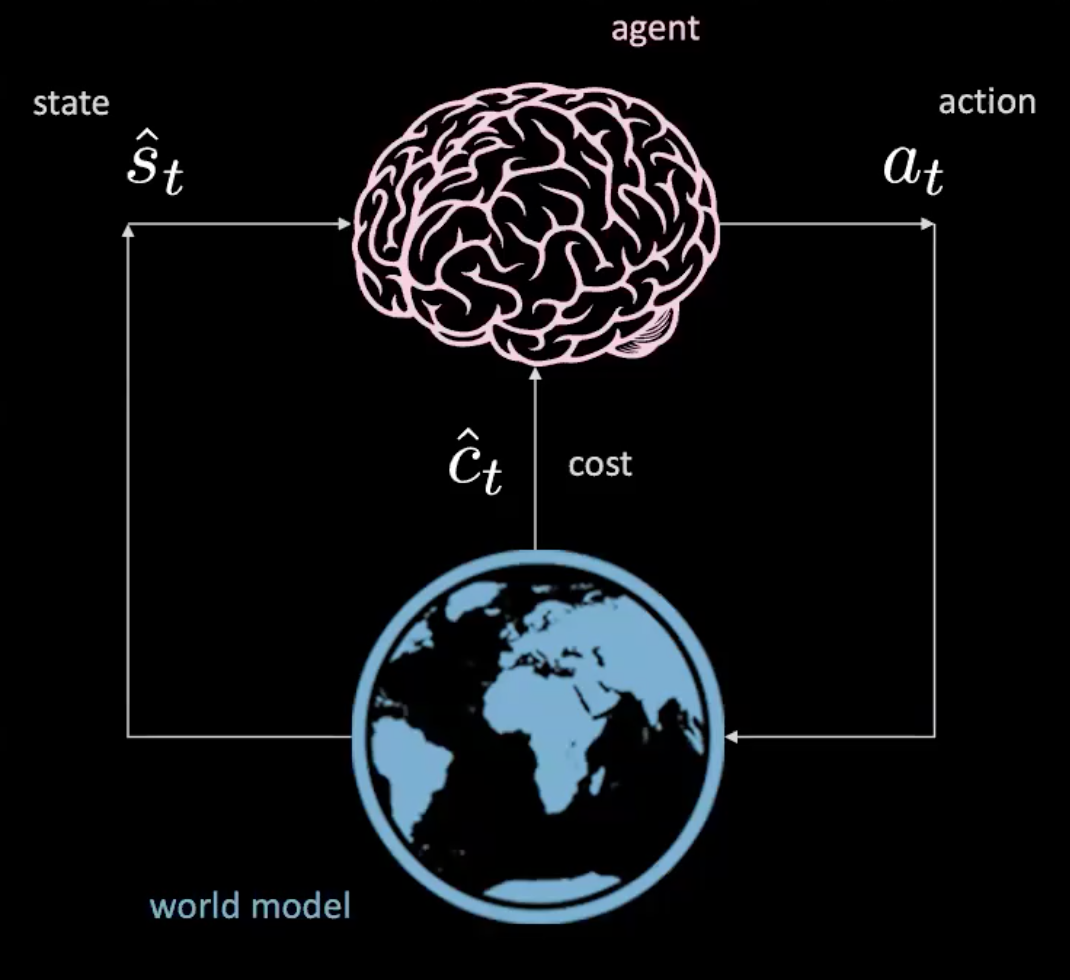
Şekil 3: Dünya modelindeki bir ajanın çizimi

Veri Kümesi

Dünya modelini nasıl öğreneceğimizi tartışmadan önce, sahip olduğumuz veri setini inceleyelim. Eyaletlerarası yola bakan 30 katlı bir binanın tepesine monte edilmiş 7 kameramız var. Yukarıdan aşağı görünümü elde etmek için kameraları ayarlıyoruz ve ardından her araç için sınırlayıcı kutuları çıkarıyoruz. Zaman $t$ , pozisyon $p_t$, hız $v_t$, anlık trafik durumunu ve etraftaki araçların durumlarını $i_t$ belirtsin.

Sürüşün kinematiğini bildiğimizden, sürücünün yaptığı eylemlerin neler olduğunu anlamak için onları tersine çevirebiliriz. Örneğin, araba doğrusal tekdüze bir hareketle hareket ediyorsa, ivmenin sıfır olduğunu anlayabiliriz (yani hiçbir eylem yok).

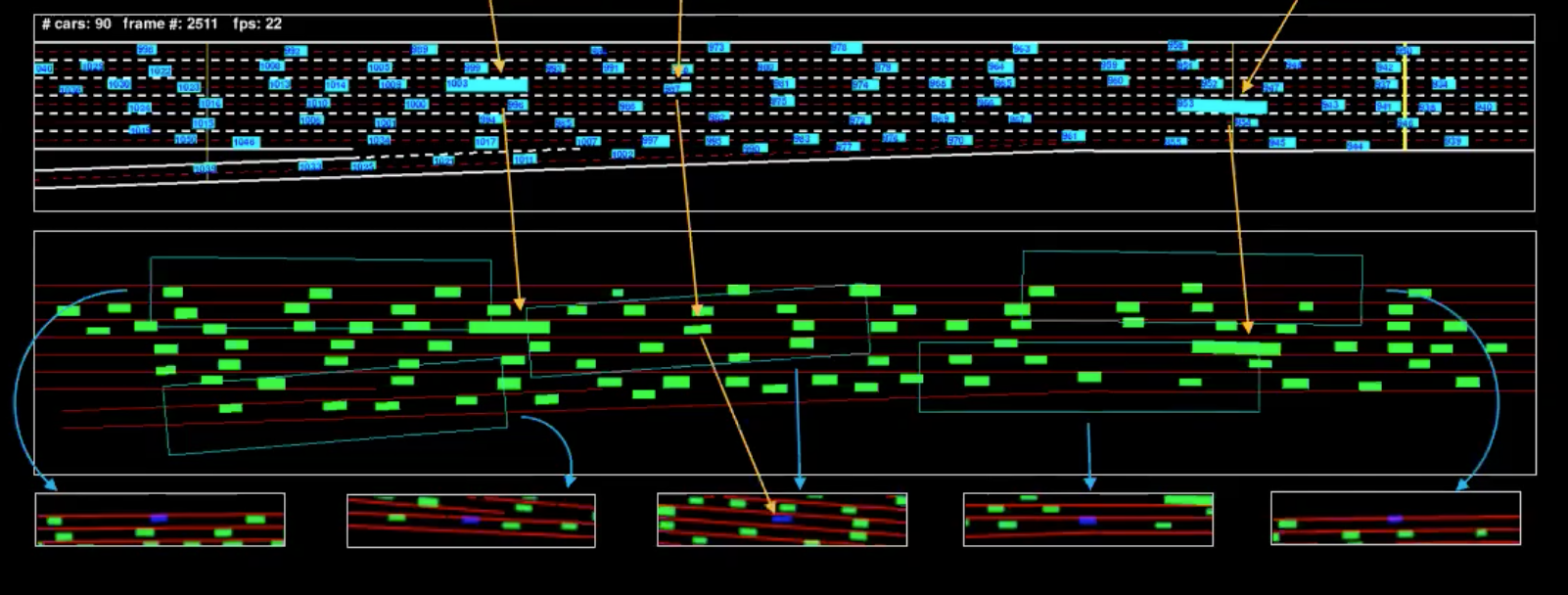
Şekil 4: Tek bir karenin makine gösterimi

Mavi renkli resime besleme, yeşil resime de makine temsili diyebilıriz. Bunu daha iyi anlamak için, birkaç aracı izole ettik (şekilde işaretlenmiştir). Aşağıda gördüğümüz görüntüler, bu araçların görüş alanlarının sınırlayıcı kutularıdır.

Maliyet

Burada iki farklı maliyet türü vardır: şerit maliyeti ve yakınlık maliyeti. Şerit maliyeti bize bir şeritte ne kadar iyi olduğumuzu söyler ve yakınlık maliyeti bize diğer arabalara ne kadar yakın olduğumuzu söyler.

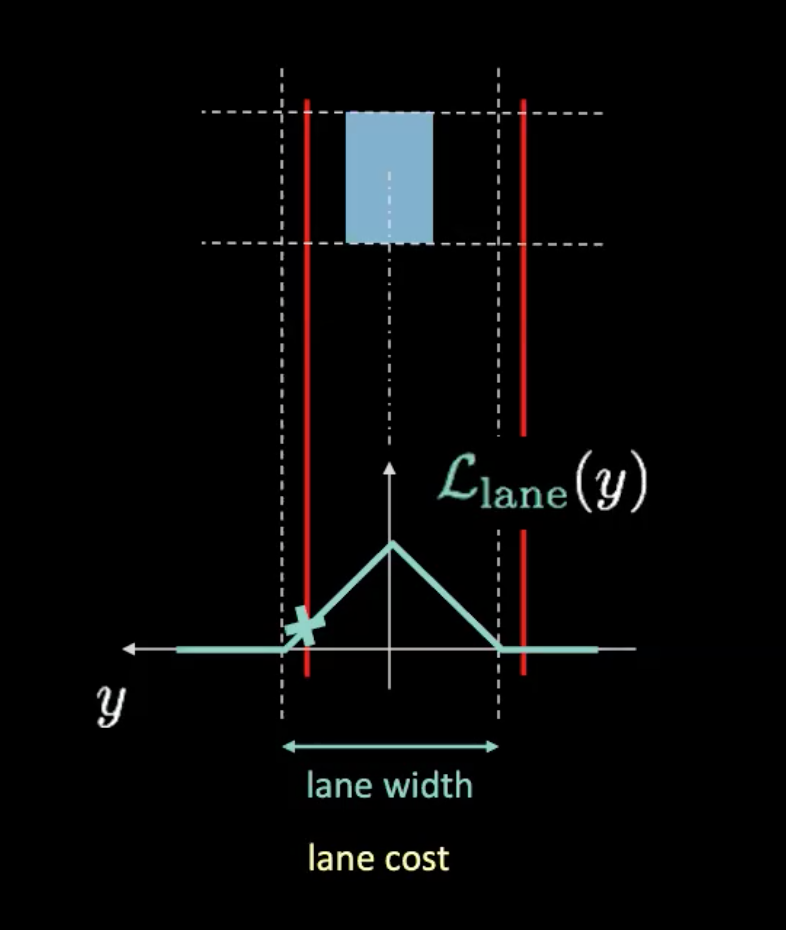
Şekil 5: Şerit maliyeti

Yukarıdaki şekilde, noktalı çizgiler gerçek şeritleri temsil eder ve kırmızı çizgiler, arabamızın mevcut konumu göz önüne alındığında şerit maliyetini anlamamıza yardımcı olur. Arabamız hareket ettikçe kırmızı çizgiler de hareket eder. Kırmızı çizgilerin potansiyel eğriyle kesişme yüksekliği (camgöbeği renginde olan alan) bize maliyeti verir. Araç şeridin merkezinde ise, her iki kırmızı çizgi de gerçek şeritlerle çakışarak sıfır maliyet verir. Öte yandan, araba merkezden uzaklaştıkça kırmızı çizgiler de hareket ederek sıfır olmayan bir maliyet oluşturur.

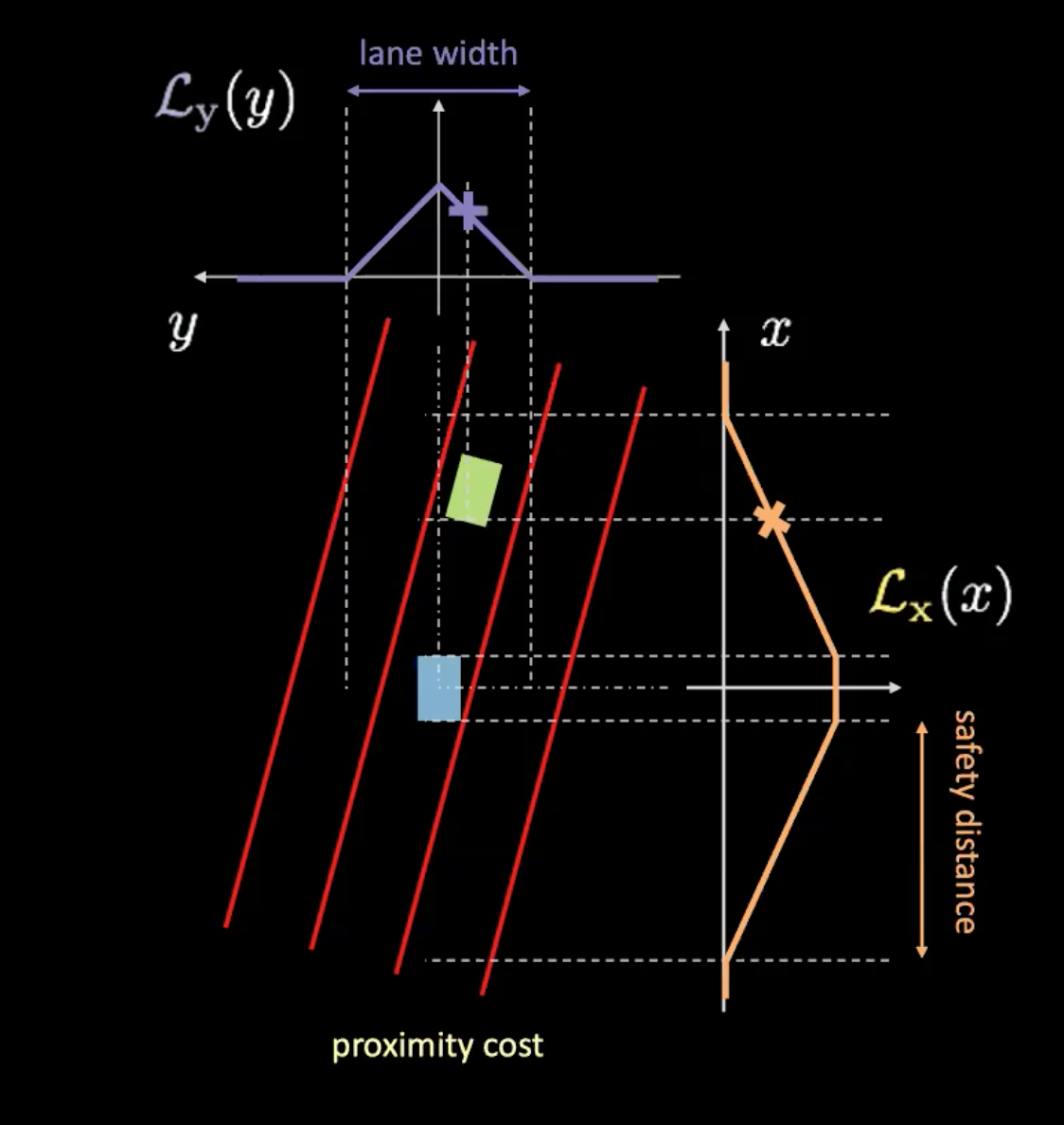
Şekil 6: Yakınlık maliyeti

Yakınlık maliyetinin iki bileşeni vardır ($\mathcal{L}_x$ and $\mathcal{L}_y$). $\mathcal{L}_y$ şerit maliyetine benzer ve $\mathcal{L}_x$ arabamızın hızına bağlıdır. Şekil 6’daki Turuncu eğri bize güvenlik mesafesini anlatır. Arabanın hızı arttıkça turuncu eğri genişler. Araba ne kadar hızlı giderse, o kadar çok ileriye ve arkaya bakmanız gerekecektir. Bir arabanın turuncu eğri ile kesişme noktasının yüksekliği $\mathcal{L}_x$’i belirler.

Bu iki bileşenin çarpımı bize yakınlık maliyetini verir.

Dünya modelini öğrenmek

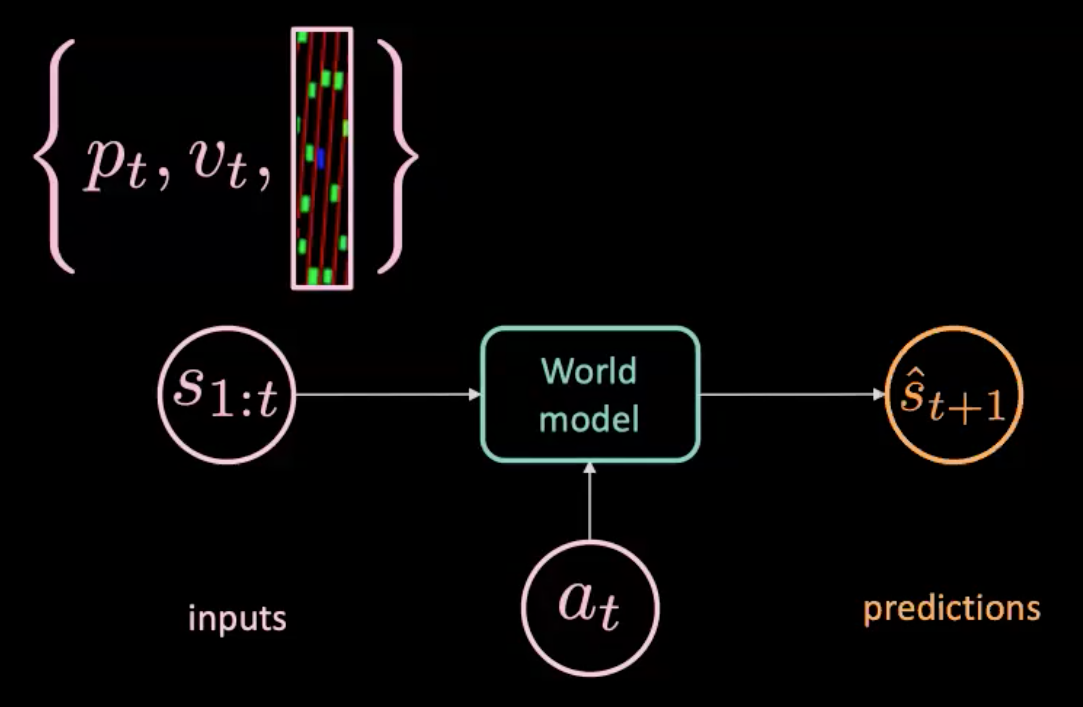
Şekil 7: Dünya modelinin çizimi

Dünya modeli bir eylemle $a_t$ (direksiyon, fren ve hızlanma) ve durumlar dizisiyle $s_{1:t}$ (Her bir durumun o andaki konum, hız ve bağlam görüntüleriyle temsil edildiği durumlar dizisi) besleniyor ve gelecek durumu $\hat s_{t+1}$ tahmin ediyor. Öte yandan, bize gerçekte ne olduğunu anlatan gerçek dünyaya da sahibiz. ($s_{t+1}$). Biz tahmin ($\hat s_{t+1}$) ve hedef ($s_{t+1}$) arasındaki MSE (Ortalama Kare Hata) optimize edereek modelimizi eğitebiliriz.

Deterministik tahminci-kod çözücü

Dünya modelimizi eğitmenin bir yolu, aşağıda açıklanacak bir tahmin-kod çözücü modeli kullanmaktır.

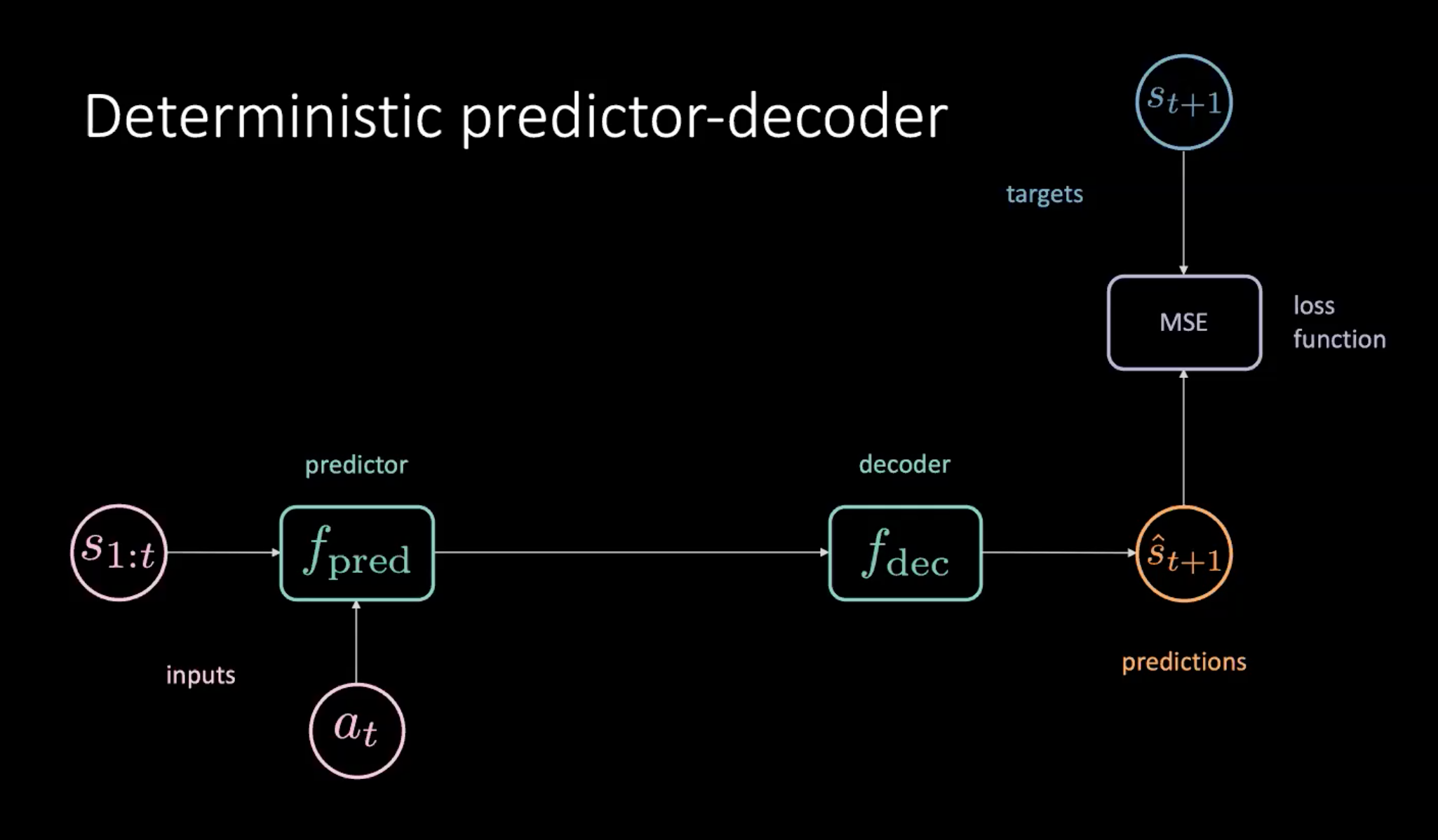
Şekil 8: Dünya modelini öğrenmek için deterministik tahmin-kod çözücü

Şekil 8’de gösterildiği gibi, tahmin modülü tarafından sağlanan bir dizi durumumuz ($s_{1:t}$) ve aksiyonumuz ($a_t$) var. Tahmin modülü , kod çözücüye aktarılan geleceğin gizli bir temsilini çıkarır. Kod çözücü, geleceğin gizli temsilinin kodunu çözer ve bir tahmin çıkarır.($\hat s_{t+1}$). Ardından, tahmin $\hat s_{t+1}$ ve hedef $s_{t+1}$ arasındaki MSE’yi en aza indirerek modelimizi eğitiyoruz.

Şekil 9: Gerçek gelecek *vs.* Deterministik gelecek

Maalesef bu işe yaramıyor!

Deterministik çıktının çok bulanık hale geldiğini görüyoruz. Bunun nedeni, modelimizin gelecekteki tüm olasılıkların ortalamasını almasıdır. Bu, daha önce birkaç derste tartışılan geleceğin multimodalitesiyle karşılaştırılabilir, orijine yerleştirilen bir kalemin rastgele düştüğü yer. Tüm lokasyonların ortalamasını alırsak, bu bize kalemin hiç hareket etmediği inancını verir ve bu yanlıştır.

Modelimize gizli değişkenler ekleyerek bu sorunu çözebiliriz.

Varyasyonel tahmin ağı

Önceki bölümde belirtilen problemi çözmek için, orijinal ağa, boyutları eşitlemek için bir genişletme modülünden $f_ {exp}$ geçen düşük boyutlu bir gizli değişken $z_t$ ekliyoruz.

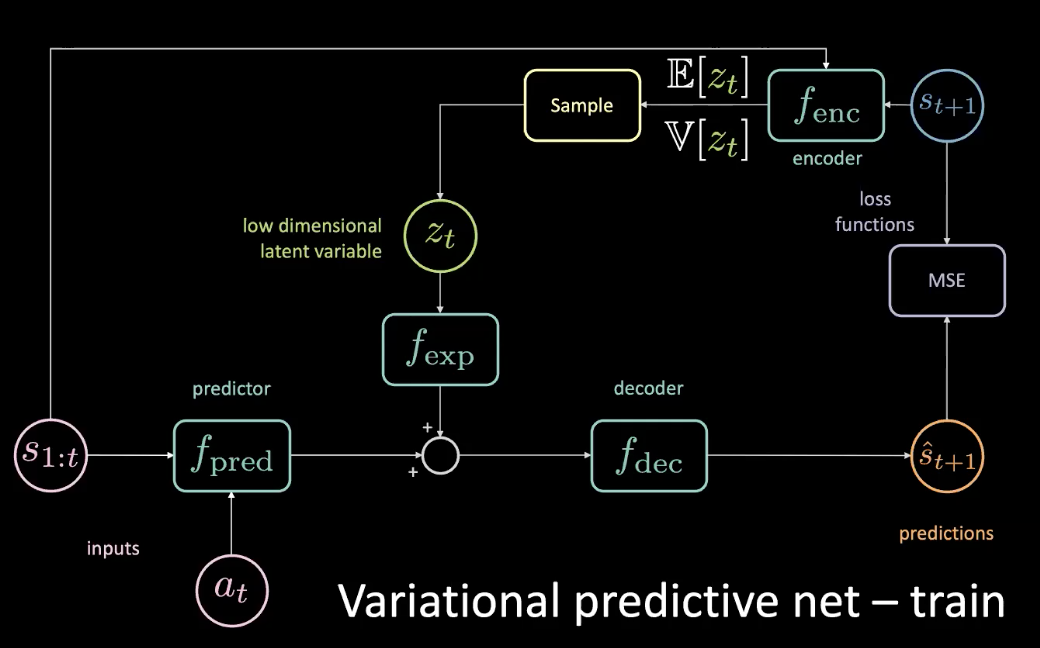
Şekil 10: Varyasyonel tahmin ağı - eğitim

$z_t$, MSE’nin belirli bir tahmin için en aza indirileceği şekilde seçilir. Gizli değişkeni ayarlayarak, gizli alanda (latent space) gradyan inişi yaparak MSE’yi sıfıra getirebilirsiniz. Ancak bu çok pahalıdır. Bir kodlayıcı kullanarak bu gizli değişkeni aslında tahmin edebiliriz. Kodlayıcı gelecek durumu alıp bize $z_t$ ‘yi örnekleyebileceğimiz ortalama ve varyansa sahip bir dağılım verir.

Eğitim sırasında, geleceğe bakarak ve kodlayıcıdan bilgi alarak neler olup bittiğini öğrenebilir ve bu bilgiyi gizli değişkeni tahmin etmek için kullanabiliriz. Ancak, test sırasında geleceğe erişimimiz yoktur. KL sapmasını optimize ederek kodlayıcıyının bize öncüle olabildiğince yakın bir ardıl dağıtım sağlamaya zorlayıp bu sorunu çözebiliriz.

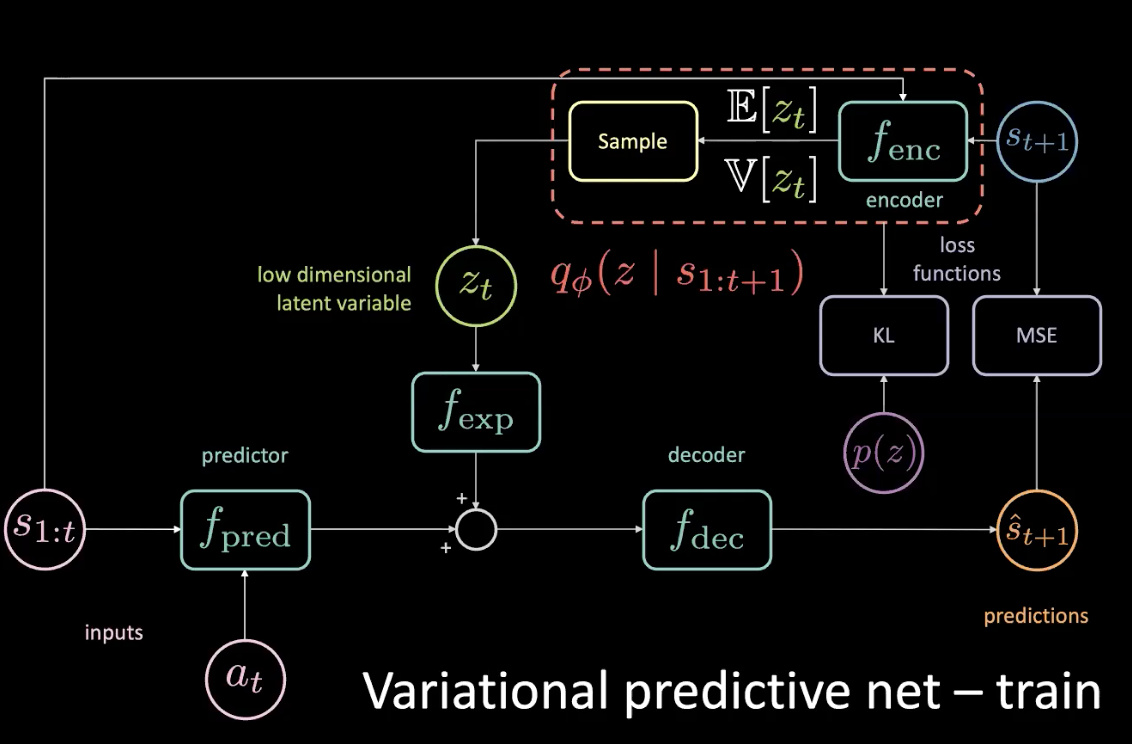
Şekil 11: Varyasyonel tahmin ağı - eğitim (öncül dağıtımla)

Şimdi, çıkarıma bakalım - Nasıl sürüyoruz?

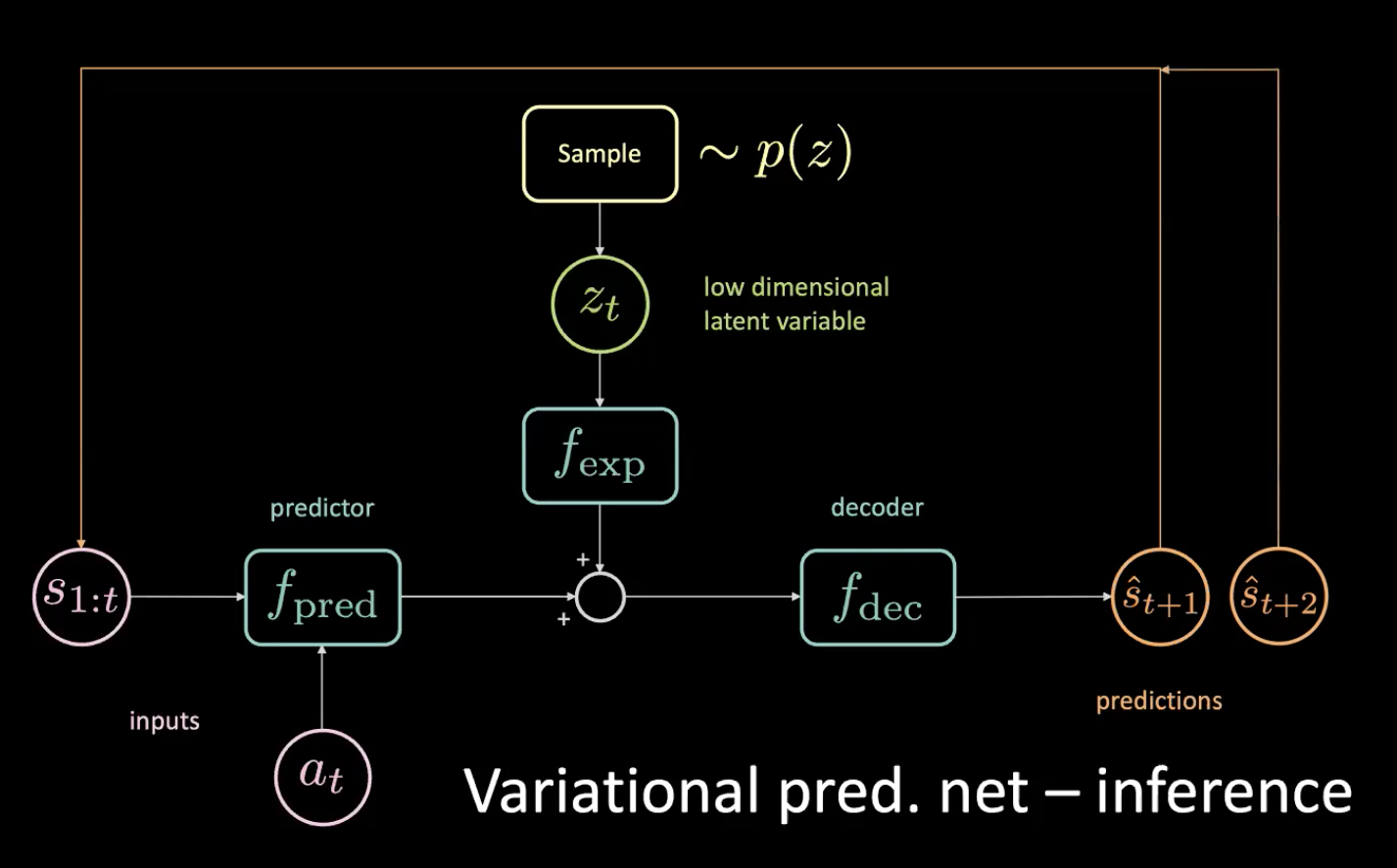
Şekil 12: Varyasyonel tahmin ağı - çıkarım

Düşük boyutlu gizli değişkeni $z_t$ kodlayıcıyı bu dağıtıma doğru çekmeye zorlayarak öncülden örnekliyoruz. Tahmini $\hat s_{t+1}$ aldıktan sonra, geri koyarız (otomatik gerileyen bir adımda) ve sonraki tahminini $\hat s_{t+2}$ alırız ve ağı bu şekilde beslemeye devam ederiz.

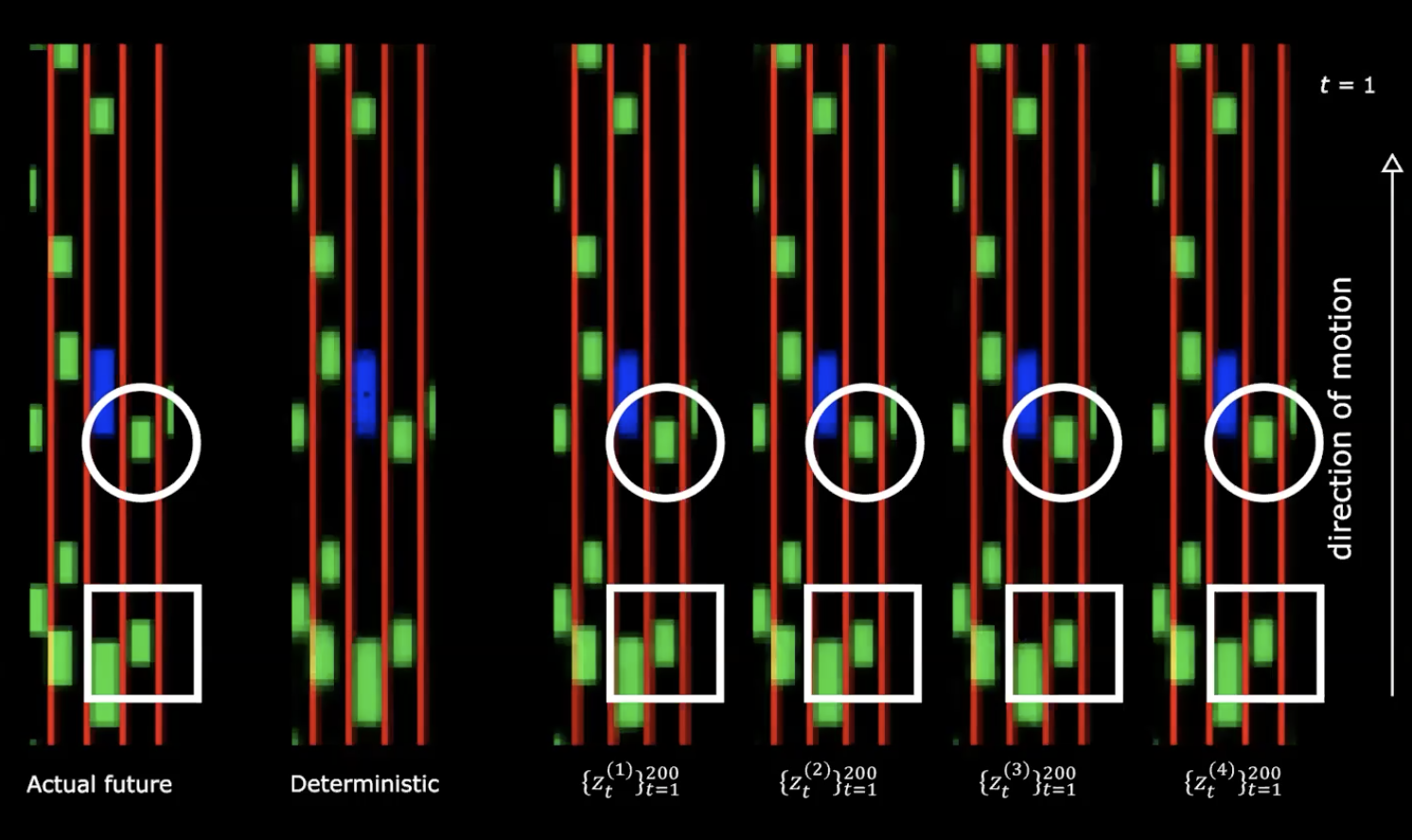
Şekil 13: Gerçek gelecek * vs * Deterministik

Yukarıdaki şekilde sağ tarafta, normal dağılımdan dört farklı çekiliş görebiliriz. Aynı başlangıç durumu ile başlıyoruz ve gizli değişkene farklı 200 değer sağlıyoruz.

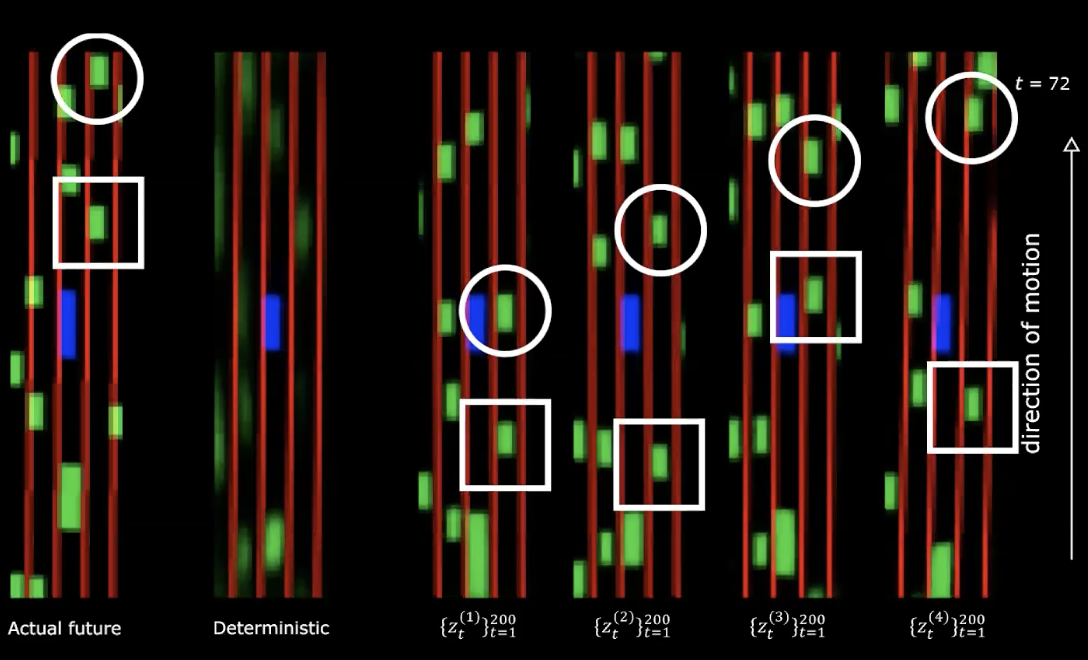
Şekil 14: Gerçek gelecek * vs * Deterministik - hareketten sonra

Farklı gizli değişkenler sağlamanın, farklı davranışlara sahip farklı durum dizileri oluşturduğunu fark edebiliriz. Bu da geleceği üreten bir ağımız olduğu anlamına geliyor. Oldukça etkileyici!

Sırada?

Artık yukarıda açıklanan şerit ve yakınlık maliyetlerini optimize ederek politikamızı eğitmek için bu büyük miktardaki veriyi kullanabiliriz.

Bu bir çok gelecek, ağa beslediğiniz gizli değişkenler dizisinden gelir. Gizli alanda, gradyan tırmanışı gerçekleştirirseniz, yakınlık maliyetini artırmaya çalışırsınız, böylece diğer arabaların size yakınlaşacağı şekilde gizli değişkenlerin sırasını elde edersiniz.

Eylem duyarsızlığı ve iletim sönümü(dropout)

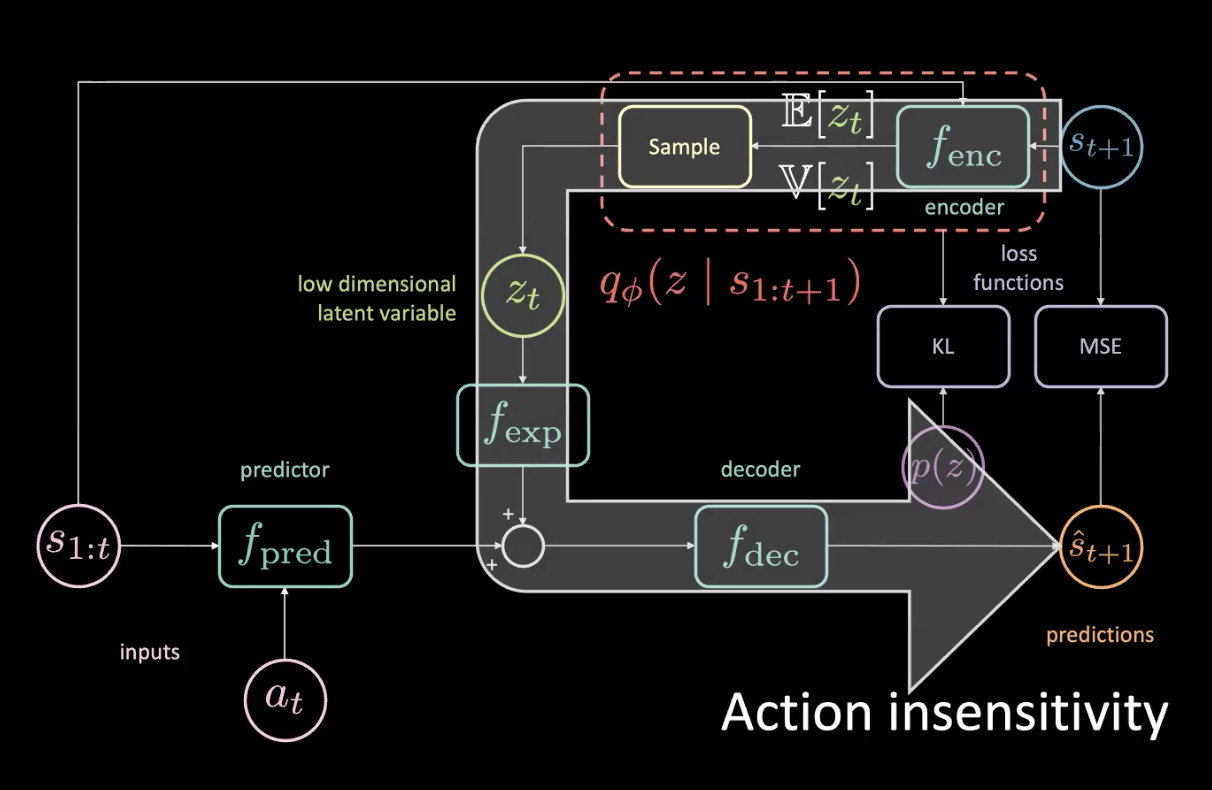
Şekil 15: Sorunlar - Eylem Duyarsızlığı

Geleceğe erişiminiz olduğu göz önüne alındığında, biraz sola dönerseniz, her şey sağa dönecektir ve bu MSE’ye çok büyük bir katkı sağlayacaktır. Gizli değişken ağın alt kısmına her şeyin sağa döneceğini bildirebilirse, MSE kaybı en aza indirilebilir - ki bu bizim istediğimiz şey değil! Her şeyin ne zaman sağa döndüğünü söyleyebiliriz çünkü bu deterministik bir iştir.

Şekil 15’teki büyük ok bir bilgi sızıntısını gösterir ve bu nedenle tahmin ediciye sağlanan mevcut eyleme artık duyarlı değildir.

Şekil 16: Sorunlar - Eylem Duyarsızlığı

Şekil 16’da, en sağdaki diyagramda, gizli değişkenlerin (en kesin şekilde geleceği elde etmemizi sağlayan gizli değişkenler) gerçek sırasına sahibiz ve ayrıca bir uzman tarafından gerçekleştirilen eylemlerin gerçek sırasına da sahibiz. Bunun solundaki iki figür, rastgele örneklenmiş gizli değişkenlere ancak gerçek eylem dizisine sahiptir, bundan dolayı direksiyon hareketini görmeyi bekliyoruz. Sol taraftaki sonuncusu, gizli değişkenlerin gerçek sırasına ancak keyfi eylemlere sahiptir. Ve dönüşün, eylemi (diğerinden örneklenen) kodlayan eylemden ziyade çoğunlukla gizli olandan geldiğini açıkça görebiliriz.

Bu sorun nasıl çözülür?

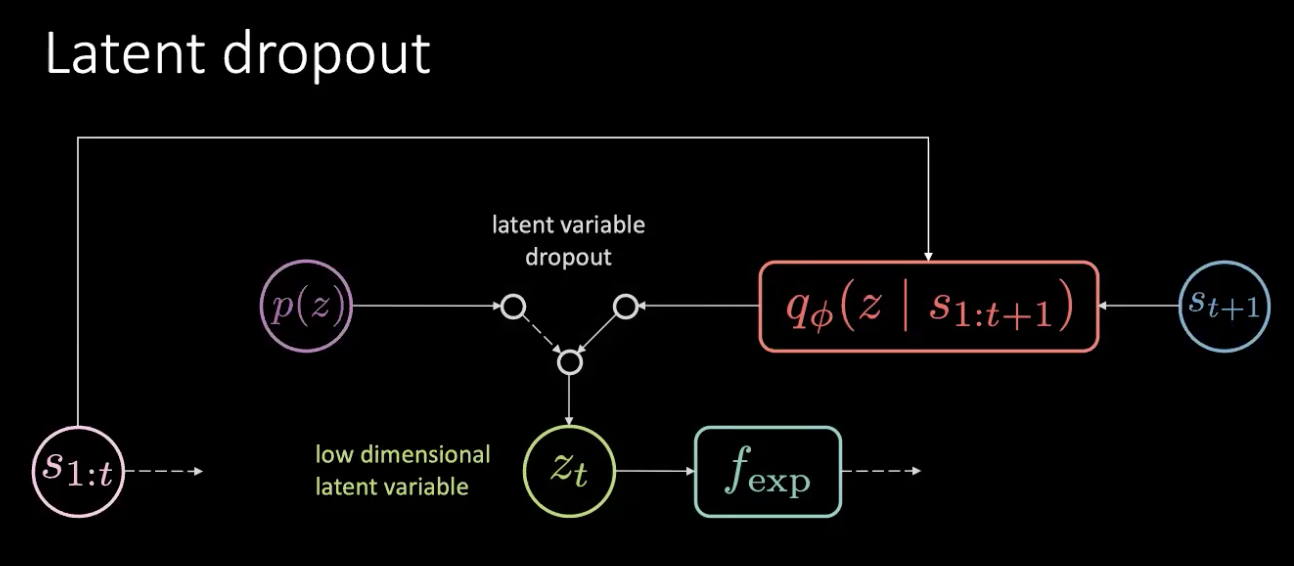
Şekil 17: Düzeltme - İletim sönümü

Sorun bellek sızıntısı değil, bilgi sızıntısıdır.Bu sorunu basitçe bu gizliliği sönümleyip öncül dağıtımdan rastgele örnekleyerek çözüyoruz. Her zaman kodlayıcının($f_{enc}$) çıktısına güvenmeyip, öncülden seçiyoruz. Bu şekilde, artık dönüşü gizli değişkende kodlayamazsınız. Bu şekilde bilgi, gizli değişken yerine eylemde kodlanır.

Şekil 18: Gizli İletim sönümü (Latent Dropout) ile performans

Sağ taraftaki son iki görüntüde, gerçek bir eylem dizisine sahip iki farklı gizli değişken kümesi görüyoruz ve bu ağlar, gizli iletim sönümü numarasıyla eğitilmiş. Artık dönüşün eylem tarafından kodlandığını gizli değişkenler tarafından kodlanmadığını görebiliriz.

Ajanın Eğitimi

Önceki bölümlerde gerçek dünya deneyimlerini simüle ederek nasıl bir dünya modeli elde edebileceğimizi gördük. Bu bölümde, ajanımızı eğitmek için bu dünya modelini kullanacağız. Amacımız, önceki durum serileri göz önüne alındığında aksiyon almak için bir politika öğrenmektir. Verilen duruma $s_t$(hız, pozisyon, resim) göre ajan bir aksiyon$a_t$ alır (hızlanma, durma, dönme), dünya modeli bir sonraki durumu ve o duruma bağlı olan yakınlık ve şerit maliyetinin kombinasyonu olan maliyeti $(s_t, a_t)$ üretir.

Önceki bölümde tartışıldığı gibi, belirsiz tahminlerden kaçınmak için, gelecek durumunun $s_{t+1}$ kodlayıcı modülünden veya öncül dağıtım $P(z)$ ‘dan gizli değişken $z_t$ örneklememiz gerekir. Dünya modeli önceki durumları $s_{1:t}$, ajanımız tarfından alınan aksiyonu, ve gizli değişken $z_t$’yi alıp gelecek durumu $\hat s_{t+1}$ ve maliyeti tahmin eder. Bu, bize nihai tahmini ve optimize etmemiz gereken zararı vermek için birden çok kez tekrarlanan (Şekil 19) bir modül oluşturur.

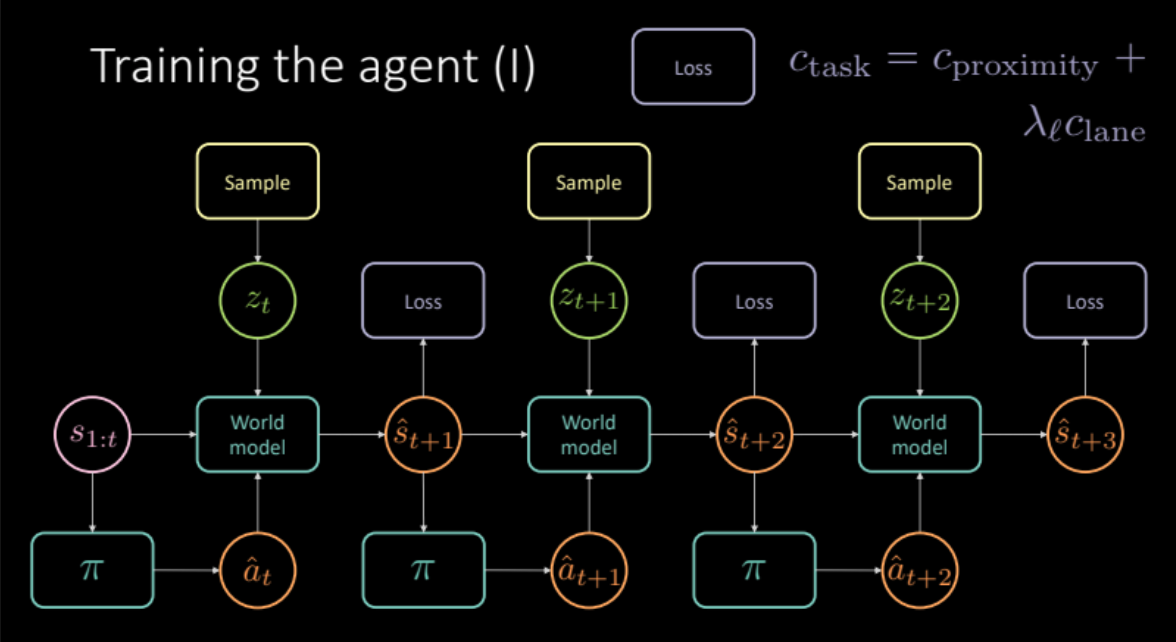
Şekil 19: Göreve özgü model mimarisi

Yani modelimizi hazırladık. Nasıl göründüğüne bakalım !!

Şekil 20: Öğrenilen politika: Ajan çarpışır veya yoldan uzaklaşır

Maalesef bu işe yaramıyor. Bu şekilde eğitilen politika, sıfır maliyetle sonuçlandığı ve her şeyi siyah olarak tahmin etmeyi öğrendiği için kullanışlı değildir.

Bu sorunu nasıl çözebiliriz? Tahminlerimizi iyileştirmek için diğer araçları taklit etmeyi deneyebilir miyiz?

Uzmanı Taklit Etmek

Buradaki uzmanları nasıl taklit ederiz? Bir durumdayken belirli bir eylem yaptıktan sonra modelimizin öngörüsünün gerçek geleceğe mümkün olduğunca yakın olmasını istiyoruz. Bu, eğitimimiz için uzman bir düzenleyici görevi görür. Maliyet fonksiyonumuz artık hem göreve özel maliyeti (yakınlık maliyeti ve şerit maliyeti) hem de bu uzman düzenleyici terimini içerir.Şimdi, gerçek geleceğe göre kaybı da hesapladığımız için, gizli değişkeni modelden çıkarmalıyız çünkü gizli değişken bize belirli bir tahmin verir, ancak bu koşullarda, sadece ortalama tahminle çalışırsak modelimiz daha iyi çalışır.

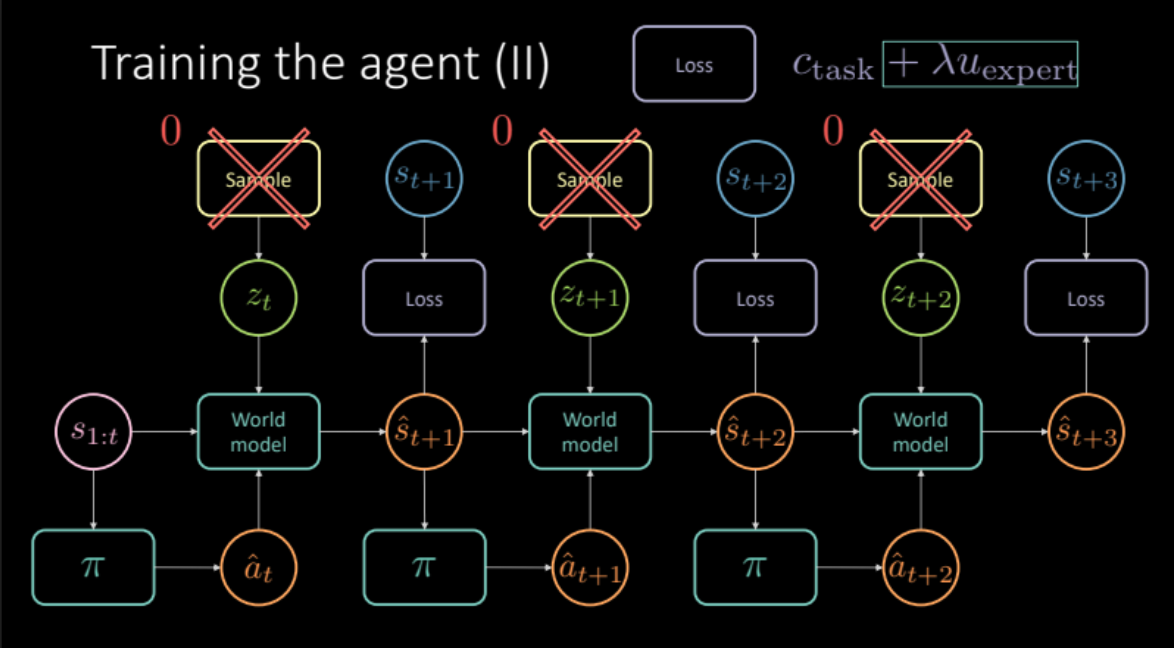
Şekil 21: Uzman düzenleme tabanlı model mimarisi

Peki bu model nasıl çalışıyor?

Şekil 22: Uzmanları taklit ederek öğrenilen politika

Yukarıdaki şekilde görebileceğimiz gibi, model aslında inanılmaz derecede iyi işliyor ve çok iyi tahminler yapmayı öğreniyor. Bu model tabanlı taklit öğrenmeydi, ajanımızı başkalarını taklit etmek için modellemeye çalıştık.

Ama daha iyisini yapabilir miyiz? Sadece sonunda kaldırmak için mi Variational Autoencoder’ı eğittik ?

İleriye dönük model tahminlerinin belirsizliğini en aza indirmeye çalışırsak, hala modelimizi iyileştirebiliriz .

İleri Model Belirsizliğini En Aza İndirmek

İleriye dönük model belirsizliğini en aza indirgemekle ne demek istiyoruz ve bunu nasıl yapacağız? Bunu yanıtlamadan önce, üçüncü hafta uygulamasında gördüğümüz bir şeyi özetleyelim.

Aynı veriler üzerinde birden fazla model eğitirsek, tüm bu modeller eğitim bölgesindeki (kırmızıyla gösterilen) noktalar üzerinde anlaşarak eğitim bölgesinde sıfır varyansla sonuçlanır. Ancak eğitim bölgesinden uzaklaştıkça, bu modellerin kayıp fonksiyonlarının yörüngeleri farklılaşmaya başlar ve varyans artar. Bu, şekil 23’te tasvir edilmiştir. Ancak varyans türevlenebilinir olduğundan, minimize etmek için varyans üzerinde gradyan inişi uygulayabiliriz.

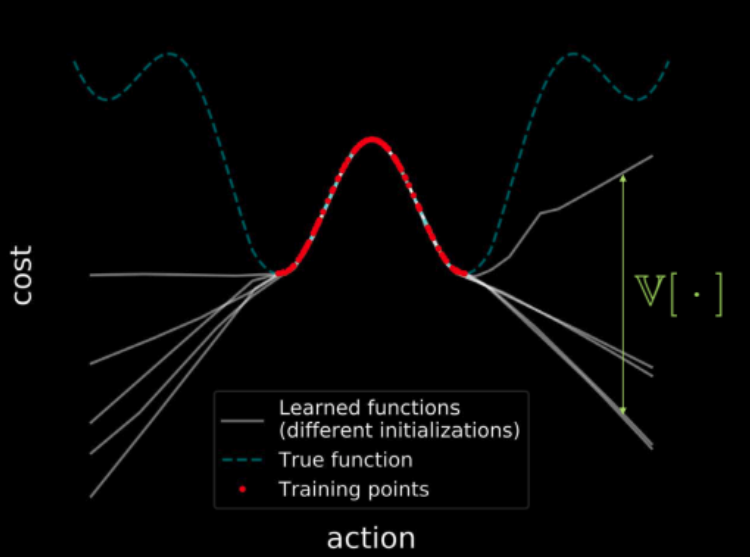
Şekil 23: Tüm girdi alanı boyunca maliyetin görselleştirmesi

Tartışmamıza geri dönersek, sadece eğitim verileri kullanarak bir politika öğrenmenin zor olduğunu gözlemliyoruz çünkü test zamanındaki durumların dağılımı, eğitim aşamasında gözlemlenenden farklı olabilir. Dünya modeli, eğitim aldığı alan dışında keyfi tahminlerde bulunabilir ve bu da yanlış bir şekilde düşük maliyetle sonuçlanabilir. Politika ağı daha sonra dinamik modeldeki bu hataları kullanabilir, aslında yanlışlıkla iyimser durumlara yol açan eylemler üretebilir.

Bunu ele almak için, dinamik modelin kendi tahminlerine ilişkin belirsizliğini ölçen ek bir maliyet öneriyoruz. Bu, aynı girdi ve eylemi birkaç farklı ileti sönümleme maskesinden geçirerek ve farklı çıktılar arasındaki varyansa bakarak hesaplanabilir. Bu, politika ağını yalnızca ileri modelin kendinden emin olduğu eylemler üretmeye teşvik eder.

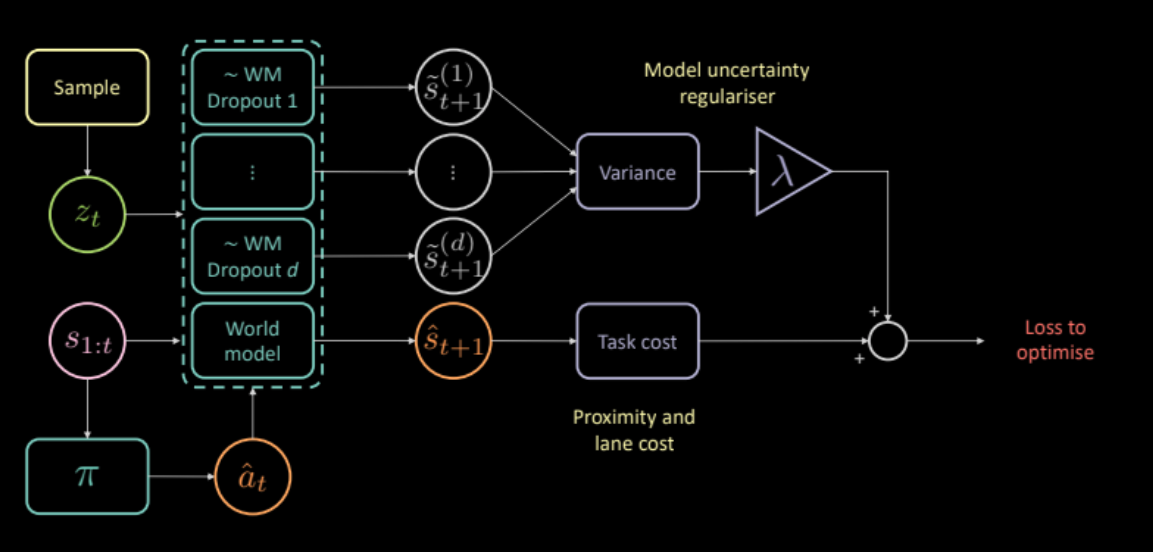
Şekil 24: Belirsizlik düzenleyici tabanlı model mimarisi

Peki, belirsizlik düzenleyici daha iyi politika öğrenmemize yardımcı olur mu?

Evet öyle. Bu şekilde öğrenilen politika önceki modellerden daha iyidir.

Şekil 25: Belirsizlik düzenleyiciye dayalı öğrenilen politika

Değerlendirme

Şekil 26, temsilcimizin yoğun trafikte araç kullanmayı ne kadar iyi öğrendiğini gösteriyor. Sarı araba orijinal sürücüdür, mavi araba öğrenilmiş temsilcimizdir ve tüm yeşil arabalar bize göre kördür (kontrol edilemez).

Şekil 26: Belirsizlik düzenleyicili modelin performansı