Aktivasyon Fonksiyonları (devam) ve Enerji Bazlı Modeller için Kayıp Fonksiyonları
🎙️ Yann LeCunBinary Cross Entropy (BCE) Kayıp Terimi - nn.BCELoss()
\[\ell(x,y) = L = \{l_1,...,l_N\}^T, \qquad l_n = -w_n[y_n\log x_n+(1-y_n)\log(1-x_n)]\]
Bu kayıp terimi, sadece iki sınıfın bulunduğu durumlarda cross entropy kayıp türünün özel bir versiyonudur ve daha basit bir fonksiyona indirgenebilinir. Bu kayıp terimi, örneğin otokodlayıcı gibi modellerde yeniden yapılanma kayıp terimi olarak kullanınır. Yukarıdaki formül $x$ ve $y$nin olasılık olduğunu varsayar, yani 0 ile 1 arasındadırlar.
Kullback-Leibler Divergence Kayıp Terimi - nn.KLDivLoss()
\[\ell(x,y) = L = \{l_1,...,l_N\}^T, \qquad l_n = y_n(\log y_n-x_n)\]
Bu, hedefiniz tek sıcak dağılım (one-hot) olduğu durumlarda basit bir kayıp terimidir. (yani. $y$ bir kategori). Yine $x$ ve $y$nin olasılık olduğunu varsayar. Bir softmax veya log-softmax ile birleştirilmemesinden dolayı dezavantajlıdır. Bu sayısal kararlılık sorunlarına yol açabilir.
BCE Loss with Logits - nn.BCEWithLogitsLoss()
\[\ell(x,y) = L = \{l_1,...,l_N\}^T, \qquad l_n = -w_n[y_n\log \sigma(x_n)+(1-y_n)\log(1-\sigma(x_n))]\]
Binary Cross Entropy kaybının bu versiyonu, softmax geçmemiş skorları alır, dolayısıyla x’in 0 ile 1 arasında olduğunu varsaymaz. Daha sonra, değerlerin bu aralıkta olduğundan emin olmak için sigmoid üzerinden geçirilir. Kayıp terimi, bu şekilde birleştirildiğinde sayısal olarak daha kararlı olur.
Marj Sıralama (Margin Ranking) Kayıp Terimi - nn.MarginRankingLoss()
\[L(x,y) = \max(0, -y*(x_1-x_2)+\text{marj})\]
Marj kayıpları, önemli bir kayıp kategorisidir. İki girişiniz varsa, bu kayıp fonksiyonu, bir girişin diğerinden en az bir marj ile daha büyük olmasını istediğinizi söyler. Bu durumda, $y$ bir ikili değişkendir $\in {-1, 1 }$. İki girdinin iki kategorinin puanları olduğunu hayal edin. Doğru kategori için puanın, yanlış kategorilerin puanından en az bir miktar daha yüksek olmasını istiyorsunuz. Hinge kaybında olduğu gibi, $y * (x_1-x_2)$ marjdan büyükse maliyet 0 olur. Daha küçükse maliyet doğrusal olarak artar. Bunu sınıflandırma için kullanacak olsaydınız, mini gruptaki en yüksek puanlı yanlış cevabın puanı $x_2$ ve doğru cevabın puanı $x_1$ olacaktı. Enerji bazlı modellerde kullanılırsa (daha sonra tartışılacaktır), bu kayıp fonksiyonu doğru cevabı $x_1$ yanlış cevabı $x_2$ e doğru zorlar.
Üçlü Marj Kayıp Terimi (Triplet Margin Loss) - nn.TripletMarginLoss()
\[L(a,p,n) = \max\{d(a_i,p_i)-d(a_i,n_i)+\text{marj}, 0\}\]
Bu kayıp, örnekler arasındaki göreceli benzerliği ölçmek için kullanılır. Örneğin, aynı kategoriye sahip iki resmi bir CNN aracılığıyla işlediğinizde ve iki vektör elde edersiniz. Bu iki vektör arasındaki mesafenin olabildiğince küçük olmasını istiyorsunuz. Bir CNN aracılığıyla da farklı kategorilere sahip iki görüntü işlediğinizde, bu vektörler arasındaki mesafenin olabildiğince büyük olmasını istersiniz. Bu kayıp işlevi, ilk mesafeyi 0’a ve ikinci mesafeyi bir marjdan daha büyük olmaya zorlar. Ancak, önemli olan tek şey, pozitif ikili arasındaki mesafenin negatif çift arasındaki mesafeden daha küçük olmasıdır.
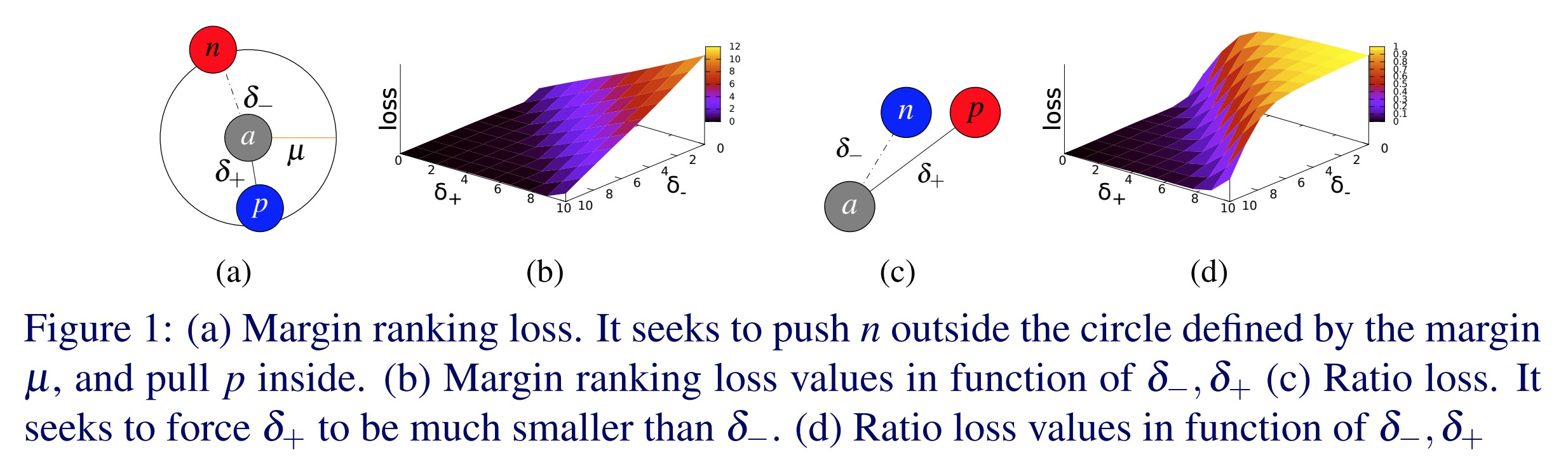
Fig. 1: Üçlü Marj Kayıp Terimi
Bu kayıp terimi Google’da resim arama sisteminde kullanılmıştır. Googleda bir resim arandığında o resim ilk olarak bir vektöre çevirilir. Daha sonra bu vektör daha önceden indekslenmiş vektörlerle karşılaştırılır ve google aradığınız resmin vektörüne en yakın resmi sonuç olarak döndürür.
Yumuşak Marjin Kayıp Terimi (Soft Margin Loss) - nn.SoftMarginLoss()
\[L(x,y) = \sum_i\frac{\log(1+\exp(-y[i]*x[i]))}{x.\text{nelement()}}\]
Giriş tensörü $x$ ve hedef tensör $y$ (1 veya -1 içeren) arasında iki sınıflı sınıflandırma lojistik kaybını optimize eden bir kriter oluşturur.
- Bu bir marj kaybının softmax versiyonudur. Softmax’tan geçirmek istediğiniz bir sürü pozitif ve bir sürü negatif olduğunu varsayın. Bu kayıp fonksiyonu daha sonra $\text{exp}(-y[i]*x[i])$ terimini doğru $x[i]$ ler için diğerlerinden daha küçük yapmaya çalışır.
- Bu kayıp fonksiyonu pozitif $y[i]*x[i]$ değerlerini birbirine yakınlaştırmaya, negatifleri uzaklaştırmaya çalışır ancak sert marjin kayıp teriminin aksine üssel olarak azalan bir etki ile sürekli bir şekilde yapar.
Çok Sınıflı Hinge Kayıp Terimi - nn.MultiLabelMarginLoss()
\[L(x,y)=\sum_{ij}\frac{max(0,1-(x[y[j]]-x[i]))}{x.\text{size}(0)}\]
Bu marj bazlı kayıp terimi, farklı girdilerin değişken miktarlarda hedeflere sahip olmasına izin verir. Bu durumda, yüksek puana sahip olmasını istediğiniz birkaç kategoriniz vardır. En sonunda tüm kategorilerdeki hinge kaybını toplar. EBM’ler için bu kayıp terimi, istenen kategorileri aşağıya ve istenmeyen kategorileri yukarıya doğru iter.
Hinge Gömü Kayıp Terimi (Hinge Embedding Loss) - nn.HingeEmbeddingLoss()
\[l_n =
\left\{
\begin{array}{lr}
x_n, &\quad y_n=1, \\
\max\{0,\Delta-x_n\}, &\quad y_n=-1 \\
\end{array}
\right.\]
İki girdinin benzer veya farklı olup olmadığını ölçmek için yarı denetimli öğrenmede kullanılan bir gömme kaybıdır. Benzer olan şeyleri bir araya getirir ve farklı olan şeyleri uzaklaştırır. $y$ değişkeni, puan çiftinin belirli bir yönde gitmesi gerekip gerekmediğini gösterir. Hinge kaybı kullanıldığında, puan $y$ 1 ise pozitif, $y$ -1 ise $\Delta$ marjı elde edilir.
Kosinüs Gömme Terimi (Cosine Embedding Loss) - nn.CosineEmbeddingLoss()
\[l_n =
\left\{
\begin{array}{lr}
1-\cos(x_1,x_2), & \quad y=1, \\
\max(0,\cos(x_1,x_2)-\text{margine}), & \quad y=-1
\end{array}
\right.\]
Bu kayıp, kosinüs mesafesini kullanarak iki girişin benzer veya farklı olup olmadığını ölçmek için kullanılır ve genellikle doğrusal olmayan gömmeleri öğrenmek veya yarı denetimli öğrenme için kullanılır.
- Başka bir şekilde düşünülürse, iki vektör arasındaki açının 1 eksi kosinüsü temelde normalleştirilmiş Öklid mesafesidir.
- Bunun avantajı, iki vektöre sahip olduğunuzda ve mesafelerini olabildiğince genişletmek istediğinizde, vektörleri çok uzun yaparak ağın bunu başarmasının çok kolay olmasıdır. Tabi ki bu bu optimal değildir. Sistemin vektörleri büyük yapmasını değil, vektörleri doğru yönde döndürmesini istersiniz, böylece vektörleri normalleştirir ve normalleştirilmiş Öklid mesafesini hesaplarsınız.
- Pozitif durumlarda, bu kayıp mümkün olduğunca vektörleri hizalamaya çalışır. Negatif çiftler için ise, kosinüsü belirli bir marjdan daha küçük yapmaya çalışır. Buradaki marj, küçük bir pozitif değer olmalıdır.
- Yüksek boyutlu bir uzayda, kürenin ekvatorunun yakınında çok fazla alan vardır. Normalleştirmeden sonra, tüm puanlarınız artık küre üzerinde normalleştirildi. İstediğiniz şey anlamsal olarak yakın olan örneklerin yakın olmasıdır. Birbirine benzemeyen örnekler ortogonal olmalıdır. Birbirlerine zıt olmalarını istemezsiniz çünkü karşı kutupta sadece bir nokta vardır. Aksine, ekvatorda çok büyük miktarda alan vardır, bu nedenle marjı küçük bir pozitif değer yaparsanız, tüm bu alandan yararlanabilirsiniz.
Bağlantısal Zamansal Sınıflandırma (CTC) Kayıp Terimi - nn.CTCLoss()
Sürekli (bölümlere ayrılmamış) bir zaman serisi ile bir hedef dizi arasındaki kaybı hesaplar.
- CTC kaybı, girdinin hedefle olası hizalanma ihtimallerini toplayarak, bir giriş düğümüne göre türevlenebilen bir kayıp değeri üretetir.
- Girişin hedefle hizalanmasının “çoktan bire” olduğu varsayılır, bu da hedef sekansın uzunluğunu giriş uzunluğundan daha az veya ona eşit olacak şekilde sınırlar.
- Çıktınız, kategori puanlarına karşılık gelen bir vektör dizisi olduğunda kullanışlıdır.

Fig. 2: Konuşma tanıma için CTC Kayıp terimi
Uygulama Örneği: Konuşma tanıma sistemi
- Hedef: Her 10 milisaniyede bir hangi kelimenin telaffuz edildiğini tahmin edin.
- Her kelime bir dizi sesle temsil edilir.
- Kişinin konuşma hızına bağlı olarak, farklı uzunluktaki sesler aynı kelimeyle eşleştirilebilir.
- Giriş dizisinden çıktı dizisine en iyi eşlemeyi bulun. Bunun için iyi bir yöntem, minimum maliyet yolunu bulmak için dinamik programlama kullanmaktır.
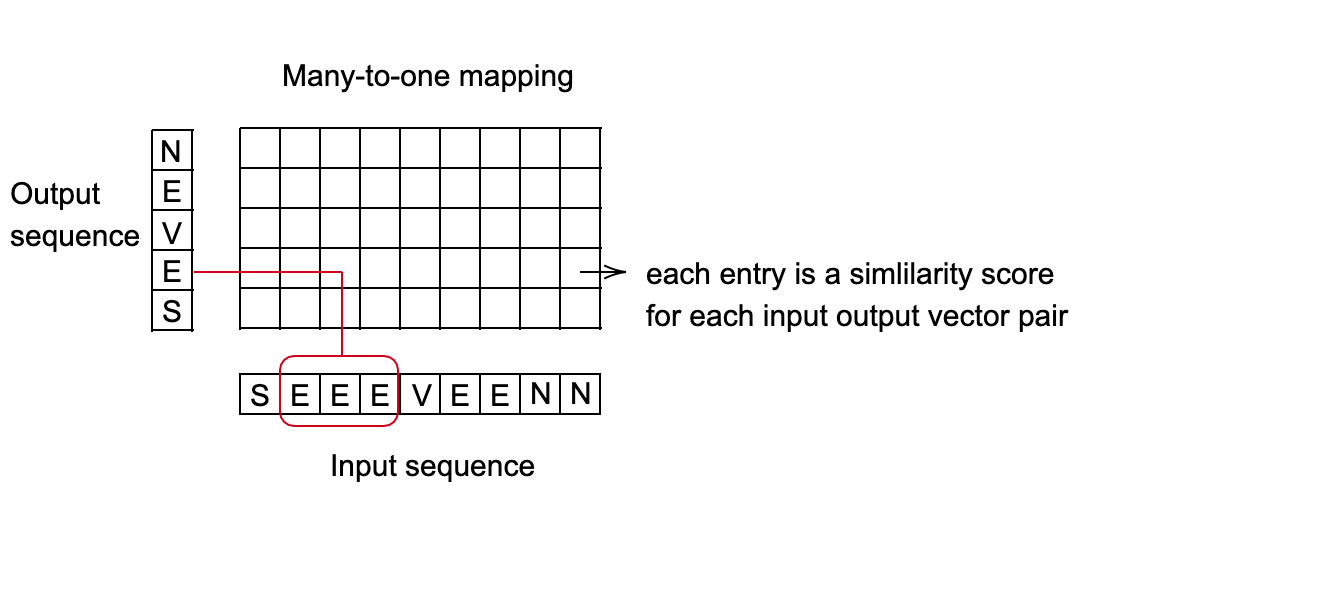
Fig. 3: Çoktan bire eşleme organizasyonu
Enerji-Bazlı Modeller (EBM) (Part IV) - Kayıp Fonksiyonu
Mimari ve Kayıp Fonksiyoneli
Enerji fonksiyonları ailesi: $\mathcal{E} = {E(W,Y, X) : W \in \mathcal{W}}$.
Eğitim seti: $S = {(X^i, Y^i): i = 1 \cdots P}$
Kayıp Fonksiyoneli: $\mathcal{L} (E, S)$
- Fonksiyonel, başka bir fonksiyonun fonksiyonu anlamına gelir. Bizim durumumuzda, fonksiyonel $\mathcal{L} (E, S)$ enerji fonksiyonunun bir fonksiyonudur $E$.
- Cünkü $E$ $W$ tarafından parametrize edilmiştir, biz bu fonksiyoneli $W$ ye bağlı bir kayıp fonksiyonuna çevirebiliriz: $\mathcal{L} (W, S)$
- Eğitim setindeki bir enerji fonksiyonunun kalitesini ölçer
- Örneklerin permütasyonları ve tekrar etmeleri durumunda değişmez.
Eğitim: $W^* = \min_{W\in \mathcal{W}} \mathcal{L}(W, S)$.
Kayıp Fonksiyonellerinin formu:
- $L(Y^i, E(W, \mathcal{Y}, X^i))$ örnek başına kayıp
- $Y^i$ istenen cevap, kategori veya tüm resim olabilir vb.
- $E(W, \mathcal{Y}, X^i)$ verilen $X_i$ değerine göre enerji yüzeyidir, $Y$ değiştiği için
- $R(W)$ düzenleyicidir
İyi Kayıp Terimi Tasarlamak
Aşşağı it doğru cevabın enerjisi üzerine.
Yukarı it yanlış cevapların enerjileri üstüne, özellikle de doğru cevaptan daha küçükse.
Örnek Kayıp Terimleri
Enerji Kayıp Terimi
\[L_{energy} (Y^i, E(W, \mathcal{Y}, X^i)) = E(W, Y^i, X^i)\]Bu kayıp fonksiyonu basitçe doğru cevabın enerjisini aşağıya iter. Ağ doğru şekilde tasarlanmamışsa, yalnızca doğru cevabın enerjisini küçük yapmaya çalıştığınız, enerjiyi başka bir yere taşımaya çalışmadığınız için, model çoğunlukla düz bir enerji üreten fonksiyon olarak sonuçlanabilir. Bundan dolayı sistem çökebilir.
Negative Log-Likelihood Loss
\[L_{nll}(W, S) = \frac{1}{P} \sum_{i=1}^P (E(W, Y^i, X^i) + \frac{1}{\beta} \log \int_{y \in \mathcal{Y}} e^{\beta E(W, y, X^i)})\]Bu kayıp fonksiyonu, olasılıkları ile orantılı olarak tüm cevapların enerjilerini yukarı doğru iterken, doğru cevapların enerjisini aşağı iter. Bu perceptron kayıp terimini $\beta \rightarrow \infty$ olduğu zaman düşürür. Yapılandırılmış çıktılarla ayrımcı eğitim için uzun süredir bir çok kominitede kullanılmaktadır.
Olasılık modeli, aşağıdakileri içeren bir EBM’dir:
- Enerji Y (tahmin edilecek değişken) üzerinden integre edilebilinir
- Kayıp işlevi, negatif log-olabilirliktir.
Perceptron Kayıp Terimi
\[L_{perceptron}(Y^i,E(W,\mathcal Y, X^*))=E(W,Y^i,X^i)-\min_{Y\in \mathcal Y} E(W,Y,X^i)\]60+ yıl önceki perceptron kayıp terimine cok benzer bir şekildedir, ve her zaman pozitiftir çünkü minumum $Y^i$ üzerinden alınır, ve $E(W,Y^i,X^i)-\min_{Y\in\mathcal Y} E(W,Y,X^i)\geq E(W,Y^i,X^i)-E(W,Y^i,X^i)=0$. Aynı denklemden anlaşılacağı üzere fonksiyon $Y^i$ doğru olduğu zaman sıfır verir.
Bu kayıp, doğru cevabın enerjisini küçültür ve diğer tüm cevapların enerjisini olabildiğince büyük hale getirir. Ancak bu kayıp, fonksiyonun her yanlış $ Y^i$ cevabına aynı değeri vermesini engellemez, dolayısıyla doğrusal olmayan sistemler için kötü bir kayıp fonksiyonudur. Bu kayıp terimini geliştirmek için, en rahatsız edici yanlış cevabı tanımlarız.
Genelleştirilmiş Marjin Kayıp Terimi
En rahatsız edici yanlış cevap: ayrık durum $Y$ ayrık bir değişken olsun. Eğitim örneği $(X^i,Y^i)$ için, en rahatsız edici yanlış cevap $\bar Y^i$ yanlış olan tüm olası cevaplar arasında en düşük enerjiye sahip cevaptır:
\[\bar Y^i=\text{argmin}_{y\in \mathcal Y\text{ and }Y\neq Y^i} E(W, Y,X^i)\]En rahatsız edici yanlış cevap: sürekli durum $Y$ sürekli bir değişken olsun. Eğitim örneği $(X^i,Y^i)$ için, en rahatsız edici yanlış cevap $\bar Y^i$ doğru yanıttan en az $\epsilon$ uzakta olan tüm yanıtlar arasında en düşük enerjiye sahip yanıttır:
\[\bar Y^i=\text{argmin}_{Y\in \mathcal Y\text{ and }\|Y-Y^i\|>\epsilon} E(W,Y,X^i)\]Ayrık durumda, en rahatsız edici yanlış cevap en küçük enerjiye sahip doğru olmayan cevaptır. Sürekli durumda, $Y^i$ ye son derece yakın $Y$ için enerji $E(W,Y^i,X^i)$ ye yakın olmalıdır. Dahası $Y^i$ ye eşit olmayan $Y$ üzerinden hesaplanan $\text{argmin}$ 0 olacaktır. Sonuç olarak, bir $\epsilon$ mesafesi seçeriz ve yalnızca $Y$’lardan en az $\epsilon$’ kadar $Y_i$ ‘dan uzak olanları “yanlış yanıt” olarak kabul ederiz. Bu optimizasyonun sadece $Y$’lerin $Y^i$ den en az $\epsilon$ uzak olanları üstünde olma nedenidir.
Enerji fonksiyonu en rahatsız edici yanlış cevabın enerjisinin doğru cevabın enerjisinden bir miktar daha yüksek olmasını sağlayabilirse, bu enerji fonksiyonu iyi çalışır.
Genelleştirilmiş Marjin Kayıp Terimleri Örnekleri
Hinge Kayıp Terimi
\[L_{\text{hinge}}(W,Y^i,X^i)=( m + E(W,Y^i,X^i) - E(W,\bar Y^i,X^i) )^+\]$\bar Y^i$ en rahatsız edici yanlış cevap tır. Bu kayıp, doğru cevap ile en rahatsız edici yanlış cevap arasındaki farkın en az $m$ olmasını zorlar.

Fig. 4: Hinge Kayıp Terimi
S:$m$’yi nasıl seçeriz?
C: Keyfi, ancak son katmanın ağırlıklarını etkiler.
Log Kayıp Terimi
\[L_{\log}(W,Y^i,X^i)=\log(1+e^{E(W,Y^i,X^i)-E(W,\bar Y^i,X^i)})\]Bu ‘yumuşak’ hinge kayıp terimi olarak düşünülünebilinir. Doğru cevap ile en rahatsız edici yanlış cevabı bir hinge ile oluşturmak yerine, şimdi yumuşak bir hinge ile oluştururuz. Bu kayıp “sonsuz bir marj” sağlamaya çalışır, ancak eğimin üstel olarak azalması nedeniyle bu gerçekleşmez.

Fig. 5: Log Kayıp Terimi
Kare-Kare Kayıp Terimi
\[L_{sq-sq}(W,Y^i,X^i)=E(W,Y^i,X^i)^2+(\max(0,m-E(W,\bar Y^i,X^i)))^2\]Kombinasyon enerjiyi en aza indirmeye çalışır ve en rahatsız edici yanlış cevap için en az $m$ marjı zorlar. Bu, Siyam ağlarında kullanılan kayba çok benzer.
Diğer Kayıp Terimleri
Bir sürü var. İşte iyi ve kötü kayıp terimlerinin bir özeti.
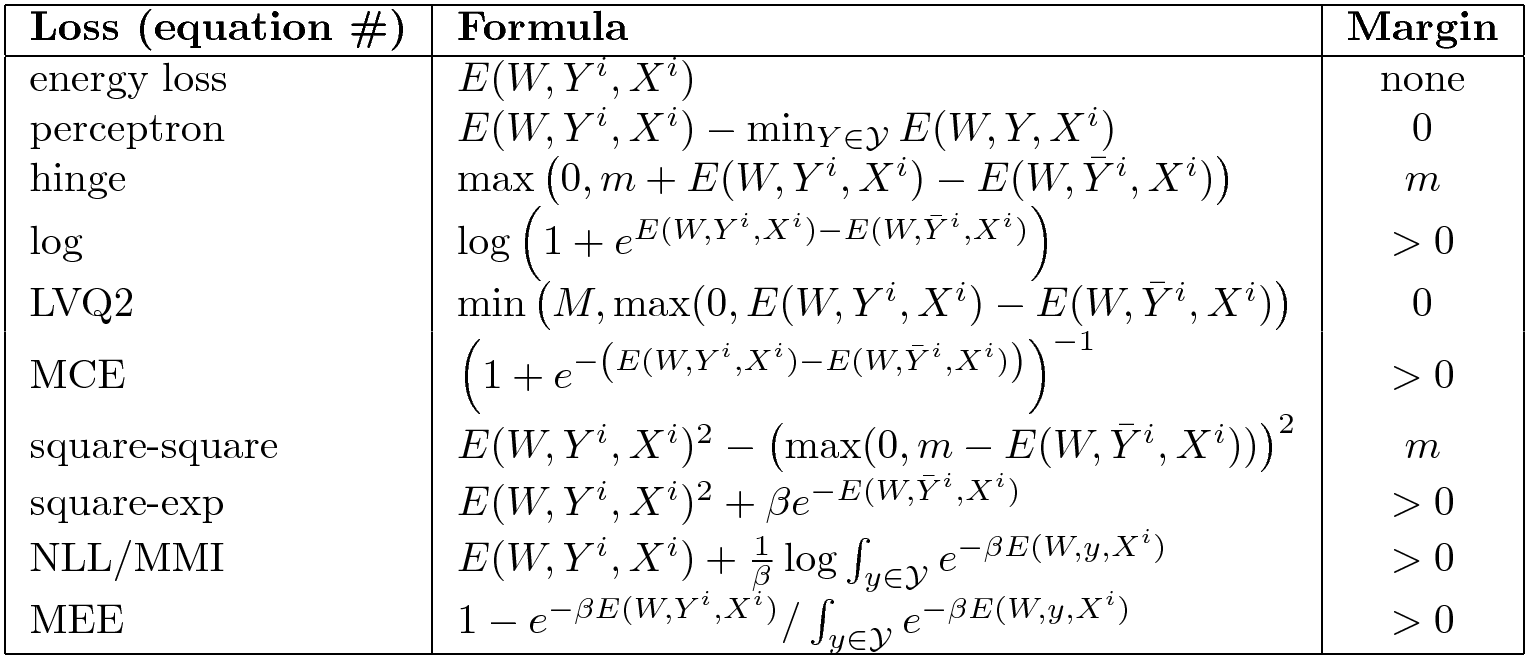
Fig. 6: EBM kayıp fonksiyonlarından seçimler
Sağ taraftaki sütun, enerji fonksiyonunun bir marj uygulayıp uygulamadığını gösterir. Basit eski enerji kaybı hiçbir yere itilmez, bu yüzden bir marjı yoktur. Enerji kaybı her problemde işe yaramaz. Perceptron kaybı, enerji doğrusal bir parametrezisyona sahipse çalışır, ancak genel olarak durum böyle değildir. Bazılarının hinge kaybı gibi sınırlı bir marjı vardır bazılarında ise yumuşak hinge gibi sonsuz bir marjı vardır.
S: Sürekli durumda en rahatsız edici yanlış cevap $ \bar Y_i$ nasıl bulunur?
C: Bir noktayı $Y^i$ den yeterince uzak bir yere itmeye çalışıyorsunuz, çünkü eğer çok yakınsa, sinir ağı tarafından tanımlanan fonksiyon “katı” olduğu için parametreler fazla hareket etmeyebilir. Ancak genel olarak, bu zordur ve kontrastlı örnekleri seçen yöntemlerin çözmeye çalıştığı problemdir. Bunu yapmanın tek bir doğru yolu yoktur.
Hinge tipi kontrast kayıpları için biraz daha genel bir form şudur:
\[L(W,X^i,Y^i)=\sum_y H(E(W, Y^i,X^i)-E(W,y,X^i)+C(Y^i,y))\]$Y$ nin ayrık olduğunu varsayarız, ancak sürekli ise, toplam integrasyon ile değiştirilir. Burda, $E(W, Y^i,X^i)-E(W,y,X^i)$ doğru ve başka bir cevap için hesaplanan $E$ nin farkıdır. $C(Y^i,y)$ marjin, ve genellikle $Y^i$ ve $y$ arasındaki mesafedir. Buradaki motivasyon, yanlış bir $y$ örneği için yükseltmek istediğimiz miktarın $y$ ile doğru örnek $Y_i$ arasındaki mesafeye bağlı olmasıdır. Bu, optimize edilmesi daha zor bir kayıp olabilir.
📝 Haochen Wang, Eunkyung An, Ying Jin, Ningyuan Huang
Mehmet Aygun
13 Apr 2020