Aktivasyon fonksiyonları (part 1)

🎙️ Yann LeCun

Aktivasyon fonksiyonları

Bugünkü derste bazı önemli aktivasyon fonksiyonlarını ve bunların PyTorch’taki uygulamalarını gözden geçireceğiz. Bu fonksiyonlar çeşitli makalelerden gelmekte ve bazı özel problemlerde daha iyi çalıştıklarını iddia etmektedirler.

ReLU - nn.ReLU()

\[\text{ReLU}(x) = (x)^{+} = \max(0,x)\]
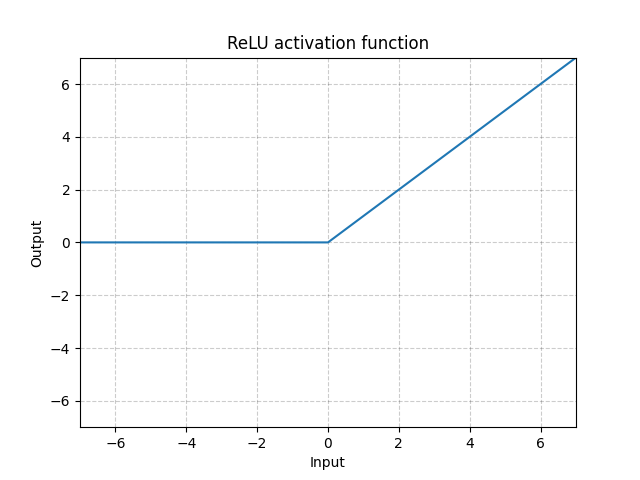
Fig. 1: ReLU

RReLU - nn.RReLU()

ReLU’nun farklı varyasyonları vardır. Rastgele ReLU (RReLU) aşağıdaki gibi tanımlanır.

\[\text{RReLU}(x) = \begin{cases} x, & \text{eğer} x \geq 0\\ ax, & \text{aksi halde} \end{cases}\]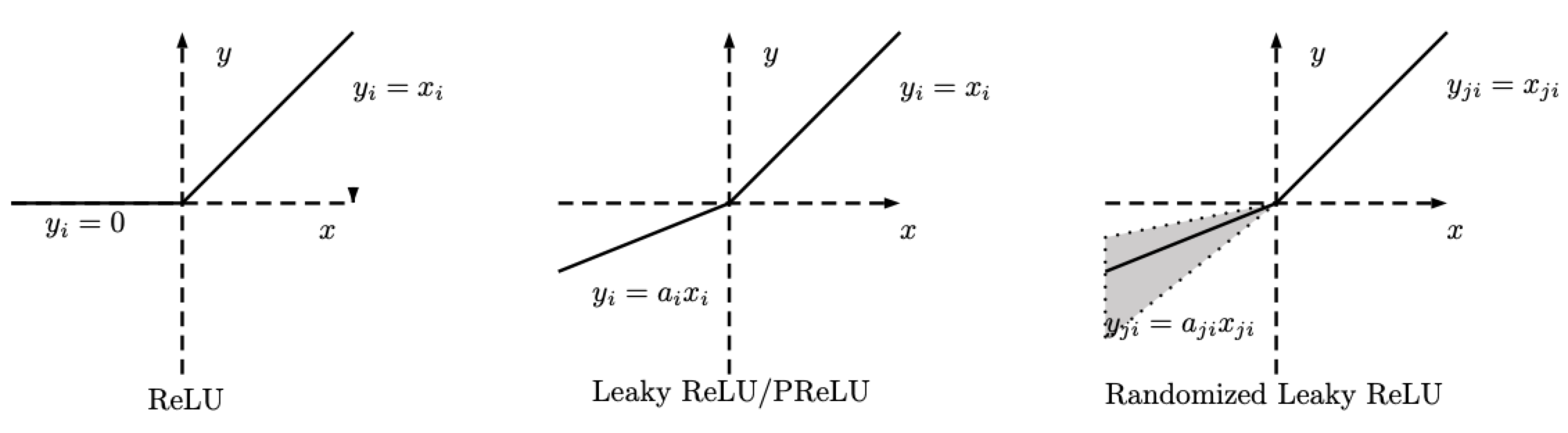
Fig. 2: ReLU, Leaky ReLU/PReLU, RReLU

RReLU için, $a$ bir rastgele değişkendir ve eğitim boyunca örneklenir, ve test aşamasında sabit kalır. PReLU için $a$ da öğrenilir, ReLU için ise $a$ sabittir.

LeakyReLU - nn.LeakyReLU()

\[\text{LeakyReLU}(x) = \begin{cases} x, & \text{eğer} x \geq 0\\ a_\text{negatif eğim}x, & \text{aksi halde} \end{cases}\]
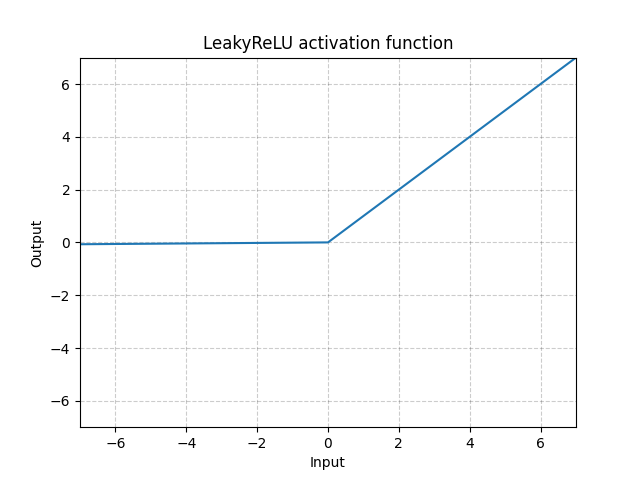
Fig. 3: LeakyReLU

Burda $a$ sabit bir değişkendir. Denklemin alt kısmı, ReLu nöronlarının inaktif hale geldiği ve hangi girdi gelirse gelsin sürekli 0 ürettiği ve ölen ReLU olarak adlandırılan problemin oluşmasını önler. Ölen ReLU’larin gradyanlari 0’dır. Negatif eğim, ağ’ın geriye doğru yayılım yapmasını ve işe yarar şeyler öğrenmesini sağlar.

LeakyReLU özellikle küçük ağlar için önemlidir. Küçük ağlarda normal ReLU kullanıldığında geriyayılım yapmak için gradyan elde etmek nerdeyse imkansızdır. LeakyReLU ile ağ tüm değerlerin sıfır olduğu alanlarda bile gradyana sahip olabilir.

PReLU - nn.PReLU()

\[\text{PReLU}(x) = \begin{cases} x, & \text{eğer} x \geq 0\\ ax, & \text{aksi halde} \end{cases}\]

Burda $a$ öğrenilenebilinir bir parametredir.

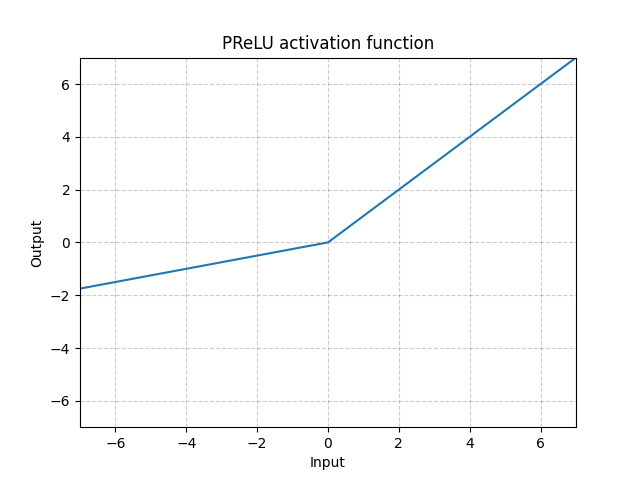
Fig. 4: ReLU

Yukarıdaki aktivasyon fonksiyonları (ör: ReLU, LeakyReLU, PReLU) ölçeğe göre değişmezdir.

Softplus - Softplus()

\[\text{Softplus}(x) = \frac{1}{\beta} * \log(1 + \exp(\beta * x))\]
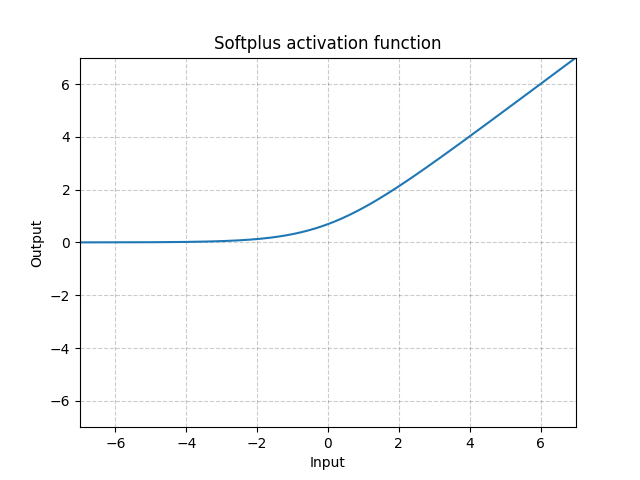
Fig. 5: Softplus

Softplus ReLU fonksiyonun pürüssüz bir yakınsamasıdır, ve makinenin sürekli pozitif çıktı vermesini zorlar.

Eüer $\beta$ yeterince büyürse, fonksiyon ReLU gibi olmaya başlar.

ELU - nn.ELU()

\[\text{ELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x) - 1)\]
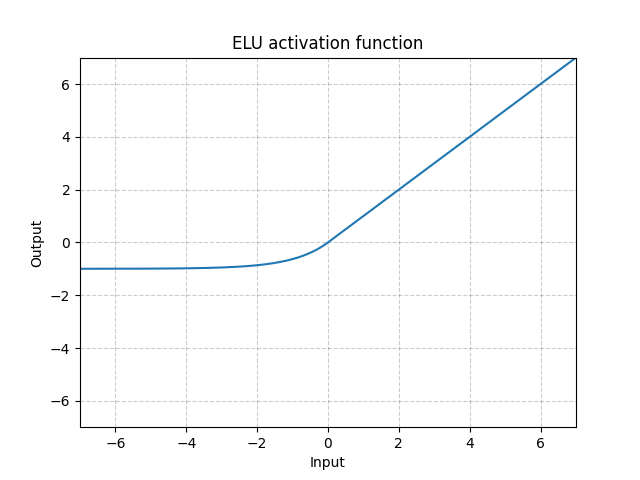
Fig. 6: ELU

ReLU’nun aksine, bu fonksiyonun değeri 0’ın altına düşebilir ve sistemin ortalama çıktısı 0’a yakın olabilir. Bundan dolayı model daha hızlı yakınsayabilir. Ve varyasyonları (CELU, SELU) sadece farklı şekilde parametrelendirilmiş versiyonlarıdır.

CELU - nn.CELU()

\[\text{CELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x/\alpha) - 1)\]
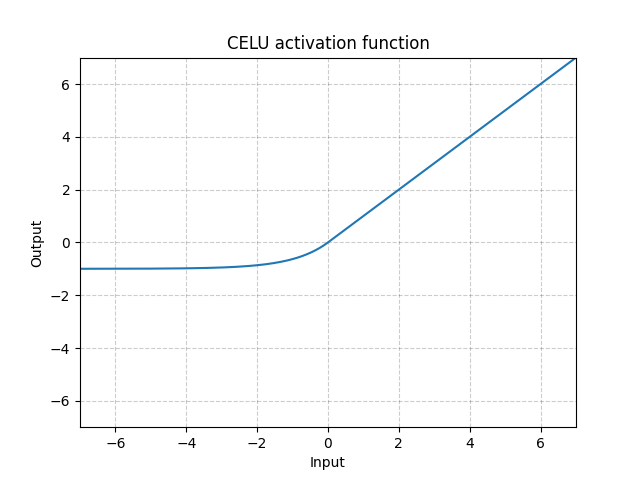
Fig. 7: CELU

SELU - nn.SELU()

\[\text{SELU}(x) = \text{scale} * (\max(0, x) + \min(0, \alpha * (\exp(x) - 1))\]
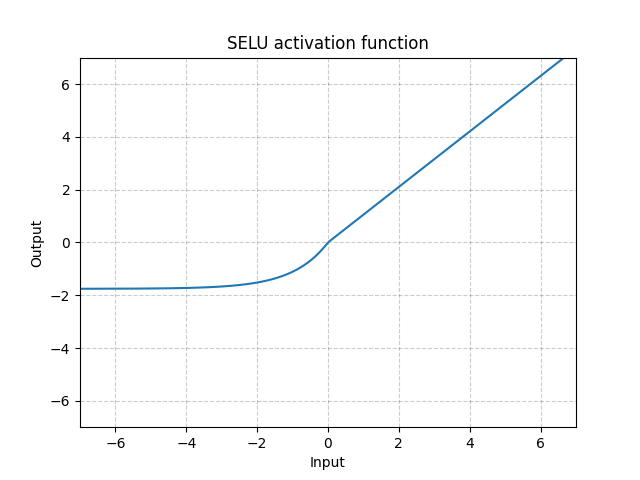
Fig. 8: SELU

GELU - nn.GELU()

\[\text{GELU(x)} = x * \Phi(x)\]

$\Phi(x)$ burada Gaussian dağılımının kümülatif dağılım fonksiyonudur.

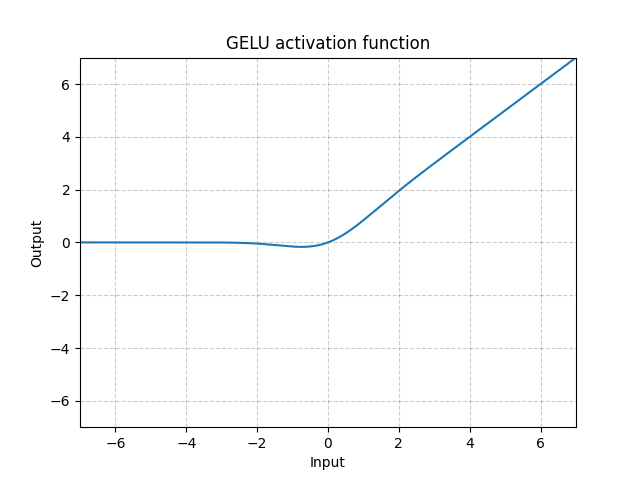
Fig. 9: GELU

ReLU6 - nn.ReLU6()

\[\text{ReLU6}(x) = \min(\max(0,x),6)\]
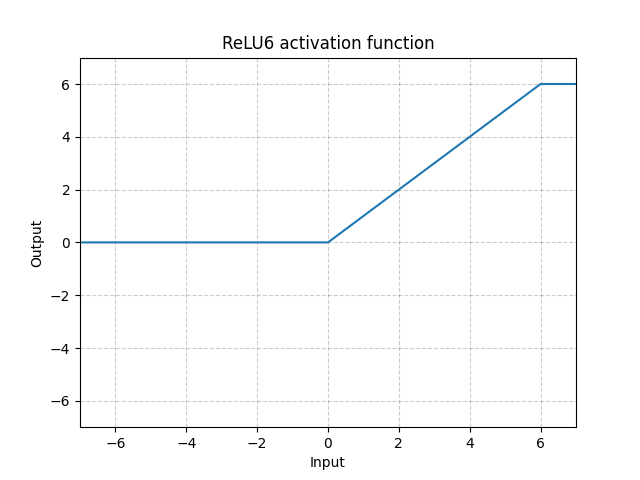
Fig. 10: ReLU6

Bu ReLU, 6 değerinde doymaya baslar. Ancak 6’nın doyma noktası olarak seçilmesi için bir neden yoktur. Bundan dolayı aşşağıdaki Sigmoid fonksiyonu ile daha iyisini yapabiliriz.

Sigmoid - nn.Sigmoid()

\[\text{Sigmoid}(x) = \sigma(x) = \frac{1}{1 + \exp(-x)}\]
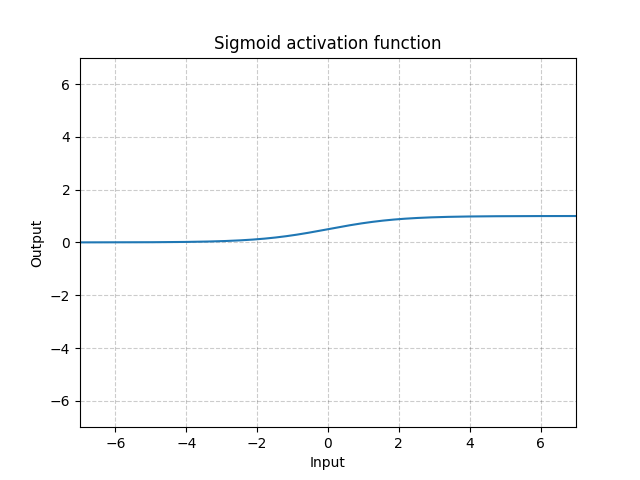
Fig. 11: Sigmoid

Sigmoidleri bir çok katmanda ard arda kullanırsak, sistemin öğrenmesi verimsiz olabilir ve ayrıca ilk değer atama aşamasında dikkatli olunması gerekir. Bunun nedeni, giriş değeri çok büyük ve sıfır olduğu zaman, sigmoid fonksiyonun gradyanının sıfır olmasıdır. Bu durumda geriye doğru gradyan akmaz ve bu durum doymuş gradyan problemi olarak adlandırılır. Bundan dolayi derin ağlarda, tek bükülmeli fonksiyonlar (ör: ReLU) tercih edilir.

Tanh - nn.Tanh()

\[\text{Tanh}(x) = \tanh(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)}\]
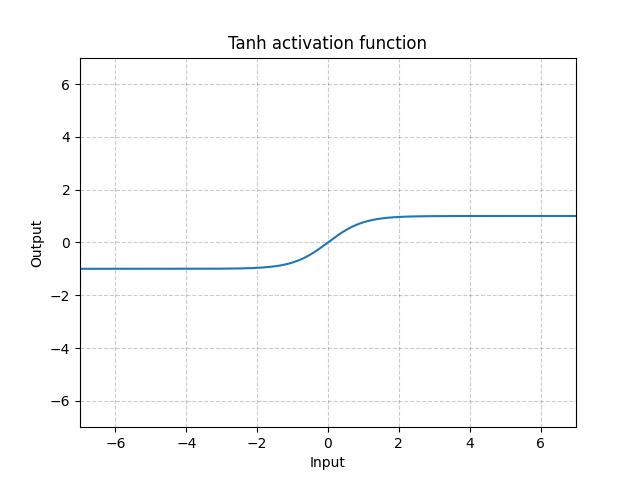
Fig. 12: Tanh

Tanh nerdeyse Sigmoid fonksiyonu ile aynıdır. Tek farkı -1 ile 1 arasına ortalanmasıdır. Fonksiyonun çıktı değerlerinin ortalaması neredeyse sıfırdır. Bundan dolayı model daha hızlı yakınsar. Not olarak, eğer tüm girdi değerlerinin ortalaması sıfıra yakınsa, yakınsama daha hızlı gerçekleşir. Bunun bir örneği yığın normalleştirmesidir.

Softsign - nn.Softsign()

\[\text{SoftSign}(x) = \frac{x}{1 + |x|}\]
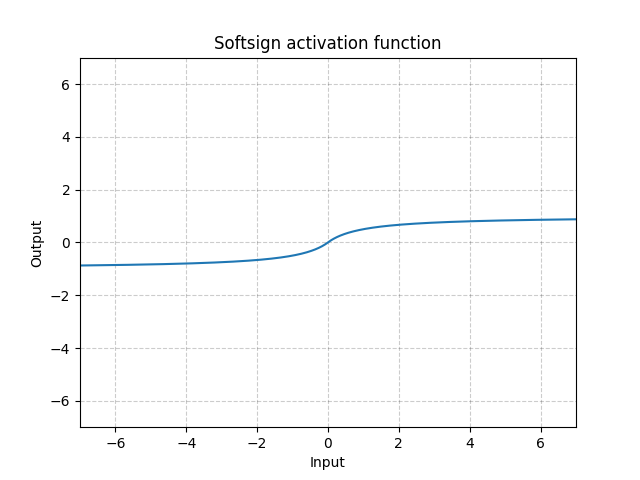
Fig. 13: Softsign

Sigmoid fonksiyonuna benzer, ancak asimptota daha yavaş ulaşır ve bu bir nebzeye kadar gradyen yok olma problemini azaltır.

Hardtanh - nn.Hardtanh()

\[\text{HardTanh}(x) = \begin{cases} 1, & \text{if} x > 1\\ -1, & \text{if} x < -1\\ x, & \text{aksi halde} \end{cases}\]

Lineer alanın aralığı [-1, 1]’den min_değer ve max_değer i değiştirerek ayarlanabilinir.

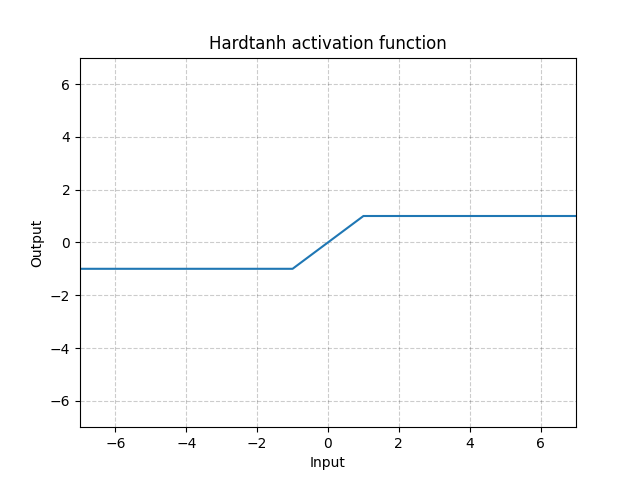
Fig. 14: Hardtanh

Bu fonskyon özellikle ağırlıkların küçük aralıklarda tutulduğu durumlarda şaşırtıcı şekilde iyi calışır.

Threshold - nn.Threshold()

\[y = \begin{cases} x, & \text{if} x > \text{threshold}\\ v, & \text{otherwise} \end{cases}\]

Çok nadir olarak kullanılır, çünkü gradyanı geri yayayamayız. Ayrıca, 60 ve 70’lerde ikili nöronlar kullanıldığından, insanların geri-yayılım kullanmasını engellemiştir.

Tanhshrink - nn.Tanhshrink()

\[\text{Tanhshrink}(x) = x - \tanh(x)\]
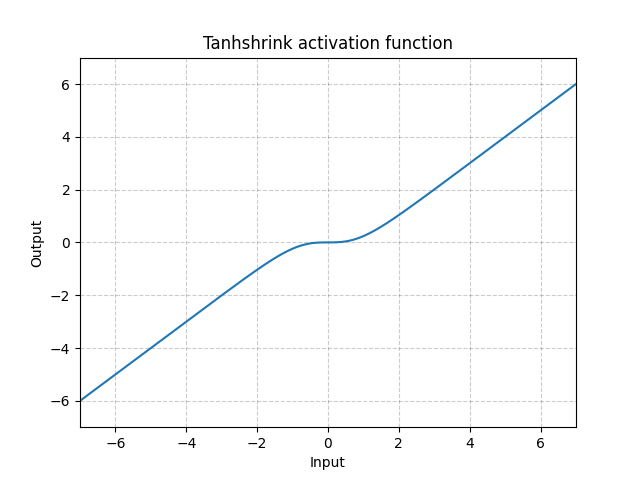
Fig. 15: Tanhshrink

Gizli değişkenin seyrek olarak kodlanması dışında çok nadir olarak kullanılır.

Softshrink - nn.Softshrink()

\[\text{SoftShrinkage}(x) = \begin{cases} x - \lambda, & \text{eğer} x > \lambda\\ x + \lambda, & \text{eğer} x < -\lambda\\ 0, & \text{aksi halde} \end{cases}\]
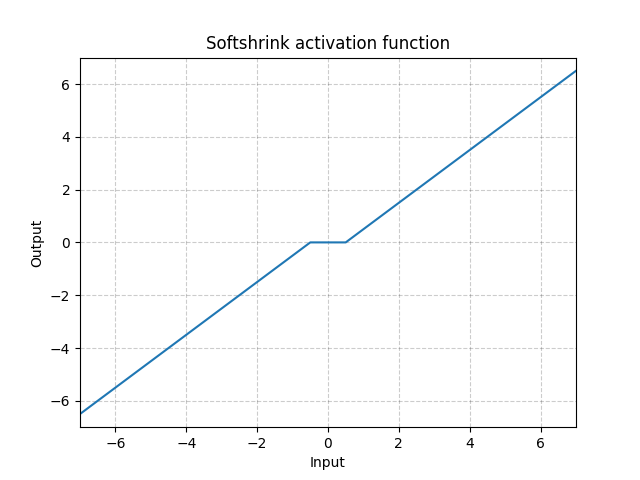
Fig. 16: Softshrink

Bu fonksiyon temelde değişkeni 0’a doğru sabit olarak küçültür ve değişken 0’a yakınsarsa çıktının 0 olmasını zorlar. Bunu $\ell_1$ in gradyanı için bir adim olarak dusunebilirsiniz. Ayrıca, Yinelemeli Büzülme-Eşikleme Algoritması (Iterative Shrinkage-Thresholding Algorithm) için de bir adımdır. Ancak standart sinir ağlarında aktivasyon olarak genellikle kullanılmaz.

Hardshrink - nn.Hardshrink()

\[\text{HardShrinkage}(x) = \begin{cases} x, & \text{eğer} x > \lambda\\ x, & \text{eğer} x < -\lambda\\ 0, & \text{aksi halde} \end{cases}\]
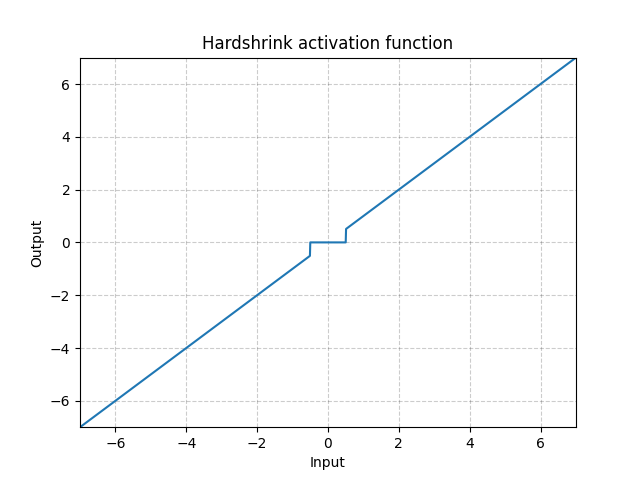
Fig. 17: Hardshrink

Seyrek kodlama dışında çok nadir kullanılır.

LogSigmoid - nn.LogSigmoid()

\[\text{LogSigmoid}(x) = \log\left(\frac{1}{1 + \exp(-x)}\right)\]
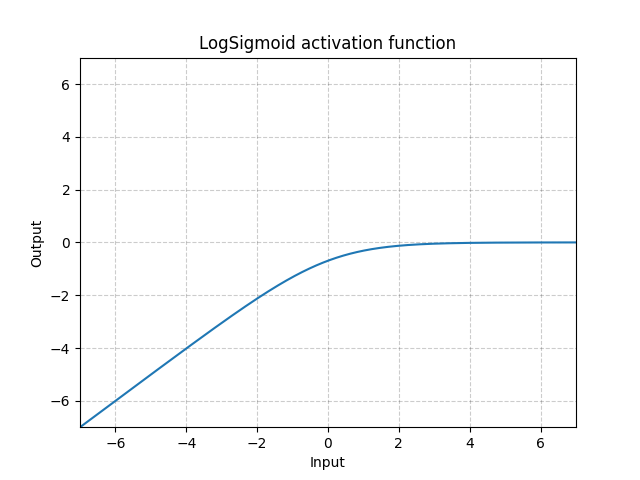
Fig. 18: LogSigmoid

Genellikle hata fonksiyonlarinda kullanılır, aktivasyon fonksiyonu olarak çok yaygın değildir.

Softmin - nn.Softmin()

\[\text{Softmin}(x_i) = \frac{\exp(-x_i)}{\sum_j \exp(-x_j)}\]

Sayıları olasılık dağılımına dönüştürür.

Soft(arg)max - nn.Softmax()

\[\text{Softmax}(x_i) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}\]

LogSoft(arg)max - nn.LogSoftmax()

\[\text{LogSoftmax}(x_i) = \log\left(\frac{\exp(x_i)}{\sum_j \exp(x_j)}\right)\]

Genellikle hata fonksiyonlarında kullanılır, aktivasyon fonksiyonu olarak çok yaygın değildir.

S&C aktivasyon fonksiyonları

nn.PReLU() ile alakalı sorular

• tüm kanallar için neden ayni $a$ değerini istiyoruz?

  Değişik kanallar değişik $a$ değerine sahip olabilir. $a$ değerini tüm birimler için parametre olarak kullanılanabilinir. Öznitelik haritası olarak da paylaşılınabilinir.

• $a$ değerini ögreniyor muyuz? $a$ değerini öğrenmek avantajlı mı?

  $a$ değerini öğrenedebilirsin, sabitleyedebilirsin. Sabitlemenin amacı, negatif eğilimin olduğu yerlerde bile eğriselliğin sıfır olmayan gradyan vermesininden emin olmaktır. $a$’yı’ öğrenilebilir hale getirmek, doğrusal olmayanlığı doğrusal haritalamaya veya tam doğrultmaya dönüştürebilir. Kenar polaritesinden bağımsız olarak bir kenar detektörü dizayn etmek gibi bazi uygulamalar için yararlı olabilir.

• Eğriselligin ne kadar karmaşık olmasını istiyoruz?

  Teorik olarak, doğrusal olmayan bir fonksiyonun tamanını yay parametreleri, Chebyshev polinomu, vb. gibi şeyleri kullanarak çok karmaşık bir şekilde parametrelendirebiliriz. Parametrelendirme, öğrenme sürecinin bir parçası olabilir.

• Sisteminizde daha fazla üniteye sahip olmanın parametrelendirmeye göre avantajı nedir?

  Bu gerçekten ne yapmak istediğine baglıdır. Örneğin, düşük boyutlu bir uzayda regresyon yaparken, parametrelendirme yardımcı olabilir. Ancak, göreviniz görüntü tanıma gibi yüksek boyutlu bir uzayın içindeyse, sadece bir tane “doğrusallık” gereklidir ve monotonik doğrusallık daha iyi çalışır. Kısacası, istediğiniz fonksiyonları parametreleştirebilirsiniz, ancak bu genellike büyük bir avantaj sağlamaz.

Bükülme ile alakali sorular

• Bir bükülme vs iki bükülme

  İkili bükülmede ölçek içinde tanımlanmıştır. Bu, giriş katmanı iki ile çarpılırsa (veya sinyal genliği iki ile çarpılırsa), çıkışların tamamen farklı olacağı anlamına gelir. Sinyal daha fazka doğrusal olmayacaktır, ve böylece çıktı tamamen farklı bir davranış gösterecektir. Oysa, sadece bir bükülmeye sahip bir fonksiyonunuz varsa, girişi iki ile çarparsanız, çıktınız da iki ile çarpılır.

• Bükülmeleri olan doğrusal olmayan bir aktivasyon ile pürüzsüz doğrusal olmayan bir aktivasyon arasındakı farklar. Neden / ne zaman diğeri tercih edilir?

  Bu bir ölçek eşit değişirlik durumudur. eğer bükülme sert ise, girdiyi ikiyle çarptiğınızda, çıktı da ikiyle çarpılır. Eğer pürüzsüz bir geçiş varsa, örneğin, girdiyi 100 ile carparsaniz, cıktıda sert bir bükülme var gibi görünüyor çünkü pürüzsüz kısım 100 kat küçülmüştür. Eğer girdiyi 100 ile bölerseniz, kıvrım çok düzgün dışbükey bir fonksiyon haline gelir. Böylece, girdinin ölçeğini değiştirerek, aktivasyon biriminin davranışını değiştirmiş olursunuz.

  Bu bazen problem olabilir. Örneğin, çok katmanlı bir sinir ağı eğitiyorsunuz ve birbiri ardına iki katmanınız var. Bir katmanın ağırlıklarının diğer katmanın ağırlıklarına göre ne kadar büyük olduğu konusunda iyi bir kontrole sahip olamazsınız. Ölçekleri önemseyen bir doğrusalsızlığınız varsa, ağınızın ilk katmanda hangi boyutta ağırlık matrisinin kullanılabileceğine dair bir seçeneği yoktur, çünkü bu davranışı tamamen değiştirecektir.

  Bu sorunu çözmenin bir yolu, her bir tabakanın ağırlıkları üzerinde sert bir ölçek oluşturmaktır, böylece yığın normalleştirmedeki gibi katmanların ağırlıklarını normalleştirebilirsiniz. Böylece, bir birime giren varyans daima sabit hale gelir. Eğer ölçeği sabitlerseniz, sistem iki bükülmeli fonksiyonda eğriselligin hangi tarafını seçeceğine dair bir kontrole sahip olamaz. Bu ‘sabitlenmiş’ kısım çok ‘doğrusal’ hale gelirse bu bir sorun olabilir. Örneğin, Sigmoid sıfıra yakın alanlarda neredeyse doğrusal hale gelir ve bu nedenle (0’a yakın) yığın normalleştirme çıkışları ‘doğrusal olmayan’ şekilde etkinleştirilemez.

  Derin ağların neden tek bükülme fonksiyonları ile daha iyi çalıştığı tam olarak belli değildir. Muhtemelen ölçek eşdeğerliği özelliğinden kaynaklanmaktadır.

soft(arg)max fonksiyonunda Sıcaklık katsayısı

• Sıcaklık katsayısını ne zaman ve neden kullanıyoruz?

  Bir dereceye kadar, gelen ağırlıklar ile sıcaklık gereksizdir. Softmax’a gelen agirlikli bir toplamınız varsa, $\beta$ parametresi ağırlıkların büyüklüğü nedeniyle gereksizdir.

  Sıcaklık, çıkış dağılımının ne kadar katı olacağını kontrol eder. $\beta$ çok büyük olduğunda, bir veya sıfıra çok yakın olur. $\beta$ küçük olduğunda, daha yumuşaktır. $\beta$’nin limiti sıfıra yakın olduğunda, neredeyse ortalama gibi davranır. $\beta$ sozsuzluğa gittiğinde, argmax gibi davranır. Artık gevşek versiyon değildir. Bu nedenle, softmax’tan önce bir çeşit normalizasyonunuz varsa, bu parametrenin ayarlanması katılığı kontrol etmenizi sağlar. Bazen, küçük bir $\beta$ ile başlayabilirsiniz. Bu sayede iyi şekilde davranan gradyan inişine sahip olabilirsiniz. Ve sistem calıştıkça, daha katı aralıklı tahminler isterseniz $\beta$ değerini arttırabilirsiniz. Böylece tahminleri keskinleştirebilirsiniz. Bu numaraya sertleştirme (annealing) denir. Öz dikkat mekanizması gibi uzman karması durumları için de yararlı olabilir.

Kayıp fonksiyonları

PyTorchda bir çok loss fonksiyonu implemente edilmiştir. Burada bazılarının üstünden geçeceğiz.

nn.MSELoss()

Bu fonksiyon girdi $x$ ve hedef $y$ arasındaki ortalama karesel hatayı (OKH) (karesel L2 norm) verir. L2 hatası olarak da adlandırılır.

$n$ adet örneği olan bir miniyığın kullanıyorsak, $n$ adet her örnek için bir kayıp olacaktır. Hata fonksiyonuna değerlerin hepsini bir vektor olarak tut veya indirge diyebiliriz.

eğer indirgenmemişse (yani fonksiyonda reduction='none' kullanılmışsa), hata terimi aşşağıdaki gibi olacaktır.

\[l(x,y) = L = \{l_1, \dots, l_N\}^\top, l_n = (x_n - y_n)^2\]

Burada $N$ yığın boyutu, $x$ ve $y$ herhangi bir şekilde n elemena sahip tensörlerdir.

İndirgeme opsiyonları aşşağıdaki gibidir (not: varsayılan değer reduction='mean' dır).

\[l(x,y) = \begin{cases}\text{mean}(L), \quad &\text{eğer reduction='mean'}\\ \text{sum}(L), \quad &\text{eğer reduction='sum'} \end{cases}\]

Toplama operatörü yine tüm elementler üzerinde çalışır, ve sonunda $n$ ile böler.

$n$ ile bölmek istemiyorsak reduction = 'sum' parametresi verilebilinir.

nn.L1Loss()

Bu fonksiyon, girdi $x$ ve hedef $y$’nin (veya istenen çıktı ve hedeflenen çıktı) tüm elementleri arasındaki ortalama mutlak hatayı (OMH) hesaplar.

eğer indirgenmemişse (eğer reduction='none' şeklinde ayarlanmışsa), hata terimi aşşağıdaki gibi hesaplanır.

\[l(x,y) = L = \{l_1, \dots, l_N\}^\top, l_n = \vert x_n - y_n\vert\]

Burada $N$ yığın boyutu, $x$ ve $y$ herhangi bir şekilde n elemena sahip tensörlerdir.

Bu fonksiyon aynı nn.MSELoss() gibi 'mean' and 'sum' ingirgeme opsiyonlarına sahiptir.

Kullanim alanı: L1 loss terimi L2 loss terimine göre aykırı veya parazit veri noktalarında daha dirençlidir. L2 hata teriminde bu aykırı/parazit noktalar karelenir, bu da hata teriminin bu noktalara aşırı hassas olmasına neden olur.

Problem: L1 hata terimi altta (0) türevlenebilir değildir. Bu nedenle gradyanlarla ugraşırken dikkatli olunması gerekir (yani Softshrink). Bu durum, aşşağıdaki SmoothL1Loss terimini kullanmak için motivasyon sağlar.

nn.SmoothL1Loss()

Bu fonksiyon eğer elemensal olarak mutlak hata 1’in altına düşerse L2, aksi halde L1 hata terimini kullanır.

\(\text{loss}(x, y) = \frac{1}{n} \sum_i z_i\) ,

\[z_i = \begin{cases}0.5(x_i-y_i)^2, \quad &\text{eğer } |x_i - y_i| < 1\\ |x_i - y_i| - 0.5, \quad &\text{aksi halde} \end{cases}\]

Bu fonksiyon ayrıca reduction (indirgeme) seçeneklerine sahiptir.

Bu, Ross Girshick tarafından ([Fast R-CNN] (https://arxiv.org/abs/1504.08083)) önerilmiştir. Pürüzsüz L1 Kaybı (SmoothL1Loss), objektif olarak kullanıldığında Huber Kaybı veya Elastik Ağ olarak da bilinir.

Kullanim Alanı: Aykırı değerlere MSELoss dan daha az duyarlıdır ve alt kısımda pürüzsüzdür. Bu fonksiyon çoğu kez aykırı değerlere karşı koruma için bilgisayarla görü alanında kullanılır.

Problem: Bu işlevin bir ölçeği vardır (yukarıdaki işlevde $0.5$).

Bilgisayarla Görüde L1 vs L2

Çok farklı tahminler yaptığımız $y$’lere sahip olduğumuz durumlarda:

• Eğer OKH kullanırsak (L2 hata terimi), sistem $y$’lerin ortalamasını üretmeye başlar, bilgisayarla görüde bu bulanık resme karşılık gelmektedir.
• Eğer L1 hata terimi kullanırsak, $y$ değerini optimize eden değer bulanik olmayan medyan değer olacaktır, ancak çoklu boyutlarda medyanı tanımlamak zordur. L1 genellikle daha keskin resim tahminlerinin ortaya çıkmasına neden olur.

nn.NLLLoss()

C sınıfa sahip sınıflandırma problemlerindeki negatif log olabilirlik kayıp terimidir.

Not olarak, matematiksel olarak, NLLLoss fonksiyonunun girdisi (log) olabilirlik değerleri olmalıdır, ancak PyTorch bunu mecburi tutmaz. Dolayısıyla etki, istenen bileşeni mümkün olduğunca büyük hale getirmektir.

İndirgenmemiş (yani reduction parametresinin 'none' olarak atandığı durumda) hata terimi aşşağıdaki gibi tanımlanabilinir:

\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - w_{y_n} x_{n,y_n}, \quad w_{c} = \text{weight}[c] \cdot \mathbb{1}\{c \not= \text{ignore\_index}\}\]

,$N$ burada mini yığın boyutudur.

eğer reduction, 'none' değilse (varsayılan 'mean'),

\[\ell(x, y) = \begin{cases} \sum_{n=1}^N \frac{1}{\sum_{n=1}^N w_{y_n}} l_n, & \text{eğer reduction} = \text{'mean';}\\ \sum_{n=1}^N l_n, & \text{eğer reduction} = \text{'sum'.} \end{cases}\]

Bu kayıp fonksiyonunun, sınıfların her birine ağırlık atayan bir bir boyutlu bir tensör kullanılarak aktarılabilen isteğe bağlı bir weight argümanı vardır. Bu, dengesiz eğitim seti ile uğraşırken kullanışlıdır.

Ağırlıklar ve Dengesiz Sınıflar:

Ağırlık vektörü, frekans her bir kategori/sınıf için farklıysa yararlıdır. Örneğin, ortalama grip sıklığı akciğer kanserinden çok daha yüksektir. Az sayıda örneği olan kategoriler için ağırlık arttırabilinir.

Bununla birlikte, ağırlığı ayarlamak yerine, eğitimdeki örneklerin görülme sıklığını eşitlemek daha iyi olur, böylece stokastik gradyanlardan daha iyi yararlanabiliriz.

Eğitimdeki sınıfları eşitlemek için her sınıfın örneklerini farklı bir arabellek içine koyulur. Bundan sonra her yığından birer örnek olarak mini yığınlar olusturulur. Küçük bellekteki örnekler bittiginde, baştan o sınıfın örneklerini kullanılmaya devam edilir. Bu işlem çok fazla örneğe sahip sınıfların belleklerindeki tüm örnekler kullanilinana kadar devam eder. Bu şekilde, tüm kategorilerin eşit frekansa sahip olması dairesel bellek kullanımı ile sağlanılır. Frekanslari eşitlemeye çalışırken büyük sınıfların bazı örneklerini kullanmayarak asla eşitleme yapmamalıyız. Datayı yerde bırakmayın !

Yukarıdaki yöntemin bariz bir sorunu, sinir ağı (NN) modelimiz gerçek örneklerin göreceli frekansını bilemeyecektir. Bunu çözmek için, en sonda sistemimizi gerçek sınıf frekansları kullanarak hassas ayar (fine-tune) yapabiliriz. Böylece sistem daha sık olan şeyleri daha sık çıktı olarak üretmek için uyum sağlar.

Bu şemanın sezgisini elde etmek için tıp fakültesine geri dönelim: öğrenciler nadir hastalıklara sık olan hastalıklarda olduğu kadar zaman harcıyorlar (hatta bazen nadir hastalıklar üzerinde daha karışık oldukları için daha fazla zaman harcıyorlar). İlk olarak hepsinin özelliklerine uyum sağlamayı, daha sonra hangisinin nadir olduğunu öğrenerek bu problemi cözüyorlar.

nn.CrossEntropyLoss()

Bu fonksiyon nn.LogSoftmax ve nn.NLLLoss fonksiyonlarını bir sınıfta topluyor. Bu fonksiyonda, doğru sınıfın puanını olabildiğince büyütür.

Burada iki işlevin birleştirilmesinin nedeni, gradyan hesaplamasının sayısal olarak daha kararlı yapmaktir. Softmax’in değeri 1 veya 0’a yaklaştığında, log değeri 0 veya $-\infty$’a yakınsar. Log’un 0’a yakın yerlerde eğimi $\infty$’e yakındır, bu da geri yayılımda ara adımlarda sayısal olarak hatalara yol açabilir. İki işlev birleştirildiğinde, gradyanlar doyar, böylece sonunda makul bir sayı elde ederiz.

Girdinin her sınıf için normalleştirilmemiş bir değer olması beklenir.

Kayıp terimi şu şekilde tanımlanabilir:

\[\text{loss}(x, c) = -\log\left(\frac{\exp(x[c])}{\sum_j \exp(x[j])}\right) = -x[c] + \log\left(\sum_j \exp(x[j])\right)\]

ya da weight argumanı verildiğinde:

\[\text{loss}(x, c) = w[c] \left(-x[c] + \log\left(\sum_j\exp(x[j])\right)\right)\]

Kayıpların, her mini yığın için ortalaması alınır.

Çapraz Entropi Kaybının(Cross Entropy Loss) fiziksel bir yorumu, iki dağılım arasındakı farklılığı ölçtüğümüz Kullback-Leibler sapması (KL sapması) ile ilgilidir. Burada, (yarı (quasi)) dağılımlar, x vektörü (tahminler) ve hedef dağılım (yanlış sınıflarda 0 ve doğru sınıfta 1 olan bir sıcak vektör) ile temsil edilir.

Matematiksel olarak,

\[H(p,q) = H(p) + \mathcal{D}_{KL} (p \mid\mid q)\]

\(H(p,q) = - \sum_i p(x_i) \log (q(x_i))\) Çapraz Entropi Kaybı, (iki dağılım arasında), \(H(p) = - \sum_i p(x_i) \log (p(x_i))\) entropi, ve \(\mathcal{D}_{KL} (p \mid\mid q) = \sum_i p(x_i) \log \frac{p(x_i)}{q(x_i)}\) KL sapmasıdır.

nn.AdaptiveLogSoftmaxWithLoss()

Bu, çok sayıda sınıf (örneğin, milyonlarca sınıf) için softmax’ın etkili bir softmax yaklaşımdır. Hesaplamanın hızını artırmak için bir çok püf nokta uygular.

Methodun detayları Edouard Grave, Armand Joulin, Moustapha Cissé, David Grangier, Hervé Jégou tarafından yazılan Efficient softmax approximation for GPUs makalesinde bulunabilinir.

---

📝 Haochen Wang, Eunkyung An, Ying Jin, Ningyuan Huang
Mehmet Aygun
13 Apr 2020