Kamyon Kasası-Ön tarafı

Kurulum

Bu görevin amacı, herhangi bir keyfi başlangıç konumundan yükleme platformuna geri dönerken kamyonun direksiyonunu kontrol eden bir öz denetimli öğrenme kontrolörü oluşturmaktır.

Figüre 1’de gösterildiği gibi sadece geri dönmeye izin verilmiş olduğu not edelim.

Fig. 1: The Truck, Trailer and Loading Dock

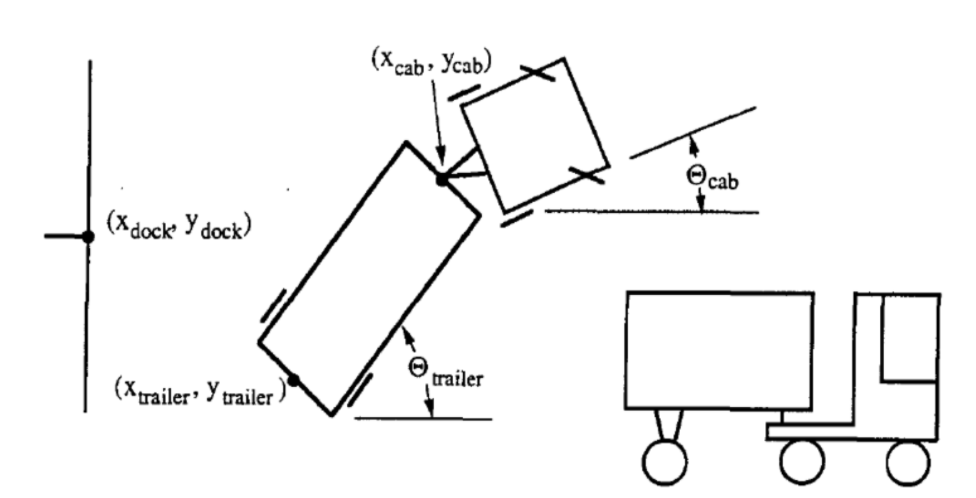Kamyonun durumu altı parametre ile temsil edilir:

• $\tcab$: Kamyonun açısı
• $\xcab, \ycab$: Boyunduruğun kartezyeni (veya römorkun önü).
• $\ttrailer$: Römorkun açısı
• $\xtrailer, \ytrailer$: Römorkun (arka) kartezyeni.

Kontrolörün hedefi her seferinde kamyon sabit küçük bir uzaklık içinde geri döndüğünde $\phi$ için uygun bir açı seçmektir. Başarı iki kritere bağlıdır:

1. Römorkun arkası duvar yükleme platformuna paraleldir, ör. $\ttrailer = 0$.
2. Römorkun arkası ($\trailer, \trailer$) yukarıda gösterildiği gibi ($ x_{dock}, y_{dock}$) noktasına mümkün olduğunca yakın.

Daha Fazla Parametre ve Görselleştirme

Fig. 2: Parameters for visualization

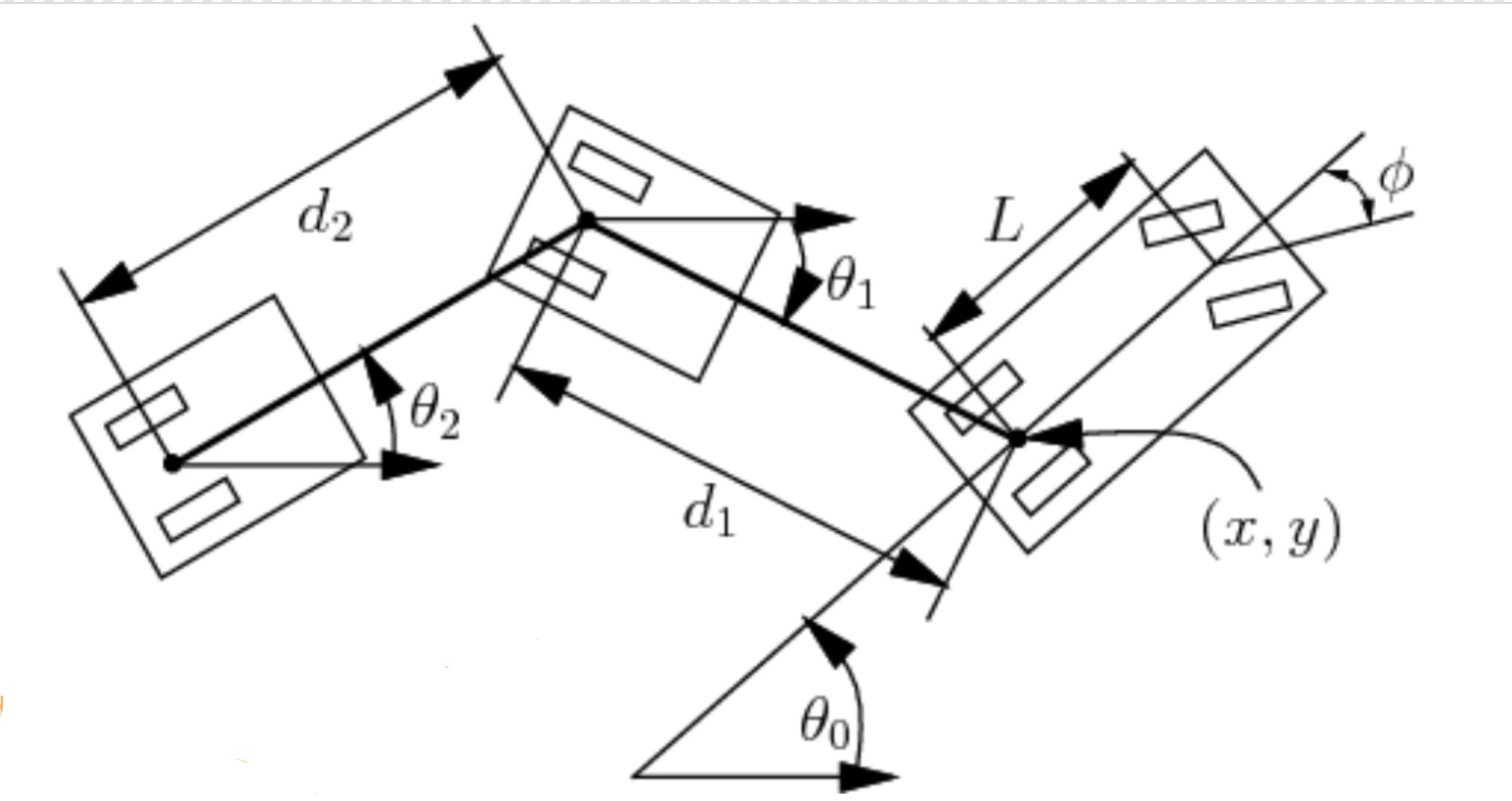Bu bölümde aynı zamanda Figür 2’de gösterilen birkaç parametreyi daha göz önüne alacağız. Arabanın uzunluğu $L$, araba ve römork arasındaki uzaklık $d_1$ ve römorkun uzunluğu $d_2$ verilmiş olsun. Bu durumda açının ve pozisyonun değişimini hesaplayabiliriz.

Burada $s$ işaretlenmiş hızı ve $\phi$ negatif direksiyon açısını gösterir.
Şimdi durumu sadece dört parametre ile gösterebiliriz: $\xcab$, $\ycab$, $\theta_0$ ve $\theta_1$. Çünkü parametre uzunulukları bellidir ve $\xtrailer, \ytrailer$ parametreleri $\xcab, \ycab, d_1, \theta_1$ parametreleri tarafından belirlenir.

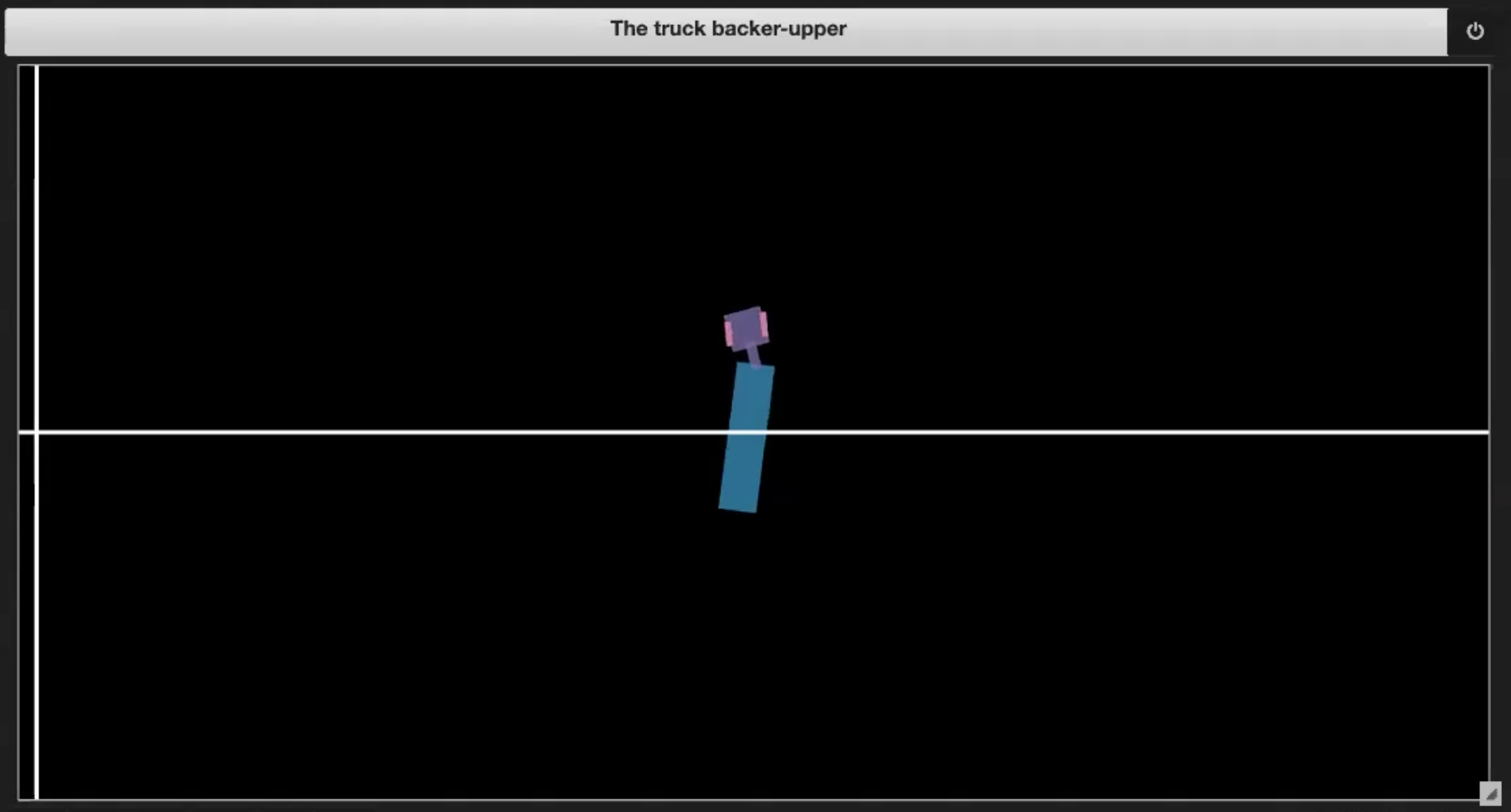
Bu Derin Öğrenme Mini Kurs’un Jupyter Notebook’da Figür 3.(1-4)’lerde gösterilen bazı örneklem ortamlarına sahibiz.

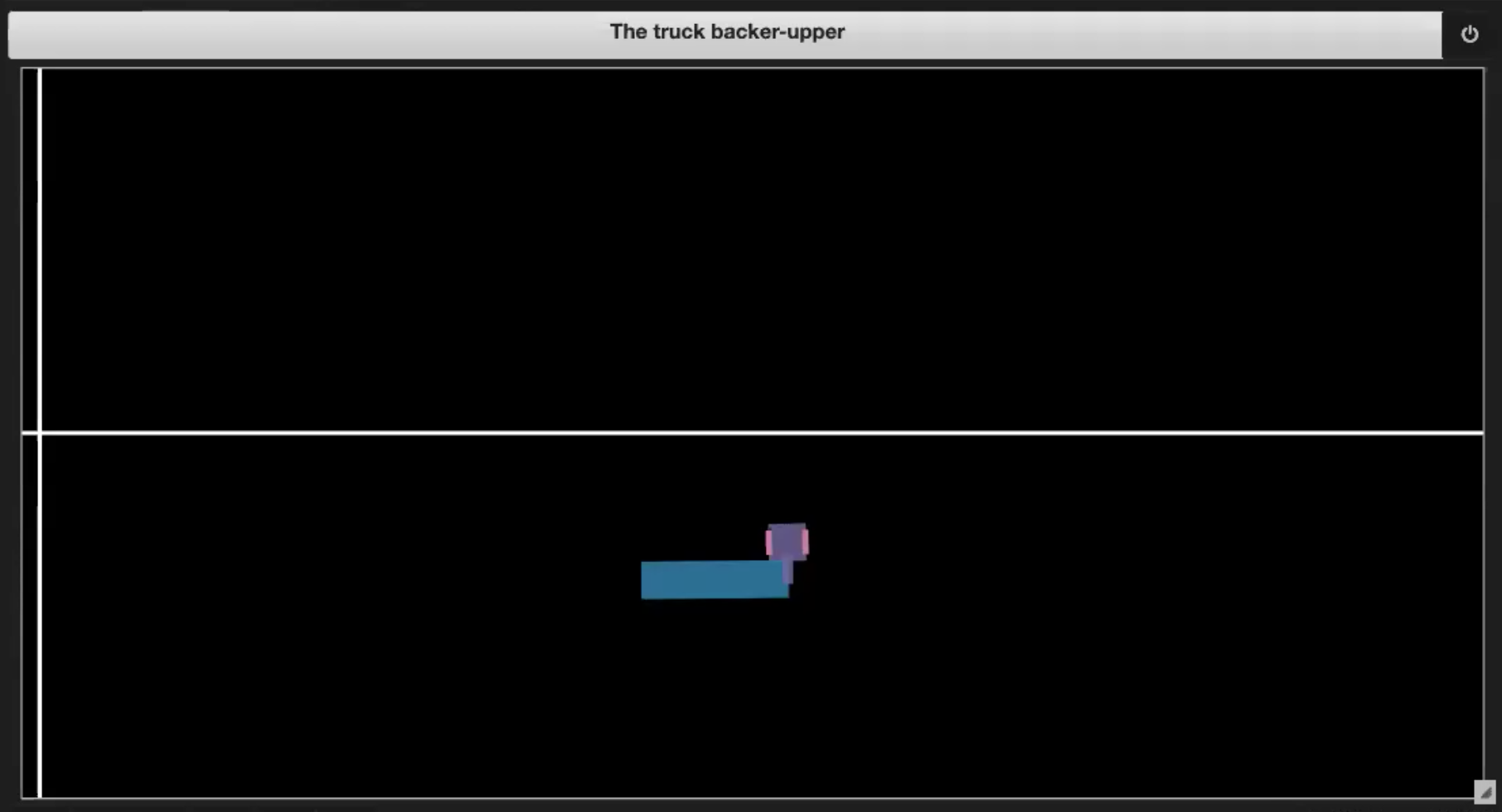Fig. 3.1: Sample plot of the environment	Fig. 3.2: Driving into itself (jackknifing)
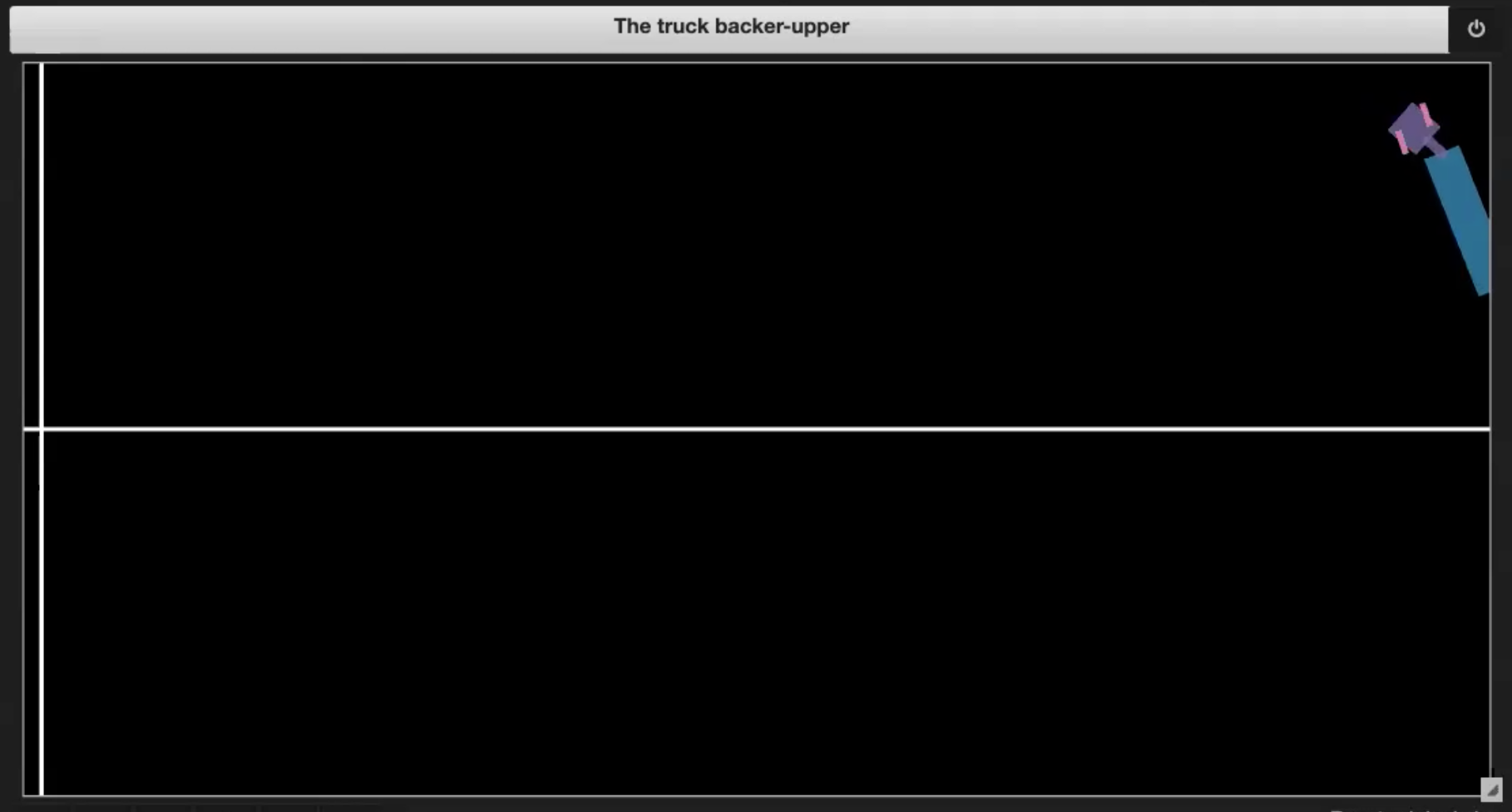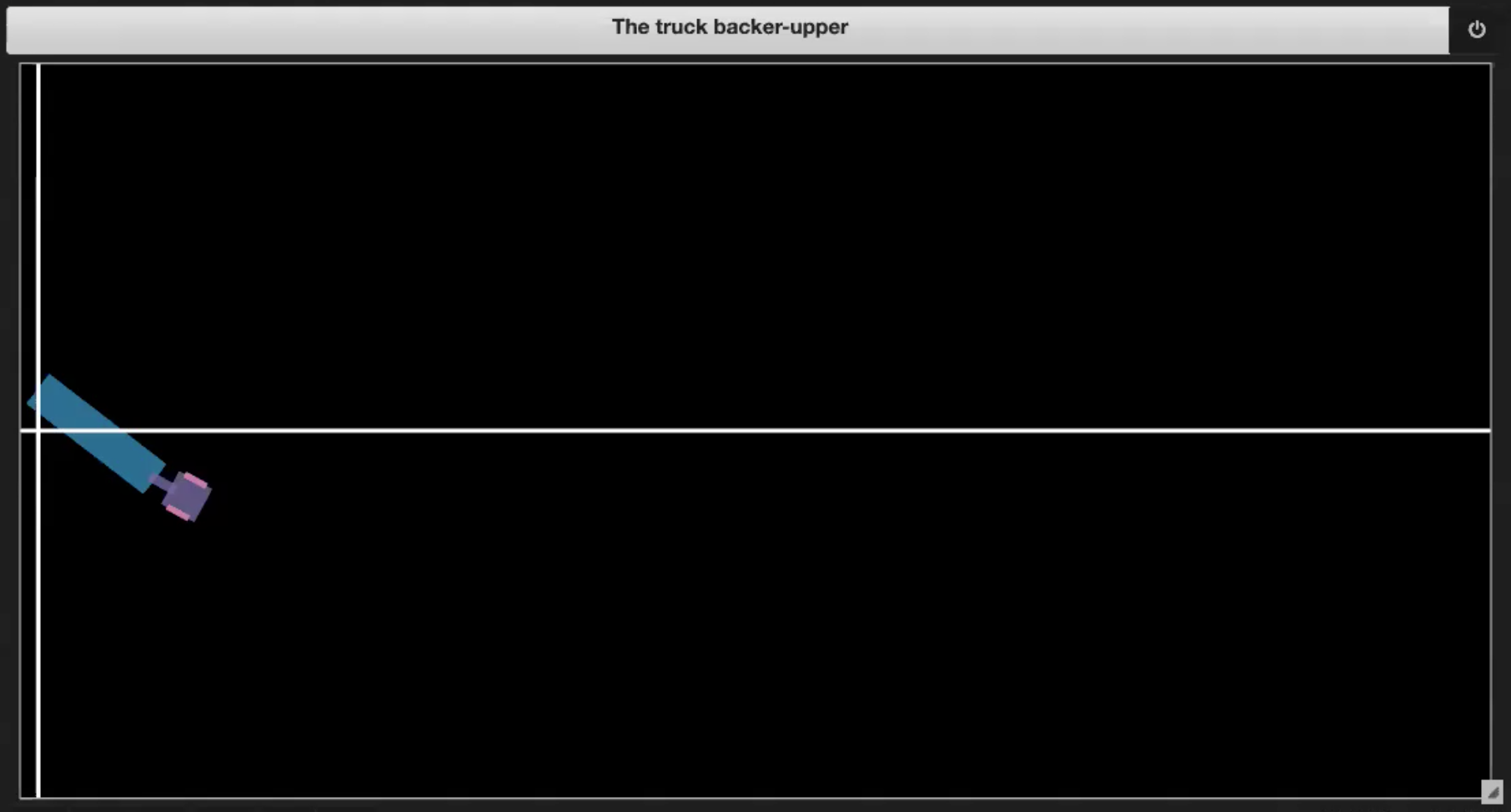Fig. 3.3: Going out of boundary	Fig. 3.4: Reaching the dock

Her bir zaman dilimi $k$’de $-\frac{\pi}{4}$ ve $\frac{\pi}{4}$ arasındaki bir direksiyon sinyali beslenecek ve kamyon uyumlu olan açıyı kullanarak geri dönecek.

Sekansın sonlanabileceği çeşitli durum var:

• Kamyonun kendine doğru sürmesi (jackknifes, as in Figure 3.2)
• Kamyon sınırların dışına çıkması (shown in Figure 3.3)
• Kamyonun platforma ulaşması (shown in Figure 3.4)

Eğitim

Eğitim işlemi 2 adımı kapsar: (1) bir sinir ağını kamyonun bir emülatörü olması için eğitmek ve (2) bir sinir ağını kamyonu kontrol etmesi için bir kontrolör olarak eğitmek.

Fig. 4: Overview Diagram

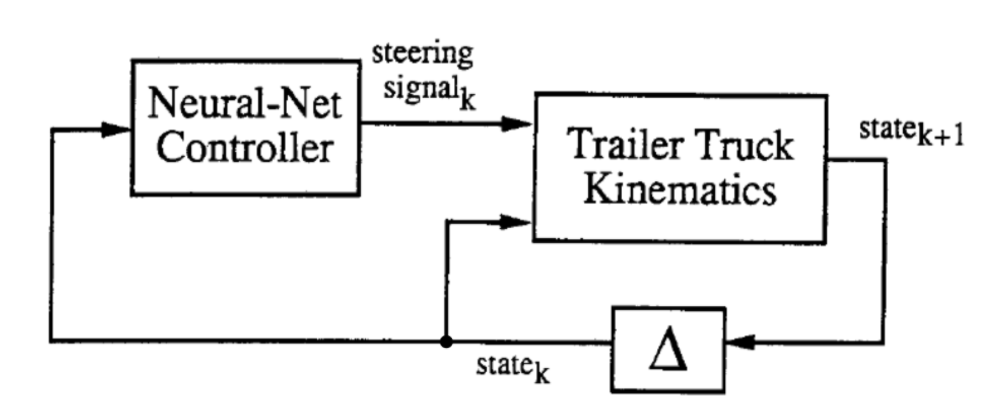Yukarıda gösterildiği gibi, soyut diyagramda, iki blok eğitilecek olan iki ağdır. Her bir zaman dilimi $k$’de “Römork Kamyon Kinematiği”, veya emülatörü nasıl adlandırdıysak, 6 boyutlu bir durum vektörü alır ve kontrolörden direksiyon sinyali üretir, ve her bir zaman dilimi $k + 1$’de yeni bir 6 boyutlu durum üretir.

Emülatör

Emülatör güncel lokastonu ($\tcab^t$,$\xcab^t, \ycab^t$, $\ttrailer^t$, $\xtrailer^t$, $\ytrailer^t$) ve direksiyon yönünü $\phi^t$ girdi olarak alır ve bir sonraki zaman dilimindeki durumu ($\tcab^{t+1}$,$\xcab^{t+1}, \ycab^{t+1}$, $\ttrailer^{t+1}$, $\xtrailer^{t+1}$, $\ytrailer^{t+1}$) çıktı olarak verir. Bir lineer gizli katmandan, ReLu aktivasyon fonksiyonu ile, ve bir lineer çıktı katmanından oluşur. Yitim fonksiyonu olarak MSE’yi kullanırız ve emülatörü rastgele gradyan inişi kullanılarak eğitiriz.

Fig. 5: Training the Neural-net Emulator

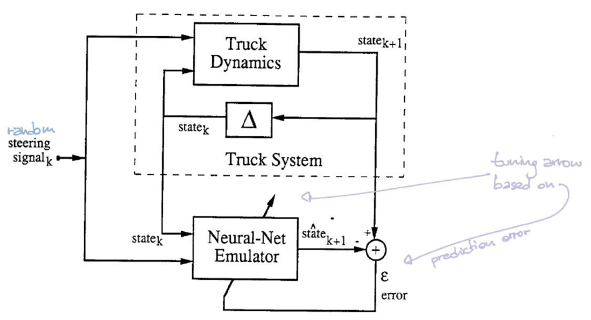Bu kurulumda simülatör, güncel lokasyon ve direksiyon açısı verildiğinde bize bir sonraki adımın lokasyonunu söyleyebilir. Bu yüzden Simülatörü taklit eden bir sinir ağına gerçekten ihtiyacımız yoktur. Bunun yanında, daha karmaşık bir sistemde, sistemin vurgulanan denklemlerine erişimimiz olmayabilir, örn. güzel hesaplanabilir bir formda evren kurallarımız yok. Sadece direksiyon sinyalleri sekanslarını ve onlara karşılık gelen yolları kaydeden bir veriyi gözlemleme şansımız olabilir. Bu durumda, bu komplex sistemin dinamiklerini taklit eden bir sinir ağını eğitmek isteyebiliriz.

Emülatörü eğitmek için Class truck içerisinde eğitimde bakmaya ihtiyaç duyduğumuz iki önemli fonksiyon var.

Birincisi step fonksiyonu ki hesaplamadan sonraki kamyonun surumunu çıktı olarak verir.

def step(self, ϕ=0, dt=1):
    
    # Check for illegal conditions
    if self.is_jackknifed():
        print('The truck is jackknifed!')
        return
    
    if self.is_offscreen():
        print('The car or trailer is off screen')
        return
    
    self.ϕ = ϕ
    x, y, W, L, d, s, θ0, θ1, ϕ = self._get_atributes()
    
    # Perform state update
    self.x += s * cos(θ0) * dt
    self.y += s * sin(θ0) * dt
    self.θ0 += s / L * tan(ϕ) * dt
    self.θ1 += s / d * sin(θ0 - θ1) * dt

İkincisi ise state fonksiyonu, ki kamyonun güncel durumunu çıktı olarak verir.

def state(self):
        return (self.x, self.y, self.θ0, *self._traler_xy(), self.θ1)

İlk olarak iki liste üretirilir. Rastgele bir şeklide üretilen direksiyon açısını ϕ ve truck.state() fonksiyonunu çalıştırarak kamyondan gelen başlangıç durumunu girdi listesine ekleyerek üretiriz. Ve truck.step(ϕ) tarafından hesaplanabilen kamyonun durumunu ekleyip bir çıktı listesi üretiriz.

Şimdi emülatörü eğitebiliriz:

cnt = 0
for i in torch.randperm(len(train_inputs)):
    ϕ_state = train_inputs[i]
    next_state_prediction = emulator(ϕ_state)
    
    next_state = train_outputs[i]
    loss = criterion(next_state_prediction, next_state)
    
    optimiser_e.zero_grad()
    loss.backward()
    optimiser_e.step()
    
    if cnt == 0 or (cnt + 1) % 1000 == 0:
        print(f'{cnt + 1:4d} / {len(train_inputs)}, {loss.item():.10f}')
    cnt += 1

torch.randperm(len(train_inputs)) fonksiyonu bize $0$’dan eğiitm girdilerinin uzunluğu eksi $1$ arasındaki indislerin bir rastgele permütasyonunu verdiğini unutmayalım. İndislerin permütasyonundan sonra her bir zaman diliminde indis i‘deki girdi listesinden ϕ_state seçilir. ϕ_state‘i lineer gizli çıktı katmanına sahip bir emülatör fonksiyonu yoluyla girdi olarak veririz ve next_state_prediction çıktısını alırız. Şunu farkedelim ki emülatör aşağıda tanımlanan bir sinir ağıdır.

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

Burada doğru sonraki durumun ve öngörülen sonraki durumun arasındaki yitimi hesaplamak için MSE’yi kullanırız, doğru sonraki durum girdi listesindeki ϕ_state‘in indisine karşılık gelen i indisi ile birlikte çıktı listesinden gelen durumdur.

Kontrolör

Bkz. Figür 5. Blok $\matr{C}$ kontrolörü temsil eder. Kontrolör güncel durumu alır ve bir direksiyon açısını çıktı olarak verir. Sonrasında blok $\matr{T}$ (emülatör) hem durumu hem de açıyı sonraki durumu üretmek için kullanır.

Fig. 5: State Transition flow diagram

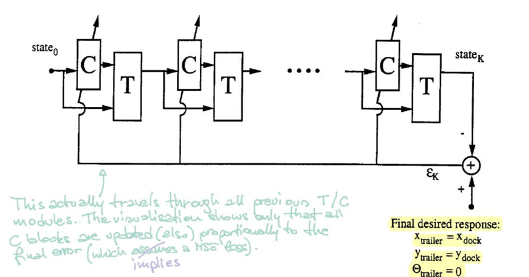Kontrolörü eğitmek için rastgele bir başlangıç durumundan başlarız ve procedure($\matr{C}$ and $\matr{T}$) fonksiyonunu tekar ederiz ta ki romörk platforma paralel olana kadar. Hata romörk lokasyonu ve platform lokasyonunu karşılaştırarak hesaplanır. Sonrasında geri yayılım kullanarak gradyanları buluruz ve SGD yoluyla kontrolörün parametrelerini güncelleriz.

Detaylı Model Yapısı

Bu ($\matr{C}$, $\matr{T}$) işleminin detaylı bir grafiğidir. Bir durum (6 boyutlu bir vektör) ile başlarız, ayarlanabilir bir ağırlık matrisi ile çarğarız ve 25 gizli birim elde ederiz. Sonrasında çıktı (direksiyon sinyali) elde etmek için başka bir ayarlanabilir ağırlık vektörü yoluyla geçiş yaptırırız. Benzer olarak sonraki adımın durumunu üretmek için iki katman yoluyla durumu ve açıyı $\phi$ (7 boyutlu vektör) girdi olarak veririz.

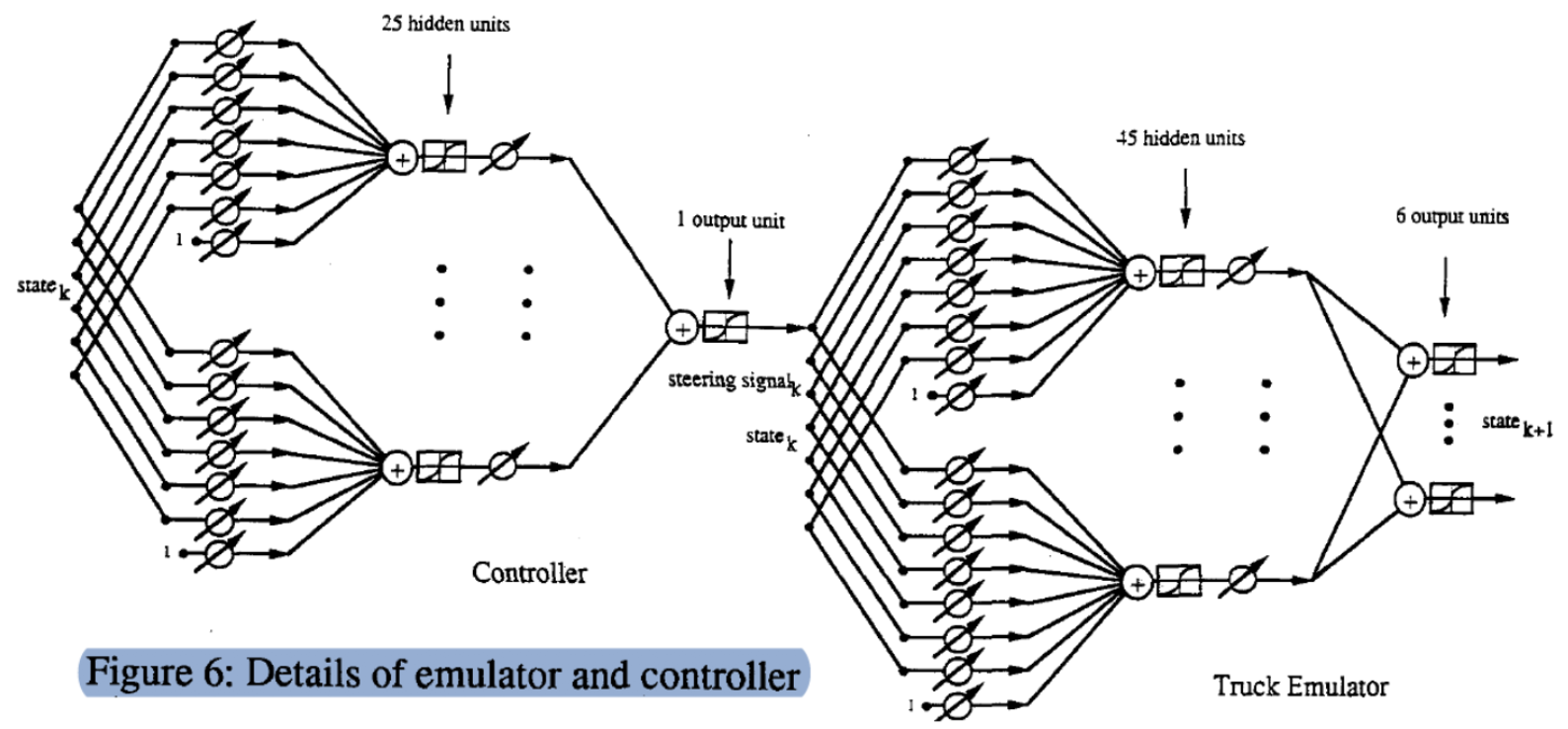
Bunu data açık bir şekilde görmek için emülatörün tam uygulamasını görebilirsiniz:

state_size = 6
steering_size = 1
hidden_units_e = 45

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

optimiser_e = SGD(emulator.parameters(), lr=0.005)
criterion = nn.MSELoss()

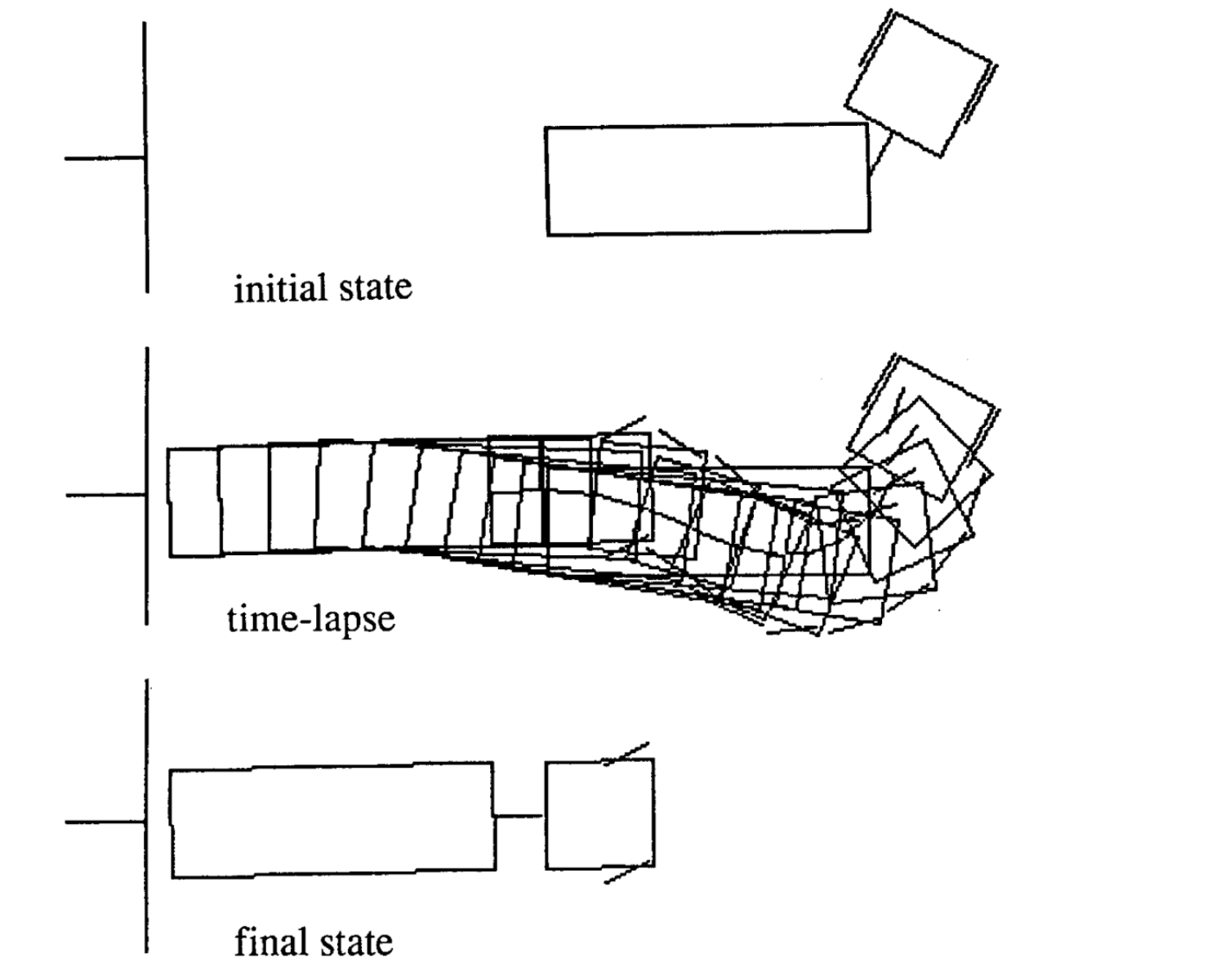
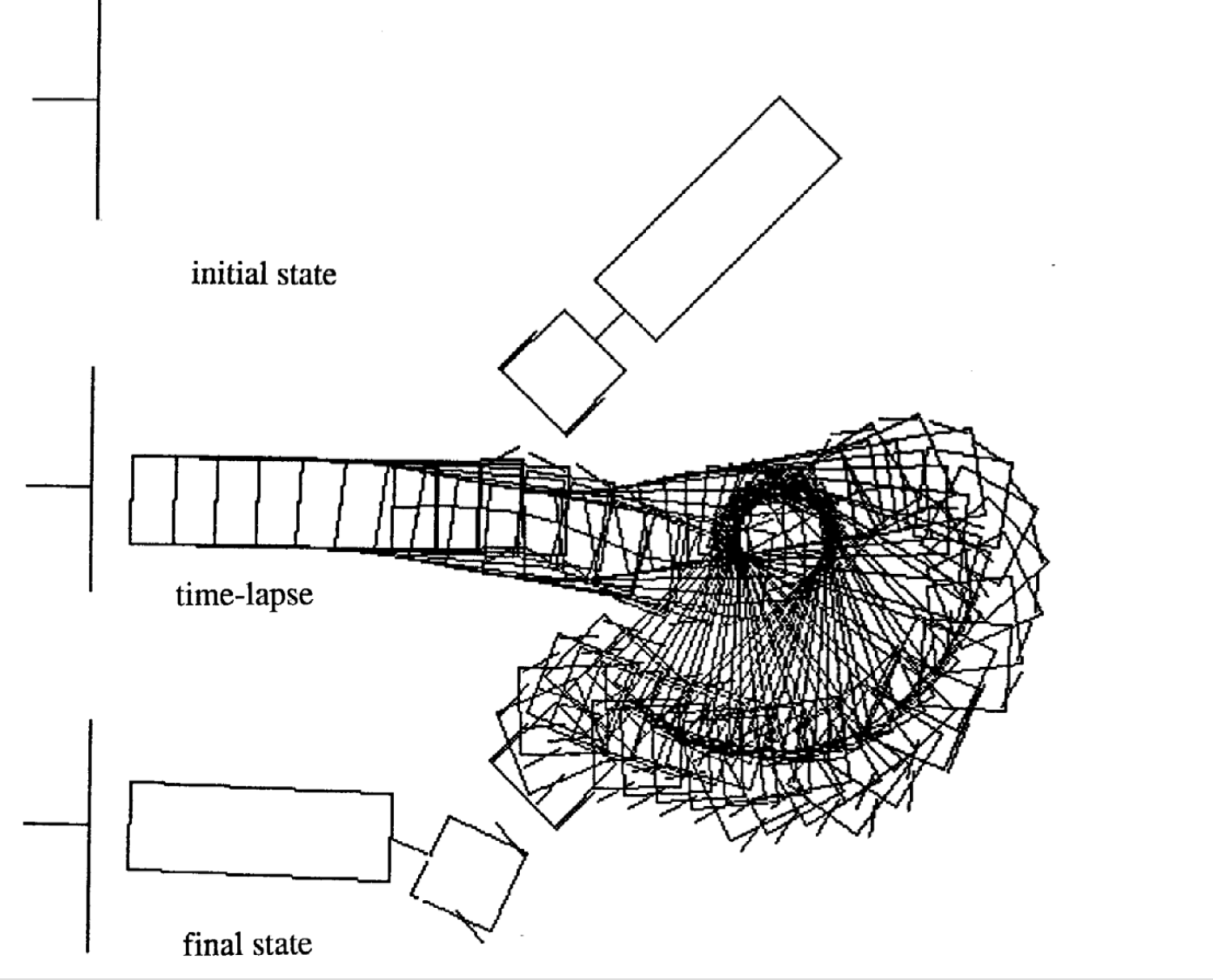
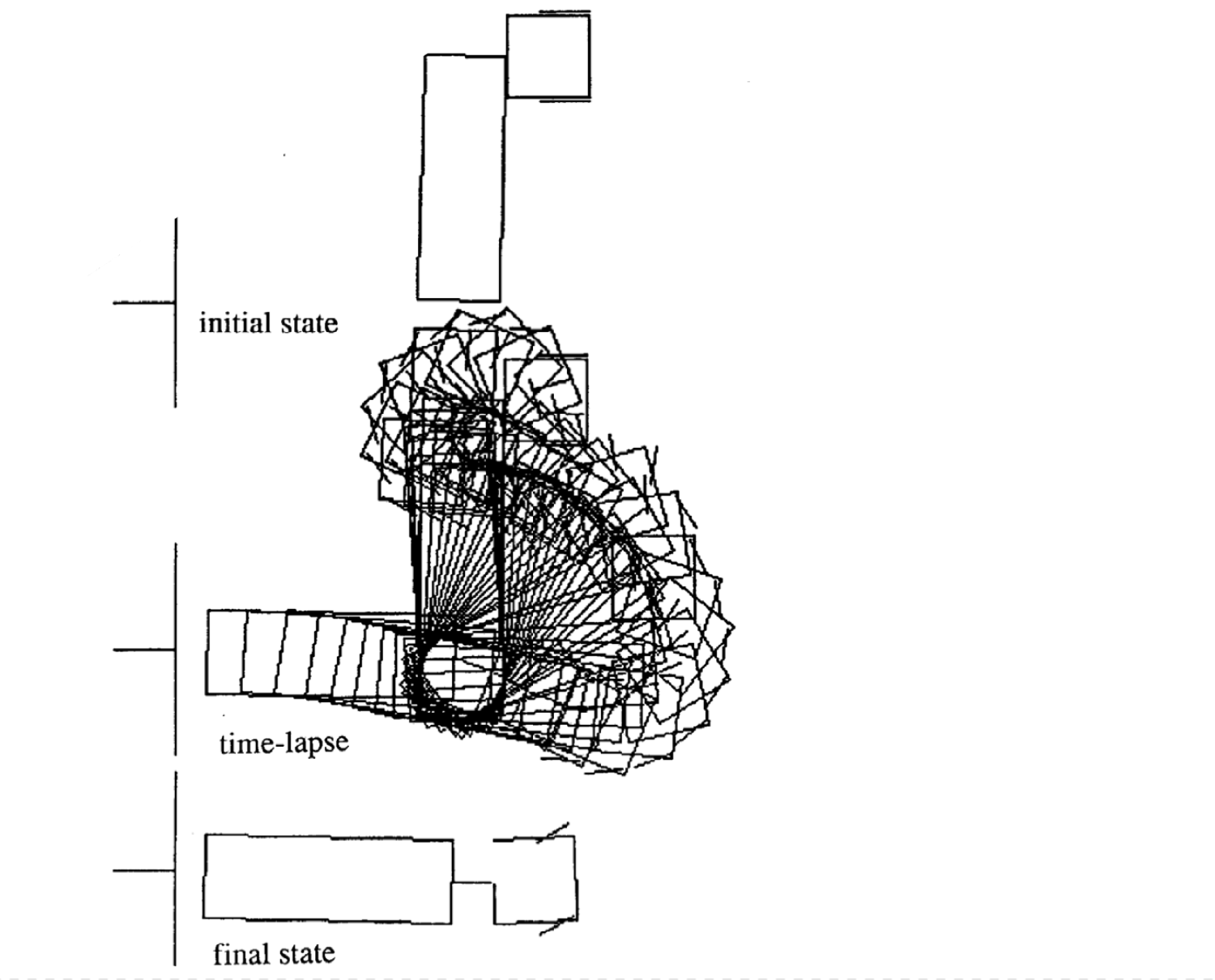
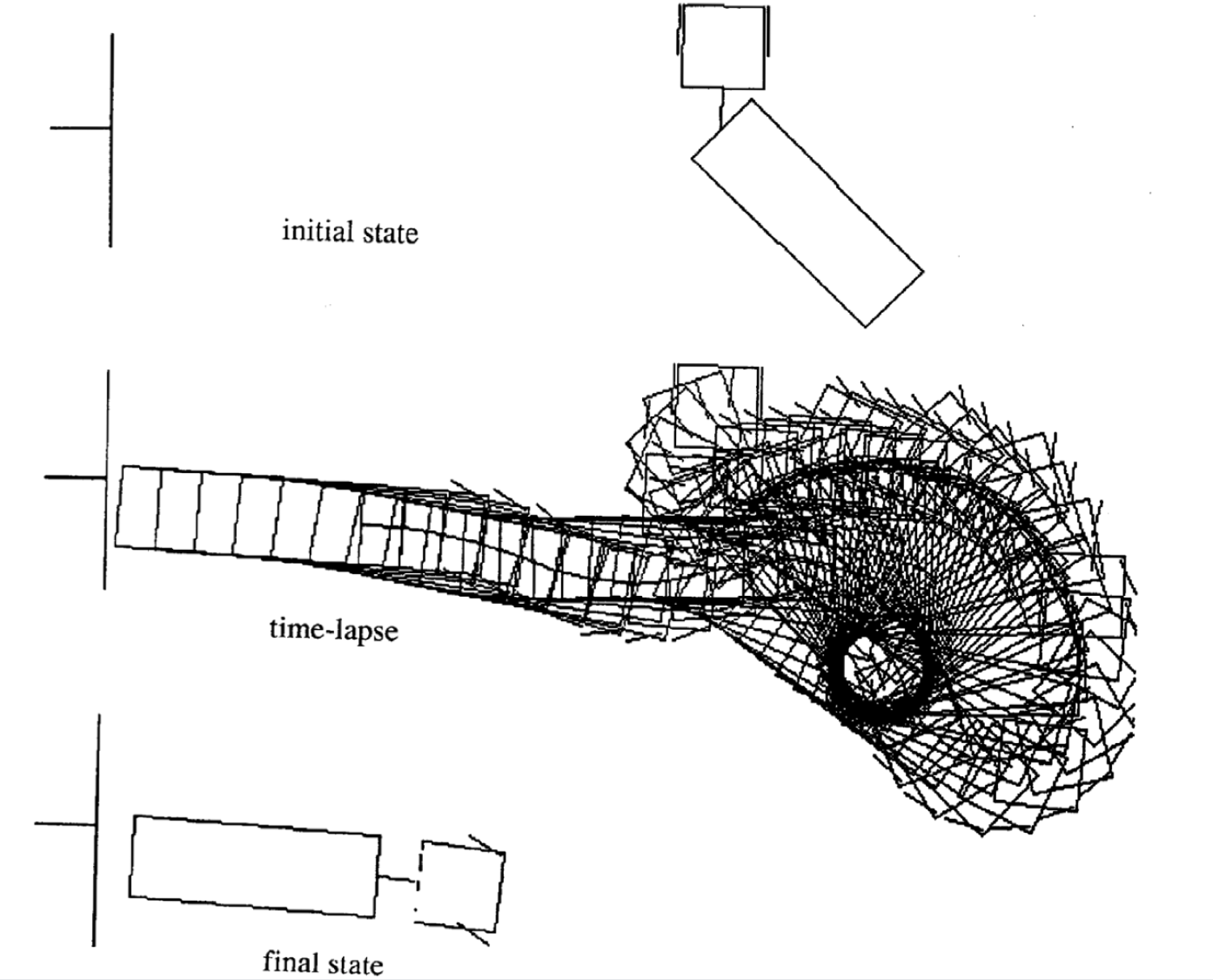
Hareketin Örneği

Örnekler farklı başlangıç durumları için 4 hareket örneğidir. Şunu farkedelim ki zaman adımlarının sayısı her parçada değişiklik gösteriyor.

Ek Kaynaklar:

Tam çalışan bir demoyu şurada bulabilirsiniz: https://tifu.github.io/truck_backer_upper/

Lütfen koda da göz atın: https://github.com/Tifu/truck_backer_upper