Üretici Çekişmeli Ağlar

Çekişmeli Üretici Ağlara Giriş (GANs)

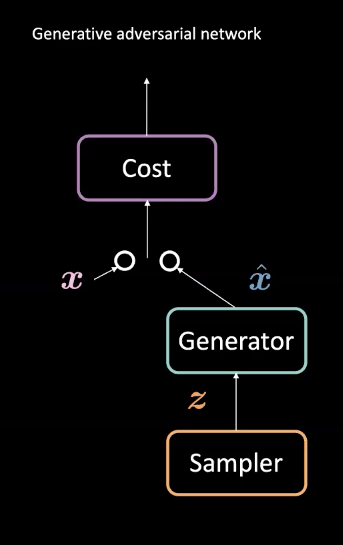
Şekil 1: GAN Yapısı

GAN’lar denetimsiz makine öğrenmesinde kullanılan bir sinir ağı türüdür. İki adet çekişmeli modülden oluşurlar: üretici (generator) ve maliyet (cost) ağları. Bu modüllerden maliyet ağı sahte örnekleri filtrelemeye çalışırken üretici ağı da gerçekçi örnekler $\vect{\hat{x}}$ üreterek maliyet ağını kandırmaya çalışır. Bu rekabet ile model gerçekçi veri üretebilen bir üretici öğrenir. Bu üreticiler geleceği tahmin etme veya belirli bir veri kümesi üzerinde eğitildikten sonra, görüntü oluşturma gibi görevlerde kullanılabilir.

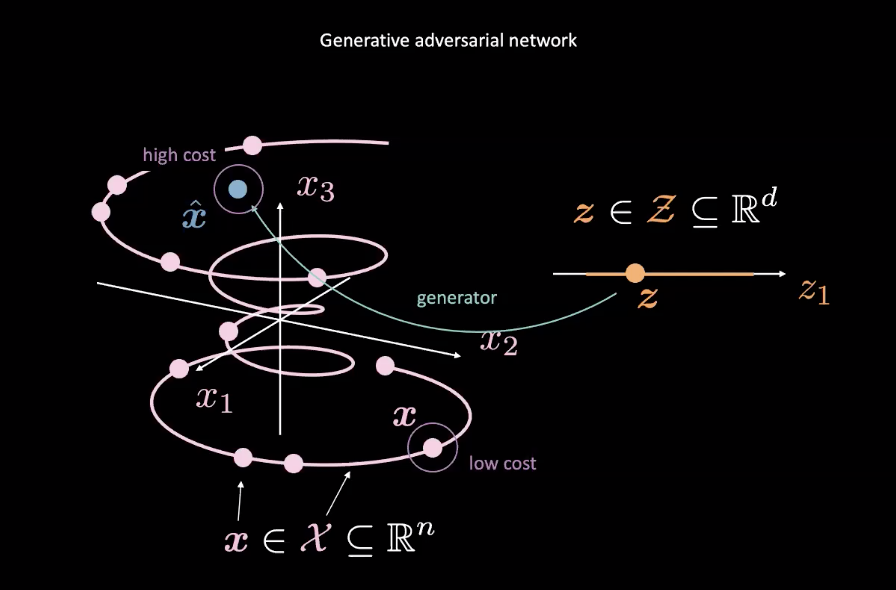
Şekil 2: Rastgele Değişkenden GAN Bağlanımı

GAN’lar, enerji bazlı modellerin (EBM) örneklerinden bir tanesidir. Öyle ki, maliyet ağı, Şekil 2’de görüldüğü üzere, pembe ile ifade edilmiş gerçek veri dağılımına $\vect{x}$ yakın girdiler için düşük maliyet üretmesi için eğitilir. Diğer dağılımlardan gelen verilerin (Şekil 2’deki mavi noktalar, $\vect{\hat{x}}$) maliyetlerinin de yüksek olması gerekir. Maliyet ağının performansını ölçmek için ortalama karesel hata (MSE) kullanılabilir. Önemli bir nokta ise, maliyet fonksiyonu belirli bir aralıkta kısıtlı, pozitif skaler değerleri çıktı olarak verir ($\text{cost} : \mathbb{R}^n \rightarrow \mathbb{R}^+ \cup {0}$). Bildiğimiz ayrıştırıcılarda ise çıktılar ayrık bir biçimde birbirlerinden ayırılır.

Üretici ağ ($\text{generator} : \mathcal{Z} \rightarrow \mathbb{R}^n$) ise rastgele değişken $\vect{z}$’yi gerçekçi üretilmiş veriye bağlayan bağlanımı iyileştirmek için eğitilir. Üretici, maliyet ağının çıktısına göre eğitilir ve $\vect{\hat{x}}$’nin enerjisini minimize etmeye çalışır. Bu enerjiyi $C(G(\vect{z}))$ ile belirtelim, burada $C(\cdot)$ maliyet ağını ve $G(\cdot)$ üretici ağını temsil etmektedir.

Maliyet ağının eğitimi MSE hatasını minimize etmeye dayalı iken üretici ağın eğitimi de maliyet ağını $C(\vect{\hat{x}})$’nin $\vect{\hat{x}}$’e göre gradyanları ile minimize ederek gerçekleşir.

Veri manifoldunun dışındaki noktalara yüksek maliyet ve manifoldun içindeki noktalara düşük maliyet atamayı sağlamak için, maliyet ağının kayıp fonksiyonu $\mathcal{L}_{C} = C(x)+[m-C(G(\vect{z}))]^+$ belli bir pozitif aralık $m$ için tanımlanmıştır. $\mathcal{L}_{C}$’yi minimize etmek, $C(\vect{x}) \rightarrow 0$ ve $C(G(\vect{z})) \rightarrow m$’yi gerektirir. Üreticinin kayıp fonksiyonu $\mathcal{L}_{G}$, üretici için $C(G(\vect{z})) \rightarrow 0$ durumu olması için teşvikleyen $C(G(\vect{z}))$ terimidir. Ancak, bu durum dengesizlik yaratmaktadır çünkü $0 \leftarrow C(G(\vect{z})) \rightarrow m$.

GAN ve VAE Arasındaki Fark

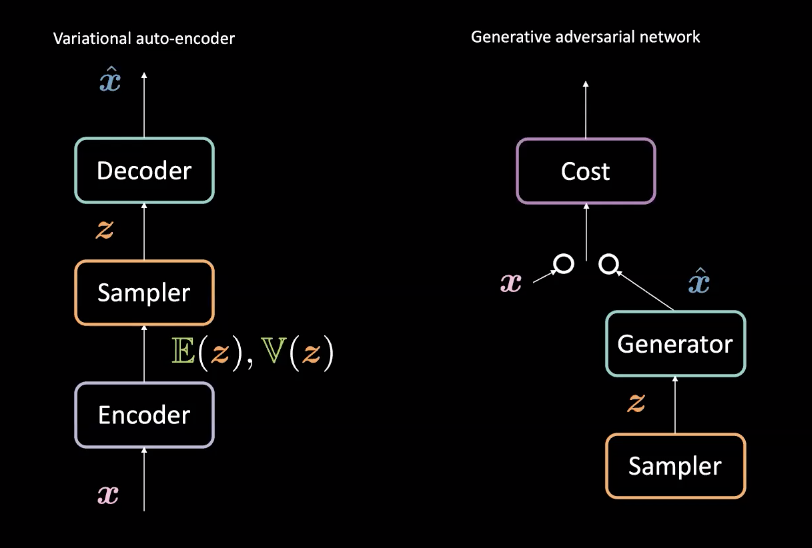
Şekil 3: VAE (solda) - GAN (sağda) - Mimari tasarım

Sekizinci haftada işlediğimiz Değişimsel Otokodlayıcılar (VAE) ile kıyaslandığında, GAN üreticileri farklı bir şekilde oluşturur. VAE’ler girdileri $\vect{x}$’i saklı uzay $\mathcal{Z}$’ye bir kodlayıcı (encoder) ile bağlar ve $\mathcal{Z}$’den veriye $\vect{\hat{x}}$ bir kodçözümleyici (decoder) ile geri bağlar. Sonra, $\vect{\hat{x}}$’i $\vect{x}$’e gerioluşturarak benzetmeye çalışır. GAN’lar ise yukarıda açıklandığı gibi rekabet eden üretici ve maliyet ağları arasındaki çekişmeli bir ortamda eğitilir. Bu ağlar, geri yayılım yoluyla peş peşe eğitilir. Bu yapıların farkları Şekil 3’te görülebilir.

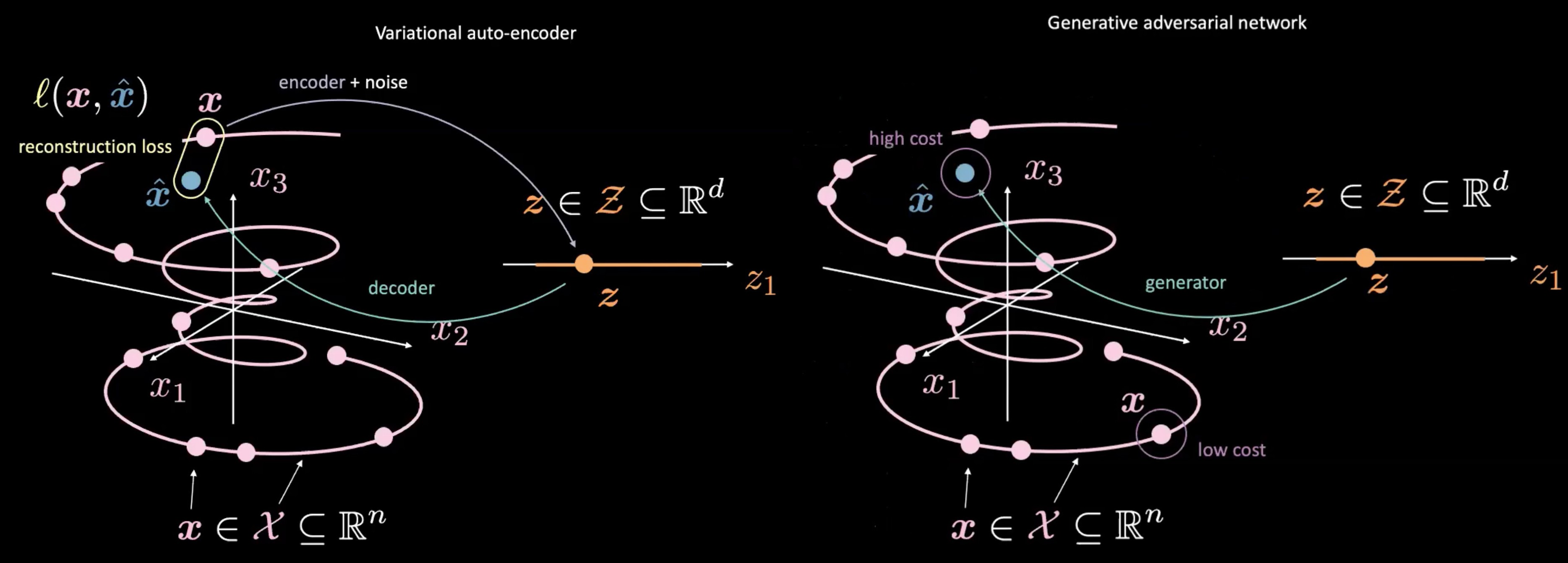
Şekil 4: VAE (solda) - GAN (sağda) - Saklı Değişken $\vect{z}$'den Bağlanım

GAN’lar $\vect{z}$’yi üretme ve kullanmaları bakımından da VAE’lerden ayrılır. GAN’lar tıpkı VAE’lerdeki saklı uzay gibi $\vect{z}$’yi örnekleyerek başlar. Sonra, üretici ağları ile $\vect{z}$’yi $\vect{\hat{x}}$’ye bağlar. Üretilen örnek $\vect{\hat{x}}$, ayrıştırıcıya ne kadar “gerçek” olup olmadığını ölçmek için gönderilir. VAE ve GAN arasındaki temel farklılıklardan biri de, gerçek çıktı $\vect{x}$ ile üretici ağın çıktısı $ \ vect {\ hat {x}} $ arasında doğrudan bir ilişki (yani yeniden yapılandırma kaybı) ölçmemize gerek olmamasıdır. Aksine, üreticiyi ayrıştırıcının $\vect{x}$ için verdiği skorlara benzer skorlar verebilen $\vect{\hat{x}}$ üretmesi için eğiterek $\vect{\hat{x}}$’i $\vect{x}$’e benzemeye zorluyoruz.

GAN’ın Önemli Sorunları

GAN’lar ile oldukça güçlü üreticilere sahip olabilsek de, GAN mimarisinde henüz çözümü olmayan önemli problemler mevcuttur.

1. Dengesiz Yakınsama (Unstable convergence)

Üretici eğitimle geliştikçe, ayrıştırıcı (discriminator) performansı kötüleşmekte çünkü ayrıştırıcı artık gerçek ile sahte veri arasındaki farkı kolaylıkla belirtemez olur. Eğer üretici mükemmel bir üretici ise, gerçek ve sahte verilerin manifoldları üst üste binmiş olacak ve ayrıştırıcı çok fazla hatalı sınıflandırma yapıcaktır.

Bu durum, GAN’ların yakınsamasında, yani sistemin bir çözüme kavuşmasında büyük bir sorun teşkil eder: ayrıştırıcının geri dönütü zamanla gücünü yitirir. Eğer GAN ayrıştırıcısı tamamiyle rastgele dönütler verirken eğitime devam edersek, üretici de çöp niteliğinde dönütler ile eğitilmeye başlar ve üreticinin kalitesi de çöküntüye uğrayabilir. [Bkz. GAN’larda eğitim yakınsaması]

Üretici ve ayrıştırıcı arasındaki rekabetçi ortamın sonucu dengeden ziyade dengesizliklere sebep vermekterdir.

2. Sönümlenen Gradyan

<–! ### 2. Vanishing gradient –>

Varsayalım ki, GAN için ikili çapraz entropi (binary cross entropy) kayıp fonksıyonu kullanıyoruz:

Ayrıştırıcı gitgide sonuçlarına güvenmeye başlayınca, $D(\vect{x})$ $1$’e ve $D(\vect{\hat{x}})$ ‘da $0$’a yaklaşacak. Ayrıştırıcının güveni, maliyet ağının çıktılarını gradyanların doyduğu düz bölgelere taşıyacak. Bu düz bölgeler, üretici ağının eğitimini aksatmasına sebebiyet verecek olan sönümlenmiş gradyanların bol olduğu bölgelerdir. Bu yüzden, GAN eğitirken, ayrıştırıcı kendine güvendikçe, hatanın da kademeli olarak arttığından emin olmalıyız.

3. Mod Çökmesi

<–! ### 3. Mode collapse –>

Eğer üretici, tüm $\vect{z}$’leri ayrıştırıcıyı kandırabilecek bir tane örneğe $\vect{\hat{x}}$’e bağlarsa, üretici sadece bu $\vect{\hat{x}}$ üretir. Eninde sonunda, ayrştırıcı da spesifik olarak bu sahte girdiyi öğrenecektir. Sonuç olarak, üretici de sonraki en uygun $\vect{\hat{x}}$’i kullanır ve bu süreç sürekli devam eder. Böylelikle, ayrıştırıcı sahte $\vect{\hat{x}}$’leri mütemadiyen ayıklarken yerel minima’dan (lokal minima) kaçamaz. Bu soruna olası bir çözüm, üreticiye farklı girdiler verildiğinde aynı çıktıyı verirse miktar ceza uygulamaktır.

Derin Evrişimsel Üretici Çekişken Ağ (Deep Convolutional Generative Adversarial Network, DCGAN) kaynak kodu

Bu örneğin kaynak kodunu burada bulabilirsiniz.

Üretici

1. Üretici girdiyi nn.ConvTranspose2d modülleriyle büyütür. Her nn.ConvTranspose2d‘ın ardından da nn.BatchNorm2d ve nn.ReLU kullanılır.
2. Sıralı (sequential) modülünün sonunda, ağ nn.Tanh() fonksiyonunu çıktıyı $(-1,1)$ aralığında sıkıştırmak için kullanır.
3. Rastgele vektör girdisinin boyutu $nz$’dir. Çıktının boyutu ise $nc \times 64 \times 64$’tür. Kanal sayısı $nc$ ile ifade edilmiştir.

class Generator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # Girdi Z, evriştirilir
            nn.ConvTranspose2d(     nz, ngf * 8, 4, 1, 0, bias=False),
            nn.BatchNorm2d(ngf * 8),
            nn.ReLU(True),
            # Aktivasyon boyutu: (ngf*8) x 4 x 4
            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 4),
            nn.ReLU(True),
            # Aktivasyon boyutu: (ngf*4) x 8 x 8
            nn.ConvTranspose2d(ngf * 4, ngf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 2),
            nn.ReLU(True),
            # Aktivasyon boyutu: (ngf*2) x 16 x 16
            nn.ConvTranspose2d(ngf * 2,     ngf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf),
            nn.ReLU(True),
            # Aktivasyon boyutu: (ngf) x 32 x 32
            nn.ConvTranspose2d(    ngf,      nc, 4, 2, 1, bias=False),
            nn.Tanh()
            # Aktivasyon boyutu: (nc) x 64 x 64
        )

    def forward(self, input):
        output = self.main(input)
        return output

Discriminator

1. Aktivasyon fonksiyonu olaraknn.LeakyReLU‘nun kullanılması, negatif rejimlerde gradyanı yok etmemek açısından oldukça önemlidir. Bu gradyanlar olmadan, üretici güncellenemez.
2. Sequential() modülünün sonunda, ayrıştırıcı nn.Sigmoid() fonksiyonu ile girdiyi sınıflar.

class Discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # Girdi boyutu (nc) x 64 x 64
            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            # Aktivasyon boyutu (ndf) x 32 x 32
            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 2),
            nn.LeakyReLU(0.2, inplace=True),
            # Aktivasyon boyutu (ndf*2) x 16 x 16
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 4),
            nn.LeakyReLU(0.2, inplace=True),
            # Aktivasyon boyutu. (ndf*4) x 8 x 8
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 8),
            nn.LeakyReLU(0.2, inplace=True),
            # Aktivasyon boyutu. (ndf*8) x 4 x 4
            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
            nn.Sigmoid()
        )

    def forward(self, input):
        output = self.main(input)
        return output.view(-1, 1).squeeze(1)

Bu sınıflar netG and netD olarak başlatılır.

GAN için Kayıp Fonksiyonu

Girdi ve çıktı arasında BCE hata fonksiyonunu kullanıyoruz.

criterion = nn.BCELoss()

Düzenek

Değişken fixed_noise‘un boyutunu opt.batchSize ve rastgele vektörün uzunluğunu nz alıyoruz. Ayrıca, sırasıyla real_label ve fake_label değişkenleri ile gerçek ve üretilmiş (sahte) verinin etiketlerini belirliyoruz.

fixed_noise = torch.randn(opt.batchSize, nz, 1, 1, device=device)
real_label = 1
fake_label = 0

Sonra, ayrıştırıcı ve üretici ağlar için eniyileştiricileri (optimizers) kuruyoruz.

optimizerD = optim.Adam(netD.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))

Eğitim

Her eğitim epoku (epoch) iki adımdan oluşur.

1. Adım ayrıştırıcı ağını güncellemektir. Bu da iki aşamada gerçekleşir. Önce, ayrıştırıcıyı dataloader modüllerinden gelen gerçek veri ile besler, çıktı ile real_label arasındaki hatayı hesaplar, ve gradyanleri geri yayılım ile biriktiririz. Sonra, ayrıştırıcıyı üretici ağın fixed_noise ile ürettiği verilerle besler, fake_label ile çıktı arasındaki hatayı hesaplar ve gradyanları biriktiririz. Sonunda, biriktirdiğimiz gradyanları, ayrıştırıcı ağın parametrelerini güncellemek için kullanırız.

Ayrıştırıcıyı eğitirken, sahte veriyi ayırmamız (detach) gerekir ki üreticinin bu adımda gradyanlara erişmesini önleyebilelim.

Ayrıca, zero_grad() metodunu bu adımın başında kullanmamız gerekiyor çünkü bir önceki güncellemeden kalan gradyanlerı kullanamayız. Her .backward() çağrıldığında .backward() metodu ayrıştırıcı ve üretici ağların gradyanlerini biriktirir. Son olarak, ayrıştırıcının parametrelerini güncellememiz için optimizerD.step()‘i çağırmamız yeterli olacaktır.

# Gerçek veri ile eğit
netD.zero_grad()
real_cpu = data[0].to(device)
batch_size = real_cpu.size(0)
label = torch.full((batch_size,), real_label, device=device)

output = netD(real_cpu)
errD_real = criterion(output, label)
errD_real.backward()
D_x = output.mean().item()

# Sahte veri ile eğit

noise = torch.randn(batch_size, nz, 1, 1, device=device)
fake = netG(noise)
label.fill_(fake_label)
output = netD(fake.detach())
errD_fake = criterion(output, label)
errD_fake.backward()
D_G_z1 = output.mean().item()
errD = errD_real + errD_fake
optimizerD.step()

2. Adım üretici ağı güncellemektir. Bu sefer, ayrıştırıcıya sahte verileri gönderiyoruz ama hatayı real_label ile hesaplıyoruz! Bunu yapmamızın sebebi üreticiyi gerçekçi $\vect{\hat{x}}$’ler ürettirebilmek için eğitmemizdir.

netG.zero_grad()
label.fill_(real_label)  #
output = netD(fake)
errG = criterion(output, label)
errG.backward()
D_G_z2 = output.mean().item()
optimizerG.step()