Dünya Modelleri ve Üretken Çekişmeli Ağlar
🎙️ Yann LeCunOtonom Kontrol İçin Dünya Modelleri
Özdenetimli öğrenmenin en önemli kullanım alanlarından biri de kontrol için dünya modellerini öğrenmektir. Biz insanlar bir eylem gerçekleştirken, dünyanın nasıl çalıştığına dair içsel bir modele sahibiz. Örneğin, henüz 9 aylıkken, çoğunlukla gözlem yoluyla fizik için bir sezgi kazanırız. Bu durum bir bakıma özdenetimli öğrenmeye benzer; neler olacağını tahmin etmeyi öğrenirken, özdenetimli öğrenmede saklı değişkenleri öğrendiğimiz gibi. Bunu ilerletirsek, içsel modeller bize dünya üzerinde bir eylem gerçekleştirebilmemizi sağlar. Mesela, öğrendiğimiz fiziksel içgüdü ile kavramayı kullanarak kaslarımızın nasıl çalıştığını tahmin edebilir ve bu bılgiyle düşen bir kalemi nasıl yakalayabileceğimizi tahmin edebiliriz.
Dünya modeli nedir?
Bir otonom zeka sistemi dört ana modülden oluşmaktadır (Şekil 1). İlk olarak, dünyayı gözlemleyen ve dünyanın durumunu temsil etmeye çalışan bir algı(perception) modülü. Bu temsil tam değildir çünkü 1) eylemci tüm evreni gözlemlemez ve 2) gözlemlerin doğruluğu sınırlıdır. Ayrıca, ileri beslemeli(feed-forward) bir modelde, algı modülü sadece ilk zaman adımında kullanılır. İkinicisi, eylemci(actor) modülü (veya politika modülü) dünyanın durum temsiline göre belli bir eylem yapmaya çalışır. Üçüncü olarak, model modülü dünyayı ifade eden durum temsilini kullanarak, ve tabii ki de var olan bazı saklı değişkenler ile, yapacağı eylemin sonucunu tahmin eder. Bu tahmin, ilk zaman adımından algılama modülünün rolünü üstlenerek, dünyanın bir sonraki durumu için tahmin olarak bir sonraki zaman adımına iletilir. Son olarak, eleştirmen modülü aynı öngörüyü önerlien eylemin maliyetine dönüştürür, örn. hız ile birlikte kalemin düştüğüne inanmam göz önüne alındığında, eğer kaslarımı bu şekilde hareket ettirirsem, kalemi ne kadar kötü bir şekilde kaçırmış olurum?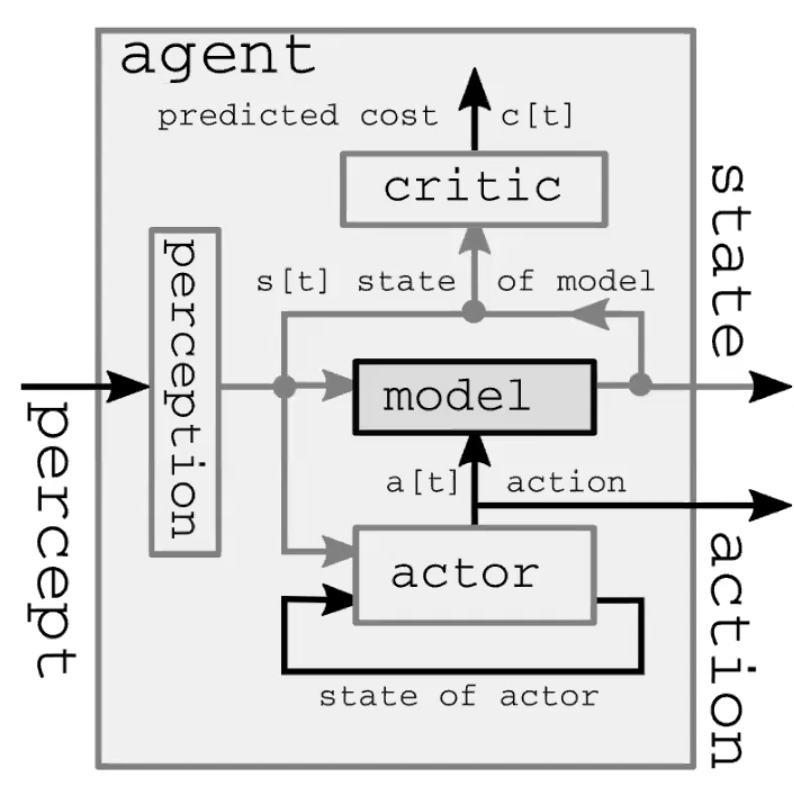
Şekil 1: Bir otonom zeka sistemi gösteriminin Dünya Modeli mimarisi.
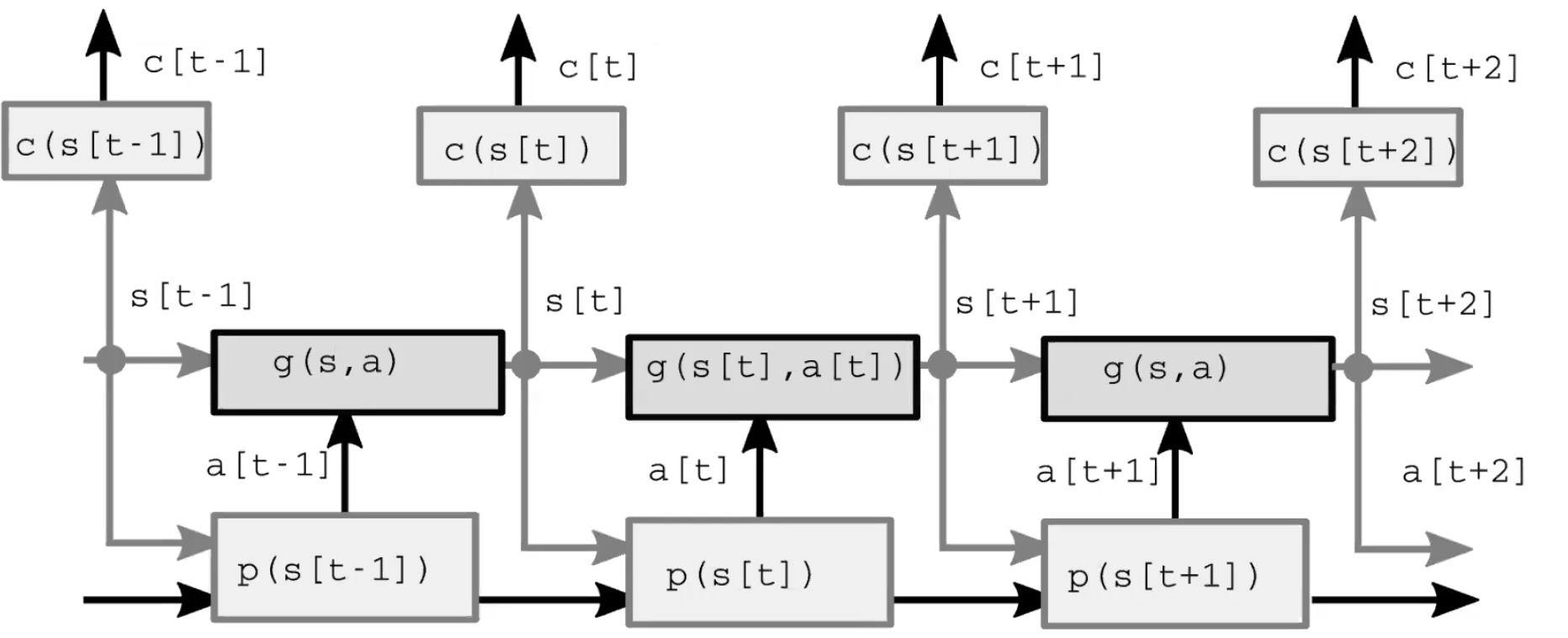
Şekil 2: Model mimarisi.
Klasik Modelleme
Klasik optimal kontrolde aktör/politika modülü yerine eylemi ifade eden bir eylem değişkeni bulunmaktadır. Bu formülasyon, 1960’larda NASA tarafından insan bilgisayarlarından (çoğunlukla Siyah kadın matematikçiler) elektronik bilgisayarlara geçtiklerinde roket yörüngelerini hesaplamak için kullanılan Model Öngörücü Kontrol(Model Predictive Control) adlı klasik bir yöntemle optimize edilmiştir. Bu sistemi zamanla açılmış bir RNN gibi, eylemleri saklı değişkenler gibi, ve geri yayılım ile gradyan yöntemlerini(veya dinamik programlama gibi yöntemleri) de zaman adımı maliyetlerinin toplamını en aza indirgeyen eylemler dizisini öngörmemizi sağlayan yöntemler olarak düşünebiliriz. Not: Saklı değişkenler ve parametrelerin optimizasyon süreçleri benzer olsa da “çıkarım”(inference) kelimesini saklı değişkenler için ve “öğrenme”(learning) kelimesini parametreler içi kullanırız. Önemli bir fark, saklı değişken her bir örnek için belli bir değer alırken parametreler tüm örnekler arasında paylaşılır.
An improvement
Şimdi, planlama yaparken, her seferinde geri yayılım gibi karmaşık bir süreçten geçmemeyi tercih ediyoruz. Bunun için, değişimsel otokodlayıcılarda kullandığımız taktiği seyrek kodlamada kullanacağız: Optimal eylem dizisini doğrudan elimizdeki dünyaya ayit temsilcilerle tahmin edebilmek için bir kodlayıcı eğiteceğiz. Burada, kodlayıcıya politika ağı adını vereceğiz.
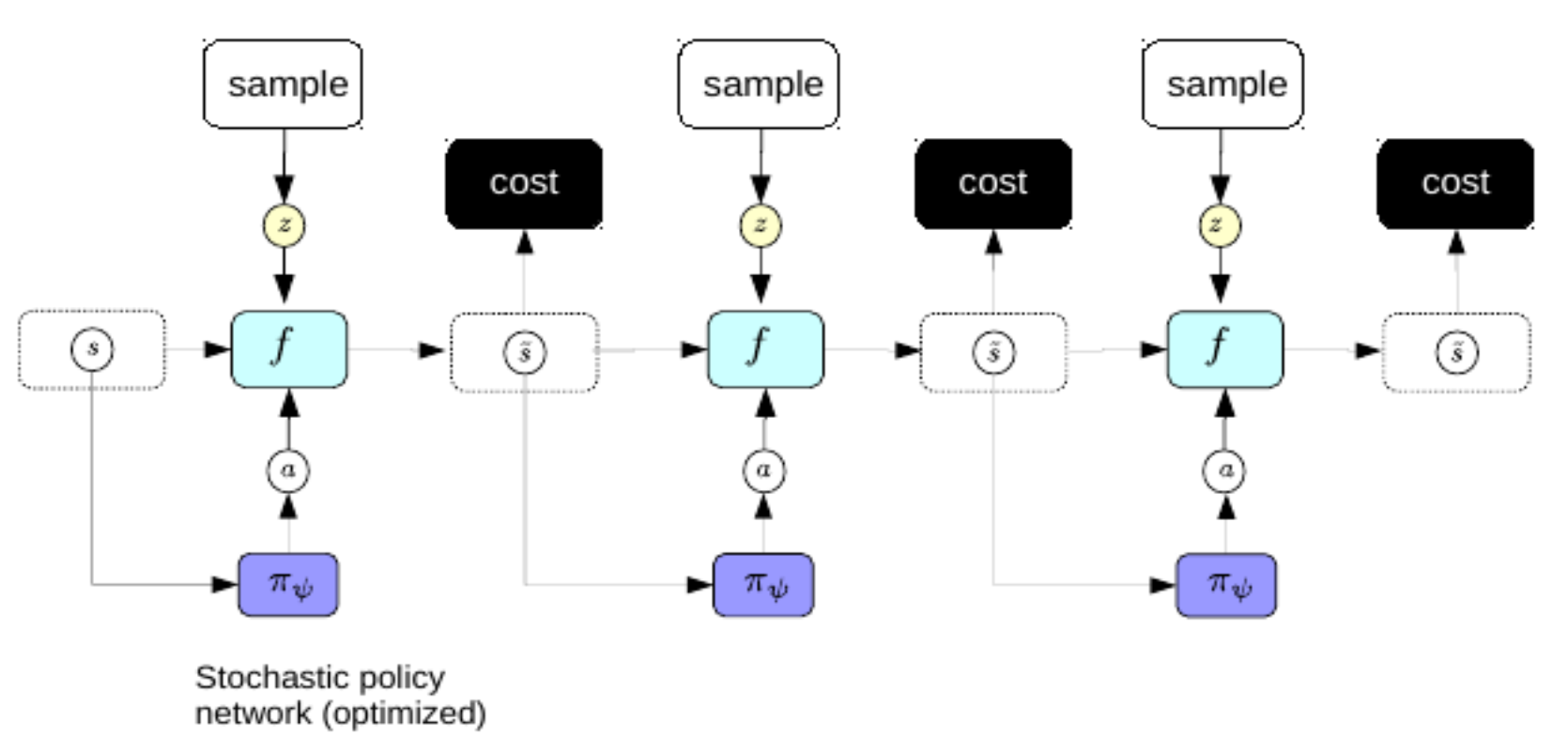
Şekil 3: Politika Ağı. ## [Pekiştirmeli Öğrenme (RL)](https://www.youtube.com/watch?v=Pgct8PKV7iw&t=3993s) Pekiştirmeli öğrenme ile şu ana kadar öğrendiklerimiz arasında iki fark vardır: 1. Pekiştirmeli öğrenmedeki ortamlarda hata fonksiyonu bir kara kutudan ibarettir. Yani, eylemcinin ödül dinamiğini anlaması mümkün değildir. 2. Pekiştirmeli öğrenmede, ortamda ilerlemek için ortamı modelleyen ileriye dönük bir model kullanmayız. Aksine, gerçek dünya ile etkileşime girer ve ne olduğunu gözlemleyerek sonucu öğreniriz. Gerçek dünyada, dünya hakkındaki ölçümlerimiz mükemmel olmadığından, ileride bundan sonra ne olacağını tahmin etmemiz her zaman mümkün değildir. Pekiştirmeli öğrenmedeki temel sorun, hata fonksiyonunun türevlenememesidir. Bu yüzden, tek yol deneme ve yanılmadan ibarettir. Burda da problem, durum uzayını verimli bir şekilde nasıl keşfecegimize dönüşüyor. Buna bir çözüm bulduktan sonra, bir sonraki konu da keşif(exploration) ve sömürü(exploitation) temel sorusudur: Çevreyi en üst düzeyde öğrenecek biçimde eylemler mi gerçekleştirmek istersin yoksa olabildiğince yüksek bir ödül almak için daha önce öğrendiklerinden yararlanmak mı istersin? Aktör-Eleştirmen(Actor-Critic) yöntemleri hem eylemci hem de eleştirmen eğiten popüler bir RL algoritmaları ailesidir. Birçok RL yöntemi, maliyet fonksiyonunun bir modelini (eleştirmen) eğiterek benzer şekilde çalışır. Aktör-Eleştirmen yöntemlerinde eleştirmenin rolü, değer onksiyonunun(value function) beklenen değerini öğrenmektir. Eleştirmen de bir sinir ağı olduğu için modül üzerinden geri yayılım mümkündür. Aktörün sorumluluğu ortamda gerçekleştirilecek eylemler önermek iken eleştirmenin görevi ise maliyet fonksiyonunun bir modelini öğrenmektir. Aktör ve eleştirmen, hiçbir eleştirmen kullanılmamış olmasından daha verimli öğrenmeye yol açacak şekilde birlikte çalışır. Dünyanın iyi bir modeline sahip değilseniz öğrenmek çok daha zordur: örn. uçurumun yanındaki araba bir uçurumdan düşmenin kötü bir fikir olduğunu bilmeyecektir. Bu, insanların ve hayvanların RL ajanlarından çok daha hızlı öğrenmelerini sağlar: kafamızda gerçekten iyi dünya modelleri var. Geleceği, dünyanın doğasında varolan belirsizliklerden (Aleatorik ve Epistemik) ötürü, her zaman tahmin etmemiz mümkün değildir. Aleatorik belirsizlik, kontrolümüzün olmadığı veya gözlemleyemediğimiz olaylardan ötürü var olan bir belirsizlik türüdür. Epistemik belirsizlik ise geleceği tahminlemek için modelin yetersizliklerinden kaynaklı belirsizlik türüdür. İleriye dönük modeller, aşağıdaki gibi tanımlıdır: $$\hat s_{t+1} = g(s_t, a_t, z_t)$$ burada $z$, değerini bilmediğimiz bir saklı değişkendir. $z$ dünya hakkında bilmemizin mümkün olmadığı fakat tahminimizi etkileyen bilgiyi(aleatorik belirsizlik) ifade eder. $z$'yi seyrelterek, gürültü ekleyerek veya kodlayıcı ile düzenlileştirebiliriz. İleriye dönük modelimizi planlamayı öğrenmesi için kullanabiliriz. Sistem bir kodçözücünün durum temsilini ve belirsizlik $z$'yi çözümlemesiyle çalışır. En iyi $z$, $\hat s_{t+1}$ ile gerçekten gözlemlenmiş $s_{t+1}$'in arasındaki farkı minimize eden $z$ olarak tanımlanmıştır. ## [Üretken Çekişmeli Ağ (GAN)](https://www.youtube.com/watch?v=Pgct8PKV7iw&t=5430s) GAN yapısının oldukça fazla varyasyonu literatğrde mevcuttur ve burada GAN'ı karşıtsal metodların kullanıldığı enerji bazlı bir model olarak ele alıyoruz. GAN, karşıt örneklerin enerjileri yukarı iterken eğitim kümesindeki örneklerin enerjilerini aşağı iter. GAN temelde iki kısımdan oluşur: karşıt örnekleri akıllıca üreten bir üretici(generator) ve enerji modeli olarak davranan, ve esasında bir kayıp fonksiyonu olan, bir ayrıştırıcı(discriminator)(bazen eleştirmen olarak da adlandırılır). Hem üretici hem de ayrıştırıcı birer sinir ağıdır. GAN'ın kullandığı iki girdi türü sırasıyla eğitim örneği ve karşıt örneğidir. Eğitim örnekleri için, GAN bu örnekleri ayrıştırıcıdan geçirir ve enerjilerini düşürmeye çalışır. Karşıt örnekler için ise GAN, belli bir dağılımdan saklı bir değişken örnekler, bu örnekleri üreticiden geçirerek eğitim örneklerine benzer örnekler üretir ve bu örnekleri ayrıştırıcıdan geçirerek enerjisini artırmaya çalışır. Ayrıştırıcı için hata fonksiyonu şu şekilde tanımlanmıştır: $$\sum_i L_d(F(y), F(\bar{y}))$$ burada $L_d$ , $F(y) + [m - F(\bar{y})]^+$ veya $\log(1 + \exp[F(y)]) + \log(1 + \exp[-F(\bar{y})])$ gibi marjin bazlı bir hata fonksiyonu olabilir. Yeter ki $F(y)$ azalsın ve $F(\bar{y})$ artsın. Bu bağlamda, $y$ bir etiket ve $\bar{y}$ ise $y$ haricinde en düşük enerjiyi sağlayan tepki değişkenidir. Üretici ağ için ise farklı bir hata fonksiyonu tanımlıdır: $$L_g(F(\bar{y})) = L_g(F(G(z)))$$ burada $z$ saklı değişken ve $G$ de üretici sinir ağıdır. Üreticinin, ağırlıklarını adapte etmesini ve ayrıştırıcıyı kandirabilecek düşük enerjili $\bar{y}$'ler üretmesini istiyoruz. Bu modelin üretken çekişmeli ağlar olarak adlandırılmasının sebebi birbiriyle uyumsuz giden iki hata fomksiyonunu aynı anda minimize etmeye çalışmamızdandır. Burdaki sorun gradyan inişi problemi değil çünkü amacımız hedef iki fonksiyon arasında bir Nash denge noktası bulmak istememiz ve gradyan inişi ile böyle bir problemi çözemeyiz. Örneklerimiz gerçek manifolda yakın olduğunda belli problemlerle karşılacağız. Varsayalım ki sonsuz ince bir manifoldumuz olsun. Ayrıştırıcının manifold dışında $0$ olasılık ve içinde ise sonsuz olasılık vermesi beklenmektedir. Bunu yapmak oldukça zor olduğundan, GAN sigmoid kullanarak manifold dışında $0$ ve üzerinde $1$ üretir. Burdaki problem ise eğer biz sistemimizi başarıı bir şekilde eğitmiş olsak dahi, manifoldun dışında ayrıştırıcı 0 değerini veriyorsa, enerji fonksiyonu bu durumda anlamını yitirmiş demektir. Bunun sebebi enerji fonksiyonu pürüzsüz(smooth) değildir ve veri manifoldunun dışında heryerde enerji sonsuz iken manifoldun üzerindeki her yerde enerji 0 olucaktır. Enerjinin bir anda $0$'dan sonsuza gitmesi fonksiyonu pürüzlüleştirir. Araştırmacılar, bu problemi çözmek için enerji fonksiyonunu düzenlileştirilmesinden geçen birçok yol önerdiler. Wasserstein GAN'da ayrıştırıcının ağırlıklarını kısıtlayan önemli bir örnektir.
📝 Bofei Zhang, Andrew Hopen, Maxwell Goldstein, Zeping Zhan
emirceyani
30 Mar 2020