Discriminative Recurrent Sparse Auto-Encoder and Group Sparsity

Ayrıştırıcı Tekrarlı Seyrek Otokodlayıcı ve Grup Seyrekliği (DrSAE, Discriminative recurrent Sparse Auto-Encoder)

DrSAE’nin felsefesi seyrek kodlamayı,veya ayrık otokodlayıcı, ayrıştırıcı eğitim ile birleştirmesinden oluşur.

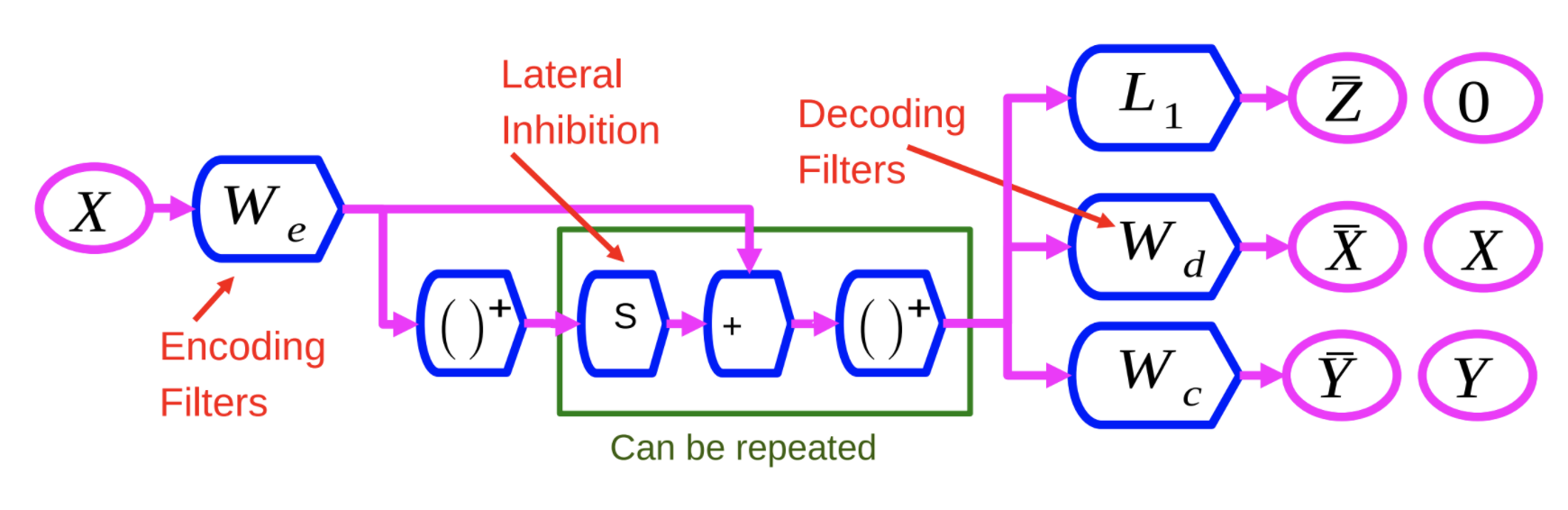
Şekil 1: Ayrıştırıcı Tekrarlı Seyrek Otokodlayıcı Ağ

Kodlayıcı, $W_e$, LISTA metodundaki kodlayıcıya benzer. X değişkeni önce $W_e$ üzerinden, daha sonra doğrusalsızlıktan geçer. Bu sonuç daha sonra bir diğer öğrenilmiş matris, S, ile çarpılır ve sonra $W_e$’ye eklenir.Daha sonra bir diğer doğrusalsızlığa gönderilir. Bu işlem her tekrarın bir katman olacağı şekilde defalarca tekrarlanabilir.

Bu sinir ağını 3 farklı kriter ile eğitiriz:

1. $L_1$: $L_1$ kriterini öznitelik vektörü X’in üzerinde onu seyrek yapmak için üzerinde uygula.
2. X’i iyileştir: Bu çıktıya göre tekrar girdi üreten kodçözücü matrisi kullanarak yapılır. Bu Şekil 1’deki $W_d$ tarafından gösterildiği gibi karesel hatayı en aza indirilerek yapılır.
3. Bir Üçüncü Terim ekle: Bu üçüncü terim, $W_c$ ile gösterilen, kategoriyi tahmin etmeye çalışan basit bir doğrusal sınıflayıcıdır.

Bu sistem bu 3 kriterin hepsini aynı anda en aza indirmek için eğitildi.

Bunun avantajı sistemi girdiyi iyileştirebilecek temsilleri bulmaya zorlamasıdır, daha sonra basitçe sistemi girdi hakkında fazlaca bilgi içeren öznitelikleri çıkarmaya doğru yön verir. Diğer bir deyişle öznitelikleri zenginleştirir.

Grup Seyrekliği

Buradaki niyetimiz seyrek öznitelikler üretmek, ama sadece evrişimlerden çıkan normal öznitelikler değil, örneklemeden sonra seyrek olan öznitelikler üretmek.

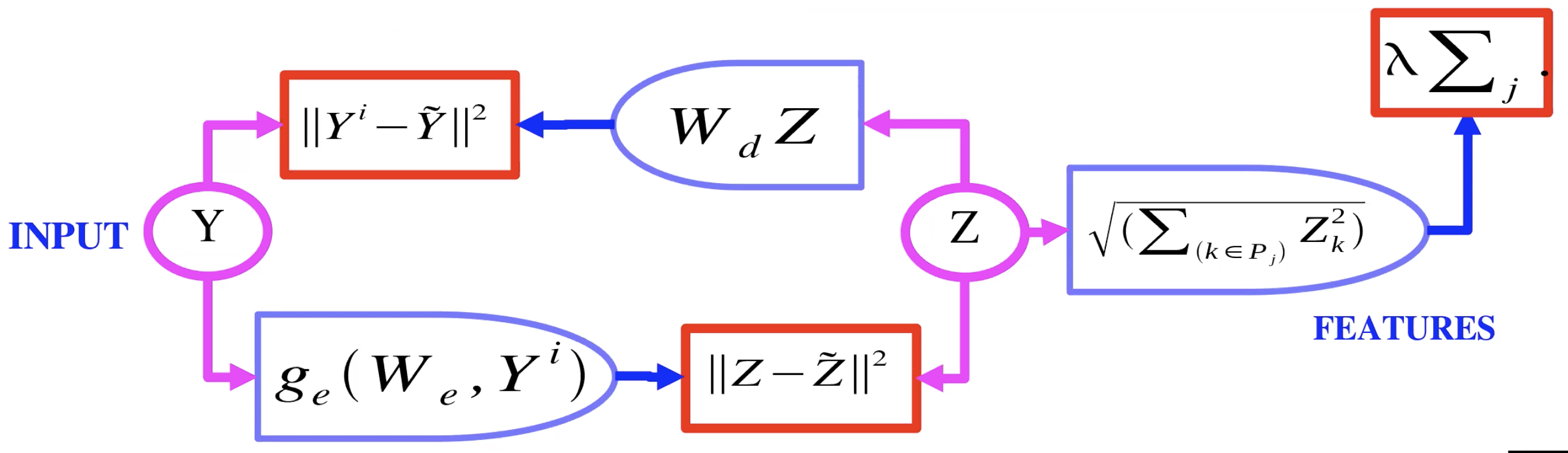
Şekil 2: Grup Seyreklikli Otokodlayıcı

Şekil 2 grup seyreklikli bir otokodlayıcının örneğini gösteriyor. Burada, saklı değişken Z bir $L_1$ üzerinden gitmek yerine gruplar üstünden bir $L_2$’ye gidiyor. Yani Z’li gruptaki her bileşen için $L_2$ büyüklüğünü alıyoruz, ve bu büyüklükleri topluyoruz. Düzenlileştirici olarak bunu kullandık şimdi Z’li gruplarda seyreklik sahibi olabiliriz. Bu gruplar, veya özniteliklerin havuzları, birbirine benzer öznitelikler ile grup oluşturma eğilimindedirler.

Grup Seyreklikli AE(AutoEncoder, Otokodlayıcı): sorular ve açıklamalar

Q: İlk slaytta sınıflayıcı ve düzenlileştirici ile kullanılan stratejiye benzer bir strateji VAE(Variational AutoEncoder, Değişimsel Otokodlayıcı) için kullanılabilir mi?

A: VAE’ye gürültü eklemek ve seyrekliğe zorlamak saklı değişken/ kod’daki bilgiyi azaltmanın iki yoludur. Kimlik fonksiyonunu öğrenmesini engeller.

Q: “Grup Seyreklikli AE” slaytındaki $P_j$ nedir?

A: p bir öznitelik havuzudur.Bir z vektörü için, z’deki değerlerin bir altkümesi olur.

Q: Öznitelik örneklemesi üzerine açıklama.

A: (Yann grup seyreklikli AE’nin temsilini çiziyor) Kodlayıcı örneklenmiş özniteliklerinin $L_2$ büyüklüklerini kullanarak düzenlileştirilmiş saklı değişken z’yi üretir. Bu z resim iyileştirilmesi için kodçözücü tarafından kullanılır.

Q: Grup düzenlileştirme benzer öznitelikleri gruplamada yardımcı oluyor mu?

A: Bunun cevabı kesin değil, buradaki çalışma işlem gücü/ veri hazır olmadan yapılmış. Teknikler ön sıralara geri getirilmemiş.

Resim düzeyi eğitimi, yerel filtreler var ama ağırlık paylaşımı yok

Yardım edip etmediğinin cevabı kesin değil. Bununla ilgilenen insanlar ya resim restorasyonuyla ya da bir tür özdenetimli öğrenme ile ilgililer. Bu veri kümesi çok küçük olduğunda iyi çalışıyor. Evrişimli bir kodlayıcı ve kodçözücüsüne sahipsiniz ve onları karmaşık hücreler üstünde grup seyrekliği ile eğitiyorsunuz, öneğitimi bitirdikten sonra, elde ettiğiniz kodçözücüden arınmış ve kodlayıcıyı da sadece özellik çıkarıcı olarak kullanan bir sistemdir, diyelim ki evrişimli bir ağın birinci katmanı var siz onun üstüne ikinci bir katman tutturuyorsunuz.

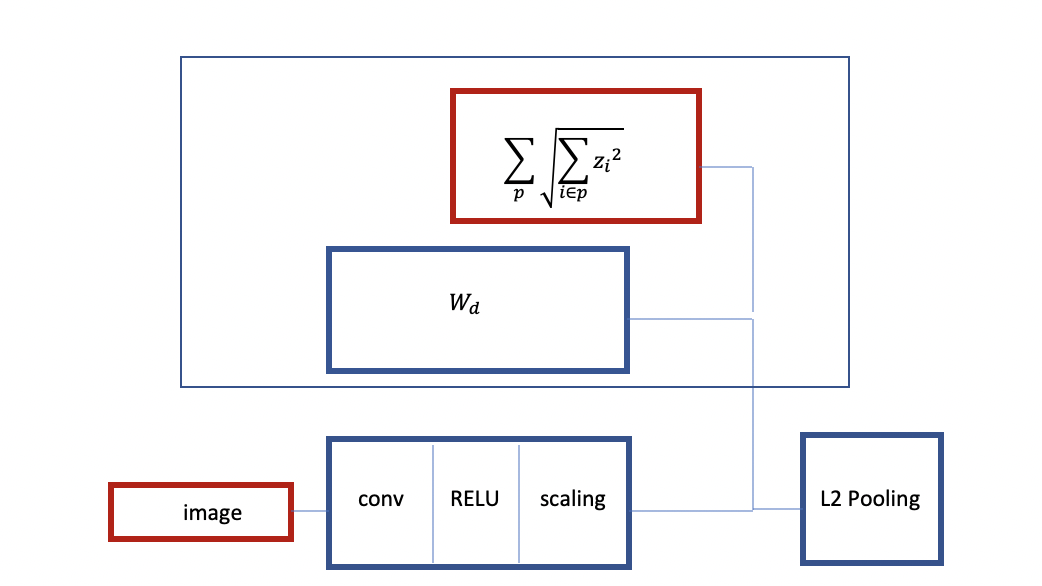
Şekil 3: Grup Seyreklikli Evrişimli RELU’nun Yapısı

Yukarıda görüleceği üzere, bir resimle başlıyorsunuz, basitçe Evrişimli RELU gibi olan bir kodlayıcınız ve bundan sonra bir çeşit ölçekleme katmanınız var. Grup seyrekliği ile eğitiyorsunuz. Doğrusal bir kodçözücü ve 1.grup kriteriniz var. Grup seyrekliğini düzenlileştirici olarak kullanıyorsunuz. Bu grup seyrekliğine benzer bir mimaride L2 örneklemesi gibidir.

Bu ağın bir diğer örneğini de eğitebilirsiniz. Bu sefer, daha fazla katman ekleyebilirsin ve L2 örnekleyici ile seyreklik kritlerli kodçözücüsüne sahip olabilirsin, onu örnekleme ile birlikte girdisini iyileştirmek için eğit. Bu öneğitilmiş 2 katmanlık evrişimli ağ oluşturacak. Bu prosedür Yığılmış Otokodlayıcı(Stacked Autoencoder) olarak da geçer. Buradaki karakteristik özellik ağın grup seyreklikli değişmez öznitelikleri üretmesi için eğitilmesidir.

Q : Mümkün olan her alt-ağacı gruplar halinde kullanmalı mıyız?

A : Bu size kalmış, isterseniz birden fazla ağacı kullanabilirsiniz. Ağacı nadir kullanılan dalları kaldıran, gerektiğinden daha büyük bir ağaç ile eğitebiliriz.

Şekil 4: Resim Düzeyi Eğitimi, yerel filtreler var ama ağırlık paylaşımı yok

Bunlar rüzgar gülü desenleri olarak adlandırılır. Bu özniteliklerin bir tür organizasyonudur. Kırmızı noktalar etrafında gezindikçe oryantasyon sürekli olarak farklıdır. Kırmızı noktalardan birini alırsak ve kırmızı noktalar etrafında küçük bir çember çizersek, hareket ettikçe çıkarıcının oryantasyonunun sürekli olarak değiştiğini fark edersin. Benzer eğilimler beyinde de gözlemlenmiştir.

Q : Grup seyrekliği terimi küçük bir değer almak üzere mi eğitilmiştir?

O bir düzenlileştiricidir. Terimin kendisi eğitilmemiştir, belirlenmiştir. O sadece grupların L2 büyüklüğüdür ve gruplar önceden belirlenmiştir. Ama, bir kriter olduğu için, kodlayıcının ve kodçözücünün ne yapacağına ve ne tür özniteliklerin çıkarılacağına karar verir.

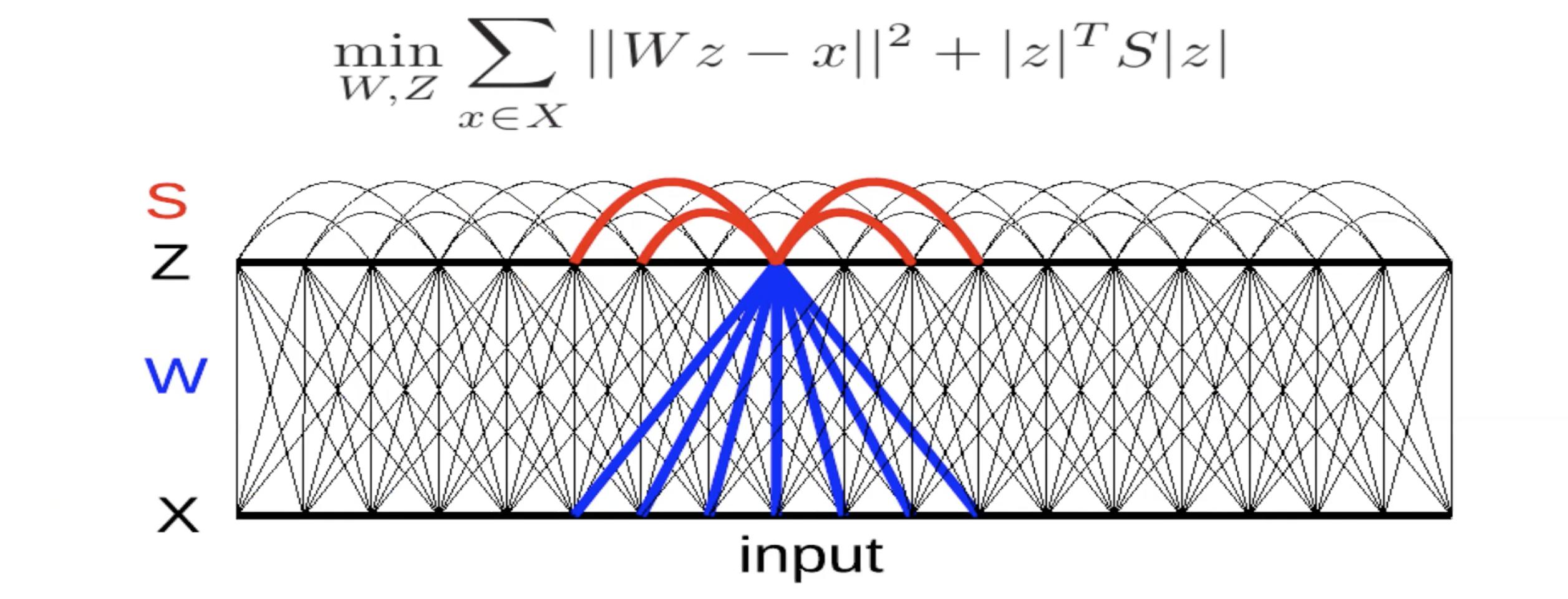
Şekil 5: Yanal Ketleme Vasıtasıyla Değişmez Öznitelikler

Burada kare yeniden oluşturma hatası veren bir doğrusal kodçözücü var. Enerjide bir kriter var. S matrisi ya elle belirlendi ya da terimi en yüksek değere çekmek için öğrendi. Eğer S’deki terimler pozitif ve büyüklerse, sistemin $z_i$’nin ve $z_j$’nin aynı anda aktif olmasını istemediği anlamına gelir. Nitekim, bu bir tür ortak ketlemedir (sinirbilimde doğal ketleme denir). Böylece, S için olabilecek en büyük değeri bulmaya çalışır.

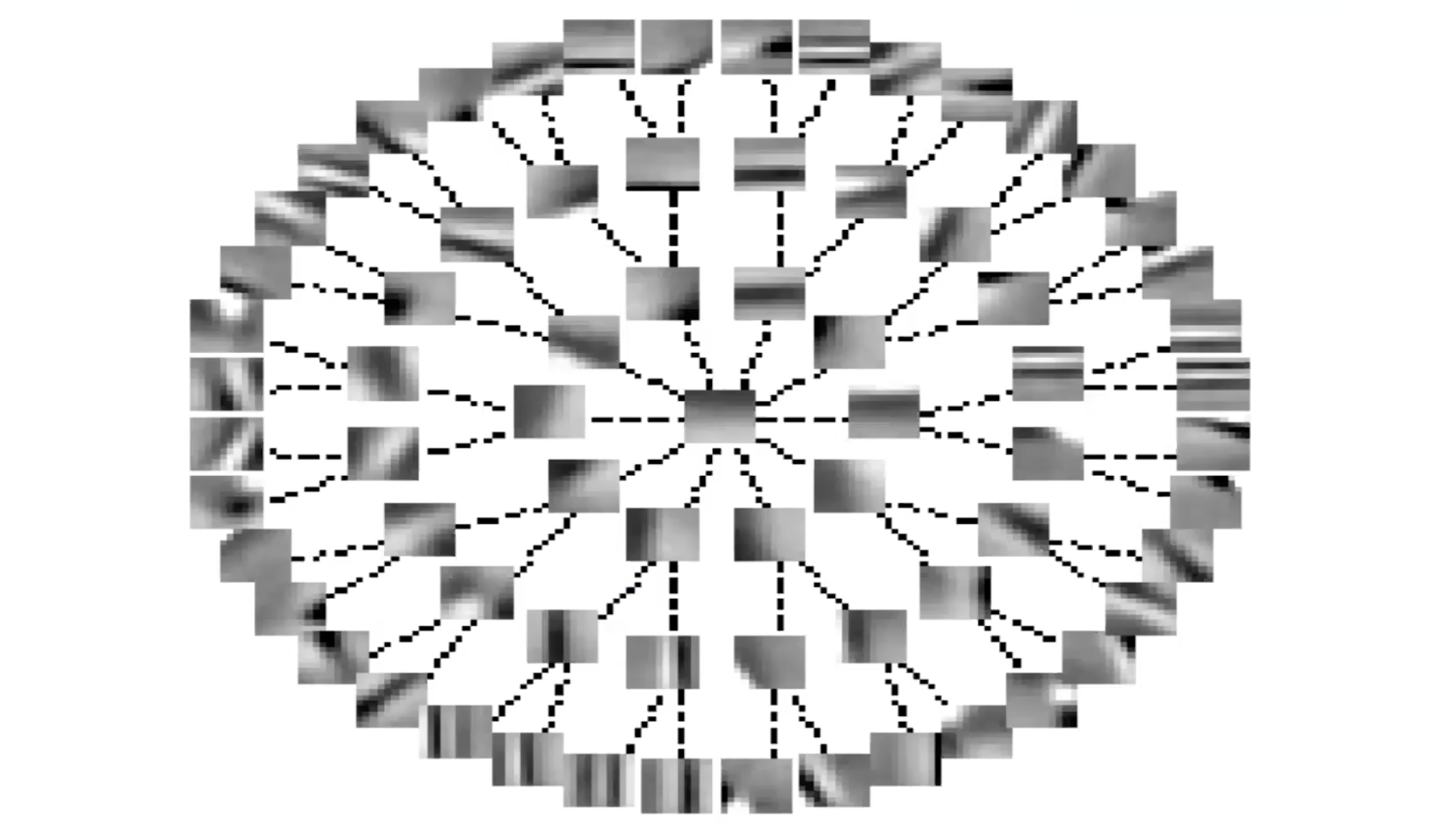
Şekil 6: Yanal Ketleme Vasıtasıyla Değişmez Öznitelikler (Ağaç Formu)

Eğer S’yi ağaç şartlarında organize ederseniz, çizgiler S matrisinde sıfır terimlerini temsil eder. Çizginiz olmadığı zaman, orada bir sıfır olmayan terim vardır. Yani, her öznitelik ağaçta kendinden yukarıda veya aşağıda olanlar hariç diğer öznitelikleri engeller. Bu grup seyrekliğinin zıttı gibidir.

Tekrar gördüğünüz gibi sistemler öznitelikleri neredeyse sürekli olarak biçimlendirir. Ağacın dalı boyunca bulunan öznitelikler aynı özniteliğin farklı seçicilikteki halini temsil ederler. Ağacın çevresinde bulunan öznitelikler neredeyse sürekli olarak farklıdır çünkü engelleme yoktur.

Bu sistemi eğitmek için, her tekrarda, bir $x$ verilir ve enerji fonksiyonunu en aza indiren $z$ bulunur. Sonra $W$’yi güncellemek için bir kez gradyan inişi yapılır. Ayrıca $S$’deki terimleri daha büyük yapmak için bir kez gradyan çıkışı da yapılabilir.