Üretici Modeller - Değişimsel Otokodlayıcılar

Hatırlatma: Otokodlayıcılar (Autoencoder - AE)

Kısaca özetlersek basit bir Otokodlayıcı şu şekilde çalışır:

• İlk olarak, otokodlayıcı bir girdi alır alır ve bunu $\boldsymbol{h} = f(\boldsymbol{W}_h \boldsymbol{x} + \boldsymbol{b}_h)$ ile ifade edilen bir afin dönüşümden geçirerek gizli bir değer ile eşleştirir. Dönüşüm formülündeki $f$ değeri eleman çapında bir aktivasyon fonksiyonudur. Bu kodlama aşamasıdır ve $\boldsymbol{h}$ değeri kod olarak adlandırılır.
• Sonrasında, kod çözme aşamasında $\hat{\boldsymbol{x}} = g(\boldsymbol{W}_x \boldsymbol{h} + \boldsymbol{b}_x)$ formülü uygulanır. Bu formülde ise $g$ aktivasyon fonksiyonudur.

Detaylı açıklama için 7. haftanın ders notlarına bakabilirsiniz.

VAE’nin temelinde yatan mantık ve klasik otokodlayılardan farkları

Şimdi bir üretici model olan Değişimsel Otokodlayıcılara (Variational Autoencoders, VAE) bakalım. Burada akla gelen ilk soru, neden üretici modellerle ilgilendiğimiz ile ilgilidir. Ayırt edici modeller verilen gözlemlere göre tahmin yapmayı öğrenir, üretici modeller ise data üretim süreçlerini simüle etmeyi amaçlar. Bunun bir etkisi olarak da üretici modeller altta yatan nedensel ilişkileri daha iyi anlayarak daha iyi genelleştirme yapar.

Değişimsel Otokodlayıcılar yapısal ve mimari benzelikleri göze alınarak Otokodlayıcı sınıfında adlandırılsa da, Şekil 1‘de görüldüğü üzere formülasyonları oldukça farklıdır.

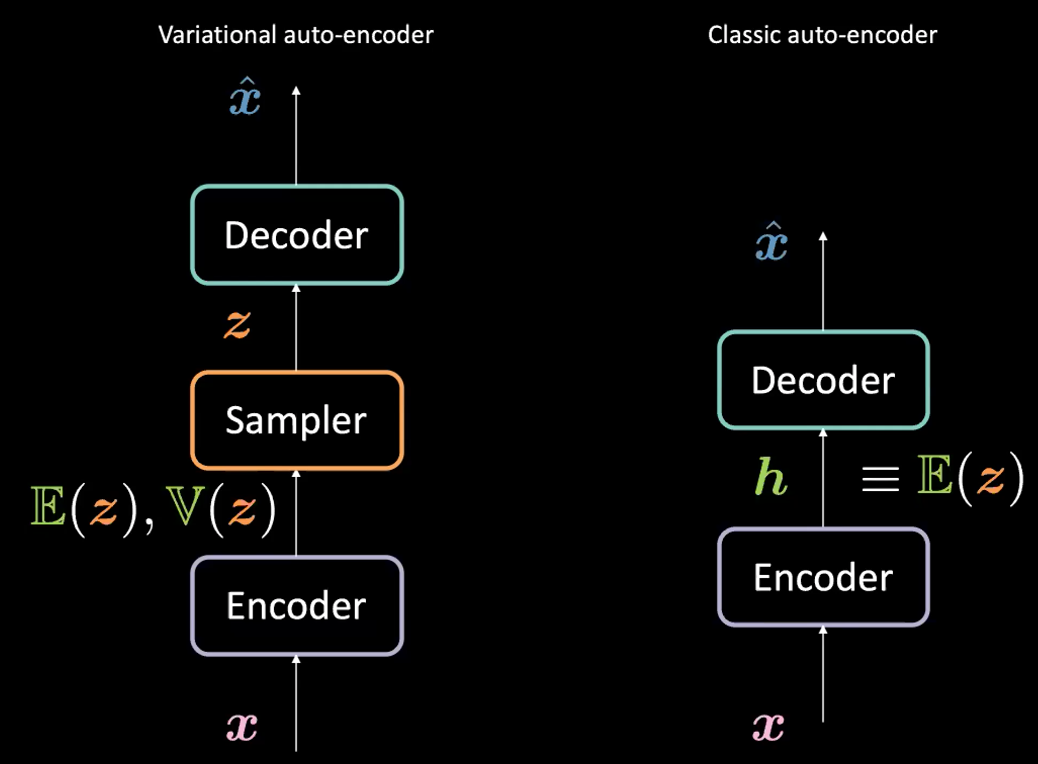
Şekil 1: Değişimsel Otokodlayıcı vs. Klasik Otokodlayıcı

Değişimsel otokodlayıcı (VAE) ile klasik otokodlayıcı (AE) arasındaki farklar nelerdir?

VAE:

• Kodlama aşaması: $\boldsymbol{x}$ girdisini kodlayıcıya veriyoruz. Klasik otokodlayıcılarda olduğu gibi bir saklı gösterim kodu $\boldsymbol{h}$ üretmek yerine, VAE’de üretilen kod 2 kısımdan oluşur: $\mathbb{E}(\boldsymbol{z})$ ve $\mathbb{V}(\boldsymbol{z})$. Burada $\boldsymbol{z}$ değeri ortalaması $\mathbb{E}(\boldsymbol{z})$ varyansı da $\mathbb{V}(\boldsymbol{z})$ olan bir Gauss dağılımına (normal dağılım) ait bir saklı rastgele değişkendir. Her ne kadar pratikte kod dağılımı olarak Gauss dağılımı kullanılsa da, diğer dağılım çeşitleri de kullanılabilir.
  • Kodlayıcı $\mathcal{X}$’ten $\mathbb{R}^{2d}$: $\boldsymbol{x} \mapsto \boldsymbol{h}$’e bir fonksiyon olarak ifade edilebilir. Burada $\boldsymbol{h}$, $\mathbb{E}(\boldsymbol{z})$ ve $\mathbb{V}(\boldsymbol{z})$) değerlerinin birleşimini ifade etmektedir.
• Sonra, $\boldsymbol{z}$ değeri yukarıda kodlayıcı tarafından parametreleştirilen dağılımdan örneklenir. Bunun için $\mathbb{E}(\boldsymbol{z})$ ve $\mathbb{V}(\boldsymbol{z})$ değerleri örnekleyici fonksiyona verilerek saklı değişken $\boldsymbol{z}$ üretilir.
• Son olarak, $\boldsymbol{z}$ kodçözücüye verilerek $\hat{\boldsymbol{x}}$ elde edilir.
  • Kodçözücü $\mathcal{Z}$’den $\mathbb{R}^{n}$: $\boldsymbol{z} \mapsto \boldsymbol{\hat{x}}$’e bir fonksiyondur.

Aslında klasik otokodlayıcılardaki $\boldsymbol{h}$’yi VAE formülasyonundaki $\E(\boldsymbol{z})$ vektörü olarak düşünebiliriz. Kısaca klasik otokodlayıcı (AE) ve değişimsel otokodlayıcı (VAE) arasındaki temel fark değişimsel otokodlayıcının (VAE) yeni data üretmeyi sağlayan üretici süreçlere izin veren iyi bir saklı uzaya sahip olmasıdır.

VAE amaç (kayıp) fonksiyonu

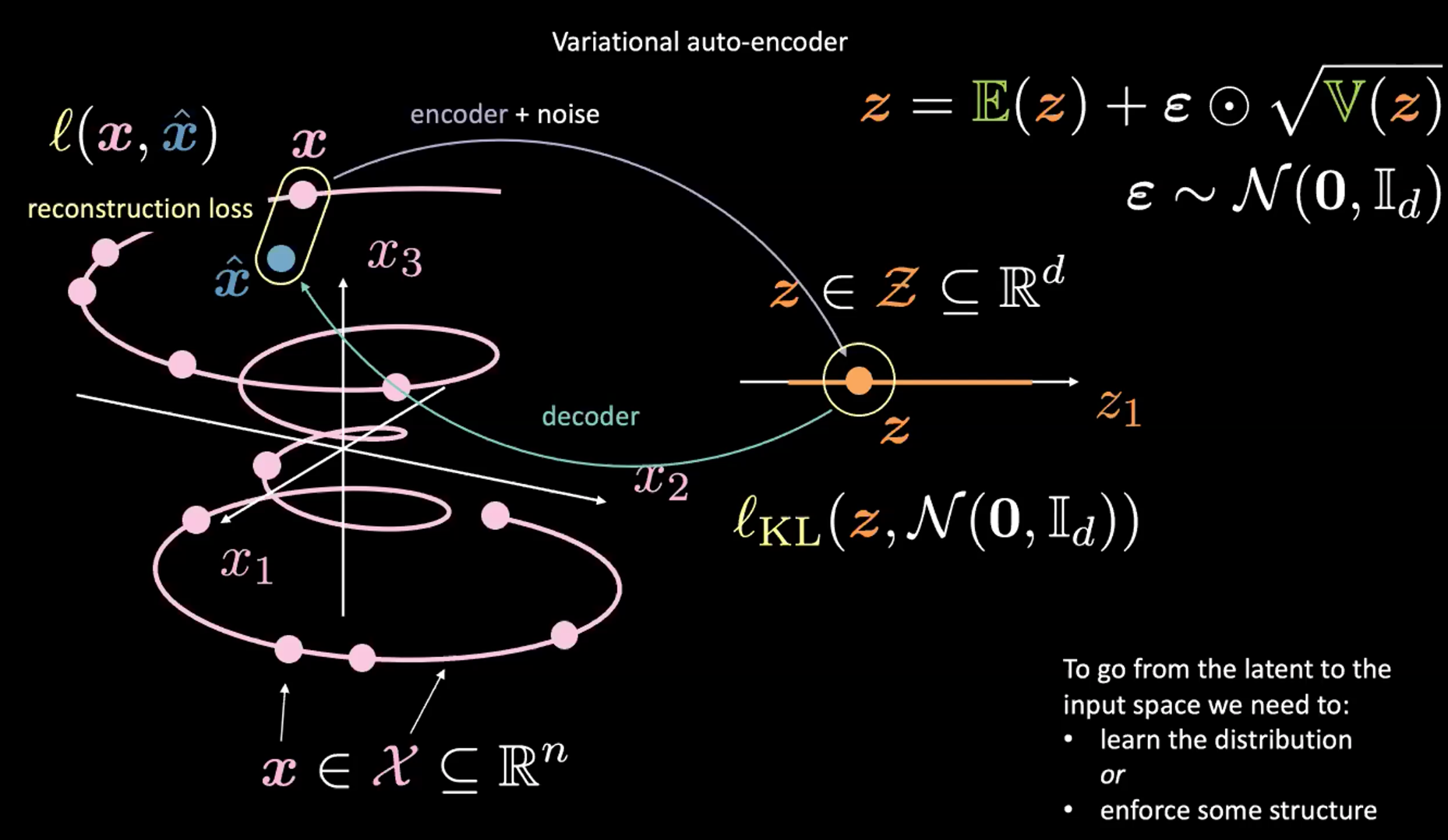
Şekil 2: Girdi uzayından saklı uzaya eşleme

Yukarıdaki Şekil 2’de sağ üst köşeyi şimdilik görmezden gelebilirsiniz. O bölümde yer alan yeniden parametreleştirme hilesi bir sonraki başlıkta açıklanacaktır.

Önce, girdi uzayından (sol) saklı uzaya (sağ) kodlayıcı ve gürültü kullanarak kodlama yapıyoruz. Sonra, saklı değer uzayından (sağ) çıktı uzayına (sol) doğru kodu çözüyoruz. Saklı değer uzayından girdi uzayına gitmek için (yeni data üretme) ya saklı değer uzayının dağılımını öğrenmek ya da belirli bir yapıya zorlamak gerekir. Bizim durumumuzda, VAE saklı değer uzayını belirli bir yapıya zorlar.

Her zaman olduğu gibi VAE’yi de eğitmek için bir kayıp fonksiyonunu küçültmemiz gerekir. Kayıp fonksiyonu yeniden oluşturma ve düzenlileştirme terimlerinden oluşur.

• Yeniden oluşturma terimi, çıktı katmanında bulunur. Şekil 2‘de sol tarafta $l(\boldsymbol{x}, \hat{\boldsymbol{x}})$ bölümü ile ifade edilir.
• Düzenlileştirme terimi saklı katmanda bulunur ve saklı değer uzayını belirli bir Gauss yapısına zorlar (Şekil 2.’de sağ tarafta). Bunu yapmak için $l_{KL}(\boldsymbol{z}, \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d))$ ceza terimini kullanırız. Bu terim olmadan VAE klasik otokodlayıcı gibi çalışır, bu da ezberlemeye sebep olabilir ve istediğimiz üretici özelliklere sahip olmaz.

$\boldsymbol{z}$’yi örneklemek (yeniden parametreleştirme hilesi)

VAE kodlayıcısı tarafından verilen dağılımdan nasıl örnek üretebiliriz? Yukarıda anlatıldığı gibi $\boldsymbol{z}$’yi elde etmek için Gauss dağılımından örnekleyebiliriz. Fakat bu problemli bir yaklaşımdır çünkü VAE’yi eğitmek için gradyan inişi kullanırsak örnekleme fonksiyonundan nasıl geri yayılım yapılabileceğini bilmiyoruz.

Bunun yerine $\boldsymbol{z}$’yi “örneklemek” için yeniden parametreleştirme hilesi kullanıyoruz. $\epsilon\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d)$ alarak $\boldsymbol{z} = \mathbb{E}(\boldsymbol{z}) + \boldsymbol{\epsilon} \odot \sqrt{\mathbb{V}(\boldsymbol{z})}$ formülünü kullanıyoruz. Bu sayede, eğitim sırasında geri yayılım mümkün oluyor. Gradyanlar bu formüldeki çarpım ve toplam işlemlerinden eleman çapında geçiyor.

VAE kayıp fonksiyonunu parçalarına ayırmak

Saklı Değişken Tahminlerini ve Yeniden Oluşturma Kaybını Görselleştirmek

Daha önce de belirtildiği gibi VAE kayıp fonksiyonu 2 kısımdan oluşur: yeniden oluşturma terimi ve düzenlileştirme terimi. Bunu şöyle ifade edebiliriz:

Kayıp fonksiyonundaki her terimin amacını görselleştirmek için tahmin edilen her $\boldsymbol{z}$ değerini 2 boyutlu uzayda daireler olarak düşünebiliriz. Bu dairelerin merkezi $\mathbb{E}(\boldsymbol{z})$, kapladığı alan da $\boldsymbol{z}$’nin $\mathbb{V}(\boldsymbol{z})$ tarafından belirlenen olası değerleri olacaktır.

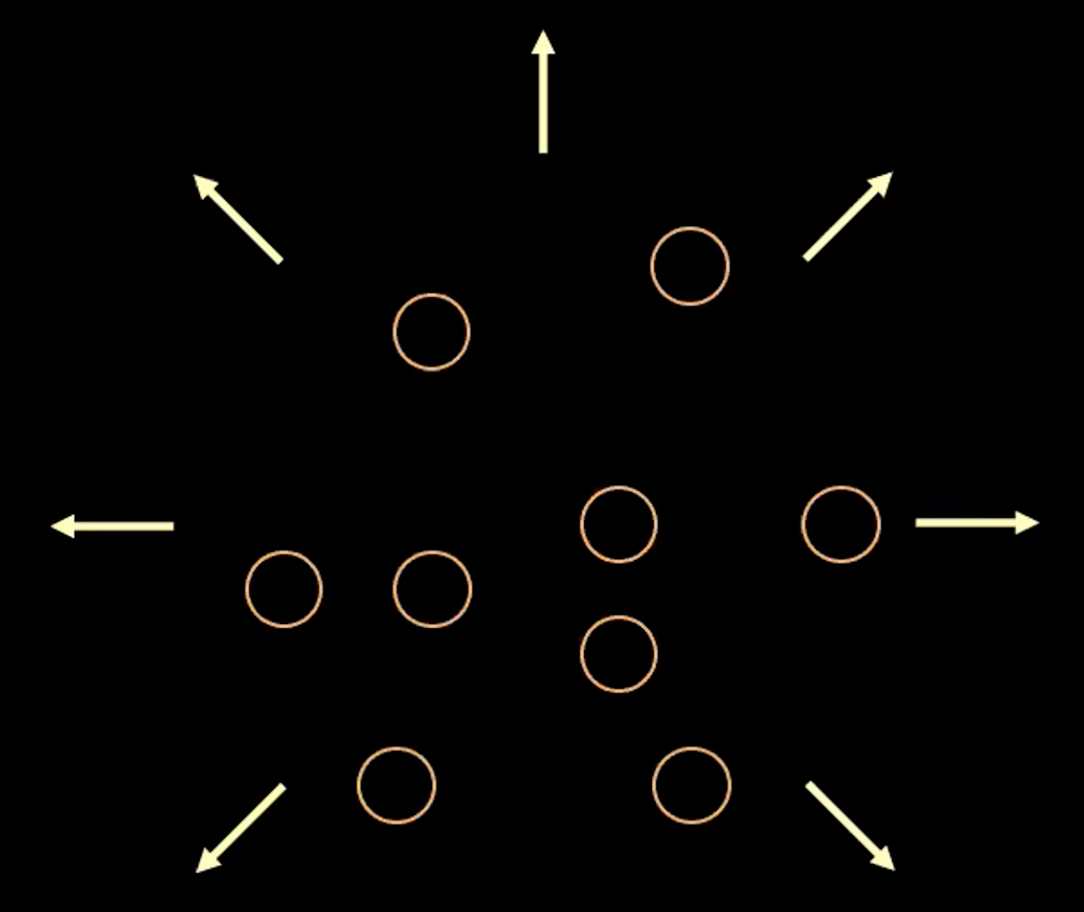
Şekil 3: z vektörünü saklı uzaydaki daireler olarak görselleştirmek

Yukarıda Şekil 3’te, her daire bir $\boldsymbol{z}$ değerinin tahmini bölgesini gösteriyor, oklar ise (aşağıda daha detaylı anlatılacaktır) yeniden oluşturma teriminin her daireyi nasıl birbirinden uzağa ittiğini gösteriyor.

Eğer herhangi iki tahmini $z$ değeri üst üste gelirse (görsel olarak iki daire üst üste gelirse) bu yeniden oluşturma için belirsizlik yaratır çünkü üst üste gelen değerler her iki orijinal girdi ile de eşleştirilebilir. Bu sebepten yeniden oluşturma kaybı bu iki noktayı birbirinden uzağa iter.

Eğer sadece yeniden oluşturma kaybını kullanırsak, tahmin edilen noktalar birbirinden uzağa itilmeye devam edecek ve sistemin dağılmasına sebep olabilecektir. Bu noktada ceza terimi devreye girer.

Not: ikili girdiler için yeniden oluşturma kaybı:

gerçek değerli girdiler için yeniden oluşturma kaybı:

Ceza terimi

İkinci terim, ortalaması $\mathbb{E}(\boldsymbol{z})$ ve varyansı $\mathbb{V}(\boldsymbol{z})$ olan bir Gauss dağılımından örneklenen $\boldsymbol{z}$ ve standart normal dağılım arasındaki göreli entropi (iki dağılım arasındaki mesafe ölçüsü) değeridir. Eğer VAE kayıp fonksiyonundaki bu ikinci terimi açarsak aşağıdaki formülü elde ederiz:

Bu formüldeki toplamda her değer dört terimden oluşur. Aşağıda, ilk üç terimi ve bunun oluşturduğu grafiği (Şekil 4) göreceksiniz

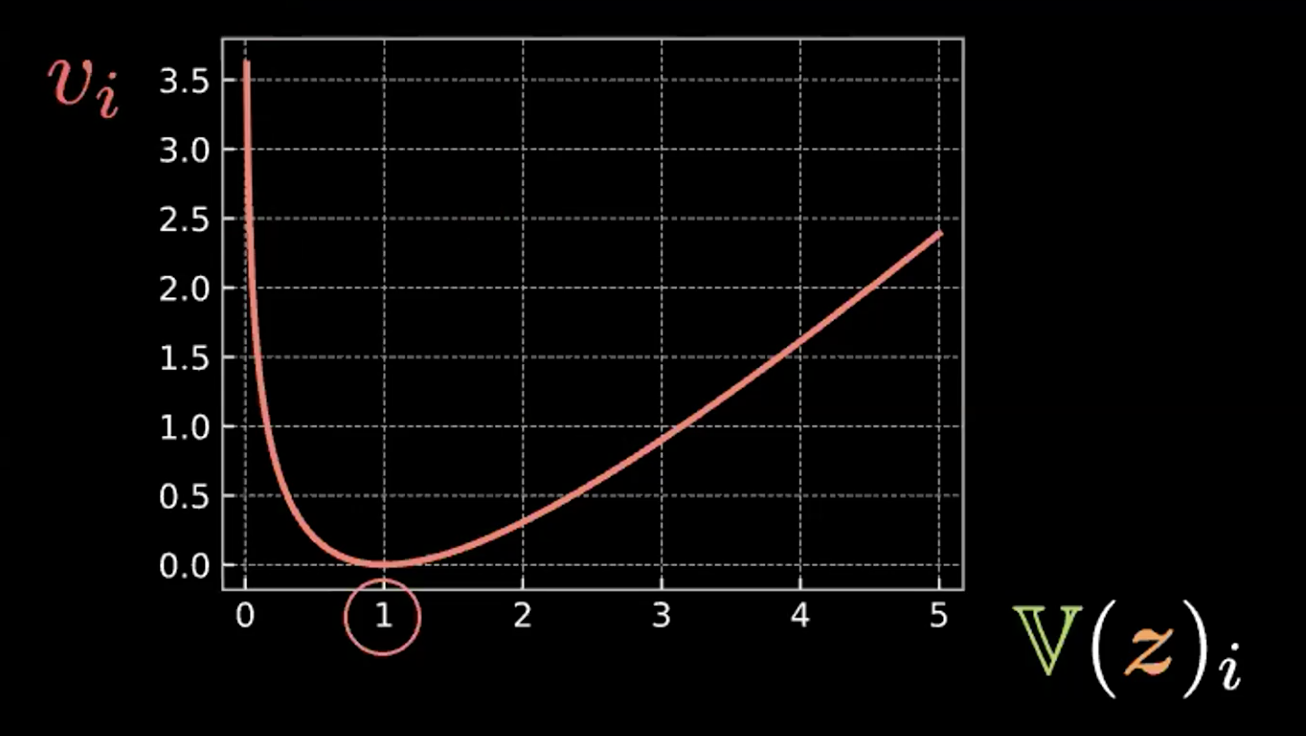
Şekil 4: Göreli entropinin dairelerin varyansını 1 olmaya zorlamasını gösteren çizim

Görebildiğimiz gibi bu ifade, $z_i$’nin varyansı 1 olunca en küçük değere sahip oluyor. Yani ceza kaybımız tahmini kayıp değişkenlerinin varyansını yaklaşık olarak 1’de tutuyor. Bu da görsel olarak yukarıdaki “dairelerin” çapının 1 civarında olması demek oluyor.

Son terim, $\mathbb{E}(z_i)^2$, $z_i$’lar arasındaki mesayi azaltıyor ve yeniden oluşturma teriminin sebep olduğu dairelerin uzaklaşarak “patlama”sını engelliyor.

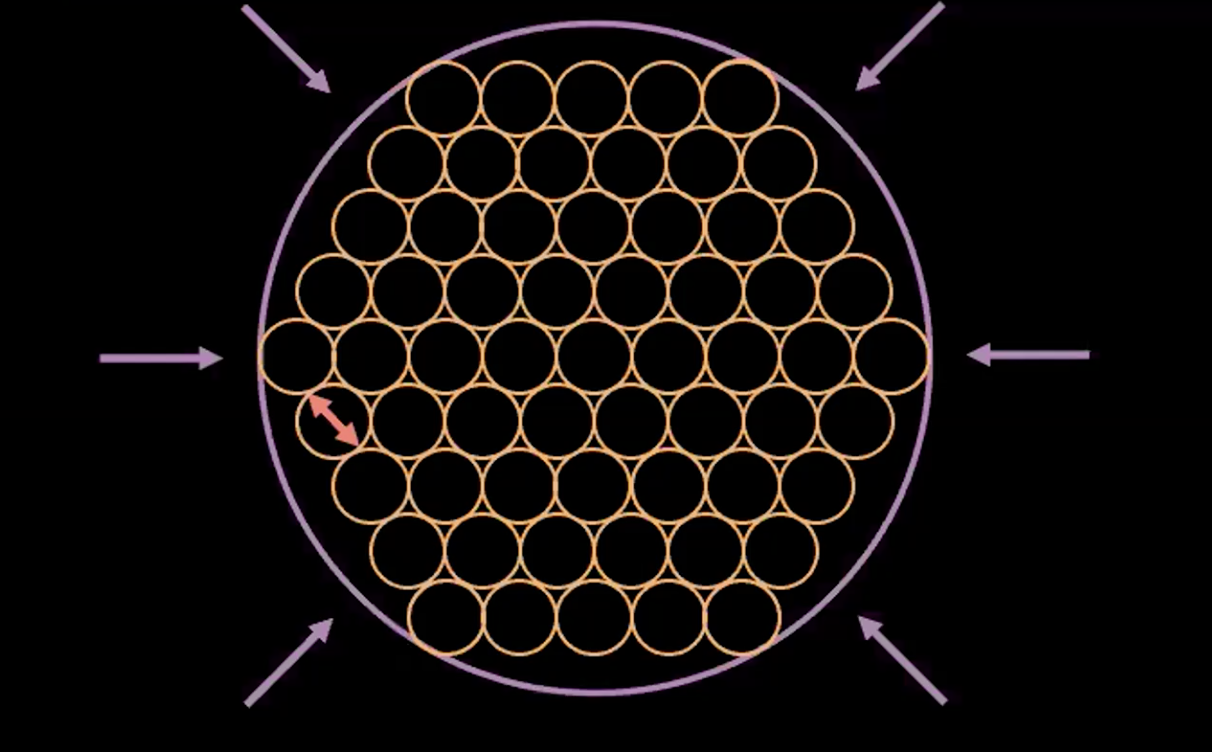
Şekil 5: VAE'nin "daire içinde daire" temsili

Yukarıda *Şekil 5, VAE’nin nasıl hiç üst üste binme olmadan ve her dairenin tahmini varyansını yaklaşık 1 seviyesinde tutarak, tahmini saklı değişkenleri mümkün olduğunca bir araya ittiğini gösteriyor.

Not: VAE kayıp fonksiyonundaki $\beta$ değeri yeniden oluşturma terimi ve ceza teriminin ağırlıklarını belirleyen bir hiperparametredir.

Değişimsel Otokodlayıcı (VAE) kodunun yazımı

İlgili Jupyter notebook’a buradan ulaşabilirsiniz.

Bu notebook’ta bir VAE kodu yazıp MNIST veri kümesi ile eğiteceğiz. Sonrasında normal dağılımdan bir $\boldsymbol{z}$ örnekleyip kodçözücüye vereceğiz ve sonuçları kıyaslayacağız. Son olarak, 2 boyutlu gösterimde $\boldsymbol{z}$nin nasıl değiştiğine bakacağız.

Not: Kullandığımız MNIST veri kümesindeki piksel değerleri $[0, 1]$ aralığına normalleştirilmiştir.

Kodlayıcı ve Kodçözücü

1. VAE modülündeki kodlayıcı ve kodçözücüyü tanımlıyoruz.
2. Kodlayıcının son doğrusal katmanında, çıktıyı 2 boyutlu olacak şekilde tanımlıyoruz. İlk boyut ortalamaları, diğer boyut da varyansları ifade edecek. Daha önce yeniden parametreleştirme hilesinde anlatıldığı gibi bu ortalama ve varyans değerleri kullanılarak $\boldsymbol{z} \in R^d$ değerini örnekliyoruz.
3. Girdi verisine benzer şekilde çıktıyı $[0, 1]$ aralığında almak için kodçözücünün son doğrusal katmanında sigmoid aktivasyon fonksiyonunu kullanıyoruz.

class VAE(nn.Module):
    def __init__(self):
        super().__init__()

        self.encoder = nn.Sequential(
            nn.Linear(784, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, d * 2)
        )

        self.decoder = nn.Sequential(
            nn.Linear(d, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, 784),
            nn.Sigmoid(),
        )

Yeniden parametreleştirme ve forward (ileri) fonksiyonu

Model eğitim modundayken, reparameterise (yeniden parametreleştir) fonksiyonu için standart sapmayı (std) varyansın logaritmasını (logvar) kullanarak hesaplıyoruz. Varyans yerine varyansın logaritmasını kullanıyoruz çünkü varyansın negatif olmadığından emin olmak istiyoruz. Ayrıca logaritmasını almak, varyansın kullandığı bütün değer aralığını kullanmamızı sağlıyor bu da eğitimi daha kararlı hale getiriyor.

Eğitim boyunca reparameterise fonksiyonu yeniden parametreleştirme hilesini uygulayacak, böylelikle eğitim için geri yayılım kullanabileceğiz. Derste anlatılan sarı daire konseptiyle bağdaştırmak gerekirse, bu fonksiyonu her çağırdığımızda bir eps = std.data.new(std.size()).normal_() noktası çekiyoruz, yani 100 defa çağırırsak normal dağılım kullandığımız için yaklaşık olarak bir küre oluşturacak 100 nokta elde ederiz. eps.mul(std).add_(mu) satırı da bu kürenin mu merkezli ve std yarıçaplı olmasını sağlıyor.

forward fonksiyonunda önce kodlayıcıyı kullanarak mu (ilk yarı) ve logvar‘ı (ikinci yarı) hesaplıyoruz. Sonra reparameterise fonksiyonu ile $\boldsymbol{z}$’yi hesaplıyoruz. Son olarak da kodçözücünün çıktısını döndürüyoruz.

def reparameterise(self, mu, logvar):
    if self.training:
        std = logvar.mul(0.5).exp_()
        eps = std.data.new(std.size()).normal_()
        return eps.mul(std).add_(mu)
    else:
        return mu

def forward(self, x):
    mu_logvar = self.encoder(x.view(-1, 784)).view(-1, 2, d)
    mu = mu_logvar[:, 0, :]
    logvar = mu_logvar[:, 1, :]
    z = self.reparameterise(mu, logvar)
    return self.decoder(z), mu, logvar

VAE’nin kayıp fonksiyonu

Burada yeniden oluşturma kaybını (ikili çapraz entropi - binary cross entropy) ve göreli entropiyi (KL ıraksama cezası - KL divergence penalty) tanımlıyoruz.

def loss_function(x_hat, x, mu, logvar):
    BCE = nn.functional.binary_cross_entropy(
        x_hat, x.view(-1, 784), reduction='sum'
    )
    KLD = 0.5 * torch.sum(logvar.exp() - logvar - 1 + mu.pow(2))

    return BCE + KLD

Yeni örneklerin üretilmesi

Modeli eğittikten sonra normal dağılım kullanarak rastgele bir $z$ örnekleyebilir ve kodçözücüye verebiliriz. Şekil 6‘da görebileceğimiz gibi bazı sonuçlar iyi değil çünkü kodçözücümüz bütün saklı değer uzayını kapsamıyor. Bu sorunu çözmek için modelimizi daha fazla eğiterek kodçözücüyü geliştirebiliriz.

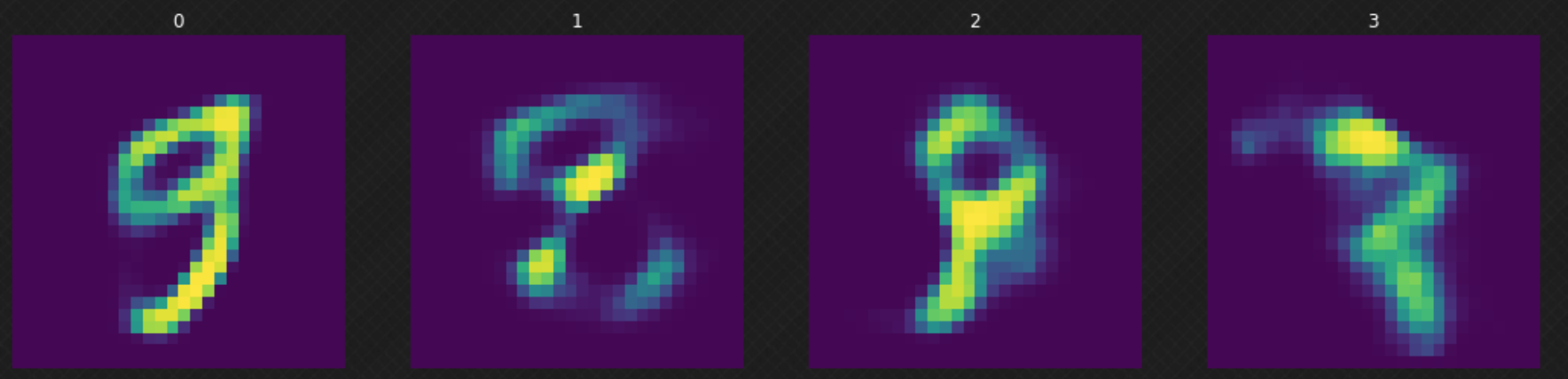
Şekil 6: Saklı değer uzayında rastgele hareket etmek

Şimdi bir rakamın öbürüne nasıl dönüştüğüne bakabiliriz, eğer klasik otokodlayıcı kullanmış olsaydık bunu görmek mümkün olmayacaktı. Saklı değer uzayında gezindiğimizde kodçözücünün çıktısının mantıklı olduğunu görebiliyoruz. Aşağıda, Şekil 7‘de $3$ rakamını $8$ rakamına nasıl dönüştürdüğümüzü görebiliriz.

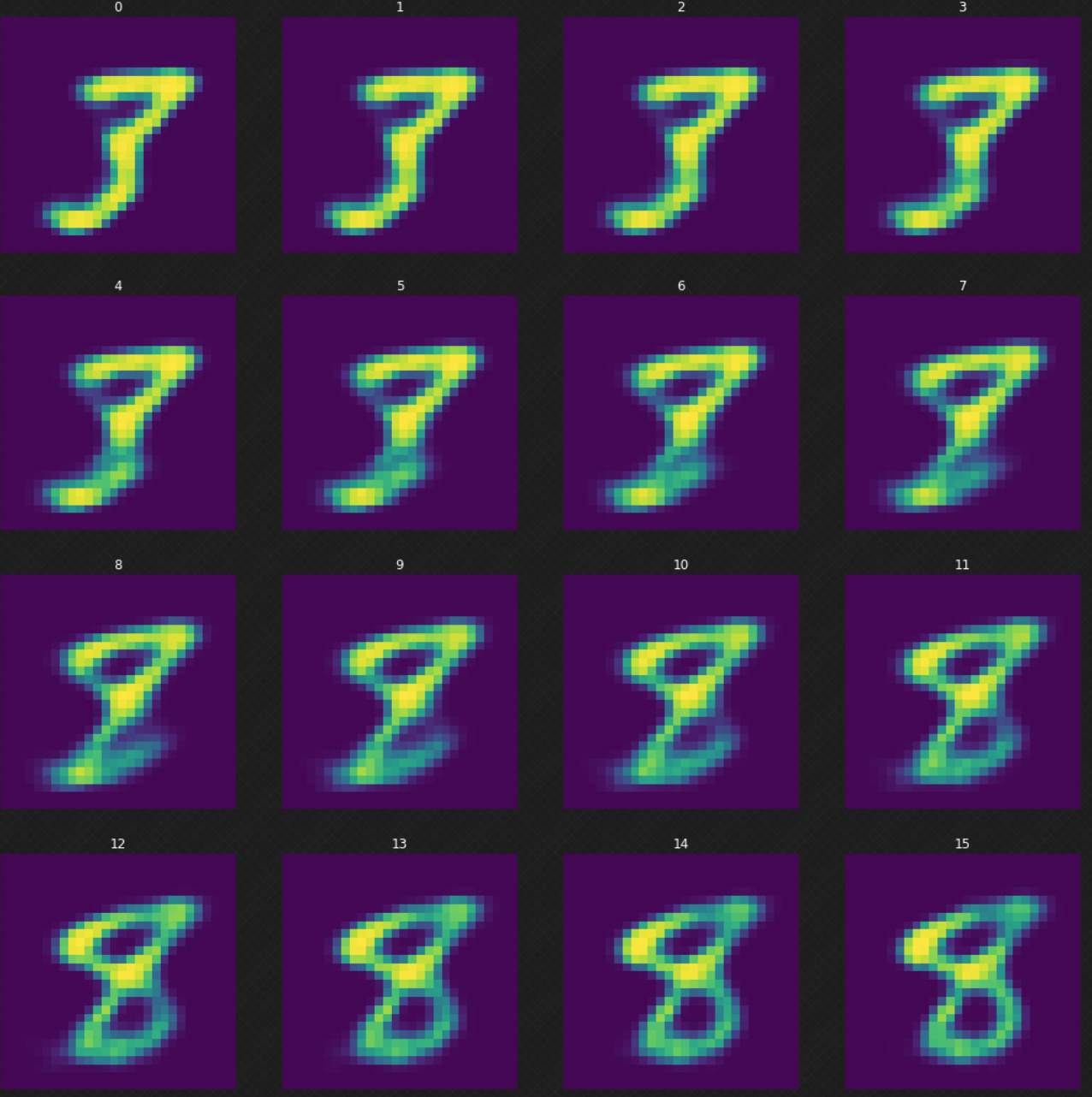
Fig. 7: 3 rakamını 8 rakamına dönüştürmek

Ortalamaların izdüşümü

Son olarak, saklı değer uzayının eğitim sırasında/sonrasında nasıl değiştiğine bakalım. Aşağıda, Şekil 8‘deki grafikler, kodlayıcı çıktısındaki ortalamaların 2 boyutlu uzaydaki izdüşümleri (her renk farklı bir rakamı temsil ediyor). Epok 0’da sınıfların çok az toplanma göstererek farklı yerlere dağıldıklarını görebiliyoruz. Model eğitildikçe saklı değer uzayı daha iyi belirleniyor ve sınıflar (rakamlar) öbekler oluşturmaya başlıyor.

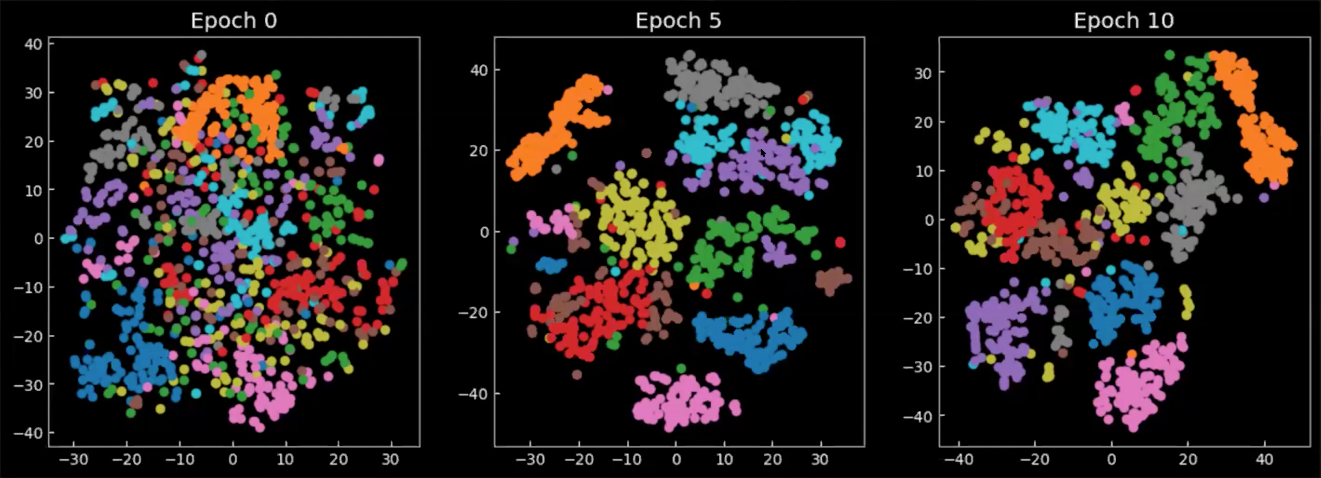
Şekil 8: Saklı değer uzayındaki $\E(\vect{z})$ ortalamaların 2 boyutlu izdüşümleri