Düzenlileştirilmiş Saklı Değişkenli Enerji Bazlı Modeller
🎙️ Yann LeCunDüzenlileştirilmiş Saklı Değişkenli EBM’ler
Saklı değişkenlere sahip modeller, kestirimlerin $\overline{y}$ gözlemlenen girdi $x$ ve ilaveten bir saklı değişken $z$’ye koşullu dağılımını üretebilir. Enerji bazlı modeller de saklı değişken(ler) içerebilir:
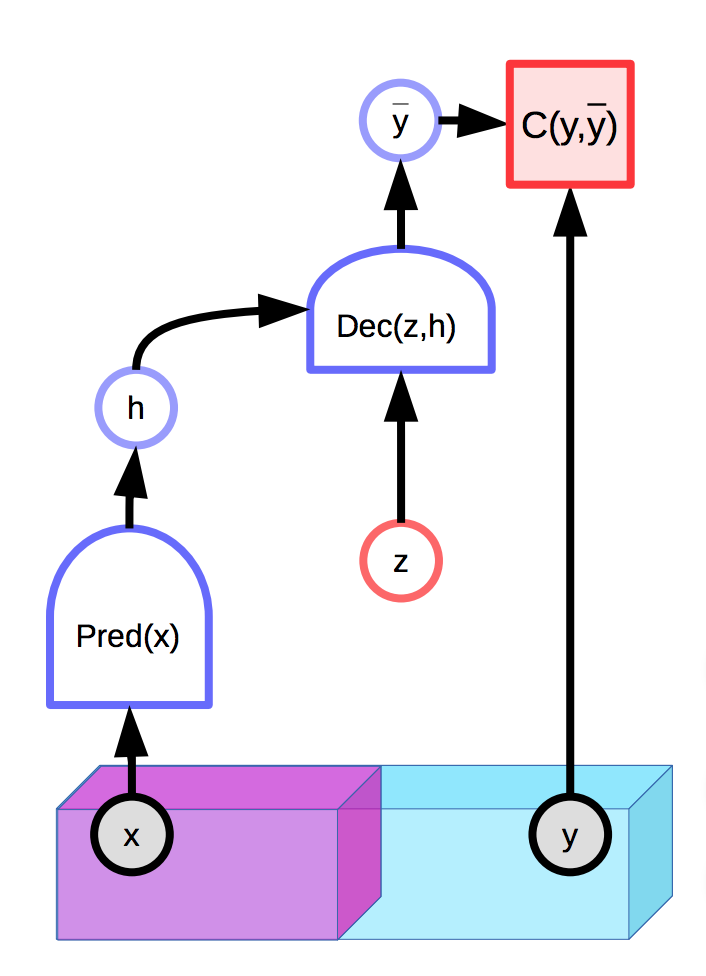
Şekil 1: Gizli değişkenli bir EBM örneği
Daha fazla detay için bir önceki dersin notlarına bakabilirsiniz.
Ne yazık ki, eğer saklı değişken $z$ nihai kestirim $\overline{y}$’nin üretim sürecini gereğinden fazla ifade ediyorsa, her gerçek çıktı $y$, girdi $x$ ve uygun bir biçimde seçilmiş $z$ sayesinde kayıpsız yeniden oluşturulabilir. Diğer bir deyişle, enerji fonksiyonu heryerde 0 değerini almış olur çünkü enerji, çıkarım (inference) esnasında $y$ ve $z$’ye göre eniyilenir (optimize edilir).
Bu durum için basit bir çözum, gizli değişken $z$’nin bilgi kapasitesini sınırlamaktır. Bunu yapmanın bir yolu da gizli değişkeni düzenlileştirmektir:
\[E(x,y,z) = C(y, \text{Dec}(\text{Pred}(x), z)) + \lambda R(z)\]Bu yöntem, küçük değerler alan z’nin uzay hacmini sınırlayacak ve bu sınırlamayla düşük enerjiye sahip y’nin uzayını da kontrol edebilmiş olacağız. Lambda’nın değeri bu dengeyi kontrol eder. Bu yöntemi, reel sayılar kümesi $R$ üzerinde anlatmış olsaydık, uygun boyutun neredeyse her yerde türevlenebilen yakınsaması olan $L_1$ normu bu yöntemi oldukça iyi anlatmış olurdu. $z$’nin $L_2$ normunu kısıtlarken üzerine gürültü eklemek de bilgi kapasitesini sınırlar (VAE).
Seyrek Kodlama (Sparse Coding)
Seyrek kodlama, veriyi parçalı bir doğrusal fonksiyon ile yakınsamaya çalışan koşulsuz düzenlileştirilmiş saklı değişkenli bir enerji bazlı modeldir.
\[E(z, y) = \Vert y - Wz\Vert^2 + \lambda \Vert z\Vert_{L^1}\]$n$ boyutlu vektör $z$, maximum sayıda sıfırdan farklı elemana $m « n$ sahiptir. Böylece, her $Wz$, $W$’nun sütünlarının $m$ tanesinin oluşturduğu uzayının içindeki bir elemanı olacaktır.
Her eniyileme adımından sonra, matris $W$ ve saklı değişken $z$, $W$’nun sütünlarının $L_2$ normları toplamı ile normalize edilir. Bu işlemi yaparak, $W$ ve $z$’nin sıfıra veya sonsuza ulaşmamasını garantilemiş oluruz.
FISTA

Şekil 2: FISTA hesaplamalı çizgesi
FISTA (fast ISTA, Hızlı ISTA) seyrek kodlama enerji fonksiyonu $E(y,z)$’i $z$’ye göre eniyilemek için $\Vert y - Wz\Vert^2$ ve $\lambda \Vert z\Vert_{L^1}$ terimlerini dönüşümlü olarak eniyileyen bir algortimadır. $Z(0)$’a ilk değerini verir ve $Z$’yi aşağıdaki kurala göre güncelleriz:
\[z(t + 1) = \text{Shrinkage}_\frac{\lambda}{L}(z(t) - \frac{1}{L}W_d^\top(W_dZ(t) - y))\]$Z(t) - \frac{1}{L}W_d^\top(W_dZ(t) - Y)$ terimi, $\Vert y - Wz\Vert^2$ terimi için bir gradyan adımıdır. $\text{Shrinkage}$ fonksiyonu değerleri sıfıra doğru iterek $\lambda \Vert z\Vert_{L_1}$ terimini eniyilemiş olur.
LISTA
FISTA’yı büyük boyutlu veri kümelerine (örn. resimler) uygulamak oldukça maliyetlidir. FISTA algoritmasını daha da verimlileştirmek için en iyi saklı değişken $z$’yı öngörmek için bir ağ eğitmektir:
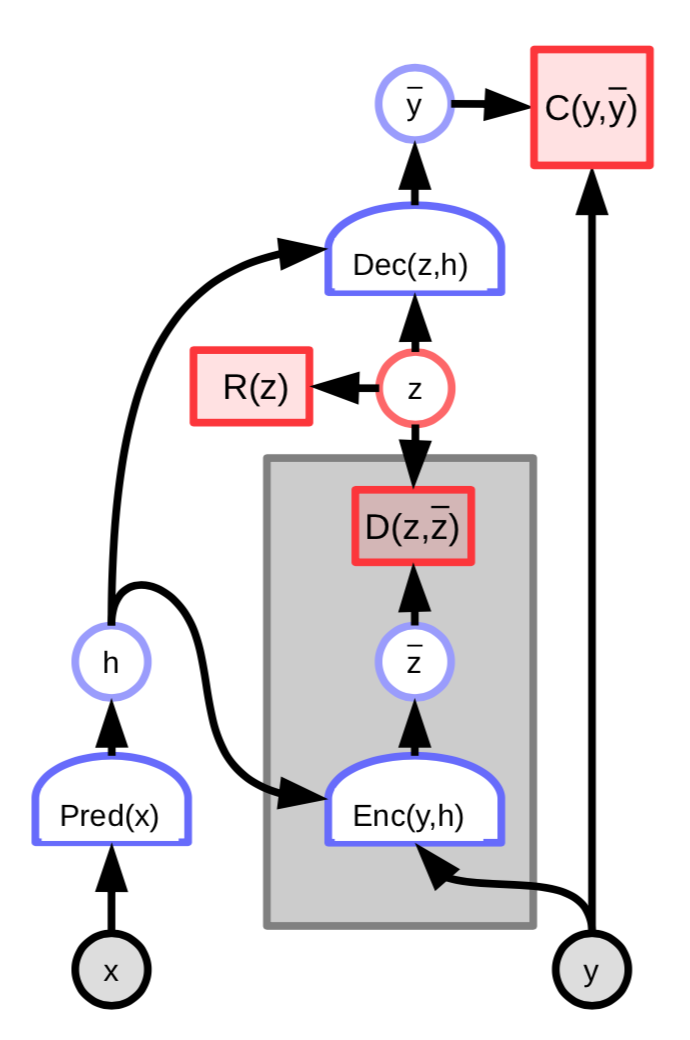
Şekil 3: Saklı değişken kodlayıcılı EBM modeli
Bu yapının enerji fonksiyonu, öngörülen gizli değişken $\ overline z $ ile optimal gizli değişken $z$ arasındakı farkı ölçen ek bir terim içerir:
\[C(y, \text{Dec}(z,h)) + D(z, \text{Enc}(y, h)) + \lambda R(z)\]Daha fazla tanımlamak gerekirse,
\[W_e = \frac{1}{L}W_d\] \[S = I - \frac{1}{L}W_d^\top W_d\]ve sonra aşağıdaki gibi yazabiliriz:
\[z(t+1) = \text{Shrinkage}_{\frac{\lambda}{L}}[W_e^\top y - Sz(t)]\]Yukarıdaki kuralı yinelemeli sinir ağı gibi yorumlamak, yani saklı değişken $z$’yi sürekli tahmin edebilmemizi sağlayan parametreleri $W_e$ öğrenmek mümkündür. Ağ, sabit sayıda $K$ adımı kadar çalıştırılır ve $W_e$’nin gradyanları zamanla geri yayılım yöntemiyle hesaplanır. Eğitilmiş ağ, FISTA algoritmasından daha kısa adımda iyi $z$’ler üretir.
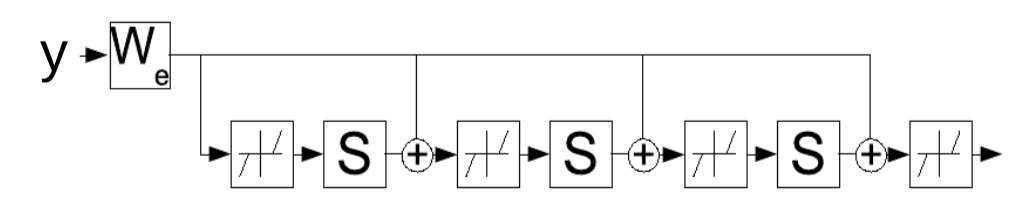
Şekil 4: Zamanla açılmış bir yinelemeli ağ olarak LISTA
Seyrek Kodlama Örnekleri
256 boyutlu bir saklı değişkene sahip seyrek kodlama sistemi MNIST veri setinde kullanıldığında, sistem eğitim kümesinin neredeyse tamamını doğrusal bir şekilde birleştirerek oluşturabilmemizi sağlayan 256 kalem vuruşunu öğrenir. Seyrek düzenleştirici ise yeni örnekleri oluştururken olabildiğince az kalem vuruşu kullanmaya zorlar.

Şekil 5: MNIST'te Seyrek Kodlama. Her bir resim W'nin öğrenilmiş sütunudur.
Seyrek kodlama sistemi, doğal görüntü yamalarında eğititldiğinde, öğrenilen öznitelikler yönlendirilmiş kenarlara sahip gabor filtreleridir. Bu öznitelikler, hayvan görme sistemlerinin ilk kısımlarında öğrenilen öznitelikleri andırmaktadır.
Evrişimsel Seyrek Kodlama (Convolutional Sparse Coding)
Diyelim ki bir resmimiz ve resmin öznitelik haritası ($z_1, z_2, \cdots, z_n$) olsun. Ardından, her bir öznitelik haritasını çekirdek $K_i$ ile evrişimleyebiliriz ($*$). Yeniden oluşturum (reconstruction) hesabı aşağıdaki gibidir:
\[Y=\sum_{i}K_i*Z_i\]Burada yeniden oluşturum, bildiğimiz seyrek kodlamadakinden, $Y=\sum_{i}W_iZ_i$, farklıdır. Seyrek kodlamada, sütünlar ve $Z_i$’nin katsayıları ile ağırlıklı toplam kullanılarak yeniden oluşturum gerçekleştirilir. Evrişimsel seyrek kodlamada, hala doğrusal bir işlem yapmaktayız, ancak sözlük (dictionary) matrisi artık öznitelik haritalarıyla ifade edilir ve her bir öznitelik haritasını tüm çekirdeklerler ile evriştirip sonuçları toplayarak yeniden oluşturum gerçekleştirilir.
Doğal Görüntülerde Evrişimsel Seyrek Özkodyalıcı

Şekil 6 Elde edlien Filtreler ve Temel Fonksiyonlar. Doğrusal Evrişimsel Kodçözücü
Kodlayıcı (encoder) ve kodçözücüdeki (decoder) filtreler görünüş itibariyle birbirlerine benzerdir. Kodlayıcı, sırasıyla evrişim üzerine doğrusal olmayan bir işlem ve bu işlemi takip eden ölçeği manipüle eden diyagonal katmandan ibarettir. Sonra, kodun kısıtlamasında seyreklik bulunmaktadır. Kodçözücü ise evrişimsel ve doğrusal bir kodçözücüdür. Geridönüştürüm kare hatasıyla gerçekleştirirlir.
Yani, sadece bir tane filtre olduğunu dayatırsak o zaman bu filtre merkezi bir filtredir. İki filtre ile değişik şekillerde filtreler elde edebiliriz. Dört filtreyle yatay ve dikey kenarlar elde edebiliriz; her filtre için 2 kutba sahip oluruz. Sekiz filtreyle sekiz farklı yönde yönlendirilmiş filtreler elde edebiliriz. On altı tane ile, merkeze doğru daha fazla yön elde ederiz. Filtre sayısını arttırdıkça, kenar dedektörlerine ek olarak daha değişik filtreler ve değişik yönlerde dedektörler elde edebiliriz.
Bu olay ilginç gözükebilir çünkü yukarıdaki filtreler ile görsel kortekste gözlemlediklerimiz aslında oldukça benzerdir. Bu da, iyi öznitelikleri tamamiyle denetimsiz bir şekilde öğrenebileceğimizin bir göstergesidir.
Eğer bu öznitelikleri evrişimsel bir ağda kullanıp bir görev için eğitirsek, baştan eğittiğimiz bir ağın performansına sahip olamayacağız. Ancak, bu öznitelikler bazı durumlarda performansı iyileştirebilir. Örneğin, elimizdeki verinin sayısı yeterli değilse veya çok az sayıda kategori varsa, denetimli öğrenme ile, işe yaramayan öznitelikler elde edebiliriz.

Şekil 7 Renkli resimde Evrişimsel Seyrek Kodlama
Yukardaki şekil, renkli görüntülerde bir başka örnektir. Kodçözücü çekirdeğin (sağ tarafta) boyutu 9’a 9’dur. Bu çekirdek tüm resme evrişimsel bir biçimde uygulanır. Soldaki resim, kodçözücüdeki seyrek kodları göstermektedir. $Z$ vektöründe bileşenlerin çok azı beyaz veya siyahtır ki bu da vektörün oldukça seyrek olduğunu göstermektedir.
Değişimsel Otokodlayıcılar
Değişimsel Otokodlayıcılar, seyreklik haricinde düzenlileştirilmiş saklı değişken enerji bazlı modelleri ile benzer bir mimariye sahiptir. Fakat bilgi, koda gürültü ekleyerek sınırlandırılır.
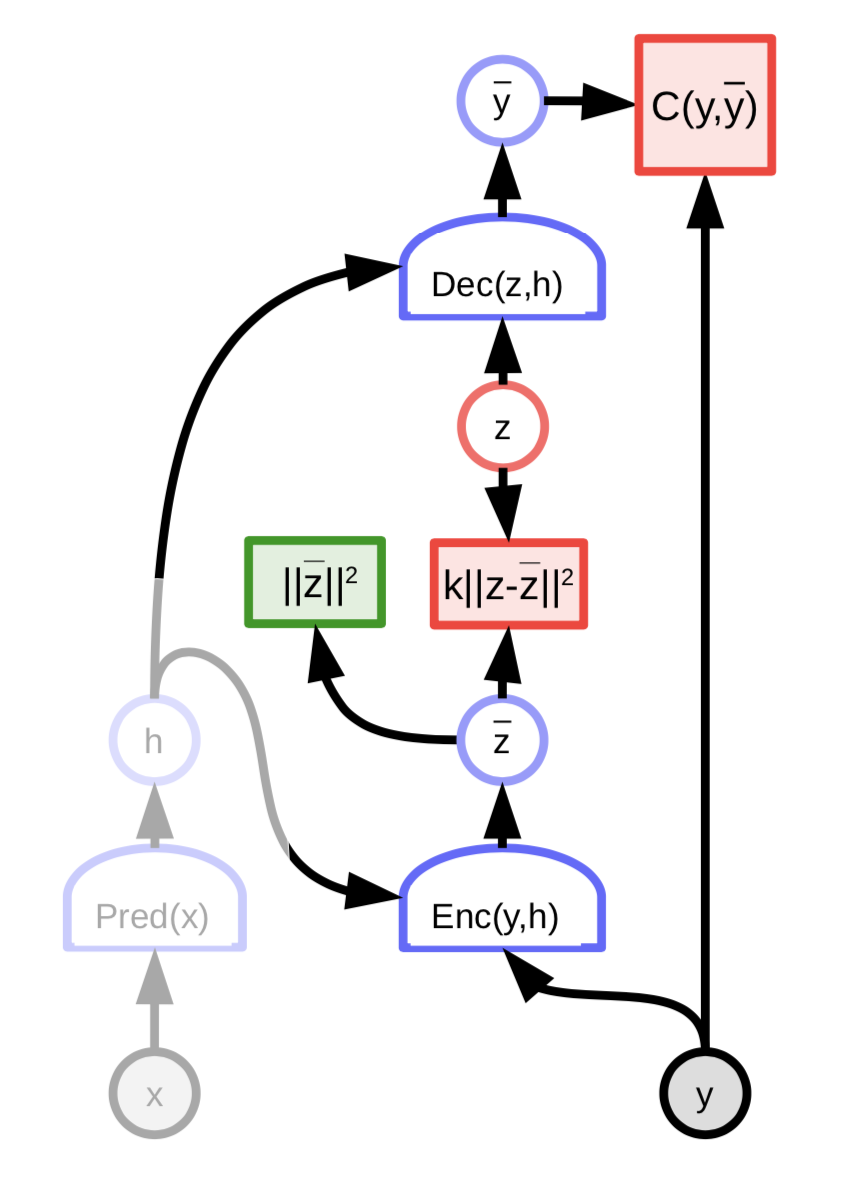
Şekil 8: Değişimsel Otokodlayıcı Mimarisi
Saklı değişken $z$, enerji fonksiyonunu $z$’ye göre minimize ederek hesaplanmaz. Burada enerji fonksiyonunu, logaritmasını aldığımızda bize ${\overline z}$’ye bağlanma bedelini veren bir dağılımdan saklı değişken $z$’nin rastgele örneklenmesi olarak düşünebiliriz. Burada dağılım, ortalaması ${\overline z}$ olan bir Gaussian dağılımıdır ve ${\overline z}$’nin üzerine Gaussian gürültüsü eklemiş oluruz.
Üzerine Gaussian gürültüsü eklenmiş kod vektörlerini Şekil 9(a)’da görebilirsiniz.
|
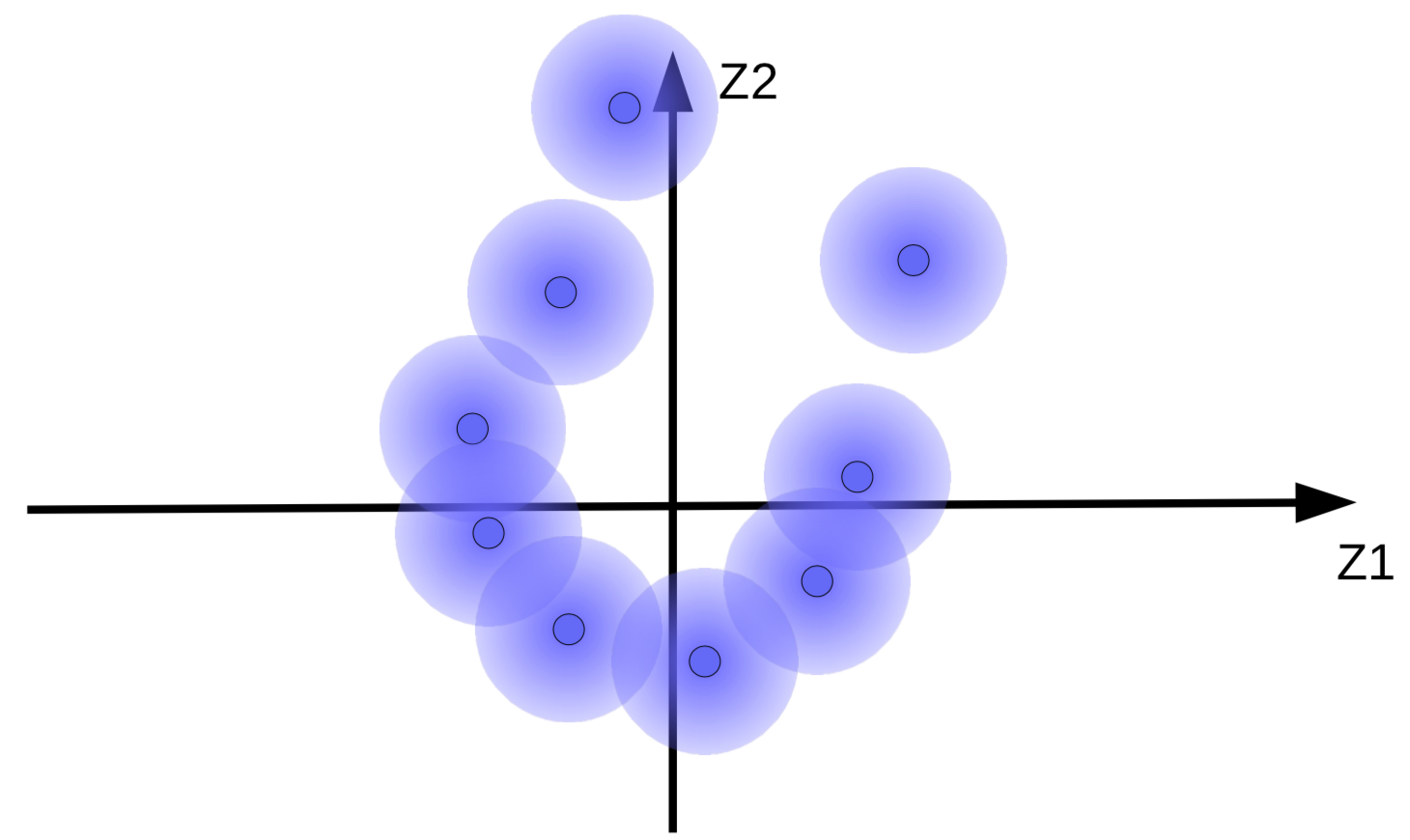
(a) Bulanık toplar kümesi
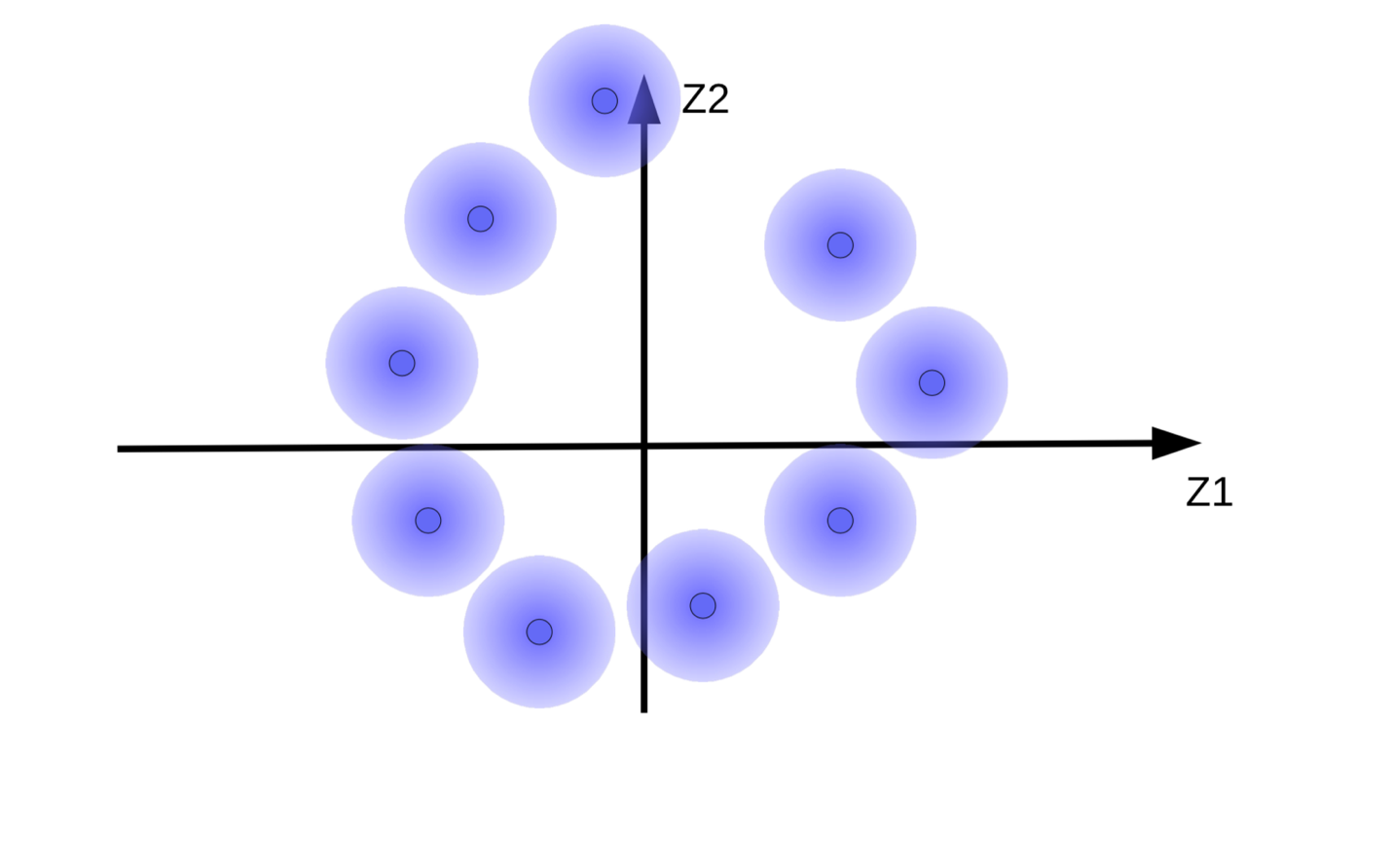
(b) Topların düzenlileştirme olmadan enerji minimizasyonu sebebiyle hareketi
Sistem, $z$’nin (gürültü) etkisini olabildiğince azaltmak için kod vektörleri ${\overline z}$’yi mümkün olduğunca büyütmeye çalışır. Bu durumu da, Şekil 9(b)’de görüldüğü gibi orjinden uzaklaşan bulanık toplar (fuzzy balls) ile anlayabiliriz. Sistemin kod vektörlerini olabildiğince büyütmek istemesinin bir diğer sebebi de bulanık topların çakışmasını engellemek, yani çözümleyicinin farklı örneklerin yeniden oluşturumu sırasında oluşabilecek karmaşayı engellemektir.
Fakat, eğer varsa, bulanık topların veri manifoldu etrafında toplanmasını isteriz. Bu yüzden, sistemin kod vektörlerini bir ortalamaya ve sıfıra yakın bir varyansları olmasına zorlamalıdır. Bu zorlamayı gerçekleştirmek için, Şekil 10’daki gibi topları, yani kod vektörlerini, orjine bir yayla bağladığımızı düşünelim.
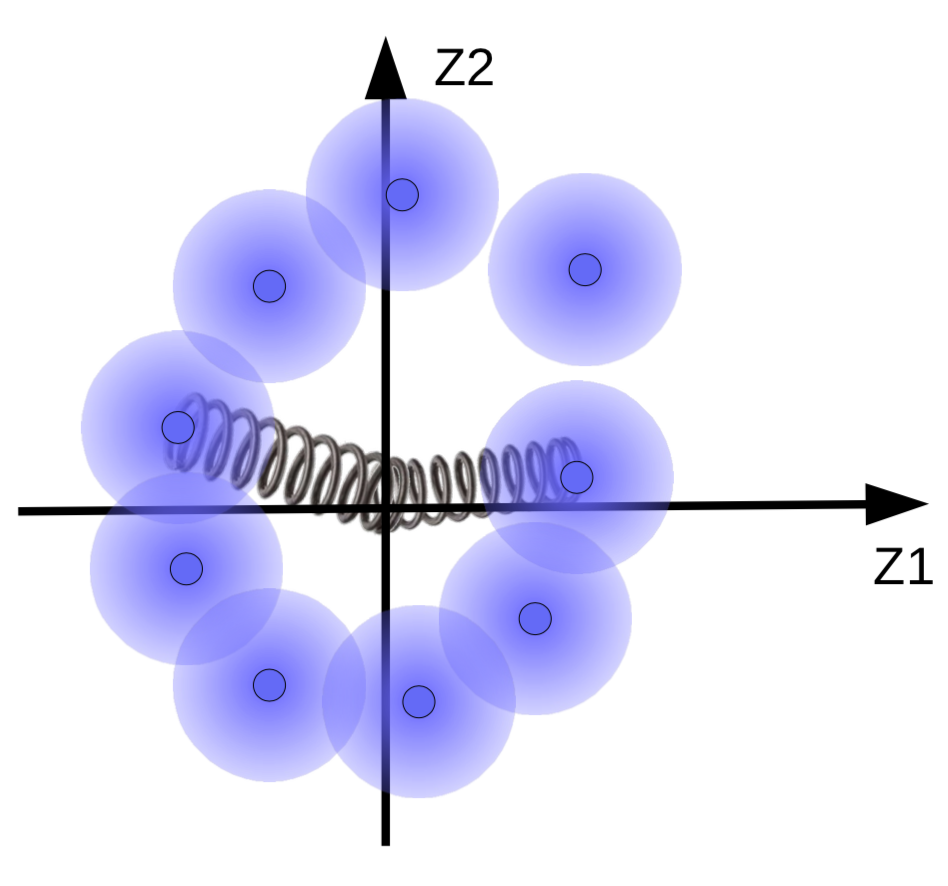
Şekil 10: Yaylarla görselleştirilen düzenlileştirmenin etkileri
Yayın gücü, bulanık topların orijine ne kadar yakın olduğunu belirler. Eğer yay çok zayıf ise, toplar orjinden uzaklaşacaktır. Eğer çok güçlüyse, toplar orjinde kümelenecektir ki bu da yüksek enerjiye sebep verecektir. Bu durumu engellemek için, sistem kürelerin örneklerinin benzer olması şartıyla üst üste gelmesine izim verecektir.
Topların boyutlarını da kontrol edebilmek mümkündür. Bu kontrol, varyansı 1’e yaklaştırmaya çalışarak topu ne çok büyütüp ne de çok küçülten KL Iraksaması (KL Divergence) ile yapılır.
📝 Henry Steinitz, Rutvi Malaviya, Aathira Manoj
emirceyani
23 Mar 2020