Otokodlayıcılara giriş

Otokodlayıcıların uygulamaları

Resim üretimi

Fig. 1’deki resimlerden hangisinin sahte olduğunu söyleyebilir misiniz? Aslında, ikisi de StyleGan2 üreticisi tarafından oluşturuldu. Yüz detayları çok gerçekçi olsa da, arkaplan garip görünüyor (sol: bulanık, sağ: şekilsiz objeler). Bunun sebebi sinir ağının yüz örnekleri üzerinde eğitilmiş olması. Arkaplanın değişkenliği çok daha yüksek. Burada data manifoldunun boyutu yaklaşık 50, yüz resminin serbestlik derecesine eşit.

Fig. 1: StyleGan2 tarafından üretilen yüzler

Piksel Uzayı ve Gizli Uzayda Ara Değer Bulmanın Farkı

Fig. 2: Bir köpek ve bir kuş

Eğer köpek ve kuş resimleri (Fig. 2) arasındaki ara değeri lineer bir şekilde piksel uzayında bulursak, Fig. 3’teki iki resmin üst üste binmiş görüntüsünü elde ederiz. Sol üstten sağ alta, köpek resminin ağırlığı azalırken kuş resminin ağırlığı artıyor.

Fig. 3: Ara değer bulmanın sonuçları

Eğer iki saklı uzay gösteriminin ara değerini bulup bunu kodçözücüye verirsek, Fig. 4’teki köpekten kediye dönüşümü elde ederiz.

Fig. 4: Kodçözücüden gelen sonuçlar

Açık bir şekilde saklı uzay resmin yapısını anlamakta daha iyi.

Dönüşüm Örnekleri

Fig. 5: Yakınlaştırma

Fig. 6: Kaydırma

Fig. 7: Parlaklık

Fig. 8: Döndürme (Dönmenin 3 boyutlu olabileceğini unutmayın)

Görüntü Süper-çözünürlüğü

Bu modelin amacı görüntüyü geliştirip orijinal yüzleri yeniden oluşturmak. Fig. 9’da soldan sağa, ilk sütun 16x16’lık girdi görüntüsü, ikincisi standart bikübik ara değer bulmadan elde ettiğimiz, üçüncüsü sinir ağı tarafından oluşturulan sonuç, en sağdaki ise orijinal resim. (https://github.com/david-gpu/srez)

Fig. 9: Orijinal yüzlerin yeniden oluşturulması

Çıktı resimlerinden eğitim verisinde önyargı olduğu çok açık, bu da yeniden oluşturulan yüzlerin hatalı olmasına sebep oluyor. Örneğin, sol üstteki Asyalı adam, dengesiz eğitim görüntülerinden dolayı çıktıda Avrupalı gibi görünüyor. Sol alttaki kadının yeniden oluşturulmuş yüzü eğitim resimlerindeki o açıdaki örnek eksikliğinden dolayı garip gözüküyor.

Görüntü Renklendirme

Fig. 10: Yüzlere gri parça konulması

Fig. 10’daki gibi yüzün üzerine gri bir parça koymak resmi eğitim manifoldundan uzaklaştırır. Fig. 11’deki gibi yüzü yeniden oluşturmak, Enerji fonksiyonunu minimize ederek en yakın örnek resmi bularak yapılıyor.

Fig. 11: Fig. 10'un yeniden oluşturulmuş görüntüsü

Açıklamadan Görüntü Oluşturmak

Fig. 12: Açıklamadan görüntü oluşturma örneği

Fig. 12’deki gibi yazılı açıklamadan görüntüyü metnin özelliklerinden önemli görsel bilgileri çıkarıp onları görüntüye çevirerek yapılıyor.

Otokodlayıcılar nedir?

Otokodlayıcılar, denetimsiz bir şekilde eğitilen, önce verimizin kodlanmış gösterimini öğrenip daha sonra bu kodlanmış gösterimden girdi verisini mümkün olan en yakın şekilde üreten yapay sinir ağlarıdır. Bu yüzden, otokodlayıcının çıktısı, girdi için bir tahmindir.

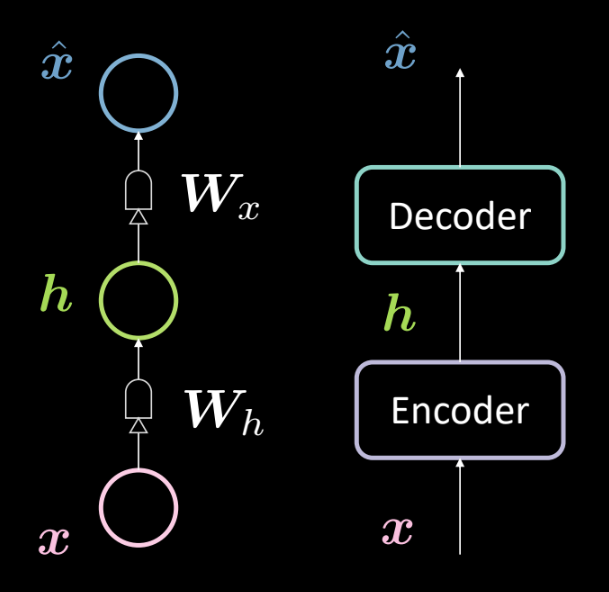
Fig. 13: Basit bir otokodlayıcının mimarisi

Fig. 13 basit bir otokodlayıcının mimarisini gösteriyor. Daha önce olduğu gibi, aşağıdan girdi $\boldsymbol{x}$ ile başlayıp, daha sonra onu otokodlayıcıya ($\boldsymbol{W_h}$ ve arkasından gelen sıkıştırma ile tanımlanan bir afin dönüşümü) veriyoruz. Bu işlemin sonucu ara gizli katman $\boldsymbol{h}$. Bu da daha sonra kodçözücüye ($\boldsymbol{W_x}$ ve arkasından gelen sıkıştırmayla tanımlanan başka bir afin dönüşümü) girdi olarak veriliyor. Buradan çıkan ise modelimizin girdisinin tahmini/yeniden üretimi olan $\boldsymbol{\hat{x}}$. Daha önce yaptığımıza benzer olarak, buna 3 katmanlı bir sinir ağı diyoruz.

Yukarıdaki ağı bu denklemlerle matematiksel olarak gösterebiliriz:

Ayrıca aşağıdaki boyutları belirtiyoruz:

Not: PCA gösteriminde, ağırlıklarımızın tanımı $\boldsymbol{W_x}\ \dot{=}\ \boldsymbol{W_h}^\top$ olabilir.

Neden otokodlayıcıları kullanıyoruz?

Bu noktada girdiyi tahmin etmenin amacını ve otokodlayıcıların uygulamalarını merak ediyor olabilirsiniz.

Otokodlayıcıların ana kullanım alanları aykırılık tespiti ve resim arıtma. Otokodlayıcının görevinin veriyi manifoldun (verdiğimiz veri manifoldu) üzerinde yeniden oluşturmak olduğunu biliyoruz. Otokodlayıcımızın sadece manifold üzerindeki girdileri üretebilmesini istiyoruz. Bu yüzden modeli eğitim sırasında gördüklerini üretecek şekilde sınırlandırıyoruz, böylece yeni girdilerde bulunan farklılıklar silinecek çünkü model böyle değişikliklere karşı duyarsız.

Otokodlayıcıların başka bir uygulaması da görüntü sıkıştırma. Eğer ara katman boyutumuz $d$ girdi boyutumuz $n$’den daha küçükse, kodlayıcı sıkıştırıcı olarak kullanılır ve saklı (kodlanmış) gösterim girdinin büyün (veya çoğu) özelliğini tutarken daha az yer kaplayacak.

Yeniden oluşturma kaybı

Şimdi de genelde kullanılan yeniden oluşturma kayıp fonksiyonlarına bakalım. Veri kümesinin tamamının kaybı örnek başına kaybın ortalamasına eşit. Yani

Girdimiz kategorilendirildiyse, Çapraz Entropi kaybını kullanarak örnek başına kaybı şu şekilde hesaplayabiliriz:

Ve girdi reel bir değer olduğunda, Ortalama Karesel Hata Kaybını kullanabiliriz:

Az ve çok doldurulmuş saklı katman

Saklı katmanın boyutu $d$ girdinin boyunu $n$’den küçük olduğu zaman, buna az doldurulmuş saklı katman diyoruz. Benzer şekilde, $d>n$ olduğunda, çok doldurulmuş saklı katman diyoruz. Fig. 14 solda az doldurulmuş, sağda da çok doldurulmuş bir saklı katman gösteriyor.

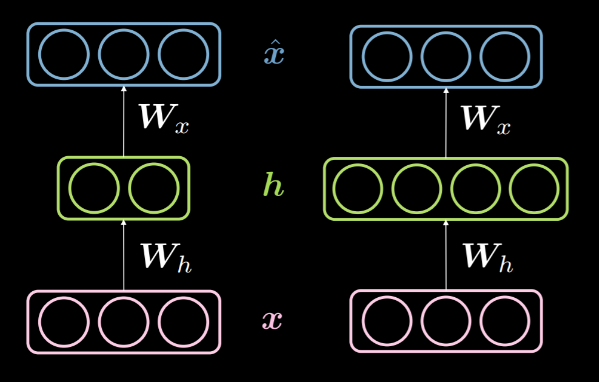
Fig. 14: Az doldurulmuş ve çok doldurulmuş saklı katmanlar

Yukarıda tartıştığımız gibi, az doldurulmuş bir saklı katman sıkıştırma için kullanılabilir, çünkü girdideki bilgiyi daha az boyuta kodluyoruz. Diğer tarafta, çok doldurulmuş bir katmanda girdiden daha çok boyutlu bir kodlama yapıyoruz. Bu da optimizasyonu kolaylaştırıyor.

Girdiyi yeniden oluşturduğumuz için, model girdi özelliklerinin hepsini saklı katmana kopyalayıp bunları çıktıya taşıyarak birim fonksiyon olarak çalışmaya yatkın. Bu modelimizin herhangi bir şeyi öğrenmesini engelleyeceği için bundan kaçınılmalı. Bu yüzden bir bilgi darboğazı kullanarak bazı ekstra kısıtlamalar getirmeliyiz. Bunu saklı katmanı sadece eğitim sırasında görülen değerlerle kısıtlayarak yapıyoruz. Bu seçici yeniden oluşturmayı (girdi uzayının bir alt kümesiyle sınırlı) sağlayıp modeli manifoldun üzerinde olmayan her şeye karşı duyarsız yapıyor.

Az doldurulmuş bir katmanın girdiyi kopyalayacak yeterince boyutu olmadığı için birim fonksiyon olarak davranamayacağına dikkat etmeliyiz. Bundan dolayı az doldurulmuş bir saklı katmanın aşırı öğrenmesi çok doldurulmuş bir saklı katmana göre daha az muhtemel, ancak yine de mümkün. Örneğin güçlü bir kodlayıcı ve kodçözücü verildiğinde, model her veri noktasına bir sayıyla eşleştirip fonksiyonu öğrenebilir. Aşırı öğrenmeyi engellemek için düzenlileştirme, mimari yöntemler, vb. kullanabiliriz.

Arıtan otokodlayıcı

Fig. 15 bir arıtan otokodlayıcının manifoldunu gösterip nasıl çalıştığı hakkında bir sezgi sahibi olmamızı sağlıyor.

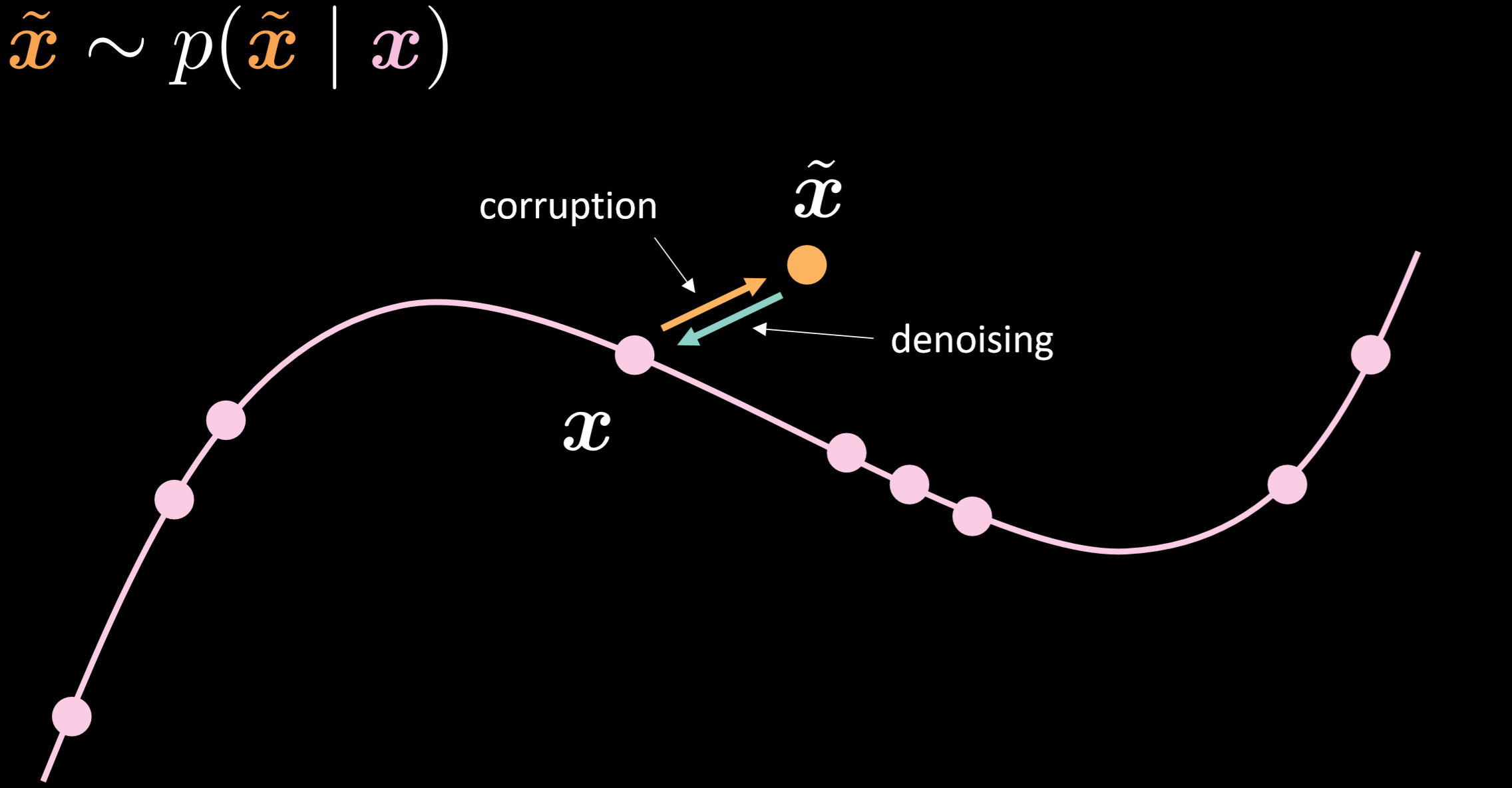
Fig. 15: Arıtan otokodlayıcı

Bu modelde, gerçekte göreceğimiz gürültülü dağılımı verdiğimizi varsayıyoruz, böylece ondan nasıl güçlü bir şekilde düzelteceğimizi öğrenebiliriz. Girdi ve çıktıyı karşılaştırarak manifoldun üzerindeki noktaların hareket etmediğini, manifolddan uzakta olan noktalarınsa çok hareket ettiğini söyleyebiliriz.

Fig. 16 girdi ve çıktı verisi arasındaki ilişkiyi gösteriyor.

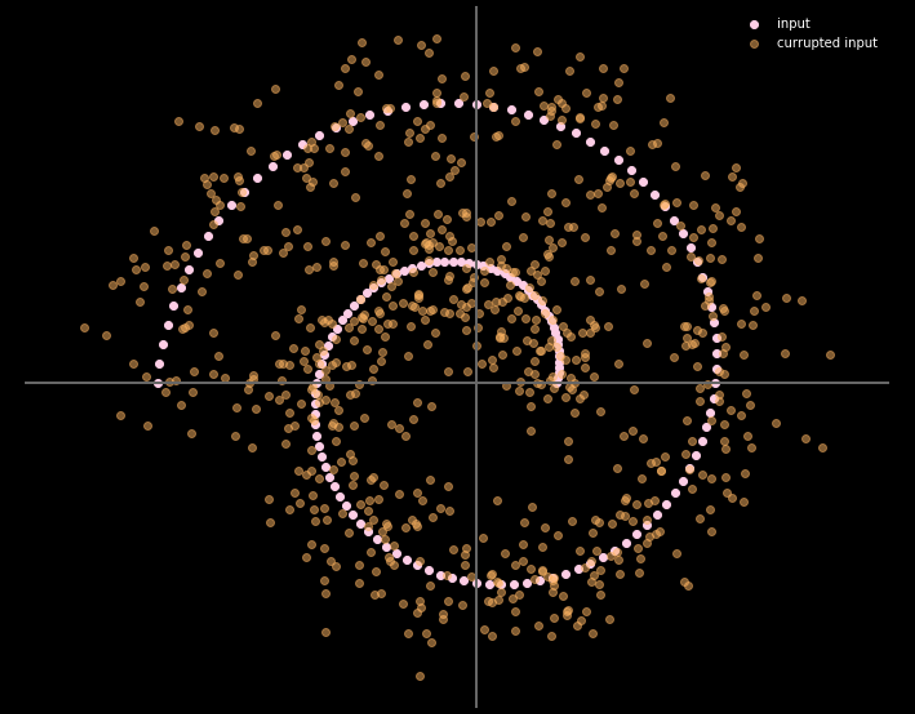
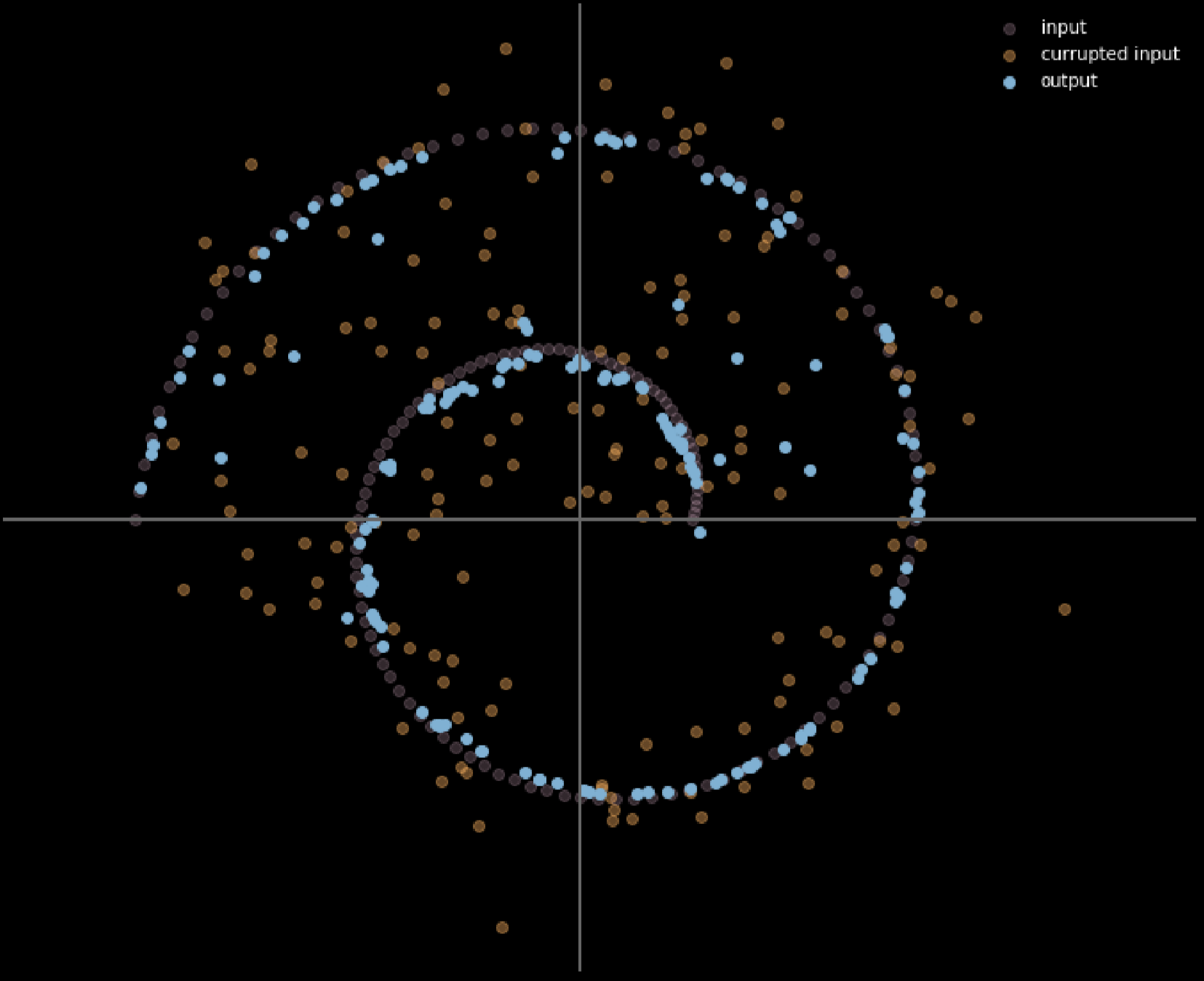
Fig. 16: Arıtan otokodlayıcının girdi ve çıktısı

Fig. 17’de olduğu gibi her girdinin hareketinin mesafesini göstermek için farklı renkler kullanabiliriz.

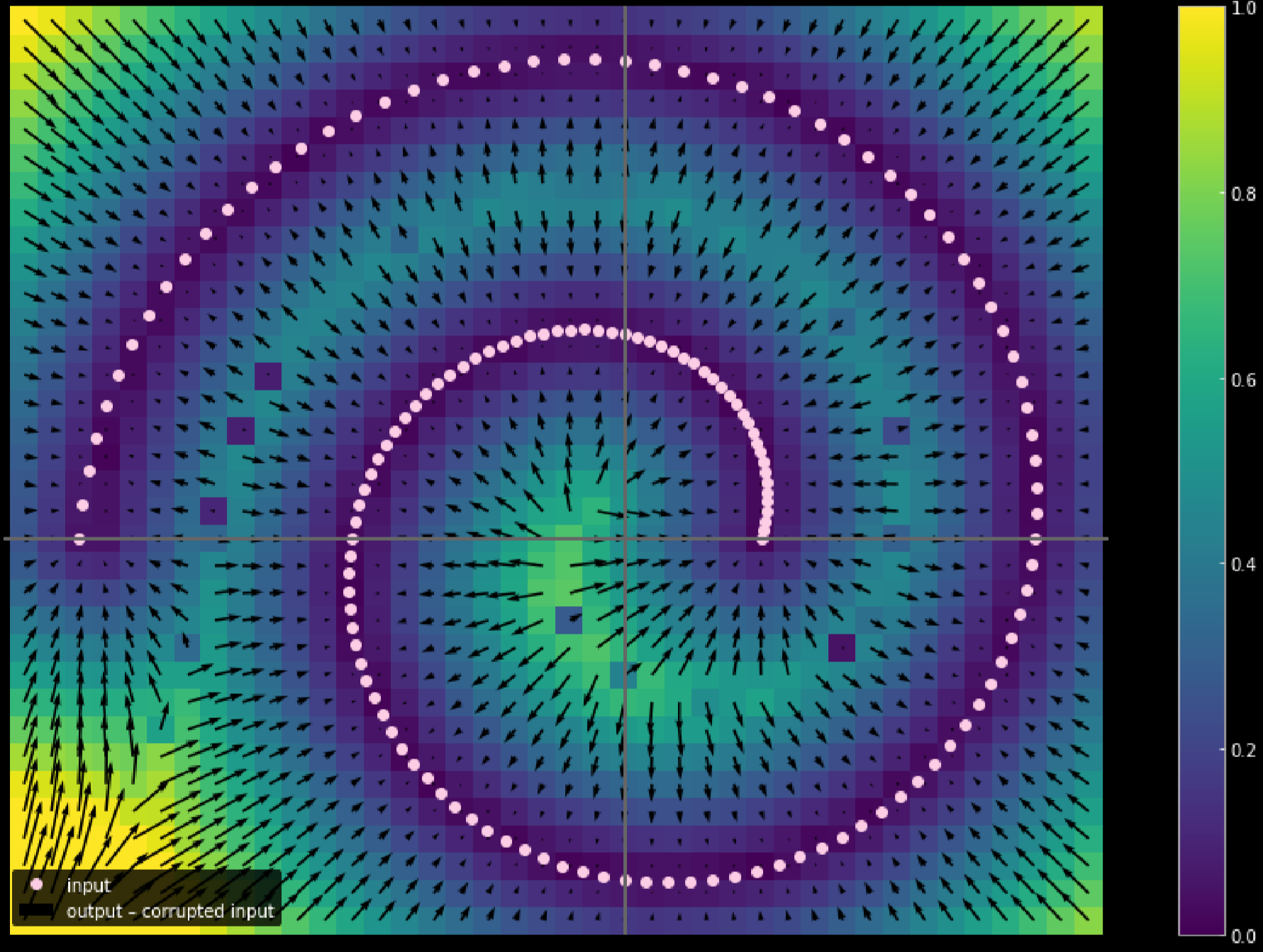
Fig. 17: Girdi verisinin hareket mesafesinin ölçülmesi

Renk açıldıkça, noktanın hareket mesafesi uzuyor. Şekilden köşelerdeki noktalarin 1 birime yakın hareket ettiğini, iki kol arasındaki noktalarınsa eğitim sırasında üst ve alt kollar tarafından çekildiği için hareket etmediğini söyleyebiliriz.

Daraltan otokodlayıcı

Fig. 18 daraltan otokodlayıcının kayıp fonksiyonunu ve manifoldu gösteriyor.

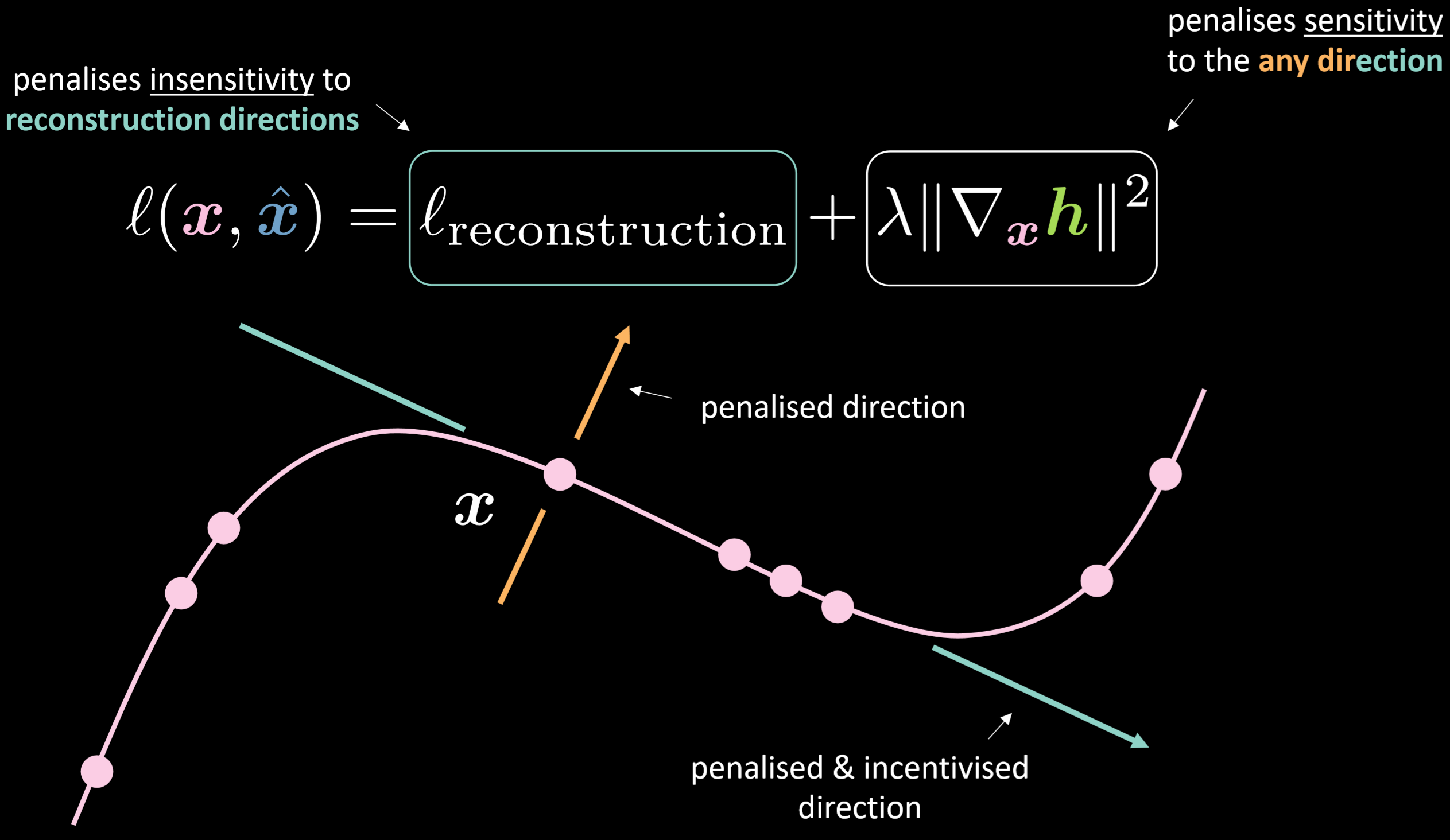
Fig. 18: Daraltan otokodlayıcı

Kayıp fonksiyonu yeniden oluşturma terimi artı saklı gösterimin girdiye göre gradyanının uzunluğunun karesini içeriyor. Bu yüzden genel kayıp girdinin değişkenliğine göre saklı katmanın değişkenliğini minimize edecek. Bunun faydası modelin yeniden oluşturma yönlerine duyarlıyken diğer olası yönlere duyarsız olması.

Fig. 19 otokodlayıcıların genel olarak nasıl çalıştığını gösteriyor.

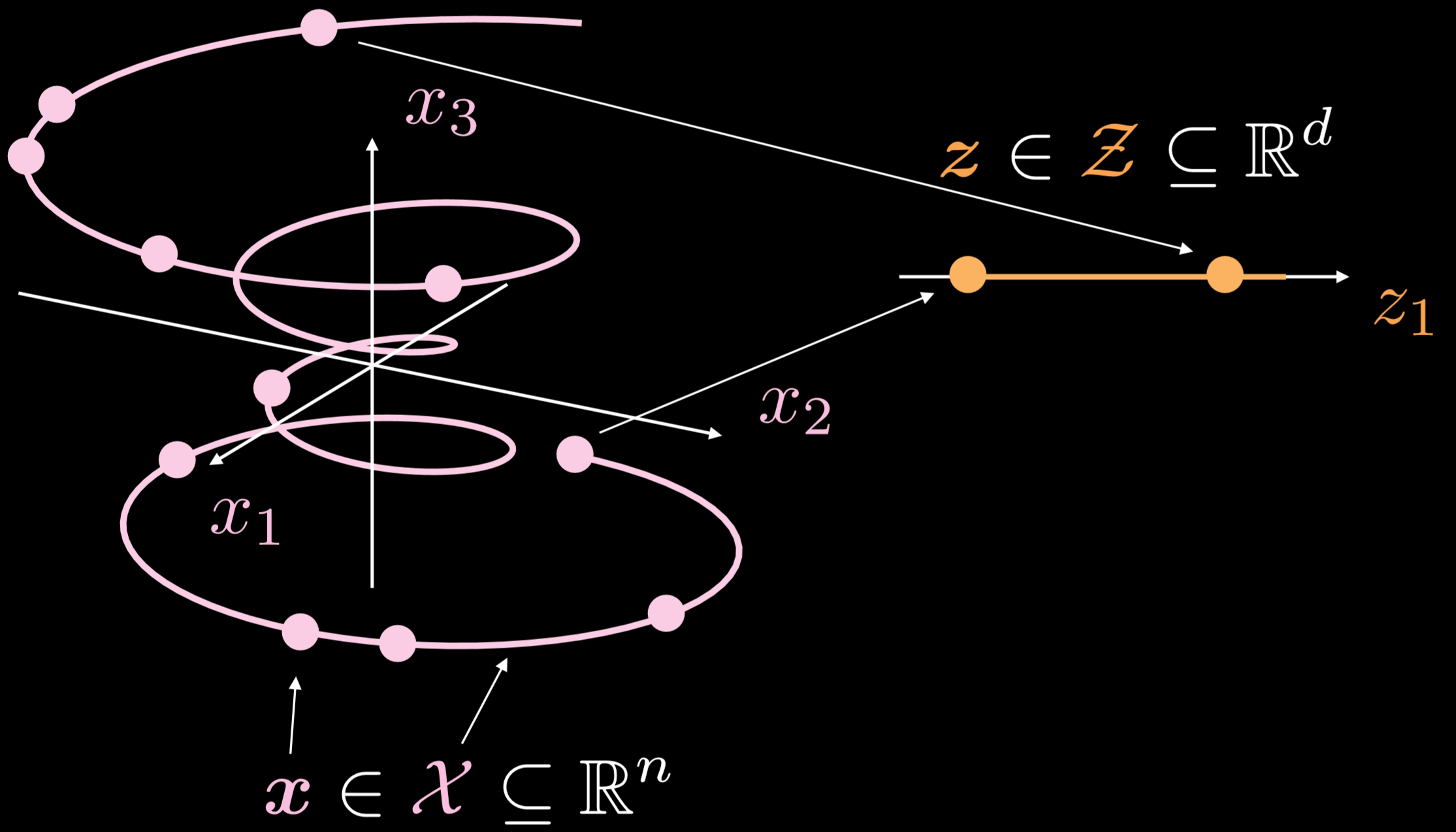
Fig. 19: Basit otokodlayıcı

Eğitim manifoldu üç boyutta ilerleyen tek boyutlu bir obje. $\boldsymbol{x}\in \boldsymbol{X}\subseteq\mathbb{R}^{n}$ ve $\boldsymbol{z}\in \boldsymbol{Z}\subseteq\mathbb{R}^{d}$ iken, otokodlayıcının hedefi kıvrımlı çizgiyi bir yönde uzatmak. Bunun bir sonucu olarak girdi katmanındaki bir nokta saklı katmandaki bir noktaya dönüştürülecek. Şimdi girdi uzayı ve saklı uzaydaki noktalar arasında bağıntımız var, ancak girdi uzayı ve saklı uzay bölgeleri arasında bir bağıntımız yok. Daha sonra, kodçözücüyü saklı saklı katmandaki bir noktadan anlamlı bir çıktı katmanı oluşturması için kullanacağız.

Otokodlayıcının uygulanması - Notebook

Jupyter notebook burada bulunabilir.

Bu çalışmada, standart bir otokodlayıcı ve bir arıtan otokodlayıcıyı yazıp çıktılarını karşılaştıracağız.

Otokodlayıcı model mimarisi ve yeniden oluşturma kaybının tanımlanması

$28 \times 28$’lik resim ve 30 boyutlu saklı katman kullanıyoruz. Dönüşüm süreci $784\to30\to784$ şeklinde. Hiperbolik tanjant fonksiyonunu kodlayıcıya ve kodçözücüye uygulayarak, çıktının görüntü kümesini $(-1, 1)$’e sınırlandırmış oluyoruz. Ortalama Karesel Hata (MSE) bu modelin kayıp fonksiyonu olarak kullanılacak.

class Autoencoder(nn.Module):
    def __init__(self):
        super().__init__()
        self.encoder = nn.Sequential(
            nn.Linear(n, d),
            nn.Tanh(),
        )
        self.decoder = nn.Sequential(
            nn.Linear(d, n),
            nn.Tanh(),
        )

    def forward(self, x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x

model = Autoencoder().to(device)
criterion = nn.MSELoss()

Standart otokodlayıcının eğitimi

PyTorch kullanarak standart otokodlayıcıyı eğitmek için sıradaki 5 fonksiyonu eğitim döngüsüne koymalısınız:

İleri gidiş:

1) Girdiyi resmini output = model(img)‘ı çağırarak modele göndermek.
2) criterion(output, img.data) kullanarak kaybı hesaplamak

Geri gidiş:

3) optimizer.zero_grad() ile gradyanı sıfırlayıp değerin toplanmasını önlemek.
4) loss.backward() kullanarak geri yayılım
5) optimizer.step() kullanarak geri adım

Fig. 20 standart otokodlayıcının çıktısını gösteriyor.

Fig. 20: Standart otokodlayıcının çıktısı

Arıtan otokodlayıcının eğitimi

Arıtan otokodlayıcı için aşağıdaki adımları eklemelisiniz:
1) nn.Dropout() kullanarak rastgele nöronları kapatmak.
2) do(torch.ones(img.shape)) kullanarak gürültü maskesi yaratmak.
3) İyi resimleri ikili maskeler img_bad = (img * noise).to(device) ile çarparak kötü resimler yaratmak.

Fig. 21 arıtan otokodlayıcının çıktısını gösteriyor.

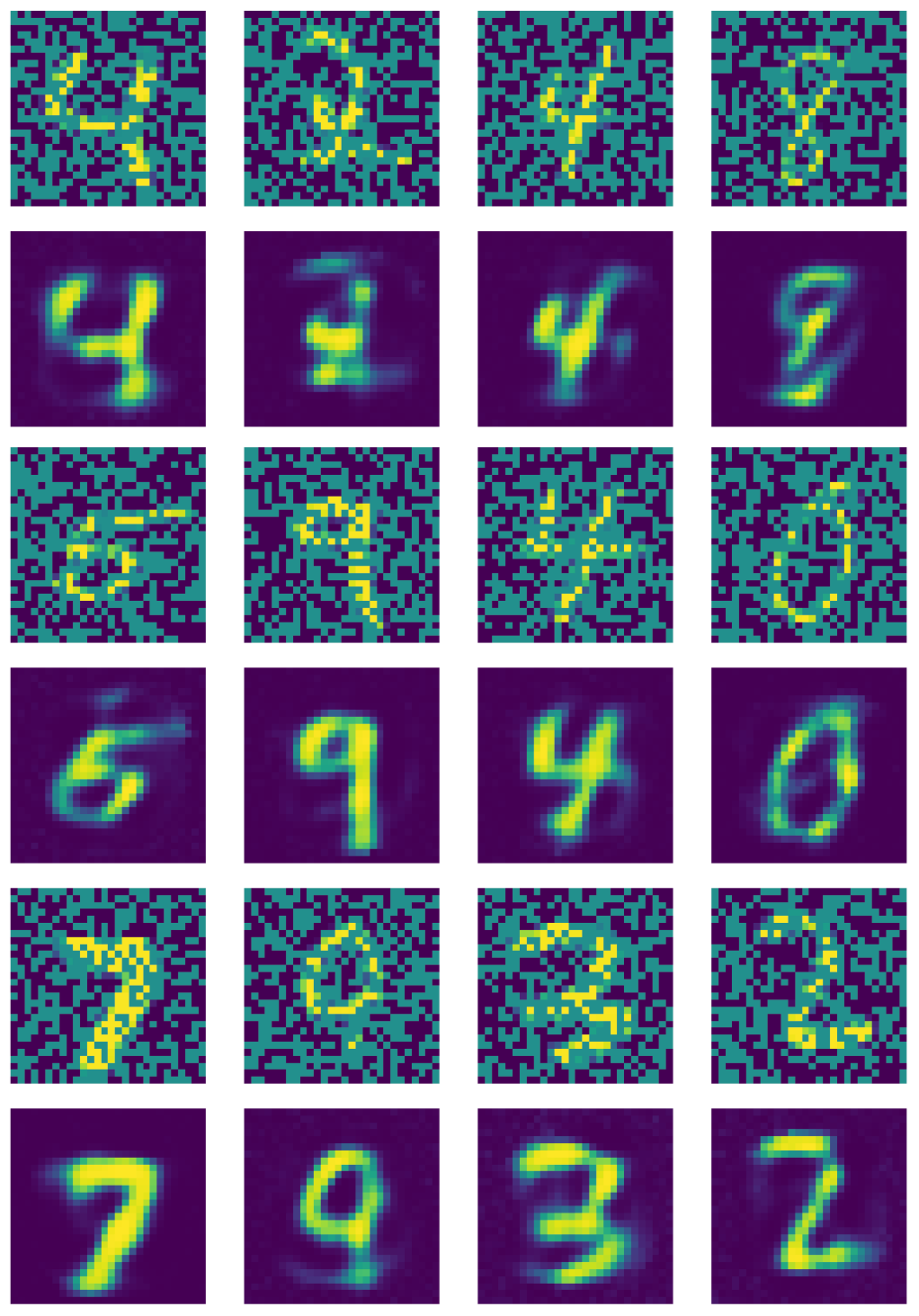
Fig. 21: Arıtan otokodlayıcının çıktısı

Çekirdeklerin karşılaştırılması

Dikkat etmemiz gereken bir şey girdinin boyutunun $28 \times 28 = 784$ ve saklı katmanın boyutunun 500 olmasına rağmen, siyah piksellerin sayısından dolayı model hala çok doldurulmuş bir katmana sahip. Aşağıdaki örnekler az doldurulmuş standart bir otokodlayıcıda kullanılan çekirdeklerin örnekleri. Açık bir şekilde sayıların bulunduğu bölgedeki pikseller bir çeşit örüntünün keşfedildiğini gösterirken, bu bölgenin dışındaki pikseller rastgele. Bu da standart otokodlayıcının sayının bulunduğu bölge dışındaki piksellerle ilgilenmediğini gösteriyor.

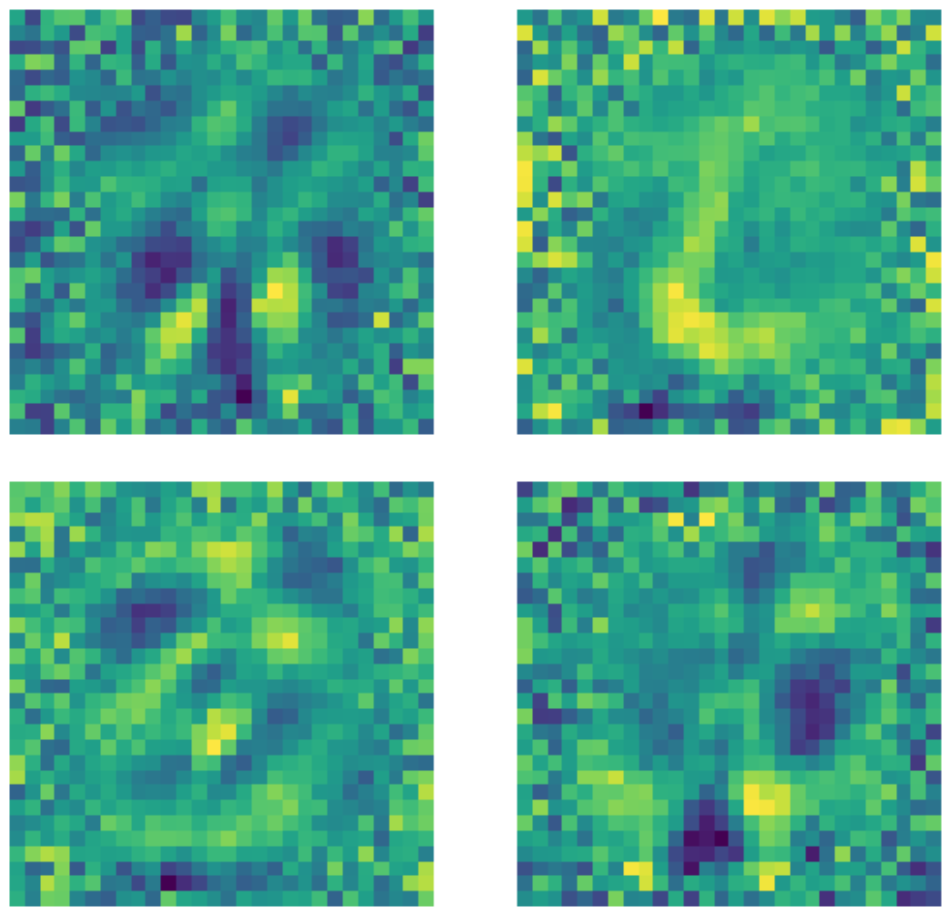
Figure 22: Standart otokodlayıcı çekirdekleri.

Diğer bir tarafta da, aynı veri iletim sönümünün her görüntüye modeli eğitmeden önce uygulandığı arıtan otokodlayıcıya verildiğinde farklı bir şey oluyor. Her çekirdek sayının bulunduğu bölgenin dışındaki pikselleri sabit bir değere eşitliyor. İletim sönümü uygulandığı için model artık sayının bulunduğu bölgenin dışındaki pikselleri de önemsiyor.

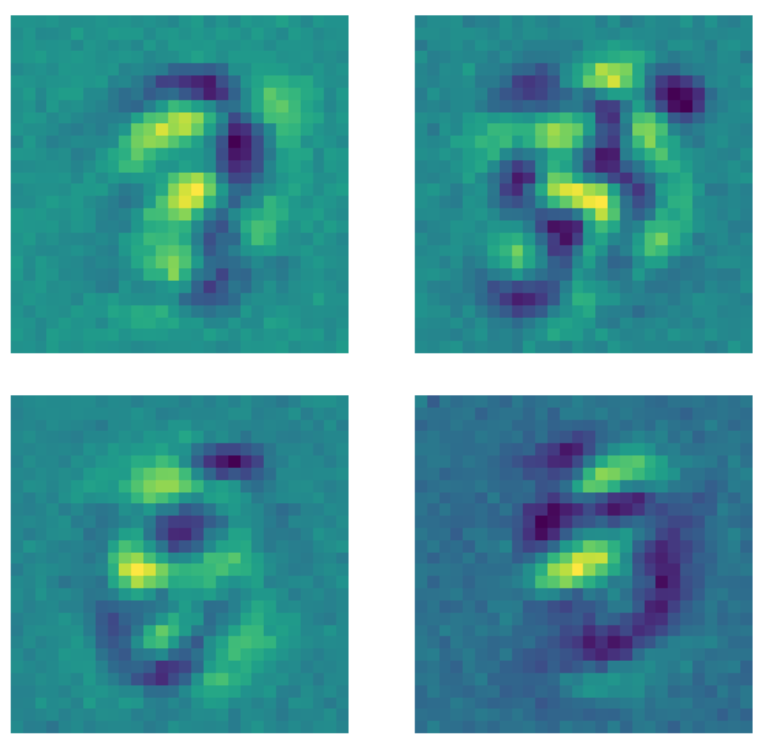
Figure 23: Arıtan otokodlayıcı çekirdekleri.

En gelişmiş yöntemlerle karşılaştırdığımızda aslında bizim otokodlayıcımız daha başarılı!! Sonuçları aşağıda görebilirsiniz.

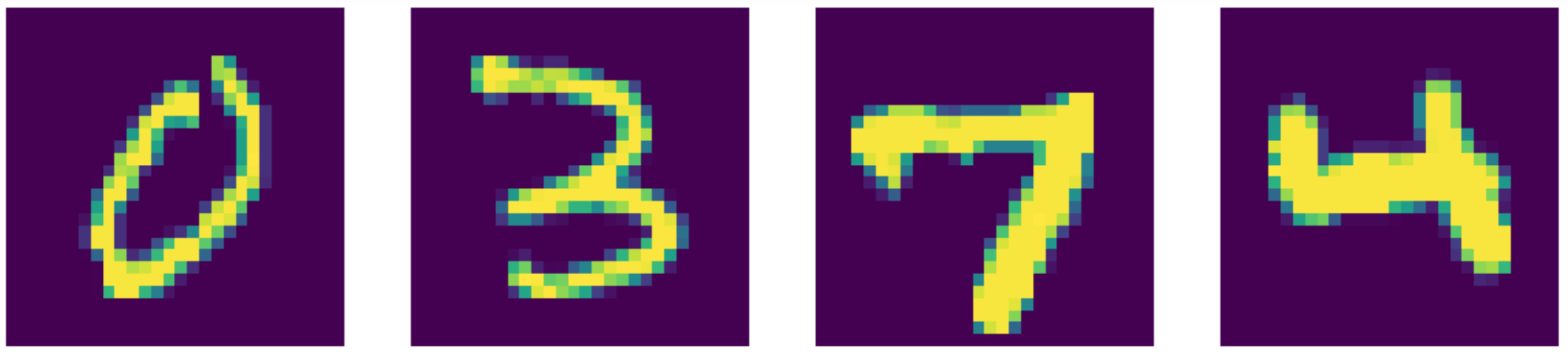
Figure 24: Girdi verisi (MNIST rakamları).

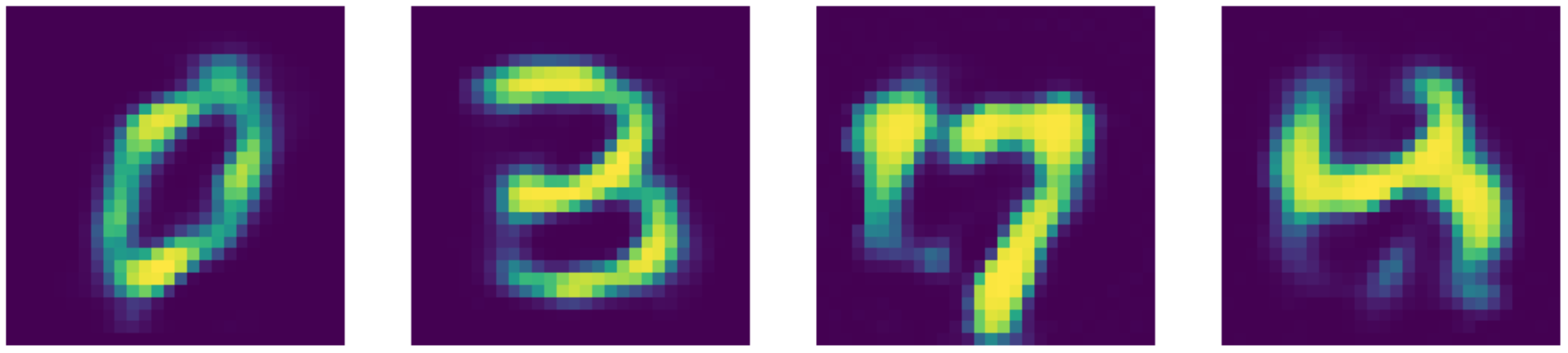
Figure 25: Arıtan otokodlayıcının yeniden oluşturdukları.

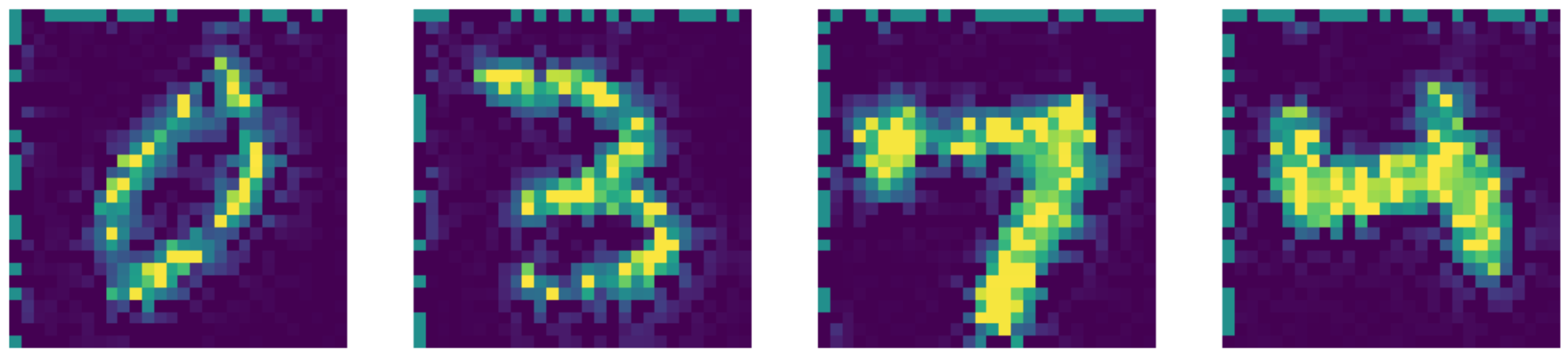
Figure 26: Telea renklendirme çıktısı.

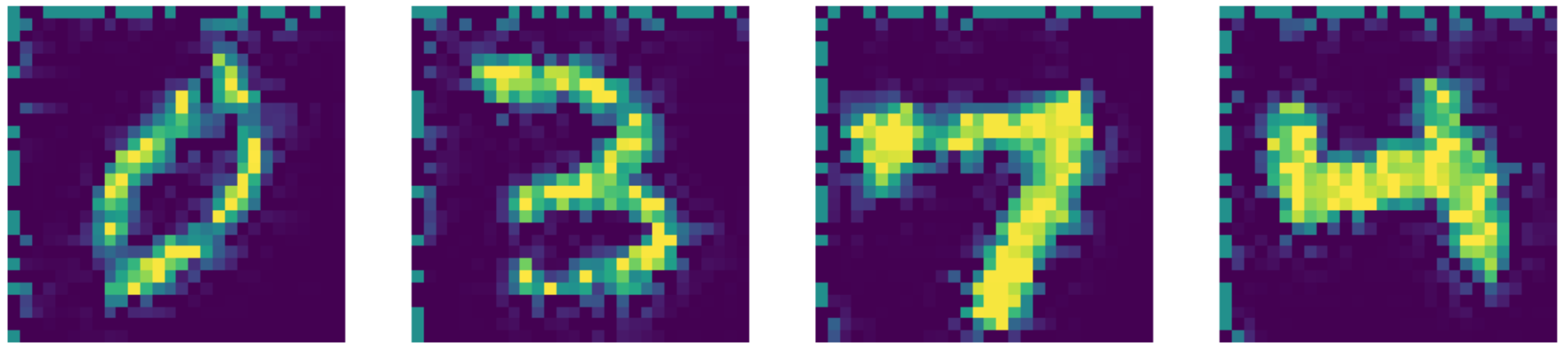
Figure 27: Navier-Stokes renklendirme çıktısı.