Örnekler ve Detaylarla SSL ve EBM

Özdenetimli Öğrenme

Özdenetimli Öğrenme (SSL) hem denetimli hem de denetimsiz öğrenmeyi kapsıyor. SSL’nin amacı girdinin iyi bir gösterimini öğrenmek, böylece daha sonra bunu denetimli görevlerde kullanılabilir. SSL’de model verinin bir kısmını tahmin etmek için geri kalan veriyi kullanarak eğitiliyor. Örneğin, BERT SSL yöntemleri kullanılarak eğitildi ve Arıtan Otokodlayıcı (DAE) bize Doğal Dil İşlemedeki (NLP) en gelişmiş sonuçları veriyor.

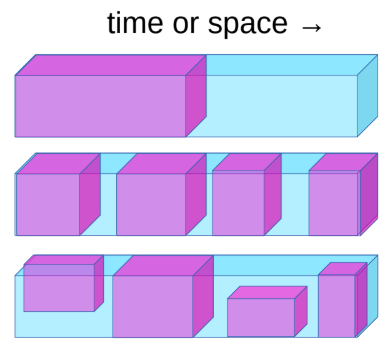
Fig. 1: Özdenetimli Öğrenme

Özdenetimli Öğrenme görevleri şunlarla tanımlanabilir:

• Geçmişi kullanarak geleceği tahmin etmek
• Görünenleri kullanarak gizli olanları tahmin etmek
• Elimizdeki her şeyi kullanarak ulaşamadığımız kısımları tahmin etmek

Örneğin, eğer bir sistem kamera hareket ettiğindeki yeni kareyi tahmin etmek için eğitildiyse, sistem dolaylı olarak derinliği ve ıraklık açısını öğrenecek. Bu da sistemi görüşünde bulunmayan objelerin yok olmadığını, hareketli, hareketsiz nesneler ve arkaplan arasındaki farkı öğrenmeye zorlayacak. Bu sayede yerçekimi gibi fizik hakkında sezgilere de sahip olabilir.

En gelişmiş NLP sistemleri (BERT) dev bir sinir ağını bir SSL göreviyle öneğitiyor. Cümleden bazı kelimeleri çıkarıp sistemin eksik kelimeleri tahmin etmesini istiyorsunuz. Bu çok başarılı oldu. Benzer fikirler bilgisayarlı görü dünyasında da denendi. Aşağıdaki resimde gösterildiği gibi, resmin bir kısmını çıkarıp modeli eksik parçayı tahmin etmesi için eğitebilirsiniz.

Fig. 2: Bilgisayarlı görüdeki eş sonuçlar

Modeller eksik kısmı doldurabilse de, NLP sistemleri kadar başarılı değiller. Eğer bu modeller tarafından oluşturulan iç gösterimleri alıp bir bilgisayarlı görü sistemine girdi olarak verirseniz, ImageNet kullanılarak denetimli bir şekilde öneğitilen sistemden daha başarısız oluyor. Buradaki fark NLP ayrık iken resimlerin sürekli olması. Başarıdaki farkın sebebi ise, ayrık durumda belirsizliği nasıl göstereceğimizi biliyorken (muhtemel çıktılar üzerinde büyük bir softmax kullanabiliriz), sürekli durumda nasıl yapacağımızı bilmiyoruz.

Zeki bir sistemin karar vermek için hareketlerinin çevresinde ve kendisine nasıl sonuçları olacağını tahmin etmesi gerekiyor. Dünya tamamen deterministik olmadığı ve makinede/insan beyninde her ihtimali hesaplayacak işlem gücü olmadığı için, yapay zeka sistemlerine belirsizlik durumunda yüksek boyutlu uzaylarda tahmin etmeyi öğretmemiz gerekiyor. Enerji temelli modeller (EBMler) bu iş için oldukça faydalı olabilir.

En küçük kareler kullanılarak videonun sıradaki karesini tahmin etmek için eğitilen bir sinir ağının ürettiği kareler bulanık resimler olacak, çünkü model geleceği tam olarak tahmin edemiyor, kaybı azaltmak için tüm olası yeni karelerin ortalamasını alıyor.

Yeni karenin tahminini yapabilmek için saklı değişkenli enerji temelli modelleri kullanmak:

Doğrusal bağlanımdan farklı olarak, saklı değişkenli enerji temelli modeller dünya hakkında bildiklerimizin yanında gerçekte ne olduğu hakkında bilgi veren saklı bir değişken de alıyor. Bu iki bilginin birleşimi gerçeğe daha yakın bir tahmin için kullanılabilir.

Bu modeller girdi $x$ ve gerçek çıktı $y$ arasındaki uyumluluğu sistemin enerjisini en aza indiren saklı değişkene bağlı olarak değerlendiren sistemler olarak düşünülebilir. Girdi $x$’i gözlemleyip girdinin ve saklı değişkenler $z$’nin farklı kombinasyonları ile muhtemel tahminler olan $\bar{y}$’leri üretip enerjiyi, tahmin hatasını en aza indireni seçiyoruz.

Çizdiğimiz saklı değişkene bağlı olarak, tüm muhtemel tahminlere sahip olabiliriz. Saklı değişken girdi $x$’te bulunmayan çıktı $y$’nin önemli bir bilgisi olarak düşünülebilir.

Skaler değerli enerji fonksiyonunun iki versiyonu bulunmakta:

1. Koşullu $F(x, y)$ - $x$ ve $y$ arasındaki uyumluluğu ölçmek
2. Koşulsuz $F(y)$ - $y$’nin bileşenleri arasındaki uyumluluğu ölçmek

Bir Enerji Temelli Modeli Eğitmek

$F(x, y)$’yi parametrize etmek için Enerji Temelli Model eğitmenin iki ayrı türü bulunmakta.

1. Karşılaştırmalı yöntemler: $F(x[i], y[i])$’de düşürüp, diğer $F(x[i], y’)$’lerde yükseltmek
2. Mimari yöntemler: Düzenlileştirme ile $F(x, y)$’yi düşük enerjili bölgeler sınırlı veya minimum olacak şekilde oluşturmak

Enerji fonksiyonunu şekillendirmek için yedi farklı strateji var. Karşılaştırmalı yöntemler yükseltecekleri noktaları seçmede farklılık gösteriyor. Mimari yöntemler ise kodun bilgisinin kapasitesini sınırlandırdığı yöntemler ile farklılık gösteriyor.

Karşılaştırmalı yöntemlerden biri En Büyük Olabilirlik öğrenmesi. Enerji normalize edilmemiş negatif log yoğunluğu olarak yorumlanabilir. Gibbs dağılımı bize verilen $x$’e göre $y$’nin olabilirliğini veriyor. Şu şekilde formülleştirilebilir:

En Büyük Olabilirlik, olabilirliği maksimuma çıkarmak için payı büyütüp paydayı küçültüyor. Bu, aşağıdaki gibi $-\log(P(Y \mid W))$’yi minimize etmeye eşdeğer.

Bir Y örneği için negatif log olabilirlik kaybının gradyanı aşağıdaki gibi:

Yukarıdaki gradyanda, gradyanın ilk terimi veri noktamız $Y$’deki, ve ikinci terimi tüm $Y$’lerdeki beklenti değerini veriyor. Bundan dolayı, gradyan inişi yaptığımızda, ilk terim veri noktamız $Y$’deki enerjiyi düşürmeye çalışırken ikinci terim diğer tüm $Y$’lerdeki enerjiyi arttırmaya çalışıyor.

Enerji fonksiyonunun gradyanı genellikle çok karmaşık, bu yüzden integrali hesaplamak, tahmin etmek veya integrale yaklaşmak genelde zorlu olduğu için çok ilgi çekicidir.

Saklı değişkenli enerji temelli model

Saklı değişkenli modellerin asıl avantajı, saklı değişken sayesinde çok sayıda tahmini mümkün kılmaktır. $z$ küme üzerinde değiştikçe, $y$ olası tahminlerin manifoldu üzerinde değişiyor. Bazı örnekler:

1. K-ortalama
2. Seyrek modelleme
3. GLO

Bunlar iki tür olabilir:

1. $y$’nin $x$’e bağlı olduğu koşullu modeller
   1. \[F(x,y) = \text{min}_{z} E(x,y,z)\]
   2. \[F_\beta(x,y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(x,y,z)}\]
2. $y$’nin bileşenleri arasındaki uyumluluğu ölçen $F(y)$ skaler enerji fonksiyonu olan koşulsuz modeller
   1. \[F(y) = \text{min}_{z} E(y,z)\]
   2. \[F_\beta(y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(y,z)}\]

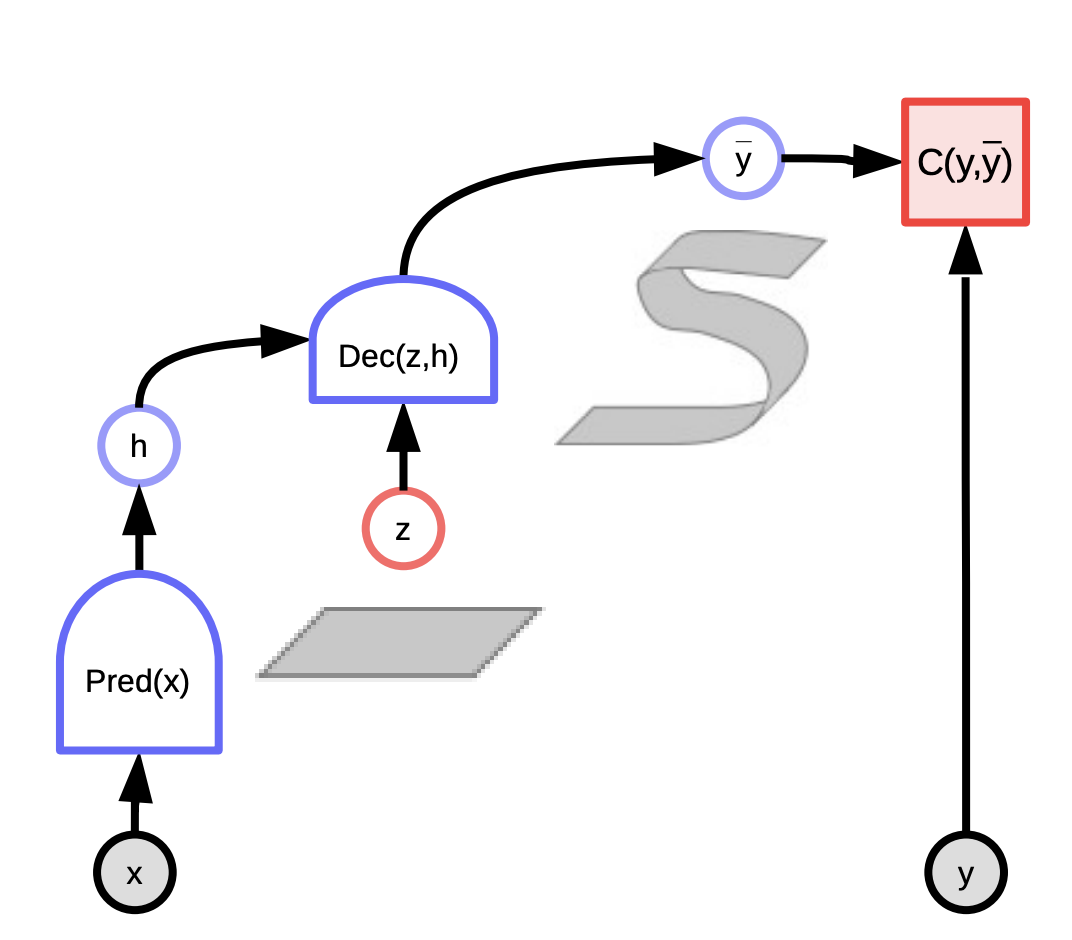
Fig. 3: Saklı Değişkenli EBM

Saklı değişkenli EBM örneği: $K$-ortalama

K-ortalama $y$ üzerindeki dağılımı modellemeye çalıştığımız bir enerji temelli model olarak düşünülebilecek basit bir kümeleme algoritmasıdır.

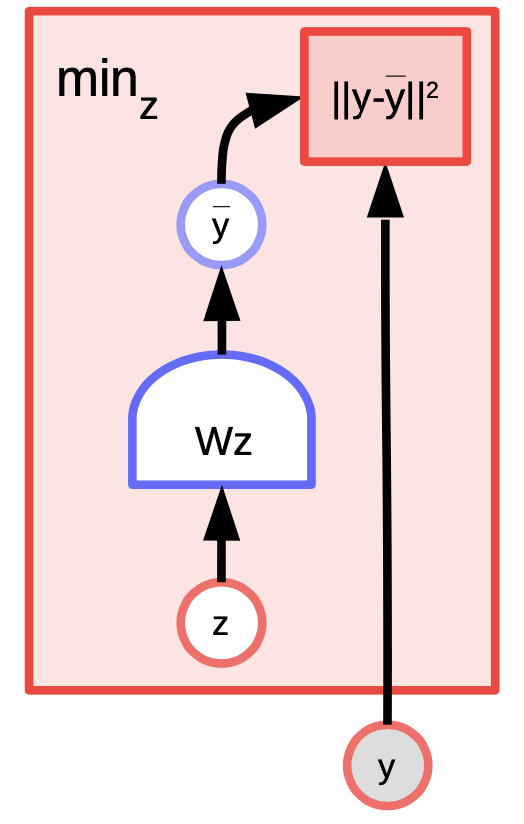
Fig. 4: K-ortalama örneği

Verilen $y$ ve $k$ değerini kullanarak, $W$’nun $k$ adet muhtemel sütunundan hangisinin yeniden üretme hatası veya enerji fonksiyonunu minimize ettiğini bulup çıkarım yapabiliriz. Algoritmayı eğitmek için yaklaşımımız $W$’nun $y$’ye en yakın sütununu seçmek için $z$’yi bulup daha sonra daha da yaklaşmak için gradyan adımı atıp işlemi tekrar edebiliriz. Ancak, koordinat gradyan inişi aslında daha iyi ve daha hızlı çalışıyor.

Aşağıdaki grafikte, pembe sarmal üzerinde veri noktalarını görebiliriz. Bu çizgiyi çevreleyen siyah damla, $W$’nun prototiplerinin etrafındaki ikinci dereceden düşüşlere karşılık geliyor.

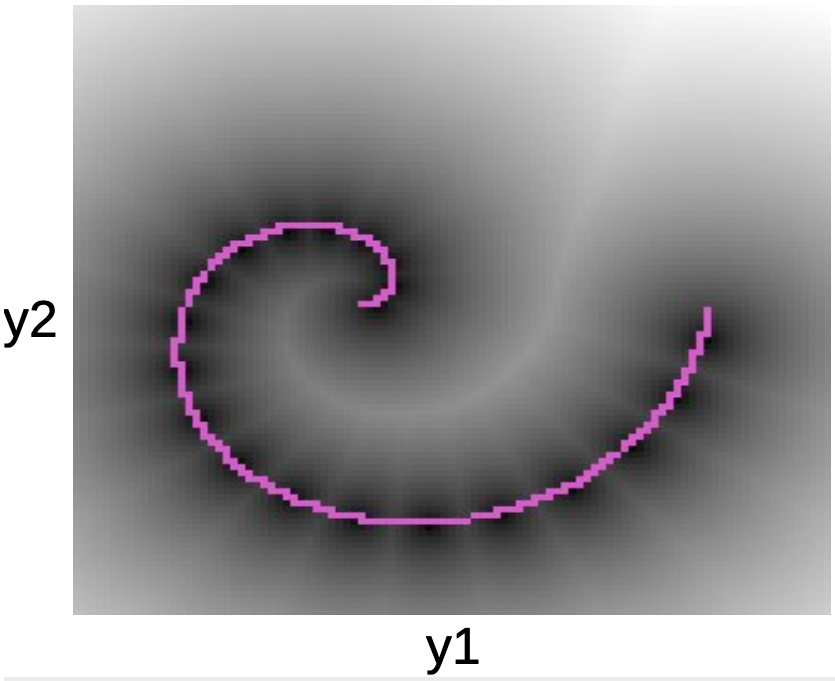
Fig. 5: Sarmal grafik

Enerji fonksiyonunu öğrendiğimizde aşağıdaki soruları ele almaya başlayabiliriz:

1. $y_1$ noktası verildiğinde $y_2$ noktasını tahmin edebilir miyiz?
2. $y$ verildiğinde, veri manifoldundaki en yakın noktayı bulabilir miyiz?

K-ortalama bir mimari yöntemdir (karşılaştırmalı yöntemlerden farklı). Yani enerjiyi herhangi bir yerde yükseltmiyoruz, tek yaptığımız enerjiyi belli bölgelerde düşürmek. Bunun bir dezavantajı $k$ değerine karar verdikten sonra, sadece $k$ adet noktada 0 enerjiye sahip olabiliriz ve bu noktalardan uzaklaştıkça karesel bir oranda artacak.

Karşılaştırmalı yöntemler

Dr Yann LeCun’a göre, herkes bir noktada mimari yöntemleri kullanacak, ama şu an resimler üzerinde karşılaştırmalı yöntemler daha iyi çalışıyor. Bazı veri noktalarını ve enerji yüzeyinin eşyükselti eğrilerini gösteren aşağıdaki şekle bakın. İdeal olarak, enerji yüzeyinin en düşük enerjiye veri manifoldu üzerinde sahip olmasını isteriz. Böylece yapmak istediğimiz şey, eğitim örneğinin etrafında enerjiyi (yani $F(x,y)$ değerini) düşürmek, ama bu tek başına yeterli olmayabilir. Bu yüzden yüksek enerjiye sahip olması gereken ama düşük enerjiye sahip olan $y$’lerde de yükseltiyoruz.

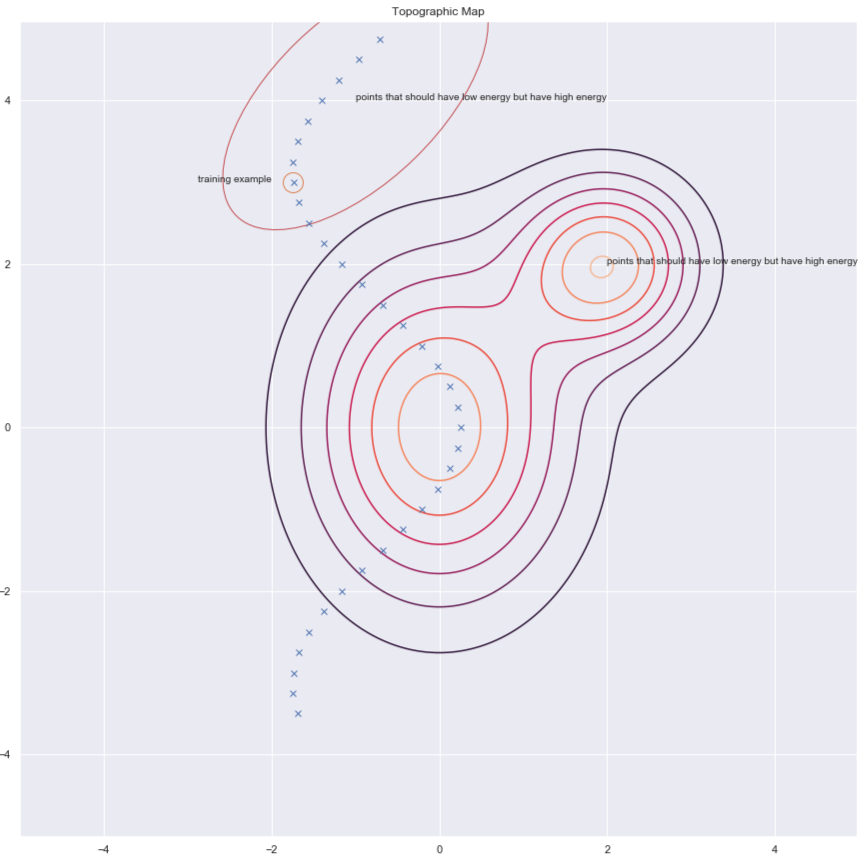
Fig. 6: Karşılaştırmalı yöntemler

Enerjiyi yükseltmek istediğimiz $y$’leri bulmak için birkaç farklı yol var. Bazı örnekler:

1. Arıtan Otokodlayıcı
2. Karşıtsal Iraksama
3. Monte Carlo
4. Markov Zincirli Monte Carlo
5. Hamiltonian Monte Carlo

Arıtan otokodlayıcı ve karşıtsal ıraksama hakkında kısaca tartışacağız.

Arıtan otokodlayıcı (DAE)

Enerjiyi arttıracağımız $y$’leri bulmanın bir yolu, aşağıdaki grafikte yeşil oklarla gösterildiği gibi eğitim örneğini rastgele bozmaktır.

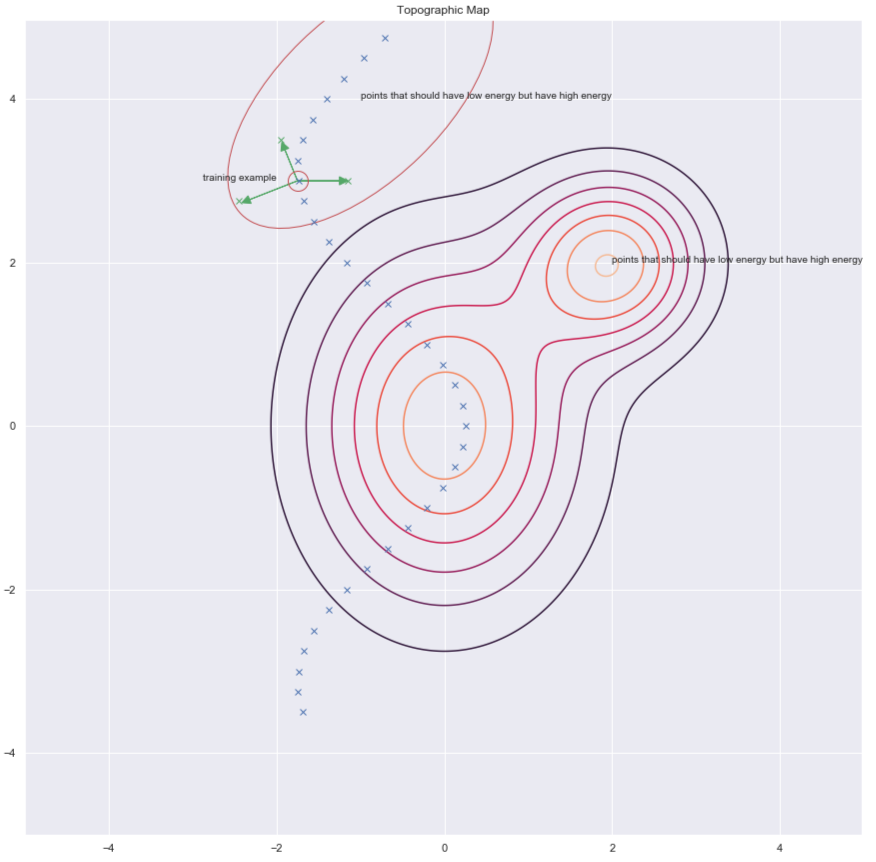
Fig. 7: Topografik harita

Veri noktasını bozduktan sonra, enerjiyi burada yükseltebiliriz. Eğer bunu her veri noktası için yeterince kez yaparsak, enerji eğitim örneklerinin yanında bükülecek. Aşağıdaki grafik eğitimin nasıl yapıldığını gösteriyor.

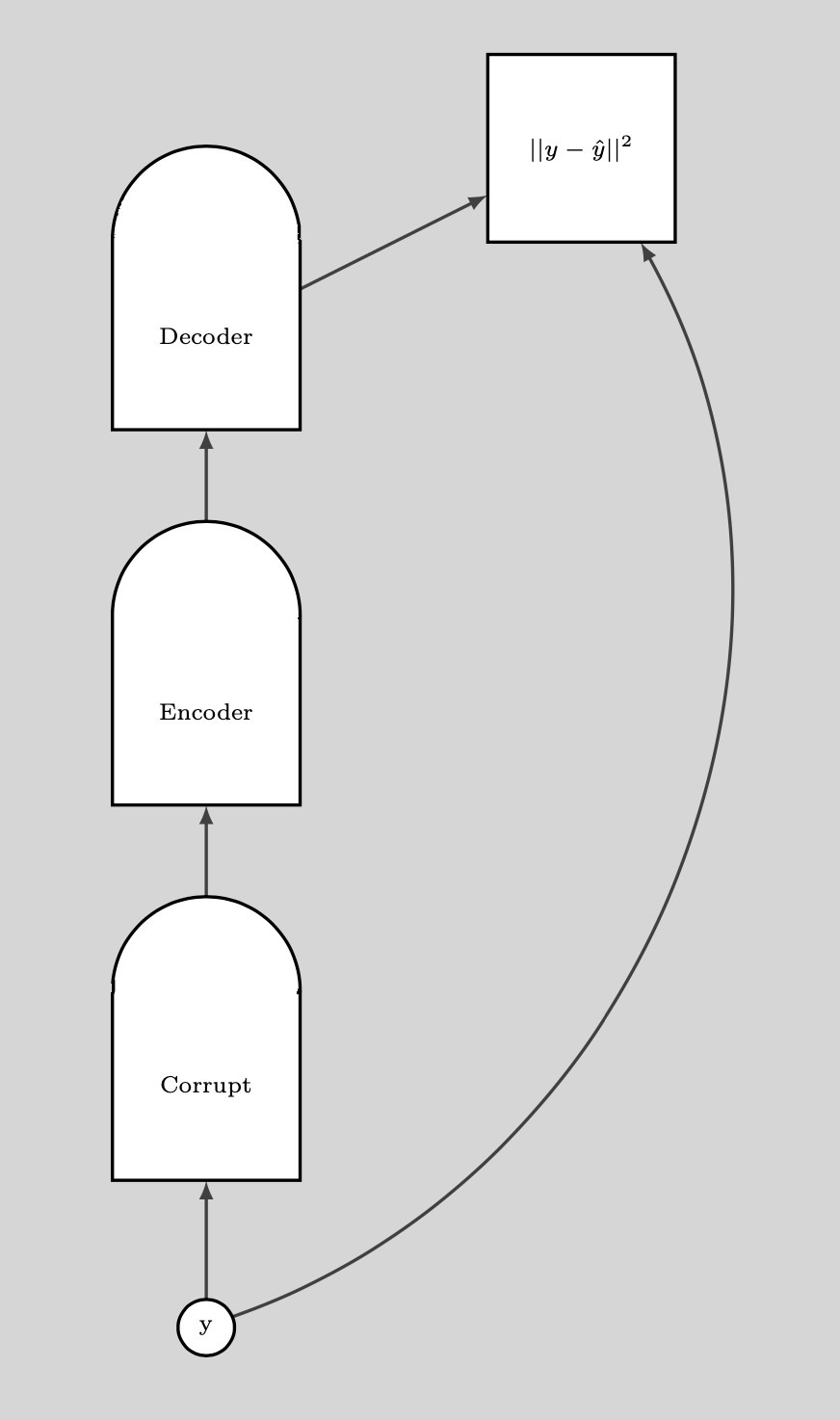
Fig. 8: Eğitim

Eğitim adımları:

1. $y$ noktasını al ve onu boz
2. Kodlayıcı ve Kodçözücüyü bozulmuş veri noktasından orijinal veri noktasını oluşturacak şekilde eğit

Eğer DAE düzgün bir şekilde eğitilirse, enerji veri manifoldundan uzaklaştıkça karesel bir şekilde büyüyecek.

Aşağıdaki grafik DAE’yi nasıl kullandığımızı gösteriyor.

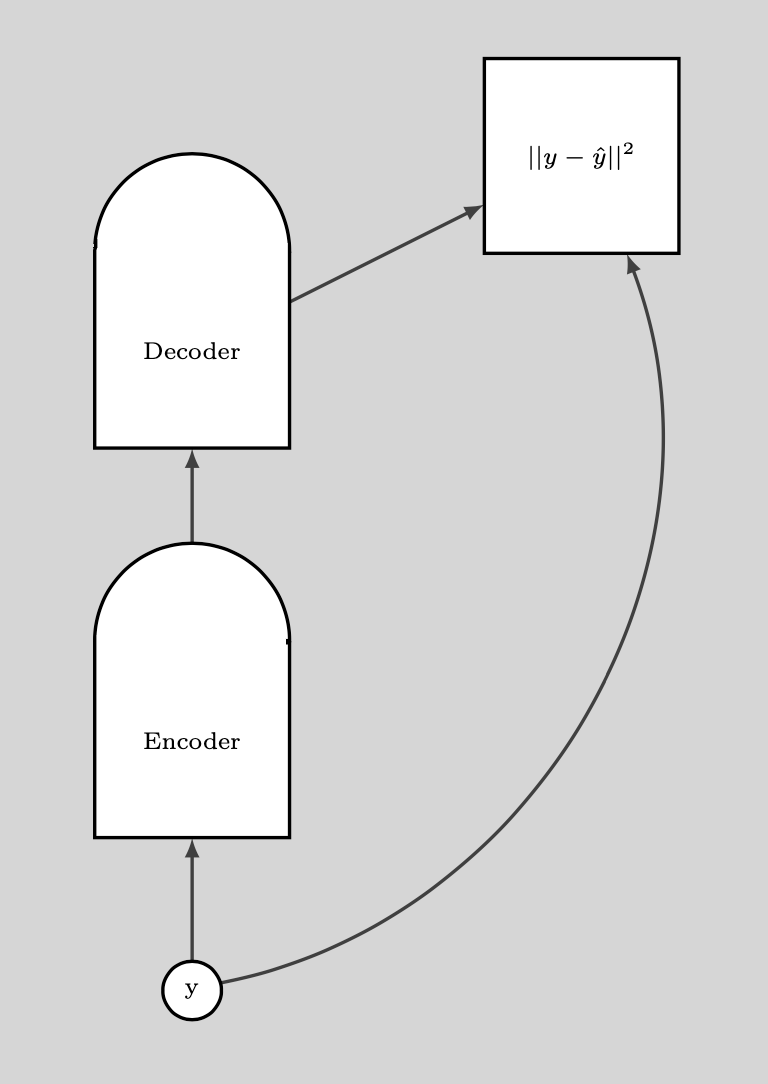
Fig. 9: DAE nasıl kullanılır

BERT

BERT benzer bir şekilde eğitiliyor, ancak bu sefer uzay ayrık ve metinle uğraşıyoruz. Bozma tekniğiyle bazı kelimeleri gizleyip, yeniden oluşturma adımında bunları tahmin etmeye çalışıyoruz. Bundan dolayı bu yöntemin başka bir adı da gizli otokodlayıcı.

Karşıtsal Iraksama

Karşıtsal ıraksama bize enerjiyi yükselteceğimiz $y$ noktalarını bulmak için daha akıllıca bir yöntem sunuyor. Eğitim noktamıza rastgele bir vuruş yapıp gradyan inişiyle enerji fonksiyonunda aşağı inebiliriz. Yolun sonunda geldiğimiz noktada enerjiyi yükseltiyoruz. Bu aşağıdaki grafikte yeşil çizgiyle gösteriliyor.

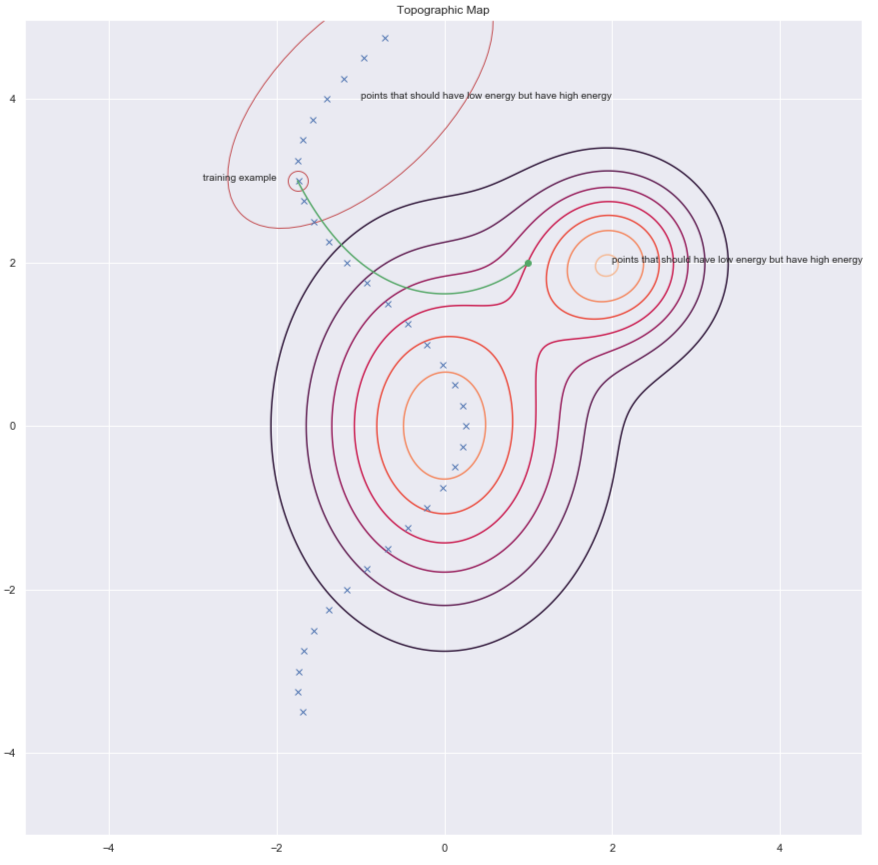
Fig. 10: Karşıtsal Iraksama