Enerji Temelli Modeller

Genel Bakış

Modelleri tanımlamak için yeni bir çatı tanıtacağız. Bu çatı; denetimli, denetimsiz ve özdenetimli modelleri tanımlaya yardımcı olacak birleştirici bir şemsiye görevi görecek. Enerji temelli modeller bir $x$ değişkenler grubunu gözlemler ve bir $y$ değişkenler grubunu çıktı verir. İleri beslemeli ağlarda 2 büyük sorun var:

1. Çıkarsama yordamı, ağırlıklı toplamların yığılmış katmanlarından daha karmaşık bir hesaplama ise ne olur?
2. Tek bir girdi için birden çok olası çıktı varsa ne olur? Örnek: Videonun gelecek çerçevelerini öngörmek. Temel olarak bir sınıflandırma ağında, bu ağı her sınıf için bir puan verecek şekilde eğitiyoruz. Bununla beraber, görüntüler gibi yüksek boyutlu bir tanım alanında bunu yapmak mümkün değildir. (Görüntüler üzerine eşiksiz en büyük koyulamaz!). Çıktı kesikli olsa bile, geniş bir örneklem uzayına sahip olabilir. Örneğin, metnin bileşimsel olması çok sayıda olası kombinasyona yol açar. Enerji temelli modeller, bu yöntemleri modellemek için daha iyi bir çatı sağlar.

EBM yaklaşımı

$x$’leri $y$’lere sınıflandırmaya çalışmak yerine, belirli bir ($x$, $y$) çiftinin birbirine uyup uymadığını tahmin etmek istiyoruz. Ya da başka bir deyişle, $x$ ile uyumlu bir $y$ bulun. Sorunu, düşük olan bazı $F($x$, $y$)$’ler için bir y bulma olarak da ortaya koyabiliriz. Örnek olarak:

• $Y$, $x$’in doğru yüksek çözünürlüklü görüntüsü mü?
• A metni, B metninin iyi bir çevirisi mi?

Yorum: Bir fonksiyonu en aza indirdiğimiz bu çıkarsama yöntemi ve geniş bir modeller sınıfı bu şekilde işler. $f(x,y)$’yi veya “enerji”‘yi en aza indirerek. Bu nedenle, çıkarsama yöntemini $f(x,y)$ ile gösterilen kısıtlamaları en aza indirerek uyguluyoruz. Bundan böyle $f(x,y)$’ye “Enerji fonksiyonu” diyoruz.

Tanım

$F(x,y)$’nin $(x,y)$ çiftleri arasındaki bağımlılık seviyesini belirteceği şekilde bir enerji fonksiyonu $F: \mathcal{X} \times \mathcal{Y} \rightarrow \mathcal{R}$ tanımlarız. (Bu enerjinin öğrenmede değil, çıkarsamada kullanıldığını dikkate alın.) Çıkarsama, aşağıdaki denklemle ifade edilebilir: \(\check{y} = \displaystyle \text{argmin}_y \left \{ F(x,y)\right \}\)

Çözüm: gradyan temelli çıkarsama

Enerji fonksiyonunun pürüzsüz ve türevlenebilir olmasını istiyoruz, böylece fonksiyonu çıkarsama için gradyan temelli yöntemleri uygulama amacıyla kullanabiliriz. Çıkarsamayı uygularken, uyumlu $y$’leri bulmak için gradyan inişini kullanarak bu fonksiyonu ararız. En düşük değeri elde etmek için gradyan yöntemlere alternatif birçok yöntem mevcuttur.

Öte yandan: Grafik modeller, Enerji temelli modellerin özel bir halidir. Enerji fonksiyonu, enerji terimlerinin bir toplamı olarak ayrışır. Her enerji terimi, ilgilendiğimiz değişkenlerin bir alt kümesini dikkate alır. Belirli bir şekilde düzenlendikleri takdirde, çıkarsamasıyla ilgilendiğimiz değişkene göre terimlerin toplamının en düşük değerini bulmak için etkili çıkarım algoritmaları mevcuttur.

Saklı Değişkenler ile EBM

$Y$ çıktısı, $x$ ve değerini bilmediğimiz ilave bir değişken olan $z$’ye (saklı değişken) bağlıdır. Bu saklı değişkenler yardımcı bilgi sağlayabilir. Örneğin, saklı bir değişken size bir metin parçasındaki kelime sınırlarının konumlarını işaret edebilir. Bu bize el yazısını boşluk bırakmadan yorumlama konusunda yardımcı olabilir. Bunun bilinmesi, deşifre edilmesi zor boşluklara sahip olan konuşmalar konusunda da yarar sağlayacaktır. Ek olarak, bazı diller çok zayıf sözcük sınırlarına sahiptir (örn. Fransızca). Bu nedenle, modelimizde bu saklı değişkenin bulunması, böyle bir girdiyi yorumlamak için çok yararlı olacaktır.

Çıkarım

EBM gizli değişkeniyle çıkarsama yapmak için, $y$ ve $z$’ye göre aynı anda enerji fonksiyonunu en aza indirmek istiyoruz.

Bu da enerji fonksiyonunu şu şekilde yeniden tanımlamakla eşdeğerdir: \(F_\infty(x,y) = \text{argmin}_{z}E(x,y,z)\), bu da eşittir: \(F_\beta(x,y) = -\frac{1}{\beta}\log\int_z \exp(-\beta E(x,y,z))\). $\beta \rightarrow \infty$ iken $\check{y} = \text{argmin}_{y}F(x,y)$ olur.

Saklı Değişkenli EBM

Saklı değişkenlerin bir başka büyük avantajı da, saklı değişkeni bir küme üzerinde değiştirerek, $y$ tahmin çıktısını olası tahminlerin manifoldu üzerinde de değiştirebilmemizdir (şerit aşağıdaki grafikte gösterilmiştir): $F(x,y) = \text{argmin}_{z} E(x,y,z)$.

Bu, makinenin sadece bir değil, birden çok çıktı üretmesine olanak sağlar.

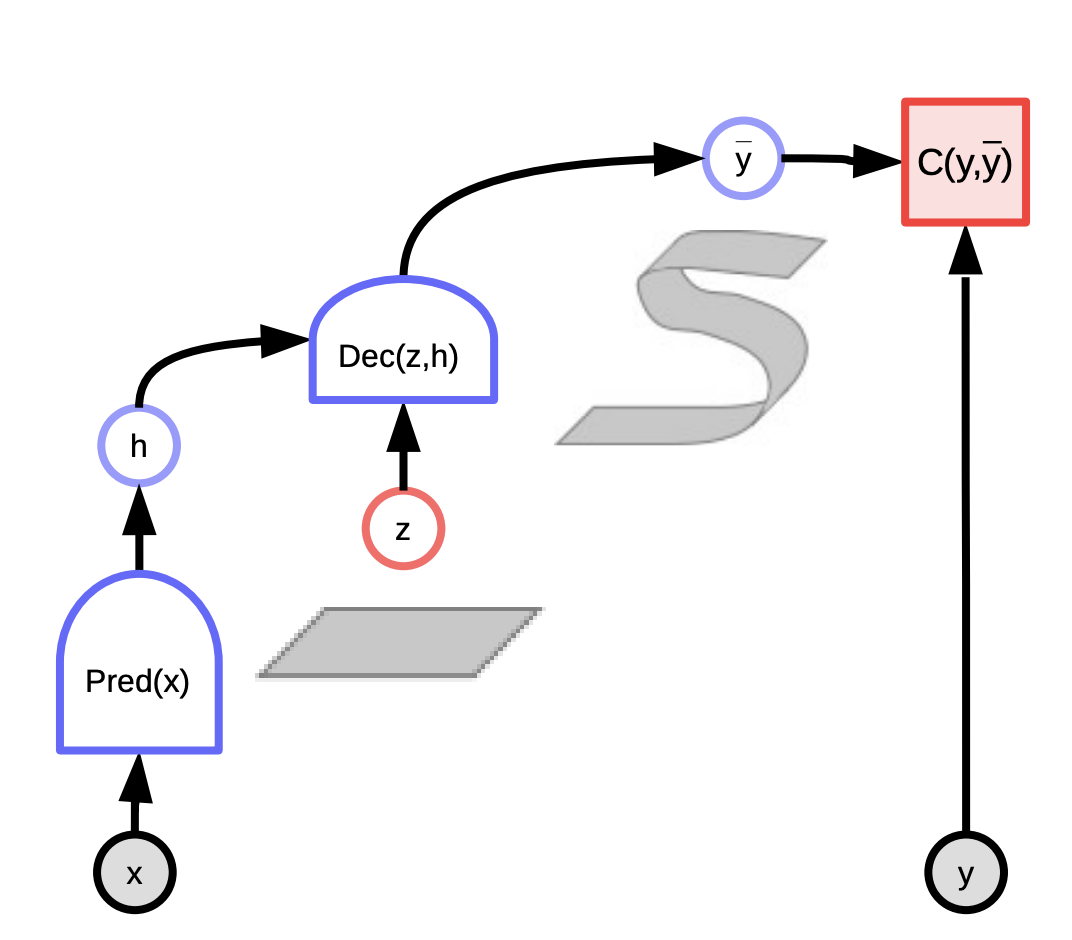
Fig. 1: Enerji Temelli Modeller için hesaplamalı çizge

Örnekler

Video tahmini bir örnek olarak verilebilir. Video tahminini kullanmamız için birçok iyi uygulama var, örneğin bir video sıkıştırma sistemi yapmak. Veya, kendi kendine giden bir arabanın videosunu kullanarak diğer arabaların ne yapacağını tahmin etmek de bir örnek olabilir. Bir başka örnek olarak da tercüme verilebilir. Bir metin parçası için bir dilden diğerine tek bir doğru çeviri olmadığından dil çevirisi her zaman zorlu bir sorun olmuştur. Genellikle, aynı fikri ifade etmenin birçok farklı yolu vardır ve insanlar neden bir yolu diğerine tercih ettiklerini muhakeme etmekte zorlanırlar. Bu nedenle, bir sistemin verilen bir metne yanıt olarak üretebileceği tüm olası tercümeleri parametreleştirmenin bir yoluna sahip olmak iyi olabilir. Diyelim ki Almanca’dan İngilizce’ye tercüme yapmak istiyoruz, İngilizce’de hepsi doğru olan birden fazla tercüme olabilir ve bazı saklı değişkenleri değiştirerek üretilen tercümeyi de değiştirebiliriz.

Enerji temelli modeller vs olasılıksal modeller

Enerjilere normalize edilmemiş negatif log olasılıkları olarak bakabilir ve normalleştirmeden sonra enerjiden olasılığa geçiş için Gibbs-Boltzmann dağılımını şu şekilde kullanabiliriz:

Bu denklemde $\beta$ pozitif sabittir ve modelinize uyacak şekilde ayarlanması gerekir. $\beta$ değeri arttıkça modelin dalgalanması artarken, $\beta$ değerinin azalmasıyla model daha pürüzsüz bi hal alır. (Fizikte $\beta$ sıcaklığın tersidir: $\beta \rightarrow \infty$ sıcaklığın sıfıra gittiği anlamına gelir).

$Y$ üzerinde tümleştirirsek: $P(y \mid x) = \int_z P(y,z \mid x)$, şu denklemi elde ederiz:

Bu nedenle, bir saklı değişken modelimiz varsa ve saklı değişken $z$’yi olasılıksal olarak doğru bir şekilde ortadan kaldırmak istiyorsak, tek yapmamız gereken enerji fonksiyonu $F_\beta$’yi yeniden tanımlamaktır.

Serbest Enerji

Bunu hesaplamak muhtemelen çoğu durumda baş edilmesi çok zor bir sorun olacaktır. Dolayısıyla, modelinizde en aza indirmek istediğiniz veya tümleştirmeye çalıştığınız (Enerji fonksiyonu $F$’yi yeniden tanımlayarak) saklı bir değişkeniniz varsa, ve en aza indirmek yukarıdaki formülde $\beta$’nın sonsuz limitine karşılık geliyorsa, o zaman yapılabilir. Yukarıdaki $F_\beta(x, y)$ tanımı göz önüne alındığında, $P(y \mid x)$’nin yalnızca Gibbs-Boltzmann formülünün bir uygulaması olduğu söylenebilir, ve $z$ de bunun içerisinde dolaylı bir şekilde tümleştirilmiştir. Fizikçiler buna ‘Serbest Enerji’ dediğinden biz de $F$ diyoruz. Yani $e$ enerji, $F$ ise serbest enerjidir.

***Soru: Enerji temelli modellerin sağladığı avantajları detaylandırabilir misiniz? Olasılık temelli modeller, üzerinde tümleştirme yapılabilen saklı değişkenler de içerebilir.

Olasılıksal modellerdeki fark, en aza indireceğiniz nesne fonksiyonunu seçme şansınızın olmamasıdır. Aynı zamanda manipüle ettiğiniz her nesnenin bir normalleştirilmiş dağılım olması gerektiğinden, olasılıksal çatıya sadık kalmanız gerekir (değişimli yöntemler vb. kullanılarak yaklaşımlanabilir). Burada, nihayetinde bu modellerle yapmak istenen şeyin karar vermek olduğunu söyleyebiliriz. Araba sürebilen bir sistem kurduysanız ve sistem size “0.8 ihtimalle sola veya 0.2 ihtimalle sağa dön” derse, sola döneceksiniz. Olasılıkların 0.2 ve 0.8 olduğu gerçeği önemsizdir. Yapmak istediğiniz şey en iyi kararı vermektir, çünkü bir karar vermek zorundasınız. Bu yüzden olasılıklar karar vermede işe yaramaz. Otomatik bir sistemin çıktısını başka bir sisteminkiyle bir araya getirmek isterseniz (örneğin bir insan, veya başka bir sistem), ve bu sistemler beraber değil, aksine ayrı ayrı eğitilmişse, o zaman ihtiyacınız olan şey iyi bir karar verebilmek için iki sistemin kalibre edilmiş puanlarını birleştirmektir. Puanları kalibre etmenin tek yolu, onları olasılığa dönüştürmektir. Diğer tüm yollar ikinci planda kalmış, uğraşmaya değmezdir. Ancak karar vermek için bir sistemi uçtan uca eğitecekseniz, en iyi karara en iyi puanı verdiği sürece hangi puanlama fonksiyonunu kullanırsanız kullanın işe yarayacaktır. Enerji temelli modeller; modeli nasıl ele alacağınız, nasıl eğiteceğiniz, ve hangi nesne fonksiyonunu kullanacağınız konusunda size çok daha fazla seçenek sunar. Modelinizin olasılıksal olması için ısrarcıysanız, en büyük olabilirlik kullanmanız gerekir. Temel olarak modelinizi, gözlemlediğiniz verilere en yüksek olasılığı verecek şekilde eğitmelisiniz. Sorun, bunun sadece modelinizin “doğru” olduğu durumda işe yaramasıdır ve modeliniz asla “doğru” değildir. Ünlü istatistikçi George Box’un da dediği gibi “Tüm modeller yanlıştır, ama bazıları faydalıdır.”. Dolayısıyla tüm olasılıksal modeller, özellikle yüksek boyutlu ve birleşimsel (metin gibi) uzaydakiler, yaklaşık modellerdir. Bu modellerin hepsi bir şekilde yanlıştır, ve bunları normalleştirmeye çalışırsanız daha da yanlış hale getirirsiniz. Yani onları normalleştirmemek daha iyidir.

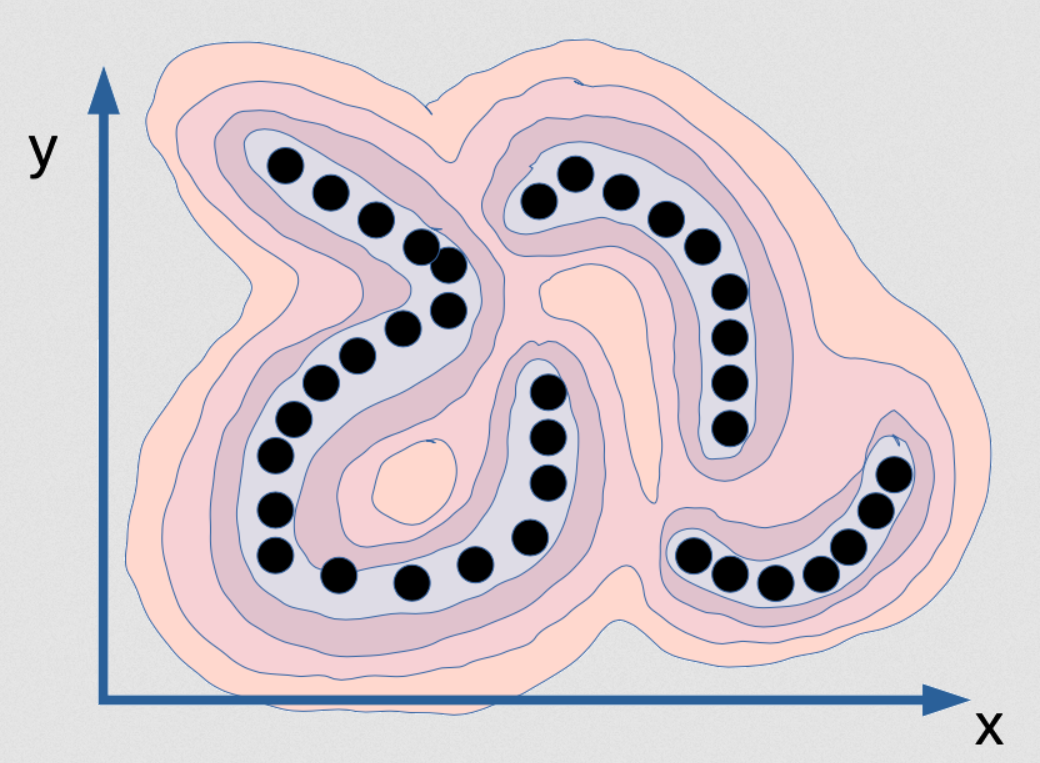
Fig. 2: x ve y arasındaki bağımlılığı ölçen enerji fonksiyonunun görselleştirilmesi

Bu, x ve y arasındaki bağımlılığı yakalamaya çalışan bir enerji fonksiyonudur. Adeta sıradağlara benzer. Vadiler siyah noktaların olduğu yerlerdir (bunlar veri noktalarıdır), ve dört bir yanı dağlarla çevrilidir. Eğer olasılıksal bir modeli bununla eğitirseniz, noktaların sonsuz incelikte bir manifoldda olduğunu hayal edin. Yani siyah noktaların veri dağılımı aslında sadece bir doğru, ve bu doğrulardan üç tane var. Aslında genişlikleri yok. Bundan yola çıkarak bir olasılıksal model eğitecek olursanız, yoğunluk modeliniz size ne zaman bu manifoldda olduğunuzu söylemeleridir. Bu manifoldda yoğunluk sonsuz, sadece epsilon kadar dışındayken ise sıfır olmalıdır. Bu dağılımın doğru modelini elde etmek bu şekilde mümkün olacaktır. Yoğunluğun sonsuz olmasının yanında, [x ve y] üzerinde integralin de 1 olması gerekir. Bunu bilgisayarda uygulamak çok zordur. Hatta sadece zor değil, imkansızdır. Diyelim ki bu fonksiyonu bir çeşit sinir ağı ile hesaplamak istiyorsunuz- sinir ağınız sonsuz ağırlığa sahip olmalı ve sistemin çıktısının tüm alan üzerindeki integrali 1 olacak şekilde ayarlanmalıdır. Bu temelde imkansızdır. Bu veri örneği ile doğru, geçerli bir olasılıksal model yaratmak mümkün değildir. En büyük olabilirlik sizden bunu üretmenizi isteyecektir, ve dünyada bu hesabı yapabilecek bir bilgisayar yoktur. Aslında bu ilginç bile değil. Bu örnek için elinizde kusursuz bir yoğunluk modeli, yani (x,y) uzayındaki ince bir levha olduğunu hayal edin, çıkarsama yapamazsınız! Size x değerini verir ve “y’nin en iyi değeri nedir?” diye sorarsam bulamazsınız çünkü sıfır olasılık kümesi haricindeki tüm y değerlerinin sıfır olasılığı vardır, ve mümkün olan sadece birkaç değer mevcuttur. Örneğin bu x değerleri için:

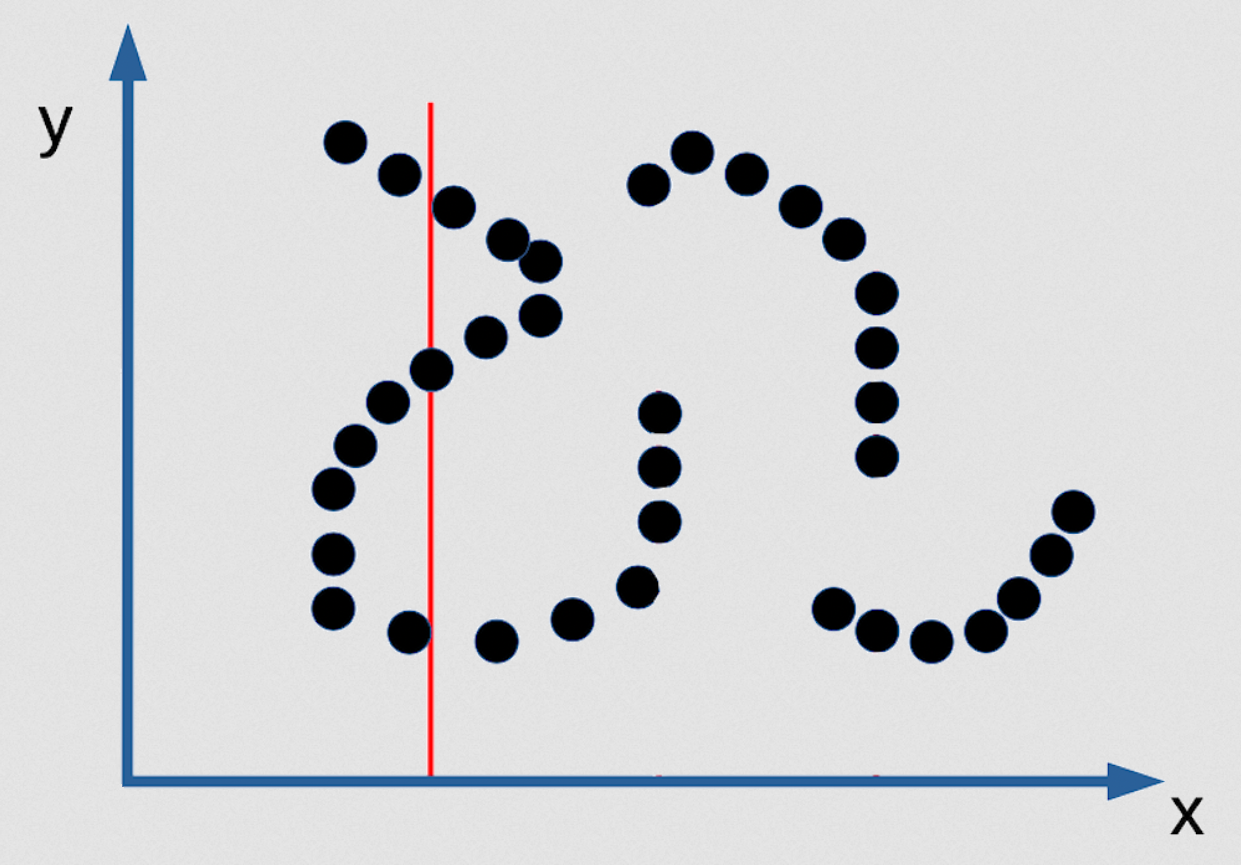
Fig. 3: Gizli bir fonksiyon olarak EBM'nin çok sayıda tahmin örnekleri

Mümkün olan 3 y değeri vardır ve bunlar sonsuz derecede dardır. Bu nedenle onları bulamazsınız. Bulmanıza yarayacak bir çıkarsama algoritması da mevcut değildir. Bu değerleri bulmanızın tek yolu zıtlık fonksiyonunuzu pürüzsüz ve türevlenebilir hale getirmektir, daha sonra istediğiniz bir noktadan başlayabilir ve gradyan inişiyle herhangi bir x değerine karşılık iyi bir y değeri bulabilirsiniz. Ancak dağılım önceden bahsettiğim şekilde ise bu, dağılımın iyi bir olasılıksal modeli olmayacaktır. Bu da iyi bir olasılıksal modele sahip olmak için ısrar etmenin aslında kötü olduğu bir durumdur. En büyük olabilirlik [bu durumda] işe yaramazdır!

Yani eğer gerçek bir Bayes’çiyseniz “ama bu, yoğunluk fonksiyonunuzun pürüzsüz olması gerektiğini söyleyen güçlü bir önsele sahip olarak düzeltilebilir” dersiniz. Bunu bir önsel olarak düşünebilirsiniz. Fakat Bayes terimleriyle yaptığınız her şeyde- logaritma almak, normalleştirmeyi unutmak- enerji temelli modeller elde edersiniz. Enerji fonksiyonunuza eklenebilecek bir düzenlileştiriciye sahip olan enerji temelli modeller, olabilirliğin enerjinin üsseli olduğu Bayes modellerine tamamıyla eşdeğerdir. Elde ettiğiniz şey $\exp(\text{energy}) \exp(\text{regularizer})$ olur, bu da şuna eşittir: $\exp(\text{energy} + \text{regulariser})$. Eğer üsseli çıkarırsanız düzenlileştirici eklenmiş bir enerji temelli model elde etmiş olursunuz.

Yani olasılıksal ve Bayesçi yöntemler arasında bir uyuşma var, ama en büyük olabilirlik için ısrarcı olmak, özellikle de olasılıksal modelinizin çok yanlış olacağı yüksek boyutlu veya birleşimsel uzayda, bazen sizin için kötü olabilir. Kesikli dağılımlarda çok yanlış değildir (sorun değil), ancak sürekli durumlarda, gerçekten yanlış olabilir. Aslında tüm modeller yanlış olacaktır.