RNN ve LSTM Modellerinin Mimarileri

Genel Bakış

RNN (Reccurrent Neural Network, Özyinelemeli Sinir Ağı) dizi şeklindeki veriyle uğraşırken kullanabileceğimiz mimarilerden biridir. CNN (Convolutional Neural Network, Evrişimli Sinir Ağı) dersinde bir sinyalin, alana göre, 1, 2, ya da 3 boyutlu olabileceğini öğrendik. Dizi şeklindeki veride ilgili alan X’in zamana göre girdileri olduğundan tek boyutlu veriyle uğraşılır. Yine de RNN’i iki yöne sahip olan 2 boyutlu veriyle de kullanabilirsiniz.

Düz Sinir Ağı vs. Özyinelemeli Sinir Ağı

Fig 1’de üç katmanlı düz bir sinir ağının diyagramını görebilirsiniz. Pembe balon girdi vektörü x’i gösterirken gizli katman ve çıktı katmanı sırasıyla yeşil ve mavi ile gösterir. Sağ taraftaki dijital elektronik örneğinde görüldüğü gibi bu kombinasyonel mantığa benzer, şimdiki çıktı sadece şimdiki girdiye bağlıdır.

Fig 1: Düz Mimari

Düz sinir ağının aksine, özyinelemeli ağlarda şimdiki çıktı sadece şimdiki girdiye değil, aynı zamanda, Fig 2.’de görüldüğü üzere, sistemin o anki durumuna bağlıdır. Bu dijital elektronikteki ardışık mantığa benzer, çıktı bir “mandal” (flip-flop, dijital elektronikte basit bir bellek ünitesi) devresine bağımlıdır. Bu yüzden buradaki ana farklılık düz sinir ağının çıktısı sadece o anki girdiye bağlıyken, özyinelemeli bir ağın çıktısının sistemin durumuna da bağlı olmasıdır.

Fig 2: RNN Mimarisi

Fig 3: Basit Sinir Ağı Mimarisi

Yann’ın diyagramı bir tensörden (vektörden) diğerine eşlemeyi göstermek için bu şekilleri nöronların arasına ekler. Örneğin, Fig 3’te, girdi vektörü x, bu eklenmiş birimden eşlenip gizli gösterim h’e gidecektir. Bu aslında bir afin dönüşümdür (yani döndürme ve sonrasında bozma). Daha sonra başka bir dönüşümle gizli katmandan son çıktıyı alırız. Benzer şekilde, RNN diyagramında görüldüğü gibi, nöronlar arasına eklenmiş şekilleri aynı şekilde görebilirsiniz.

Fig 4: Yann'ın RNN Mimarisi

Dört RNN Türü ve Örnekleri

İlk durum vektörden diziyedir. Burada girdi bir balondur ve devamında sistemin içsel durumunun evrimi yeşil balonlarla gösterilmiştir. Sistem evrildikçe, her zaman adımında belirli bir çıktı olacaktır.

Fig 5: Vektörden Diziye

Bu tip mimarinin örneği girdi olarak bir görüntü alıp çıktı olarak görüntünün kelime dizisi halinde İngilizce açıklamasının üretilmesidir. Fig 6’yı kullanarak açıklayacak olursak, her bir mavi balon İngilizce kelimelerin İngilizce sözlükteki indeksi olabilir. Örneğin, eğer çıktı “This is a yellow school bus” cümlesiyse, öncelikle “This” kelimesinin indeksini, sonra “is” kelimesinin indeksini alarak devam edersiniz. Bu ağdan elde edilen bazı sonuçlar aşağıda gösterilmiştir. Örneğin, ilk sütunda son resim için üretilen açıklama, “A herd of elephants walking across a dry grass field.” (“Bir fil sürüsü kurak yeşillik alan boyunca yürüyor.”), epey detaylı. İkinci sütunda ilk resim için “Two dogs play in the grass.” (“İki köpek çimenlik alanda oynuyor.”) cümlesi üretiliyor, ancak resimde aslında üç köpek var. Son sütunda, “A yellow school bus parked in a parking lot.” (“Yeşil bir okul servisi otoparka park edilmiş.”) gibi, daha yanlış örnekler var. Genel olarak, bu sonuçlar bu ağın sert bir şekilde başarısız olabileceğini ve aynı zamanda bazen de iyi çalışabileceğini gösteriyor. Bu girdinin sadece tek bir vektör, resmin gösterimi, çıktınınsa bir dizi sembol, örneğin İngilizce cümleleri oluşturan kelimeleri oluşturan karakterler, olduğu bir örnek. Bu tür mimarilere otoregresif ağ denir. Bir otoregresif ağ bir önceki adımda süretilen çıktının bir sonraki adıma girdi olarak verildiği ağdır.

Fig 6: Vektörden Diziye Örnek: Resimden Metine

İkinci türde bir diziden bir vektör üretilir. Bu ağ bir dizi sembolü besler ve sadece son adımda bir çıktı üretir. Bu tür bir uygulama Python yorumlamak için kullanılabilir. Örneğin girdiler bir Python programının satırları olabilir.

Fig 7: Diziden Vektöre

Fig 8: Python kodunun girdi satırları

Ağ bu programın doğru çözümünü verecektir. Daha karmaşık bir program aşağıdaki gibi olabilir:

Figure 9: Daha karmaşık bir durum için Python girdi satırları

Bu durumda çıktı 12184 olmalıdır. Bu iki örnek bir sinir ağını bu tür bir uygulama için eğitebileceğinizi gösteriyor. Sadece bir sembol dizisi besleyip çıktının belli bir sayı olmasını sağlamalıyız.

Üçüncü durumda, Fig 10’da görüldüğü gibi, sekanstan vektör vektörden sekans üretilir. Bu mimari eskiden makine tercümesi için kullanılan standart mimariydi. Burada pembeyle gösterildiği gibi bir dizi sembolle başlarsınız. Her şey son bir h vektöründe toplanır ve bu vektör bir konsepti temsil eder. Örneğin, bir cümleyi girdi olarak alıp, cümlenin anlamını ve vermek istediği mesajı temsil eden, geçici bir vektöre sıkıştırabiliriz. Daha sonra herhangi bir dösterimde bu anlamı aldıktan sonra, ağ başka bir dilde onu açabilir. Örneğin “Today I’m very happy” (“Bugün çok mutluyum”) İtalyanca ya da Çince’ye çevrilebilecek bir İngilizce kelime dizisidir. Son olarak, ağ aynı sıkıştırılmış versiyon verildiğinde bir kodçözme işlemi uygular. Son zamanlarda, bir sonraki derste işleyeceğimiz, Dönüştürücü (Transformer), gibi ağların tercüme görevlerinde bu metoddan daha iyi sonuçlar aldığını gördük. Bu mimari 2018 yılında en iyi çalışan yöntemdi.

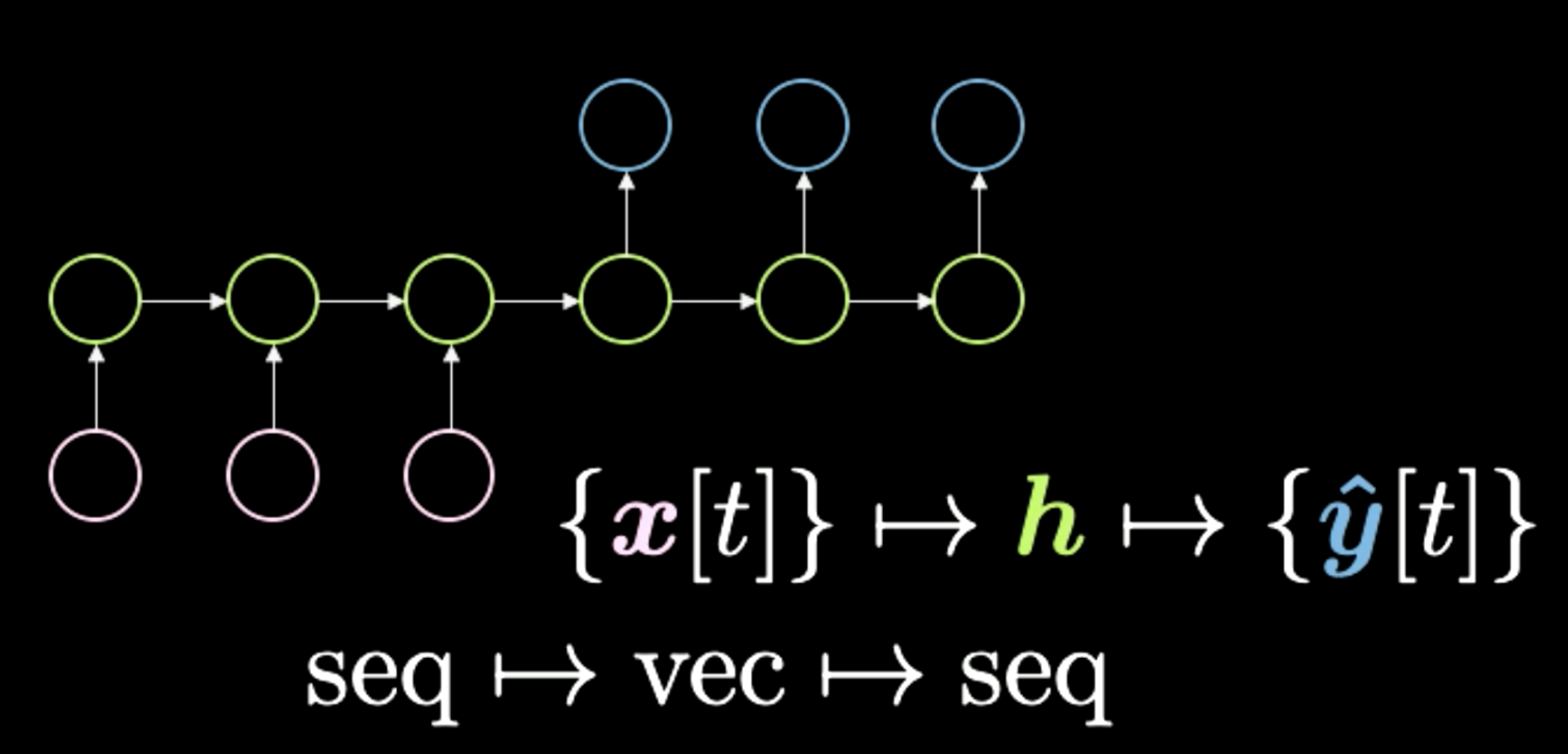
Figure 10: Sekanstan Vektöre Vektörden Sekansa

Eğer saklı uzayda PCA (Principle Component Analysis, Temel Bileşen Analizi) uygularsanız, grafikte görüldüğü gibi, kelimelerin anlamlarına göre gruplandığını görürsünüz.

Fig 11: PCA sonrası anlamlarına göre gruplanmış kelimeler

Yaklaştığımızda aynı alanda “January” (Ocak) ve “November” (Kasım) gibi ayların olduğunu görürüz.

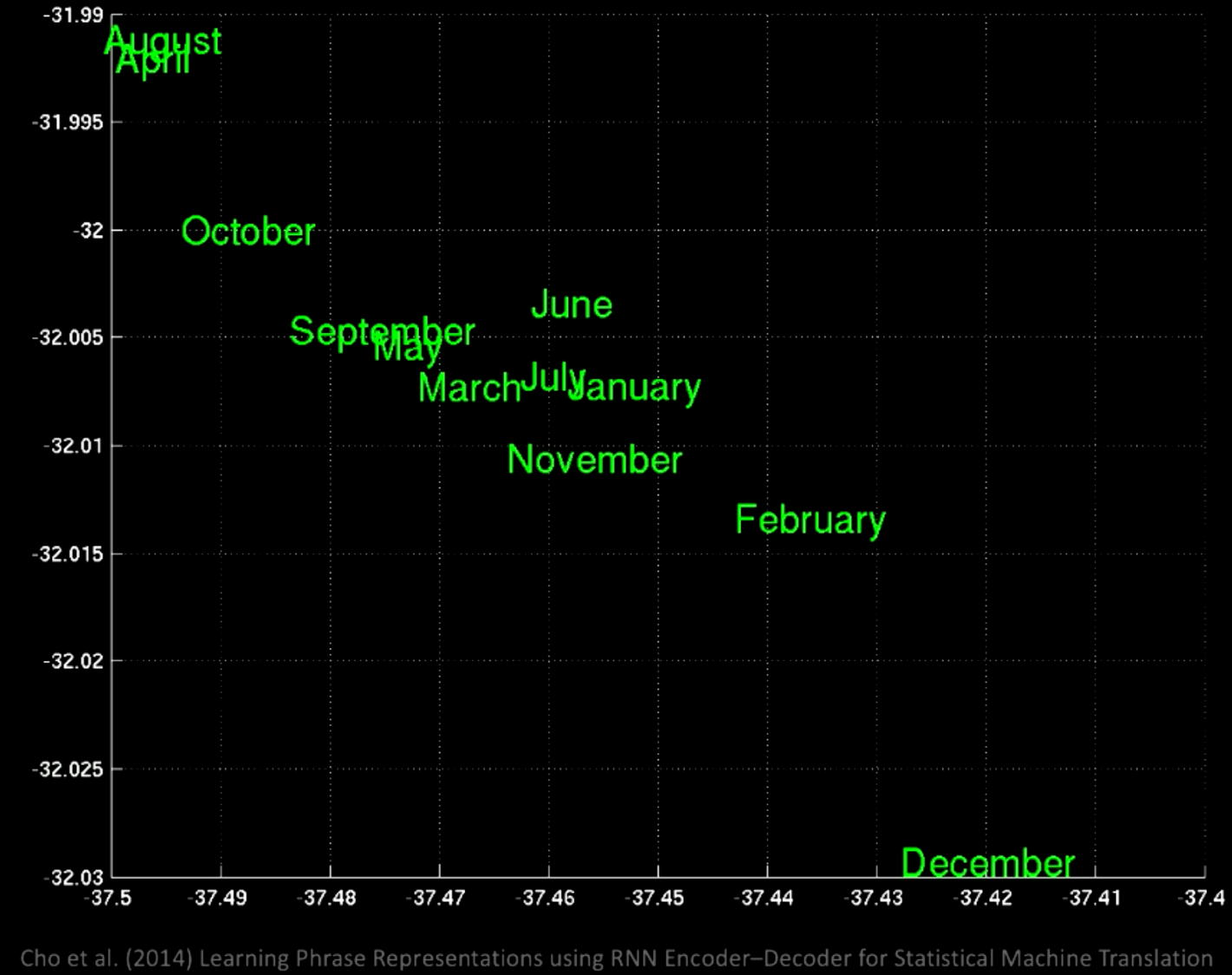
Fig 12: Kelime gruplarına yakından bakış

Başka bir alana bakarsanız, “a few days ago” (birkaç gün önce) “the next few months” (gelecek birkaç ayda) gibi kalıpları görebilirsiniz.

Fig 13: Başka bir bölgedeki kelime grupları

Bu örneklerden görüldüğü gibi farklı alanlar belirli paylaşılan anlamları kapsar.

Fig 14. bu tür bir ağ eğiterek nasıl anlamsal özelliklerin yakalanabildiğini gösterir. Örneğin, bu örnekte bir vektörün “man” (adam) ve “woman” (kadın) kelimelerini “king” (kral) ve “queen” (kraliçe) kelimelerine benzer bir şekilde bağladığını görebilirsiniz. Bu gömülmelerde erkek-kadın ilişkilerinde benzer uzaklıkları elde edersiniz. Bir başka örnek “walking” (yürüyor-) “walked” (yürüdü-) ve “swimming” (yüzüyor-) “swam” (yüzdü-) arasında görülebilir. Bu türk doğrusal dönüşümleri uygularak bir kelimeden diğerine ya da bir ülkeden başkentine geçebilirsiniz.

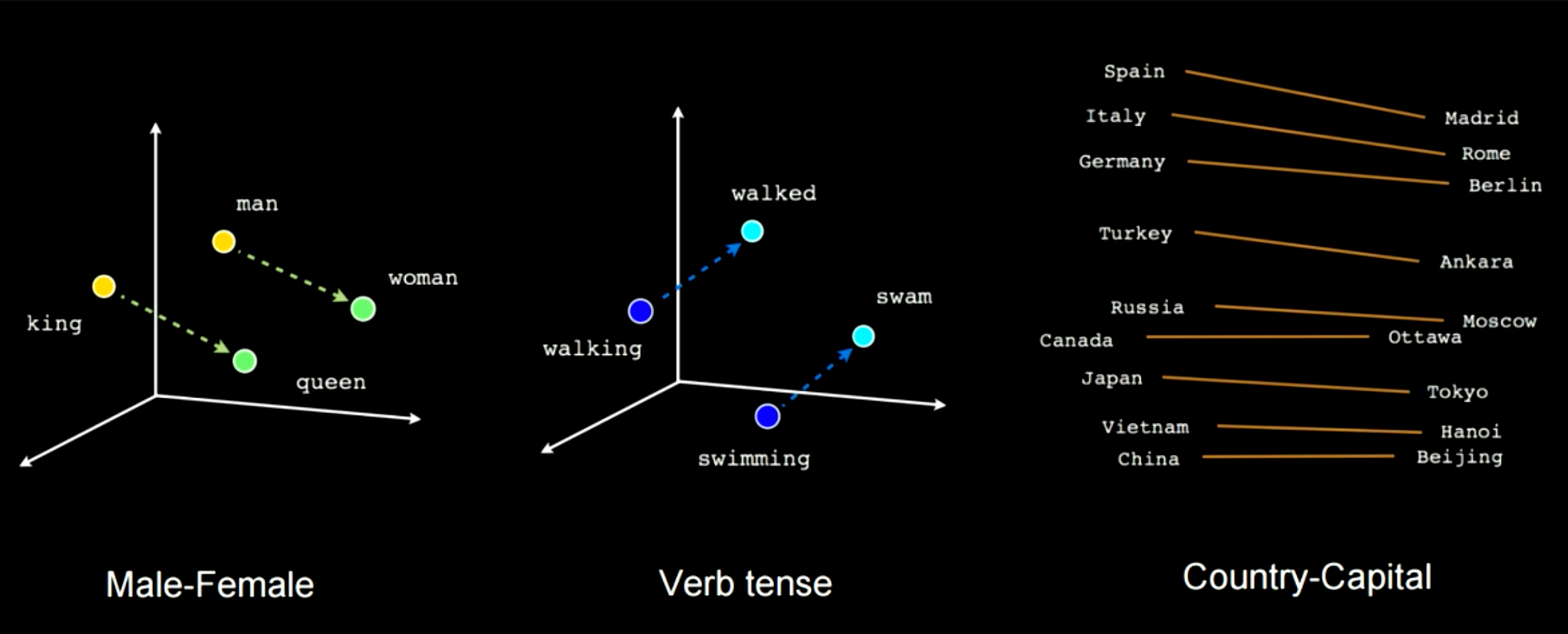
Fig 14: Eğitim esnasında yakalanan anlamsal özellikler

The fourth and final case is sequence to sequence. In this network, as you start feeding in input the network starts generating outputs. An example of this type of architecture is T9, if you remember using a Nokia phone, you would get text suggestions as you were typing. Another example is speech to captions. One cool example is this RNN-writer. When you start typing “the rings of Saturn glittered while”, it suggests the following “two men looked at each other”. This network was trained on some sci-fi novels so that you can just type something and let it make suggestions to help you write a book. One more example is shown in Figure 16. You input the top prompt and then this network will try to complete the rest.

Dördüncü ve son durumda diziden dizi üretilir. Bu ağda girdi beslendikçe ağ çıktı üretir. Bu tür mimarinin örneği T9’dur. Nokia telefonları hatırlıyorsanız, siz yazdıkça telefonun öneride bulunduğunu hatırlarsınız. Bir başka örnek konuşmadan altyazı oluşturmaktır. Havalı bir örnek yazar-RNN’dir. “the rings of Saturn glittered while” yazdığınızda size “two men looked at each other” cümlesi önerilir. Bu ağ bilimkurgu romanları üzerinde eğitildiğinden bir şeyler yazıp size bir kitap yazmanızda yardım edecek öneriler alabilirsiniz. Bir başka örnek Fig 16’da görülebilir. Üstteki cümle verildiğinde ağ kalanını tamamlamaya çalışır.

Fig 15: Diziden diziye

Fig 16: Diziden diziye modelle metin tamamlama modeli

Zamanda Geri Yayılım

Model Mimarisi

Bir RNN eğitmek için zamanda geri yayılım (BPTT, Back Propagation Through Time) kullanılmalıdır. RNN mimarisi aşağıdaki figürde berilmiştir. Soldaki dizayn döngü gösterimini kullanırken, sağdaki döngüyü açarak zamanda bir doğru üzerinde gösterir.

Fig 17: Zamanda geri yayılım

Gizli gösterimler şöyle gösterilmiştir

İlk denklem doğrusal olmayan bir fonksiyonun girdinin yığın şeklinde, gizli katmanın bir önceki konfigürasyonun sona eklendiği versiyonunun döndürülmüş haline uygulanışını gösterir. Başta, $h[0]$’a sıfır atanmıştır. Denklemi sadeleştirmek için, $W_h$, $\left[ W_{hx}\ W_{hh}\right]$ olarak iki ayrı matris halinde yazılabilir ve bazen dönüşüm şu şekilde ifade edilebilir.

bu girdinin yığın halinde gösterilişine denk gelir.

$y[t]$ son döndürmede hesaplanır ve sonrasında zincir kuralını kullanarak bir önceki zaman adımına hatayı geri yayabiliriz.

Dil Modellemede Yığınlaştırma (Batch-ification)

Bir sembol dizisiyle uğraşırken metni çeşitli boyutlarda yığınlaştırabiliriz. Örneğin, dizilerle uğraşırken, aşağıdaki figürde gösterildiği gibi, önce yığınlaştırma uygulanarak dikeyde zaman alanı korunabilir. Bu örnekte yığın boyutu dört olarak belirlenmiştir.

Figure 18: Yığınlaştırma

Eğer BPTT periodu $T$’ye 3 atanmışsa, RNN’deki ilk girdi $x[1:T]$ ve çıktı $y[1:T]$ şöyle belirlenir

RNN ilk yığın üzerinde çalışırken, önce $x[1] = [a\ g\ m\ s]$ beslenir ve çıktının $y[1] = [b\ h\ n\ t]$ olması sağlanır. Gizli gösterim $h[1]$, $x[2]$’den $y[2]$’nin üretilebilmesi için bir sonraki adıma iletilir. $h[T-1]$, son girdi olan $x[T]$’den son çıktı $y[T]$’nin üretilebilmesi için bir sonraki adıma iletildiğinde gradyanların sonsuza kadar yayılmasını önlemek için hem $h[T]$ hem $h[0]$ için gradyan yayılımı işlemi kesilir (PyTorch’ta .detach()). Tüm süreç aşağıdaki figürde gösterilmiştir.

Figure 19: Yığınlaştırma

Kaybolan ve Patlayan Gradyan

Problem

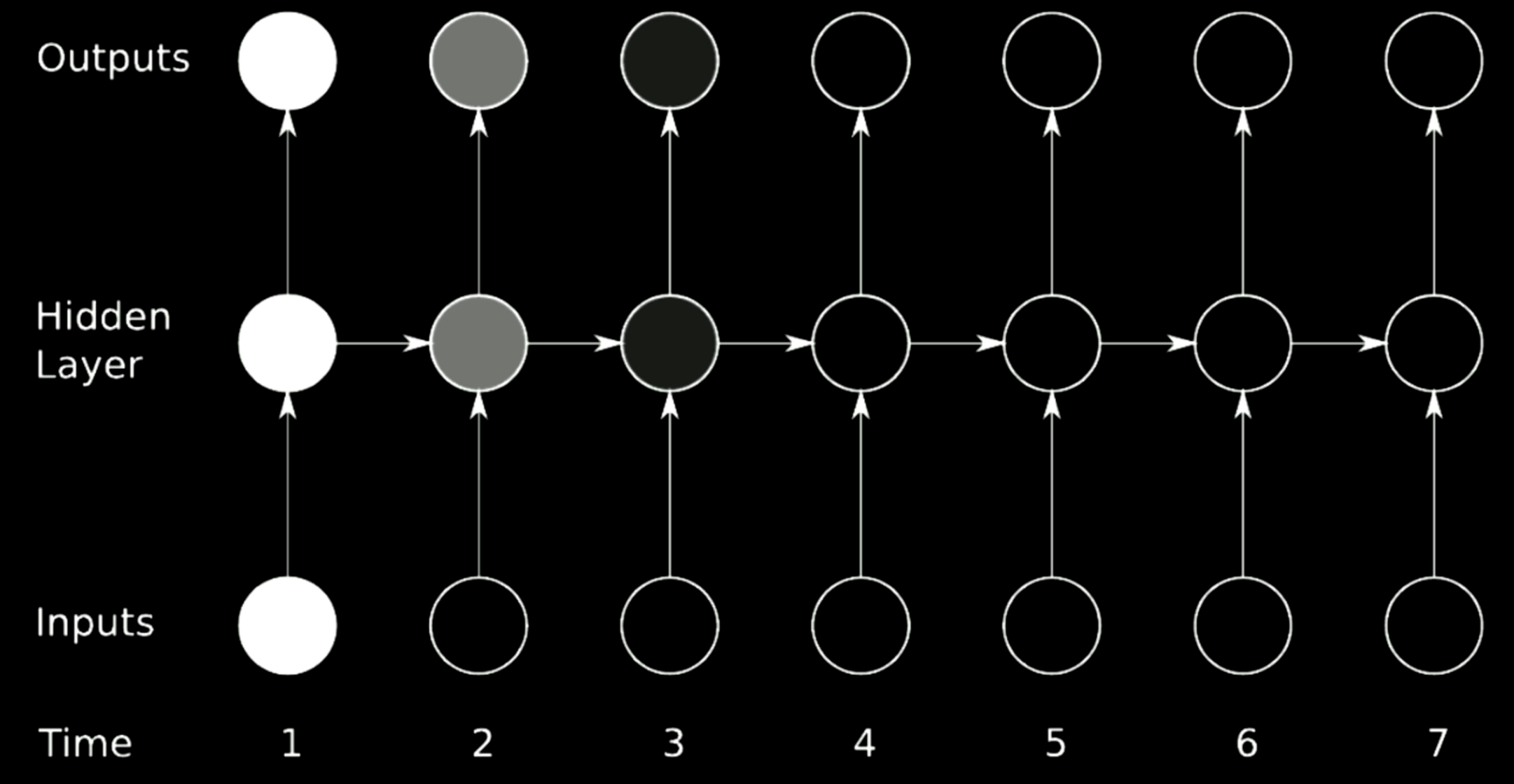
Figure 20: Kaybolma Problemi

Yukarıdaki figür tipik bir RNN mimarisidir. RNN’de önceki adımlardan döndürme yapılabilmesi için, yukarıdaki modelde yatay oklarla gösterilen matrisleri kullanırız. Matrisler çıktıların boyutlarını değiştirebileceğinden, eğer seçtiğimiz determinant 1’den büyükse, gradyan zamanla büyüyecek ve gradyan patlamasına sebep olacaktır. Başka bir deyişle, eğer seçtiğimiz özdeğer 0 boyunca küçükse, yayılım süreci gradyanları küçültecek ve gradyan kaybolmasına sebep olacaktır.

Tipik RNN’lerde, gradyanlar tüm olası oklar üzerinden iletilir ve bu gradyanların kaybolması veya patlaması için büyük olanak sağlar. Örneğin, parlak rengin gösterdiği üzere zaman 1’de gradyan büyüktür. Bir rotasyondan geçtiğinde epey küçülür ve zaman 3’te tamamen ölür.

Çözüm

Gradyanların patlamasını ve kaybolmasını önlemenin yollarından biri atlamalı bağlantılardır. Bunu sağlamak için birden fazla ağ kullanılabilir.

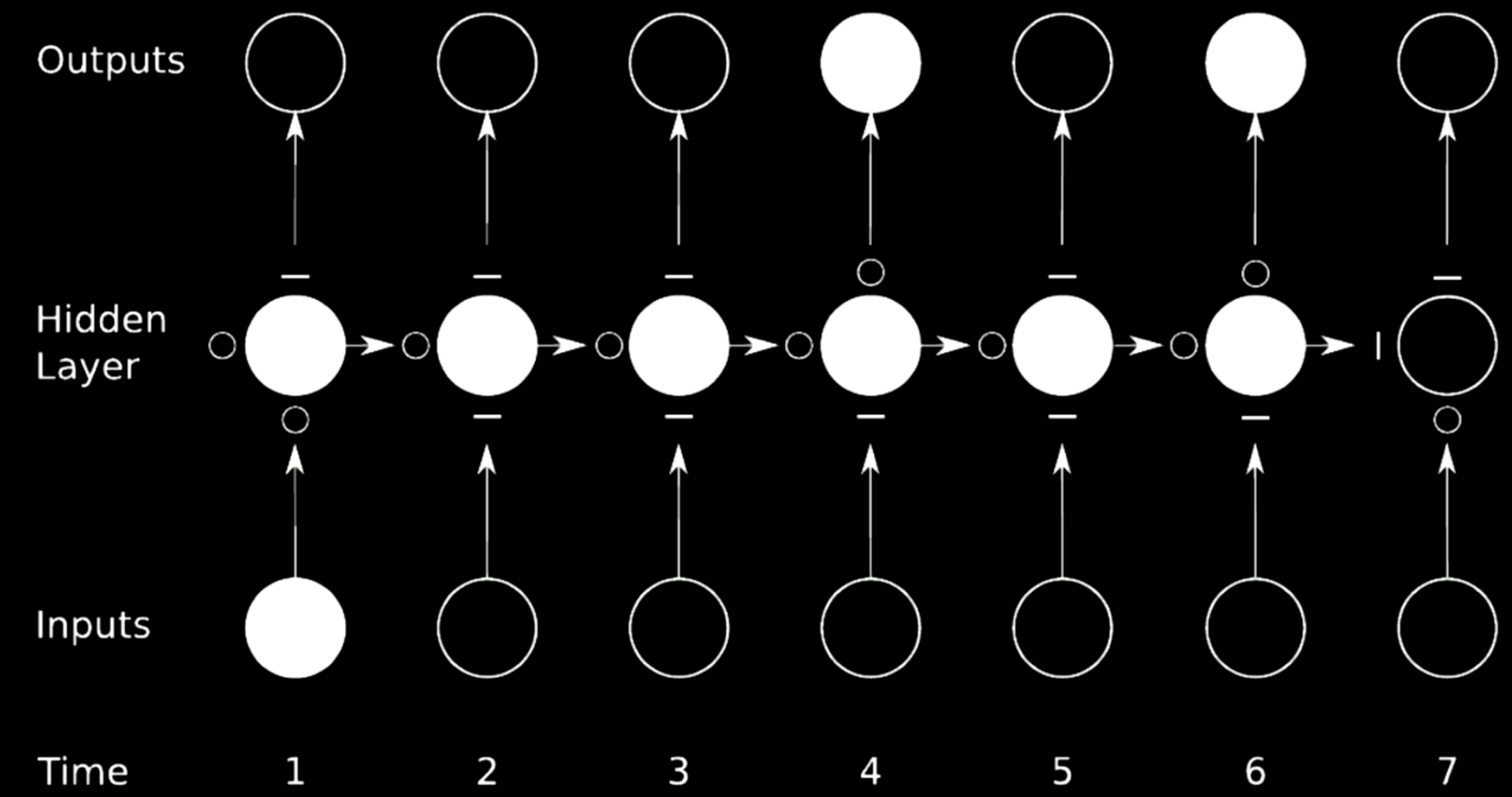
Figure 21: Atlamalı bağlantı

Yukarıdaki örnekte, orijinal ağ dört ağa bölünmüştür. İlk ağı ele alalım. Zaman 1’den bir değer alır ve çıktıyı gizli katmandaki ilk ara duruma gönderir. Durum, $\circ$ların gradyanların geçmesini sağladığı, $-$lerinse önlediği, üç ağ içerir. Bu tekniğe kapılı yinelemeli ağ denir.

LSTM yaygın bir kapılı RNN’lerden biridir ve bir sonraki bölümlerde detaylı olarak anlatılmıştır.

Uzun Ömürlü Kısa Dönem Bellek

Model Mimarisi

Aşağıdaki denklemler LSTM’i ifade eder. Girdi kapısı, afin transformasyon olacak olan, sarı kutularla gösterilmiştir. Bu transformasyon, aday kapımız olan $c[t]$ ile çarpılacaktır.

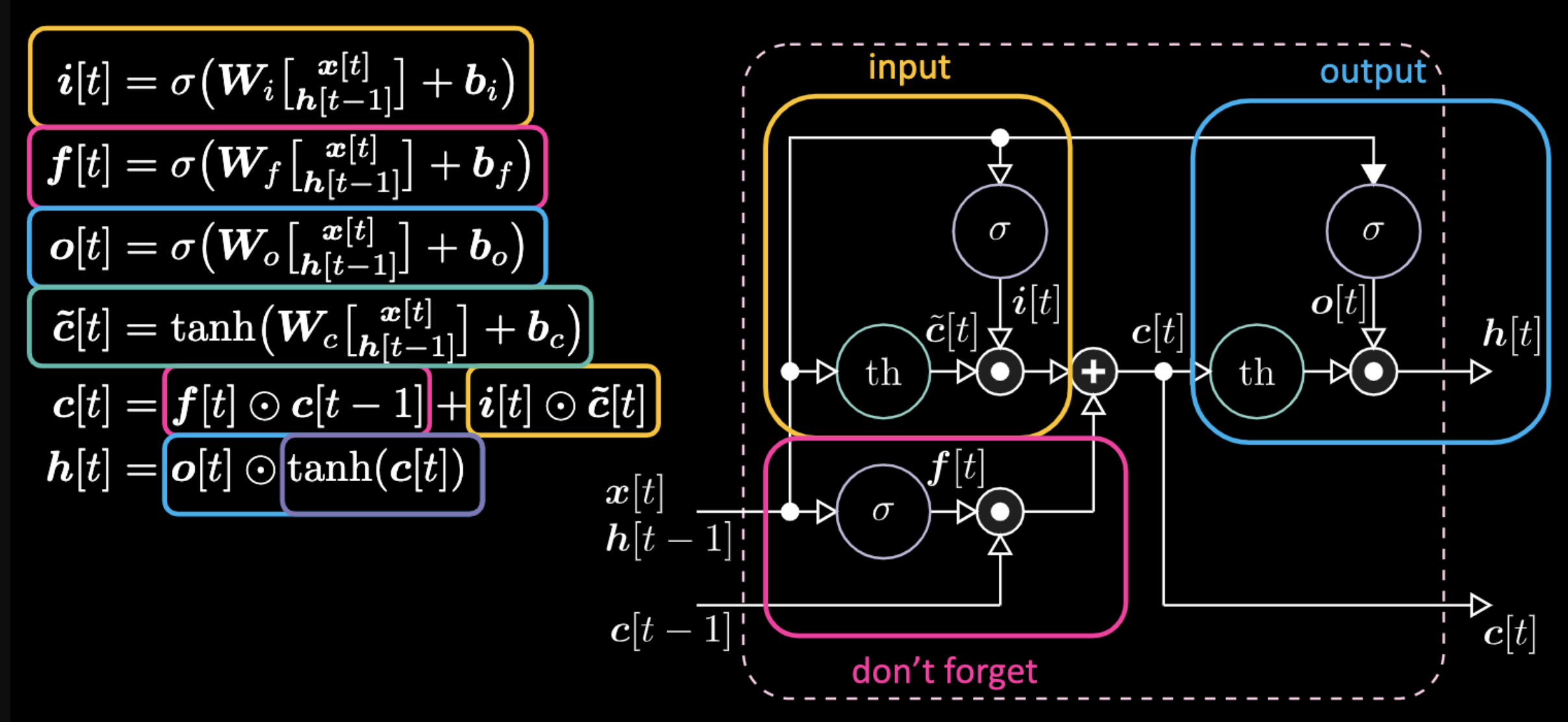
Figure 22: LSTM Mimarisi

Unutmama kapısı önceki hücre belleği $c[t-1]$ ile çarpılacaktır. Toplam hücre değeri $c[t]$ girdi ve unutmama kapılarının toplamıdır. Son izli durum gösterimi çıktı kapısı $o[t]$ ile $c[t]$’nin hiperbolik tanjant versiyonunun Hadamard çarpımıdır. Son olarak, basitçe, $\tilde{c}[t]$ bir yinelemeli ağdır. Yani çıktıyı modüle etmek için bir $o[t]$, unutmama kapısını modüle etmek için bir $f[t]$, ve girdiyi modüle etmek için bir $i[t]$’yi kullanırız. Tüm bu bellek ve kapılar arasındaki etkileşimler çarpımsal etkileşimlerdir. $i[t]$, $f[t]$ ve $o[t]$ sıfırdan bire kadar değerler alan sigmoidlerdir. Dolayısıyla, sıfırla çarparken kapalı bir kapı elde edersiniz, birle çarparken açık bir kapı elde edersiniz.

Peki çıktıyı nasıl kapatırız? Mor bir iç gösterim olan $th$’yi ele alalım ve çıktı kapısına sıfır verelim. Çıktı sıfırla bir şeyin çarpımı olur ve sıfır elde ederiz. Eğer çıktı kapısına bir verirsek mor gösterimle aynı değeri elde ederiz.

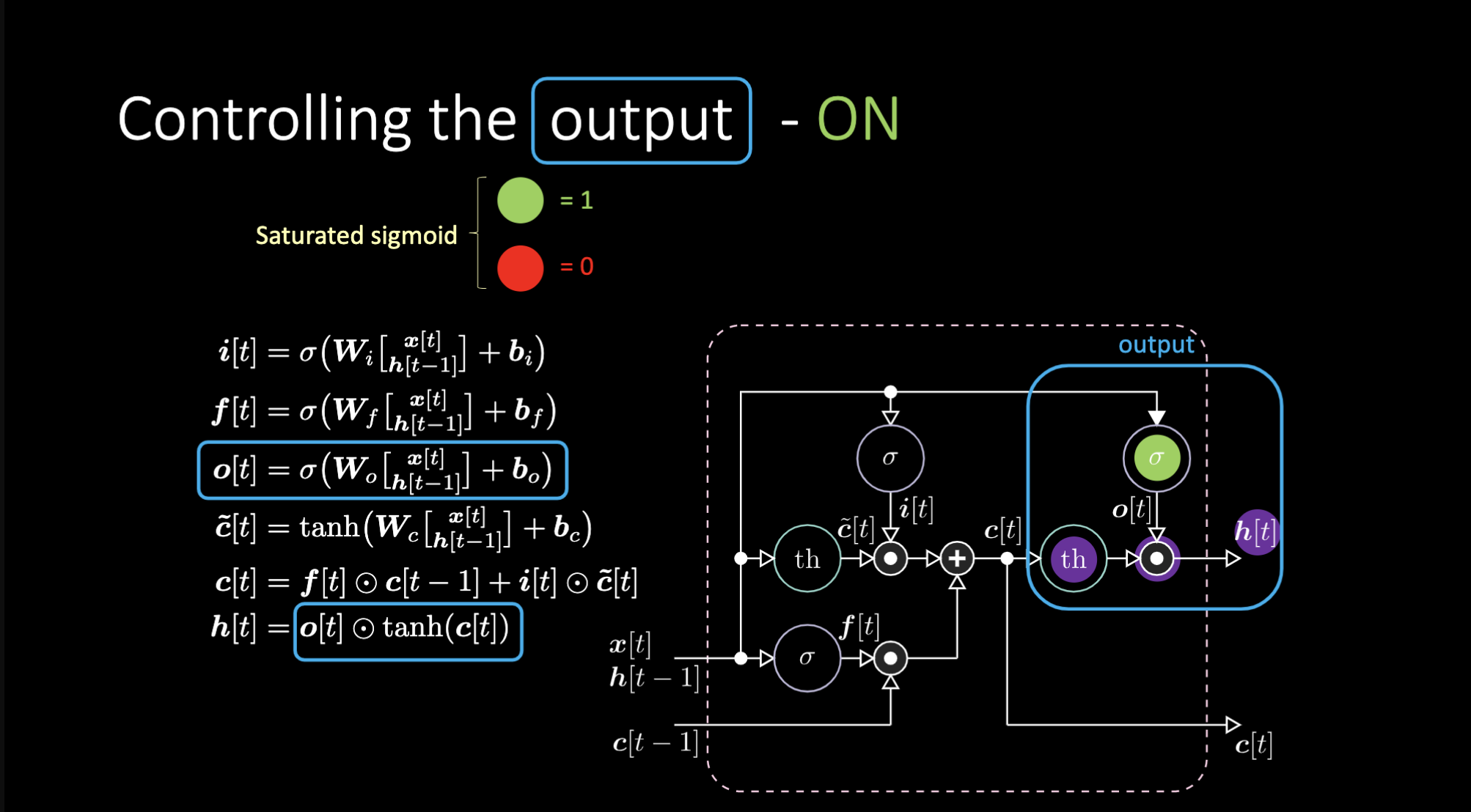
Fig 23: LSTM Mimarisi - Çıktı açık

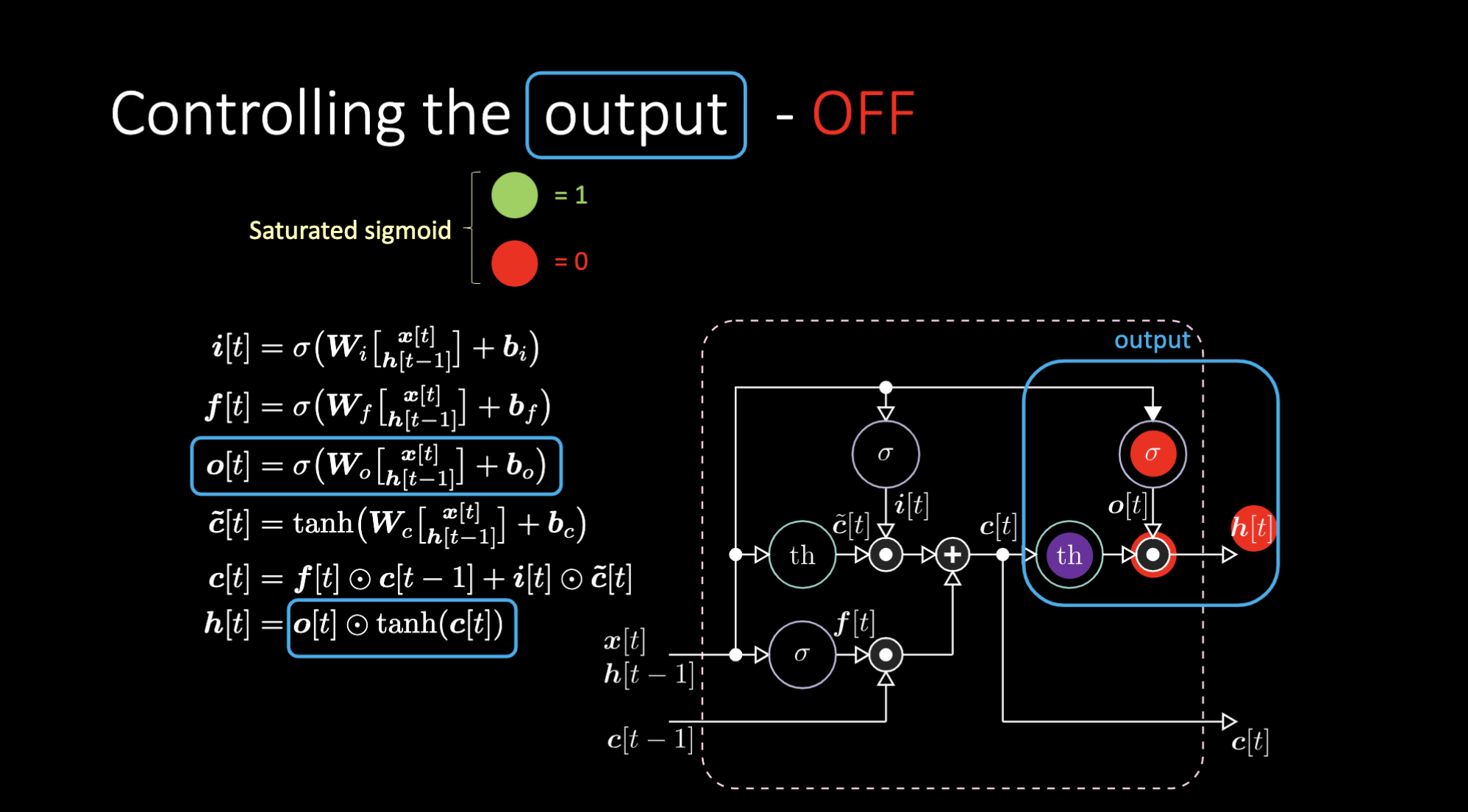
Fig 24: LSTM Mimarisi - Çıktı kapalı

Benzer bir şekilde belleği de kontrol edebiliriz. Örneğin $f[t]$ ve $i[t]$’yi sıfır yaparak belleği sıfırlayabiliriz. Çarpım ve toplamadan sonra bellekte sıfır elde ederiz. Öte yandan iç gösterim $th$’yi sıfır tutarken $f[t]$’ye bir vererek bellek içeriğini koruyabiliriz. Bu yüzden toplam $c[t-1]$ değerini alır ve iletmeye devam eder. Son olarak, girdi kapısında bir elde edecek, çarpımın mor değeri alabileceği ve unutmama kapısına sıfır vererek aslında unutmasını sağlayacak şekilde belleğe yazabiliriz.

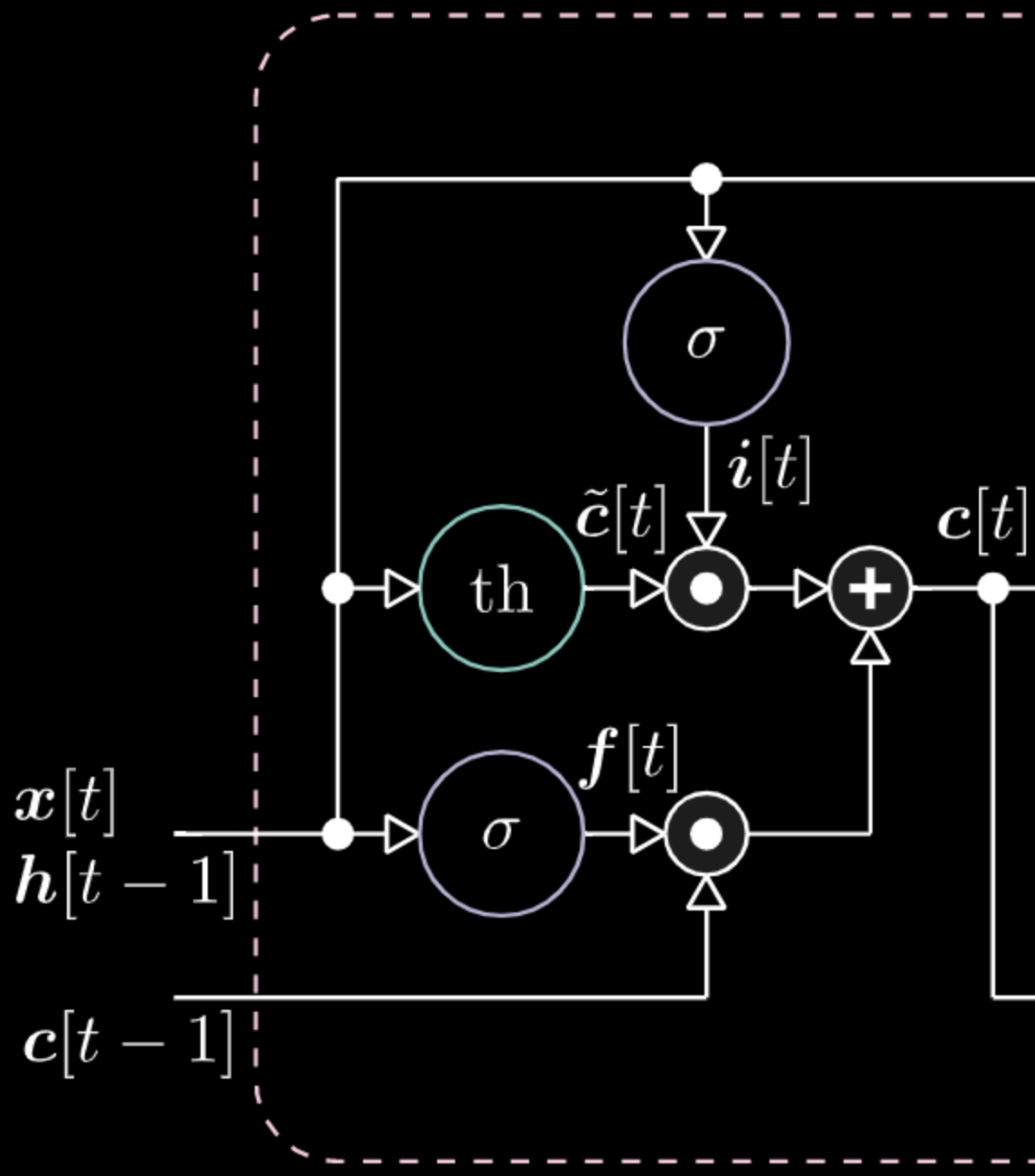
Fig 25: Bellek hücresinin görselleştirilmesi

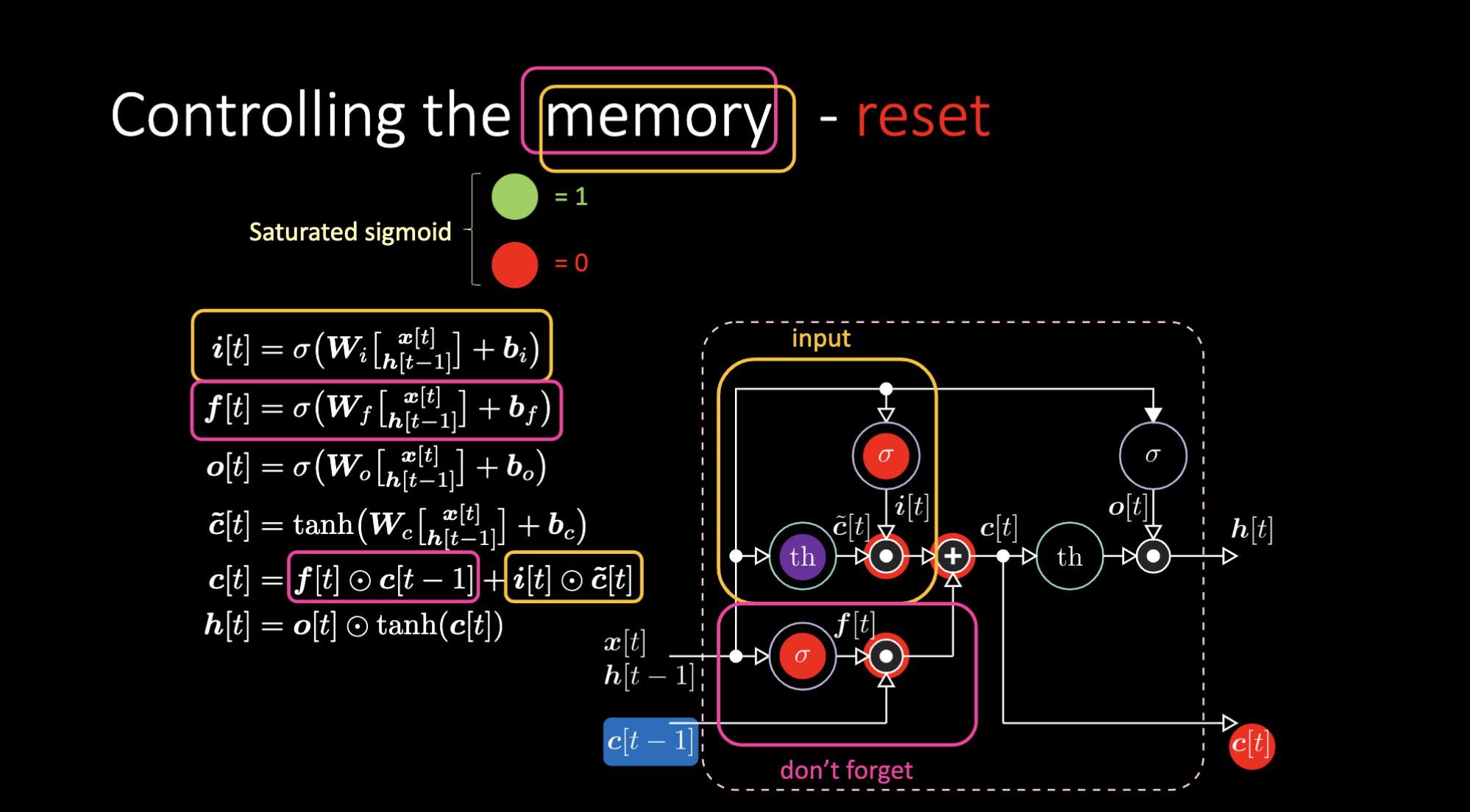
Fig 26: LSTM Mimarisi - Belleğin sıfırlanması

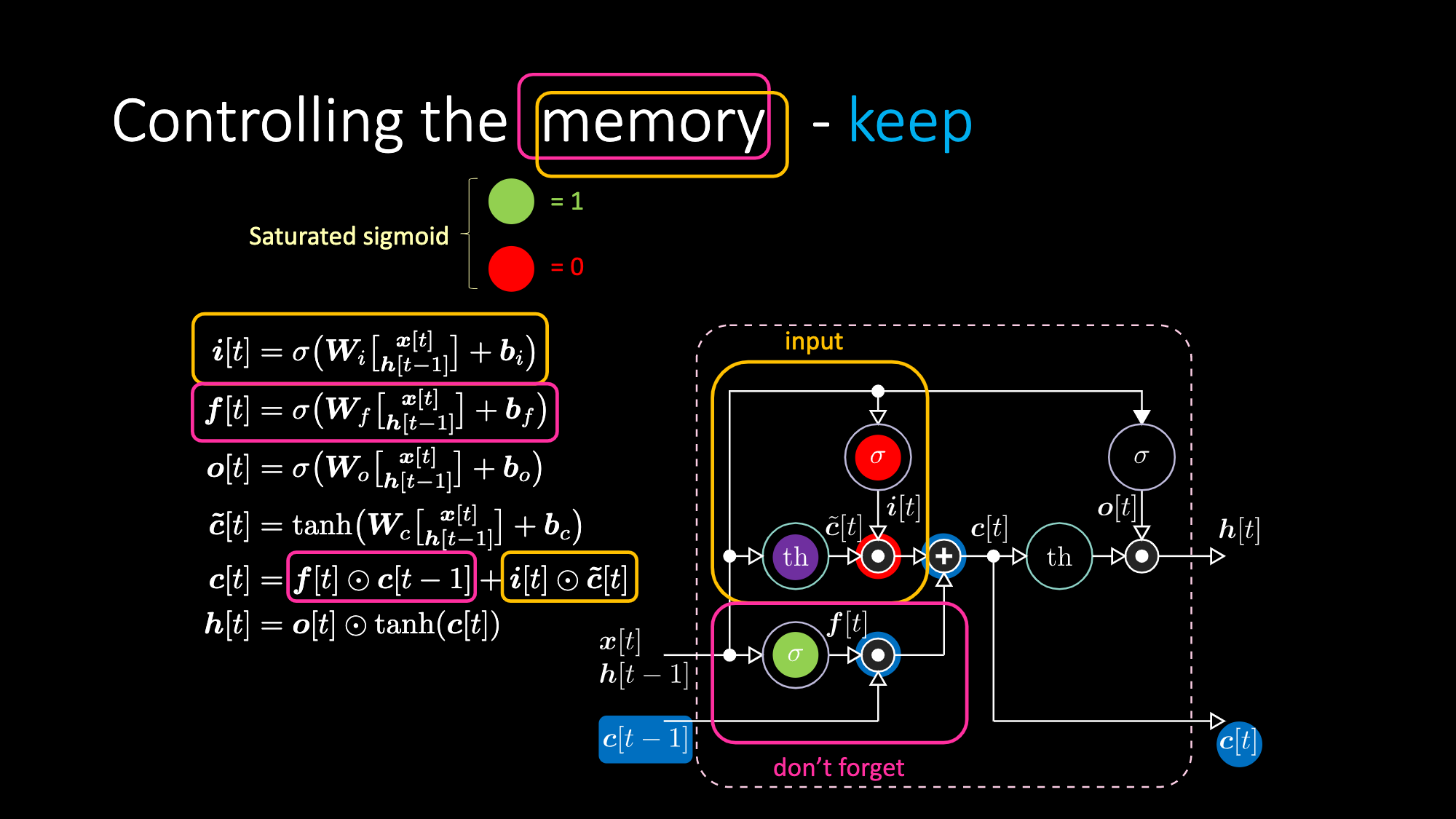
Fig 27: LSTM Mimarisi - Belleğin korunması

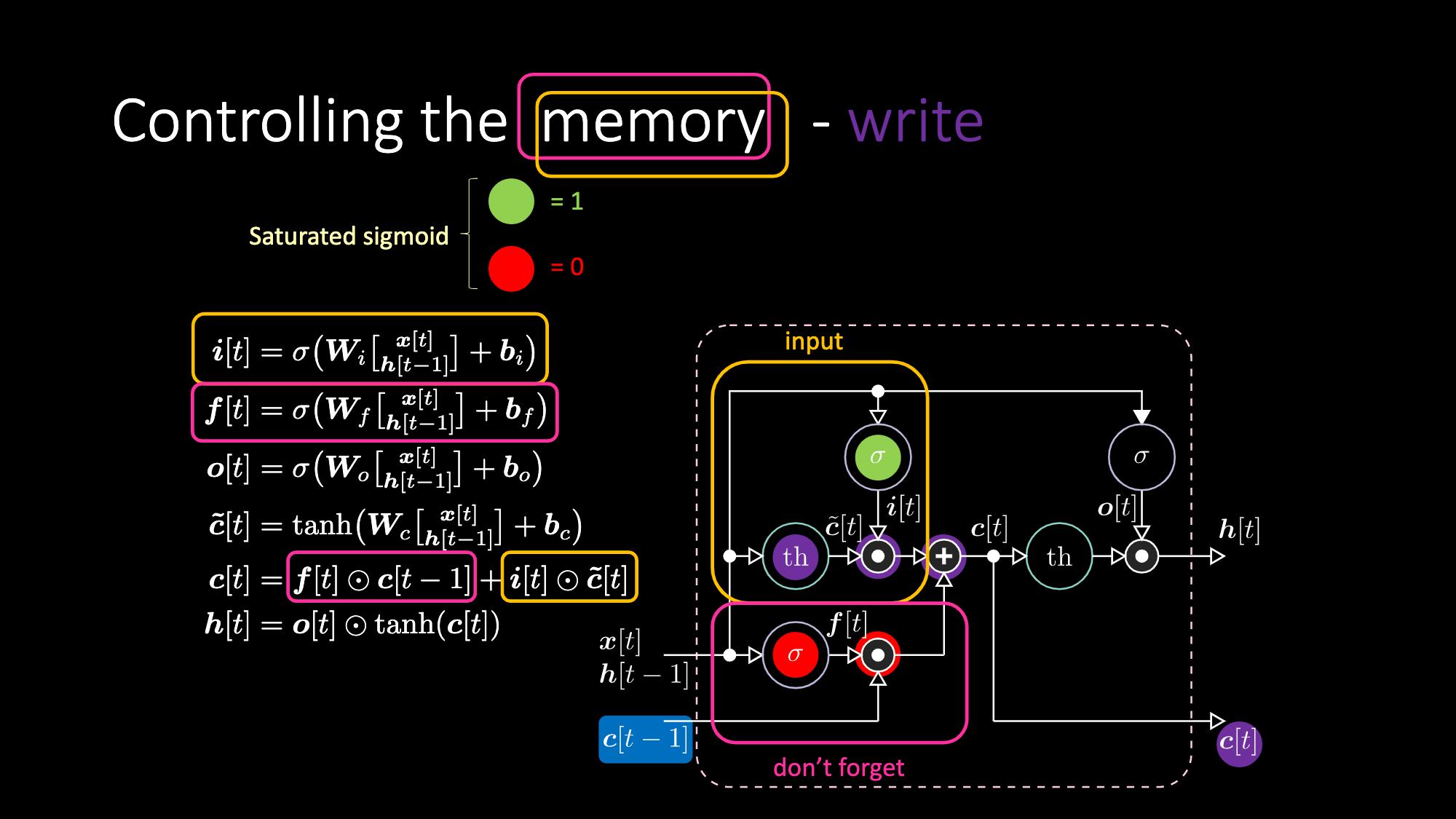
Figure 28: LSTM Mimari - Belleğe yazma

Notebook Örnekleri

Dizi Sınıflandırma

Burada amaç dizileri sınıflandırmaktır. Elemanlar ve hedefler yerel olarak temsil edilir (sadece bir elemanı sıfır olmayan vektörler halinde). Dizi bir B ile başlar, bir E ile biter (“tetik sembolü”) ve $t_1$ ve $t_2$ pozisyonlarında X veya Y karakterlerinden birini alan karakterleri dışındaki diğer karakterleri {a, b, c, d} kümesinden rastgele seçilen karakterlerden oluşur. DifficultyLevel.HARD (“ZorlukSeviyesi.ZOR”) örneğinde dizi uzunluğu 100-110 arasından , $t_1$ 10-20 arasından ve $t_2$ 50-60 arasından rastgele seçilir. Dört dizi sınıfı Q, R, S ve U X ve Y‘nin zamansal sıralarına bağlıdır. Kurallar şöyledir: X, X -> Q; X, Y -> R; Y, X -> S; Y, Y -> U.

1). Verikümesi İncelemesi

Veri oluşturucusundan döndürülen tip uzunluğu 2 olan bir demettir (tuple). Demetin ilk elemanı $(32, 9, 8)$ şeklindeki dizi yığınıdır. Bu veri ağa beslenir. Her satırda sekiz farklı sembol bulunur (X, Y, a, b, c, d, B, E). Her satır bir one-hot vektördür. Bir satır dizisi bir sembol dizisini gösterir. İlk tamamen sıfırdan oluşan satır dolgulamayı gösterir. Dolgulama dizinin boyu kısa olduğunda maksimum boyuta tamamlamak için kullanılır. Demetin ikinci elemanı yığına karşılık gelen, dört sınıfımız olduğu için (Q, R, S, and U), $(32, 4)$ şeklindeki sınıf etiketleridir. İlk dizi BbXcXcbE‘dir. Kodçözülmüş sınıf etiteti ise Q‘ya karşılık gelen $[1, 0, 0, 0]$ vektörüdür.

Fig 29: Girdi vektörü örneği

2). Modelin Tanımlanması ve Eğitimi

Basit bir özyinelemeli ağ, bir LSTM, tanımlayalım ve 10 epok boyunca eğitelim. Eğitim döngüsünde aşağıdaki beş adıma dikkat etmeliyiz:

• Modelin ileri geçişi
• Kaybın hesaplanması
• Gradyan önbelleğinin sıfırlanması
• Kaybın parametrelere göre kısmi türevlerinin geri yayılımla hesaplanması
• Gradyanların tersi yönde güncelleme

Fig 30: Basit RNN vs LSTM - 10 Epok

Basit zorluk seviyesinde, 10 epoktan sonra, RNN %50 doğruluk oranına ulaşırken LSTM %100’e ulaşır. Ama LSTM RNN’in dört katı ağırlığa sahiptir ve iki gizli katmandan oluşur, bu nedenle bu adil bir karşılaştırma değildir. 100 epoktan sonra RNN de %100 doğruluk oranına erişir ve LSTM’e göre daha uzun sürede eğitilir.

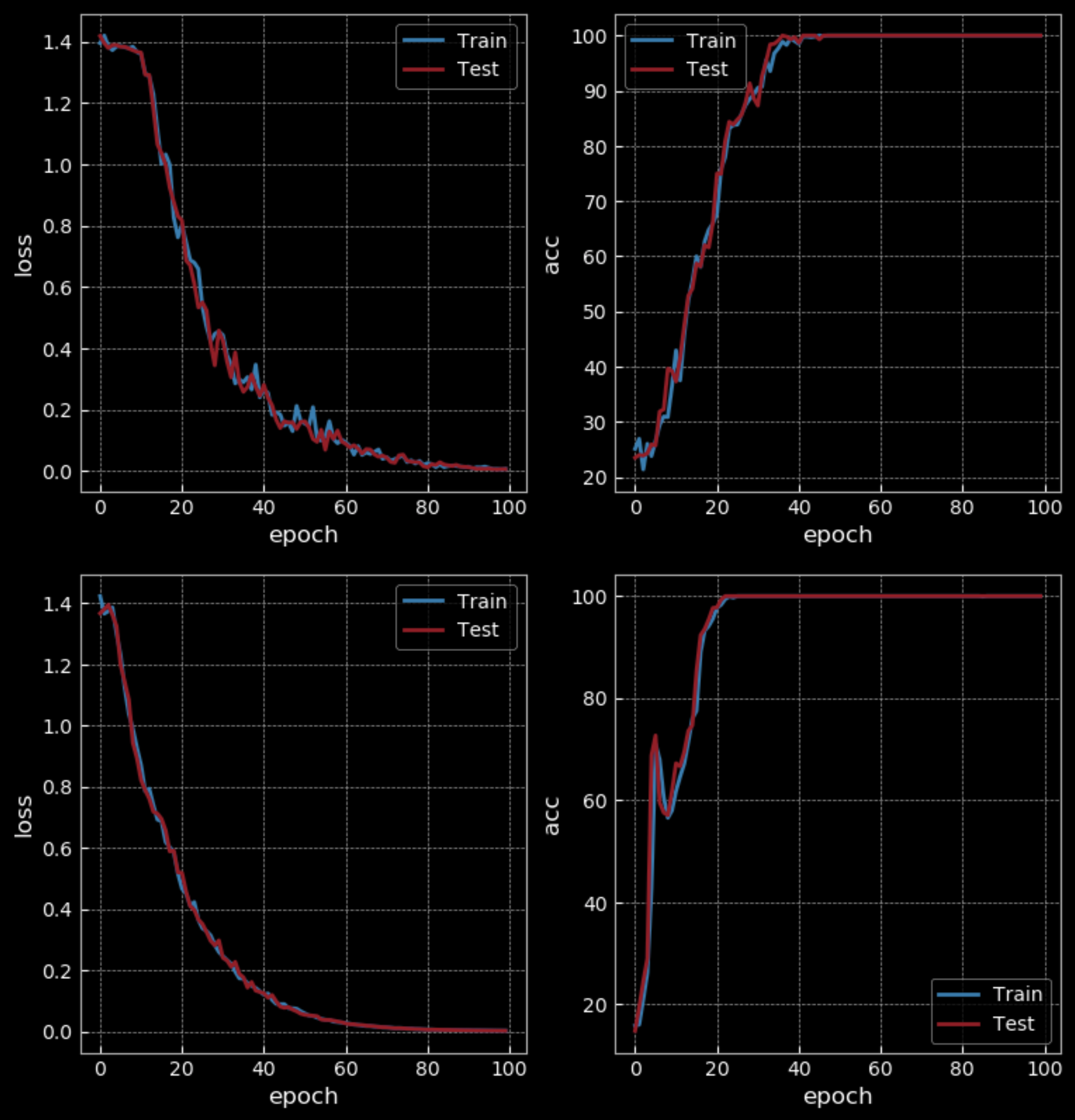
Fig 31: Basit RNN vs LSTM - 100 Epok

Daha uzun diziler kullanarak eğitimdeki zorluk seviyesini artırdığımızda LSTM çalışmaya devam ederken RNN’in başarısız olduğunu görürüz.

Fig 32: Gizli durum değerinin görselleştirilmesi

Yukarıdaki görsel LSTM’in gizli durumunun zamana göre değişimini gösterir. Girdileri tanh üzerinden göndeririz, böylece $-2.5$’in altındaki değerler $-1$’e, $2.5$ üzerindeki değerler $1$’e eşlenir. Bu örnekte X için bir gizli katmanın seçildiğini (resimdeki beşinci satır) ve sonrasında başka bir X değeri için kırmızı olduğunu görebiliriz. Yani, hücrenin beşinci gizli biriminin X‘i gözlemlediğinde tetiklendiğini ve diğer X‘i gördükten sonra sessizleştiğini görebiliriz. Bu bizim sekansın sınıfını tanımamızı sağlar.

Sinyal Yankılama

Sinyali n adım yankılama senkonize çoktan-çoğa görevlere örnektir. Bir örnekte, ilk girdi dizisi "1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 1 1 1 ...", ilk hedef dizisi "0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 ..."‘dir. Bu örnekte çıktı üç adım gecikmelidir. Yani bu bilgiyi tutabilmek için bir kısa-dönem belleğe ihtiyaç duyarız. Bir dil modelindeyse daha önceden henüz söylenmemiş bir şeyi söyler.

Tüm diziyi ağa göndermeden ve son hedefi bir şey olması için zorlamadan önce, uzun dizileri küçük parçalara ayırmamız gerekir. Yeni bir parçayı beslerken, bir sonraki yeni parçayı beslerken iç duruma girdi olarak verebilmek için gizli durumu takip etmemiz gerekir. LSTM’de yeterince kapasiteye sahip olduğunuz sürece belleği uzun süre koruyabilirsiniz. RNN belli bir uzunluğa eriştikten sonra geçmişte ne olduğunu unutmaya başlar.