RNN'ler, GRU'lar, LSTM'ler, Dikkat, Diziden Diziye (Seq2Seq), ve Bellek Ağları

Derin Öğrenme Mimarileri

Derin öğrenmede farklı fonksiyonların gerçeklenmesi için farklı modüller bulunur. Derin öğrenmede uzmanlaşmanın gerekliliklerinden biri belirli görevleri yerine getirebilmek için mimariler tasarlamaktır. Tıpkı eskilerde bilgisayarlara yönergeler vermek için algoritmaların kullanıldığı programların yazıldığı gibi, derin öğrenme karmaşık bir fonksiyonu, fonksiyonlarının öğrenme ile belirlendiği, (yüksek ihtimalle dinamik) fonksiyonel modüllerden oluşan grafiklere indirger.

Evrişimli ağlarda gördüğümüz üzere, ağ mimarisi önemlidir.

Yinelemeli Ağlar

Evrişimli sinir ağlarında grafikler ya da modüller arasındaki bağlantılar döngü içeremez. Çıktıları hesaplarken girdilerin hazır olabilmesi için en azından kısmi bir sıralama bulunur.

Fig. 1’de gösterildiği gibi, yinelemeli ağlarda döngüler bulunur.

Fig. 1. Döngü içeren bir yinelemeli ağ

• $x(t)$ : zamana göre değişen girdi
• $\text{Enc}(x(t))$: girdi için bir gösterim üreten kodlayıcı
• $h(t)$: girdinin gösterimi
• $w$: eğitilebilir parametreler
• $z(t-1)$: önceki gizli durum
• $z(t)$: şimdiki gizli durum
• $g$: karmaşık bir sinir ağı olabilecek fonksiyon; girdilerinden biri bir önceki zaman adımı olabilecek olan $z(t-1)$
• $\text{Dec}(z(t))$: çıktı üreten kodçözücü

Yinelemeli Ağlar: Döngünün açılımı

Döngüyü zaman içinde açın. Girdisi bir sıralı dizidir $x_1, x_2, \cdots, x_T$.

"
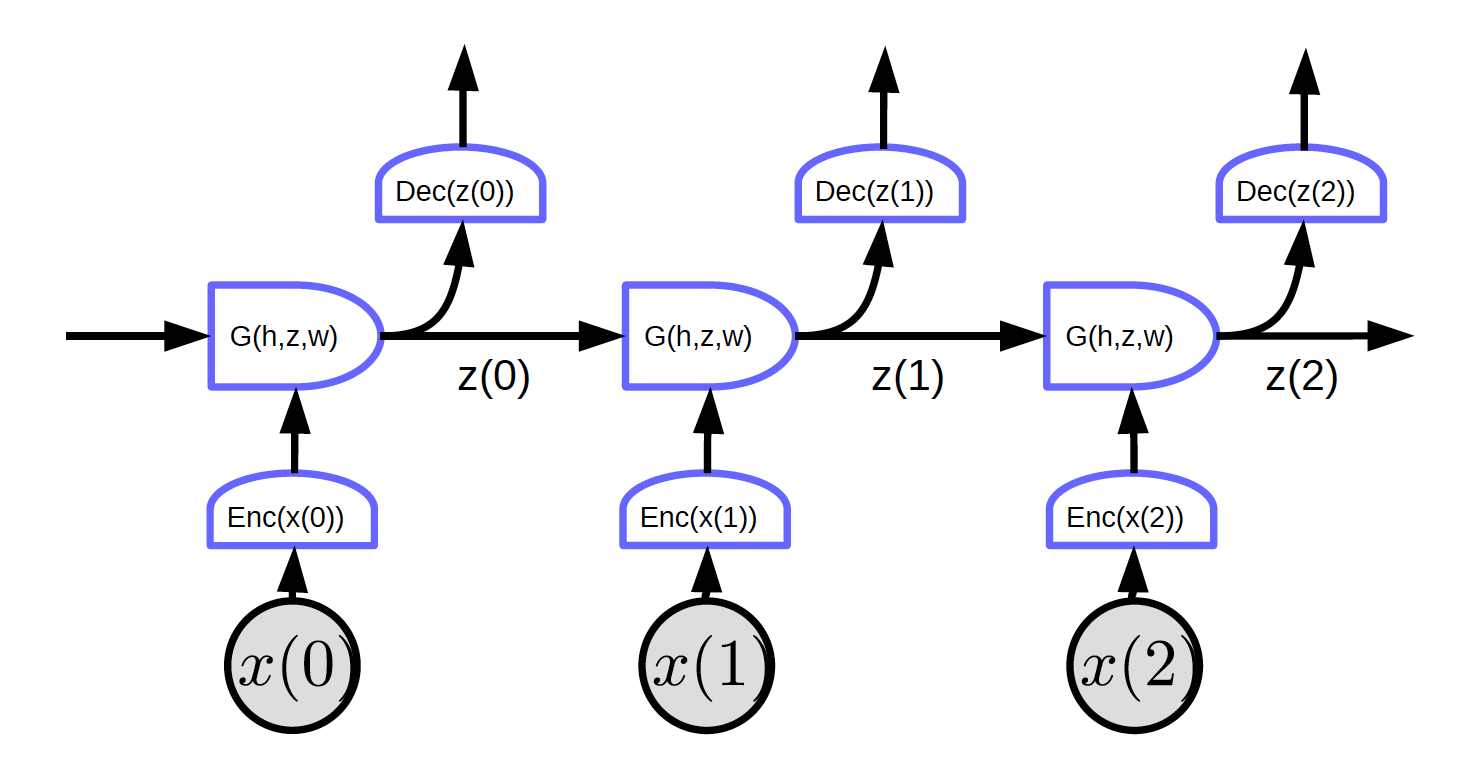
Fig. 2. Döngüsü açılmış yinelemeli ağlar

Fig. 2’de girdi $x_1, x_2, x_3$ şeklindedir.

t=0 zamanında, $x(0)$ girdisi kodlayıcıya iletilir ve kodlayıcı $h(x(0)) = \text{Enc}(x(0))$ gösterimini üretip gizli durumu ($z(0) = G(h_0, z’, w)$) üretmesi için G’ye iletir. t=0 zamanında $G$’deki $z’$ değerlerine ilk değerleri 0 olarak veya rastgele atanır.

Bu ağda döngüler bulunmadığından, geri yayılımı gerçekleştirebiliriz.

Fig. 2 belirli bir özelliğe sahip olan bir yinelemeli ağı gösteriyor: Tüm bloklar aynı ağırlıkları paylaşıyor. Üç kodlayıcı, kodçözücü ve G fonksiyonları farklı zaman adımlarında aynı ağırlıklara sahip.

BPTT: Zaman boyunca geri yayılım (backprop through time). Ne yazık ki, BPTT RNN’lerin saf formunda çok iyi çalışmaz.

RNN’lerin problemleri:

1. Kaybolan Gradyanlar:
   • Uzun bir sıralı dizide, her zaman adımında gradyanlar (transpoze edilmiş) bir ağırlık matrisiyle çarpılır. Eğer ağırlık matrisinde küçük değerler varsa, gradyanların normları gittikçe, üstel bir şekilde, küçülür.
2. Patlayan Gradyanlar:
   • Eğer büyük bir ağırlık matrisimiz varsa ve yinelemeli katmandaki eğrisellik (non-linearity) doymuyorsa, gradyanlar patlayacaktır. Her güncelleme adımında ağırlıklar ıraksayacaktır. Gradyan inişinin çalışabilmesi için çok küçük bir öğrenme hızı kullanmamız gerekebilir.

RNN’leri kullanmak için sebeplerden biri geçmişteki bilgiyi hatırlamının sağladığı avantajdır. Ancak bazı püf noktaları uygulanmadan RNN’ler uzun zaman önceki bilgileri hatırlayamayabilir.

Kaybolan gradyan problemine bir örnek:

Girdi bir C programından karakterlerdir. Sistem verilen programın sentaktik açıdan doğru bir program olup olmadığını söyleyecektir. Sentaktik açıdan doğru bir program geçerli sayıda parantezlere sahip olmalıdır. Bu sebeple, ağ kaç tane açık parantez olduğunu ve bunları kapatıp kapatmadığını hatırlamalıdır. Ağ bu bilgiyi bir sayaçta tutar gibi gizli durumunda tutmalıdır. Ancak uzun bir programda, kaybolan gradyanlar yüzünden, bu bilgiyi muhafaza etmekte zorlacaktır.

RNN’ler için Püf Noktaları

• Gradyanları kesmek: (patlayan gradyanları önlemek için) Çok büyük hale geldiklerinde gradyanları kes.
• İlk değer ataması: (doğru bir değerle başlamak kaybolan/patlayan gradyanları önler) Normu bir dereceye kadar korumak için ağırlık matrislerine ilk değer ata. Örneğin, ortogonal ilk değer ataması değer matrisine rastgele bir ortogonal matris olacak şekilde değerler atar.

Çarpımsal Modüller

Çarpımsal modüllerde girdilerin ağırlıklı toplamlarını hesaplamaktansa, girdilerin çarpımlarının ağırlıklı toplamları hesaplanır.

Varsayın ki $x \in {R}^{n\times1}$, $W \in {R}^{m \times n}$, $U \in {R}^{m \times n \times d}$ ve $z \in {R}^{d\times1}$. Burada U bir tensördür.

, $s_i = w_{i}^\top x = \sum_j w_{ij}x_j$.

Sistemin çıktısı girdilerin ve ağırlıkların klasik ağırlıklı toplamıdır. Ağırlıklar da girdilerin ve ağırlıkların ağırlıklı toplamıdır.

Hiperağ mimarisi: Ağırlıklar başka bir ağ tarafından hesaplanır.

Dikkat

$x_1$ ve $x_2$ vektördür, $w_1$ ve $w_2$ softmax’ten sonraki skalerlerdir ve $w_1 + w_2 = 1$ denklemini sağlar, $w_1$ ve $w_2$ aynı zamanda 0 ve 1 arasındadır.

$w_1x_1 + w_2x_2$, i $x_1$ ve $x_2$’nin $w_1$ ve $w_2$ katsayıları tarafından ağırlıklarındırılmış ağırlıklı toplamıdır.

$w_1$ and $w_2$’nin göreceli büyüklüğünü değiştirerek, w_1x_1 + w_2x_2$’nin çıktısını $x_1$ ya da $x_2$’ye veya $x_1$ ve $x_2$’nin herhangi bir lineer kombinasyonuna dönüştürebiliriz.

Girdiler birden fazla $x$ vektörü içerebilir ($x_1$ ve $x_2$’den daha fazla). Sistem bunların uygun bir kombinasyonunu seçecektir ve bu seçim başka bir parametre olan z tarafından belirlenecektir. Bir dikkat mekanizması sinir ağının dikatinin belirli girdilere odaklanırken diğerlerini yoksaymasını sağlar.

Dikkat NLP dönüştürücü (transformer) mimarileri ya da diğer dikkat tiplerini kullanan NLP (Natural Language Processing, Doğal Dil İşleme) sistemlerinde giderek daha da önemli hale gelmektedir.

Ağırlıklar veriye bağlı değildir, çünkü z veriye bağlı değildir.

Gated Recurrent Units, Kapılı Yinelemeli Üniteler (GRU)

Yukarıda belirtildiği üzere, RNN kaybolan/patlayan gradyanlar sorunları yaşar ve durumları uzun süre hatırlayamaz. GRU, Cho, 2014, bu sorunları çözmeyi deneyen çarpımsal modellerin bir uygulamasıdır. GRU bellekli yinelemeli ağların bir örneğidir (bir diğeri LSTM’dir). Bir GRU ünitesinin yapısı aşağıda görülebilir:

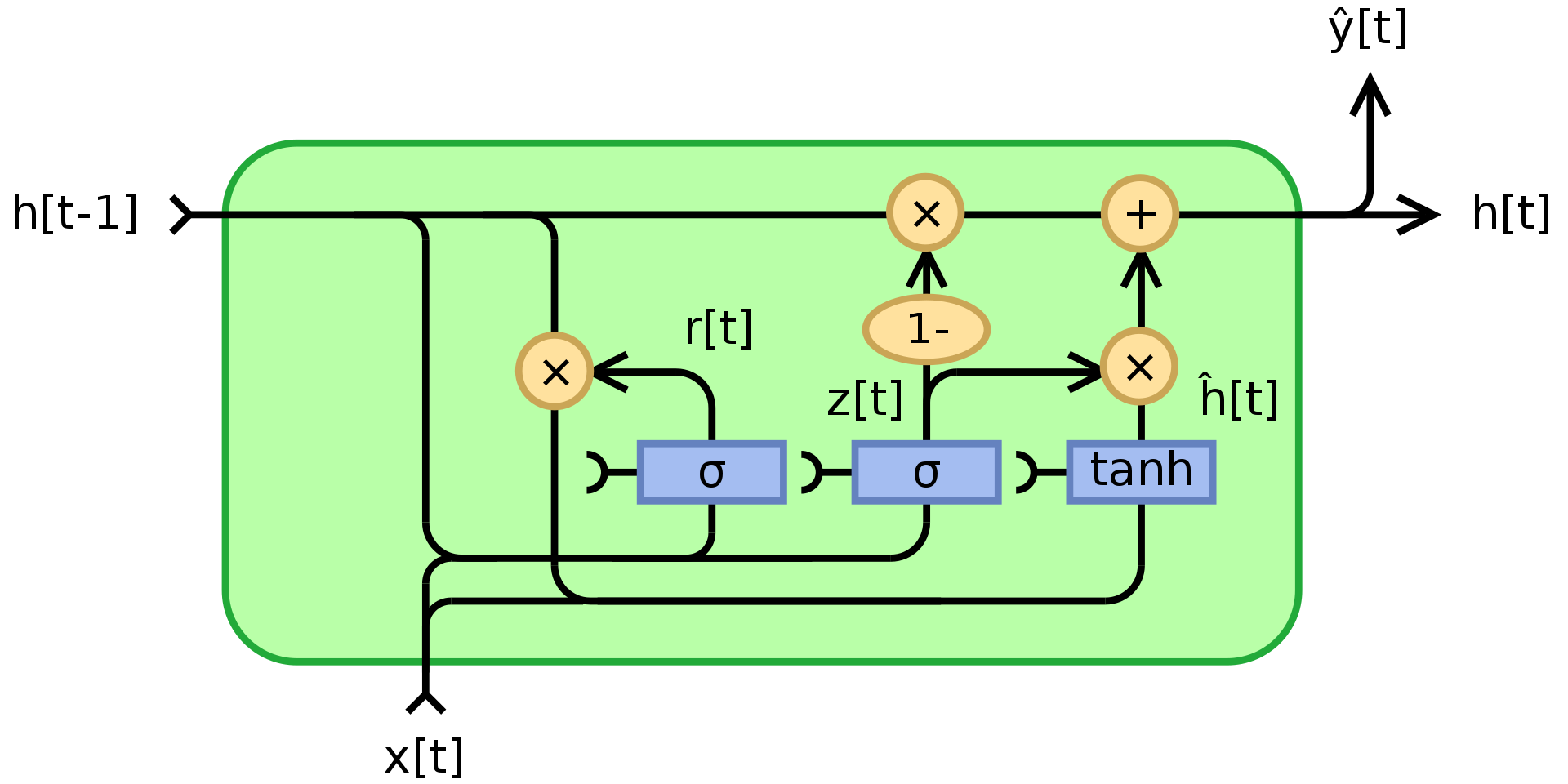
Fig. 3. Kapılı Yinelemeli Ünite [GRU]

burada $\odot$ Hadamard çarpımını, $x_t$ girdi vektörünü, gösterir, $h_t$ çıktı vektörünü, $z_t$ güncelleme kapısı vektörünü, $r_t$ sıfırlama kapısı vektörünü, $\phi_h$ hiperbolik tanh’yi, $W$,$U$,$b$ öğrenilebilir parametreleri gösterir.

Spesifik olmak gerekirse, $z_t$ geçmiş bilginin ne kadarının geleceğe aktarılması gerektiğini belirleyen bir kapı vektörüdür. İki lineer katmanın toplamına sigmoid fonksiyonunu, $x_t$ girdisine ve geçmiş $h_{t-1}$ durumuna yanlılık uygular. Sigmoidin uygulanmasının bir sonucu olarak $z_t$ 0 ve 1 arasında katsayılar içerir. Son çıktı durumu $h_t$, $h_{t-1}$ ve $z_t$ ile elde edilmiş olan $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$ ifadesinin lineer bir kombinasyonudur. Katsayı 1’se, şimdiki birimin çıktısı önceki durumun bir kopyasıdır ve (varsayılan davranış olarak) görmezlikten gelinir. 1’den daha azsa, girdiden gelen yeni bilginin bir kısmı dikkate alınır.

Sıfırlama kapısı $r_t$ geçmiş bilginin ne kadarının unutulması gerektiğini belirler. Yeni bellek içeriğinde, $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$, $r_t$ katsayısı 0’sa geçmişten gelen bilgi kullanılmaz. Aynı zamanda $z_t$’de 0’sa, $h_t$ sadece girdiye bakacağından tüm sistem tamamen sıfırlanır.

LSTM (Long Short-Term Memory, Uzun Ömürlü Kısa-Dönem Belleği)

GRU aslında kendisinden çok önce çıkmış olan LSTM’in basitleştirilmiş bir halidir Hochreiter, Schmidhuber, 1997. LSTM’ler geçmiş bilgiyi koruyan bellek hücreleri oluşturarak, aynı zamanda RNN’lerde görünen uzun süreli bellek kayıplarını da çözmeyi hedefler. LSTM’lerin yapısı aşağıda gösterilmiştir.

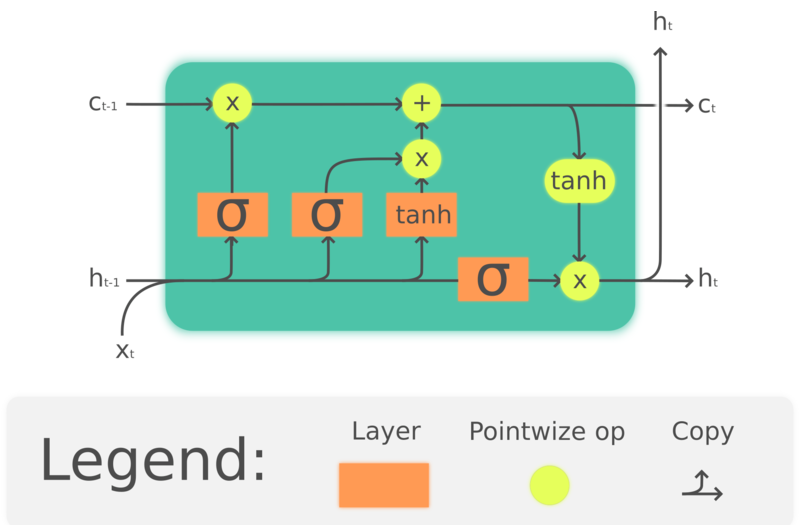
Fig. 4. LSTM

burada $\odot$ Hadamard çarpımını, $x_t\in\mathbb{R}^a$ LSTM biriminin girdilerinden birini, $f_t\in\mathbb{R}^h$ unutma kapısının aktivasyon vektörünü, $i_t\in\mathbb{R}^h$ girdi/güncelleme kapısının aktivasyon vektörünü, $o_t\in\mathbb{R}^h$ çıktı kapısının aktivasyon vektörünü, $o_t\in\mathbb{R}^h$ gizli durum vektörünü (ve aynı zamanda o birimin çıktısını), $c_t\in\mathbb{R}^h$ ise hücrenin durum vektörünü gösterir.

Bir LSTM ünitesi ünite içerisinde bilgiyi iletmek için hücre durumu $c_t$’yi kullanır. Kapı isimli yapıları kullanarak bilginin hücre durumunda korunup korunmayacağını düzenler. Unutma kapısı şimdiki girdi ve önceki gizli duruma bakarak $f_t$ bir önceki hücre durumu $c_{t-1}$’den ne kadar bilgi tutmak istediğimize karar verir ve $c_{t-1}$. katsayısı ile bunu 0 ve 1 arasında bir değerle ifade eder. $\tanh(W_cx_t + U_ch_{t-1} + b_c)$ hücre durumunu güncellemek için bir aday hesaplar, ve unutma kapısında olduğu gibi, girdi kapısı $i_t$ ne kadar güncelleme uygulanacağını belirler. Son olarak, çıktı $h_t$, hücre durumu $c_t$ temel alınarak hesaplanır, ancak sonrasında $\tanh$’tan geçirilip çıktı kapısı $o_t$ tarafından filtrelenir.

Her ne kadar LSTM’ler NLP’de sıkça kullanılıyor olsalar da, popülerlikleri azalmaktadır. Örneğin, konuşma tanıma zamansal CNN’lere, NLP ise dönüştürücülere (transformers) yönelmektedir.

Sequence to Sequence (Diziden Diziye) Modeli

Sutskever NIPS 2014 tarafından önerilen yaklaşım klasik yöntemlerle karşılaştırılabilecek performansa sahip olan ilk sinirsel makine tercüme sistemidir. Bu yöntem bir hem kodlayıcının hem de kodçözücünün çok katmanlı LSTM’lerden oluştuğu bir kodlayıcı-kodçözücü mimarisine sahiptir.

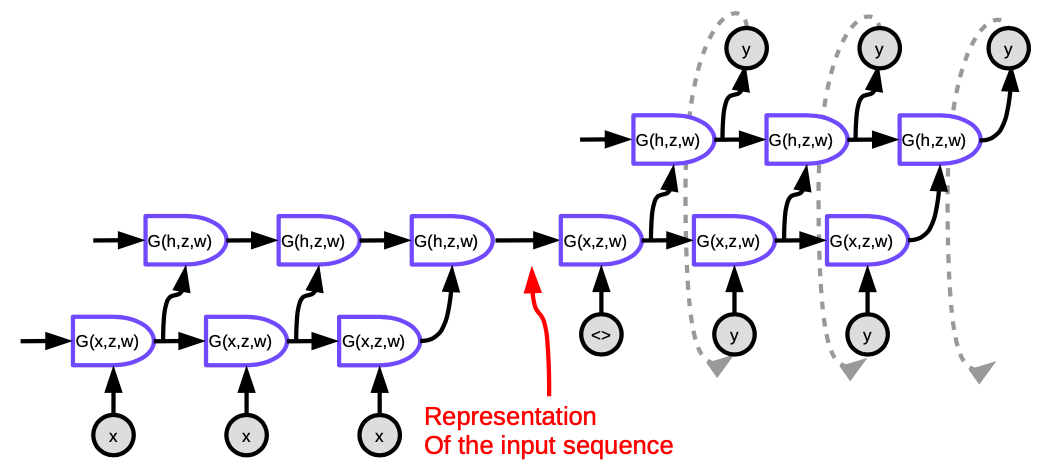
Fig 5. Seq2Seq

Fig. 5’teki tüm hücreler birer LSTM’dir. Kodlayıcı için (sol taraftaki kısım), zaman adımı sayısı çevirilecek cümlenin uzunluğuna eşittir. Her zaman adımında, bir önceki LSTM’in gizli durumunun bir sonrakine iletildiği LSTM yığınları bulunur (yayına göre dört katman). Son zaman adımındaki son katman tüm cümlenin anlamını temsil eden bir vektör oluşturur ve hedef dildeki kelimeleri üreten bir başka çok katmanlı LSTM’e (kodçözücü) iletilir. Kodçözücüde metin ardışık bir şekilde üretilir. Her bir zaman adımında bir kelime üretilir ve bir sonraki adıma girdi olarak verilir.

Bu mimari iki açıdan tatmin edici değildir: İlk sebep, cümlenin tüm anlamının kodlayıcı ve kodçözücü arasındaki gizli durum vektörüne sıkıştırılmak zorunda olmasıdır. İkinci sebepse, LSTM’lerin yaklaşık olarak 20 kelimeden fazla bilgiyi tutmakta zorlanmalarıdır. Bu sorunlar ters yönlerde iki LSTM kullanan Bi-LSTM’le çözülebilir. Bi-LSTM’de anlam biri soldan sağa, diğeri sağdan sola çalışan iki LSTM tarafından oluşturulan iki vektöre kodlanabilir. Bu yöntem çok bilgi kaybetmeden cümlenin uzunluğunun iki katına çıkarılabilmesini sağlar.

Dikkatli Seq2seq

Yukarıda bahsedilen yöntemin başarısı kısa sürdü. Bahdanau, Cho ve Bengio‘nun yayınında tüm cümlenin anlamını bir vektöre sıkıştıran devasa bir network yerine her adımda dikkati orijinal dildeki denk anlamlara sahip alakalı yerlere yoğunlaştırmanın daha manalı olduğu gösterildi (yani dikkat mekanizması).

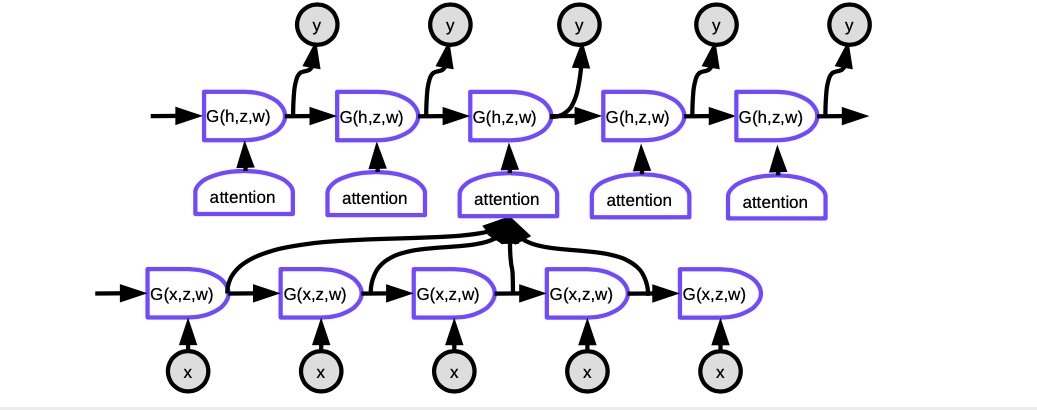
Fig 6. Dikkatli Seq2Seq

Dikkatte, her bir adımda şimdiki kelimeyi üretmek için öncelikle girdi cümlesindeki hangi kelimelerin gösterimlerine odaklanmamız gerektiğine karar vermemiz gerekir. Aslında, ağımız hangi kodlanmış girdinin, kodlayıcının şu anki çıktısıyla ne kadar eşleştiğini gösteren bir skor hesaplamayı öğrenir. Bu skorlar bir softmax ile normalize edilir ve sonrasında katsayılar kodlayıcıdaki farklı zaman adımlarının gizli durumlarının ağırlıklı toplamlarını hesaplamak için kullanılır. Sistem ağırlıkları ayarlayarak dikkat edilecek alanı ayarlamış olur. Bu mekanizmanın sihri katsayıları hesaplamak için kullanılan ağın geri yayılımla eğitilebilmesidir. Bu mekanizmaları elle oluşturmaya gerek yoktur!

Dikkat mekanizmaları sinirsel makine tercümesini baştan aşağı değiştirdi. Sonrasında, Google bir yayınla, Attention Is All You Need, nöron gruplarının dikkati gerçeklediği dönüştürücüyü (transformer) öne sürdü.

Bellek Ağı

Bellek ağları Facebook’ta Antoine Bordes tarafından 2014’te ve Sainbayar Sukhbaatar tarafından 2015’te başlatılan çalışmalara dayanır.

Bellek ağının arkasındaki fikir beyninizde iki önemli bölümün bulunmasıdır: biri uzun dönemli belleğin bulunduğu kortekstir. Hipokampus adında bir ayrı bir nöron yığını neredeyse korteksteki her yerle bağlantı kurar. Hipokampusun kısa süreli hafıza için kullanıldığı düşünülmektedir, buradaki şeyler görece kısa bir süre hatırlanır. Yaygın teoriye göre uyuduğunuzda büyük miktarda bilgi, hipokampusun kapasitesi sınırlı olduğundan, uzun süreli hafızada pekiştirilmek üzere hipokampustan kortekse transfer edilir.

Bir bellek ağı için, (belleğin bir adresi olarak düşünülebilecek) bir $x$ girdisi vardır ve bu $x$ $k_1, k_2, k_3, \cdots$ (“anahtarlar”) vektörleriyle skaler çarpım kullanılarak karşılaştırılır. Softmax’ten geçirildiğinde toplamları bire eşit olan bir sayı dizisi elde edilir. Bir diğer vektör kümesi de $v_1, v_2, v_3, \cdots$’dir (“değerler”). Bu vektörlerin softmax’ten gelen vektörlerle çarpılıp toplanması (dikkate olan benzerliğe dikkat edin) sonucu verir.

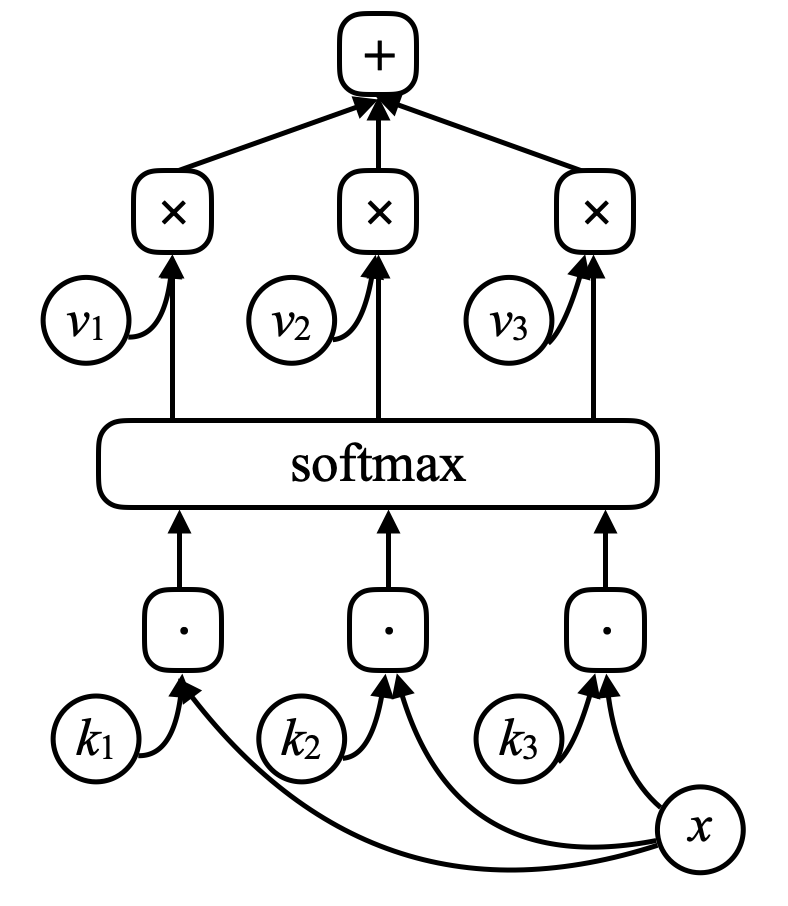
Fig 7. Bellek ağı

Eğer anahtarlardan biri ((mesela $k_i$)) $x$ ile tam olarak eşleşirse, bu anahtarla ilişkili katsayı bire çok yakın olacaktır. Yani, sistemin çıktısı esasen $v_i$ olacaktır.

Bu adreslenebilir ilişkisel bellektir (“addressable associative memory”). İlişkisel bellekte eğer girdiniz bir anahtarla eşleşirse o değeri alırsınız. Gördüğümüz hali bunun yumuşak, türevlenebilir halidir, bu şekliye geri yayılım uygulayabilmenizi ve vektörleri gradyan inişiyle değiştirebilmenizi sağlar.

Yazarların yaptığı şey sisteme bir cümle dizisi vererek bir hikaye anlatmaktı. Cümleler önceden eğitilmemiş bir sinir ağı kullanılarak vektörlere kodlanmıştı ve bu şekilde belleğe gönderilmişti. Bu sisteme bir soru sorduğunuzda, soruyu kodlayarak sinir ağına girdi olarak verirsiniz, ağ belleğe bir $x$ üretir ve bellek bir değer döndürür.

Bu değer, ağın önceki durumuyla birlikte, belleğe tekrar erişmek için kullanılır. Tüm ağı sorunuza bir cevap üretmesi için eğitirsiniz. Kapsamlı bir eğitimden sonra model hikayeleri hafızada tutmayı ve soruları cevaplamayı öğrenir.

Bellek ağında, bir girdi alıp bellek içinde bir adres üretip değeri ağa geri getiren ve devam ederek sonunda bir çıktı üreten bir ağ bulunur. Bu bir bilgisayara çok benzer çünkü bilgisayarda da bir işlemci ve yazma ve okuma işlemlerinin gerçekleştirildiği bir harici bellek bulunur.

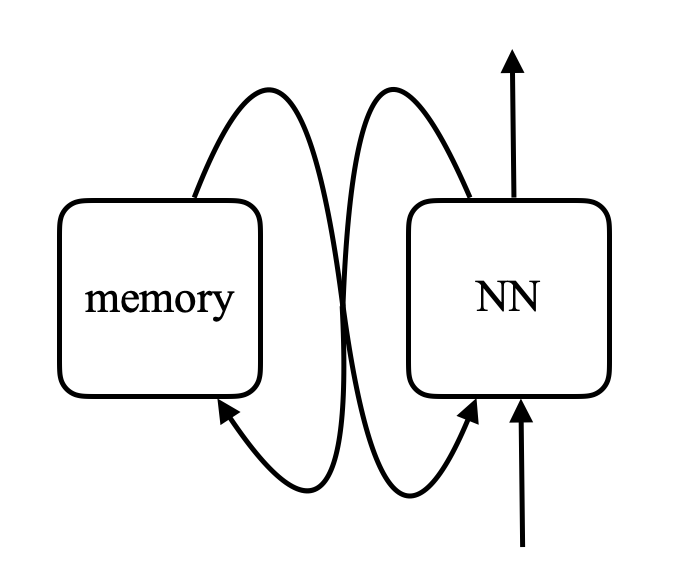
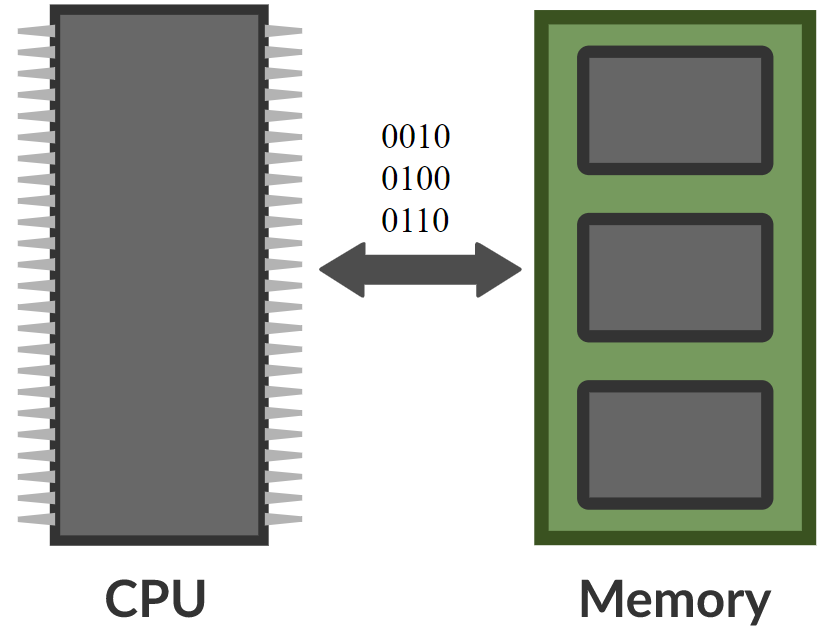
Fig 8. Bellek ağı ve bilgisayarın karşılaştırılması (Resim kaynağı: Khan Academy)

Bunu kullanarak türevlenebilir bilgisayarlar yapılabileceğini düşünen insanlar var. Bir örnek, Facebook’un yayını arXiv’da yayınlandıktan üç gün sonra tanıtılan, DeepMind’ın Neural Turing Machine ‘idir.

Buradaki fikir girdileri anahtarlarla karşılaştırmak, katsayılar üretmek ve değerler oluşturmaktır - tam da dönüştürücülerin yaptığı gibi! Dönüştürücü, en basit tabirle, her nöron grubunun bu ağlardan biri olduğu bir ağdır.