Evrişimleri ve otomatik fark alma motorunu anlamak

1 boyutlu evrişimleri anlamak

Bu bölümde verilerin esnekliğini, durağanlığını, bileşimini öğrenebilmek için öncelikle evrişimi tartışacağız.

Önceki hafta bahsedilen $A$ matrisini kullanmak yerine matris genişliğini çekirdek boyutu $k$ ile değiştireceğiz. Burada matrisin her satırı bir çekirdektir. Çekirdekleri istifleyerek ve kaydırarak kullanabiliriz (bkz. Şekil 1). Böylece $n-k+1$ uzunluğunda $m$ katmanımız olur .

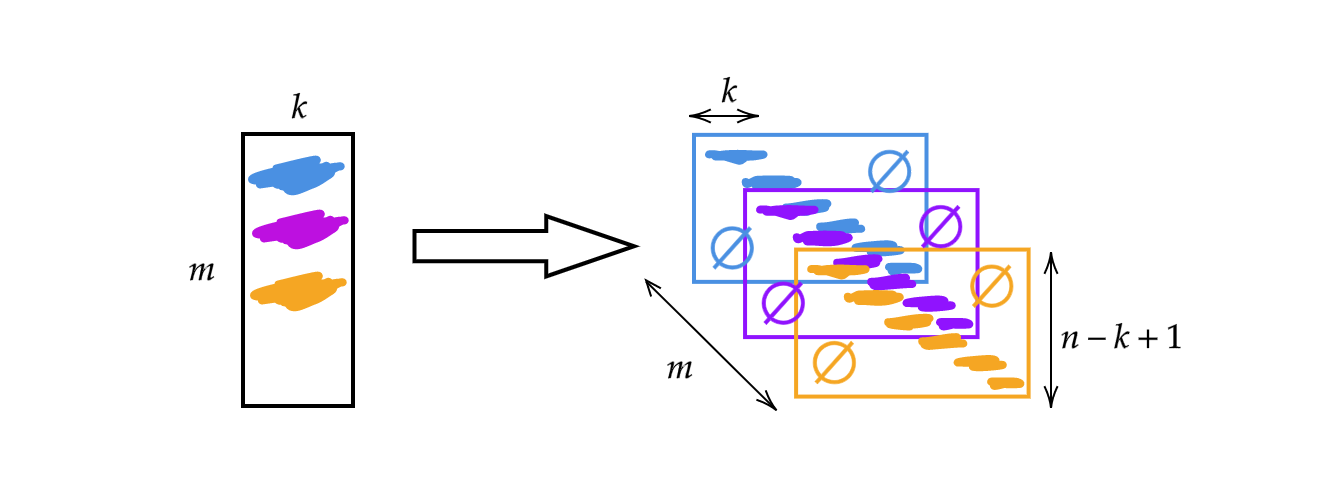
Şekil 1: 1 boyutlu evrişimin gösterimi

Çıktı, $n-k+1$ boyutunda $m$ adet (kalınlık) vektördür.

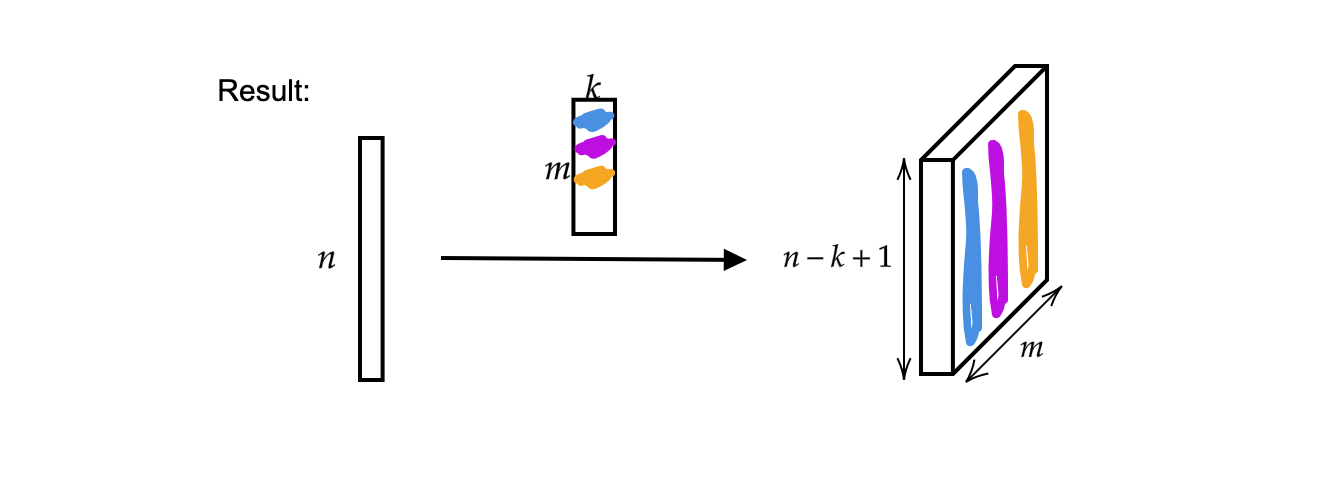
Şekil 2: 1 boyutlu evrişimin sonucu

Ayrıca tek bir giriş vektörü monofonik bir sinyal olarak görülebilir.

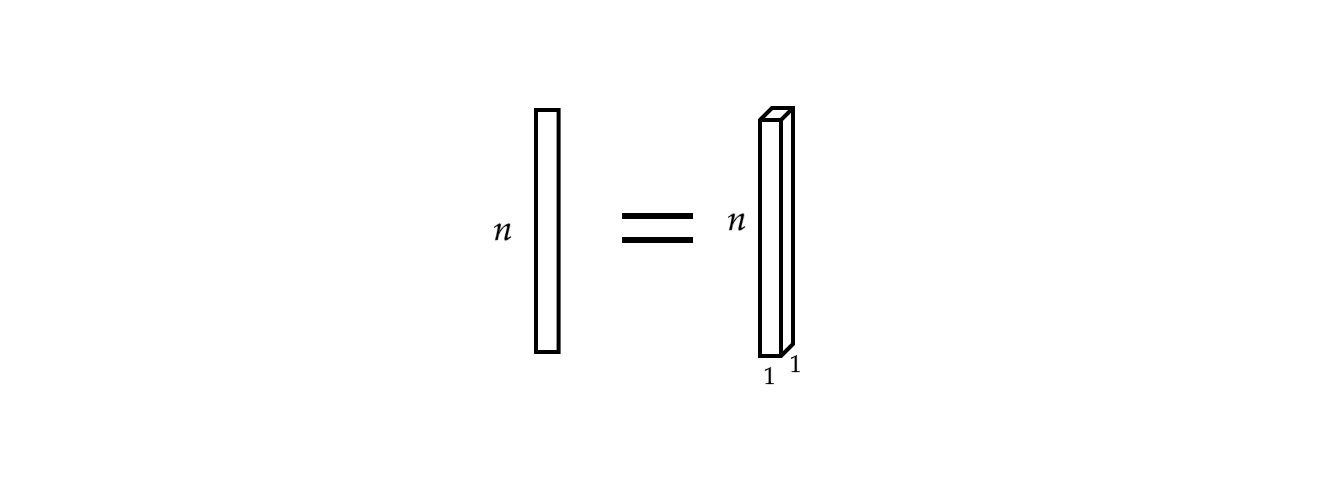
Şekil 3: Monofonik sinyal

Artık $x$ girdisi bir eşlemedir.

burada $\Omega = \lbrace 1, 2, 3, \cdots \rbrace \subset \mathbb{N}^1$ ($1$ boyutlu sinyal olduğu için / $1$ boyutlu bir alanda olduğu için) ve bu durumda kanal sayısı $c$ $ $1$’dir. $c = 2$ olduğunda bu bir stereofonik sinyal olur.

1 boyutlu evrişim için sadece her bir çekirdek için skaler çarpımı hesaplayabiliriz (bkz. Şekil 4).

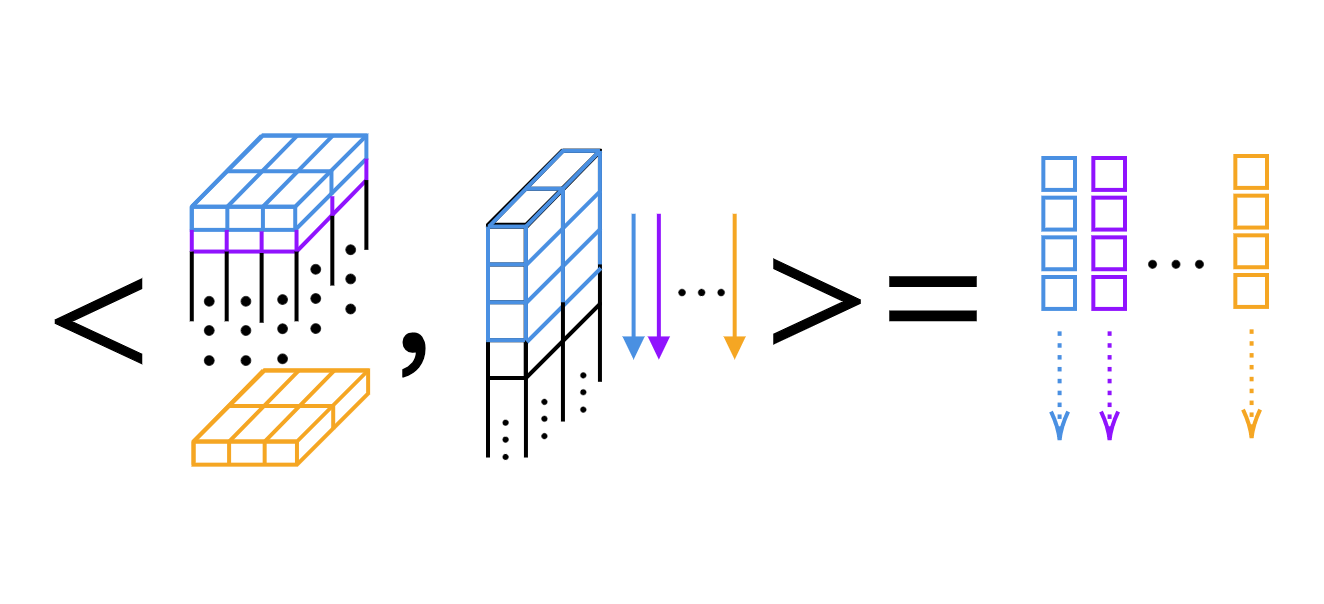
Şekil 4: 1 boyutlu evrişimin katman katman skaler çarpımı

PyTorch’ta çekirdeklerin boyutu ve çıktı genişliği

İpucu: Fonksiyonların dokümanlarına erişmek için IPython’da soru işaretini kullanabiliriz. Örneğin,

Init signature:
nn.Conv1d(
	in_channels,           # number of channels in the input image
	out_channels,          # number of channels produced by the convolution
	kernel_size,           # size of the convolving kernel
	stride=1,              # stride of the convolution
	padding=0,             # zero-padding added to both sides of the input
	dilation=1,            # spacing between kernel elements
	groups=1,              # nb of blocked connections from input to output
	bias=True,             # if `True`, adds a learnable bias to the output
	padding_mode='zeros',  # accepted values `zeros` and `circular`
)

1 boyutlu evrişim

$2$ kanaldan (stereofonik sinyal) $16$ kanala ($16$ çekirdeğe) giden, çekirdek boyutu $3$ ve adım boyutu $1$ olan $1$ boyutlu evrişimimiz var. Bir de kalınlığı $2$ ve uzunluğu $3$ olan $16$ adet çekirdeğimiz var. Giriş sinyalinin $1$ büyüklüğünde bir grup(tek bir sinyal), $2$ kanal ve $64$ örneğe sahip olduğunu varsayalım. Ortaya çıkan çıkış katmanı $1$ sinyal, $16$ kanal ve sinyalin uzunluğu $62$ ($=64-3+1$). Ayrıca yanlılık boyutu, ağırlık başına bir yanlılığa sahip olduğumuz için $16$ olarak bulunur.

conv = nn.Conv1d(2, 16, 3)  # 2 channels (stereo signal), 16 kernels of size 3
conv.weight.size()          # output: torch.Size([16, 2, 3])
conv.bias.size()            # output: torch.Size([16])

x = torch.rand(1, 2, 64)    # batch of size 1, 2 channels, 64 samples
conv(x).size()              # output: torch.Size([1, 16, 62])

conv = nn.Conv1d(2, 16, 5)  # 2 channels, 16 kernels of size 5
conv(x).size()              # output: torch.Size([1, 16, 60])

2 boyutlu evrişim

İlk olarak girdi verisini yüksekliği $64$ ve genişliği $128$ olan $20$ kanallı (diyelim ki hiperspektral görüntü kullanıyoruz) $1$ örnek olarak tanımlıyoruz. 2 boyutlu evrişim girişten $20$ kanal ve $3 \times 5$ boyutunda $16$ çekirdeğe sahiptir. Evrişimden sonra çıktı verisi, yüksekliği $62$ ($=64-3+1$) ve genişliği $124$ ($=128-5+1$) olan $16$ kanallı $1$ örnek olur.

x = torch.rand(1, 20, 64, 128)    # 1 sample, 20 channels, height 64, and width 128
conv = nn.Conv2d(20, 16, (3, 5))  # 20 channels, 16 kernels, kernel size is 3 x 5
conv.weight.size()                # output: torch.Size([16, 20, 3, 5])
conv(x).size()                    # output: torch.Size([1, 16, 62, 124])

Çıkışta aynı boyuta ulaşmak istiyorsak dolgu(padding) yapabiliriz. Yukarıdaki koda devam ederek evrişim işlevine yeni parametreler ekleyebiliriz: stride = 1 ve padding = (1, 2), yani $y$ yönünde $1$ sıra (en üstten $1$ ve en alttan $1$) ve $x$ yönünde $2$ sıra. Böylece çıkış sinyali, giriş sinyali ile aynı boyutta olur. 2 boyutlu evrişim gerçekleştirirken çekirdek koleksiyonunu saklamak için gereken boyut sayısı $4$’tür.

# 20 channels, 16 kernels of size 3 x 5, stride is 1, padding of 1 and 2
conv = nn.Conv2d(20, 16, (3, 5), 1, (1, 2))
conv(x).size()  # output: torch.Size([1, 16, 64, 128])

Otomatik gradyan nasıl çalışır?

Bu bölümde kısmi türevleri hesaplayabilmemiz için Torch’un tensörler üzerindeki tüm hesaplamaları kontrol etmesini isteyeceğiz.

• Gradyan biriktirme özelliklerine sahip $2\times2$ boyutlarında bir $\boldsymbol{x}$ tensörü oluşturun;
• $\boldsymbol{x}$’ın tüm öğelerinden $2$ çıkartın ve $\boldsymbol{y}$’yi elde edin; (y.grad_fn‘yi basarsak, <0x12904b290'da SubBackward0 object> alırız, yani ynin $\boldsymbol{x}-2$ çıkartma modülü tarafından üretildiği anlamına gelir. Ayrıca orijinal tensörü elde etmek için y.grad_fn.next_functions[0][0].variableı da kullanabiliriz.)
• Biraz daha işlem yapın: $\boldsymbol{z} = 3\boldsymbol{y}^2$;
• $\boldsymbol{z}$’nin ortalamasını hesaplayın.

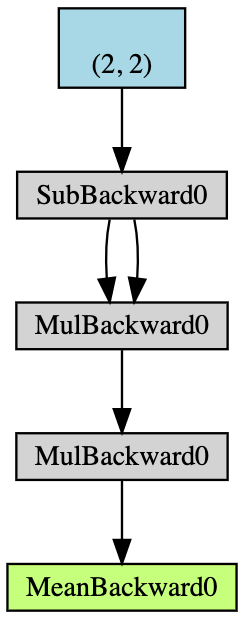
Şekil 5: Otomatik Gradyan Örneğinin Akış Şeması

Gradyanları hesaplamak için geri yayılım kullanılır. Bu örnekte geri yayılım işlemi $\frac{d\boldsymbol{a}} {d\boldsymbol{x}}$ gradyanını hesaplamak olarak görülebilir. $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$ doğrulama amaçlı elle hesapladıktan sonra, a.backward() in çalıştırılmasının hesaplamamızdaki x.grad ile aynı değeri verdiğini bulabiliriz.

Elle geri yayılımı hesaplama süreci şöyledir:

PyTorch’ta kısmi türev kullandığınızda orijinal verilerle aynı şekli alırsınız. Ancak esas Jacobian bunun transpozudur.

Temelden daha çılgınlığa

Şimdi $1\times3$ boyutunda $x$ vektörümüz var, iki $x$’i $y$’ye atarız ve normu $1000$’den küçük olana kadar $y$’i ikiyle çarpmaya devam ederiz. $x$ için rastgeleliğe sahip olmamız nedeniyle prosedür sona erdiğinde yineleme sayısını doğrudan bilemeyiz.

x = torch.randn(3, requires_grad=True)

y = x * 2
i = 0
while y.data.norm() < 1000:
    y = y * 2
    i += 1

Ancak elimizdeki gradyanları bilerek bunu kolayca çıkarabiliriz.

gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)

print(x.grad)
tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])
print(i)
9

Çıkarıma gelince, aşağıda gösterildiği gibi gradyan birikimini izlemek istediğimizi belirlemek için requires_grad=True değerini kullanabiliriz. $x$ veya $w$’nin tanımlanmasında requires_grad=True atamasını yapmadan $z$ üzerinde backward() çağırırsak, $x$ veya $w$ üzerinde gradyan birikimimiz olmadığı için çalışma zamanı hatası alırız.

# Gradyan birikmesine izin veren x vez w
x = torch.arange(1., n + 1, requires_grad=True)
w = torch.ones(n, requires_grad=True)
z = w @ x
z.backward()
print(x.grad, w.grad, sep='\n')

Ve with torch.no_grad () ile gradyan birikimini tutmayabiliriz.

x = torch.arange(1., n + 1)
w = torch.ones(n, requires_grad=True)

# Tüm Torch tensörlerinde gradyan birikimi olmayacaktır
with torch.no_grad():
    z = w @ x

try:
    z.backward() # z'nin gradyan birikimi olmadığı için PyTorch burada bir hata verir.
except RuntimeError as e:
    print('RuntimeError!!! >:[')
    print(e)

Daha fazlası – özel gradyanlar

Ayrıca temel sayısal işlemler yerine sinir ağı grafına kendi tanımladığımız modülleri/fonksiyonları bağlayabiliriz. İlgili Jupyter Notebook’u burada bulabilirsiniz.

Bunu yapmak için, torch.autograd.Function öğesini miras almalı ve forward() ve backward () fonksiyonlarını tekrar yazmalıyız(override). Örneğin ağları eğitmek istiyorsak, ileri geçişi almalıyız ve girişin çıkışa göre kısmi türevlerini bilmeliyiz, böylece bu modülü kodun herhangi bir noktasında kullanabiliriz. Girdinin çıktıya göre kısmi türevlerini bildiğimiz sürece geri yayılım (zincir kuralı) kullanarak bunu işlem zincirinin herhangi bir yerine bağlayabiliriz.

Bahsedilen notebookta, add, split ve max modüllerinde üç adet özel modül örneği vardır. Örneğin, özel ekleme(add) modülü:

# Custom addition module
class MyAdd(torch.autograd.Function):

    @staticmethod
    def forward(ctx, x1, x2):
        # ctx is a context where we can save
        # computations for backward.
        ctx.save_for_backward(x1, x2)
        return x1 + x2

    @staticmethod
    def backward(ctx, grad_output):
        x1, x2 = ctx.saved_tensors
        grad_x1 = grad_output * torch.ones_like(x1)
        grad_x2 = grad_output * torch.ones_like(x2)
        # need to return grads in order
        # of inputs to forward (excluding ctx)
        return grad_x1, grad_x2

İki şeyi toplayarak bir çıktı almamız durumunda, ileri yayılım fonksiyonunu bu şekilde yeniden yazmamız gerekir. Ve geri yayılım yapmak için döndüğümüzde, gradyanlar her iki tarafa kopyalanmıştır. Bu yüzden geri yayılım fonksiyonunu kopyalayarak yeniden yazıyoruz.

split ve max modüllerinde ileri ve geri fonksiyonlarını nasıl yeniden yazdığımızı görmek için notebooktaki kodlara bakın. Bir şeyi split ile böldüysek, aşağı gidişte gradyan alırken onları eklemeli / toplamalıyız. argmax, en yüksekteki şeyin dizinini verir, yani en yüksektekinin dizini $1$, diğerleri ise $0$ olarak döner. Farklı özel modüllerin kendi ileri geçişini ve geriye doğru fonksiyonda gradyanları nasıl aldığını yeniden yazmamız gerektiğini unutmayın.