Optimizasyon Yöntemleri 2

Adaptif yöntemler

Momentumlu SGD şu anda birçok makine öğrenmesi problemi için en iyi optimizasyon yöntemidir. Ancak Adaptif Yöntemler adı verilerek yıllar boyunca geliştirilen başka yöntemler de vardır. Bu yöntemler özellikle şartları zayıf belirlenmiş problemler için SGD işe yaramazsa kullanılır.

SGD formülasyonunda, ağdaki her bir ağırlık aynı öğrenme oranına sahip bir denklem kullanılarak güncellenir (global $\gamma$). Adaptif yöntemlerde ise, her bir ağırlık için ayrı bir öğrenme oranı uyarlanır. Bu amaçla her ağırlık için gradyanlardan aldığımız bilgiler kullanılır.

Uygulamada sık kullanılan ağların farklı bölümlerinde farklı yapıları vardır. Örneğin, CNN’in ilk bölümlerinde büyük görüntülerde çok sığ evrişim katmanları varken daha sonraki bölümlerinde küçük görüntülerde çok sayıda kanalın evrişimleri olabilir. Bu işlemlerin her ikisi de çok farklı olduğundan ağın başlangıcı için iyi çalışan bir öğrenme oranı ağın sonraki bölümleri için iyi çalışmayabilir. Bu katmana göre uyarlanan öğrenme oranlarının yararlı olabileceği anlamına gelir.

Ağın ikinci kısmındaki ağırlıklar (aşağıdaki Şekil 1’de 4096) doğrudan çıktıyı belirler ve çok güçlü bir etkiye sahiptir. Bu nedenle bunlar için daha düşük öğrenme oranları gerekir. Aksine ilk kısımdaki ağırlıkların çıktı üzerindeki bireysel etkileri özellikle de rastgele başlatıldığında daha küçük olacaktır.

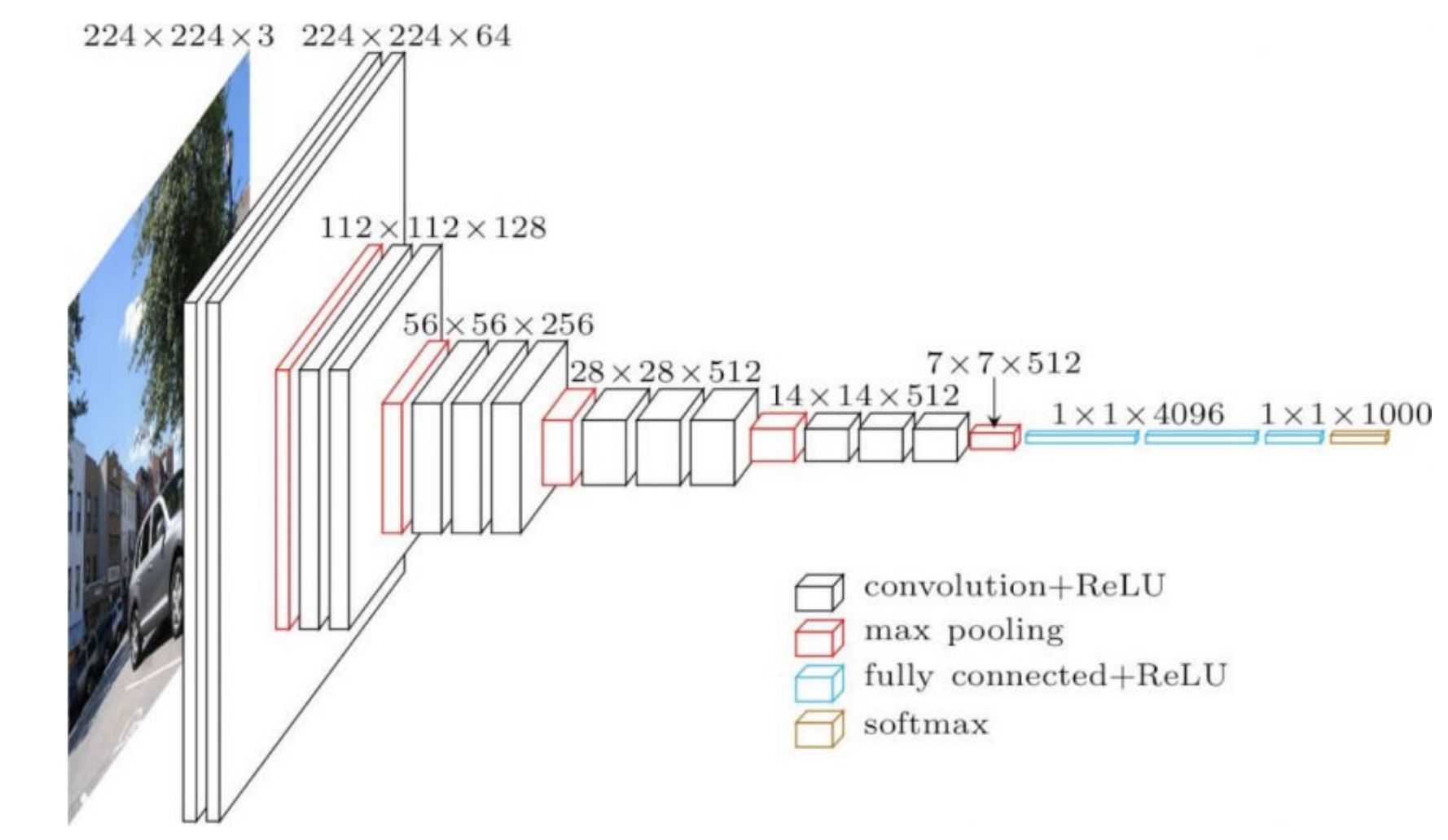
Şekil 1: VGG16

RMSprop

Karelerin ortalamasının karekökü yayılımı(Root Mean Square Propagation) nın ana fikri, gradyanın karelerin ortalamasının karekökü ile normalize edilmesidir.

Aşağıdaki denklem gradyanın karesinin alınması sırasında vektörün her bir elemanının ayrı ayrı karelerinin alındığını gösterir.

burada $\gamma$ küresel öğrenme oranı, $\epsilon$, $\epsilon$ makinesine yakın bir değerdir ($10^{-7}$ veya $10^{-8}$ türünden) – sıfıra bölünme hatalarından kaçınmak için, $v_{t+1}$ ise 2. moment tahminidir.

Üstel hareketli ortalama(exponential moving average) (zaman içinde değişebilecek bir miktarın ortalamasını korumak için standart bir yöntem) yoluyla bu gürültülü miktarı tahmin etmek için $v$ değerini güncelliyoruz. Daha fazla bilgi sağladıkları için yeni değerlere daha büyük ağırlıklar vermeliyiz. Bunu yapmanın bir yolu, eski değerlerin ağırlıklarını üstel olarak düşürmektir. $v$ hesaplamasında çok eski olan değerler 0 ile 1 arasında değişen bir $\alpha$ sabiti ile her adımda azalacak şekilde ağırlıklandırılır. Bu sayede eski değerler artık üstel hareketli ortalamanın önemli bir parçası olmayıncaya kadar azalmış olur.

Orijinal yöntem merkezi olmayan bir ikinci momentin üstel hareketli ortalamasını tutar yani ortalamayı çıkartmaz. İkinci moment gradyanı eleman bazında normalize etmek için kullanılır, yani gradyanın her elemanı ikinci moment tahmininin kareköküne bölünür. Gradyanın beklenen değeri(expectation) küçükse, bu işlem gradyanın standart sapmaya bölünmesine benzer.

Paydada küçük bir $\epsilon$ kullanmak fark etmez çünkü $v$ çok küçük olduğunda zaten momentum da çok küçük olur.

ADAM

ADAM yani Adaptif Moment Tahmini(Adaptive Moment Estimation) RMSprop yöntemine momentum ekleyen ve daha yaygın kullanılan bir yöntemdir. Momentum güncellemesi üstel hareketli ortalama ile yapılır ve $\beta$ ile uğraşırken öğrenme oranını değiştirmemiz gerekmez. Tıpkı RMSprop’ta olduğu gibi burada da gradyanın karesinin üstel hareketli ortalamasını alırız.

burada $m_{t+1}$, momentumun üstel hareketli ortalamasıdır.

Başlangıçtaki iterasyonlarda hareketli ortalamayı tarafsız tutmak için kullanılan yanlılık düzeltmesi(bias correction) burada gösterilmemiştir.

Uygulama tarafı

Sinir ağlarının eğitim sürecinin başlangıcında SGD genellikle yanlış yöne giderken, RMSprop doğru yönde ilerler. Bununla birlikte, RMSprop da klasik SGD gibi gürültüden etkilenir, yani yerel bir minimum bulduğunda optimumun etrafında yaptığı sıçramalar kritik sonuçlara yol açar. Tıpkı SGD’ye momentum eklediğimizde olduğu gibi, ADAM ile de aynı iyileştirmeyi elde ederiz. Bu çözümün gürültülü olmayan iyi bir tahminidir, bu nedenle ADAM genellikle RMSprop üzerinden önerilir.

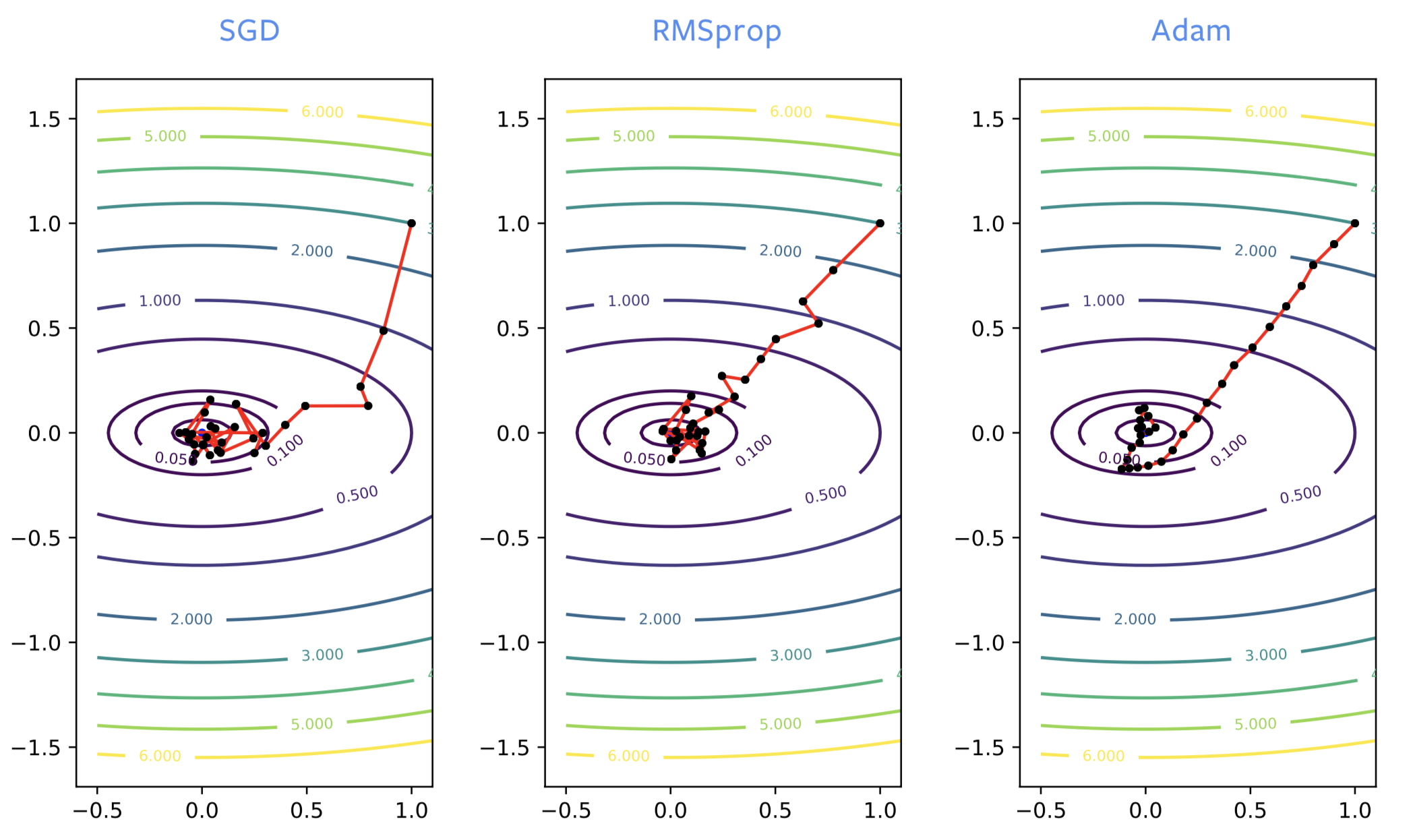
Şekil 2: SGD, RMSprop ve ADAM karşılaştırması

ADAM, dil modellerini kullanırken bazı ağları eğitmek için gereklidir. Sinir ağlarını optimize etmek için genellikle momentumlu SGD veya ADAM tercih edilir. Bununla birlikte, ADAM’ın yayınlardaki teorisi iyi anlaşılmamıştır ve bazı dezavantajları da vardır:

• Çok basit test problemlerinde yöntemin yakınsamadığı görülebilir.
• Genelleme hataları verdiği bilinmektedir. Sinir ağı, eğitim için kullanılan verilerde sıfır kayıp verecek şekilde eğitilmişse daha önce hiç görmediği diğer veri noktalarında sıfır kayıp vermeyecektir. Özellikle görüntü problemlerinde SGD kullandığımızdakinden daha kötü genelleme hataları almamız oldukça yaygındır. Örneğin ADAM veya yapısındaki faktörler, en yakın yerel minimumu bulmayı yani daha gürültüsüz olmayı içerebilir.
• ADAM da 3 tampon bulundurmamız gerekirken, SGD 2 tampon gerektirir. Birkaç gigabayt boyutundaki bir modeli eğitmediğimiz sürece çok önemli değildir ancak böyle bir durumda belleğe sığmayabilir.
• 1 yerine 2 momentum parametresi ayarlanmalıdır.

Normalizasyon katmanları

Normalizasyon katmanları optimizasyon algoritmalarını iyileştirmek yerine, ağ yapısının kendisini iyileştirir. Bunlar mevcut katmanlar arasındaki ek katmanlardır. Amaçları optimizasyon ve genelleme performanslarını iyileştirmektir.

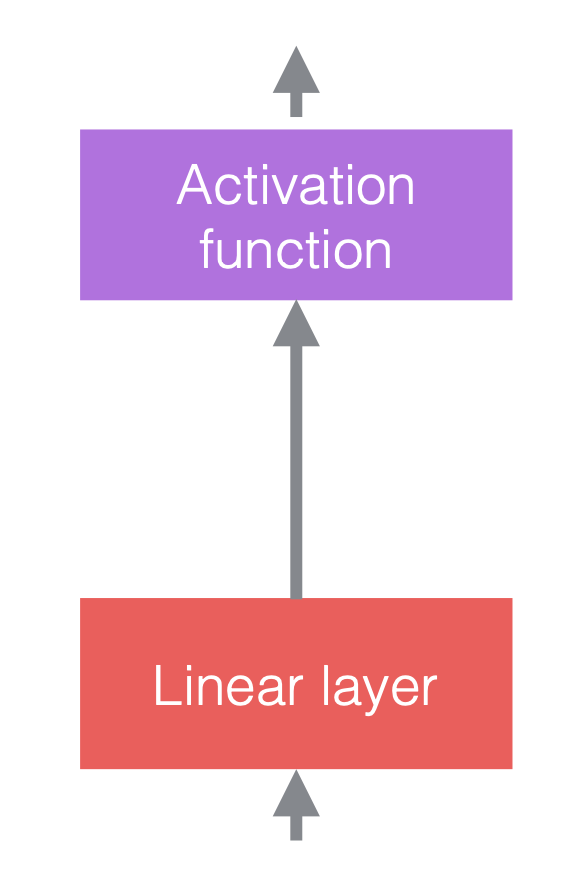
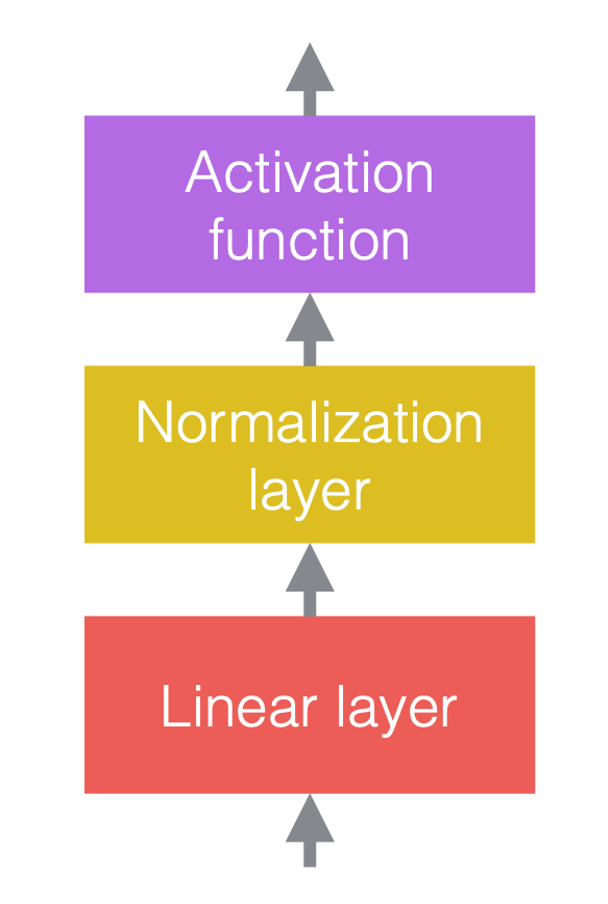
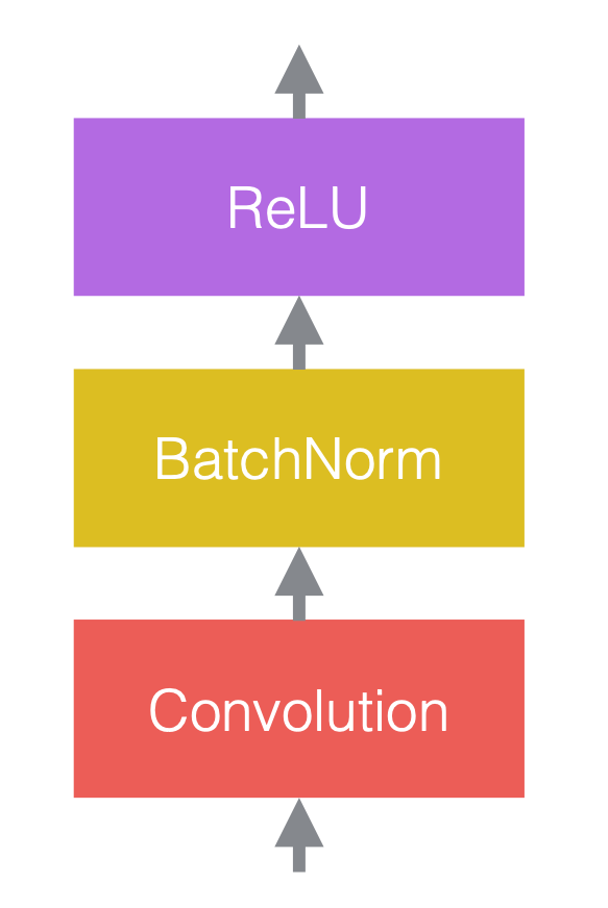
Sinir ağlarında tipik olarak doğrusal işlemleri doğrusal olmayan işlemlerle değiştiririz. Doğrusal olmayan işlemler aktivasyon fonksiyonları olarak da bilinir, ör.ReLU. Normalizasyon katmanlarını doğrusal katmanlardan önce veya aktivasyon fonksiyonlarından sonra yerleştirebiliriz. En yaygın uygulama aşağıdaki şekilde olduğu gibi doğrusal katmanlar ve aktivasyon fonksiyonları arasına yerleştirmektir.

(a) Normalizasyonu eklemeden önce	(b) Normalizasyonu ekledikten sonra	(c) CNN’lerde bir örnek

Şekil 3(c)’de, evrişim doğrusal katmandır, bunu toplu normalizasyon ve ardından ReLU takip eder.

Şunu unutmayın ki, normalizasyon katmanları üzerinden geçen verileri etkiler, yani ağın gücünü değiştirmez, ağırlıkların düzgün ayarlanmasıyla normalize edilmemiş bir ağ da normalize bir ağ ile aynı çıkışı verebilir.

Normalizasyon işlemleri

Normalizasyonun genel gösterimi:

burada $x$ girdi vektörü, $y$ çıktı vektörü, $\mu$, $x$’in tahmini ortalaması, $\sigma$, $x$’in tahmini standart sapması(std) , $a$ öğrenilebilir ölçeklendirme faktörü ve $b$ öğrenilebilir yanlılık(bias) terimidir.

Öğrenilebilir parametreler $a$ ve $b$ olmadan çıkış vektörü $y$ nin dağılımı sabit ortalama=0 ve std=1’e sahip olacaktır. Ölçeklendirme faktörü $a$ ve yanlılık terimi $b$ ağın temsil gücünü sağlar, yani çıkış değerleri herhangi bir aralıkta olabilir. $a$ ve $b$ normalizasyonu tersine çevirmez, çünkü bunlar öğrenilebilir parametrelerdir ve $\mu$ ve $\sigma$ ‘dan çok daha kararlıdır.

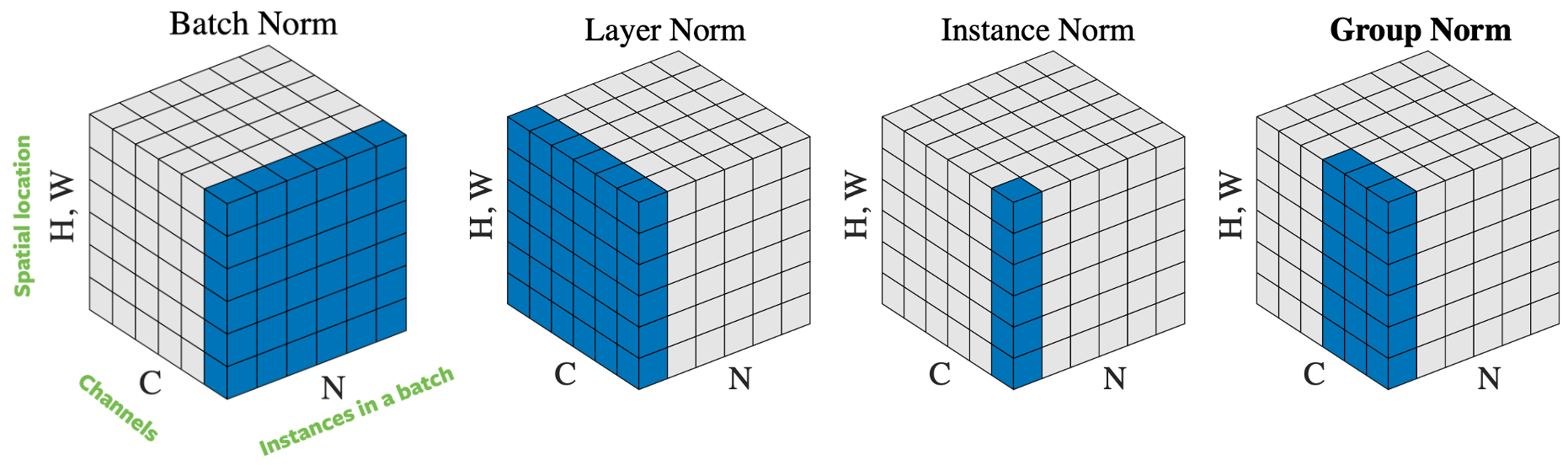
Şekil 4: Normalizasyon işlemleri.

Giriş vektörünü normalize etmek için normalizasyon örneklerinin nasıl seçileceğine bağlı birkaç yol vardır. Şekil 4’te $H$ yüksekliğindeki ve $W$ genişliğindeki $N$ görüntüden oluşan bir mini-grup için $C$ kanallı 4 farklı normalleştirme yaklaşımı görülmektedir:

• Toplu norm(Batch norm): normalizasyon girişin yalnızca bir kanalına uygulanır. Bu ilk önerilen ve en iyi bilinen yaklaşımdır. Daha fazla bilgi için lütfen [ResNet 7’nizi Nasıl Eğitirsiniz: Toplu Norm] (https://myrtle.ai/learn/how-to-train-your-resnet-7-batch-norm/) sayfasını okuyun.
• Katman normu(Layer norm): normalleştirme bir görüntü içindeki tüm kanallara uygulanır.
• Örnek normu(Instance norm): normalleştirme yalnızca bir görüntü ve bir kanal üzerine uygulanır.
• Grup normu(Group norm): normalizasyon bir görüntüye ancak birkaç kanala uygulanır. Örneğin, 0’dan 9’a kadar olan kanallar bir gruptur, 10 ile 19 arası başka bir gruptur vb. Uygulamada grupların büyüklüğü hemen hemen her zaman 32’dir. Bu yaklaşım uygulamada iyi bir performansa sahip olduğu ve SGD ile çelişmediği için Aaron Defazio tarafından önerilmiştir.

Uygulamada toplu norm ve grup normu bilgisayarlı görme problemleri için iyi çalışırken, katman normu ve örnek normu çoğunlukla dil problemleri için kullanılmaktadır.

Normalizasyon neden işe yarar?

Normalizasyon pratikte iyi çalışıyor olsa da etkinliğinin ardındaki nedenler hala tartışmalıdır. Başlangıçta normalizasyon “iç ortak değişken kaymasını(internal covariate shift)” azalttığı için önerilmiştir, ancak bazı araştırmacılar deneylerinde bunun yanlış olduğunu kanıtlamıştır. Bununla birlikte normalizasyonun aşağıdaki faktörlerin bir kombinasyonuna sahip olduğu açıktır:

• Normalizasyon katmanlarına sahip ağların optimize edilmesi daha kolaydır ve daha büyük öğrenme oranlarının kullanılması mümkündür. Normalizasyon sinir ağlarının eğitimini hızlandıran bir optimizasyon etkisine sahiptir.
• Ortalama/std tahminleri, gruplardaki örneklerin rastgele olması nedeniyle gürültülüdür. Bu ekstra “gürültü” bazı durumlarda daha iyi genelleme sağlar. Normalizasyonun bir düzenlileştirme(regularization) etkisi vardır.
• Normalizasyon ağırlıkların başlangıç durumuna bağlı olan duyarlılığı azaltır.

Sonuç olarak, normalizasyon daha “dikkatsiz” olabilmenizi sağlar –neredeyse tüm sinir ağlarını bloklar halinde bir araya getirebilir ve ne kadar kötü şartlandırılmış olduğunu düşünmek zorunda kalmadan eğitme şansınız olabilir.

Uygulamada dikkat edilecek hususlar

Geri yayılımın da normalizasyon uygulaması gibi ortalama ve standart sapma hesaplamasıyla yapıldığına dikkat etmeliyiz: çünkü başka şekilde yapılırsa ağ eğitimi sapacaktır. Geri yayılım hesaplaması oldukça zor ve hataya açıktır ancak PyTorch bunu bizim için otomatik olarak hesaplayabilir, bu da çok işimize yarar. PyTorch’ta bulunan iki normalizasyon katmanı sınıfı aşağıda listelenmiştir:

torch.nn.BatchNorm2d(num_features, ...)
torch.nn.GroupNorm(num_groups, num_channels, ...)

Toplu norm, ilk olarak geliştirilen ve en yaygın olarak bilinen yöntemdir. Ancak Aaron Defazio bunun yerine grup normu kullanılmasını önerir. Bu yöntem daha kararlı, teorik olarak daha basittir ve genellikle daha iyi çalışır. Grup büyüklüğünün 32 seçilmesi iyi bir varsayılan değerdir.

Toplu norm ve örnek normu için kullanılan ortalama/standart sapma, ağın her test edilmesinde yeniden hesaplanmasın diye eğitimden sonra sabitlenir. Çünkü normalizasyonu gerçekleştirmek için birden fazla eğitim örneği gereklidir. Grup normu ve katman normu için bu gerekli değildir, çünkü onlarda normalizasyon sadece bir eğitim örneğinin üzerindendir.

Optimizasyonun Ölümü

Bazen hakkında hiçbir şey bilmediğimiz bir alana girebilir ve şu anda uygulamakta oldukları şeyleri geliştirebiliriz. Böyle bir örnek, Manyetik Rezonans Görüntüleme (MRI) alanında MRI görüntülerinin yapılandırmasını hızlandırmak için derin sinir ağlarının kullanılmasıdır.

Şekil 5: Bazen gerçekten işe yarıyor!

MRI Yapılandırması

Geleneksel MRI yapılandırma probleminde ham veriler bir MRI makinesinden alınır ve basit bir boru hattı/algoritma kullanılarak yeniden bir görüntü oluşturulur. MRI makineleri, verileri her seferinde bir satır veya bir sütun (birkaç milisaniyede bir) olmak üzere 2 boyutlu bir Fourier alanında yakalar. Bu ham girdi, bir frekans ve bir faz kanalından oluşur ve değeri, belirli bir frekans ve faza sahip bir sinüs dalgasının büyüklüğü(magnitude) ile temsil edilmektedir. Basitçe söylemek gerekirse gerçek ve hayali birer kanala sahip karmaşık değerli bir görüntü olarak düşünülebilir. Bu girişe bir Ters-Fourier dönüşümü uygularsak, yani değerlerine göre ağırlıklandırılmış tüm bu sinüs dalgalarını toplarsak, orijinal anatomik görüntüyü elde edebiliriz.

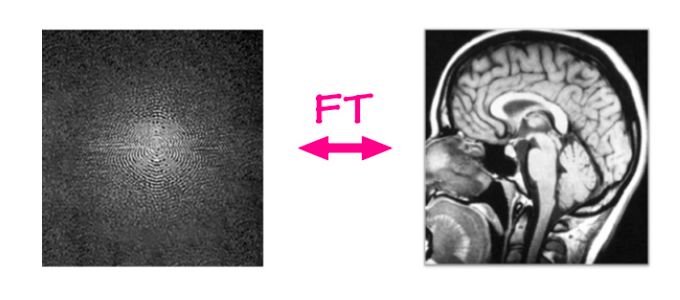
<bŞekil 6:</b> MRI yapılandırması

Fourier alanından görüntü alanına gitmek için halihazırda doğrusal bir eşleme(linear mapping) vardır. Bu yöntem çok etkilidir ve görüntü ne kadar büyük olursa olsun tam anlamıyla milisaniyeler almaktadır. Sorun şu, bunu daha da hızlı yapabilir miyiz?

Hızlandırılmış MRI

Çözülmesi gereken yeni sorun hızlandırılmış MRI’dır, burada hızlandırma ile MRI yapılandırma sürecini çok daha hızlı hale getirmeyi kastediyoruz. Makineleri daha çabuk çalıştırarak yine aynı kalitede görüntüler üretmeyi hedefliyoruz. Bunu yapabilmemizin bir yolu ve şimdiye kadarki en başarılı yolu, MRI taramasındaki tüm sütunları yakalamamaktır yani rastgele bazı sütunları atlayabiliriz. Görüntü hakkında çok fazla bilgi içerdiklerinden pratikte orta sütunları yakalamak daha elverişlidir, ancak bunların dışındakileri rastgele yakalarız. Sorun şu ki, görüntüyü yeniden yapılandırmak için artık doğrusal eşlemeyi kullanamayız. Şekil 7’de en sağdaki görüntü alt örneklenmiş Fourier uzayına uygulanan doğrusal bir eşlemenin çıktısını göstermektedir. Bu yöntemin bize çok faydalı çıktılar vermediği ve biraz daha akıllıca bir şeyler yapmak gerektiği açıktır.

Şekil 7: Alt örneklenmiş Fourier uzayında doğrusal eşleme

Sıkıştırılmış algılama

Sıkıştırılmış algılama, uzun zamandır teorik matematikteki en büyük atılımlardan biri olmuştur. Candes ve arkadaşlarının bir makalesi alt örneklenmiş Fourier alanı görüntüsünden mükemmel bir yeniden yapılandırma elde edebileceğimizi teorik olarak gösterdi. Başka bir deyişle, yeniden yapılandırmaya çalıştığımız sinyal, seyrek veya seyrek yapılandırılmışsa, daha az ölçüm kullanarak mükemmel bir şekilde yeniden yapılandırılması mümkündür. Ancak bunun çalışması için uygulamada bazı gereksinimler vardır – rastgele örnekleme değil, aksine tutarsız örnekleme gerekir – her ne kadar uygulamada insanlar rastgele örnekleme yapsalar da. Ayrıca tam bir sütunu veya yarım sütunu örneklemek aynı zamanı alır, bu nedenle uygulamada tüm sütunları örnekleriz.

Başka bir koşul, görüntümüzde seyreklik olması gerektiğidir, burada seyreklik görüntüde çok sayıda sıfır veya siyah piksel anlamına gelir. Dalga boyu ayrışımı(wavelength decomposition) yaparsak ham girdi seyrek olarak temsil edilebilir, ancak bu ayrışma bile bize tam olarak seyrek değil yaklaşık seyrek bir görüntü verir. Bu nedenle bu yaklaşım bize Şekil 8’de görebileceğimiz gibi oldukça iyi ama mükemmel olmayan bir yeniden yapılandırma sağlar. Bununla birlikte giriş, dalga boyu alanında çok seyrek olsaydı, kesinlikle mükemmel bir görüntü elde ederdik.

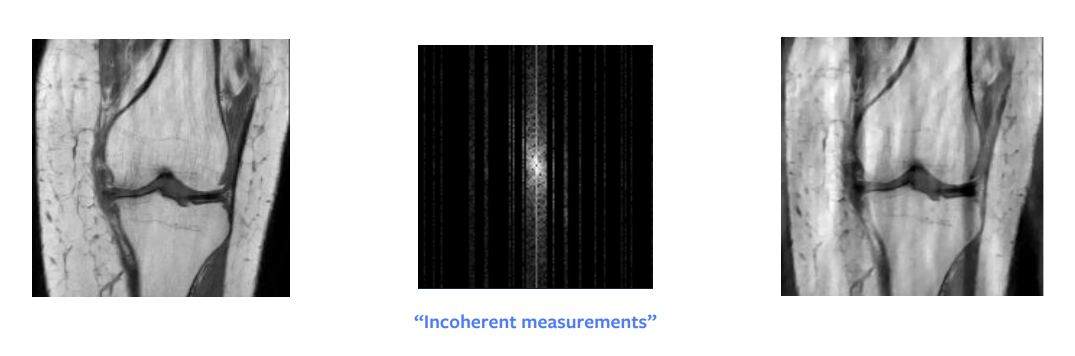
Şekil 8: Sıkıştırılmış algılama

Sıkıştırılmış algılama optimizasyon teorisine dayanır. Bu yeniden yapılandırmayı elde etmenin yolu, ek bir düzenlileştirme terimi olan bir mini optimizasyon problemini çözmektir:

burada $M$ örneklenmemiş girdileri sıfırlayan maske fonksiyonu, $\mathcal{F}$ Fourier dönüşümü, $y$ gözlemlenen Fourier alanı verileri, $\lambda$ düzenlileştirme cezasının gücü ve $V$ düzenlileştirme fonksiyonudur.

Optimizasyon problemi MRI taramasındaki her bir zaman adımı veya “dilim” için çözülmelidir ve bu genellikle taramanın kendisinden çok daha uzun sürer. Bu da daha iyi bir şey bulmamız için başka bir nedendir.

Optimizasyon kime lazım?

Her bir zaman adımında küçük optimizasyon problemlerini çözmek yerine, gerekli çözümü doğrudan üretmek için büyük bir sinir ağını neden kullanmayalım? Umudumuz, temelde optimizasyon problemini bir adımda çözecek ve her bir adımda küçük bir optimizasyon probleminin çözülmesinden elde edilen çözüm kadar iyi bir çıktı üretecek bir sinir ağını yeterli karmaşıklıkla eğitebilmektir.

burada $B$ derin öğrenme modelimiz ve $y$ ise gözlemlenen Fourier alanı verileridir.

15 yıl önce bu yaklaşım zordu – ancak bugünlerde uygulanması çok daha kolay. Şekil 9, bu sorunun bir derin öğrenme yaklaşımıyla elde edilen sonucunu göstermektedir. Çıktının sıkıştırılmış algılama yaklaşımından çok daha iyi olduğunu ve gerçek taramaya çok benzediğini görebiliyoruz.

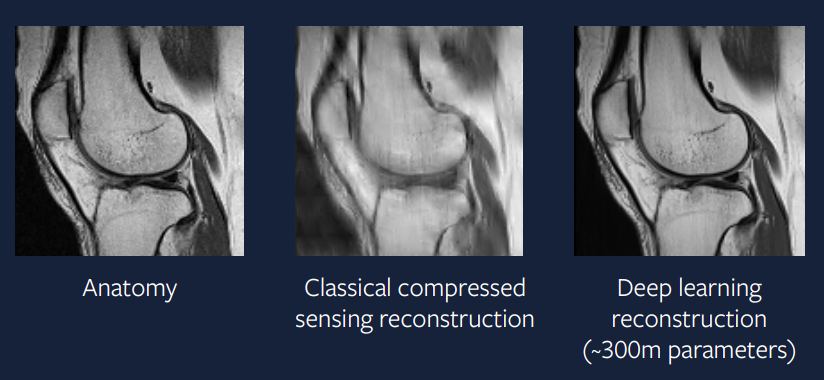
Şekil 9: Derin Öğrenme yaklaşımı

Bu yapılandırmayı oluşturmak için kurulan model bir ADAM optimizasyonu, grup normu kullanılan normalizasyon katmanları ve U-Net tabanlı evrişimli sinir ağı içerir. Böyle bir yaklaşım pratik uygulamalara çok yakındır. Umarız bu hızlandırılmış MRI taramalarının birkaç yıl içinde klinik uygulamada gerçekleştiğini göreceğiz. –>