Optimizasyon Yöntemleri 1
🎙️ Aaron DefazioGradyan inişi
Optimizasyon Yöntemleri dersine birçok yöntem içinde en basit ve en kötü (neden olduğundan bahsedeceğiz) yöntem olan Gradyan İnişi ile başlayacağız.
Problem:
\[\min_w f(w)\]Tekrarlamalı Çözüm:
\[w_{k+1} = w_k - \gamma_k \nabla f(w_k)\]burada,
- $k$-ıncı iterasyondan sonra güncellenmiş değer $w_{k+1}$,
- $k$-ıncı iterasyondan önceki başlangıç değeri $w_k$,
- $\gamma_k$ adım boyutu,
- $\nabla f(w_k)$ ise $f$’in gradyanı.
Burada $f$ fonksiyonunun sürekli ve türevlenebilir olduğu varsayılmaktadır. Amacımız optimizasyon fonksiyonunun en düşük noktasını (vadi) bulmaktır. Ancak, bu vadiye giden kesin yön bilinmemektedir. Yalnız bölgesel olarak bakılınca negatif gradyanın yönü sahip olduğumuz en iyi bilgidir. Ancak bu yönde küçük bir adım atmak bizi minimuma yaklaştırır. Bir kez küçük bir adım attıktan sonra, tekrar yeni gradyanı hesaplarız ve tekrar bu yönde küçük bir miktar hareket ederiz, ta ki vadiye ulaşıncaya kadar. Aslında temel olarak gradyan inişinin yaptığı şey en dik iniş (negatif gradyan) yönünü takip etmektir.
Tekrarmalı güncelleme denklemindeki $\gamma$ parametresine adım boyutu denir. Genelde optimal adım boyutunun değeri bilinmez; bu yüzden farklı değerler denemek zorunda kalırız. Standart uygulama, bir log-ölçeğinde bir grup değeri denemek ve en iyisini kullanmaktır. Bu durumda oluşabilecek birkaç farklı senaryo vardır. Yukarıdaki görüntü 1 boyutlu ikinci dereceden (quadratic) bir fonksiyon için bu senaryoları göstermektedir. Öğrenme hızı çok düşük olursa minimum seviyeye doğru istikrarlı bir ilerleme kaydedebiliriz. Ancak bu ideal olandan daha fazla zaman alabilir. Bizi doğrudan minimuma indirecek bir adım boyutu elde etmek genellikle çok zordur (veya imkansızdır). Bu durumda ideal olarak isteyeceğimiz şey, optimalden biraz daha büyük bir adım boyutudur. Pratikte bu en hızlı yakınsamayı sağlar. Bununla birlikte çok büyük bir öğrenme oranı kullanırsak iterasyonlar sonunda minimumdan uzaklaşırız ve sapmış oluruz. Dolayısıyla uygulamada bizi saptıracak değerden biraz daha düşük bir öğrenme hızı kullanmak isteriz.
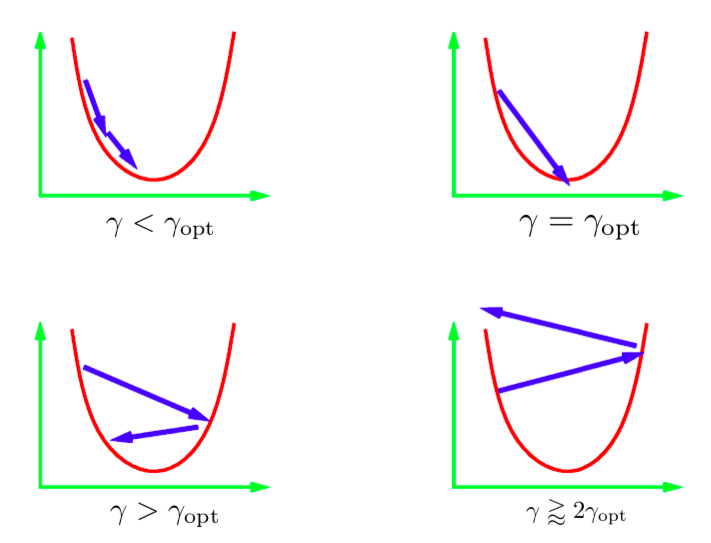
Şekil 1: 1 boyutlu ikinci dereceden fonksiyon için adım miktarları
Stokastik gradyan inişi
Stokastik gradyan inişinde gerçek gradyan vektörünü stokastik bir tahmini ile değiştiriyoruz. Özellikle bir sinir ağı için, stokastik tahmin tek bir veri noktasının (tek örnek) kaybının (loss) gradyanı anlamına gelir.
$i$-inci örnek için ağın kaybını $f_i$ ile gösterelim.
\[f_i = l(x_i, y_i, w)\]Nihai olarak en aza indirmek istediğimiz fonksiyon, tüm örneklerin toplam kaybı olan $f$ ‘dir.
\[f = \frac{1}{n}\sum_i^n f_i\]SGD’de, $f_i$ üzerindeki gradyana (toplam kayıp $f$’in gradyanını kullanmak yerine) göre ağırlıkları güncelliyoruz.
\[\begin{aligned} w_{k+1} &= w_k - \gamma_k \nabla f_i(w_k) & \quad\text{(i rastgele birbiçimli olarak seçilir)} \end{aligned}\]Eğer $i$ rastgele seçilirse, $f_i$, $f$’in gürültülü (noisy) ama tarafsız bir tahminleyicisidir ve matematiksel olarak şu şekilde yazılır:
\[\mathbb{E}[\nabla f_i(w_k)] = \nabla f(w_k)\]Bunun sonucu olarak, SGD’nin beklenen $k$-ıncı adımı, tam gradyan inişin $k$-ıncı adımı ile aynıdır:
\[\mathbb{E}[w_{k+1}] = w_k - \gamma_k \mathbb{E}[\nabla f_i(w_k)] = w_k - \gamma_k \nabla f(w_k)\]Bu nedenle, herhangi bir SGD güncellemesi, beklentide tam-toplu (full-batch) güncelleme ile aynıdır. Ancak, SGD sadece gürültülü ve daha hızlı gradyan inişi değildir. Daha hızlı olmanın yanı sıra, SGD bize tam-toplu gradyan inişten daha iyi sonuçlar verebilir. SGD’deki gürültü sığ yerel minimumlardan kaçınmak ve daha iyi (daha derin) bir minimum bulmak için yardımcı olabilir. Bu olaya tavlama denir.
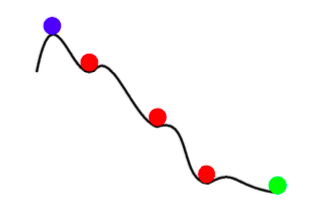
Şekil 2: SGD'de tavlama
Özet olarak, Stokastik Gradyan İnişinin avantajları aşağıdaki gibidir:
- Örnekler arasında çok fazla gereksiz bilgi vardır. SGD bu gereksiz hesaplamaların çoğunu önler.
- Erken aşamalarda gürültü, gradyandaki bilgilere kıyasla küçüktür. Bu nedenle, bir SGD adımı neredeyse bir GD adımı kadar iyidir.
- Tavlama - SGD güncellemesindeki gürültü, kötü (sığ) bir yerel minimumda yakınsamayı önleyebilir.
- Stokastik Gradyan İnişini hesaplamak büyük ölçüde daha ucuzdur (tüm veri noktalarının üzerinden geçmediğiniz için).
Mini-gruplama
Mini gruplamada, tek bir örnek üzerinden hesaplamak yerine, rastgele seçilmiş birden çok örnek üzerindeki kaybı dikkate alırız. Bu adım güncellemesinde oluşan gürültüyü azaltır.
\[w_{k+1} = w_k - \gamma_k \frac{1}{|B_i|} \sum_{j \in B_i}\nabla f_j(w_k)\]Genellikle tek bir örnek yerine mini gruplar oluşturarak donanımımızı daha iyi kullanabiliriz. Örneğin, tek örnekli eğitim kullandığımızda GPU’lardan yetersiz faydalanılmaktadır. Dağıtılmış (distributed) ağlar için sunulan eğitim teknikleri, büyük bir mini grubu bir makine kümesine paylaştırır ve sonra ortaya çıkan gradyanları toplar. Facebook yakın zamanda dağıtılmış eğitim yöntemlerini kullanarak bir saat içinde ImageNet verileri ile bir ağ eğitmiştir.
Gradyan İnişin tam boyutlu gruplar ile hiçbir zaman kullanılmaması gerektiğini belirtmek önemlidir. Tam toplu boyutta eğitim yapmak istiyorsak, LBFGS adlı bir optimizasyon tekniğini kullanırız. PyTorch ve SciPy’da bu tekniğin uygulamaları bulunmaktadır.
Momentum
Momentum’da bir yerine iki adet her iterasyonda değeri değişen değer ($p$ ve $w$) vardır. Güncellemeler aşağıdaki gibidir:
\[\begin{aligned} p_{k+1} &= \hat{\beta_k}p_k + \nabla f_i(w_k) \\ w_{k+1} &= w_k - \gamma_kp_{k+1} \\ \end{aligned}\]$p$, SGD momentumu olarak adlandırılır. Her güncelleme adımında, stokastik gradyan $\beta$ çarpanıyla (0 ile 1 arasında bir değer) sönümlendikten sonra momentumun eski değerine eklenir. $p$ gradyanların sürekli hesaplanan ortalaması olarak düşünülebilir. Sonunda $w$ yeni momentum $p$ yönünde hareket ettirilir.
Alternatif Yapı: Stokastik Ağır Top Metodu
\[\begin{aligned} w_{k+1} &= w_k - \gamma_k\nabla f_i(w_k) + \beta_k(w_k - w_{k-1}) & 0 \leq \beta < 1 \end{aligned}\]Bu yapı, matematiksel olarak önceki yapıyla eşdeğerdir. Burada bir sonraki adım, önceki adımın yönünün ($w_k - w_ {k-1}$) ve yeni negatif gradyanın birleşimidir.
Sezgisel Yaklaşım
SGD Momentum fizikteki momentum kavramına benzer. Optimizasyon süreci tepeden aşağı yuvarlanan ağır bir topa benzer. Momentum topu gittiği yönde devam edecek şekilde hareket ettirir. Gradyan ise topu başka bir yöne iten bir kuvvet olarak düşünülebilir.

Şekil 3: Momentumun Etkisi
Source: distill.pub
Momentum gidişat yönünde (soldaki şekilde olduğu gibi) etkili değişiklikler yapmak yerine, mütevazı değişiklikler yapar. Momentum tek başına SGD kullandığımızda çoğunlukla karşımıza çıkan salınımları sönümler.
$\beta$ parametresine Sönümleme Faktörü denir. $\beta$ sıfırdan büyük olmalıdır, sıfıra eşit olursa sadece gradyan inişi yapmış oluruz. Ayrıca 1’den küçük olmalıdır, aksi takdirde her şey patlar. $\beta$ ‘nın daha küçük değerleri, yönün daha çabuk değişmesine neden olur. Daha büyük değerler için güncellemenin başka yöne dönmesi daha uzun sürer.
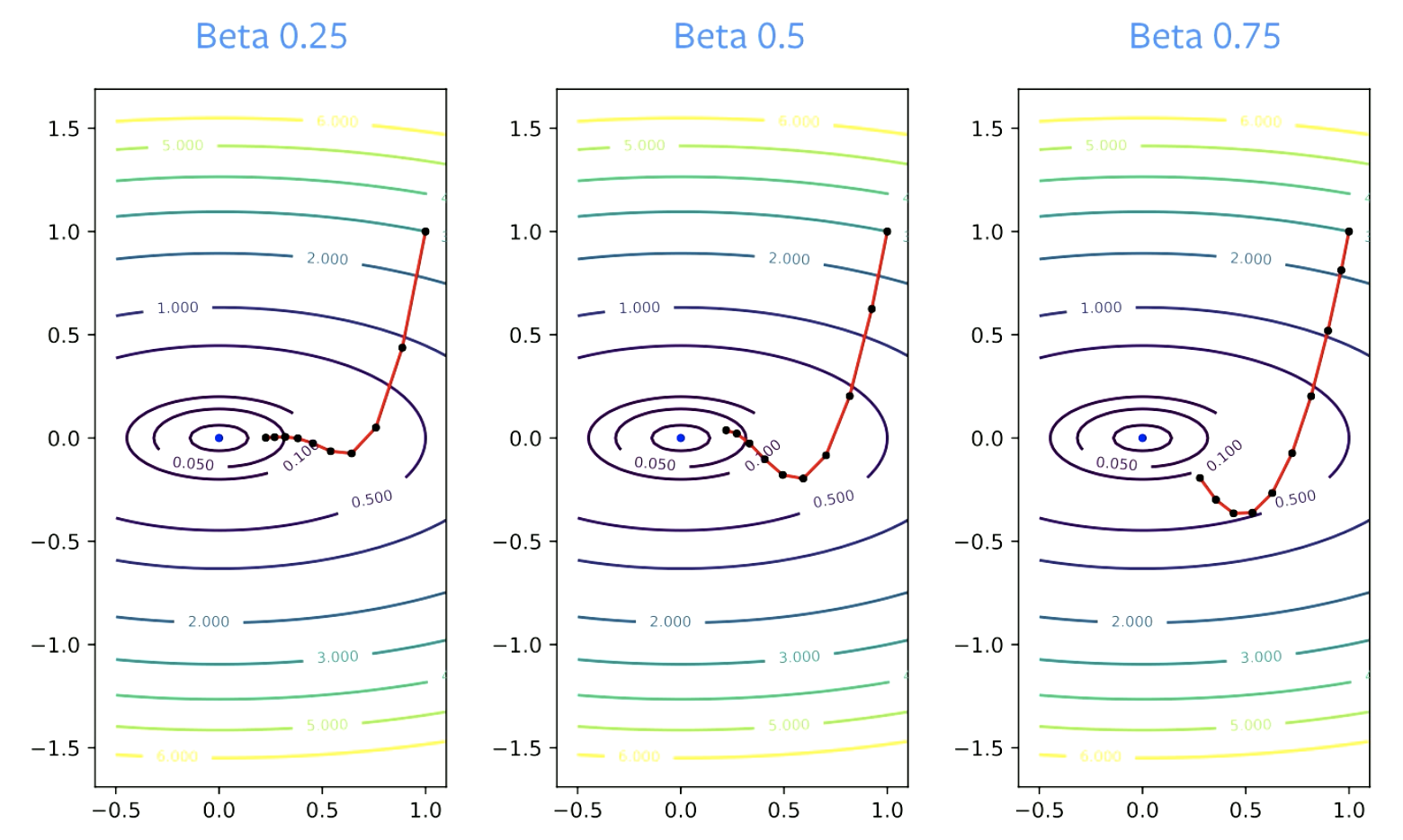
Şekil 4: Beta'nın Yakınsamadaki Etkisi
Uygulama Yönergeleri
Momentum hemen hemen her zaman stokastik gradyan inişi ile birlikte kullanılmalıdır. $\beta$ = 0.9 veya 0.99 neredeyse her zaman iyi çalışır.
Yakınsamayı sağlamak için momentum parametresi artırıldığında adım boyutu parametresinin genellikle azaltılması gerekir. $\beta$ 0,9’dan 0,99’a değiştirilirse, öğrenme oranı 10 kat azaltılmalıdır.
Momentum neden çalışıyor?
Hızlandırma
Aşağıda Nesterov momentumu için güncelleme kuralları verilmiştir.
\[p_{k+1} = \hat{\beta_k}p_k + \nabla f_i(w_k) \\ w_{k+1} = w_k - \gamma_k(\nabla f_i(w_k) +\hat{\beta_k}p_{k+1})\]Nesterov Momentumu ile sabitleri çok dikkatli seçerseniz hızlandırılmış yakınsama elde edebilirsiniz. Ancak bu sadece dışbükey problemler için geçerlidir, sinir ağları için geçerli değildir.
Birçok insan normal momentumun da hızlandırılmış bir yöntem olduğunu söyler. Ancak gerçekte sadece ikinci derece fonksiyonlar için hızlandırma sağlanır. Ayrıca, SGD gürültüye sahip olduğundan ve hızlandırma gürültüyle iyi çalışmadığından hızlandırma SGD ile iyi çalışmaz. Bu nedenle Momentum SGD ile bir miktar hızlanma mevcut olsa da, bu durum tek başına tekniğin yüksek performansı için iyi bir açıklama değildir.
Gürültü Yumuşatma
Momentumun çalışmasının muhtemelen daha pratik ve daha olası bir nedeni Gürültü Yumuşatmadır.
Momentum gradyanları ortalar. Her adım güncellemesinde sürekli çalışan ortalama bir gradyandır.
Teorik olarak, SGD’nin çalışması için tüm adım güncellemelerinin ortalamasını almalıyız.
\[\bar w_k = \frac{1}{K} \sum_{k=1}^K w_k\]SGD’nin momentumla birlikte kullanılmasının en güzel yanı, bu ortalama hesaplamasının artık gerekli olmamasıdır. Momentum optimizasyon sürecine yumuşatma ekleyerek her güncellemeyi çözüme iyi bir yaklaşım haline getirir. SGD ile bir sürü güncellemeyi ortalamak ve daha sonra bu yönde bir adım atmak amaçlanır.
Hem Hızlanma hem de Gürültü yumuşatma, momentum ile yüksek performans elde etmeye katkıda bulunur.
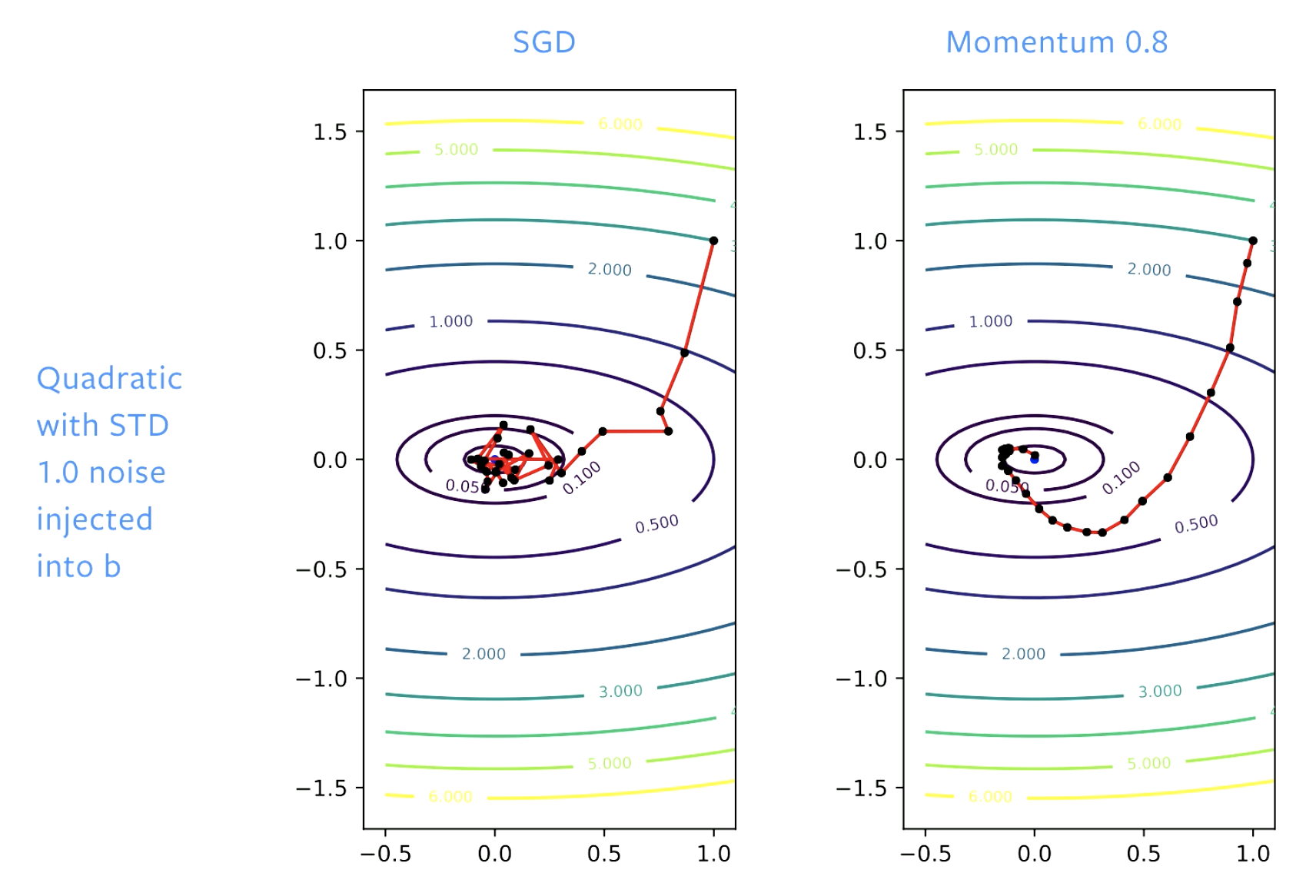
Şekil 5: SGD vs. Momentum
SGD ile başlangıçta çözüme doğru iyi bir ilerleme kaydediyoruz ancak kaseye (vadi tabanına) ulaştığımızda bu zeminin etrafında zıplıyoruz. Öğrenme hızını ayarlarsak, etrafında daha yavaş zıplarız. Momentum ile adımları yumuşatırız, böylece zemin etrafında zıplama olmaz.
📝 Vaibhav Gupta, Himani Shah, Gowri Addepalli, Lakshmi Addepalli
melikenurm
24 Feb 2020