Lineer Cebir ve Evreşim

🎙️ Alfredo Canziani

Lineer cebirin tekrarı

Bu bölüm, sinir ağları bağlamında temel lineer cebirin bir özetidir. Basit bir saklı katman $\boldsymbol{h}$ ile başlıyoruz:

\[\boldsymbol{h} = f(\boldsymbol{z})\]

Çıktı, $z$ vektörüne uygulanan doğrusal olmayan bir $f$ fonksiyonudur. Burada $z$, $\boldsymbol{x} \in\mathbb{R^n}$ vektörüne uygulanan bir $\boldsymbol{A} \in\mathbb{R^{m\times n}}$ afin dönüşümünün sonucudur:

\[\boldsymbol{z} = \boldsymbol{A} \boldsymbol{x}\]

İşlemlerin basit olması için sapmaları göz ardı ediyoruz. Lineer denklem şu şekilde genişletilebilir:

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\x_n \end{pmatrix} = \begin{pmatrix} \text{---} \; \boldsymbol{a}^{(1)} \; \text{---} \\ \text{---} \; \boldsymbol{a}^{(2)} \; \text{---} \\ \vdots \\ \text{---} \; \boldsymbol{a}^{(m)} \; \text{---} \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = \begin{pmatrix} {\boldsymbol{a}}^{(1)} \boldsymbol{x} \\ {\boldsymbol{a}}^{(2)} \boldsymbol{x} \\ \vdots \\ {\boldsymbol{a}}^{(m)} \boldsymbol{x} \end{pmatrix}_{m \times 1}\]

$\boldsymbol{a}^{(i)}$, $\boldsymbol{A}$ matrisinin $i$’nci satırını ifade ediyor.

Bu dönüşümü anlamak için, $\boldsymbol{z}$’nin $a^{(1)}\boldsymbol{x}$ bileşenini inceleyelim. $n$’in 2 olduğunu varsayarsak, $\boldsymbol{a} = (a_1,a_2)$ ve $\boldsymbol{x} = (x_1,x_2)$

$\boldsymbol{a}$ ve $\boldsymbol{x}$ 2 boyutlu düzlemde vektörler olarak çizilebilirler. Eğer $\boldsymbol{a}$ ve $\hat{\boldsymbol{\imath}}$ arasındaki açı $\alpha$ ve $\boldsymbol{x}$ ve $\hat{\boldsymbol{\imath}}$ arasındaki açı $\xi$ ise, trigonometrik formulleri kullanarak $a^\top\boldsymbol{x}$ genişletilebilir:

\[\begin {aligned} \boldsymbol{a}^\top\boldsymbol{x} &= a_1x_1+a_2x_2\\ &=\lVert \boldsymbol{a} \rVert \cos(\alpha)\lVert \boldsymbol{x} \rVert \cos(\xi) + \lVert \boldsymbol{a} \rVert \sin(\alpha)\lVert \boldsymbol{x} \rVert \sin(\xi)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \big(\cos(\alpha)\cos(\xi)+\sin(\alpha)\sin(\xi)\big)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \cos(\xi-\alpha) \end {aligned}\]

Çıktı, girdinin $\boldsymbol{A}$ matrisinin belirli bir satırına ne kadar hizalandığını gösteriyor. Bu iki vektör arasındaki açı $\xi-\alpha$’yı gözlemleyerek anlaşılabilir. $\xi = \alpha$ olduğunda, vektörler tamamen hizalanmış ve en büyük değer elde edilmiş oluyor. Eğer $\xi - \alpha = \pi$ ise, $\boldsymbol{a}^\top\boldsymbol{x}$ en küçük değerini alıyor ve iki vektör birbirinin tam tersine doğrulmuş durumdadır. Aslında lineer dönüşüm, girdinin $A$ tarafından tanımlanan çeşitli yönlere izdüşümünü görmemizi sağlıyor. Bu sezgimiz daha yüksek boyutlara da genişletilebilir.

Lineer dönüşümü anlamanın başka bir yolu da $\boldsymbol{z}$’nin ayrıca şu şekilde genişletilebildiğini farketmektir:

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} \vert & \vert & & \vert \\ \boldsymbol{a}_1 & \boldsymbol{a}_2 & \cdots & \boldsymbol{a}_n \\ \vert & \vert & & \vert \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = x_1 \begin{matrix} \rvert \\ \boldsymbol{a}_1 \\ \rvert \end{matrix} + x_2 \begin{matrix} \rvert \\ \boldsymbol{a}_2 \\ \rvert \end{matrix} + \cdots + x_n \begin{matrix} \rvert \\ \boldsymbol{a}_n \\ \rvert \end{matrix}\]

Sonuç $\boldsymbol{A}$ matrisinin sütunlarının ağırlıklı toplamına eşit. Bu yüzden sinyal girdinin bileşiminden başka bir şey değil.

Lineer cebirin evrişime genişletilmesi

Şimdi, lineer cebiri bir ses verisi analizi örneğiyle evrişime genişletiyoruz. Bir tam bağlantılı katmanı matris çarpımı olarak ifade ederek başlıyoruz: -

\[\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ w_{31} & w_{32} & w_{33}\\ w_{41} & w_{42} & w_{43} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

Bu örnekte, ağırlık matrisinin boyutu $4 \times 3$, girdi vektörünün boyutu $3 \times 1$ ve çıktı vektörünün boyutu ise $4 \times 1$.

Ancak, ses verisi bundan çok daha uzun (3 örnek uzunduğunda değil). Ses verisindeki örneklerin sayısı sesin süresi (örneğin 3 saniye) ve örnekleme oranının (örneğin 22.05 kHz) çarpımına eşit. Aşağıda gösterildiği gibi, girdi $\boldsymbol{x}$ vektörü oldukça uzun olacak. Buna bağlı olarak, ağırlık matrisi “şişmanlayacak”.

\[\begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} & \cdots &w_{1k}& \cdots &w_{1n}\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

Yukarıdaki formülasyonu eğitmesi zor olacak. Neyse ki basitleştirmek için yöntemler bulunuyor.

Özellik: yerellik

Verinin yerelliğinden dolayı (diğer bir deyişle birbirinden uzakta bulunan veri noktalarını önemsemiyoruz) yukarıdaki ağırlık matrisindeki $w_{1k}$, $k$ görece büyük olduğunda 0’lar ile doldurulabilir. Bu yüzden, matrisin ilk satırı 3 büyüklüğünde bir çekirdek (kernel) oluyor. Bu 3 büyüklüğündeki çekirdeği $\boldsymbol{a}^{(1)} = \begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} \end{bmatrix}$ olarak gösterelim.

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & \cdots &0& \cdots &0\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

Özellik: durağanlık

Doğal veri sinyalleri durağanlık (diğer bir deyişle bazı örüntüler tekrar ediyor) özelliğine sahip. Bu, daha önce tanımladığımız $\mathbf{a}^{(1)}$ çekirdeğini tekrar kullanmamızı sağlıyor. Bu çekirdeği her seferinde bir adım ileriye alarak kullanıyoruz (diğer bir deyişle adım kaydırma 1’e eşit). Sonuç şu:

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & 0 & 0 & 0&\cdots &0\\ 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&0&\cdots &0\\ 0 & 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&\cdots &0\\ 0 & 0 & 0& a_1^{(1)} & a_2^{(1)} &a_3^{(1)} &0&\cdots &0\\ 0 & 0 & 0& 0 & a_1^{(1)} &a_2^{(1)} &a_3^{(1)} &\cdots &0\\ \vdots&&\vdots&&\vdots&&\vdots&&\vdots \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix}\]

Matrisin hem yukarı-sağ hem de aşağı-sol kısımları yerellik özelliği sayesinde 0’larla dolduruldu, bu da matrisin seyrekleşmesine yok açtı. Bir çekirdeğin tekrar tekrar kullanımına ağırlık paylaşımı denir.

Toeplitz matrisinin çoklu katmanları

Bu değişikliklerden sonra, elimizde kalan değişken sayısı 3 ($a_1,a_2,a_3$). 12 değişkeni ($w_{11},w_{12},\cdots,w_{43}$) olan önceki ağırlık matrisiyle karşılaştırdığımızda, şimdiki değişken sayımız çok kısıtlayıcı ve aynı şekilde genişletmek istiyoruz.

Önceki matris çekirdeği $\boldsymbol{a}^{(1)}$ olan bir katman olarak düşünülebilir (bir evrişimli katman). Daha sonra değişken sayısını arttırarak farklı $\boldsymbol{a}^{(2)}$, $\boldsymbol{a}^{(3)}$, v.s. çekirdekleriyle çoklu katmanlar oluşturabiliriz.

Her katmanda defalarca tekrarlanmış bir çekirdeği içeren bir matris var. Bu matrise Toeplitz matrisi deniyor. Her Toeplitz matrisindeki soldan sağa inen tüm köşegenler sabit bir sayıdır. Burada kullandığımız Toeplitz matrisleri aynı zamanda seyrek matrisler.

İlk çekirdek $\boldsymbol{a}^{(1)}$ ve girdi vektörü $\boldsymbol{x}$ verildiğinde, bu katman tarafından verilen çıktının ilk elemanı $a_1^{(1)} x_1 + a_2^{(1)} x_2 + a_3^{(1)}x_3$. Böylece, çıktı vektörünün tamamı şu şekilde gözüküyor:

-

\[\begin{bmatrix} \mathbf{a}^{(1)}x[1:3]\\ \mathbf{a}^{(1)}x[2:4]\\ \mathbf{a}^{(1)}x[3:5]\\ \vdots \end{bmatrix}\]

Benzer sonuçlar almak için aynı matris çarpma yöntemi sonraki evrişimli katmanlarda başka çekirdeklerle ($\boldsymbol{a}^{(2)}$ ve $\boldsymbol{a}^{(3)}$) uygulanabilir.

Evrişimleri dinlemek - Jupyter Notebook

Jupyter Notebook’a buradan ulaşabilirsiniz.

Burada evrişimi ‘hareketli skaler çarpım’ olarak inceleyeceğiz.

librosa kütüphanesi $\boldsymbol{x}$ ses kaydını ve onun örnekleme oranını yüklememizi sağlıyor. Bu örnekte, 70641 örnek var, örnekleme oranı 22.05kHz ve kaydın toplam uzunluğu 3.2 saniye. Yüklenmiş ses sinyali dalgalı (Fig 1’e bakın) ve $y$ ekseninin büyüklüğüne bakarak neye benzediğini tahmin edebiliriz. Ses sinyali $x(t)$ aslında Windows sistemi kapatıldığında çalan ses (Fig 2’ye bakın).

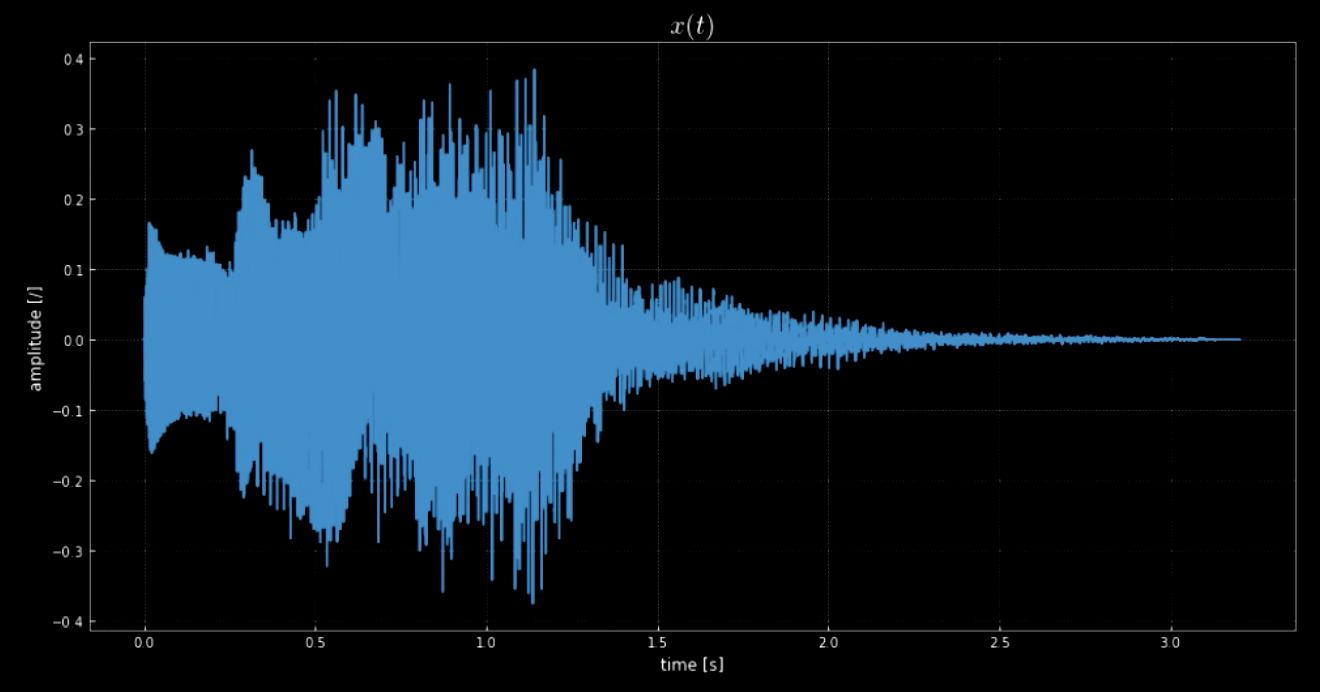
Fig. 1: Ses sinyalinin görselleştirilmesi.

Fig. 2: Üstteki ses sinyalinin notaları.

Notaları dalga şeklinden ayırabilmemiz gerekiyor. Bunu başarmak için Fourier dönüşümünü kullansaydık tüm notalar bir araya gelirdi ve perdelerin zamanını ve yerini tam olarak bulmak zor olurdu. Bu yüzden bir yerelleştirilmiş Fourier dönüşümüne ihtiyacımız var (başka bir adıyla spektogram). Spektogramda görüldüğü gibi (Fig 3’e bakın), farklı perdeler farklı frekanslarda (örneğin ilk perde 1600’de zirveye ulaşıyor) en yüksek değerinde. 4 perdeyi frekanslarında bir araya getirerek orijinal sinyalin perdeli versiyonunu elde ediyoruz.

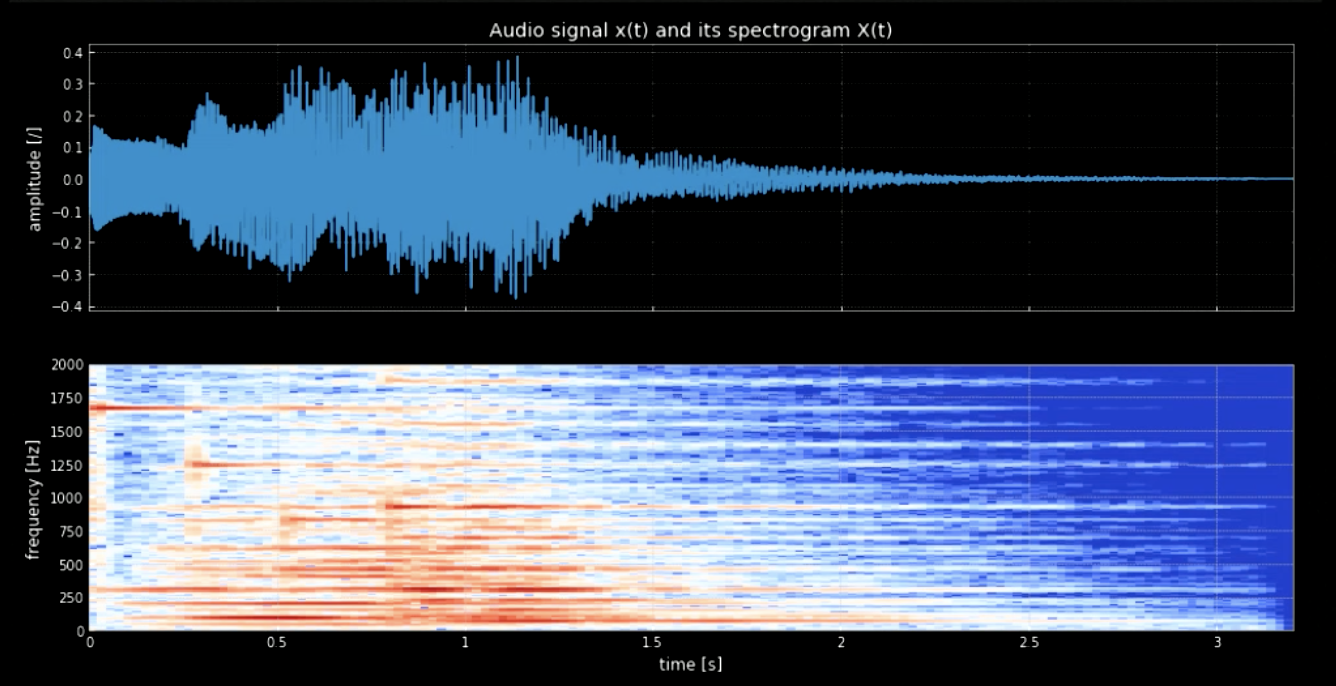
Fig. 3: Ses sinyali ve spektrogramı.

Girdi sinyalinin tüm perdelerle (örneğin piyanonun tüm tuşları) evrişimi, girdideki tüm notaların çıkarılmasını (sesin bir çekirdekle eşleşmesiyle) sağlayabilir. Orijinal sinyalin spektogramları ve bir araya gelmiş perdelerin sinyali Fig 4’te gösterilirken, orijinal sinyal ve 4 perdenin frekansları Fig 5’te gösteriliyor. Dört çekirdeğin girdi sinyaliyle (orijinal sinyal) evrişiminin çizimi Fig 6’da gösteriliyor. Fig 6 ile birlikte evrişimin ses kaydı notaların çıkarılmasında evrişimin ne kadar etkili olduğunu gösteriyor.

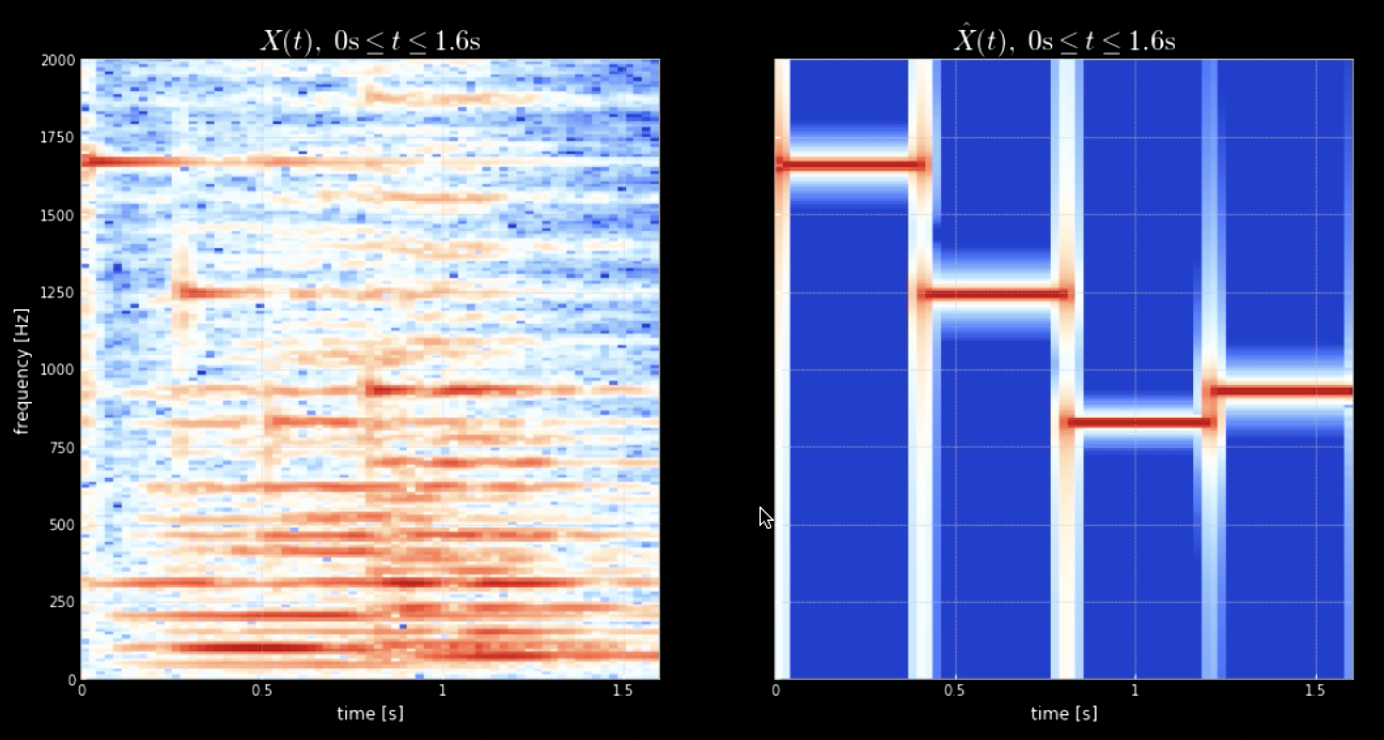
Fig. 4: Orijinal sinyalin spektogramı (sol) ve Bir araya gelmiş perdelerin spektogramı (sağ).

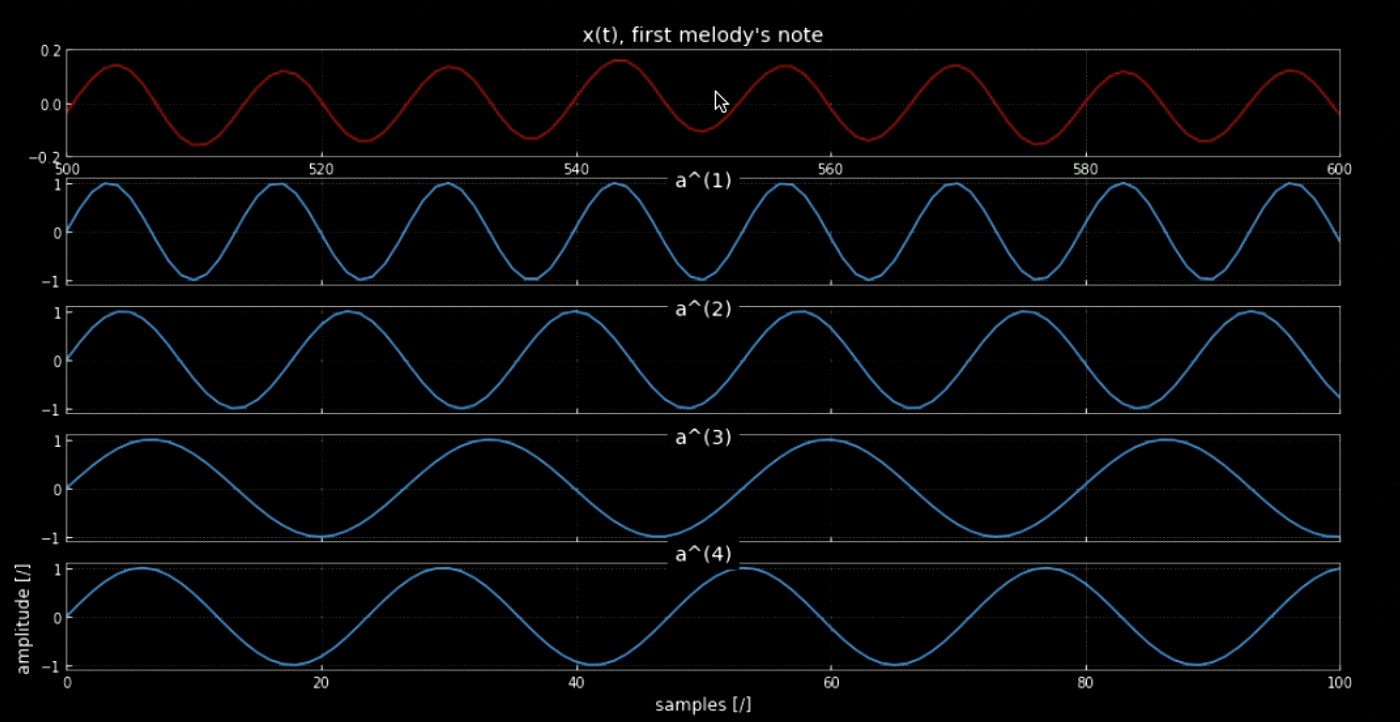
Fig. 5: Melodinin ilk notası.

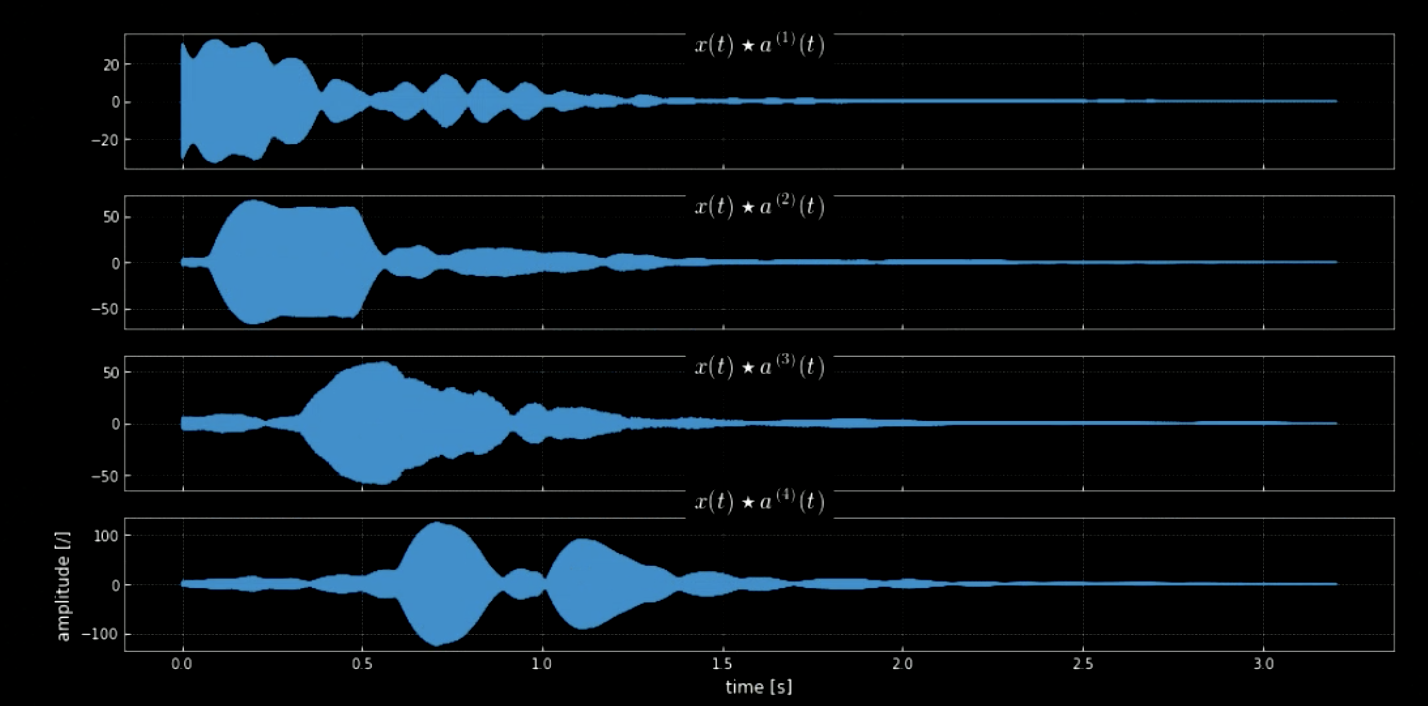
Fig. 6: Dört çekirdeğin evrişimi.

Farklı veri setlerinin boyutsallığı

Son bölüm, farklı boyutsallık gösterimleri ve bunun örnekleri için kısa bir incelemedir. Burada girdi kümesi $X$, tanım kümesi $\Omega$’dan kanal $c$’ye olan fonksiyonlardan oluşuyor.

Örnekler

• Ses verisi: tanım kümesi 1 boyutlu, zamana bağlı ayrık sinyal; kanal sayısı $c$ 1 (mono), 2 (stereo), 5+1 (Dolby 5.1), v.s. olabilir
• Görsel veri: tanım kümesi 2 boyutlu (pikseller); $c$’nin değerleri 1(gri tonlama), 3(renkli), 20(hiperspektral), v.s.
• Özel görelilik: tanım kümesi $\mathbb{R^4} \times \mathbb{R^4}$ (uzay-zaman $\times$ dört-ivme); $c = 1$ olduğu zaman Hamiltonian denir.

Fig. 7: Farklı türde sinyallerin farklı boyutları.

---

📝 Yuchi Ge, Anshan He, Shuting Gu, and Weiyang Wen
yavuzdrmzksr
18 Feb 2020