ConvNet Gelişmeleri, Mimarileri, Uygulama Detayları ve Avantajları.

İlkel CNN’ler ve modern CNN’lere gelişimi

Küçük veri kümelerinde ilkel evrişimli sinir ağları

Fukushima’nın görsel korteks modelleme konusundaki çalışmalarından esinlenerek, denetimli eğitim ve geri yayılım ile birleştirilmiş basit/karmaşık hücre hiyerarşisini kullanmak, Prof. Yann LeCun tarafından Toronto Üniversitesi’nde ‘88 -‘89’da ilk CNN’in gelişmesine yol açtı. Deneylerde 320 ‘mouser-written’ basamaklı küçük bir veri kümesi kullanılmıştır. Aşağıdaki mimarilerin performansları karşılaştırıldı:

1. Tek FC(tam bağlantılı) Katman
2. İki FC Katman
3. Paylaşılan ağırlıklar olmadan Yerel Bağlantılı Katmanlar
4. Ağırlıklar ve yerel bağlantılarla kısıtlanmış ağ
5. Paylaşılan ağırlıklar ve yerel bağlantılar ile kısıtlı ağ 2 (daha fazla öznitelik haritası)

En başarılı ağlar (paylaşılan ağırlıklarla kısıtlanmış ağ) en güçlü genelleştirilebilirliğe sahipti ve modern CNN’lerin temelini oluşturdu. Bu arada, tek FC katmanı aşırı öğrenme eğilimi gösterir.

Bell Laboratuarlarında ilk “gerçek” ConvNet

Bell Labs’a taşındıktan sonra LeCunn’un araştırmalarında, daha büyük bir CNN eğitmek için el yazısı posta kodlarını kullanmaya başladı:

• 256 (16$\times$16) giriş katmanı
• 12 5$\times$5 kernels with stride 2 (stepped 2 pixels): sonraki katman düşük çözünürlüklüdür
• Ayrıca bir örnekleme yöntemi KULLANILMADI

Örneklemeli evrişimsel ağ mimarisi

Ertesi yıl bazı değişiklikler yapıldı: ayrı örnekleme yöntemi getirildi. Ayrı örnekleme yöntemi, giriş değerlerinin ortalaması alınarak, bir yanlılık ekleyerek ve doğrusal olmayan bir fonksiyona (hiperbolik tanjant fonksiyonu) geçerek yapılır. 2$\times2$ örneklemesi 2 adımlı aralıklarıla gerçekleştirildi, dolayısıyla çözünürlükleri yarı yarıya düşürdü.

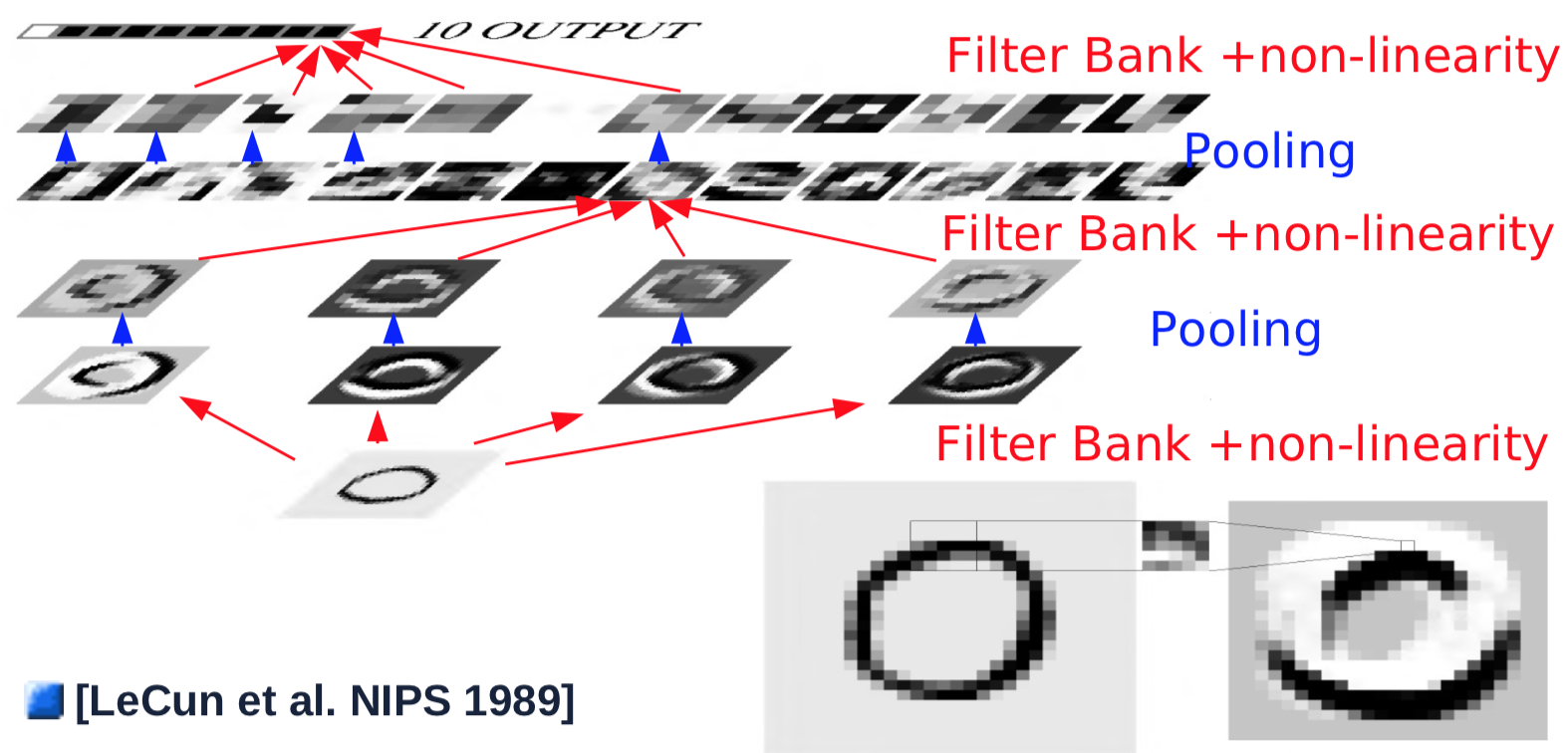
Fig. 1 ConvNet Mimarisi

Tek bir evrişimsel katman örneği aşağıdaki gibidir:

1. 32$\times$32 boyutunda bir girdi alır
2. Evrişimsel katmanı görüntü üzerinde adım 1 ile 5$\times5$ çekirdeği geçer ve sonuçta çıkan öznitelik harita boyutu 28$\times$28 olur
3. Öznitelik haritasını doğrusal olmayan bir fonksiyona aktarır: 28$\times$28
4. Adım 2 ile 2$\times$2 penceresinin ortalaması olan örnekleme katmanına geçer: 14$\times$14
5. 4 çekirdek için 1-4’ü tekrarlar

Birinci katman, basit evrişimsel/örneklem kombinasyonları genellikle kenar algılama gibi basit öznitelikleri algılar. İlk evrişimsel/örnekleme katmanından sonra amaç, önceki katmanlardan öznitelik kombinasyonlarını tespit etmektir. Bunu yapmak için, 2’den 4’e kadar olan adımlar, önceki katman öznitelik haritalarında birden çok çekirdekle tekrarlanır ve yeni bir öznitelik haritasında toplanır:

1. Yeni bir 5$\times$5 çekirdeği, önceki katmanlardaki tüm öznitelik haritalarının üzerine kaydırılır ve sonuçlar toplanır. (Not: Prof. LeCun’un 1989’daki deneyinde, nöral ağ hesaplama amacıyla tam bağlantılı değildi. Modern mimarilerde genellikle tam bağlantılı katmanlar kullanılır ): boyut 10$\times$10
2. Evrişimin çıktısını doğrusal olmayan bir işleve geçirin: boyut 10$\times$10
3. 16 çekirdek için 1/2’yi tekrarlayın.
4. Sonucu, 2 adım kaydırma ile ortalama 2$\times$2 penceresinin üzerinde olan örnekleme katmanına iletin: her öznitelik haritasınun boyutu 5$\times$5

Bir çıktı üretmek için, tam bağlantılı gibi görünen ama gerçekte evrişimsel olan son evrişim katmanı gerçekleştirilir.

1. Son evrişim katmanı, tüm öznitelik haritaları üzerinde 5$\times5$ çekirdeği kaydırılır ve sonuçlar toplanır: boyut 1$\times$1
2. Doğrusal olmayan fonksiyondan geçirilir: boyutu 1$\times$1
3. Bir kategori için tek bir çıktı oluştulur.
4. 10 kategorinin her biri için tüm adımları tekrarlayın (paralel olarak)

Evrişimsel katmanların bir sonraki katmanın öznitelik haritalarının şeklini nasıl değiştirdiğini öğrenmek için Andrej Karpathy’nin web sitesinde bulunan [bu animasyonu] (http://cs231n.github.io/convolutional-networks/) inceleyebilirsiniz. Tam makale buradan bulunabilir.

Shift equivariance

Fig. 2 Shift Equivariance

Slaytlardaki animasyonla gösterildiği gibi (burada başka bir örnek), girdi görüntüsünün çevrilmesi öznitelik haritalarının aynı çevirisiyle sonuçlanır. Ancak, öznitelik haritalarındaki değişiklikler evrişim/örnekleme işlemleriyle ölçeklendirilir. Örneğin. adım 2 ile 2$\times$2 havuzu, aşağıdaki özellik haritalarında giriş katmanındaki 1 piksel kaydırmayı 0,5 piksel kaydırmaya düşürür. Daha sonra uzamsal çözünürlük, artan sayıda öznitelik türü ile değiştirilir, yani temsilleri daha soyut hale getirilmesi ve kayma ve bozulmalara daha az duyarlı hale getirilmesi.

Genel mimari dökümü

Genel CNN mimarisi birkaç temel katman modeline ayrılabilir:

• ** Normalleştirme **
  • Beyazlatma ayarı (isteğe bağlı)
  • Çıkarma yöntemleri ör. ortalama çıkarma, yüksek geçiren filtreleme
  • Bölücü: yerel kontrast normalizasyonu, varyans normalizasyonu
• ** Filtre Bankaları **
  • Boyutsallığı artırın
  • Aşırı tamamlama temelinde projeksiyon
  • Kenar algılamaları
• ** Doğrusal olmayanlar **
  • Seyreltme
  • Genellikle Doğrultulmuş Doğrusal Birim (ReLU): $\text{ReLU}(x) = \max(x, 0)$
• ** Örnekleme **
  • Öznitelik haritası üzerinde toplama

  • Maksimum Örnekleme: $\text{MAX}= \text{Max}_i(X_i)$

  • LP-Norm Örnekleme: \(\text{L}p= \left(\sum_{i=1}^n \|X_i\|^p \right)^{\frac{1}{p}}\)

  • Log-Prob Örnekleme: $\text{Prob}= \frac{1}{b} \left(\sum_{i=1}^n e^{b X_i} \right)$

LeNet5 ve rakam tanıma

LeNet5 mimarisinin PyTorch üzerinde geliştirilmesi

LeNet5 aşağıdaki katmanlardan oluşur (1 en üstteki katmandır):

1. Log-softmax
2. 500$\times10$ boyutlarında tam bağlantılı katman
3. ReLu
4. (4$\times$4$\times50$)$\times500 boyutlarında tam bağlantılı katman
5. 2$\times$2 boyutlarında 2 adım kaydırmalı max örnekleme.
6. ReLu
7. 20 çıkış kanallı evrişimsel katman, 5$\times$5 çekirdek, 1 adım kaydırmalı.
8. 2$\times$2 boyutlarında 2 adım kaydırmalı max örnekleme.
9. ReLu
10. 20 çıkış kanallı evrişimsel katman, 5$\times$5 çekirdek, 1 adım kaydırmalı.

Girdi , 32$\times$32 gri tonlu bir görüntüdür (1 giriş kanalı).

LeNet5 mimarisinin PyTorch kodu aşağıdadır:

class LeNet5(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(1, 20, 5, 1)
        self.conv2 = nn.Conv2d(20, 20, 5, 1)
        self.fc1 = nn.Linear(4*4*50, 500)
        self.fc2 = nn.Linear(500, 10)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = F.max_pool2d(x, 2, 2)
        x = F.relu(self.conv2(x))
        x = F.max_pool2d(x, 2, 2)
        x = x.view(-1, 4*4*50)
        x = F.relu(self.fc1)
        x = self.fc2(x)
    return F.logsoftmax(x, dim=1)

fc1 ve fc2 tam bağlantılı katmanlar olmasına rağmen, çekirdekleri tüm girdiyi kapsayan evrişimsel katmanlar olarak düşünülebilir. Tam bağlantılı katmanlar verimlilik amacıyla kullanılır.

Aynı kod nn.Sequential kullanılarak ifade edilebilir, ancak bu yöntem güncel değildir.

CNN’lerin Avantajları

Tamamen evrişimsel bir ağda, girdinin boyutunu belirtmeye gerek yoktur. Ancak, girişin boyutunu değiştirmek çıktının boyutunu değiştirir.

Bir el yazısı tanıma sistemini düşünün. Giriş görüntüsünü parçalara ayırmak zorunda değiliz. CNN’i görüntünün tamamına uygulayabiliriz: çekirdekler, görüntünün tüm konumlarını kaplar ve desenin bulunduğu yerden bağımsız olarak aynı çıktıyı kaydeder. CNN’i bir görüntünün tamamına uygulamak, görüntüyü birden çok konuma ayrı ayrı uygulamaktan çok daha ucuzdur. Önceden bölümleme gerekmemektedir, bu bir rahatlamadır çünkü bir görüntüyü bölümleme görevi bir görüntüyü tanımaya benzer.

Örnek: MNIST

LeNet5, görüntünün ortasındaki rakamları sınıflandırmak için 32$\times$32 boyutundaki MNIST görüntüleri üzerinde eğitilmiştir. Veri artırma, rakamı kaydırarak, rakamın boyutunu değiştirerek, yana rakamlar ekleyerek uygulandı. Ayrıca yukarıdakilerin hiçbirini temsil etmeyen 11. kategori ile eğitildi. Bu kategoriye göre etiketlenmiş görüntüler boş görüntüler üretilerek veya rakamları merkeze değil yan tarafa yerleştirerek oluşturuldu.

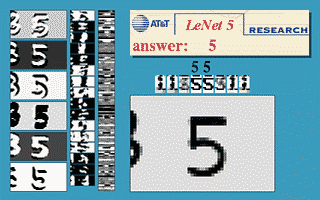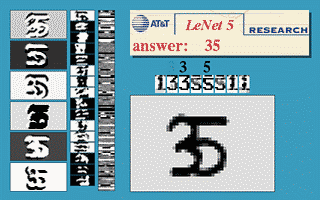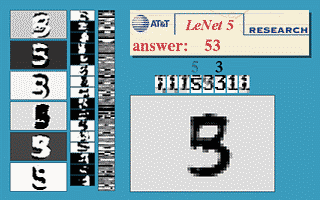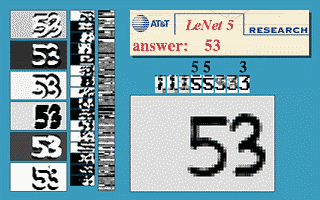
Fig. 3 ConvNet kayan pencere

Yukarıdaki görüntü, 32$\times$32 üzerinde eğitilmiş bir LeNet5 ağının, basamağı birden fazla yerde tanımak için 32$\times$64 giriş görüntüsüne uygulanabileceğini göstermektedir.

Öznitelik bağlama problemi

Öznitelik bağlama problemi nedir?

Görsel sinir bilimcileri ve bilgisayar görme insanları nesneyi bir nesne olarak tanımlama sorununa sahiptir. Nesne özniteliklerin bütünüdür, ancak bu nesneyi oluşturmak için tüm öznitelikler nasıl bir araya gelir?

Nasıl çözülür?

Bu özellik bağlama problemini çok basit bir CNN kullanarak çözebiliriz: CNN’imizi eğitmek için yeterli doğrusallık ve verilere sahip olduğumuz göz önüne alındığında, sadece iki katmanlı örneklemeli evrişimsel katmanı ile spesifik bir mekanizması olmayan iki katmanlı tam bağlantılı mimari yeterlidir.

Fig. 4 ConvNet Addressing Feature Binding

Yukarıdaki animasyon, CNN’nin tek bir konturu hareket ettirerek farklı basamakları tanıma, öznitelik bağlama problemlerini, yani özellikleri hiyerarşik, bileşiksel bir şekilde tanıma yeteneğini gösterme yeteneğini göstermektedir.

Örnek: dinamik giriş boyutu

Adım 1 ile 2 evrişim katmanı ve adım 2 ile 2 örnekleme katmanı ile bir CNN oluşturabiliriz, böylece genel adım kaydırma 4’tür. Bu nedenle, yeni bir çıktı almak istiyorsak, giriş penceremizi 4’e kaydırmamız gerekir. Daha açık bir şekilde, aşağıdaki rakamı görebiliriz (yeşil birimler). İlk olarak, 10 boyutunda bir girdimiz var ve 8 birim elde etmek için 3 boyutunda evrişim gerçekleştiriyoruz. Bundan sonra, 4 adet elde etmek için 2 büyüklüğünde örnekleme yapıyoruz. Benzer şekilde, evrişimi ve örneklemeyi tekrarlıyoruz ve sonunda 1 çıktı alıyoruz.

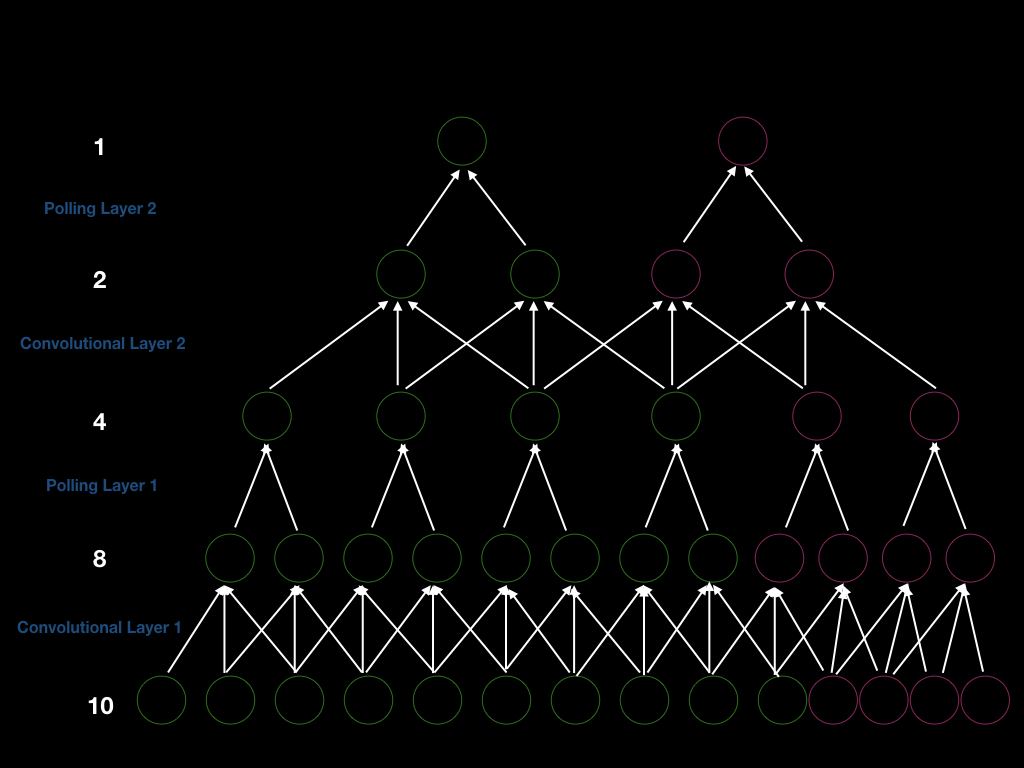
Fig. 5 Değişken Giriş Boyutlarıyla ConvNet Mimarisi

Diyelim ki giriş katmanına 4 birim ekledik (yukarıdaki pembe birimler), böylece ilk evrişim katmanından sonra 4 birim daha, ilk örnekleme katmanından sonra 2 birim daha, ikinci evrişim katmanından sonra 2 birim ve 1 fazla çıktı daha alabileceğimizi varsayalım. Bu nedenle, yeni bir çıktı oluşturmak için pencere boyutu 4’tür (2 adım $\times$2) <! - girişten çıkışa gösterdiğimiz toplam alt örnekleme 4’tür (2x2) ->. Dahası, bu, girdinin boyutunu artırırsak, her katmanın boyutunu artıracağımızın, CNN’lerin dinamik uzunluk girişlerini işleme yeteneğini kanıtlayacağımızın bir göstergesidir.

CNN’ler ne için kullanılır?

CNN’ler, çok boyutlu diziler şeklinde gelen ve üç temel özelliğe sahip doğal sinyaller için kullanılır:

1. ** Yerellik **: Birincisi, değerler arasında güçlü bir yerel korelasyon olmasıdır. Doğal bir görüntünün yakındaki iki pikselini alırsak, bu piksellerin aynı renge sahip olma olasılığı yüksektir. İki piksel birbirinden uzaklaştıkça, aralarındaki benzerlik azalacaktır. Yerel korelasyonlar, CNN’lerin yaptığı yerel özellikleri tespit etmemize yardımcı olabilir. Görüntünün piksellerini karıştırarak girdi olarak verdiğimizde, CNN görüntüyü tanımada iyi performans iyi performans göstermezken, FC mimarisi etkilenmez. Yerel korelasyon yerel bağlantıları anlamlandırır.
2. ** Durağanlık **: İkinci temel özellik, özniteliklerin gerekli olması ve paylaşılan ağırlıkları ve örneklemeyi savunarak görüntünün herhangi bir yerinde görünebilmesidir. Dahası, istatistiksel sinyaller homojen bir dağılım gösterir, başka bir deyişle görüntünün her bölgesi için öznitelik çıkarmayı tekrarlamamız gerekir.
3. ** Bileşimsellik **: Üçüncü karakter, doğal görüntülerin bileşimsel olması, yani özelliklerin bir görüntüyü hiyerarşik bir şekilde oluşturmasıdır. Bu, Hubel ve Weisel’in basit ve karmaşık hücreler üzerindeki araştırmalarına da yakın olan çoklu nöron katmanlarının kullanımını savunur.

Ayrıca, CNN’ler videolarda, görüntülerde, metinlerde ve konuşma tanımada kullanır.