Sinir Ağlarındaki Parametre Transformasyonunun Görselleştirilmesi ve Evrişimin Temel Konseptleri

Sinir Ağlarının Görselleştirilmesi

Bu bölümde, sinir ağlarının içinde olanları görselleştireceğiz.

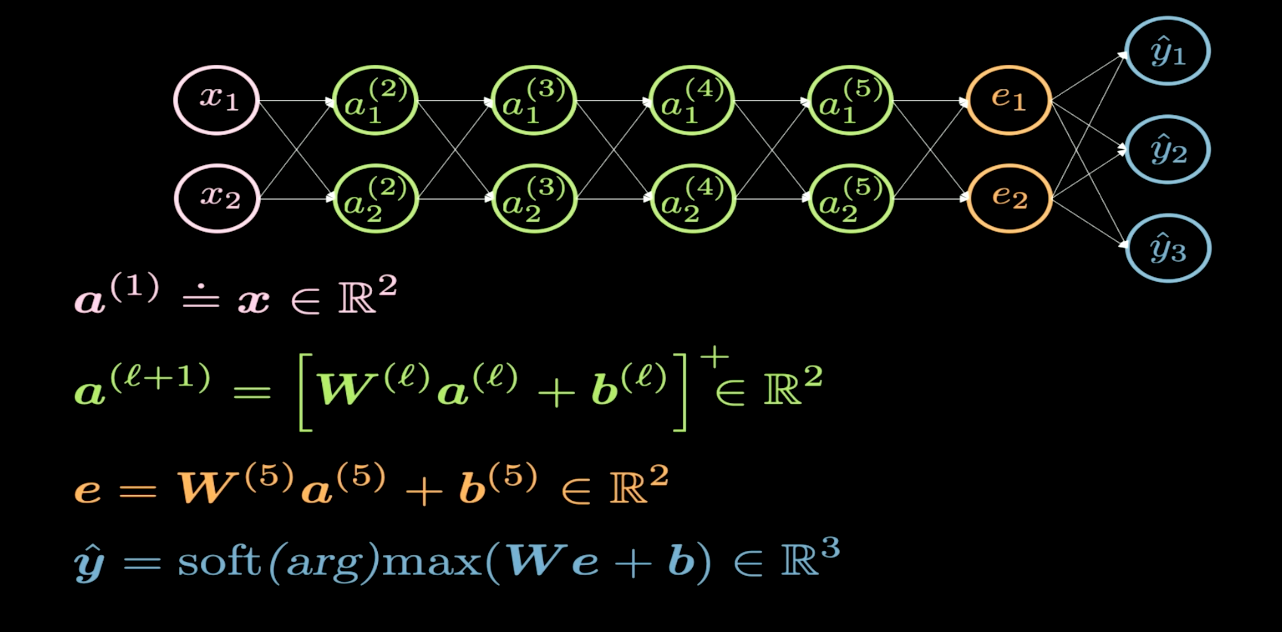
Şekil 1: Ağ Yapısı

Şekil 1, görselleştirmek istediğimiz sinir ağının yapısını betimliyor. Genellikle bir sinir ağının yapısını çizdiğimizde, girdileri aşağıda ya da solda; çıktıları yukarıda ya da sağda gösteririz. Figür 1’de, pembe nöronlar girdileri, mavi nöronlar ise çıktıları gösteriyor. Bu ağda, 4 adet saklı katman var (yeşiller), yani toplamda 6 tane katman var (4 saklı katman + 1 girdi katmanı + 1 çıktı katmanı). Bu örnekte, her gizli katmanda 2’şer nöron var, yani ağırlık matrisi ($W$)nın boyutu her katmanda 2 ye 2. Bunun nedeni ise giriş düzlemini görselleştirebileceğimiz bir düzleme dönüştürebilmek istememiz.

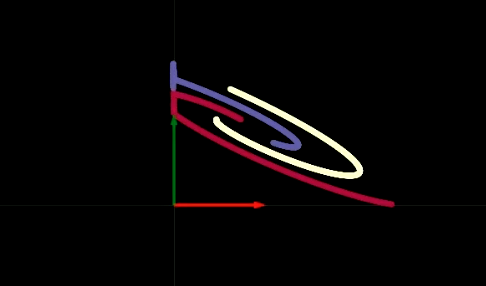
Şekil 2: Katlanma uzayının görüntülenmesi

Her katmanın dönüşümü (transformation), Şekil 2’de gösterildiği gibi, düzlemimizi belli yerlerinden katlamaya benziyor. Bu katlamalar çok keskin, çünkü bütün dönüşümler 2 boyutlu katmanda gerçekleşiyor. Deney sonucunda şunu fark ediyoruz ki eğer saklı katmanda sadece 2 nöron olursa, optimizasyon daha uzun sürüyor; eğer saklı katmanda daha çok nöron olursa optimizasyon kolaylaşıyor. Bu da aklımıza şu soruyu getiriyor: Neden saklı katmanında daha az nöron olan bir ağı eğitmek daha zor? Bu soruyu kendi kendinize düşünmelisiniz, $\texttt{ReLU}$’nun (rectified linear unit, düzeltilmiş lineer birim) görselleştirmesinden sonra buna geri döneceğiz.

| | | |(a)|(b)|

Ağın her saklı katmanına teker teker baktığımızda, her katmanın önce bir afin (affine, ilgin ) dönüşüm sonrasında lineer olmayan ReLU operasyonu yaptığını görüyoruz, ReLU operasyonu negatif değerleri yok ediyor. Şekil 3(a) ve (b) de, ReLU operatörünün nasıl göründüğünü görebiliriz. ReLU operatorü lineer olmayan dönüşümler yapmamıza yarar. Çok sayıda afin dönüşüm uygulayıp sonrasında ReLU operatörünü uyguladığımızda, Şekil 4’te de görülebileceği gibi veriyi lineer olarak doğrular ile ayırmayı başarabiliyoruz.

Şekil 4: Çıktıların Görselleştirilmesi

Bu bize neden 2 nöronlu saklı katmanların daha zor eğitildiği hakkında fikir veriyor. 6 katmanlı ağımızın her saklı katmanında birer yanlılığı (bias) var. Bu nedenle eğer bu yanlılıkların herhangi biri sağ üstteki çeyrek düzlemin dışında bir yere işaret ediyorsa, ReLU operatörü bu noktaları sıfırlayacaktır. Sonrasında, ne kadar ileride olursa olsun, katmanların veriye yapacağı dönüşümler sonrasında bu noktalar sıfır kalmaya devam edecektir. Bir sinir ağını daha “şişman” yaparak (saklı katmanlara daha çok nöron ekleyerek) daha kolay eğitilmesini sağlayabiliriz, ya da daha çok saklı katman ekleyebiliriz, ya da bu iki yöntemin bir kombinasyonunu kullanabiliriz. Beklemeyin ve görün, bu ders boyunca bize verilen probleme göre en iyi ağ yapısının ne olduğuna karar vermeyi keşfedeceğiz.

Parametre dönüşümleri (Parameter Transformations)

Genel olarak parametre dönüşümü, parametre vektörü $w$’nin bir fonksiyonun sonucu olduğu anlamına gelir. Bu dönüşüm ile, orijinal parametre uzayını başka bir uzaya eşleştirebiliriz. Şekil 5’teki $w$, $H$nin $u$ parametresiyle olan halinin çıktısı. $G(x,w)$ bir ağ ve $C(y,\bar y)$ bir maliyet fonksiyonu. Geri yayılım (backpropagation) formülü \(u \leftarrow u - \eta\frac{\partial H}{\partial u}^\top\frac{\partial C}{\partial w}^\top\)

\(w \leftarrow w - \eta\frac{\partial H}{\partial u}\frac{\partial H}{\partial u}^\top\frac{\partial C}{\partial w}^\top\) şeklinde yazılabilir. Bu formüller matris formunda uygulanırlar. Terimlerin boyutlarının birbirine uyması gerektiğine dikkat edelim. $u$,$w$,$\frac{\partial H}{\partial u}^\top$,$\frac{\partial C}{\partial w}^\top$ , sırayla $[N_u \times 1]$,$[N_w \times 1]$,$[N_u \times N_w]$,$[N_w \times 1]$ boyutlarına sahip. Bu nedenle geri yayılım formülümüzün boyutları birbiriyle uyuşuyor.

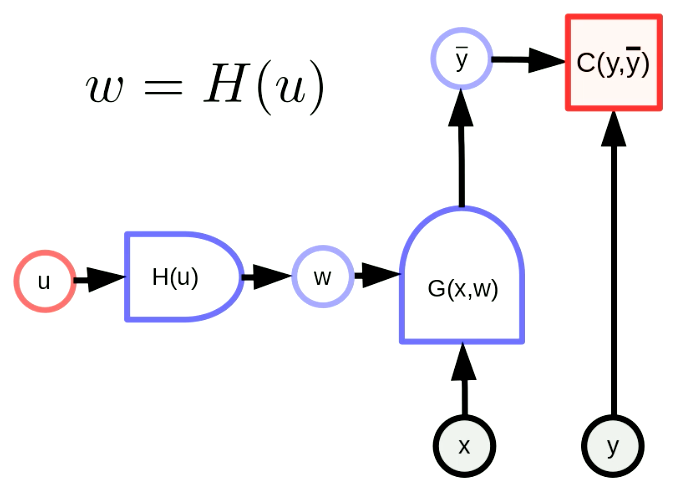
Şekil 5: Parametre Dönüşümlerinin Genel Formu

Kolay bir parametre dönüşümü: Ağırlık Paylaşma

Ağırlık paylaşma dönüşümü, $H(u)$ ‘nun, $u$’nun bir bileşenini $w$’nın birden çok bileşenine kopyaladığı anlamına gelir. $H(u)$, $u_1$’i, $w_1$, $w_2$’ye kopyalayan bir Y kısmı gibi. Bunu şu şekilde ifade edebiliriz: \(w_1 = w_2 = u_1, w_3 = w_4 = u_2\) Paylaşılan parametrelerin eşit olmasını zorunlu kılıyoruz, böylece paylaşılan parametlere göre alınan gradyan (eğim), geri yayılımda toplanmış olacak. Örneğin maliyet fonksiyonu $C(y, \bar y)$ ‘nun $u_1$’a göre gradyanı, $C(y, \bar y)$’nın $w_1$ ‘a göre olan gradyanı ve $C(y, \bar y)$’nın $w_2$’ye göre olan gradyanının toplamına eşit olacak.

Hiperağ (Hypernetwork)

Bir ağın ağırlıkları diğer ağın çıktısı ise buna hiperağ adı verilir. Şekil 6 bir “hiperağ”ın hesaplama grafiğini gösteriyor. Burada $H$ fonksiyonu, $u$ parametre vektörüne ve $x$ girdisine sahip bir ağ. Sonucunda, $G(x,w)$’nin ağırlıkları $H(x,u)$ ağı tarafından dinamik olarak ayarlanıyor. Bu eski bir fikir olsa da hala çok güçlü olan bir fikir.

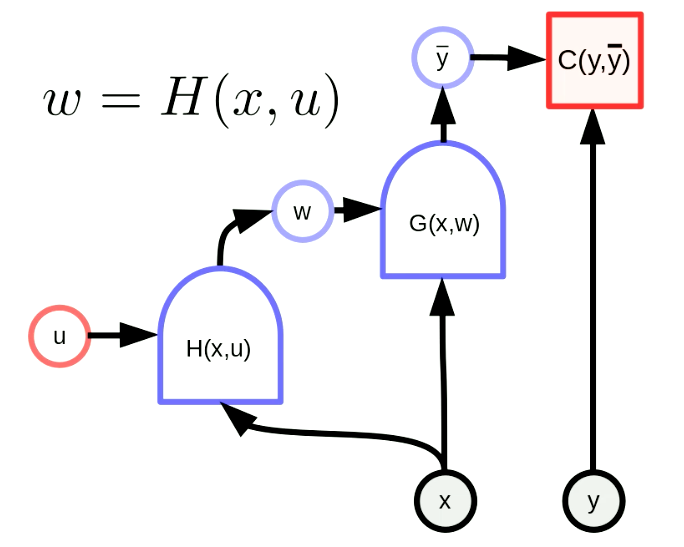
Şekil: 6 "Hiperağ"

Sıralı verilerde motifler bulma

Ağırlık paylaşımı dönüşümü, motif bulmaya uygulanabilir. Motif bulma, konuşma ya da yazı gibi sıralı verilerdeki motifleri bulma anlamına gelir. Bunu yapmanın bir yolu, Şekil 7’de görüldüğü gibi, verinin üzerinden bir pencere kaydırmak, bu da ağırlık paylaşma fonksiyonunu belli bir motifi bulması için kaydırıyor (örn. bir konuşma sinyali içindeki belli bir ses), böylece çıktılar (örn. bir skor) maksimum fonksiyonuna doğru gidiyor.

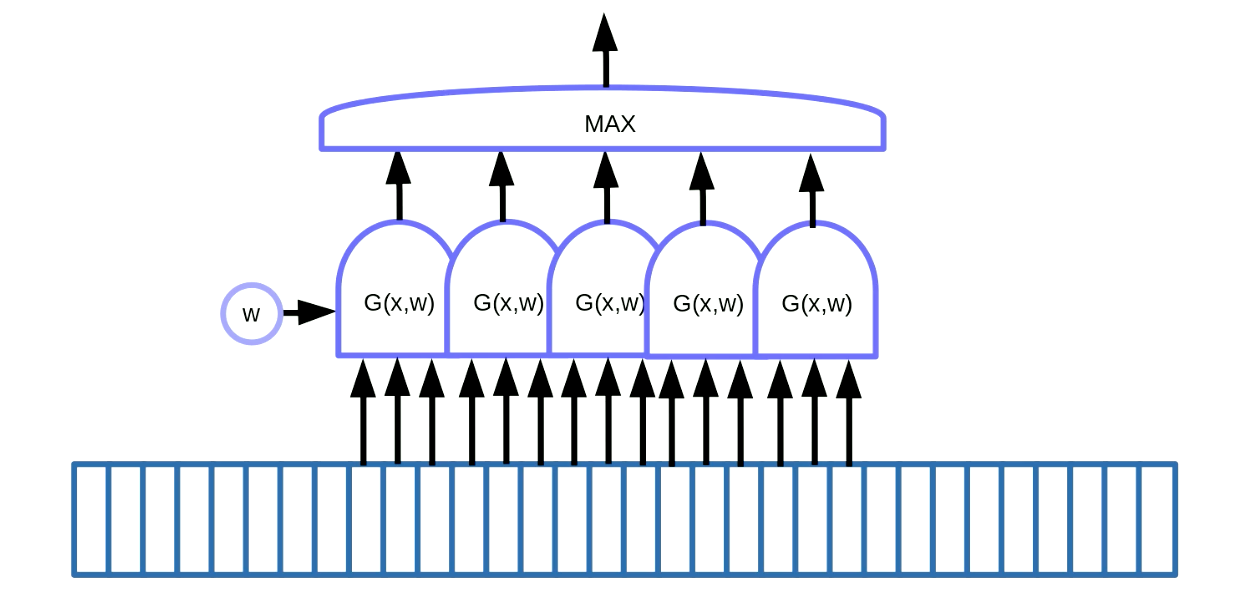
Şekil: 7 Sıralı Verilerde Motifler Bulma

Bu örnekte bu fonksiyonlardan elimizde 5 adet var. Bu sonuca göre, beş gradyanı topluyoruz ve hatayı geri yayılım yapıp $w$ parametresini güncelliyoruz. Bunu PyTorch’ta kodlarken, bu gradyanların dolaylı olarak yığılmasını önlemeliyiz, bu yüzden gradyanların ilk değerlerini atamak için zero_grad()‘ı kullanmalıyız.

Resimlerde motifler bulma

Motif bulmanın diğer bir yararlı uygulaması resimlerde motif bulma. Resimlerin üzerinden “şablon”ları kaydırarak, yer ve bozukluklarından bağımsız olarak şekilleri bulabiliriz. Şekil 8’de görüldüğü gibi, “C” ile “D” yi ayırt etmek basit bir örnek. “C” ile “D” arasındaki fark, “C” nin iki ucunun, “D”nin iki köşesinin olması. Böylelikle “uç şablonları” ve “köşe şablonları” tasarlayabiliriz. Eğer önümüzdeki şekil “şablon”lara benziyorsa, eşikte olan çıktılar verecek. Böylece bu çıktıları toplayarak harfleri ayırt edebiliriz. Şekil 8’de, ağ iki adet uç ve sıfır köşe buluyor, böylece “C”yi aktive ediyor.

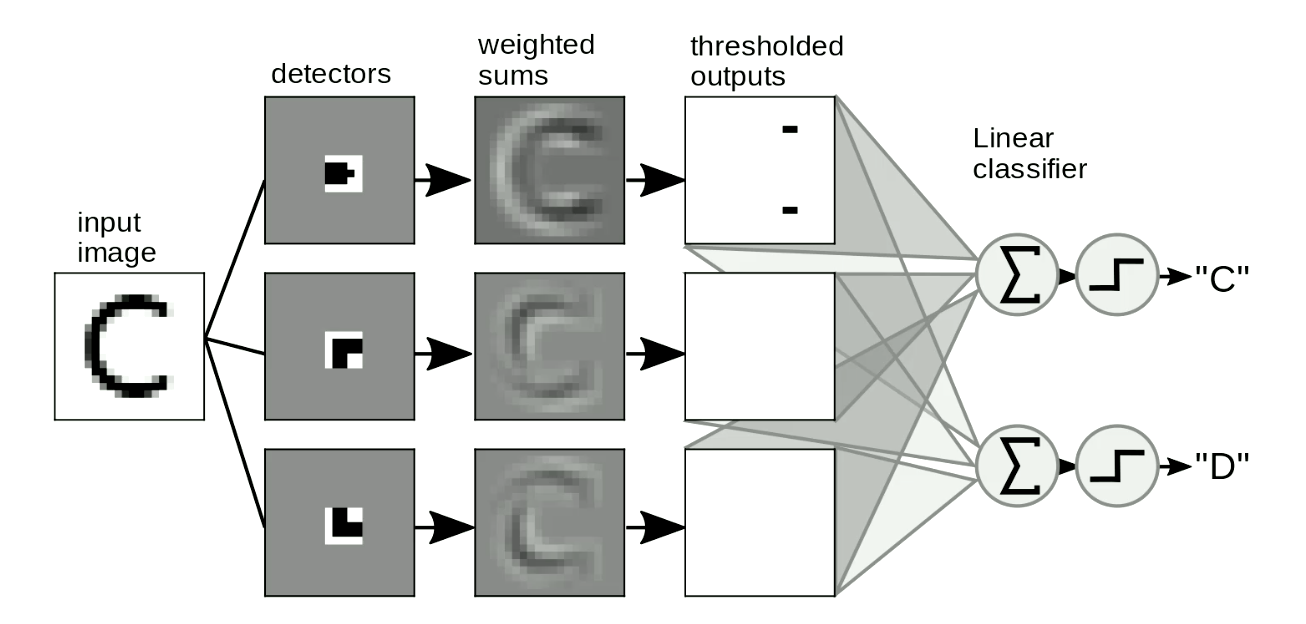
Şekil 8: Resimlerde motifler bulma

“Şablon eşleştirme”mizin kaydırma ile değişmez olması da önemli - yani girdiyi kaydırdığımızda, çıktı (örn. bulunan harf) değişmemeli. Bu ağırlık paylaşma transformasyonuyla çözülebilir. Şekil 9’da da görüldüğü gibi, “D”nin yerini değiştirdiğimizde, kaydırılmış olmalarına rağmen hala köşe motiflerini algılayabiliyoruz. Bu motifleri topladığımızda, toplam “D” harfini algılayacak şekilde ağı aktive edecek.

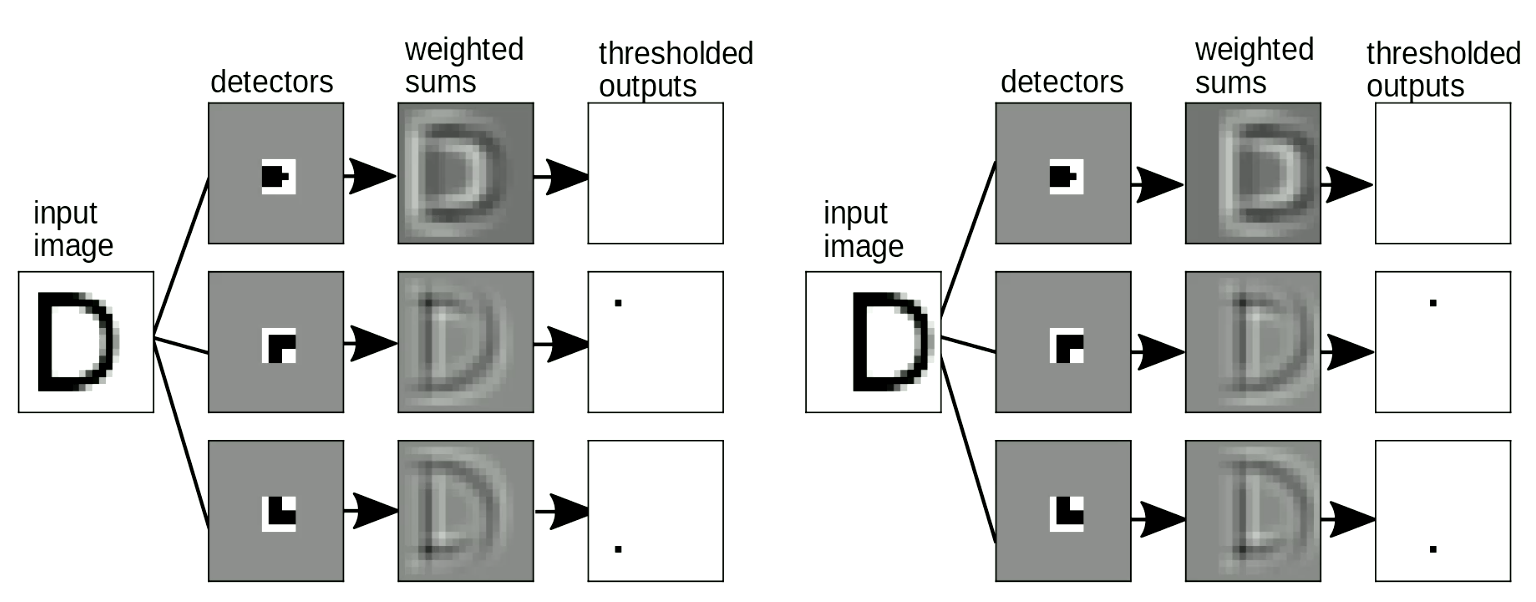
Şekil 9: Kayma Değişmezliği *(Shift Invariance)*

Bu elle oluşturulmuş, yerel dedektörleri kullanıp toplamı ile rakamı algılama metodu senelerdir kullanılıyor. Ama bize şöyle bir problem sunuyor: Bu “şablon”ları nasıl otomatik olarak dizayn edebiliriz? Sinir ağlarını bu “şablon”ları öğrenmek için kullanabilir miyiz? Sırada, evrişim konsepti var, bu da resimleri “şablonlar” ile eşleştirmek için kullandığımız operasyon.

Ayrık zamanlı evrişim (Discrete convolution)

Evrişim (Convolution)

Tek boyutlu düzlemde, girdi $x$ ile, $w$ arasındaki evrişimin tam olarak matematiksel tanımı şu şekildedir: \(y_i = \sum_j w_j x_{i-j}\) Kelimelerle ifade edersek, $i$’nci çıktı, ters çevrilmiş $w$ ile $x$ boyutundaki bir pencerenin arasındaki iç çarpım ile hesaplanabilir. Bütün çıktıyı hesaplamak için, pencere en baştan başlar, $x$ tamamlanana kadar bu pencere birer girdi kaydırılır ve bu şekilde tekrar edilir.

Çapraz korelasyon (Cross-correlation)

Pratikte, derin öğrenme alanındaki PyTorch gibi yazılımlarda kabul edilen tanım biraz farklıdır. Evrişim, PyTorch’ta $w$nin ters çevrilmemiş hali ile kodlanmıştır: \(y_i = \sum_j w_j x_{i+j}\) Matematikçiler bu formülasyona “çapraz korelasyon” derler. Bizim bağlamımımızda, bu fark sadece bir kural farkıdır. Pratik olarak çapraz korelasyon ve evrişim, bilgisayar hafızasındaki ağırlıkları baştan sona ya da sondan başa okuyarak, birbiri yerine kullanılabilir. Bunun farkında olmak önemlidir, mesela biri matematiksel bir makale üzerinden evrişim/korelasyon’un özelliklerinden faydalanmak isterse bunu göz önüne almalıdır.

Yüksek boyutlarda evrişim

Resimler gibi iki boyutlu girdilerde iki boyutlu evrişimden yararlanırız:

\(y_{ij} = \sum_{kl} w_{kl} x_{i+k, j+l}\) Bu tanım, iki boyuttan üç ve dört boyuta da kolayca taşınabilir. Bu tanımda $w$’ye evrişim çekirdeği (convolution kernel) adı verilir.

DCNN’lerde evrişim operatörüyle yapılabilecek değişiklikler

1.Adım Kaydırmak (striding): Pencereyi her seferinde $x$ üzerinde bir girdi kaydırmak yerine, daha büyük adımlarla da yapabiliriz (örneğin her seferinde iki ya da üç girdi kaydırmak gibi). Örnek: Farz edelim ki $x$ tek boyutlu ve 100 boyutunda, $w$ de 5 boyutunda olsun. (Stride) 1 ve 2 ile olacak çıktı aşağıdaki tabloda gösterilmiştir:

1. Dolgulama (padding): Derin Sinir Ağlarını dizayn ederken çoğu zaman evrişimdeki çıktının girdiyle aynı boyutta olmasını isteriz. Bunu girdinin iki tarafını da (genelde) sıfırlarla doldurarak yapabiliriz. Dolgulama çoğunlukla kolaylık olsun diye yapılır. Bazen performansı etkileyebilir, kenarlarda tuhaf efektlere yol açabilir; ama ReLU aktivasyonu kullanıldığında sıfırla dolgulama mantıksız değildir.

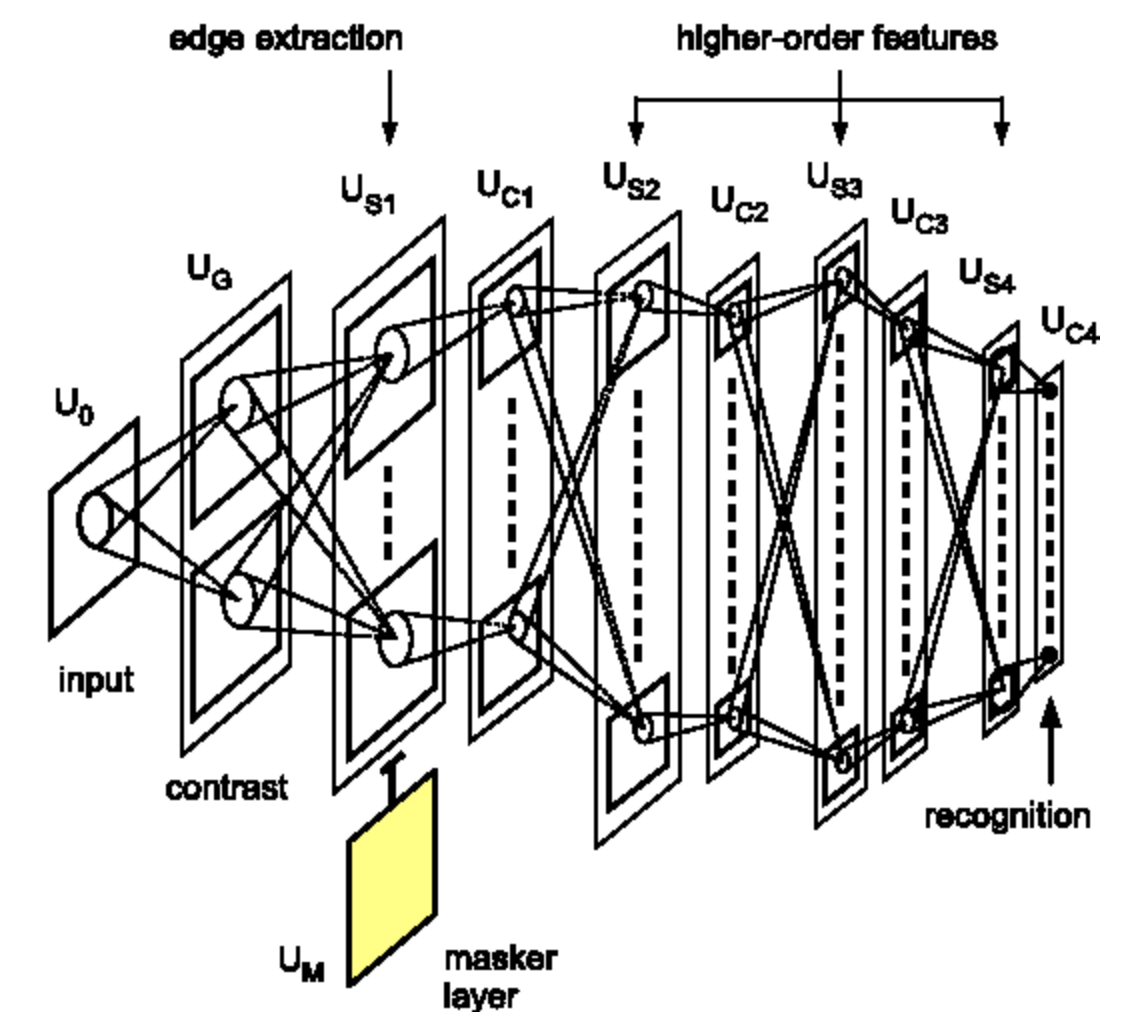
Derin Evrişimli Sinir Ağları (DCNNs)

Daha önceden de açıklandığı gibi, derin sinir ağları genelde tekrar tekrar birbirini takip eden lineer operatörler ve noktasal olarak lineer olmayan (pointwise nonlinear) katmanlardan oluşturulur. Evrişimli sinir ağlarında, bu lineer operatör, yukarda açıklanan evrişim operatörüdür. Bir de üçüncü bir katman çeşidi olan örnekleme (pooling) katmanı vardır.

Bu şekilde katmanları üst üste dizmemizin sebebi verinin hiyerarşik bir gösterimini oluşturmak istememizdir. CNN’ler sadece resimleri değil, konuşma ve dil verilerini de başarıyla işleyebilirler. Teknik olarak dizi (array) şeklinde olan herhangi bir veriye uygulanabilirler, yine de bu diziler belli özelliklere sahip olmalıdır.

Neden dünyanın hiyerarşik bir gösterimini oluşturmak istiyoruz? Çünkü üstünde yaşadığımız dünya birleşimsel bir yapı. Önceki bölümlerde de bunu ima etmiştik. Bu hiyerarşik yapı, yakın piksellerin birleşerek yönlü kenarlar gibi basit motifler oluşturduğu gerçeğinden anlaşılabilir. Bu kenarlar da birleşerek yerel çapta köşeler, T-kesişim noktaları gibi özellikleri oluştururlar. Bu köşeler birleşerek daha da soyut olan motifleri oluşturur. Böyle hiyerarşik şekilde inşa etmeye devam ederek sonuçta gerçek hayattaki objeleri oluşturmuş oluruz.

Şekil 10: Imagenet verisi üzerinde eğitilmiş evrişimli ağın öznitelik görselleştirilmesi [Zeiler & Fergus 2013]

Dolayısıyla doğada gözlemlediğimiz bu hiyerarşik ve birleşimsel yapı, sadece bizim görsel algımızın bir sonucu değil, fiziksel seviyede de doğru bir şey. En basit haliyle tanımlarsak, elimizde basit partiküller var, bunlar birleşerek atomları, atomlar birleşerek molekülleri oluşturuyorlar; bu şekilde ilerleyerek materyalleri, objelerin kısımlarını ve sonuçta da gerçek hayattaki bir objenin tamamını oluşturuyoruz.

Dünyanın bu birleşimsel yapısı, Einstein’ın insanların yaşadıkları dünyayı nasıl anladıkları ile ilgili retorik sorusunun cevabı olabilir:

Evrenle ilgili en anlaşılmaz şey anlaşılabilir olmasıdır.

Yann’a göre, bu birleşimsel yapı sayesinde dünyanın insanlar tarafından anlaşılabilir olması hala bir komplo teorisi gibi duruyor. Yine de tartışılır, birleşme olmadan, insanların yaşadıkları dünyayı anlamaları için çok daha fazla sihir olması gerek. Büyük matematikçi Stuart Geman’ın sözleri ile:

Ya dünya birleşimsel ya da Tanrı var.

Biyolojiden İlhamlar

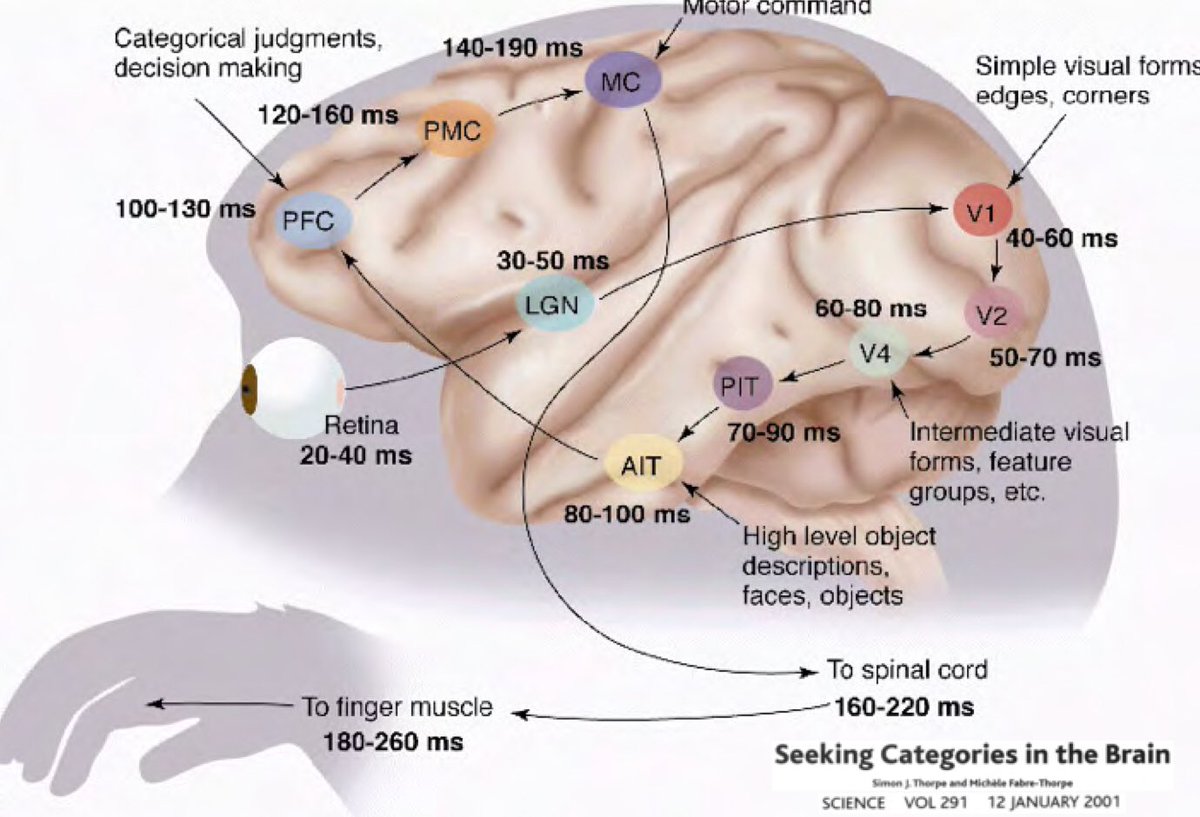
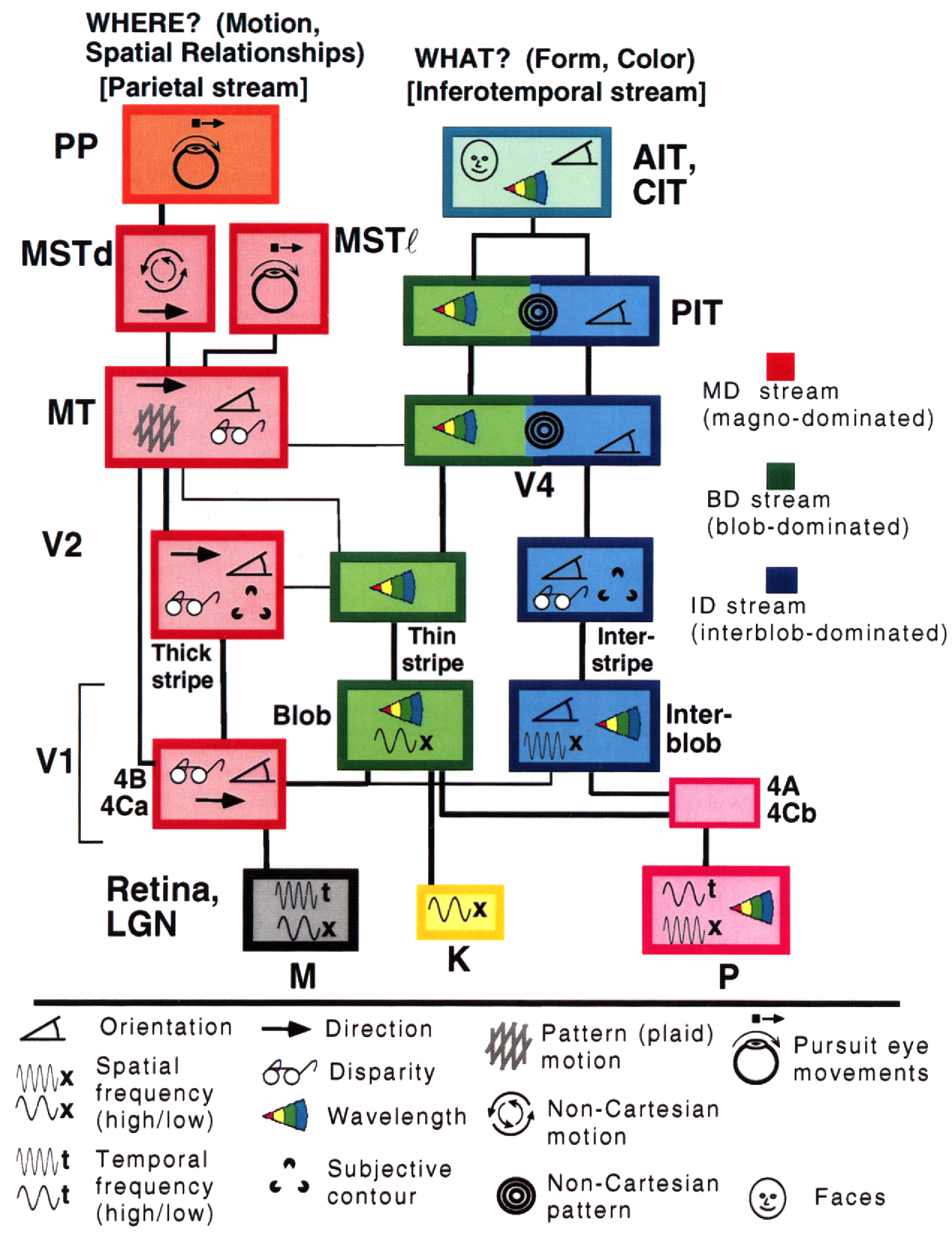
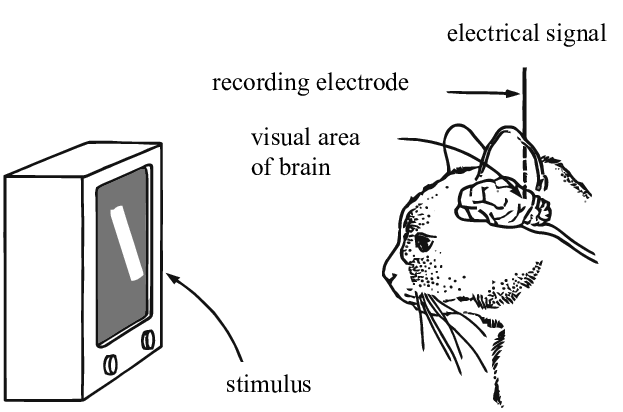
Peki neden Derin Öğrenme, dünyamızın anlaşılabilir ve birleşimsel bir yapısı olduğu fikrinin üzerine kurulmuş olmak zorunda olsun? Simon Thorpe’un araştırması bunu motive etmeye daha da yardımcı oldu. Araştırma etrafımızdaki objeleri aşırı hızlı tanıdığımızı gösterdi. Thorpe deneylerinde insanlara her 100ms’de bir resim göstererek onların resmin ne olduğunu söylemelerini istedi, ve insanlar da bunu başarıyla gerçekleştirdiler. Bu da onların objelerin ne olduğunu 100ms gibi bir sürede anladığını gösterdi. Buna ek olarak, aşağıdaki diyagramda beyinin bir bölgesinden diğerine ne kadar sürede nöronlarla iletim olduğunu görebilirsiniz:

Şekil 11: Simon Thorpe'un beyindeki görsel bilgi akışı modeli

Sinyaller retinadan LGN'ye (konstrast artırımı, kontrol gibi konularda yardımcı bölüm), sonra da V1 primer görme korteksi, V2, V4 ve sonrasında inferotemporal kortekse (PIT), yani beyinde kategorilerin tanımlandığı yere iletilir. Açık beyin ameliyatlarındaki gözlemlerin gösterdiğine göre, bir insana film izletildiğinde, PIT'deki nöronlar sadece belli görseller algılandığında ateşleniyorlar --Jennifer Aniston ya da kişi anneannesini gördüğünde-- ve diğer hiçbir görselde bu olmuyor. Nöronların ateşlenmesi, pozisyon, boyut, ışıklandırma gibi şeylerle, anneannenizin hangi yöne baktığı, ya da ne giydiğiyle de değişmiyor.

Şekil 12: Gallen & Van Essen'in beyne giden dorsal ve ventral yol modeli

Sağ kısım ventral yolu gösteriyor, yani size neye baktığınızı söyleyen şey. Sol kısım dorsal yolu gösteriyor, yani yeri, geometriyi ve hareketi algılayan şey. İnsan ve primat görsel kortekslerinde bu yollar ayrı gibi gözüküyorlar (tabii aralarında birkaç etkileşim olsa da). ### Hubel & Weisel'in katkıları (1962)

Şekil 13: Hubel & Weisel'in kedi beynindeki görsel uyarıcılarla olan deneyleri

Hubel ve Weisel, kedi beyninin görsel uyarıcılara verdiği nöron ateşlemelerini ölçmek için deneylerinde elektrotları kullandılar. V1 bölgesindeki nöronların görsel alandaki yalnızca belli alanlara duyarlı olduğunu keşfettiler ("reseptif alanlar", *receptive fields*), ve o alanlarda nöronların yönlü kenarlar algıladığını fark ettiler. Örneğin, kediye dik duran bir sopa gösterip sopayı döndürmeye başlarsanız, belli bir açıda nöronlar ateşlenir. Benzer olarak o açıdan uzaklaştıkça o nörondaki aktivasyon da azalır. Hubel ve Weisel bu aktivasyonlara duyarlı nöronlara yerel özellikleri algılayabildikleri için "basit hücreler" adını verdiler. Eğer sopayı reseptif alandan çıkarırsanız, önceki nöronun artık ateşlenmediğini, ama farklı bir nöronun ateşlendiğini keşfettiler. Görsel alanın her yerine denk gelen yerel özellik algılayıcıları vardır, insan beyninin de görsel bilgiyi "evrişim" koleksiyonlarından ibaret olarak işlediği fikri de burdan gelir. Hubel ve Weisel'in "karmaşık hücreler" diye adlandırdığı, diğer bir nöron türü ise, belli alandaki birden fazla basit hücrenin çıktısını biriktirir. Bu hücreleri, aktivasyonların birikmiş hallerini hesaplıyor gibi düşünebiliriz, maksimum, toplam, kareler toplamı, ya da sıraya bağlı olmayan herhangi bir diğer fonksiyon kullanarak. Bu karmaşık hücreler bir alandaki kenarları ve yönlenmeleri, uyarıcının tam olarak nerede olduğuna bağlı kalmadan algılarlar. Diğer bir deyişle girdinin pozisyonundaki küçük değişikliklere karşı kayma değişmezliğine sahiptirler *(shift invariance)*. ### Fukushima'nın katkıları (1982)

Şekil 14: Fukushima'nın CNN modeli

Fukushima, basit ve karmaşık hücrelerin birden fazla katmanla bilgisayar modellerinde kodlanması fikrinin ilk sahibiydi, ve bunun için elle yazılmış rakam verilerini kullandı. Bu öznitelik algılayıcılarının bazıları özel olarak oluşturulmuş ve öğrenilmişti; ama denetimsiz *(unsupervised)* öbekleme *(clustering)* algoritmalarını kullanıyordu, her katman için ayrı ayrı eğitiliyordu ve geri yayılım da henüz kullanımda değildi. Yann LeCun birkaç sene sonra aynı yapıyı kurdu, ama bu sefer denetimli *(supervised)* olarak geri yayılımla eğitti. Bu, evrişimli sinir ağlarının başlangıcı sayılmaktadır. (Not: Riesenhuber MIT'de 1999'da bu yapıyı tekrardan keşfetti fakat geri yayılımı kullanmadı.)