Yapay Sinir Ağları (ANNs)

🎙️ Alfredo Canziani

Sınıflama için denetimli öğrenme

Aşağıdaki Fig. 1(a)yı değerlendirelim. Grafikteki noktalar spiraldeki kollar gibi uzanır ve $\R^2$ içinde yaşar. Her renk sınıf etiketini verir. Özgün sınıf sayısı $K = 3$. Matematiksel olarak Eqn. 1(a) da anlatılmıştır.

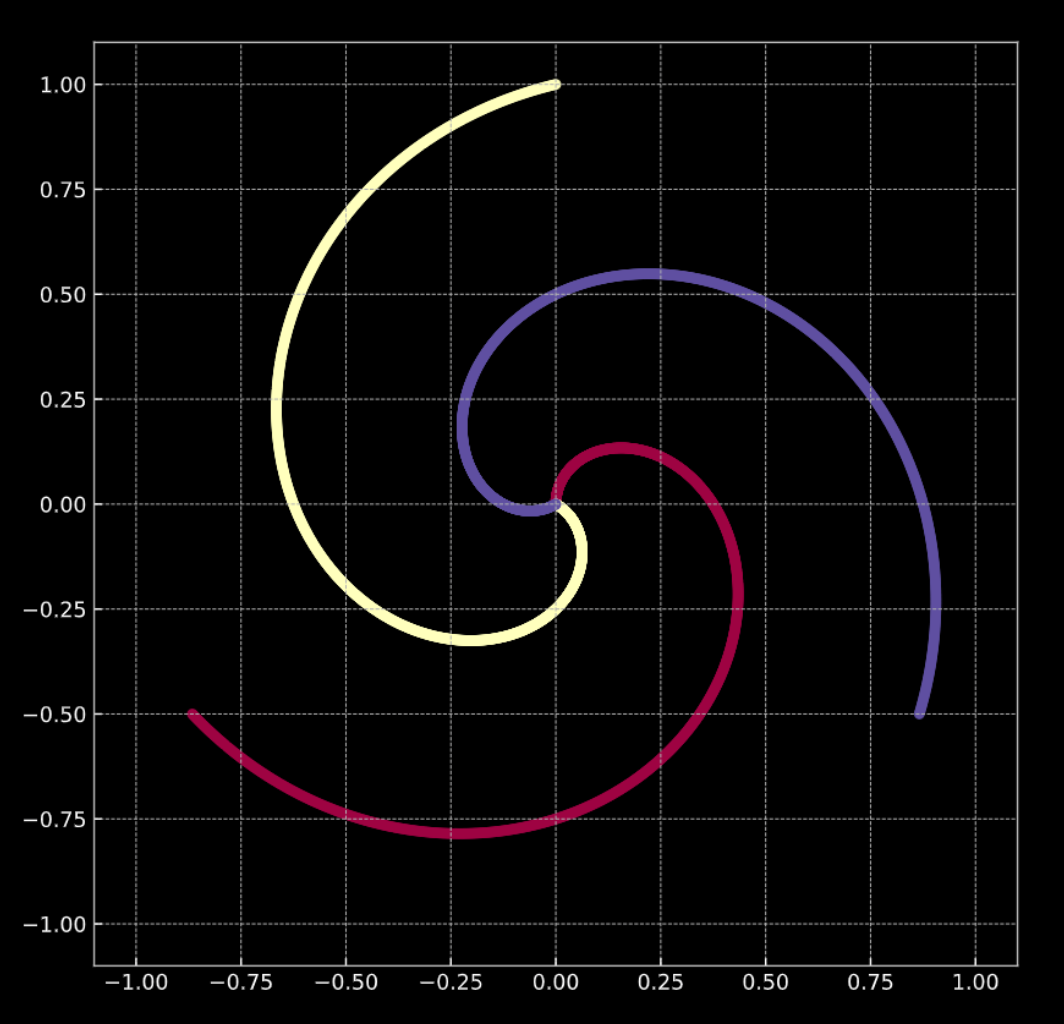Fig. 1(a) "Clean" 2D spiral

Fig. 1(b) "Noisy" 2D spiral

\[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1)\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1)\right]}\end{array}\right) \\ 0 \leq t \leq 1, \quad k=1, ..., K\] Eqn. 1(a) \[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]}\end{array}\right)\\0 \leq t \leq 1, \quad k=1, ..., K\] Eqn. 1(b)

Sınıflama yapmak ne demektir? Lojistik regresyonu düşünelim. Sınıflama için bu veriye lojistik regresyon uygulanmış olsaydı, veriyi sınıflarına ayırmak için bir grup doğrusal düzlem (karar sınırları) oluşturacaktır. Bu çözümdeki sorun her bölgede her sınıftan noktalar olmasıdır. Spiralin kolları doğrusal karar verme sınırlarını aşar. Bu iyi bir çözüm değildir!

Bu nasıl düzeltilir? Girdi alanını veri doğrusal bir şekilde ayrışabiliyormuş gibi zorlayarak dönüştürürüz. Eğitim sonunda sinir ağı karar sınırlarını eğitim verisinin dağıtımına uyduracak şekilde karar sınırlarını öğrenerek yapar

Eğitim verisi

Geçen hafta, yeni başlatılmış yapay sinir ağlarının girdilerini gelişigüzel dönüştürdüğünü gördük. Bu dönüşüm hesaplamayı elle yaptığı için aslında özünde yardımcı değildir. Girdi dönüşümlerinin el lle hesaplanan göreve göre anlamlı bir şekilde yapmaya zorlayacağız ve bunları veriyi kullanarak keşfedeceğiz.

• $\vect{X}$ girdi verisi, $m$ (eğitilen veri noktası sayıları) x $n$ (her girdi noktasının boyutu) matris boyutlarında. Figür 1(a) ve 1(b) de görünen verilere göre, $n = 2$.

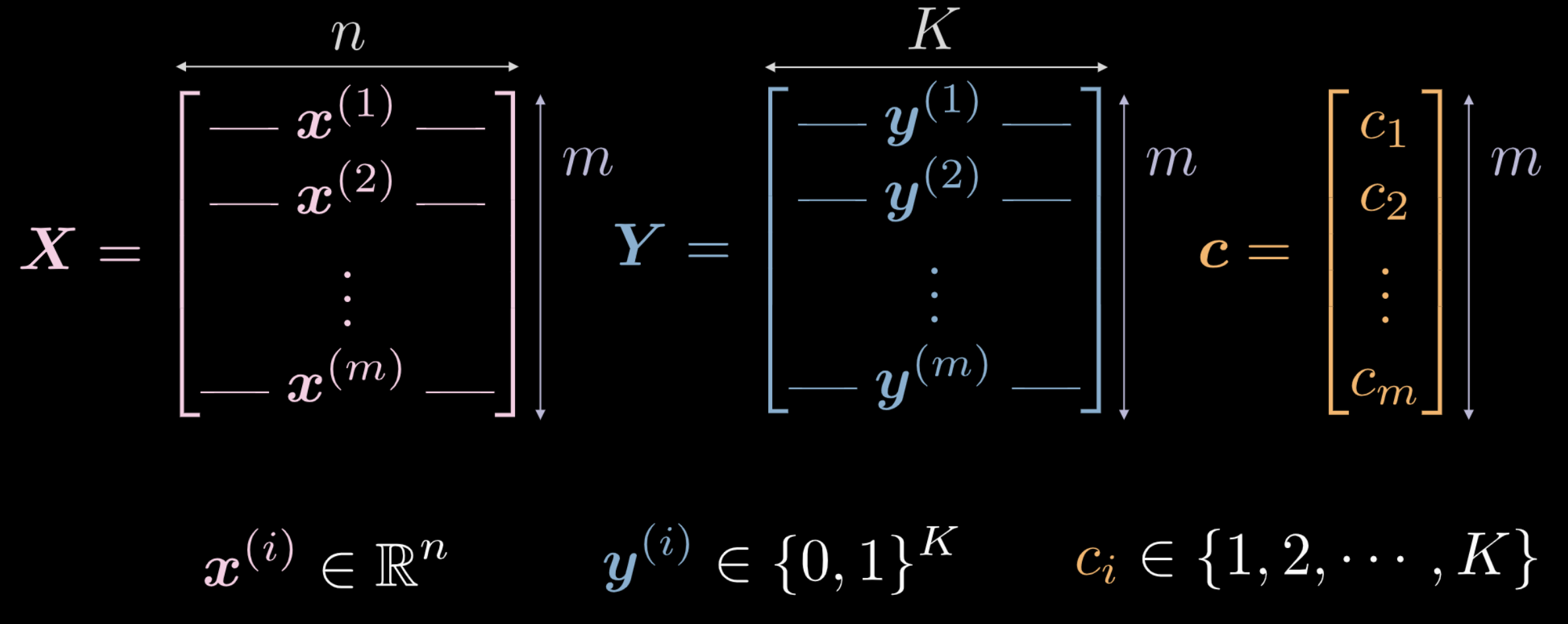
Fig. 2 Training data

• $\vect{c}$ vektörü ve $\boldsymbol{Y}$ matrisi her ikisi de $m$ veri noktalarına karşılık gelen sınıf etiketlerini ifade eder. Yukarıdaki örnekte $3$ farklı sınıf vardır.

  • $c_i \in \lbrace 1, 2, \cdots, K \rbrace$,ve $\vect{c} \in \R^m$. $\vect{c}$ eğitim verisi olarak kullanılamayabilir. Eğer farklı sayısal sınıf etiketleri $c_i \in \lbrace 1, 2, \cdots, K \rbrace$, kullanılırsa, ağ veri dağılımına uygun olmayan şekilde sıralamalı tahmin edebilir.
  • Bu problemin üstesinden gelmek için ikili karakter gizleme. Her $c_i$ verisi için, $K$ boyutlu bir sıfır vektörü $\vect{y}^{(i)}$ yapılır, bunun $c_i$-ıncı elemanı $1$e eşitlenir ( Fig. 3 ).

Fig. 3 One hot encoding

• $\boldsymbol Y \in \R^{m \times K}$. Bu matris olasılıksal ağırlığa sahiptir ve bu ağırlıklar $K$ noktalarındadır.

Tamamen bağlı (Fully Connected-FC) katmanlar

Tamamen bağlı (FC) ağları ve nasıl çalıştıklarını inceleyeceğiz.

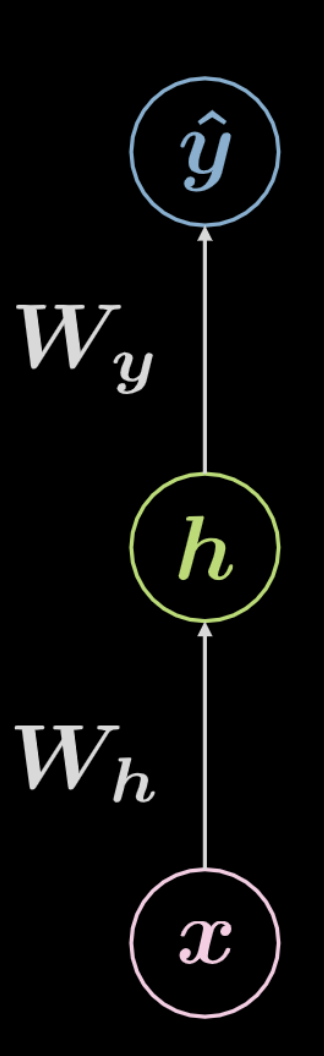
Fig. 4 Fully connected neural network

Yukarıdaki Fig. 4‘de girdi verisi, $\boldsymbol x$, $\boldsymbol W_h$, tarafından tanımlanan afin dönüşümü yapar ve liner olmayan diğer dönüşümler bunu takip eder. Bu non-lineer dönüşümler sonucunda $\boldsymbol h$, saklı çıktıyı gösterir, yani ağ dışından görünmeyen çıktı. Bu tekrar bir başka afin dönüşüm ($\boldsymbol W_y$), ve takip eden dönüşüme uğrar, sonundaki nihai çıktı: $\boldsymbol{\hat{y}}$. Bu ağ matematiksel olarak Eqn. 2 de ifade edilmiştir. $f$ ve $g$ her ikiside lineer olmayan kısımlardır.

\[\begin{aligned} &\boldsymbol h=f\left(\boldsymbol{W}_{h} \boldsymbol x+ \boldsymbol b_{h}\right)\\ &\boldsymbol{\hat{y}}=g\left(\boldsymbol{W}_{y} \boldsymbol h+ \boldsymbol b_{y}\right) \end{aligned}\] Eqn. 2 Mathematics behind a FC network

Yukarıda gösterildiği gibi bir basit sinir ağı birbirini takip eden çiftlerden oluşur, her çift afin dönüşüm ve lineer olmayan operasyon (sıkıştırma) içerir. ReLU, sigmoid, hiperbolik tanjant ve softmax sıklıkla kullanılan lineer olmayan operasyonlardır.

Yukarıdaki ağ üç katmanlıdır:

1. girdi nöronu
2. saklı noron
3. çıktı nöronu

$3$ katmanlı ağ $2$ afin dönüşüm içerir. Bu $n$ katmanlı bir ağ olacak kadar genişletilebilir.

Şimdi daha karmaşık bir durumu inceleyelim.

3 saklı katmanlı, her katmanı tamamen bağlı bir ağ olsun, şekli Fig. 5 de görülmektedir.

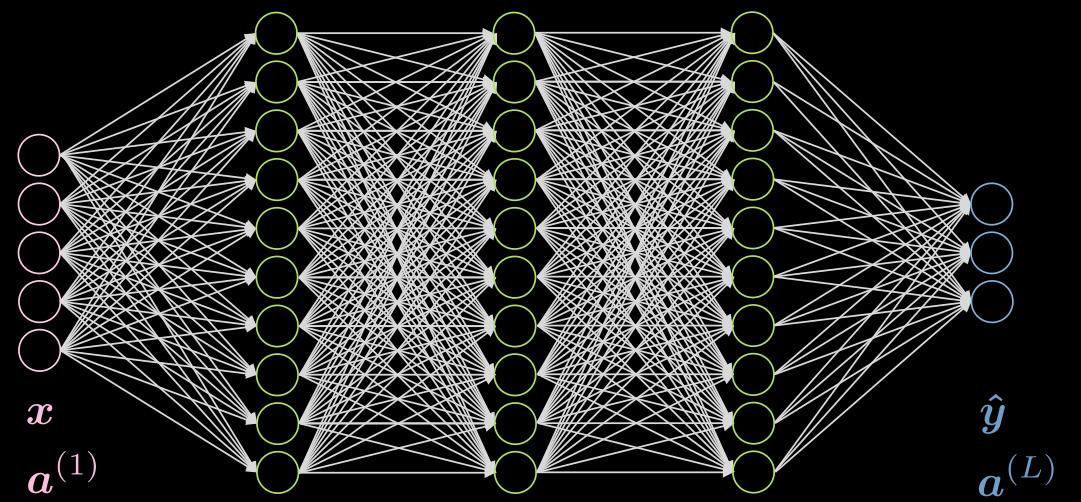
Fig. 5 Neural net with 3 hidden layers

İkinci katmandaki nöron $j$’yi düşünelim ve bunun aktivasyon fonksiyonu:

\[a^{(2)}_j = f(\boldsymbol w^{(j)} \boldsymbol x + b_j) = f\Big( \big(\sum_{i=1}^n w_i^{(j)} x_i\big) +b_j ) \Big)\]

olur. $\vect{w}^{(j)}$, $\vect{W}^{(1)}$ vektrörünün $j$. denklemidir.

Girdi katmanının aktivasyonu yalnızca kendisidir. Saklı katmanlarda ReLU, tanjant hiperbolik, sigmoid, soft(arg)max gibi fonksiyonlar olabilir.

Buradaki Piazza duyurusunda açıklandığı gibi, son katmandaki aktivasyon kullanım durumuna bağlıdır.

Sinir ağı (çıkarım)

Fig. 6‘da görünen üç katmanlı (girdi, saklı, çıktı)yapay sinir ağını düşünelim:

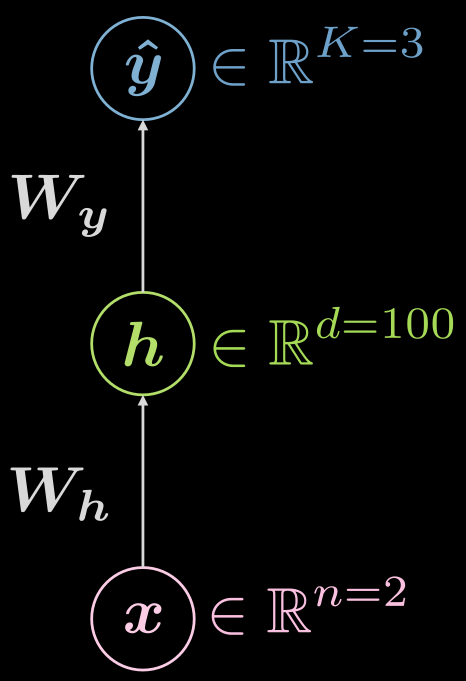
Fig. 6 Üç katmanlı sinir ağı

Ne çeşit fonksiyonlara bakarız?

\[\boldsymbol {\hat{y}} = \boldsymbol{\hat{y}(x)}, \boldsymbol{\hat{y}}: \mathbb{R}^n \rightarrow \mathbb{R}^K, \boldsymbol{x} \mapsto \boldsymbol{\hat{y}}\]

Saklı katmanı aşağıdaki gibi açarak düşünmek görselleştirmemize yardım edecektir.

\[\boldsymbol{\hat{y}}: \mathbb{R}^{n} \rightarrow \mathbb{R}^d \rightarrow \mathbb{R}^K, d \gg n, K\]

Örnek konfigürasyon nasıl olmalıdır? Bu durumda girdi iki boyutludur ($n=2$), tek saklı katmanın boyutu 1000’dir, ($C=3$) üç sınıf vardır . Saklı katmanda çok fazla nöron bulunmamamasının pratik sebepleri vardır, tek saklı katmanı 10 nöronlu üç farklı katmana bölmek mantıklı bir hamledir ($1000 \rightarrow 10 \times 10 \times 10$) .

Sinir ağı (eğitim I)

Tipik bir eğitim nasıl görünmektedir? Kayıp fonksiyonları açısından bu durumu formüllendirmek kullanışlıdır.

İlk olarak, soft (arg)max’ı hatırlayalım ve bunun son katmanda özel olarak kullanılan bir aktivasyon fonksiyonu olduğunu göz önünde bulunduralım, özellikle çoklu sınıf sınıflamalarında negatif log-benzerlilik kayıp fonksiyonu ile birlikte. Profesör LeCun’un belirttiği şekilde softmax ile sigmoidlere oranla daha iyi gradyanlar hesaplanır. Ek olarak, son katman uygun gradyan metodları ile normalize edilecektir (son katmandaki tüm nöronların toplamı 1 olacak şekilde ve açık normalizasyon kullanılmadan).

Soft (arg) max son katmandaki logitleri verir:

\[\text{soft{(arg)}max}(\boldsymbol{l})[c] = \frac{ \exp(\boldsymbol{l}[c])} {\sum^K_{k=1} \exp(\boldsymbol{l}[k])} \in (0, 1)\]

Üssel fonksiyonun pozitif özelliği gereği set kapalı değildir.

$\matr{\hat{Y}}$ seti tahminlerine göre kayıp fonksiyonu:

\[\mathcal{L}(\boldsymbol{\hat{Y}}, \boldsymbol{c}) = \frac{1}{m} \sum_{i=1}^m \ell(\boldsymbol{\hat{y}_i}, c_i), \quad \ell(\boldsymbol{\hat{y}}, c) = -\log(\boldsymbol{\hat{y}}[c])\]

$c$ tam sayı etiketidir.

Şimdi iki örnek inceleyelim, birinde girdi doğru sınıflanmış olsun diğerinde ise yanlış.

Varsayalım ki;

\[\boldsymbol{x}, c = 1 \Rightarrow \boldsymbol{y} = {\footnotesize\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}}\]

Örnek bazında kayıp nedir?

Neredeyse mükemmel tahmin durumunda ($\sim$ yaklaşık olarak ifade eder)

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow 0^{+}\]

Neredeyse tamamamen tahmin durumunda:

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow +\infty\]

Yukarıdaki örneklerde $\sim 0 \rightarrow 0^{+}$ ve $\sim 1 \rightarrow 1^{-}$ bu neden böyledir? Bir dakika düşünelim.

Not: CrossEntropyLoss kullanılınca LogSoftMax ve negatif yanlılık fonksiyonu NLLLoss ile birlikte sonuç verir, iki kere yapılmamalıdır.

Sinir ağı (eğitim II)

Eğitim için tüm eğitilebilir parametreleri bir $\mathbf{\Theta} = \lbrace\boldsymbol{W_h, b_h, W_y, b_y} \rbrace$ koleksiyonuna ekliyoruz. – ağırlık matrisleri ve yanlılık değerleri ile – Bu durum hedef fonksiyonunu veya kayıp fonksiynonunu şu şekilde yazmamızı sağlar:

\[J \left( \mathbf{\Theta} \right) = \mathcal{L} \left( \boldsymbol{\hat{Y}} \left( \mathbf{\Theta} \right), \boldsymbol c \right) \in \mathbb{R}^{+}\]

Bu duruma göre kayıp fonksiyonu ağın çıktısına bağlıdır, $\boldsymbol {\hat{Y}} \left( \mathbf{\Theta} \right)$, ve bu bir optimizasyon sorunu olarak tanımlanabilir.

Fig. 7‘de görüldüğü üzere $J(\vartheta)$’ minimize edeceğimiz fonksiyondur, tek parametresi $\vartheta$’dır.

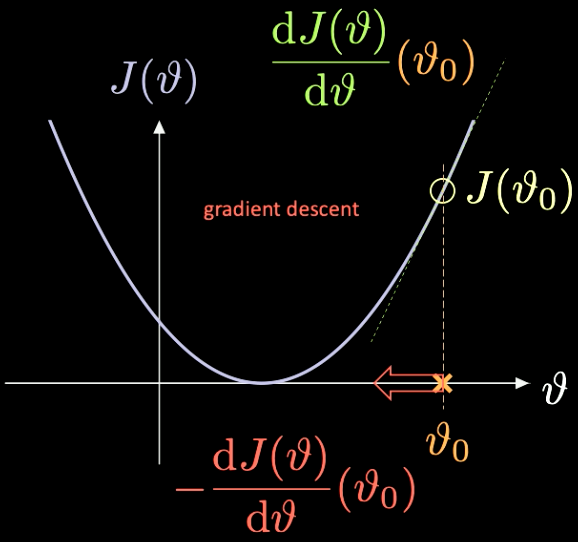
Fig. 7 Optimizing a loss function through gradient descent.

$\vartheta_0$ rastgele başlatılır, ilgili kayıp fonksiyonu $J(\vartheta_0)$’dır. Bunun türevini $J’(\vartheta_0) = \frac{\text{d} J(\vartheta)}{\text{d} \vartheta} (\vartheta_0)$. noktasında hesaplayabiliriz. Bu durumda türevin eğimi pozitiftir, dolayısıyla bu yönde en dik inişle adım adım ilerlemek gerekir. Böylece $-\frac{\text{d} J(\vartheta)}{\text{d} \vartheta}(\vartheta_0)$ bulunur.

Literatürde bu iteratif işleme gradyan inişi denir. Gradyan yöntemleri yapay sinir ağlarını eğitmek için en uygun araçlardır.

Uygun gradyanları hesaplamak için geri yayılım algoritmasını kullanırız:

\[\frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_y}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol{W_y}} \quad \quad \quad \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_h}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol h} \;\frac{\partial \, \boldsymbol h}{\partial \, \boldsymbol{W_h}}\]

Spiral Sınıflama - Jupyter defteri

Dersin Jupyter deftter burada. Bu defteri yürütmek için README.md dökümanında tarif edildiği gibi ‘the dl-minicourse’ ortamının olduğundan emin olun. ‘torch.device()’ın nasıl kullanılacağının bir öğrenği geçen haftanın notları‘nda bulunabilir.

Daha önce de olduğu gibi $\mathbb{R}^2$ noktalarında üç farklı kategoride etiketle – kırmızı, sarı ve mavi — gösterilen sınıflarda çalışacağız: Fig. 8.

Fig. 8 Spiral sınıflama verisi.

nn.Sequential()nodülleri inşa ediciye taşıyan bir konteyner, ‘nn.linear()’ girdiye afin dönüşümü yapan yanlış isimlendirilmiş modüldür: $\boldsymbol y = \boldsymbol W \boldsymbol x + \boldsymbol b$. Daha fazla bilgi için burayı PyTorch documentation inceleyebilirsiniz.

Afin dönüşüm beş şeyi yapar: döndürme, yansıtma, dönüştürme, boyutlama ve kesme.

Fig.9‘da görüldüğü üzere, ‘nn.linear()’ modüllerini kullanarak hiç bir non-lineerite eklemeden elde edebileceğimiz en iyi doğruluk $50\%$.

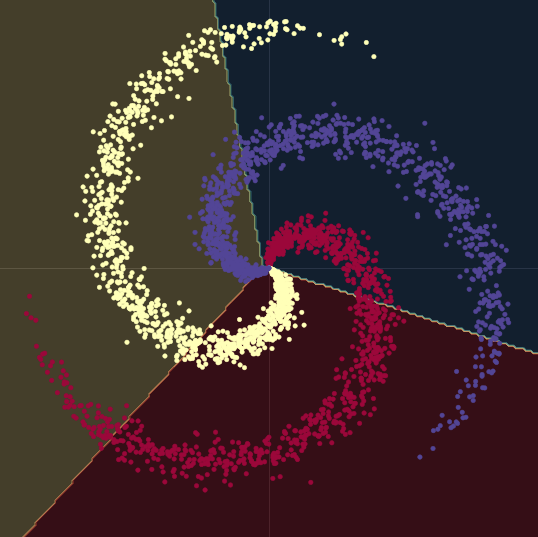
Fig. 9 Lineer karar sınırları.

Tek katmanlı lineer modelden içinde iki ‘nn.linear()’ olan iki katmanlı ve aralarında ‘nn.ReLU()’ olan modele geçersek doğruluk $95\%$’a çıkar. Bu lineer olmayan sınırların spiral veriye daha iyi uyum sağlaması kaynaklıdır.

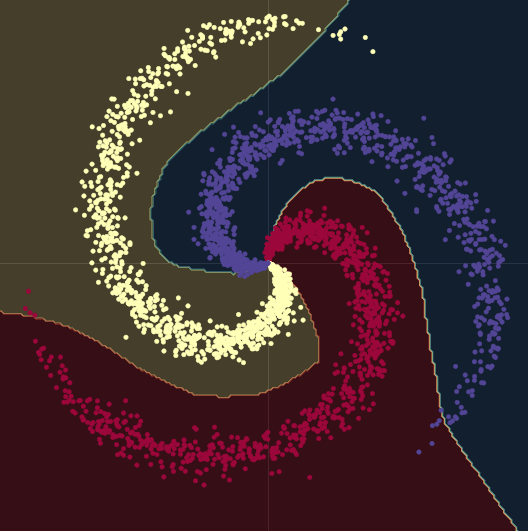
Fig. 10 Lineer olmayan karar sınırları.

Lineer regresyonla doğru bir şekilde çözülemeyen ancak yapay sinir ağıyla çözülebilen bir regresyon probleminin bir örneği olarak bu deftere ve Fig. 11‘e bakabilirsiniz. Yarısı ‘nn.ReLU()’ diğer yarısı ‘nn.Tanh()’ içeren 10 farklı ağ yapısı örneklenmiştir. Önceki parçalı lineer fonksiyonsundur, sonraki ise sürekli düz regresyondur.

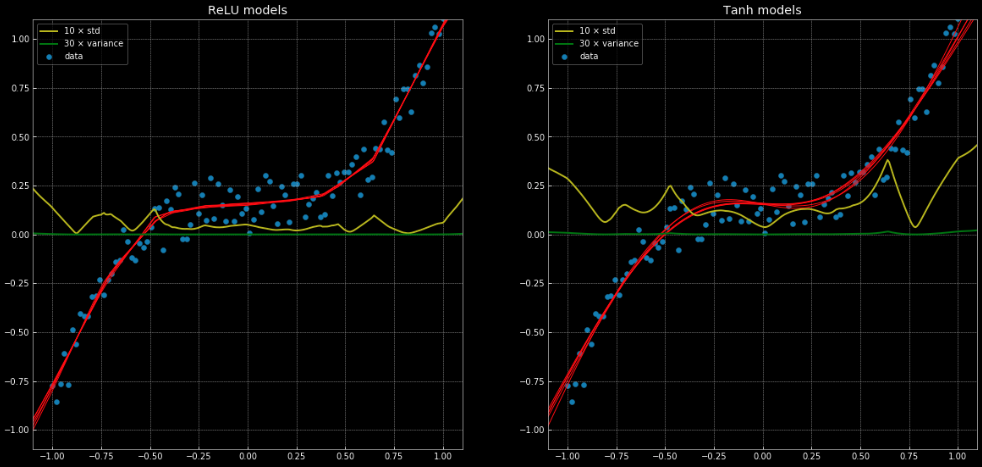
Fig. 11: 10 Yapay sinir ağları, varyans ve standart sapmaları ile.
Sol: Beş ReLU networks. Sağ: Beş tanh networks.

Sarı ve yeşil çizgiler yapay sinir ağının standart sapma ve varyansının gösterir. Bu bilgiler tek tahminli çıktılı fonksiyonlarda “güven aralığı”na benzer şekilde kolaylık sağlar. Grup varyans tahmini her tahmin için kesinliği tahmin etmeyi sağlar. Bunun önemi Fig.12‘de gösterilmiştir, karar fonksiyonlarını eğitim sınırından $+\infty, -\infty$ doğru genişletirsek:

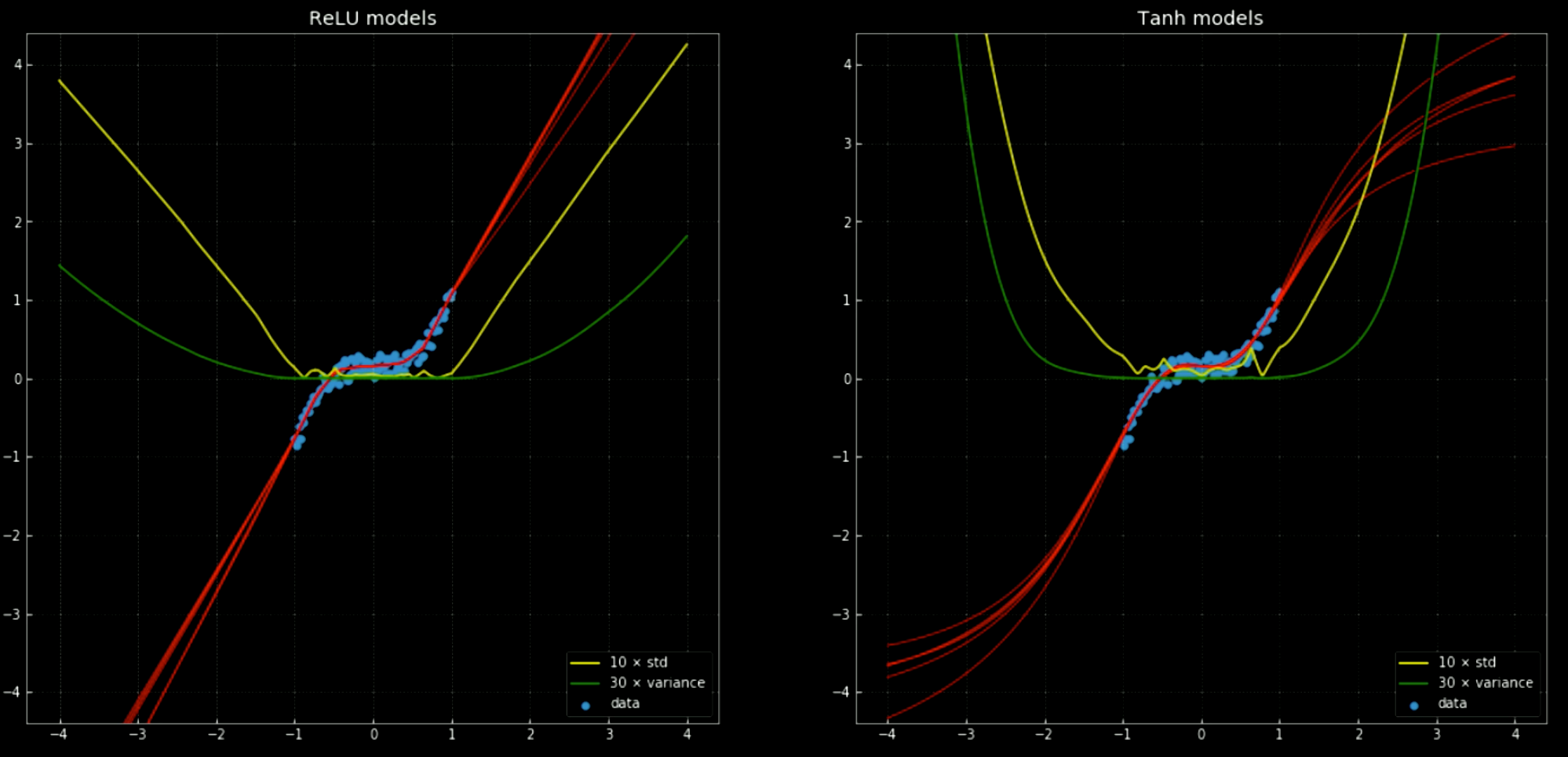
Fig. 12 Neural networks, with mean and standard deviation, outside training interval.
Left: Five ReLU networks. Right: Five tanh networks.

PyTorch’da yapay sinir ağlarını eğitirken eğitim aşamasında 5 temel adımı kullanırız.

1. output = model(input) modelin ileri eğitim geçişidir, girdiyi alır, çıktı oluşturur.
2. J = loss(girdi, hedef <veya> etiket) model çıktısını alır ve gerçek hedef veya etikete göre eğitim kayıp fonksiyonunu hesaplar.
3. model.zero_grad() gradyan hesaplanmasını temizler ve bunlar bir sonraki geçişte birikmezler.
4. J.backward() geriyayılım ve birikmeyi yaparlar: $\texttt{x}$ verisi `requires_grad=True iken her veri için $\nabla_\texttt{x} J$ hesaplar. Bunlar her değişkenin birikimli gradyanıdır: $\texttt{x.grad} \gets \texttt{x.grad} + \nabla_\texttt{x} J$.
5. optimiser.step() gradyan inişinin olduğu basamaktır: $\vartheta \gets \vartheta - \eta\, \nabla_\vartheta J$.

Yapay sinir ağı eğitilirken bu beş basamağa ihityaç duyulması çok yaygındır.

---

Melvin Selim Atay
4 Feb 2020