NN modüllerinde Gradyan Hesaplama ve Geri Yayılım için Kısa Yollar

Geriyayılımın somut örneği ve basit yapay sinir ağlarına giriş

Örnek

Görsel bir grafik yardımıyla somutlaştırılmış geri yayılım örneğini inceliyoruz. $C$ maliyet fonksiyonuna bir girdi olarak bir $G(w)$ fonksiyonu olsun, bu fonksiyon bir grafik şeklinde gösterilebilir. Jacobian matrislerinin çarpımlarını manipüle ederek bu grafiği, ters dönerek gradyan hesaplayacak olan grafiğe dönüştürebiliriz. (PyTorch ve TensorFlow bunu otomatik olarak yapabilmektedir, ileri grafik otomatik olarak ters çevirilir ve geri yayılım gradyanı olan türevlenmiş grafik ortaya çıkar.)

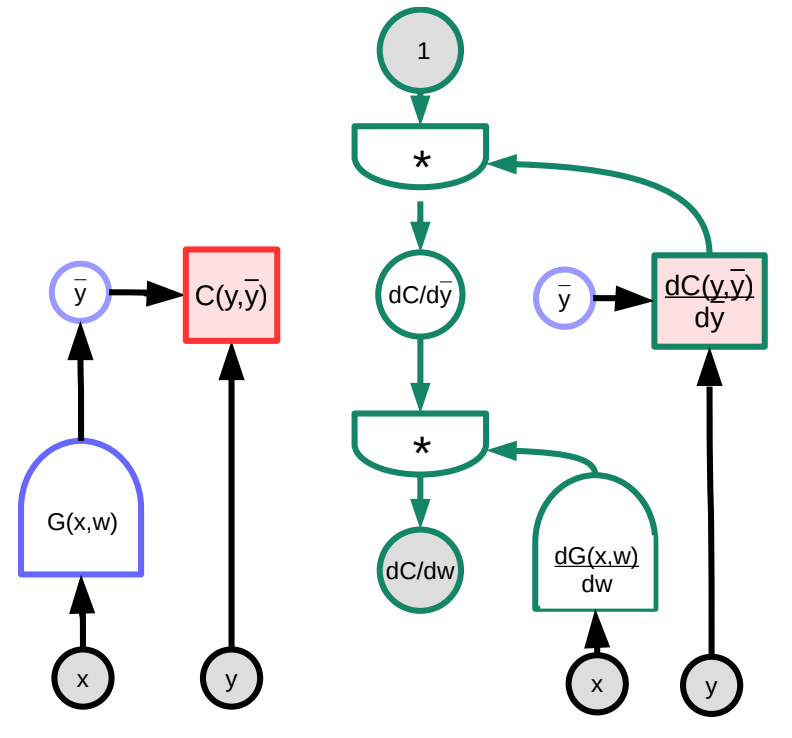
Bu örnekte, sağdaki yeşil grafik gradyan grafiğidir Yanındaki grafik de en tepedeki boğumdan bunu takip eder

Boyut olarak ele alınırsa $\frac{\partial C(y,\bar{y})}{\partial w}$ satır vektörüdür ve büyüklüğü $1\times N$ where $N$ is the number of components of $w$; $\frac{\partial C(y,\bar{y})}{\partial \bar{y}}$ ise sütun vektörüdür ve büyüklüğü $1\times M$, where $M$ çıktı boyutudur; $\frac{\partial \bar{y}}{\partial w}=\frac{\partial G(x,w)}{\partial w}$ matris boyutu ıse $M\times N$, where $M$ is the number of outputs of $G$ and $N$ is the dimension of $w$ ‘olur’.

Grafiğin mimarisi sabit değil veriye bağlı ise çeşitli karışıklıklar oluşabilir. Örneğin yapay sinir ağı modlülünü girdi vektörü uzunluuna göre seçebiliriz. Bu mümkün olsa da bu değişimi yönetmek döngü sayısı arttıkça fazlasıyla zorlaşır.

Basit yapay sinir ağı modülleri

Tanıdık Lineer ve ReLU modulleri dışında önceden inşa edilmiş pek çok farklı yapay sinir ağı modülü vardır. Bu modüller ilgili fonksiyonları yapmak için özgün bir şekilde optimizedirler ve bu yönleriyle kullanışlıdırlar. (birbirinin kombinasyonu gibi üretilmiş, orta düzey modüllere zıt olarak).

• Lineer: $Y=W\cdot X$

  \[\begin{aligned} \frac{dC}{dX} &= W^\top \cdot \frac{dC}{dY} \\ \frac{dC}{dW} &= \frac{dC}{dY} \cdot X^\top \end{aligned}\]

• ReLU: $y=(x)^+$

  \[\frac{dC}{dX} = \begin{cases} 0 & x<0\\ \frac{dC}{dY} & \text{otherwise} \end{cases}\]

• Eşleme: $Y_1=X$, $Y_2=X$

  • “Y - ayırıcısına” benzer şekilde ve her çıktı birbirine eşit. .

  • Geri yayılım yaparken gradyanlar toplanır

  • Birbirine benzer şekilde $n$ tane dallanırlar

    \[\frac{dC}{dX}=\frac{dC}{dY_1}+\frac{dC}{dY_2}\]

• Toplama: $Y=X_1+X_2$

  • Ikı değişken toplandığında bir değişken perturbe ise çıktı da aynı değerde perturbedir örneğin:

    \[\frac{dC}{dX_1}=\frac{dC}{dY}\cdot1 \quad \text{and}\quad \frac{dC}{dX_2}=\frac{dC}{dY}\cdot1\]

• Maks: $Y=\max(X_1,X_2)$

  • Bu fonksiyon şu şeklide de ifade edilir
  \[Y=\max(X_1,X_2)=\begin{cases} X_1 & X_1 > X_2 \\ X_2 & \text{else} \end{cases} \Rightarrow \frac{dY}{dX_1}=\begin{cases} 1 & X_1 > X_2 \\ 0 & \text{else} \end{cases}\]

  • Sonuç olarak zincir kuralıyla,

    \[\frac{dC}{dX_1}=\begin{cases} \frac{dC}{dY}\cdot1 & X_1 > X_2 \\ 0 & \text{else} \end{cases}\]

LogSoftMax vs. SoftMax

Bir PyTorch modülü olan SoftMax, toplamı bir olan, $0$ ve $1$ arasındaki olan pozitif sayıları dönüştürmenin kolay bir yoludur. Bu sayılar olasılık dağılımı olarak anlaşılabilir. Sonuç olarak bu yöntem, sınıflama problemlerinde yaygın olarak kullanılır. Aşağıdaki denklemdeki $y_i$ tüm kategorilerdeki olasılıkların vektörüdür.

Aşağıdaki denklem ise aynı denklemin bir başka halidir. Aşağıdaki figür, $\log(1 + \exp(s))$ fonksiyonun kısmını gösterir. $s$ çok küçük olduğunda değeri $0$, ve $s$ çok büyükse değeri $s$ olur. Sonuç olarak fonksiyon hiçbir zaman doygunluğa ulaşamaz ve yok olan gradyan probleminden kaçınılmış olur.

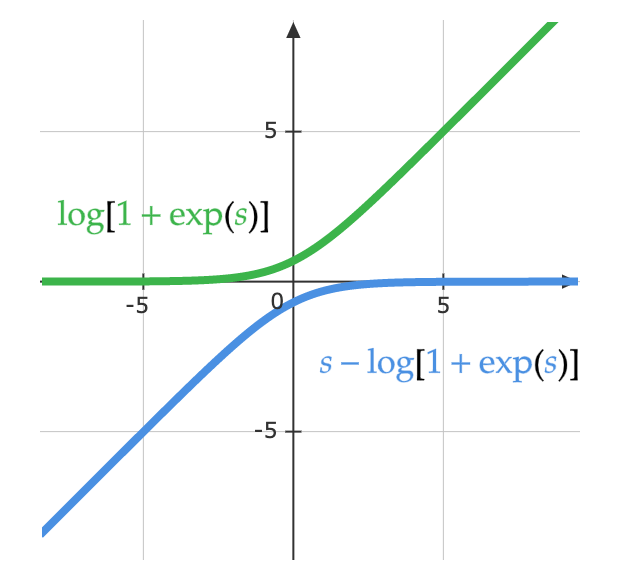
Geriyayılım için pratik hileler

Lineer olmayan aktivasyon fonksiyonu olarak ReLU kullan

Çok katmanlı ağlarda ReLU, sigmoid fonksiyon veya hiperbolik tanjant $\tanh(\cdot)$ gibi alternatiflerine göre en iyi sonucu verir. ReLU’nun bu kadar iyi çalışmasının nedeni yapısındaki tek kırgınlığın ölçek eşdeğerliğine yol açmasıdır.

Sınıflama problemlerinde amaç fonksiyonu olarak çapraz düzensizlik kullan

Bu derste daha önce bahsetmiş olduğumuz Log softmax, çapraz etropi kaybının özel bir örneğidir. PyTorch’da çapraz entropi kaybını log softmax girdisi ile tanımladığınıza emin olun (normal softmax’a zıt olarak).

Parçalı eğitim sırasında rastgele gradyan azalması kullan

Daha önce bahsedildiği gibi parçalı eğitim, veri fazla olduğunda daha etkili eğitime olanak verir; her adımda gradyan tahmininde her bir gözlem için kayıp fonksiyonunu hesaplayıp tahmin etme zorunluluğunu kaldırır.

Çapraz düzensizlik azalması kullanırken eğitim örneklerinin sırasını karıştır

Sıralama önemlidir. Model eğitim sırasındaki her adımda, tek bir sınıfa ait örnekleri görürse, yalnızca o sınıfa özgü sınıfı tahmin etmeyi neden o sınıfı tahmin ettiğiine bakılmaksızın öğrenir. Örneğin, MNIST verisetinde sayıları sınıflamaya çalışıyorsan ve veri karıştırılmamışsa, son katmandaki yanlılık parametreleri her zaman basitçe sıfırı tahmin edecektir, sonra bir, sonra iki… En uygun koşulda her parçalı eğitim adımında tüm sınıflardan örnekler bulunmalıdır. Buna rağmen, her döngüde örneklerin sıralamasının değiştirilip değiştirilmemesi gerekliliği halen devam eden bir tartışma konusudur.

Girdilerin ortalaması sıfır ve standart sapma bir olacak şekilde normalize et

Eğitimden önce her girdi özniteliğini ortalaması sıfır ve standart sapması bir olacak şekilde normalize etmek kullanışlıdır. RGB resim verisinde her kanalın ortalamasını ve standart sapmasını tek tek hesaplamak ver resmi kanal bakımından normalize etmek çok kullanılan bir yöntemdir. Örneğin verisetindeki tüm mavi değerlerinin $m_b$ ortalama ve $\sigma_b$ standart sapmasını alalalım ve her bir resimdeki mavi değerlerini normalize edelim;

$\epsilon$ ise sıfırla bölmeden kaçınmak için seçilen keyfi bir küçük sayı değeri olsun. Bu işlemin aynısını yeşil ve kırmızı kanalları için tekrarlayalım. Farklı ışıklandırmalarda çekilen resimlerden anlamlı sinyal almak için bu işlem gereklidir, örneğin gün ışığında çekilen resimlerin çok kırmızı pikseli olurken su altında çekilenlerde neredeyse hiç yoktur.

Öğrenme hızını azaltmak için programla

Eğitim devam ettikçe öğrenme hızı azalmalıdır. Uygulamada, en gelişmiş modeller sabit öğrenme hızındaki SGD yerine Adam gibi algoritmaları kullanarak eğitilirler.

Ağırlık azalması için L1 ve/veya L2 düzenlileştirmelerini kullan

Yitim fonksiyonundaki yüksek ağırlıklara ekstra bir yitim eklenebilir. Örneğin, L2 düzenlileştirmesi kullanarak, burada yitim $L$ ve güncellenecek ağırlıklar $w$ şöyle tanımlanır:

\(L(S, w) = C(S, w) + \alpha \Vert w \Vert^2\\ \frac{\partial R}{\partial w_i} = 2w_i\\ w_i = w_i - \eta\frac{\partial L}{\partial w_i} = w_i - \eta \left( \frac{\partial C}{\partial w_i} + 2 \alpha w_i \right)\) Buna neden ağırlık azalması dendiğini anlamak için yukarıdaki formülü tekrar yazmalı ve güncelleme sırasında $w_i$’yi birden küçük bir sabitle çarpmalıyız. \(w_i = (1 - 2 \eta \alpha) w_i - \eta\frac{\partial C}{\partial w_i}\)

L1 düzenlileştirmesi (Lasso) benzerdir, ancak burada $\Vert w \Vert^2$ yerine $\sum_i \vert w_i\vert$ kullanırız.

Temelde, düzenlileştirme sisteme yitim fonksiyonunu mümkün olan en kısa ağırlık vektörüyle küçültmesini söyler. L1 düzenlileştirmesinde ağırlıklar kullanışlı değildir ve $0$’a küçülürler.

Ağırlık başlangıcı

Ağırlıklar rastgele başlatılmalıdır, ancak çıktının girdiye oranla varyansını etkileyecek şekilde çok büyük veya çok küçük olmamalıdırlar. Başlangıç için pek çok yöntem vardır. Derin öğrenme modellerinde iyi çalışan bunlardan bir tanesi ise ağırlıkların varyansının girdi sayısının kare köküne ters orantılı olduğu Kaiming başlangıcıdır.

Seyreltme yap

Seyreltme düzenlileştirmenin bir diğer formudur. Yapay sinir ağının diğer bir katmanı gibi eğitilebilir, girdiyi alır ve içlerinden $n/2$ kadarını rastgele sıfıra eşitler ve sonucu çıktı olarak verir. Bu durum, katmandaki tüm ünitelerdeki bilgiyi bozarak, sistemin girdi birimlerinin küçük bir kısmına bağlı kalması yerine sistemi tüm girdi ünitelerinden bilgi almaya zorlar. Bu yöntem Hinton et al (2012) tarafından önerilmiştir.

Daha fazla hile için LeCun et al 1998 incelenebilir.

Sonuçta, geri yayılım yalnızca yığıtlanmış modellerde değil, eğer modüller arası göreceli bir kademe varsa yönlendirilmiş akrilik grafikler(DAG)’de kullanılabilir.