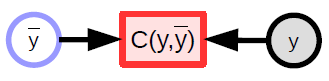Gradyan İnişi ve Geri Yayılım Algoritmalarına Giriş

Gradyan İnişi Optimizasyon Algoritması (Gradient Descent optimization algorithm)

Parametrik Modeller

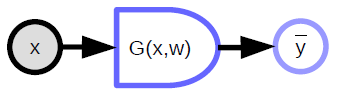
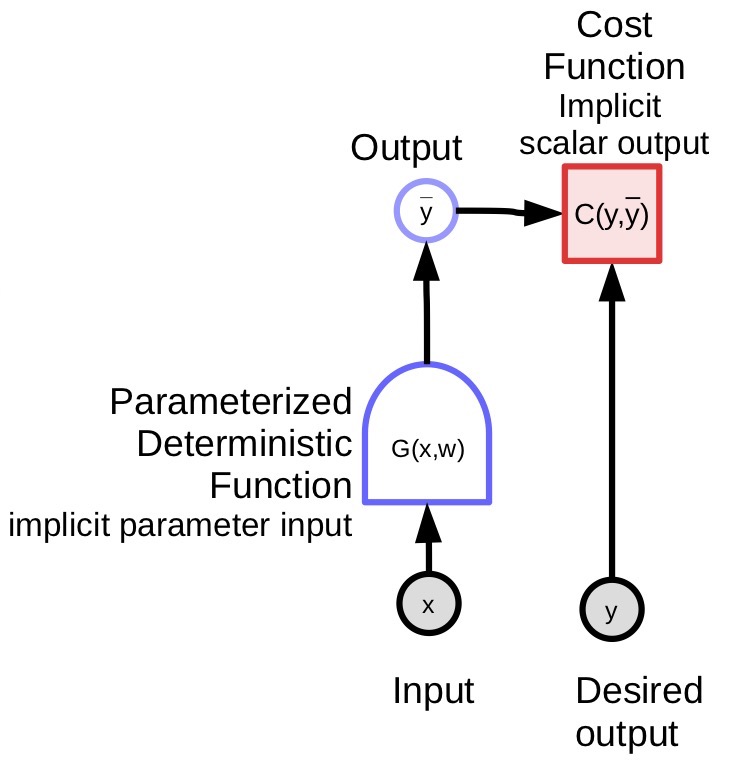
Basit bir şekilde, parametrik modeller girdilere ve eğitilebilir parametrelere bağlı olan modellerdir. İkisi arasında eğitilebilen parametreler eğitim örnekleri arasında paylaşılırken, girdilerin örnekten örneğe değişmesi dışında bir fark yoktur. Çoğu derin öğrenme küyüğhanesinde parametreler üstü kapalıdır, yani fonksiyon çağrıldığında argüman olarak verilmez. Modellerin obje yönelimli versiyonlarında “fonksiyonun içine kaydedilmiş” olduklarını söyleyebiliriz.

Parametrik model bir girdi alır, bir parametre vektörüne sahiptir ve bir çıktı üretir. Denetimli öğrenmede bu girdi gerçek çıktıyla (${y}$) model tarafından üretilen çıktıyı ($\bar{y}$) karşılaştıran maliyet fonksiyonuna girer. Bu model için hesaplama çizgesi Fig. 1’de gösterilmektedir.

Fig. 1: Parametrik Model için Hesaplama Çizgesii Gösterimi

Parametrik fonksiyonlara örnekler -

• Lineer model - Girdi vektörünün elemenlarının ağırlıklı toplamı

  \[\bar{y} = \sum_i w_i x_i, C(y,\bar{y}) = \Vert y - \bar{y}\Vert^2\]

• En yakın komşu - Girdi $\vect{x}$ ve satırları $k$ ile indekslenen ağırlık matrisi $\matr{W}$ bulunur. Çıktı $\matr{W}$ matrisinin $\vect{x}$ vektörüne en yakın satırının $k$ değeridir.

  \[\bar{y} = \underset{k}{\arg\min} \Vert x - w_{k,.} \Vert^2\]

  Parametrik modeller daha karmaşık fonksiyonları da içerebilir.

Hesaplama Çizgeleri için Blok Diyagramı Notasyonları

• Değişkenler (tensör, skaler, sürekli, ayrık)
  • sistemin gözlemlenen girdisi
  • deterministik bir fonksiyon tarafından üretilen bir hesaplanmış değişken.

• Deterministik fonksiyonlar

  

  • Birden fazla girdi alır ve birden fazla çıktı üretir
  • Üstü kapalı bir parametre değişkeni vardır (${w}$)
  • Yuvarlanan taraf hesaplaması kolay olan yönü gösterir. Yukarıdaki diyagramda ${\bar{y}}$’nin ${x}$’ten hesaplanması aksi yönden daha kolaydır.

• Skaler değerli fonksiyon

  

  • Maliyet fonksiyonlarını göstermek için kullanılır
  • Üstü kapalı bir skaler çıktısı vardır
  • Birden fazla girdi alır ve tek bir çıktı verir (genellikle girdiler arası uzaklık)

Kayıp Fonksiyonu

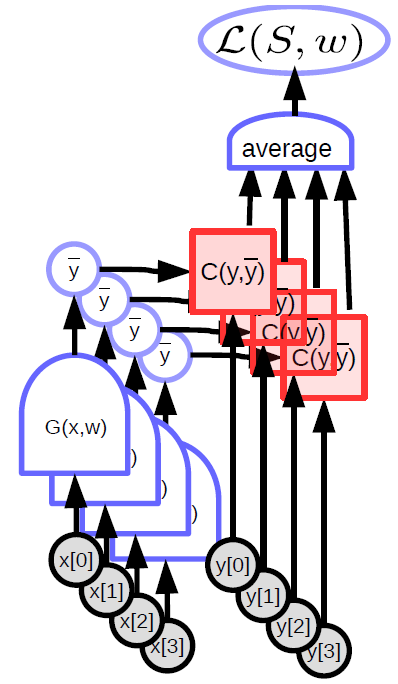
Kayıp fonksiyonu eğitim süresince azaltılan bir fonksiyondur. İki tür kayıp vardır:

1) Örnek başına kayıp - \(L(x,y,w) = C(y, G(x,w))\) 2) Ortalama kayıp -

​ Tüm örnek kümeleri için \(S = \{(x[p],y[p]) \mid p=0,1...P-1 \}\)

​ Küme için hesaplanan ortalama kayıp şu şekilde verilir : \(L(S,w) = \frac{1}{P} \sum_{(x,y)} L(x,y,w)\)

Fig. 2: Ortalama kayıplı model için hesaplama çizgesi

Standart denetimli öğrenme paradigmalarında (örnek başına) kayıp basitçe maliyet fonksiyonunun çıktısıdır. Makine öğrenmesi büyük oranda fonksiyonların optimize edilmesidir (genellikle azaltılması). GAN’lerde (Generative Adverserial Network) olduğu gibi Nash dengesini bulmayı da içerebilir. Bu, mutlaka gradyan inişi olmamakla beraber, gradyan temelli metotlarla yapılır.

Gradyan İnişi

Bir Gradyan Temelli Metot, fonksiyonun gradyanının basit bir şekilde hesaplanacağı varsayılırsa, bir fonksiyonun minimasını bulan metot/algoritmadır. Fonksiyonun sürekli ve neredeyse her yerde türevlenebilir (her yerde türevlenebilir olmak zorunda değil) olduğunu varsayar.

Gradyan İnişi Sezgisi - Sisli bir gecede bir dağın ortasında olduğunuzu hayal edin. Aşağıdaki köye gitmek istediğinizden ve kısıtlı görüşe sahip olduğunuzdan, yakınınıza bakıp en dik inişi bulup o yönde aşağı doğru adım atarsınız.

Gradyan İnişi için Farklı Metotlar

• Tam (yığın) gradyan inişi güncelleme kuralı : \(w \leftarrow w - \eta \frac{\partial L(S,w)}{\partial w}\)

• SGD (Stokastik Gradyan İnişi, Stochastic Gradient Descent) için güncelleme kuralı şu hale gelir :

  • Pick a $p$ in $\text{0…P-1}$, then update \(w \leftarrow w - \eta \frac{\partial L(x[p], y[p],w)}{\partial w}\)

Burada \({w}\) optimize edilecek parametreyi gösterir.

$\eta \text{ burada sabit, ama daha sofisyike algoritmalarda bir matris olabilir.}$.

Eğer bu bir pozitif yarı-tanımlı matrisse, yine de aşağı doğru ilerleriz, ancak mutlaka en dik iniş yönünü takip etmeyiz. Hatta inmek istediğimiz yön her zaman en dik inişin yönü olmayabilir.

Eğer fonksiyon türevlenebilir değilse, yani merdiven gibiyse, içinde bir delik varsa ya da düzse, gradyan inişi bize bir bilgi vermez ve diğer metotları kullanırız. Bunlara Sıfırıncı Derece Metotlar ya da Gradyansız Metotlar denir. Derin öğrenme tamamen gradyan temelli metotlarla ilgilidir.

Ancak RL (Pekiştirmeli Öğrenme, Reinforcement Learning) gradyanın açık formu olmadan Gradyan Tahminini içerir. Buna örnek olarak robotun düşe kalka bisiklet sürmeyi öğrenmeye çalışması verilebilir. Amaç fonksiyonu bisikletin düşmeden ne kadar süre dik kalabildiğini ölçer. Ne yazık ki amaç fonksiyonu için bir gradyan yoktur. Robotun farklı şeyler denemesi gerekir.

RL maliyet fonksiyonu çoğu zaman türevlenebilir değildir ama çıktıyı hesaplayan ağ gradyan temellidir. Denetimli öğrenmeyle pekiştirmeli öğrenme arasındaki ana fark budur. İkincisinde maliyet fonksiyonu C türevlenebilir değildir, hatta tamamen bilinmezdir. Sadece, adeta bir kara kutu gibi, bir girdi verildiğinde bir çıktı üretir. Bu onu fazlasıyla verimsiz hale getirir ve bu RL’deki temel engellerden biridir -özellikle parametre vektörü yüksek boyutlu olduğunda (bu aranacak dev bir çözüm uzayı olduğunu ima eder ve nereye hareket edileceğinin bulunmasını zorlaştırır).

RL’de en popüler yöntemlerden biri Aktör Kritik Metotlardır. Bir kritik metodu basitçe eğitilebilir ve bilinen ikinci bir C modülüne sahiptir. C modülü türevlenebilirdir ve maliyet/ödül fonksiyonunu yaklaşık olarak hesaplamak için eğitilebilir. Ödül negatif maliyettir ve daha çok bir cezadır. Bu maliyet fonksiyonunu türevlenebilir yapabilmenin, ya da en azından geri yayılımın kullanılabilmesi için türevlenebilir bir fonsiyonla yaklaşmanın, bir yoludur.

SGD’nin Avantajları ve Geleneksel Sinir Ağları İçin Geri Yayılım

Stokastik Gradyan İnişinin Avantajları (Stochastic Gradient Descent, SGD)

Pratikte amaç fonksiyonunun parametrelere göre gradyanını hesaplamak için stokastik gradyan inişini kullanırız. Amaç fonksiyonun tüm gradyanını hesaplamaktansa (tüm örneklerin ortalaması), stokastik gradyan inişi bir örnek için kaybı ve gradyanı hesaplar ve gradyanın negatif yönünde adıma atar.

Formülde $w$’ya $w$ eksi adım büyüklüğü çarı örnek başına kayıp fonksiyonu gradyanı ile yaklaşılır, ($x[p]$,$y[p]$).

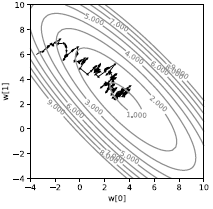
Bunu tek bir örnek için yaparsak Fig. 3’te görüldüğü gibi gürültülü bir yörünge elde ederiz. Kayıp direkt olarak aşağı doğru gitmektense stokastik bir şekilde gider. Her örnek kaybı farklı bir yöne yönlendirecektir. Bizi ortalamanın minimumuna ulaştıran ortalamadır. Her ne kadar verimsiz görünse de makine öğrenmesi bağlamında örnekler fazlalık içerdiğinde yığın gradyan inişinden daha hızlıdır.

Fig. 3: Örnek başına güncelleme için stokastik gradyan inişi yörüngesi

Pratikte tek bir örnek yerine bir yığın örnek kullanarak stokastik gradyan inişini kullanırız. Bir örnek yerine bir yığın için ortalama gradyanı hesaplayıp bir adım atarız. Bunu yapmamızın sebebi yığınları kullandığımızda paralelleştirmenin daha kolay olması ve elimizdeki donanımı daha verimli kullanmaktır (i.e. GPU, çok çekirdekli CPU).

Geleneksel Sinir Ağı

Geleneksel sinir ağları serpiştirilmiş doğrusal ve noktasal doğrusal olmayan işlemlerden oluşan katmanlardır. Doğrusal işlemler için, kavramsal olarka sadece bir matris çarpımıdır. Girdi vektörünü ağırlık matrisiyle çarparız. İkinci tür işlem vektörlerin ağırlıklı toplamını alıp basit bir doğrusal olmayan fonksiyondan geçirmektir (i.e. $\texttt{ReLU}(\cdot)$, $\tanh(\cdot)$, …).

Fig 4: Geleneksel sinir ağı

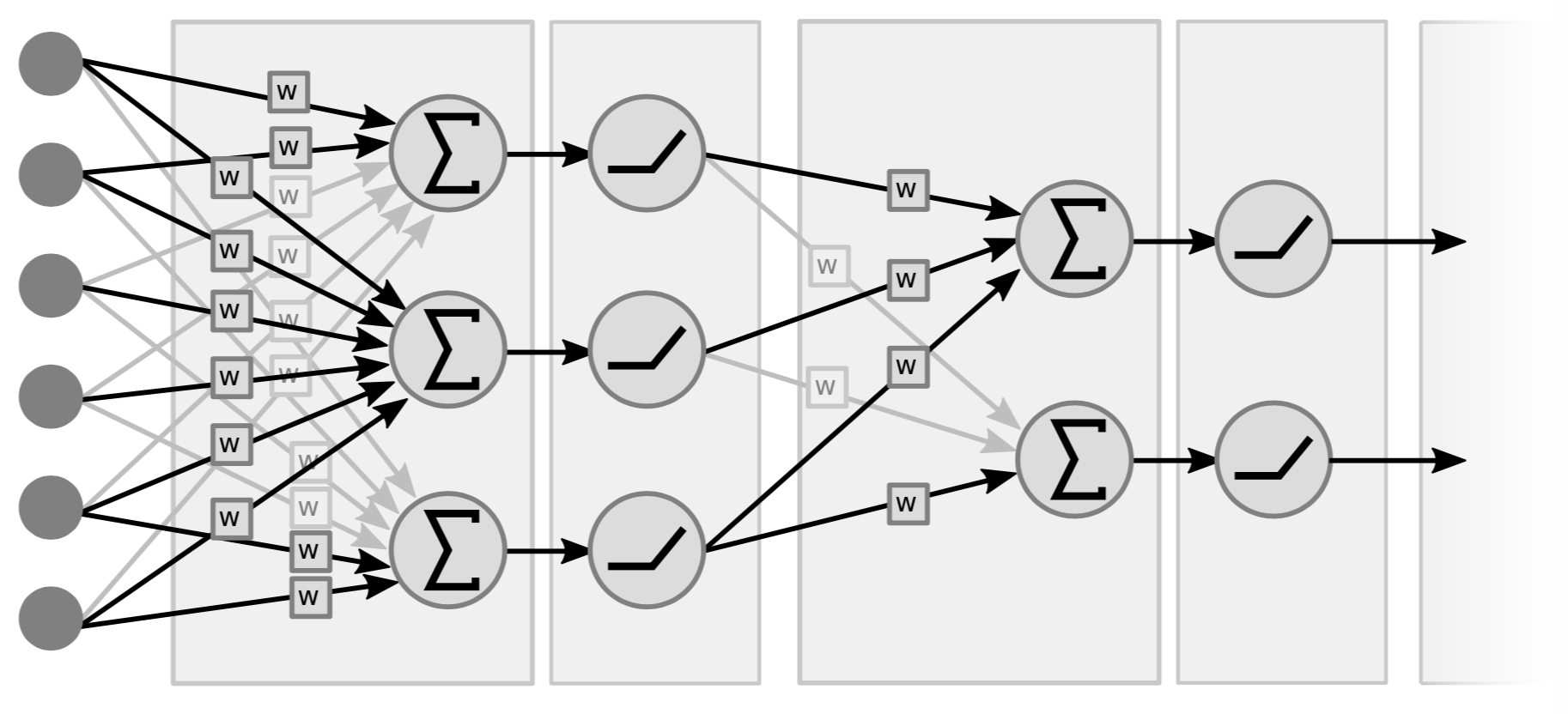Fig. 4 iki katmanlı bir ağa örnektir, çünkü önemli olan çiftlerdir (yani doğrusal ve doğrusal olmayan). Bazıları değişkenleri de sayarak bu ağa üç katmanlı der. Orta katmanda hiçbir doğrusal olmayan fonksiyon yoksa bu ağa tek katmanlı ağ diyebiliriz, çünkü bu durumda sadece iki doğrusal fonksiyonun çarpımı yine bir doğrusal fonksiyondur.

Fig. 5 ağın doğrusal ve doğrusal olmayan fonksiyonel bloklarını göstermektedir:

Fig. 5: Doğrusal ve doğrusal olmayan bloklara bir bakış

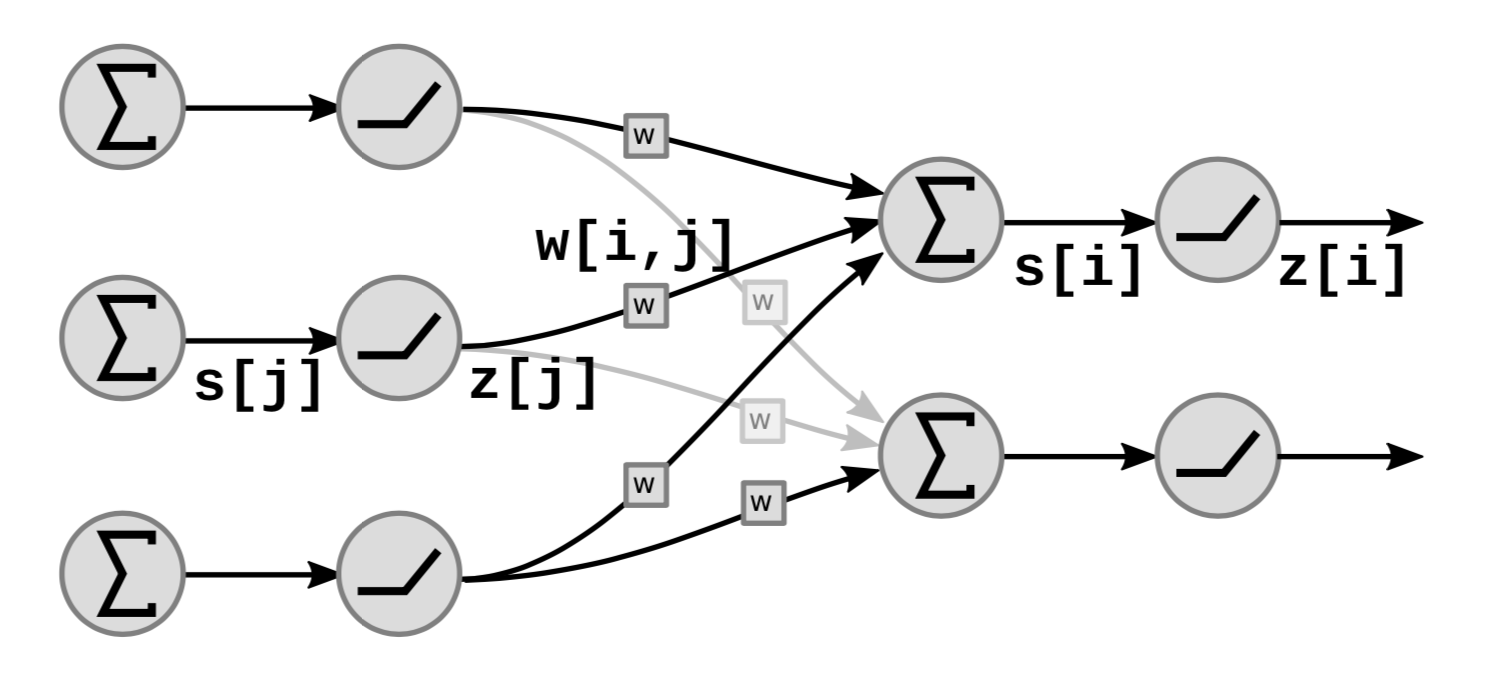Çizgede $s[i]$ ${i}$’nin ağırlıklı toplamıdır ve şöyle hesaplanır:

$UP(i)$ $i$’nin öncellerini gösterir ve $z[j]$ önceki katmanın $j$. çıktısıdır.

Çıktı $z[i]$ şöyle hesaplanabilir:

$f$ doğrusal olmayan bir fonksiyondur.

Doğrusal Olmayan Fonksiyonla Geri Yayılım

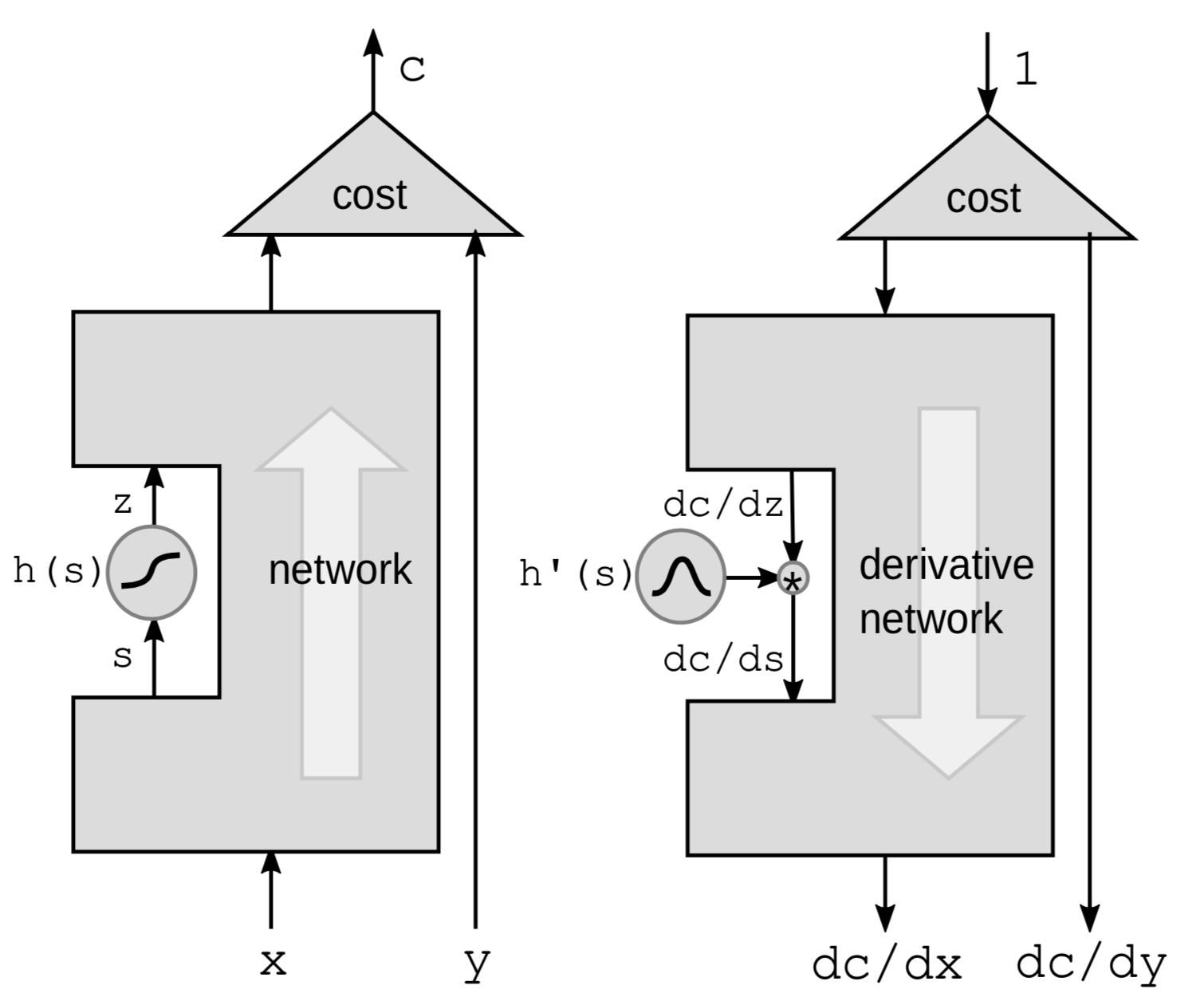
The first way to do backpropagation is to backpropagate through a non linear function. We take a particular non-linear function $h$ from the network and leave everything else in the blackbox.

Geri yayılımı gerçekleştirmenin ilk yolu doğrusal olmayan bir fonksiyon ile geri yayılımı gerçekleştirmektir. Ağdan belirli bir doğrusal olmayan $h$ fonksiyonu alıp, geriye kalan her şeyi kara kutu olarak bırakıyoruz.

Fig. 6: Doğrusal olmayan fonksiyonla geri yayılım

Zincir kuralını kullanarak gradyanları hesaplacağız:

$h’(s)$ $z$’nin $\frac{\mathrm{d}z}{\mathrm{d}s}$ ile gösterilen $s$’ye göre türevidir.

Türevlerin arasındaki ilişkiyi daha net hale getirmek için formülü tekrar şöyle yazabiliriz:

Bundan dolayı ağda bu fonksiyonların zincirleri varsa, tüm ${h}$ fonksiyonlarının türevlerini birbiri ardına çarparak geri yayılımı gerçekleştirebiliriz.

Bunu sarsımlar şeklinde düşünmek daha sezgiseldir. $s$’yi $\mathrm{d}s$ ile sarsmak $z$’yi

ile sarsacaktır.

Bu da C’yi

ile sarsacaktır.

Bir kez daha yukarıdakiye aynı formüle ulaşırız.

Ağırlıklı Toplamla Geri Yayılım

Doğrusal bir modül için geri yayılımı ağırlıklı toplamla gerçekleştiririz. Burada bir ${z}$ değişkeninden $s$ değişkenlerine olan bağlantılar hariç tüm ağa kara kutu olarak bakacağız.

Fig. 7: Ağırlıklı toplamla geri yayılım

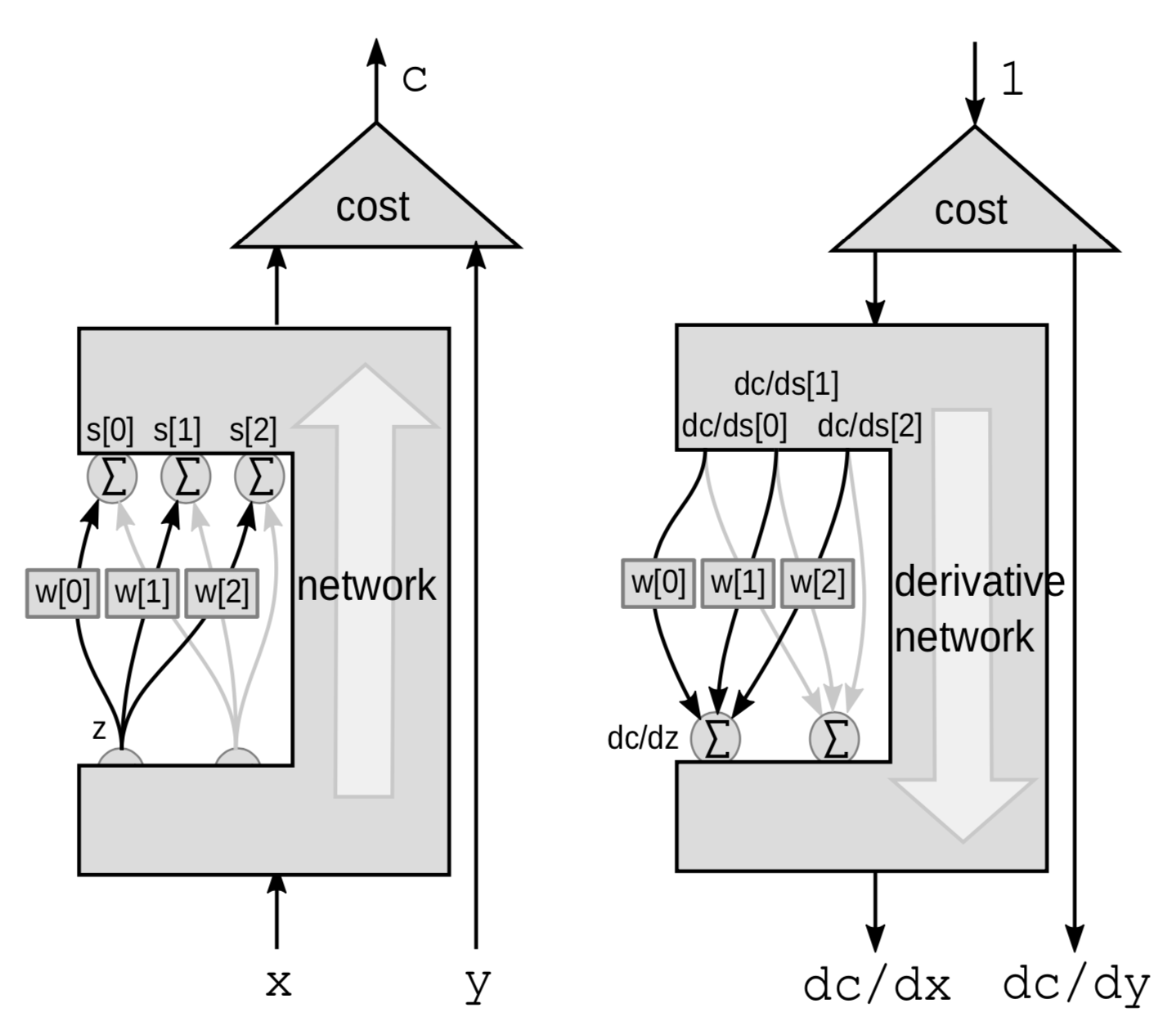Bu sefer sarsım bir ağırlıklı toplamdır. Z birden fazla değişkeni etkiler. $z$’yi $\mathrm{d}z$ ile sarsmak $s[0]$, $s[1]$ ve $s[2]$’yi:

ile sarsacaktır.

Bu C’yi \(\mathrm{d}C = \mathrm{d}s[0]\cdot \frac{\mathrm{d}C}{\mathrm{d}s[0]}+\mathrm{d}s[1]\cdot \frac{\mathrm{d}C}{\mathrm{d}s[1]}+\mathrm{d}s[2]\cdot\frac{\mathrm{d}C}{\mathrm{d}s[2]}\)

ile sarsacaktır.

Dolayısıyla C üç sarsımın toplamıyla değişecektir. \(\frac{\mathrm{d}C}{\mathrm{d}z} = \frac{\mathrm{d}C}{\mathrm{d}s[0]}\cdot w[0]+\frac{\mathrm{d}C}{\mathrm{d}s[1]}\cdot w[1]+\frac{\mathrm{d}C}{\mathrm{d}s[2]}\cdot w[2]\)

Sinir Ağının PyTorch ile Gerçeklenmesi ve Bir Genelleştirilmiş Geri Yayılım Algoritması

Geleneksel Sinir Ağının Blok Diyagramı

• Doğrusal bloklar $s_{k+1}=w_kz_k$

• Doğrusal olmayan bloklar $z_k=h(s_k)$

  

$w_k$: matris $z_k$: vektör $h$: skalerin uygulanması ${h}$ tüm bileşenler için bir fonksiyon. Bu doğrusal ve doğrusal olmayan fonksiyon çiftlerinden oluşan üç katmanlı bir sinir ağıdır. Çoğu modern sinir ağında doğrusal ve doğrusal olmayan ayrımı bu kadar net değildir ve çok modern ağlar çok daha karmaşıktır.

PyTorch Uygulaması

import torch
from torch import nn
image = torch.randn(3, 10, 20)
d0 = image.nelement()

class mynet(nn.Module):
    def __init__(self, d0, d1, d2, d3):
        super().__init__()
        self.m0 = nn.Linear(d0, d1)
        self.m1 = nn.Linear(d1, d2)
        self.m2 = nn.Linear(d2, d3)

    def forward(self,x):
        z0 = x.view(-1)  # flatten input tensor
        s1 = self.m0(z0)
        z1 = torch.relu(s1)
        s2 = self.m1(z1)
        z2 = torch.relu(s2)
        s3 = self.m2(z2)
        return s3
model = mynet(d0, 60, 40, 10)
out = model(image)

• Sinir ağlarını PyTorch ile nesne tabanlı sınıflar halinde gerçekleyebiliriz. Öncelikle sinir ağı için bir sınıf tanımlayıp doğrusal katmanları önceden tanımlanmış olan nn.Linear sınıfını kullanarak tanımlayabiliriz. Lineer katmanlar her biri bir parametre vektörü içerdiğinden ayrı nesneler olarak tanımlanmalıdır. Ayrıca nn.Linear önyargı vektörünü örtülü bir şekilde ekler. Daha sonra çıktıları hesaplamak için $\text{torch.relu}$’yu doğrusal olmayan aktivasyon olarak kullanarak bir “ileri” (forward) fonksiyonu tanımlarız. Relu fonksiyonu parametre içermediğinden ayrı olarak tanımlanmasına gerek yoktur.

• PyTorch geri yayılımın nasıl gerçekleştirileceğini ve verilen ileri fonksiyonu için gradyanların nasıl hesaplanacağını bildiğinden bizim gradyanları hesaplamamıza gerek yoktur.

Fonksiyonel Modüllerle Geri Yayılım

Geri yayılımın daha genelleştirilmiş bir halini sunuyoruz.

Fig. 8: Fonksiyonel modüllerle geri yayılım

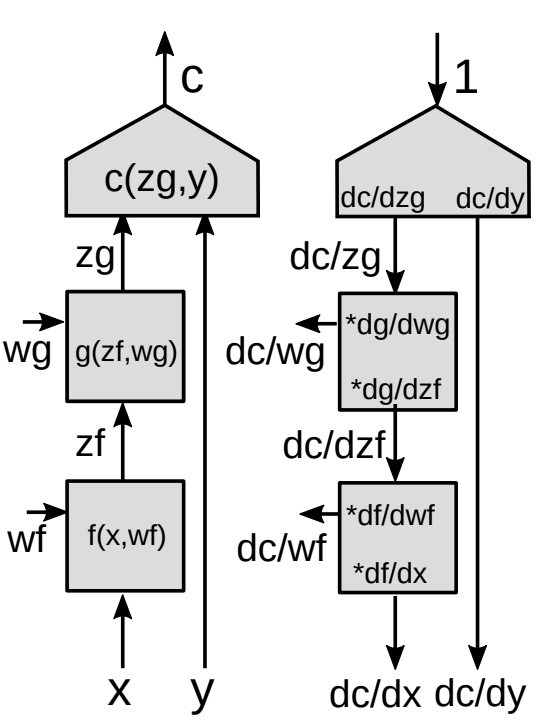• Zincir kuralını kullanarak vektör fonksiyonları için

  \[z_g : [d_g\times 1]\] \[z_f:[d_f\times 1]\] \[\frac{\partial c}{\partial{z_f}}=\frac{\partial c}{\partial{z_g}}\frac{\partial {z_g}}{\partial{z_f}}\] \[[1\times d_f]= [1\times d_g]\times[d_g\times d_f]\]

  This is the basic formula for $\frac{\partial c}{\partial{z_f}}$ using the chain rule. Note that the gradient of a scalar function with respect to a vector is a vector of the same size as the vector with respect to which you differentiate. In order to make the notations consistent, it is a row vector instead of a column vector.

  Bu zincir kuralının $\frac{\partial c}{\partial{z_f}}$ için basit formülüdür. Bir skaler fonksiyonun bir vektöre göre gradyanının kendisine göre türevini aldığınız aynı boyutlarda bir vektör olduğuna dikkat edin. Notasyonu tutarlı tutabilmek için bu bir sütun vektör yerine bir satır vektördür.

• Jacobi matrisi

  \[\left(\frac{\partial{z_g}}{\partial {z_f}}\right)_{ij}=\frac{(\partial {z_g})_i}{(\partial {z_f})_j}\]

  Kayıp fonksiyonunun $z_g$’ye göre gradyanı verildiğinde kayıp fonskyionunun $z_f$’ye göre gradyaını hesaplamak için $\frac{\partial {z_g}}{\partial {z_f}}$’ye ihtiyacımız vardır. Her $ij$ girdisi çıktının $i$. bileşeninin girdinin $j$. bileşenine göre kısmi türevini gösterir.

  Eğer kademeli modüllerimiz varsa, aşağıya gittikçe tüm modüllerin Jacobi matrislerini çarparak devam ederek tüm iç değişkenlerin gradyanlarını elde ederiz.

Çok Aşamalı Çizgede Geri Yayılım

Fig. 9’daki gibi bir ağdaki yığın halindeki modülleri düşünün.

Fig. 9: Çok aşamalı çizgede geri yayılım

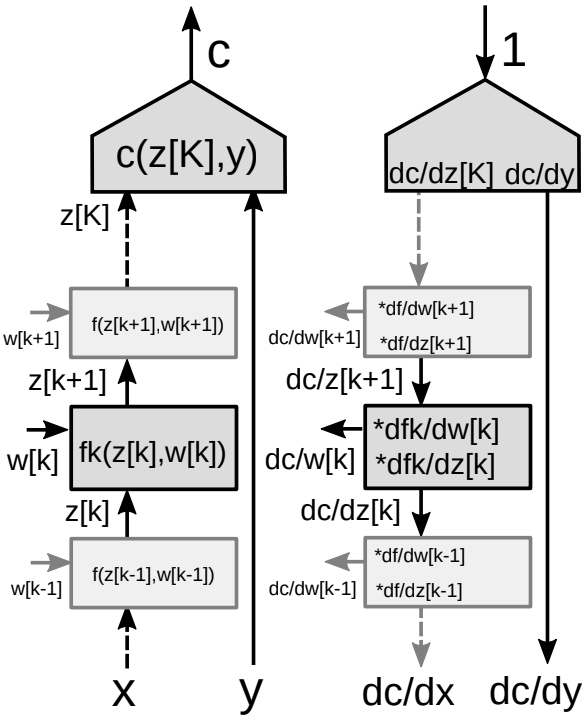Geri yayılım algoritması için iki grup gradyana ihtiyacımız vardır, bir tane durumlara göre (ağdaki her bir modül için), bir tane de ağırlıklara göre (belirli bir modüldeki tüm parametreler için). Böylelikle her bir modül için bir Jacobi matrisi elde ederiz ve geri yayılım için zincir kuralını kullanabiliriz.

• Vektör fonksiyonları için zincir kuralını kullanarak \(\frac{\partial c}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {z_k}}\)

  \[\frac{\partial c}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {w_k}}\]

• Modül için iki Jacobi matrisi

  • Bir tane $z[k]$’ye göre
  • Bir tane $w[k]$’ye