Overfitting and regularization

過学習

回帰問題を考えてみましょう。モデルは、学習不足、適切な学習、過学習のいずれかになります。

モデルの表現力がデータに対して不十分な場合、過少適合となります。モデルがデータよりも表現力が高い場合（ディープニューラルネットワークの場合のように）、過剰適合（オーバーフィッティング）のリスクがあります。

この場合、モデルは元のデータとノイズの両方を適合させるのに十分な力を持っているので、手元のタスクに対する貧弱な解を生み出します。

理想的には、モデルがノイズではなく基礎となるデータにフィットして、データに良好なフィットをもたらすことが望まれます。特に、モデルのパワーを下げることなく、これを実現したいと考えています。ディープラーニングモデルは非常に強力で、多くの場合、データを学習するために厳密に必要とされる以上のパワーを持っています。そのパワーを維持しつつ（訓練を容易にするために）、過学習と戦いたいと考えています。

デバッグのための過学習

過学習は、デバッグ中など、いくつかのケースで有用です。学習データの小さな部分集合（単一のバッチやランダムなノイズテンソルのセットでさえも）でネットワークをテストして、ネットワークがこのデータにオーバーフィットできることを確認することができます。学習に失敗した場合は、バグがある可能性があることを示しています。

正則化

正則化を導入することで過学習に対抗しようとすることができます。正則化の量はモデルの検証性能に影響を与えます。正則化が弱すぎると、過学習問題の解決に失敗します。正則化が強すぎると、モデルははるかに効果的ではなくなります。

正則化は、モデルに事前知識を追加します。すなわち、パラメータに事前分布が指定されます。これは、学習可能な関数の集合に対する制限として機能します。

Ian Goodfellowによる正則化のもう一つの定義は次のようなものです。

正則化とは、学習アルゴリズムの汎化誤差を減らすことを意図するが、訓練誤差を減らすことは意図していないような、学習アルゴリズムに行う修正のことです。

初期化テクニック

特定の分布に従って重みを初期化することで、ネットワークパラメータの優先順位を選択することができます。Xavierの初期化は、この選択肢の一つです。

重み減衰による正則化

重み減衰は我々の最初の正則化手法です。重み減衰は機械学習では広く使われていますが、ニューラルネットワークではあまり使われていません。 PyTorchでは、オプティマイザのパラメータとして重み減衰が提供されています（例えば、 SGDのweight_decayパラメータを参照してください）。

これは以下のようにも呼ばれています。

• L2
• リッジ
• ガウス事前分布

パラメータに作用する目的関数を考えることができます。

すると、次の更新式が得られます

重み減衰では、ペナルティ項を導入します。

これから、次の更新式が得られます

この更新式の新しい項は、パラメータ $\theta$ をわずかにゼロに向けて動かし、更新のたびに重みにいくつかの「減衰」を追加します。

L1正則化

PyTorchのoptimizersにも選択肢として用意されています . <!– Also called:

• LASSO: Least Absolute Shrinkage Selector Operator
• Laplacian prior
• Sparsity prior

Viewing this as a Laplace distribution prior, this regularization puts more probability mass near zero than does a Gaussian distribution.

Starting with the same update as above we can view this as adding another penalty: –>

これは次のようにも呼ばれています。

• LASSO: Least Absolute Shrinkage Selector Operator
• ラプラシアン事前分布
• スパース事前分布

これをラプラス分布を事前分布として用いたものとして見ると、この正則化は、ガウス分布よりも多くの確率質量をゼロに近づけます。

上と同じ更新から始めて、これを別のペナルティを追加したと見ることができます。

これは次の更新式を生み出します。

$L_2$ 重み減衰とは異なり、$L_1$ 正則化はパラメータ空間の軸に近い成分を「殺す」のであって、パラメータベクトルの長さを均等に減らすのではありません。

ドロップアウト

ドロップアウトでは、訓練中に特定の数のニューロンをランダムにゼロに設定します。これにより、ネットワークは入力から出力への特異な経路を学習することができなくなります。同様に、ニューラルネットワークのパラメトリゼーションが大きいため、ニューラルネットワークが入力を効果的に記憶することが可能です。しかし、ドロップアウトの場合、ドロップアウトは毎回異なる無限個のネットワークを効果的に訓練するので入力は毎回異なるネットワークに投入されることになり、これははるかに困難となります。したがって、ドロップアウトは、過学習を制御する強力な方法となり、入力の小さな変動に対してより強固なものとなります。

図1: ドロップアウトのあるネットワーク

図2: ドロップアウトのあるネットワーク

PyTorchでは、ニューロンのランダムなドロップアウト率を設定することができます。

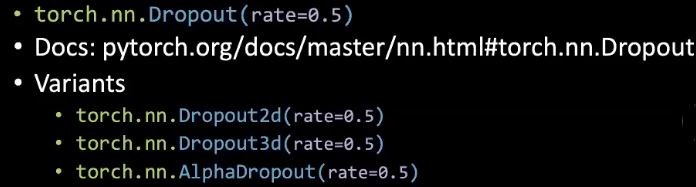
図3: ドロップアウトのコード

訓練後、推論中には、ドロップアウトはもう使いません。推論のための最終的なネットワークを作成するために、ドロップアウト中に作成された個々のネットワークをすべて平均化し、推論に使用します。同様に、すべての重みに $1/1-p$ をかけます。ただし$p$ はドロップアウト率です。

早期打ち切り

訓練中に、検証誤差が増加し始めたら、訓練を中止して、これまでに見つかった最も良い重みを使用します。これにより、重みが大きくなりすぎて、ある時点で検証性能に支障をきたし始めるのを防ぐことができます。実際には、一定の間隔で検証性能を計算し、検証誤差が減少しなくなったら停止するのが一般的です。 <!–

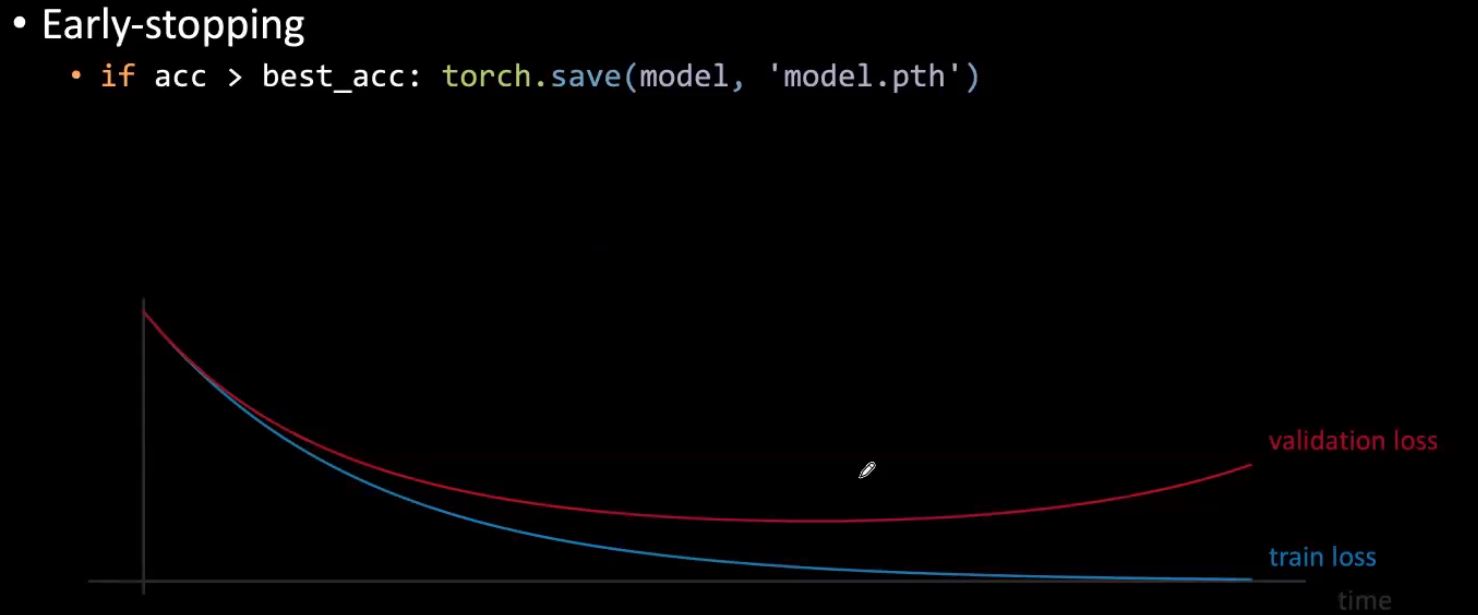
Figure 4: Early stopping

–>

図 4: 早期打ち切り

間接的に過学習と戦う

それ自体は正則化ではないけれど、パラメータを正則化する副作用を持つテクニックがあります。

バッチ正規化

質問：バッチ正規化はどのようにして訓練を効率化するのですか？

答え：バッチ正規化を適用すると、より大きな学習率を使うことができます。

バッチ正規化はニューラルネットワークの内部共変量シフトを防ぐために使われますが、実際にこれを行うのかどうか、本当の効果は何なのかについては多くの議論があります。

図5: バッチ正規化

バッチ正規化は、基本的にニューラルネットワークの入力を正規化するロジックを、ネットワーク内の各隠れ層の入力を正規化することに拡張したものです。基本的な考え方は、ニューラルネットワークの後続の各層に固定された分布を与えることです。というのも、固定された分布を持っているときに学習が最もうまくいくからです。これを行うために、各隠れ層の前に各バッチの平均と分散を計算し、これらのバッチ固有の統計量で入力値を正規化します。

各バッチが異なるため、正規化効果に関しては、各サンプルはそのバッチに基づいてわずかに異なる統計量で正規化されます。 そのため、ネットワークは1つの入力の様々なわずかに変化したバージョンを見ることになり、入力のわずかな変化に対してよりロバストな学習を行い、過学習を防ぐことができます。

バッチ正規化のもう一つの利点は、訓練が非常に速くなることです。 <!–

More data

Gathering more data is a easy way to prevent overfitting but can be expensive or not feasible.

Data-augmentation

Transformations using Torchvision can have a regularizing effect by teaching the network to learn how to be insensitive to perturbations. –>

より多くのデータ

より多くのデータを収集することは、過学習を防ぐための簡単な方法ですが、コストがかかる場合もありますし、実現不可能な場合もあります。

データを増やすことで、過学習を防ぐことができます。

Torchvisionを使用した変換は、摂動に鈍感になる方法をネットワークに教えることで、正規化の効果を得ることができます。

図6: Torchvisionによるデータ拡張

転移学習 (TF) fine-tuning (FT)

転移学習 (TF) は，事前に学習されたネットワークの上に最終的な分類器を学習することを意味します（一般的にデータが少ない場合に使用されます）。

Fine-tuning (FT) は，事前に学習されたネットワークの一部または全部を学習することを指します（一般的にデータが多い場合に用いられます）。

質問： 一般的に、どういう時に事前学習したモデルの層を学習しないようにさせるのですか？

答え：学習データが少ない場合です。

4つの一般的なケース。 1) 似たような分布に従うデータが少ない場合は、単に転移学習を行うことができます。 2) 似たような分布に従う多くのデータがあれば，特徴抽出器の性能を向上させるためにfine-tuningを行うことができます。 3) データが少なく、分布が異なる場合は、特徴抽出器の最終的な学習層の一部を削除すべきです。 4) 多くのデータがあり、それらが異なる分布からのものであれば、すべての部分を学習することができます。

注意：パフォーマンスを向上させるために、異なる層に対して異なる学習率を使用することもできます。

過学習と正則化についての議論をさらに深めるために、以下の可視化を見てみましょう。これらの可視化は、Notebookのコードを使用して生成されました。

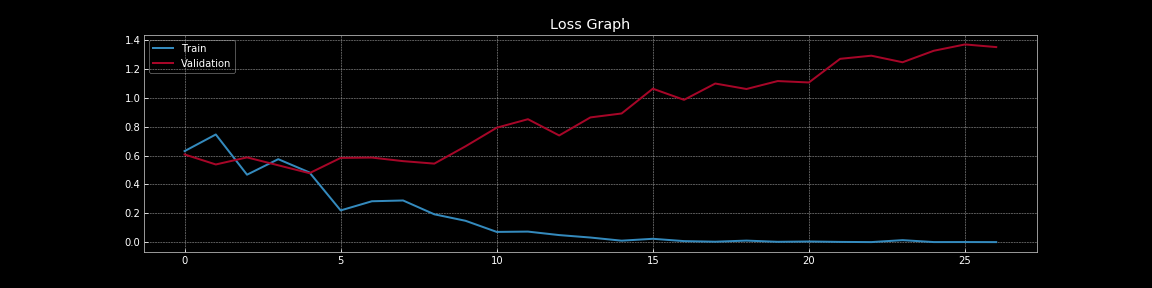
図7: ドロップアウトがない場合の誤差曲線

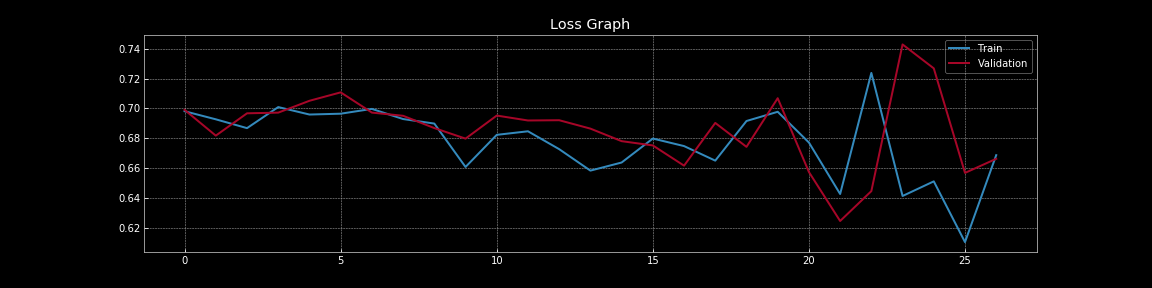
図8: ドロップアウトがある場合の誤差曲線

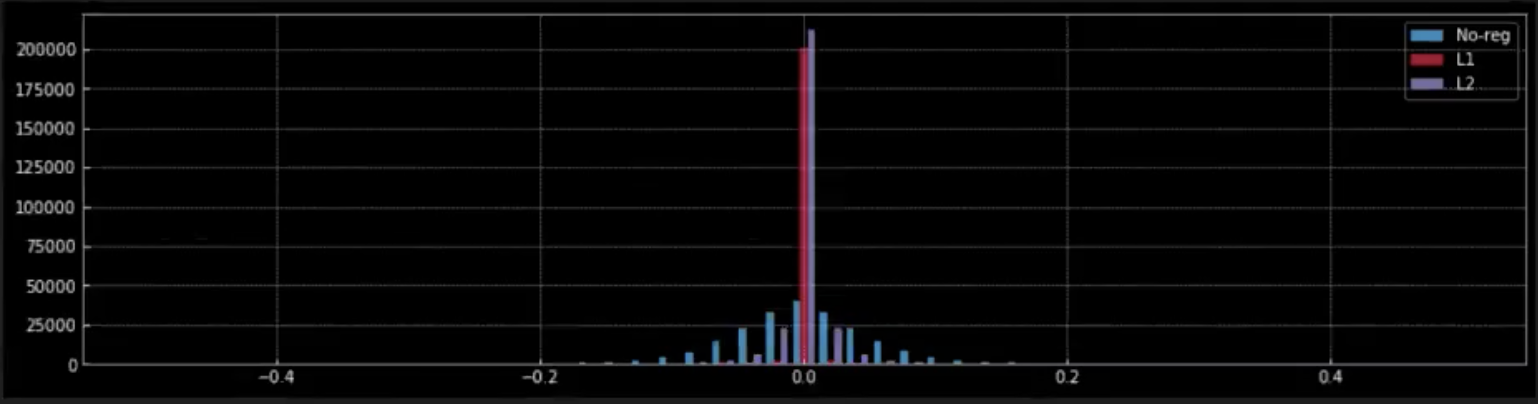
図9: 重みに対する正則化の効果

図7と図8から、ドロップアウトが汎化誤差、すなわち訓練損失と検証損失の差に与える劇的な効果を理解することができます。図7では、ドロップアウトがない場合、訓練誤差は検証誤差よりもはるかに低いため、明らかに過学習が見られます。しかし、図8では、ドロップアウトがある場合、訓練誤差と検証誤差はほぼ連続的に重なっており、モデルがサンプル外集合の代理である検証集合にうまく汎化していることを示しています。もちろん、別のホールドアウトテスト集合を使用して、実際のサンプル外集合に対する性能を測定することができます。

図9では、正則化（L1とL2）がネットワークの重みに与える効果を観察しています。

• L1正則化を適用すると、ゼロの赤いピークから、ほとんどの重みがゼロであることがわかります。ゼロに近い小さな赤い点は、モデルの非ゼロの重みです。

• 対照的に、L2正則化では、ゼロに近い青いピークから、重みのほとんどがゼロに近いがゼロではないことがわかります。

• 正則化がない場合（ラベンダー）、重みは、はるかに柔軟で、正規分布に似た形でゼロの周りに広がっています。

ベイズニューラルネットワーク：予測の不確実性の推定

ニューラルネットワークの不確実性に注目しているのは、ネットワークがどの程度の確信度を持って予測しているかを知る必要があるからです。

例：車の操縦を予測するためにニューラルネットワークを構築する場合、ネットワークの予測がどれだけ確信度が高いかを知る必要があります。

ドロップアウトを持つニューラルネットワークを使って、予測値の信頼区間を求めることができます。ここでは、ドロップアウトのあるネットワークを訓練してみましょう。

通常、推論の際には、ネットワークを検証モードに設定し、すべてのニューロンを使って最終的な予測を行います。予測を行う際には、訓練中にニューロンが落ちてしまうことを考慮して、重み $\delta$ を $\dfrac{1}{1-r}$ でスケーリングします。

この方法では、各入力に対して1つの予測が得られます。しかし、予測の信頼区間を得るためには、同じ入力に対して複数の予測が必要です。そこで、推論中にネットワークを検証モードに設定する代わりに、訓練モードのままにします。このドロップアウトネットワークを使って複数回予測を行うと、同じ入力に対して、ドロップされるニューロンに応じて異なる予測が得られます。これらの予測を使用して、最終的な予測の平均値とその周りの信頼区間を推定します。

以下の画像では、ネットワークの予測値の信頼区間を推定しています。これらの可視化は、Bayesian Neural Networks Notebookのコードを使用して生成されました。赤い線が予測値を表しています。予測値の周りの紫色の網掛け領域は、不確実性、すなわち予測値の分散を表しています。

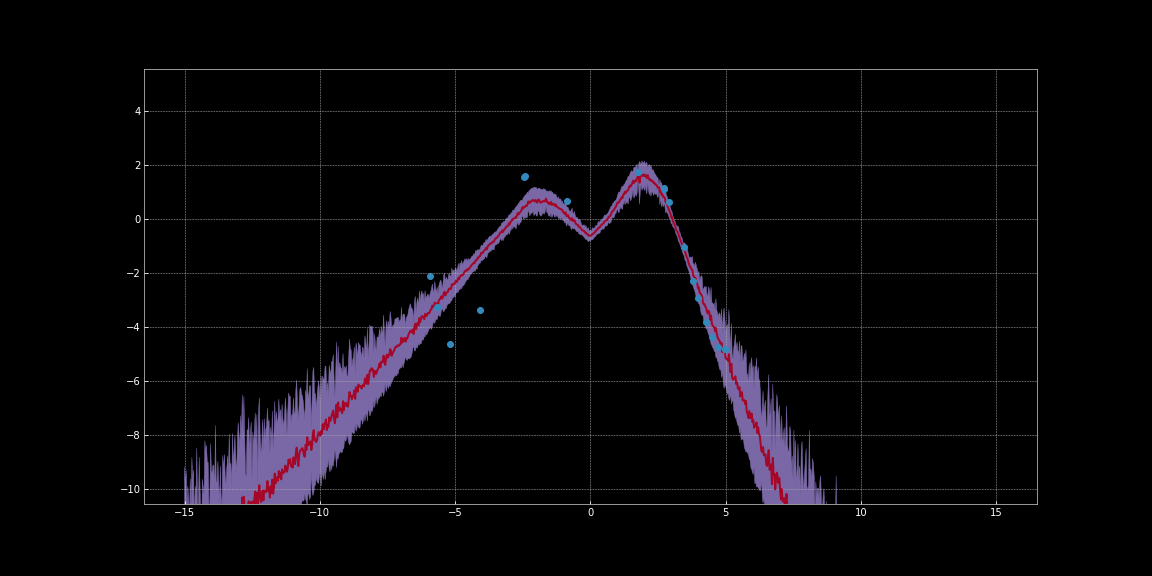
図10: ReLU活性化関数を使った不確実性の推定

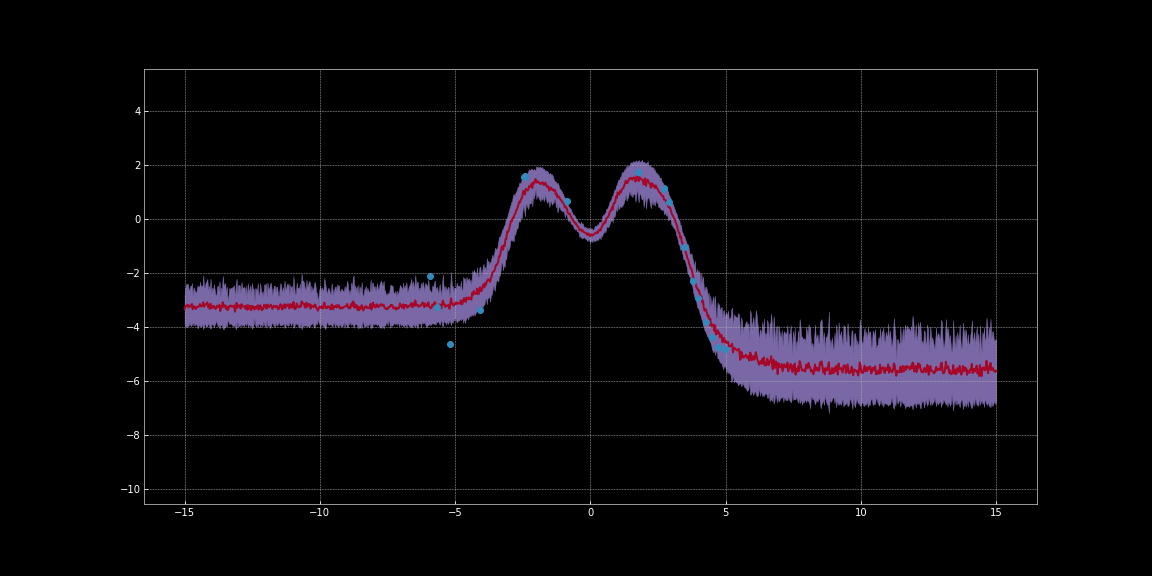
図11: Tanh活性化関数を使った不確実性の推定

上の画像で観察できるように、これらの不確かさの推定は較正されていません。活性化関数の違いによって異なります。画像の中で注目すべきは、データ点の周りの不確かさが低いことです。さらに、観察できる分散は微分可能な関数です。そのため、この分散を最小化するために勾配降下法を実行することができます。そうすることで、より信頼性の高い予測が可能になります。

EBMモデルにおいて、総損失に寄与する複数の項がある場合、それらはどのように相互作用するのでしょうか？

EBMモデルでは、総損失を推定するために、異なる項を単純かつ便利に合計することができます。

余談：潜在変数の長さを罰する項は、モデル内の多くの損失項の1つとして機能します。ベクトルの長さは、それが持つ次元の数にほぼ比例します。したがって、次元の数を減らすと，ベクトルの長さは減少し、その結果、より少ない情報を符号化します。オートエンコーダーの設定では、これによりモデルが最も重要な情報を保持していることが確認されます。したがって、潜在空間の情報をボトルネックにする1つの方法は、潜在空間の次元数を減らすことです。

正則化のためのハイパーパラメータはどのようにして決定すればよいのでしょうか？

実際には、正則化に最適なハイパーパラメータ、すなわち正則化の強さを決定するには、以下の方法を用いることができます。

• ベイズハイパーパラメータ最適化
• グリッドサーチ
• ランダムサーチ

これらの探索を行っている間、通常、最初の数エポックあれば正則化がどのように機能しているかの感覚を得るのに十分です。ですから、モデルを網羅的に訓練する必要があります。