Graphical Energy-based Methods

誤差を比較する

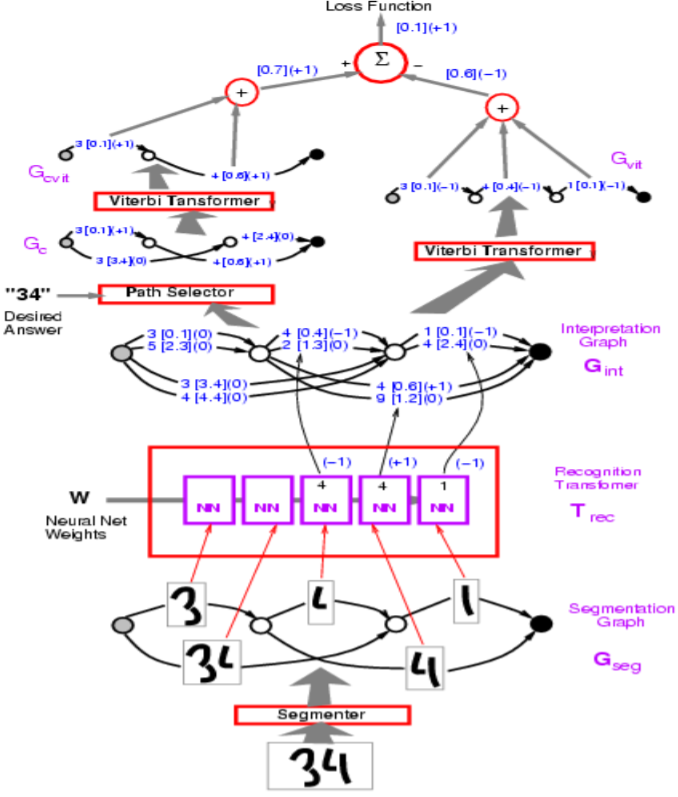
図1: ネットワークアーキテクチャ

上の図では、正しくないパスには-1がつきます。

LeCun教授は、上の図のグラフtransformerモデルの例で使われているパーセプトロン損失から始めます。目的は、間違った答えのエネルギーを大きくし、正しい答えのエネルギーを小さくすることです。

実装の面では、円弧の可視化をベクトルで表現します。各カテゴリごとに別々の弧を描くのではなく、1つのベクトルにカテゴリと各カテゴリのスコアの両方が含まれています。

Q: 上記のモデルでは、セグメンテーションはどのように実装されていますか？

A: セグメンテーションは手作りのヒューリスティックで行われます。エンドツーエンドで学習可能にする方法もありますが、このモデルでは手動で作られたセグメントを使用しています。この手動のアプローチは、文字識別のためのスライディングウィンドウアプローチに取って代わられました。

損失のおさらい

| 名前 | 式 | マージン | | :—- | :—-: | —:| | Energy Loss | $\text{E}(\text{W}, \text{Y}^i, \text{X}^i)$ | None | | Perceptron | $\text{E}(\text{W}, \text{Y}^i, \text{X}^i)-\min\limits_{\text{Y}\in\mathcal{Y}}\text{E}(\text{W}, \text{Y}, \text{X}^i)$ | 0 | | Hinge | $\max\big(0, m + \text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)$ | $m$ | | Log | $\log\bigg(1+\exp\big(\text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)$ | >0 | | LVQ2 | $\min\bigg(M, \max\big(0, \text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)$ | 0 | | MCE | $\bigg(1+\exp\Big(-\big(\text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\Big)\bigg)^{-1}$| >0 | | Square-Square | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i)^2-\bigg(\max\big(0, m - \text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)^2$ | $m$ | | Square-Exp | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i)^2 + \beta\exp\big(-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)$ | >0 | | NNL/MMI | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i) + \frac{1}{\beta}\log\int_{y\in\mathcal{Y}}\exp\big(-\beta\text{E}(\text{W}, y,\text{X}^i)\big)$ | >0 | | MEE |$1-\frac{\exp\big(-\beta E(W,Y^i,X^i)\big)}{\int_{y\in\mathcal{Y}}\exp\big(-\beta E(W,y,X^i)\big)}$ | >0 |

上の表のパーセプトロン損失にはマージンがないため、損失が破綻する危険性があります。

• ヒンジ損失は最も問題のある答えと正しい答えのエネルギーを取り、その差を計算します。直感的には、マージンがmの場合、ヒンジは、正解のエネルギーが最も問題のあるエネルギーよりも少なくともm以上低い場合にのみ、損失が0になります。
• MCE損失は音声認識に使用され、シグモイドに似ています。
• NLL損失は、正解のエネルギーを小さくし、方程式の対数成分を大きくすることを目的としています。

Q: ヒンジ損失はどうにしてNLL損失よりも優れているのでしょうか？

A: NLL損失は正解と他の解答の差を無限大にしようとするのに対し、ヒンジ損失はそれをある値(マージンm)よりも大きくしようとするだけなので、NLLよりも優れています。

定義：

デコーダは、個々の音や画像のスコアやエネルギーを示す一連のベクトルを入力として受け、可能な限り最適な出力を選び出します。

Q: デコーダを利用できる問題の例を教えてください。

A: 言語モデリング、機械翻訳、系列へのタグ付けなどです。

グラフtransformerネットワークにおける順伝播アルゴリズム

グラフの合成

グラフの合成では、2つのグラフを組み合わせることができます。この例では、$trie$（グラフ）として表現された言語モデルの辞書と、ニューラルネットワークによって生成された識別グラフを見ることができます。

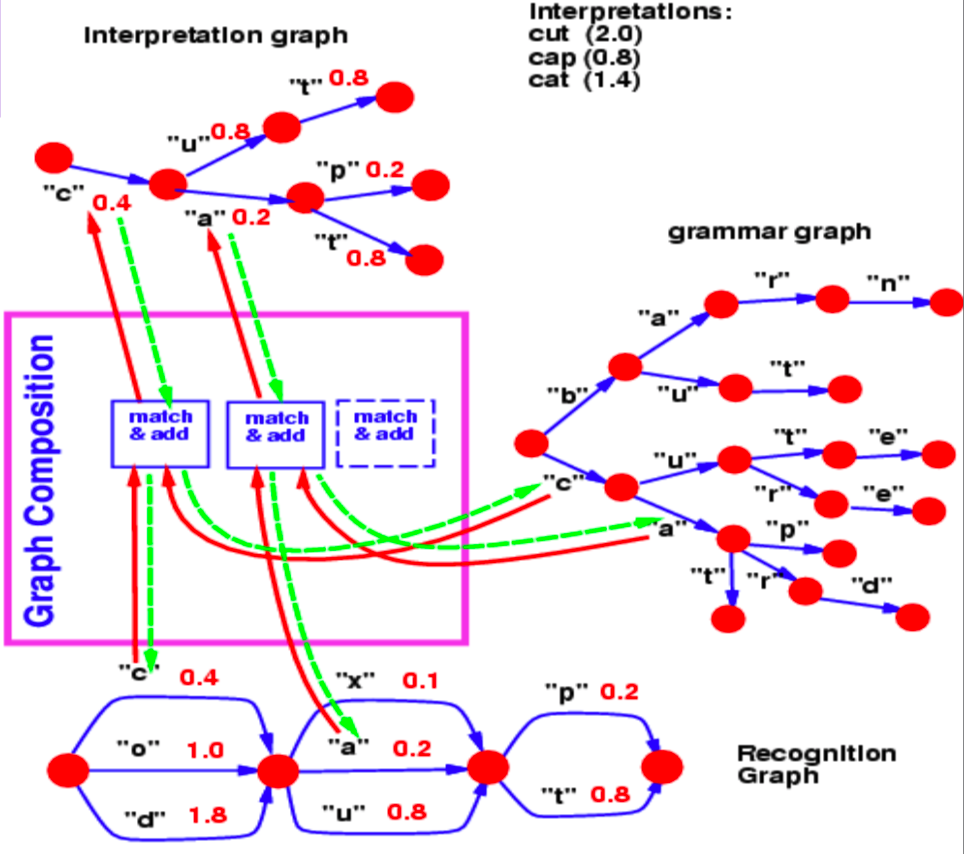
図2: グラフの合成

識別グラフは、（各円弧に関連付けられた）異なるエネルギー値で、ある文字が特定のステップでどの程度の可能性があるかを指定します。

さて、この例では、グラフの合成操作で答える質問は、この識別グラフの中で、私たちの辞書と一致する最良のパスは何か、ということです。

識別グラフと文法の間のステップ1からステップ2への共通ホップは、エネルギー0.4の文字$c$です。したがって、我々の解釈グラフには、ステップ 1 とステップ 2 の間に $c$ に対応する円弧が 1 つだけ含まれています。同様に、ステップ2とステップ3の間にあり得る文字は、識別グラフでは、$x$, $u$, $a$です。文法グラフの$c$に続く枝には、$u$と$a$が含まれています。そこで、グラフ合成演算は、解釈グラフに存在する円弧 $u$ と $a$ を選び出します。また、識別グラフからコピーした円弧を、それらのエネルギー値に関連付けます。

もし文法にも円弧に関連するエネルギー値が含まれていたとしたら、グラフの合成はエネルギー値を追加するか、他の演算子を使ってそれらを結合していたでしょう。

同様の流れで、グラフの合成はまた、ニューラルネットワークによって表現される２つの知識ベースを結合することを可能にします。上で説明した例では、文法は本質的に次の文字を予測するニューラルネットワークとして表現することができます。NNのsoftmax出力は、与えられたノードから次の文字への遷移確率を提供してくれます。

余談ですが、この例で示されている言語モデルがニューラルネットワークであれば、構造全体を誤差逆伝播することができます。これは、ループ、if条件、再帰などを含むプログラムを逆伝播する微分可能なプログラムの例になります。

90年代半ばのチェックリーダー

90年代半ばのチェックリーダーの全体のアーキテクチャは非常に複雑ですが、私たちが主に興味を持っているのは、識別グラフを生成する文字識別器から始まる部分です。

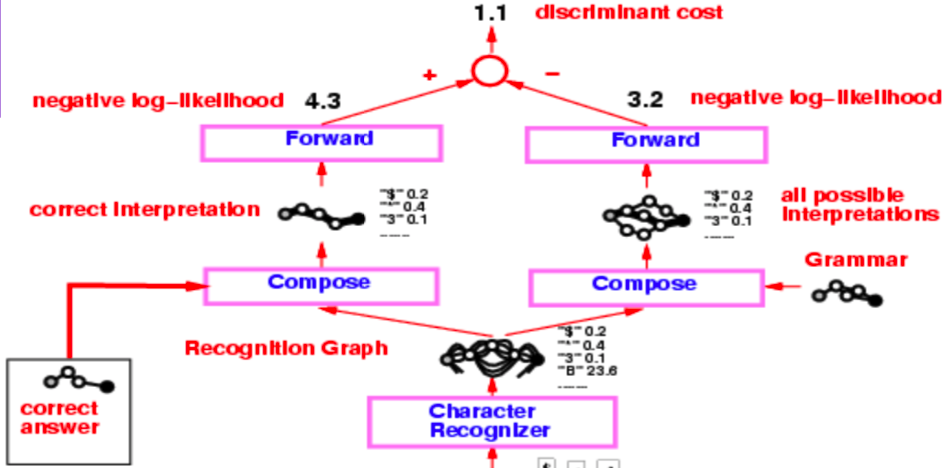
図3: チェックリーダー

この識別グラフは、2つの別々の合成操作を受けます。1つは正しい解釈（または真の値）で、2つ目は文法で、これによってすべての可能な解釈のグラフを作成します。

システム全体は負の対数尤度損失関数を使って学習されます。負の対数尤度を用いるとはつまり、解釈グラフの各パスが可能な解釈であり、そのパスに沿ったエネルギーの総和がその解釈のエネルギーであるということです。

ここで、ビタビアルゴリズムの代わりに、フォワードアルゴリズムを使用します。以下のサブセクションでは、2つのアプローチの違いを議論します。

ビタビアルゴリズム

ビタビアルゴリズムは、与えられたグラフの中で最も可能性の高いパス（またはエネルギーが最小となるパス）を見つけるために使用される動的計画法です。これは、潜在変数 $z$ に関するエネルギーを最小化します。

フォワードアルゴリズム

一方、フォワードアルゴリズムは、すべてのパスの負のエネルギーの指数の和の対数を計算します。これは、以下の式で簡単にわかります。

これは、解釈グラフのパスを定義する潜在変数$z$を周辺化しています。このアプローチでは，特定のノードへのすべての可能なパスについて，この対数和指数値を計算します。これは、ソフトミニマムな方法で、すべての可能なパスのコストを計算するようなものです。

フォワードアルゴリズムは実装が安価で、ビタビアルゴリズムよりもコストがかかりません。また、グラフ上のノードを経由して誤差逆伝播することも可能です。

フォワードアルゴリズムの動作は、解釈グラフ上に定義された以下の例を用いて示すことができます。

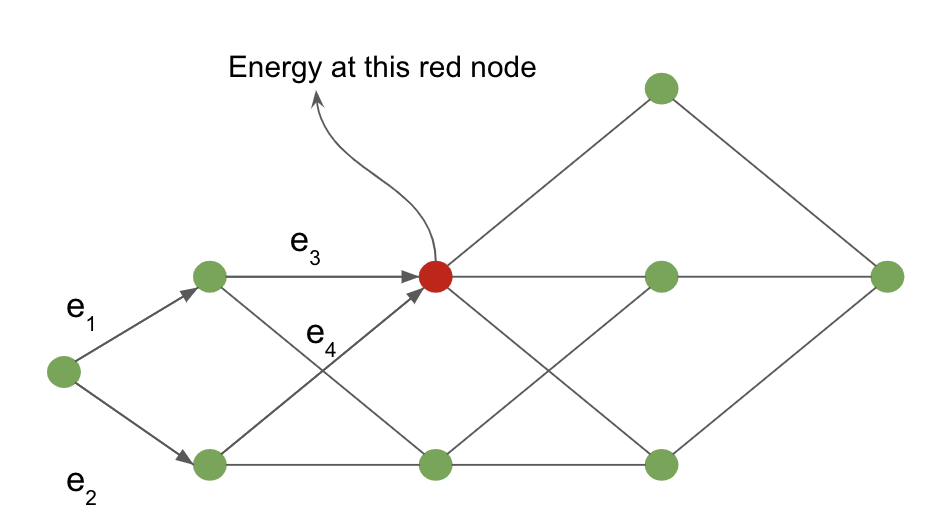
図4: 解釈グラフ

入力ノードから赤い網掛けのノードまでのコストは、赤いノードに到達する可能性のあるすべてのパスを周辺化することによって計算されます。赤いノードに入る矢印は、この例ではこれらの可能なパスを定義しています。

赤色のノードでは、ノードでのエネルギーの値は次のように与えられます。

フォワードアルゴリズムのアナロジーとしてのニューラルネットワーク

フォワードアルゴリズムは、基礎となるグラフが鎖グラフである場合の信念伝播アルゴリズムの特殊なケースです。このアルゴリズム全体は、各ノードでの関数が指数と加算項の対数和であるフィードフォワードニューラルネットワークとして見ることができます。

解釈グラフの各ノードについて、変数$\alpha$を維持します。

ここで、$e_{ki}$は、ノード$k$からノード$i$へのリンクのエネルギーです。

このニューラルネットワークにおいて、$\alpha_i$はノード$i$の活性を形成し、$e_{ki}$はノード$k$とノード$i$の間の重みです。この定式化は、対数領域における通常のニューラルネットワークの重み付き和と代数的に等価です。

フォワードアルゴリズムを適用した動的解釈グラフ（例から例へと変化するので）を誤差逆伝播することができます。解釈グラフのエッジを定義する $e_{ki}$ の重みを用いて、グラフの最後のノードで計算された $F(x, y)$ の勾配を計算することができます。

図5: チェックリーダー

チェックリーダーの例に戻り、2つのグラフ合成にフォワードアルゴリズムを適用し、対数和指数を使用して最後のノードでのエネルギー値を求めます。これらのエネルギー値の差が負の対数尤度損失です。

正解グラフと識別グラフの間のグラフ構成にフォワードアルゴリズムを適用して得られる値は、正解の対数和指数値です。対照的に、識別グラフと文法の間のグラフ構成の最後のノードでの対数和指数値は、すべての可能性のある有効な解釈にわたって周辺化された値です。

誤差逆伝播のラグランジアンによる定式化

入力 $x$ と目標出力 $y$ に対して、ネットワークを関数 $f_k$ と重み $w_k$ の集合として定式化すると、ネットワークの連続するステップが $z_{k+1} = f_k(z_k, w_k)$ で $z_k$ を出力するようになります。教師あり学習の場合では、ネットワークの目標は、ネットワークの $n$番目の出力のコストである $C(z_n, y)$ を、真の値に対して最小化することです。これは、制約 $z_{k+1} = f_k(z_k, w_k)$ と $z_0 = x$ に対して $C(z_n, y)$ を最小化する問題と等価です。

ラグランジアンは次のように書くことができます： \(\mathcal{L}(x, y, \lambda_i, z_i, w_i) = C(z_n, y) + \sum\limits_{k=0}^{n-1} \lambda^T_{k+1}(z_{k+1} - f_k(z_k, w_k))\) ここで $\lambda$ の項はラグランジュの未定乗数を表します（Calc 3 を受けたのが少し前であれば、Paul’s online notesを参照してください）。

$\mathcal{L}$を最小化するためには、$\mathcal{L}$の偏微分を、それぞれの引数についてゼロにして解く必要があります。

• $\lambda$について、単に制約: $\frac{\partial{\mathcal{L}}}{\partial \lambda_{k+1}} = 0 \rightarrow z_{k+1} = f_k(z_k, w_k)$を復元します。
• $z_k$について、$\frac{\partial \mathcal{L}}{\partial z_k} = 0 \rightarrow \lambda^T_k - \lambda^T_{k+1} \frac{\partial f_k(z_k, w)}{\partial z_k} \rightarrow \lambda_k = \frac{\partial f_k(z_k, w_k)^T}{\partial z_k}\lambda_{k+1}$。これは、単なる普通の誤差逆伝播の式です。

このアプローチは、古典力学の文脈でラグランジュとハミルトンに由来します。そこでは最小化はシステムのエネルギーについて行っており、$\lambda$項は、システムの物理的な制約を示しています。例えば二つの球を金属の棒でくっつけることで、二つの球が固定した距離を保っているように強制するようなものです。

時間ステップごとに $k$ のコスト $C$ を最小化する必要がある状況では、ラグランジアンは次のようになります \(\mathcal{L} = \sum_k \left(C_k(z_k, y_k) + \lambda^T_{k+1}(z_{k+1} - f_k(z_k, w_k)) \right)\)

Neural Ordinary Differential Equation

この誤差逆伝播の式を使って、ニューラルODEという新しいクラスのモデルについて話すことができます。これらは、基本的にはリカレントネットワークであり、 $t$ における状態 $z$ は次のように与えられます： $z_{t+\text{d}t} = z_t + f(z_t, W) dt$。ここで、$W$ は固定パラメータの集合を表します。これは，常微分方程式（偏微分なし）で表現することもできます： $\frac{\text{d}z}{\text{d}t} = f(z_t, W)$。

このようなラグランジュ方程式を用いたネットワークの学習は非常に簡単です。目標$y$があり、システムの状態が時間$T$までに$y$に到達するようにしたい場合、コスト関数を$z_T$と$y$の間の距離として設定するだけです。ネットワークのもう一つの目的は、システムの安定した状態、つまり、ある点を境に変化しなくなる状態を見つけることかもしれません。数学的には、これは $\frac{\text{d}z}{\text{d}t} = f(y, W) = 0$ とするのと同じです。一般的に、この方程式の解 $y$ を見つけることは、時間の逆伝播よりもはるかに簡単です。なぜなら、ネットワークは、全シーケンスに関する勾配を記憶する必要がなく、 $f$ または $\lvert f \rvert^2$ を最小化すればよいからです。固定点に到達するためのニューラルODEの訓練については、 (Lecun88)を参照してください。

エネルギーの意味における変分推論

導入

ある初等的なエネルギー関数 $E(x,y,z)$ を、変数 $z$ に対して周辺化して、 $x$ と $y$ と $L(x,y)$ だけの損失を得るには、次の計算をしなければなりません。

$\frac{q(z)}{q(z)}$をかけると、 次の式を得ます \(L(x,y) = -\frac{1}{\beta}\int_z q(z) \frac{\exp({-\beta E(x,y,z)})}{q(z)}\)

$q(z)$を$z$上の確率変数とすると、書き直した損失関数の積分を、 分布$\frac{\exp({-\beta E(x,y,z)})}{q(z)}$に関する期待値として解釈することができます。

この解釈、イェンセンの不等式、サンプリングに基づく近似を用いて、間接的に損失関数を最適化します。

イェンセンの不等式

イェンセンの不等式は、次のようなことを述べる幾何学的な観察です：凸関数がある場合、その関数の期待値は、ある範囲にわたって、範囲の最初と最後に評価された関数の平均値よりも小さくなります。幾何学的に説明すると、これは非常に直感的です。

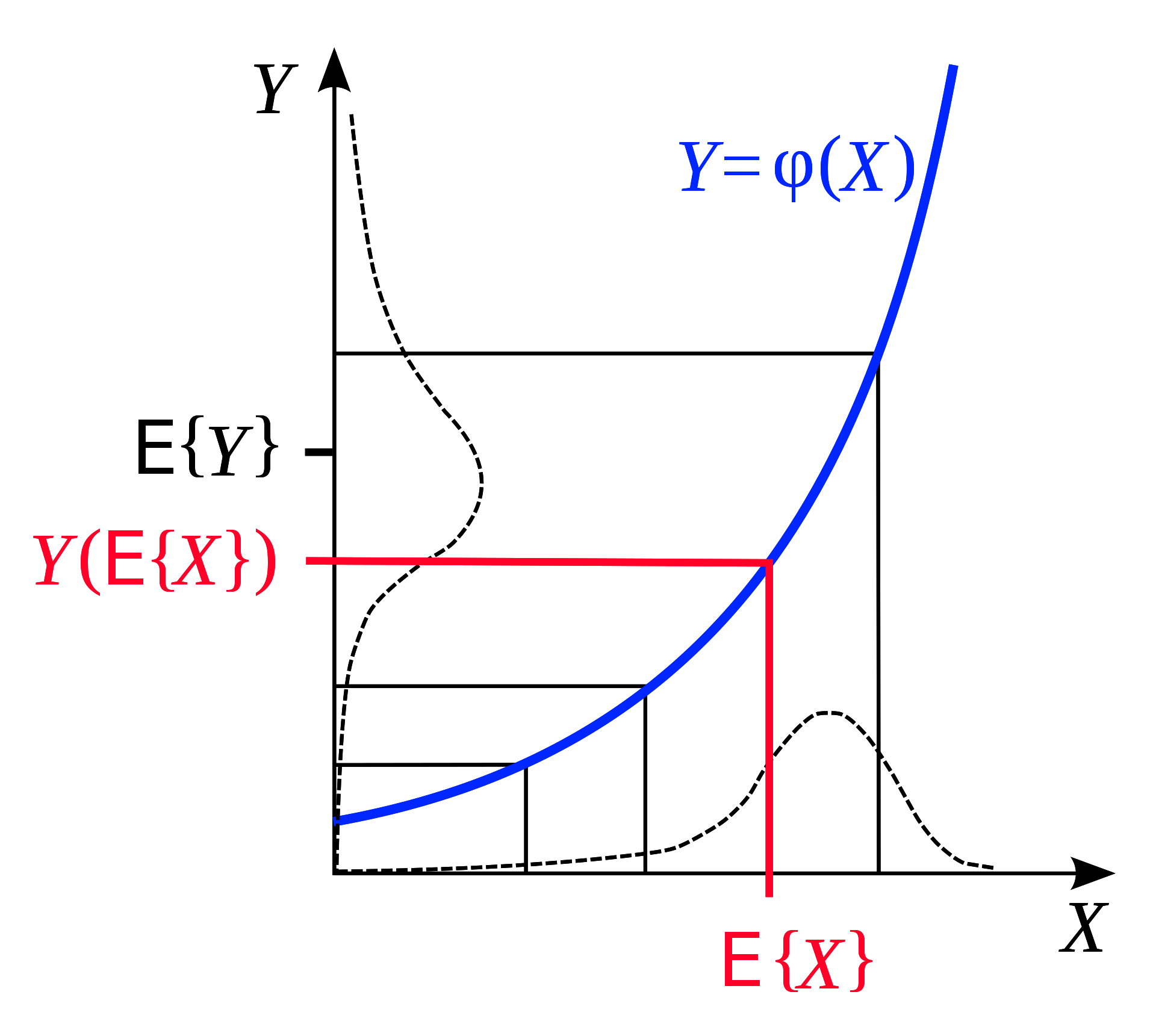
図6: イェンセンの不等式([Wikipedia](https://en.wikipedia.org/wiki/Jensen%27s_inequality)から)

同様に、$F$が凸である場合、固定された確率分布 $q$ に対して、イェンセンの不等式から、 $z$ の範囲にわたって、 $f$ が凸であることが推論できます。

今、$\frac{q(z)}{q(z)}$がかけられた後の、周辺化された$L(x,y)$は、次のようになることを思い出してください \(L(x,y) = -\frac{1}{\beta}\int_z q(z) \frac{\exp({-\beta E(x,y,z)})}{q(z)}\)

$h(z) = -\frac{1}{\beta} \frac{\exp({-\beta E(x,y,z)})}{q(z)}$とすると、イェンセンの不等式$(1)$から、次のことがわかります

引き続き、具体的な凸な損失関数として $F(x) = -\log(x)$ を使ってみましょう。

すばらしい！これで損失関数 $L(x,y)$の上限がわかりました。 上限は私たちが知っている2つの項で構成されています 最初の項 $\int_z q(z)E(x,y,z)$ は 平均 エネルギーです。 そして、２番目の項 $\frac{1}{\beta}\int_z\log(q(z))$ は、いくつかの因子($-\frac{1}{\beta}$)に、分布$q$のエントロピーをかけたものです。

要点は何でしょうか？

これで、複雑な積分を避けることができるように上界を定式化することができました。複雑な積分をする代わりに、我々の選択した代理分布($q(z)$)からサンプリングすることで、これらの値を単純に近似することができます!

上界の関数の最初の項の値を得るために、その分布からサンプリングし、サンプリングした $z$ を適用して得られる $L$ の平均値を計算します。

2番目の項（エントロピーの因子）は、分布族の性質であり、同様に $q$ のランダムサンプリングで近似することができます。

最後に、パラメータ（例えば、ネットワーク $W$ の重み）に関して $L$ を最小化することで、 $L$ を最小化することができます。この最小化は、2つの変数を更新することで行います。(1) $q$のエントロピー、(2)モデルのパラメータ$W$です。

まとめ

これは「エネルギーの視点から見た」変分推論です。指数の和の対数を計算する必要がある場合、関数の平均にエントロピー項を加えたものに置き換えます。これにより、上界が得られます。そして、この上界を最小化することで、実際に関心のある関数を最小化することができます。