構造化予測のための深層学習

構造化予測

構造化予測という問題は、スカラーの離散値や実数値ではなく、相互に依存し、相互に制約をしあってる入力xに対して、変数yを予測するという問題です。出力変数は単一のカテゴリに属するものではなく、指数関数的な値を持つこともあれば、無限に多くの種類の値をとりうることもあります。 例：音声/手書き文字の認識や自然言語翻訳の場合、出力は文法的に正しくなければならず、とりうる出力の数を制限することはできません。モデルが解くタスクは、問題の領域における逐次構造、空間構造、または組み合わせ構造を捉えることです。

構造化予測の初期の研究

モデルシステムの場合カテゴリを表すsoftmaxと比較することができる特徴ベクトルを与えるTDNNに、ベクトルが入力されます。発音された単語を認識する場合に問題となるのは、同じ単語でも人によって発音の仕方や速さが異なることです。これを解決するために、動的時間伸縮法（Dynamic Time Warping）が使用されます。

これは、誰かによって記録されたシーケンスまたは特徴ベクトルに対応する事前に記録されたテンプレートをシステムに提供するという考え方です。ニューラルネットワークはテンプレートと同時に訓練され、システムは異なる発音の単語を認識するように学習します。潜在変数により、テンプレートの長さに一致するように特徴ベクトルをタイムワープ（時系列の別の時刻に、該当する特徴ベクトルに対応するものを考えることができることを意味していると思われる）させることができます。

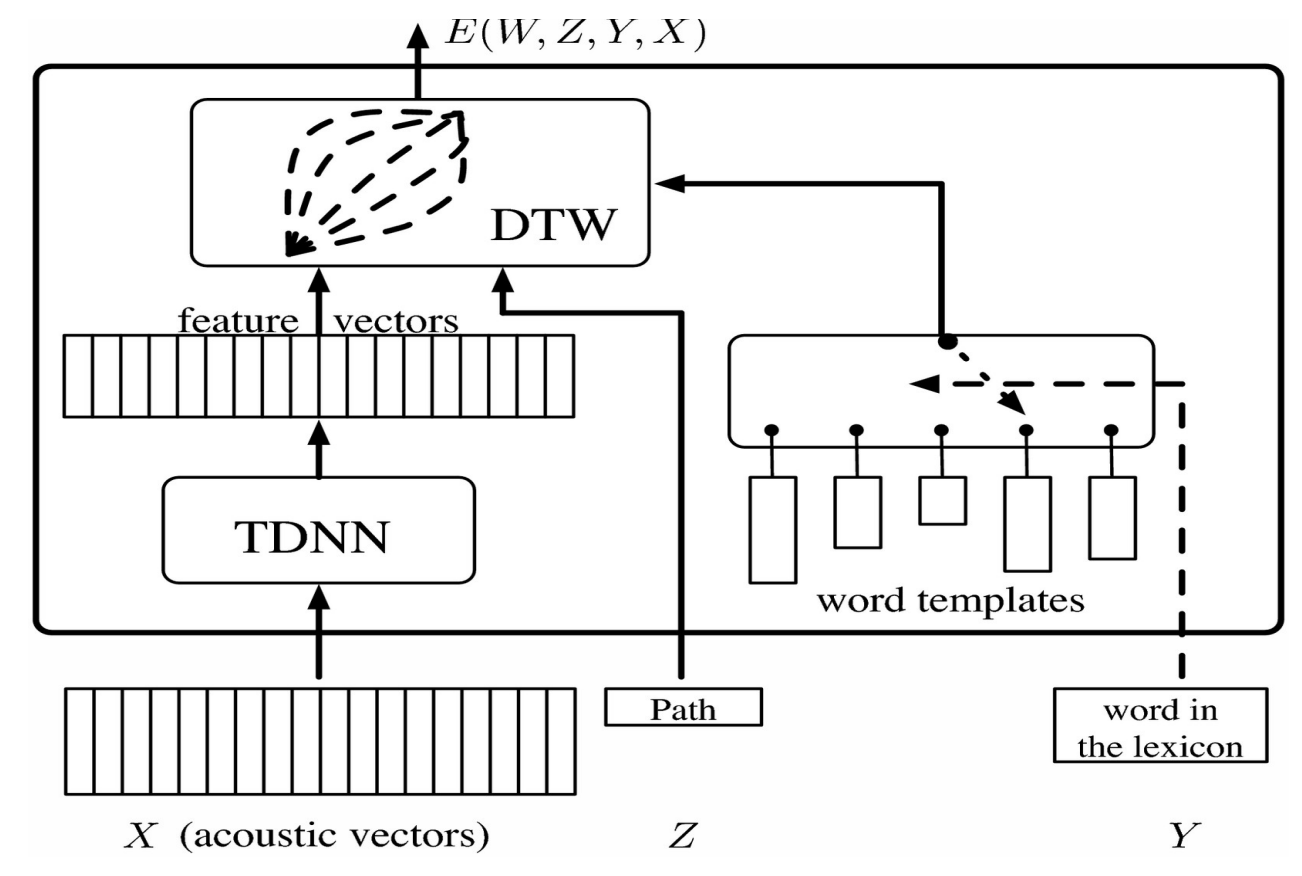
図1

これはTDNNの特徴ベクトルを水平方向に、単語テンプレートを垂直方向に並べることで、行列として可視化することができます。行列の各エントリーは特徴ベクトル間の距離に対応しています。これは、左下からスタートし、距離を最小にするパスを通って右上に到達することを目的としたグラフ問題として可視化することができます。

この潜在変数モデルを訓練するために、正解のエネルギーを可能な限り小さくしながら誤ったものに対してはエネルギーをより大きくする必要があります。これを行うために、入力された間違った単語のテンプレートを現在の特徴量の列から押しのける目的関数を用いて、勾配を逆伝播させます。

エネルギーベース因子グラフ

エネルギーベース因子グラフの背後にある考え方は、エネルギーが部分的なエネルギー項の和であったり、確率が因子の積である場合に、エネルギーベースモデルを構築することです。これらのモデルの利点は、効率的な推論アルゴリズムを採用できることです。

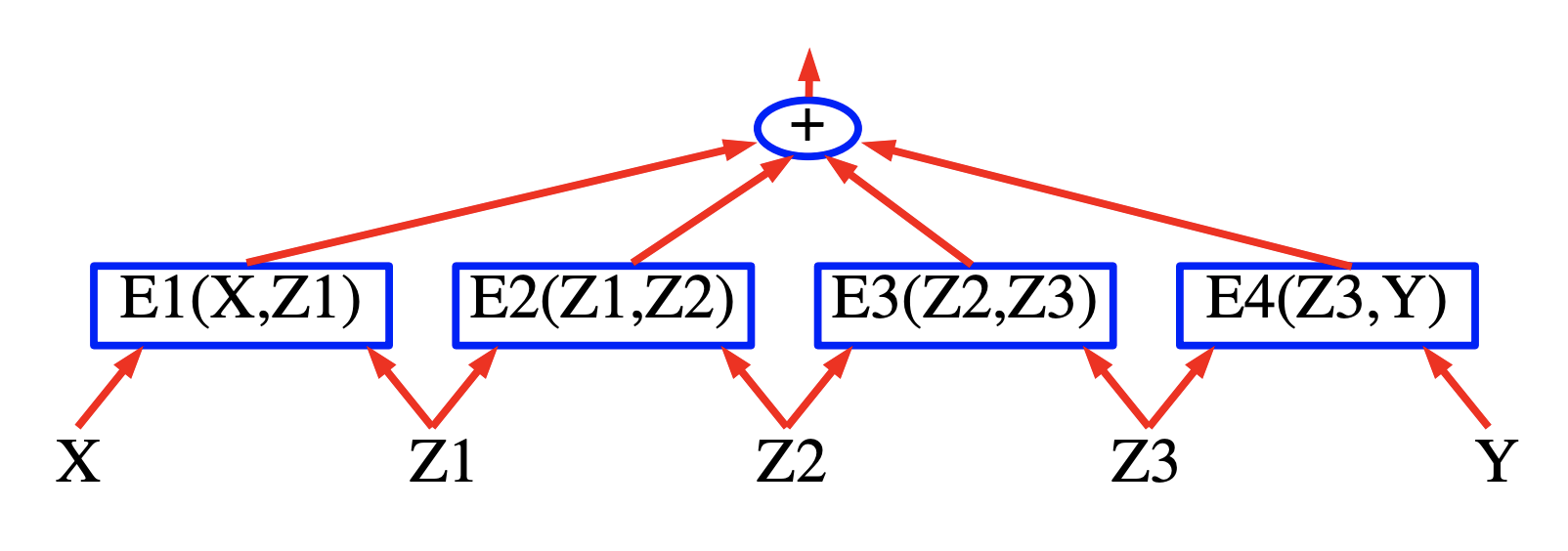
図2

シーケンスのラベル付け

このモデルは、入力音声信号Xを受けて、総エネルギー項を最小化するようなラベルYを出力します。

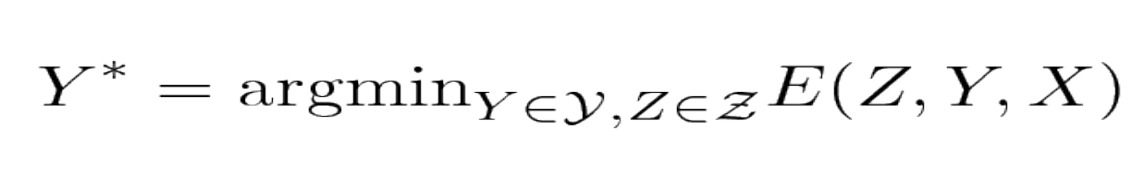
図3

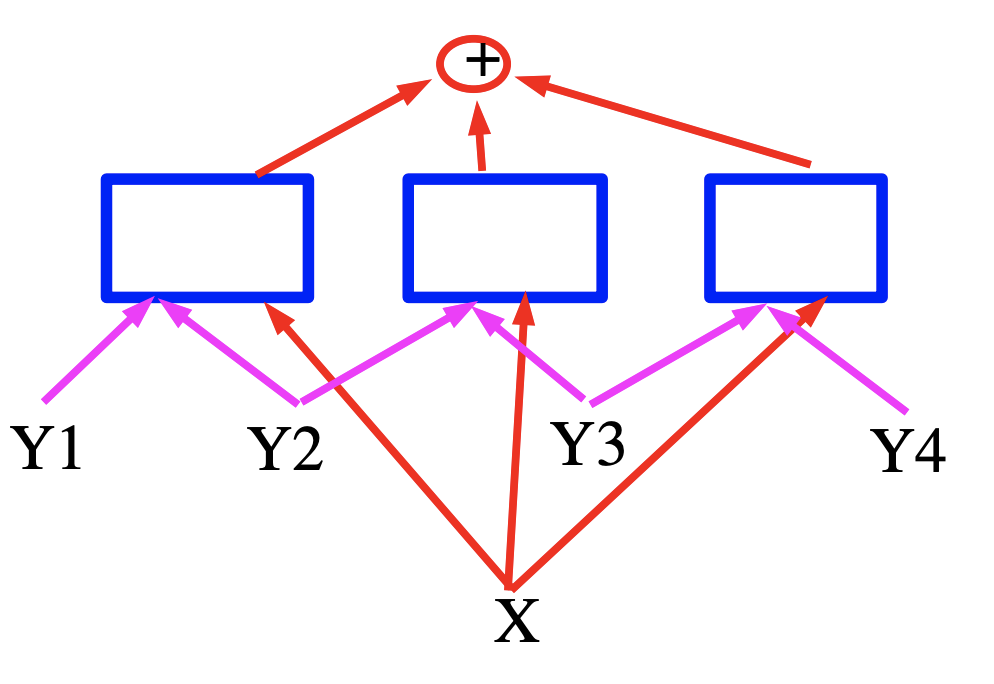
図4

この場合、エネルギーは、入力変数の特徴ベクトルを生成するニューラルネットワークである青い四角で表される３つの項の和です。音声認識の場合、Xは音声信号と考えることができ、四角は文法的制約を実装し、Yは生成された出力ラベルを表します。

エネルギーベース因子グラフの効率的な推論

A Tutorial on Energy-Based Learning (Yann LeCun, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, and Fu Jie Huang 2006):

エネルギーベースモデルを用いた学習と推論においては、答えの集合 $\mathcal{Y}$ と潜在変数 $\mathcal{Z}$ の上のエネルギーを最小化します。この最小化は、$\mathcal{Y}\times \mathcal{Z}$の濃度が大きい場合には、難解な問題となります。エネルギー関数の構造を利用して効率的に最小化を行うのがこれに対処する一つの方法です。この構造を利用できる1つのケースは、エネルギーがYとZの変数の異なる部分集合にそれぞれ依存する個々の関数（因子と呼ばれる）の和として表現できる場合です。これらの依存関係は因子グラフの形で最もよく表現することができます。因子グラフは、グラフィカルモデルまたは信念ネットワークの一般的な形式です。

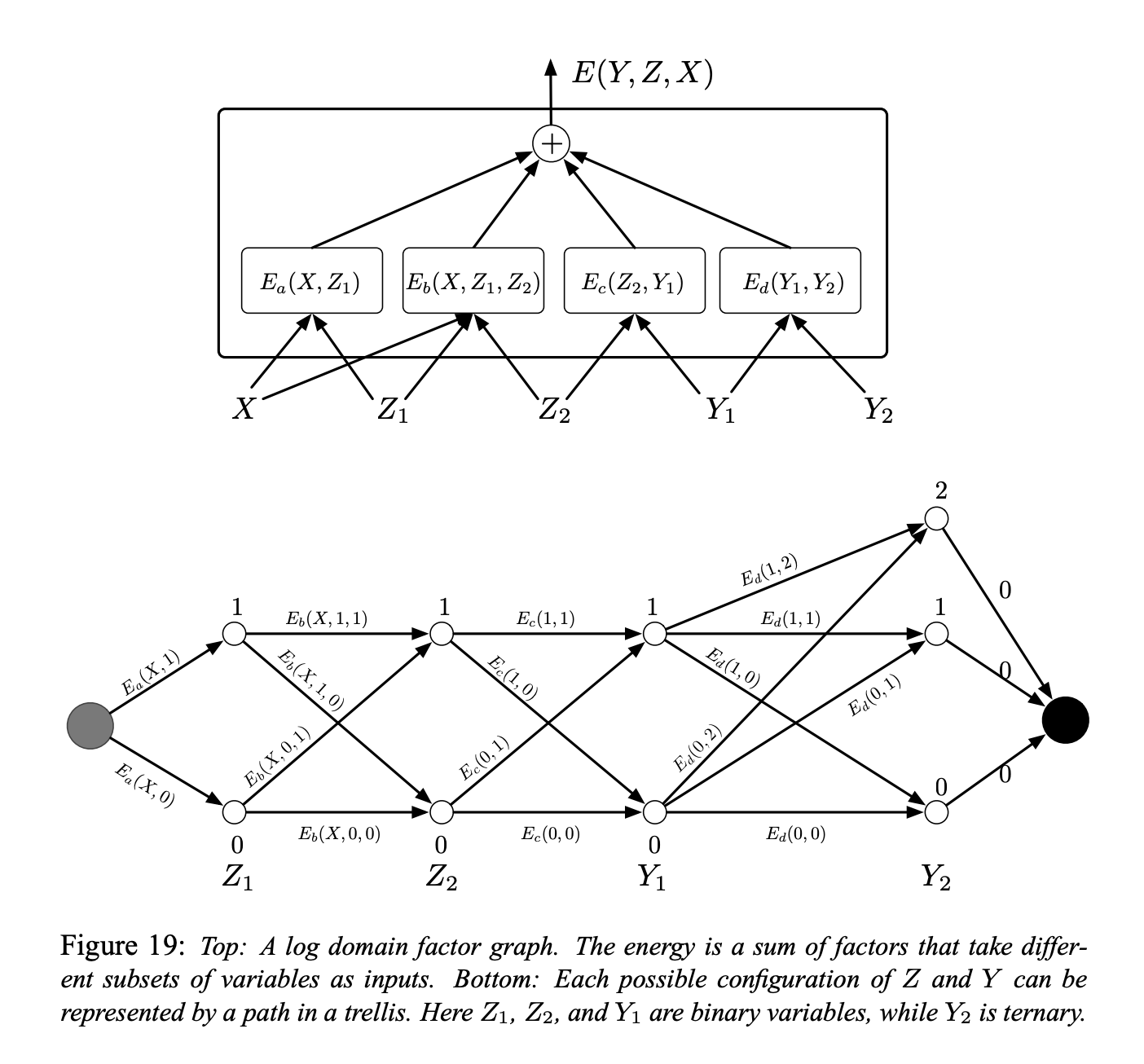
図5

因子グラフの簡単な例を図19（上）に示します。エネルギー関数は4つの因子の和です。

ここで、 $Y = [Y_1, Y_2]$ は出力変数であり、 $Z = [Z_1, Z_2]$ は潜在変数です。各因子は、入力変数の値の間のソフトな制約を表していると見ることができます。推論は、以下を見つけることで行われます。

ここで、 $Z_1$, $Z_2$, $Y_1$ が離散的な二項変数であり、 $Y_2$ が三値変数であるとします。X は常に観測されるので、 $X$ のドメインの濃度は重要ではありません。Xが与えられたときの $Z$ と $Y$ の可能な構成の数は、 $2 \times 2 \times 2 \times 3 = 24$ です。全状態探索による愚直な最小化アルゴリズムでは、エネルギー関数全体を24回評価することになります(96回の因子の評価)。

しかし、与えられた $X$ に対して、 $E_a$ は、 $Z_1 = 0$ と $Z_1 = 1$ の2つの入力の構成しかありえないことに気づきます。同様に、 $E_b$ と $E_c$ は4つの入力の構成しかなく、 $E_d$ は6つの入力の構成しかないことがわかります。したがって、$2 + 4 + 4 + 6 = 16$以上の単一の因子の評価は必要ありません。

したがって、図19(下)に示すように、16個の因子の値を事前に計算して格子の円弧上に置くことができます。

各列のノードは、1つの変数の可能な値を表します。各エッジは、その入力変数の対応する値に対する因子の出力エネルギーによって重み付けされます。この表現では、開始ノードから終了ノードまでの1本のパスが、すべての変数の1つの可能な構成を表します。パスに沿った重みの合計は、対応する構成の総エネルギーに等しくなります。したがって、推論問題は、このグラフ内の最短パスを探す問題に落とし込む事ができます。これは、ビタビアルゴリズムやA*アルゴリズムのような動的計画法を用いて行うことができます。コストは辺の数(16)に比例しますが，これは一般にパスの数よりも指数関数的に小さくなります。

$E(Y, X) = \min_{z\in Z} E(Y, z, X)$を計算するには、同じ手順に従いますが、グラフを、$Y$の所定の値と互換性のある円弧の部分集合に制限します。

上記の手順は、最小和アルゴリズムと呼ばれることもありますが、これは従来のグラフィカルモデルの最大積アルゴリズムの対数領域版です。この手順は、因子が2つ以上の変数を入力とする因子グラフや、連鎖構造ではなく木構造を持つ因子グラフに簡単に一般化できます。

しかし、これは、（ループのない）二部木の因子グラフにのみ適用されます。グラフにループが存在する場合、最小和アルゴリズムは、繰り返し適用する事で近似解を与えるかもしれないし、全く収束しないかもしれません。この場合、焼きなまし法のような降下アルゴリズムが使用されます。

「浅い」因子を持つ単純なエネルギベース因子グラフ

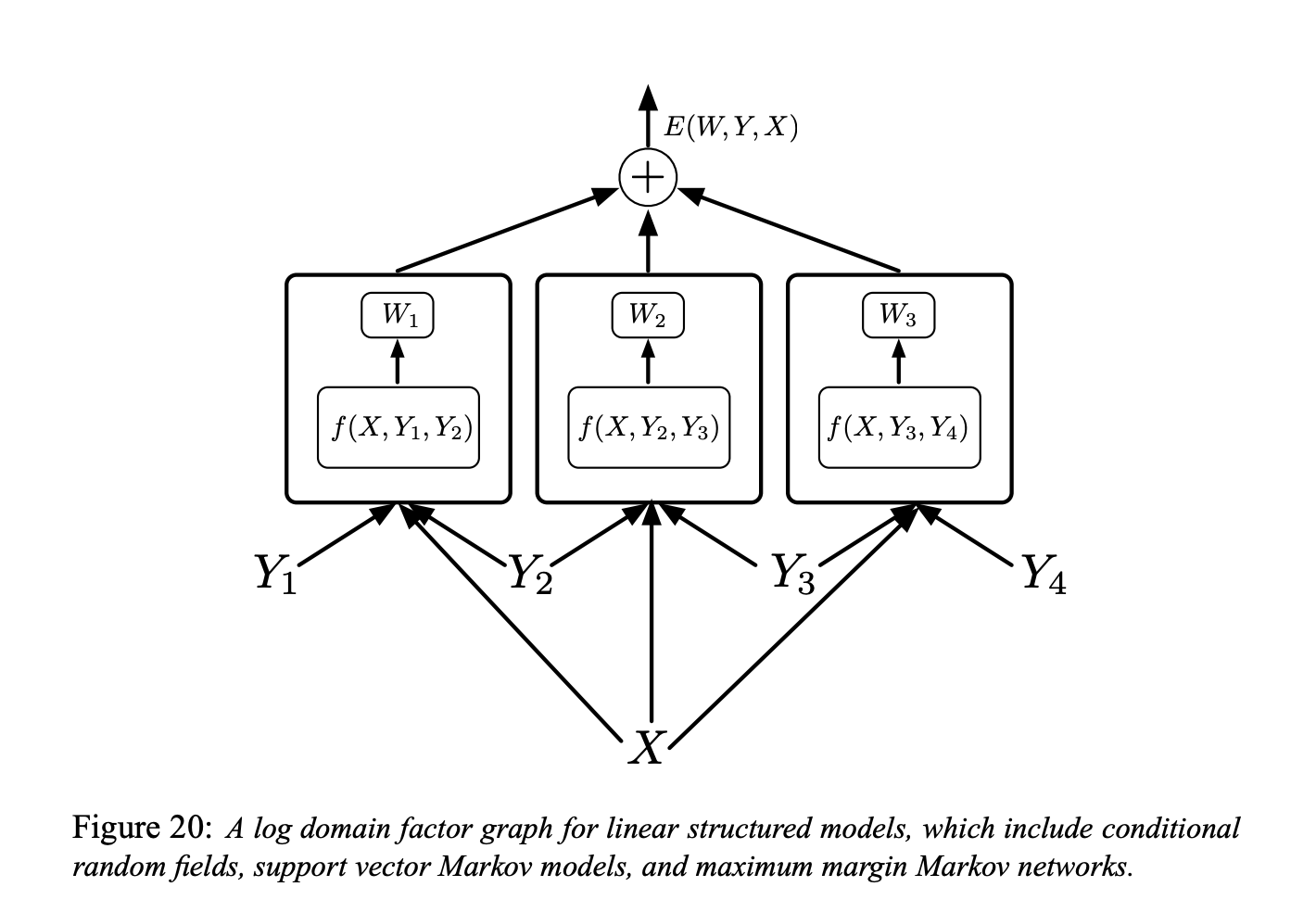
図6

図20に示す因子グラフは、線形構造化モデル（我々が話している「単純なエネルギーベース因子グラフ」）の対数領域の因子グラフです。

各因子は、訓練可能なパラメータの線形関数です。それは、入力とラベルのペア $(Y_m, Y_n)$ に依存します。一般的に、各因子は2つ以上のラベルに依存し得ますが、表記を簡単にするために2つで1組の因子に限定します。

ここで、$\mathcal{F}$は因子の集合（直接的な相互の依存性を持つ個々のラベルの組の集合）を表し、$W_{m n}$は因子$(m, n),$のパラメータベクトルであり、$f_{m n} \left(X, Y_{m}, Y_{n}\right)$は（固定された）特徴ベクトルです。グローバルパラメータベクトル $W$ は、すべての $W_{m n}$ を連結したものです。

そして、どのようなタイプの損失関数があるかを考えます。ここで、いくつかのモデルが出てきます。

条件付きランダム場

線形構造化モデルを訓練するために負の対数尤度損失関数を使うことができます。

これが、条件付きランダム場です。

直感的には、正解のエネルギーを以下のようにして、正解を含むすべての解の指数の対数を大きくしたいということです。

以下に負の対数尤度損失関数の正式な定義を示します。

最大マージンマルコフネットと潜在SVM

また、最適化のためにヒンジ損失関数を使用することもできます。

その背後にある直感は、正解のエネルギーを低くして、そして全ての間違った答えやよくない答えの構成の中で、最もエネルギーが低いものを探すというものです。そして、答えのエネルギーを押し上げていきます。他の悪い解答のエネルギーを押し上げる必要はありません。

これが最大マージンマルコフネットと潜在SVMです。

構造化パーセプトロンモデル

線形構造化モデルはパーセプトロン損失を用いて学習することができます。

Collins [Collins, 2000, Collins, 2002]は、NLPの文脈で線形構造化モデルに使用することを提唱しています。

ただし $Y^{* i}=\operatorname{argmin}_{y \in \mathcal{Y}}$で、$E\left(W, y, X^{i}\right)$ はシステムの出力した答えです。

音声・手書き文字識別のための訓練の初期段階の軌跡

最小経験誤差関数 (Ljolje, and Rabiner 1990):

シーケンスレベルで学習することで、この音やあの場所をシステムに教えるのではなく、入力文と単語の書き起こしを与え、タイムワープをしてシステムに理解するように求めます。彼らは二ューラルネットを使用しておらず、別の方法で音声信号を音声のカテゴリに変換しています。

Graph Transformer Net

ここでの問題は、入力に数字の列があるがセグメンテーションの方法がわからないということです。そこでできることは、各パスが文字列を分割する方法となるようなグラフを構築することです。これがどのように機能するのか、具体的な例を示します。

入力画像34があるとします。これをセグメンテーションツールでセグメント分けすると、複数の代替的なセグメンテーションが得られます。これらのセグメンテーションは、これらをグループ化する方法です。セグメンテーショングラフの各パスは、インクの塊をグループ化する特定の方法に対応しています。

図7

それぞれを同じ文字識別畳み込みニューラルネットで実行し、10 点のスコアのリストを得ます（ここでは 2 点ですが、本質的には 10 のカテゴリを表す 10 点でなければなりません）。例えば、1 [0.1]はカテゴリ1のエネルギーが0.1であることを意味します。このようにしてグラフが得られますが、これは少し変わったテンソルだと考えることができます。これは実際には疎なテンソルです。これはこの変数の可能な各構成について、その変数のコストが何かを教えるように要求するテンソルです。エネルギーの話をしているので、テンソルの分布というよりも、対数分布のようなものです。

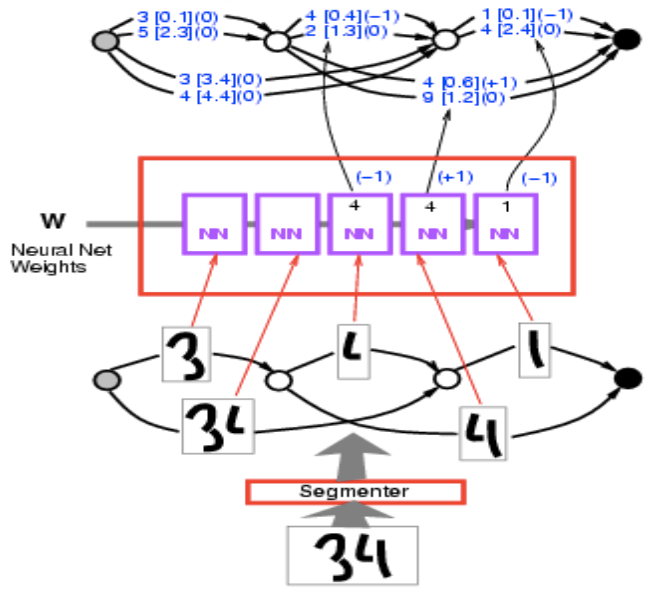
図8

このグラフを見て 正解のエネルギーを計算してみましょう 正解は34です。それらのパスの中から選んで、34と書いてあるものを見つけてください。 それら2つのうち1つはエネルギーが3.4 + 2.4 = 5.8で、もう一つは、0.1 + 0.6 = 0.7です。エネルギーが最も低いものを選びます。ここでは、エネルギーが0.7のパスが出てきます。

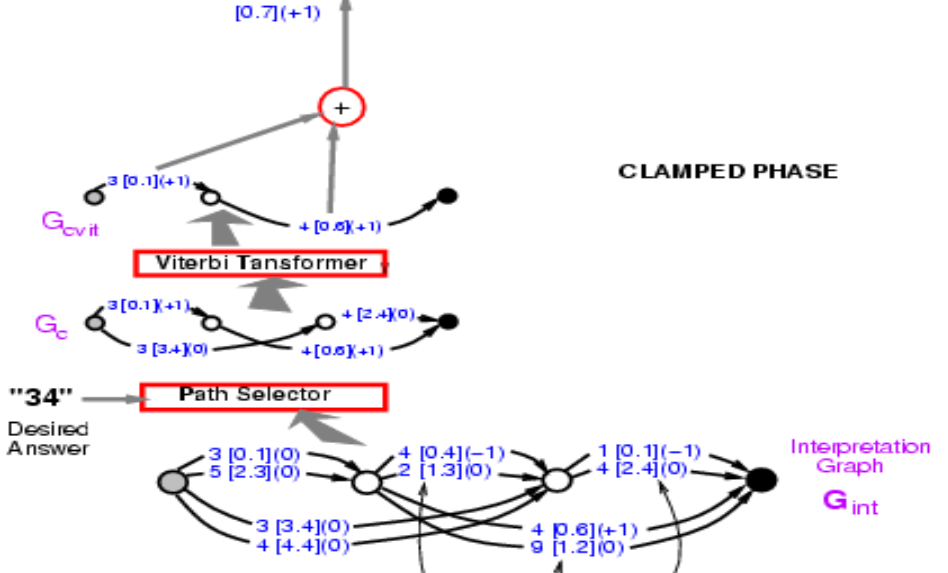
図9

したがって、パスを見つけることは、どのパスを選ぶかを表す潜在変数について最小化するようなものです。概念的には、潜在変数をパスとするエネルギーモデルです。

これで、正しいパスのエネルギーは0.7になりました。ここで必要なのは、最終的なエネルギーが下がるように畳み込みニューラルネットの重みを変えることができるようにこの構造全体を通して勾配を逆伝播することです。難しそうに見えますが、完全に可能です。このシステム全体は既に知っている要素で構築されているので、二ューラルネットは通常通りで、パス選択器とビタビ変換器は基本的に特定のエッジを選ぶかどうかのスイッチです。

では、どうやって逆伝播するのでしょうか。点0.7は0.1と0.6の和です。つまり、点0.1と0.6の両方が勾配+1を持っています。これはブラケットで表現します。すると、ビタビ変換器は2つのパスのうち1つのパスを選択します。なので、入力グラフの対応する辺の勾配をコピーして、選択されていない他のパスの勾配を0に設定するだけです。これはMax-PoolingやMean-Poolingで行っていることと全く同じです。パスを選択するものも同じで、正解を選択するシステムになっているだけです。グラフの3 [0.1] (0)はこの段階では3 [0.1] (1)であるべきで、あとで後者に戻ってくることに注意してください。これで正解のエネルギーが小さくなります。

ここで重要なのは、新しい入力を入れると二ューラルネットのインスタンスの数がセグメンテーションの数と一緒に変化して、導出されたグラフも同様に変化するという意味で、この構造が動的であるということです。この動的な構造で誤差逆伝播をする必要があります。これがPyTorchのようなものが非常に重要になるところです。

この誤差逆伝播の段階は、正解のエネルギーを小さくしてくれます。そして、不正解のエネルギーを大きくするという段階もあります。この場合、システムに好きな答えを選ばせます。これは、知覚損失を利用した構造予測のための識別訓練の簡略化された形になりそうです。

二つ目の段階のはじめは、最初の段階と全く同じです。ここでのビタビ変換器は、エネルギーが最も低い最良のパスを選ぶだけで、そのパスが正しいパスかどうかは気にしません。ここで得られるエネルギーは、可能なすべてのパスの中で最も小さいので、第一段階から得られるエネルギーと同じか、それより小さくなるでしょう。

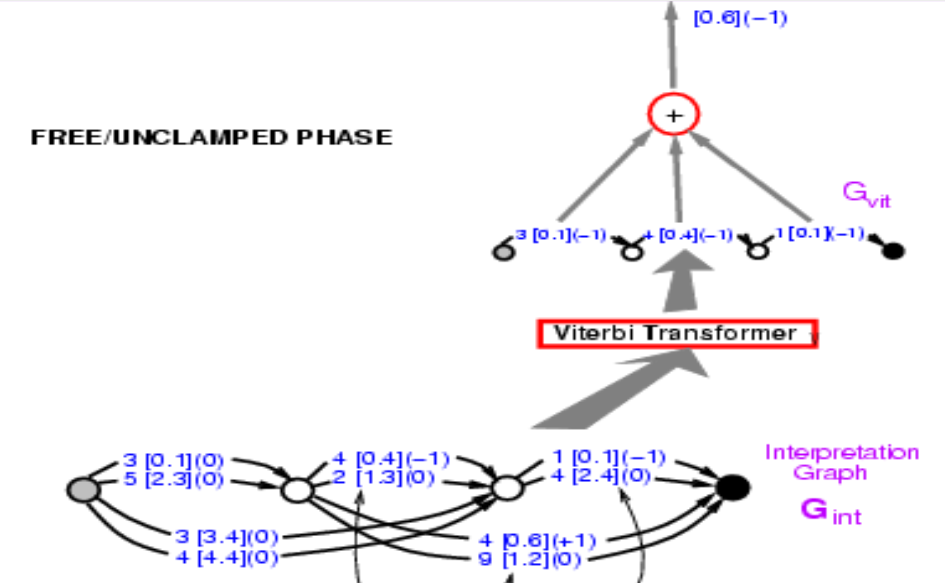
図10

段階1と2を一緒にします。損失関数は energy1 - energy2 とします。 前回は左の部分を逆伝播する方法を紹介しましたが、今回は構造全体を逆伝播する必要があります。左側のパスは+1、右側のパスは-1となり、両方のパスに3 [0.1]が出現するので、勾配は0となります。 このようにすれば、システムは最終的に、正解のエネルギーと最良解のエネルギーの差を最小化することになります。ここでの損失関数は知覚損失です。

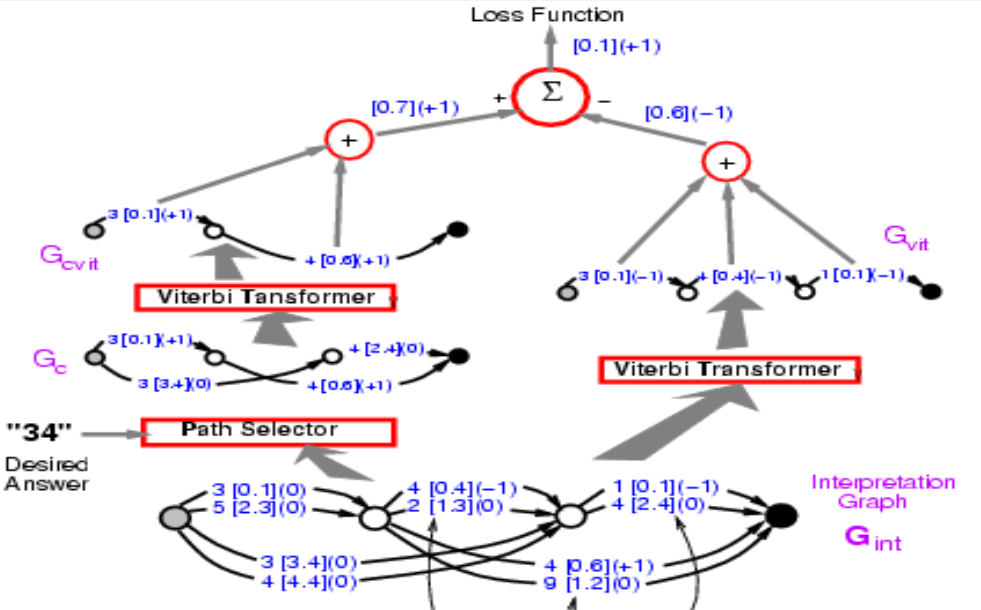
図11

質問と回答

質問1: なぜエネルギーベース因子グラフにおいて推論が簡単になるのですか？

潜在変数を持つエネルギーベースのモデルの場合の推論では、エネルギーを最小化するために勾配降下法のような全探索的な手法を使用しますが、この場合のエネルギーは因子の総和であるため、動的計画法のような手法を代わりに使用することができます。

質問2: 因子グラフの潜在変数が連続変数だったらどうなるのですか？まだ和を最小化するアルゴリズムを使えるのですか？

できません。すべての因子値に対して可能なすべての組み合わせを検索することができないからです。しかし、この場合でも、独立した最適化を行うことができるという利点があります。図19の$Z_1$と$Z_2$の組み合わせは、$E_b$にしか影響しないようなものです。独立した最適化と動的計画法で推論を行うことができます。

質問3: 図中のNNの箱は別々の畳み込みニューラルネットを表しているのですか?

共有されています。同じ畳み込みニューラルネットの複数のコピーです。ただの文字識別ネットワークです。