Graph Convolutional Networks (GCNs) - An Insight

スペクトルグラフ畳み込みニューラルネット (GCNs)

前のセクションでは、グラフの畳み込みを定義する2つの方法のうちの1つであるグラフスペクトル理論について説明しました。

通常のスペクトルGCN

グラフスペクトル畳み込み層を定義し、 $h^l$ が与えられた層の活性が次のようになるようにします：

ここで、$\eta$は非線形活性化関数、$w^l$は空間フィルタです。方程式の右辺は、$\eta(\hat{w}^l(\Delta)h^l)$と等しく、$\hat{w}^l$はスペクトルフィルタ、$\Delta$ はラプラシアンです。方程式の右辺をさらに分解すると、$\eta(\boldsymbol{\phi} \hat{w}^l(\Lambda)\boldsymbol{\phi^\top} h^l)$となります。ここで、$\boldsymbol{\phi}$ はフーリエ行列、$\Lambda$ は固有値です。これで、最終的な活性方程式は以下のようになります。

目的は、フィルタを作り込む代わりに誤差逆伝播を使ってスペクトルフィルタ$\hat{w}^l(\lambda)$を学習することです。

この手法は畳み込みニューラルネットで使われた最初のスペクトル手法ですが、いくつかの限界があります。

• フィルタの空間的な位置を保証するものではありません。
• 各層$O(n)$個のパラメータを学習する必要があります(($\hat{w}(\lambda_1)$ to $\hat{w}(\lambda_n)$)。
• $\boldsymbol{\phi}$ は密な行列なので、 学習率は$O(n^2)$です。

スプラインGCN

スプラインGCNは、局所的な空間フィルタを得るために、滑らかなスペクトルフィルタを計算します。周波数領域の滑らかさと空間位置の関係は、パーセバルの等式（ハイゼンベルグの不確かさの原理）に基づいています：スペクトルフィルタの微分が小さいほど（より滑らかな関数ほど）、空間フィルタの分散が小さくなります（位置の揺らぎが小さくなる）。

滑らかなスペクトルフィルタを得るにはどうしたらいいでしょうか？スペクトルフィルタを、$K$個の滑らかなカーネル$\boldsymbol{B}$ (スプライン)の線形結合に分解して、$\hat{w}^l(\Lambda)=diag(\boldsymbol{B}w^l)$となるようにします。活性方程式は次のようになります。

バックプロパゲーションで学習するパラメータは、層ごとに $O(1)$（定数 $K$）しかありません。しかし、計算量はやはり $O(n^2)$ です

LapGCNs

線形時間 $O(n)$ (グラフサイズ $n$) で学習するにはどうすればよいのでしょうか？$O(n^2)$の計算は、ラプラシアンの固有ベクトルを使うことによる直接的な結果です。固有分解を避ける必要がありますが、これはラプラシアンの関数を直接学習することで実現できます。スペクトル関数は、ここに示すように、ラプラシアンの単項式になります。

1つの良い特徴は、フィルターがまさにkごとのサポートに局在していることです。

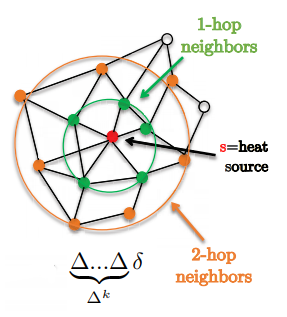
図1: 1-hop と 2-hop の近傍の表示

式 $\Delta^kh$ を $X_k$ に置き換えます。再帰的式は次のように定義されます

計算量は、スパースな(実世界の)グラフの場合、 $O(E.K)=O(n)$になりました。$X_k$ を $\bar{X}$ に再整形して、線形演算にすることができます。これで、次のような活性方程式ができました。

注：ラプラシアン固有分解が使用されていないため、すべての演算は空間領域（スペクトル領域ではない）にあるので、Spectral GCNと呼ぶのは間違っているかもしれません。さらに、LapGCNのもう一つの欠点は、畳み込み層にはスパースな線形演算が含まれており、GPUが完全に最適化されていないことです。

我々は、局所化されたフィルタ（$K$ホップサポート）、層ごとの$O(1)$個のパラメータ、$O(n)$だけの計算量の学習によって、通常のGCNの3つの限界を解決しました。しかし、LapGCNの限界は、単項基底($\Delta^0,\Delta^1,\ldots$)を使うことで、直交しなくなる(1つの係数を変えると関数の近似が変わる)ため、最適化が不安定になることです。

ChebNets

不安定な基底の問題を解決するために、我々は、任意の正規直交基底を使用することができますが、それは計算量が線形であることを保証するために再帰的な方程式を持っている必要があります。ChebNetsでは、チェビシェフ多項式を使用し、LapGCNのように$T_k(\Delta)h$ ($h$に適用されるチェビシェフ関数)を$X_k$で表現し、再帰方程式を定義します。

これで、係数に摂動が与えられた下での安定性が得られました。

ChebNetsは、任意のグラフ領域に使用できるGCNですが、等方的であるという制限があります。ユークリッドグリッドには方向があるので、標準的な畳み込みニューラルネットは、異方性のフィルタを生成しますが、スペクトルGCNは、グラフには方向（上下、左、右）の概念がないので、等方性のフィルタを計算します。

ChebNetsを2次元スペクトルフィルタを使って複数のグラフに拡張することができます。これは、例えば、映画のグラフやユーザーのグラフがある推薦システムなどで有用です。複数グラフのChebNetsは、以下のような活性式を持ちます。

CayleyNets

ChebNetsは、関心のある周波数帯（グラフコミュニティ）を持つフィルタを生成する（局所化する）ためには不安定です。CayleyNetsでは、代わりに、正規直交基底を用いたケイリー変換を用いています。

CayleyNetsは、ChebNetsと同じ性質を持っています（等方性です）が、周波数が局在しており（スペクトルズームがあります）、より豊富なクラスのフィルタを提供します（同じ次数$K$に対して）。

空間的グラフ畳み込みニューラルネットワーク

テンプレートマッチング

空間的グラフ畳み込みニューラルネットを理解するために、畳み込みニューラルネットのテンプレートマッチングの定義に戻ります。

グラフのテンプレートマッチングを行う際に問題となるのは、テンプレートにノードの順序や位置がないことです。ノードのインデックスしかなく、ノード間の情報をマッチングさせるには十分ではありません。どのようにしてテンプレートマッチングを設計すれば、ノードのリパラメトライゼーションに対して不変になるのでしょうか？つまり、あるグラフがあってそのノードの1つが任意のインデックス（例えば6）を持っていた場合、このインデックスは122となっていた可能性もあります。ですから、ノードのインデックスに依存しないテンプレートマッチングを実行できることが不可欠です。

これを行う最も簡単な方法は、 $w_{j1}$,$w_{j2}$, $w_{j3}$ などのテンプレートベクトルを持つのではなく、 $w^l$ だけを持つことです。そして、このベクトル $w^l$ を、グラフ上の他のすべての特徴と一致させます。今日のほとんどのグラフニューラルネットワークは、この性質を利用しています。

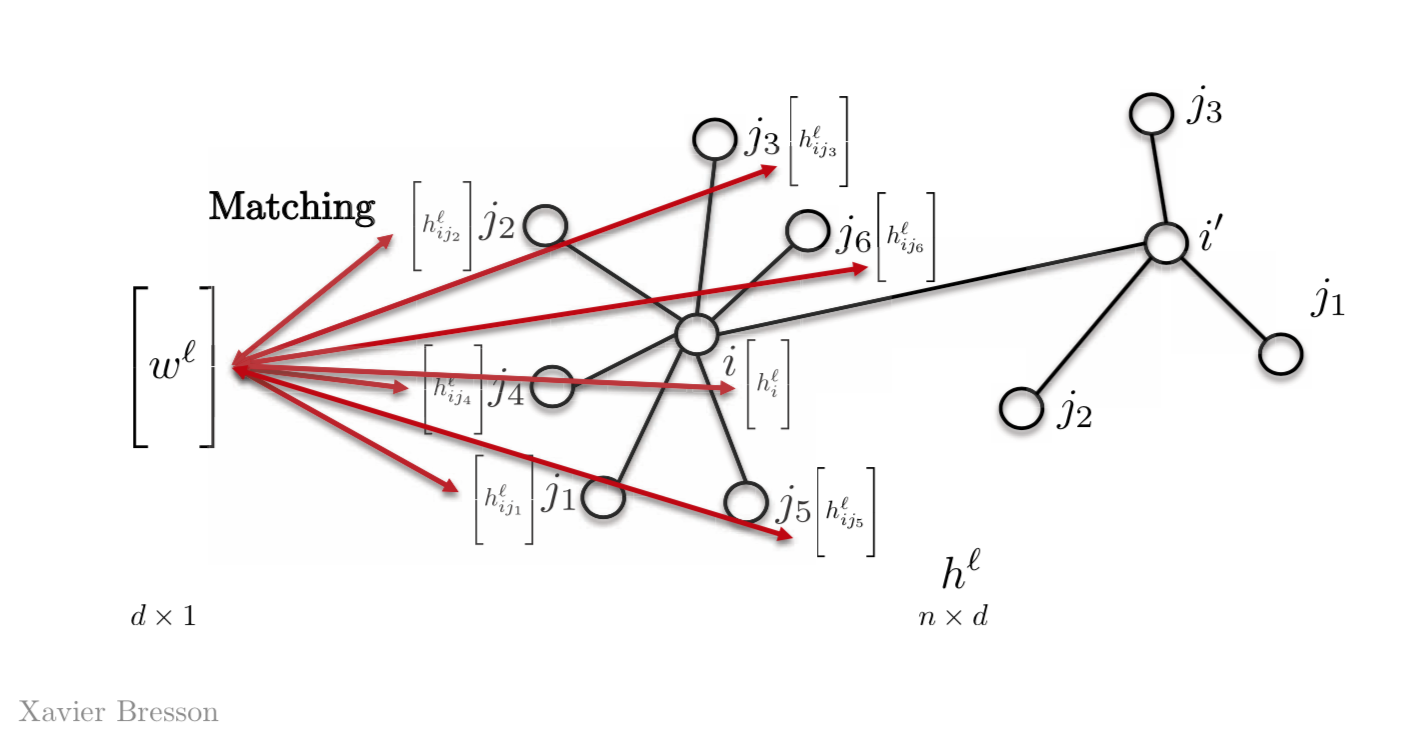
図2: テンプレートベクトルを用いたテンプレートマッチング

数学的には、一つの特徴に対して、以下を得ることになります。

ただし$w^l$は$l$層目の$d \times 1$次元のテンプレートベクトルで、$h_{ij}^l$はノード$j$の$d \times 1$次元ベクトルで、これは$i$番目のノードについてスカラー値$h_{i}^{l+1}$を返します。

より多くの($d$の)特徴量については、以下のようになります。

\(h_{i}^{l+1}=\eta\bigg(\sum_{j \in N_{i}} \boldsymbol{W}^l,h_{ij}^l\bigg)\) <!– where, $\boldsymbol{W}^l$ is of the dimensionality $d \times d$ and $h_{i}^{l+1}$ is $d \times 1$

for a vectoral representation,

where, $\boldsymbol{A}$ is the adjacency matrix of dimensions $n \times n$, $h^l$ is the activation function at the layer $l$ with dimensions $n \times d$.

Based on this definition of Template Matching we can define two types of Spatial GSNs – Isotropic GCNs and Anisotropic GCNs. –>

ここで、$\boldsymbol{W}^l$ は、次元数 $d \times d$ であり、$h_{i}^{l+1}$ は、あるベクトル表現

に対して、次元数$d \times 1$ です。ここで、$\boldsymbol{A}$は次元数$n \times n$の隣接行列であり、$h^l$は次元数$n \times d$の$l$層目の活性化関数です。

このテンプレートマッチングの定義に基づいて、等方的グラフ畳み込みニューラルネットと異方的グラフ畳み込みニューラルネットの２種類の空間的グラフ畳み込みニューラルネットが定義できます。

等方的グラフ畳み込みニューラルネット

通常の空間的グラフ畳み込みニューラルネット

これは前と同じ定義ですが、式の中に対角行列を加えて、近傍の平均値を求めるようにしています。

すると、行列表現は次のようになります

ここで、$\boldsymbol{A}$の次元は、$n \times n$、$h^{l}$の次元は、$n \times d$ 、$W^{l}$の次元は、$d \times d$となり、$n \times d$次元の行列$h^{l+1}$となります。

そして、ベクトル表現は次のようになります

ここで、$h_{i}^{l+1}$は、$d \times 1$次元です。

ベクトル表現は、ノードのリパラメトライゼーションの際に不変である、ノードの順序がない場合の処理を担当しています。つまり、前の例に加えて、もしノードが6であり、これが122 に変更された場合、次の層の$h^{l+1}$ での活性化関数の計算では何も変わりません。

異なる大きさの近傍を扱うこともできます。つまり、4ノードでも10ノードでも何も変わらないということです。

その構成からして局所的受容野が与えられているということになります。つまり、グラフニューラルネットワークでは、近傍を考慮するだけでよいのです。

重みを共有しているので、グラフの位置に関係なく、すべての特徴表現に対して同じ行列$\boldsymbol{W}^{l}$が得られます。これは畳み込み演算の性質です。

すべての演算が局所的に行われるので、この定式化はグラフの大きさにも依存しません。

これは等方的なモデルなので、隣り合う行列は同じ 行列$\boldsymbol{W}^{l}$を持つことになります。

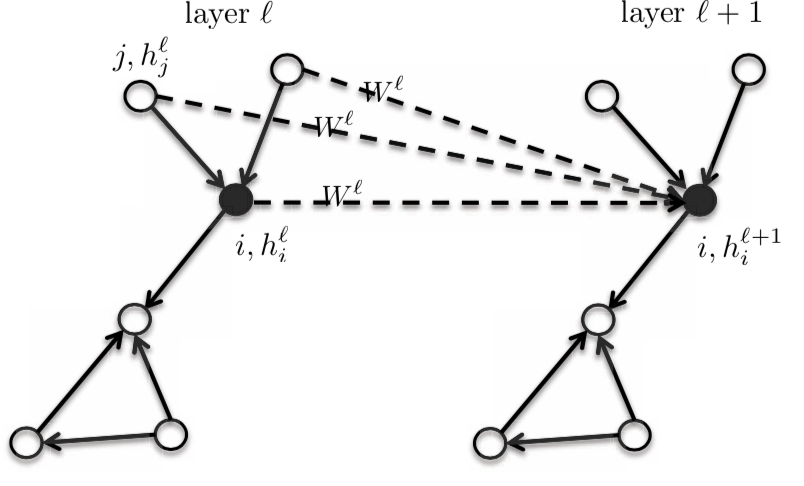
図3: 等方的なモデル

つまり、ノード $i$ と その近傍においては、次の層の活性 $h_{i}^{l+1}$ は、前の層の活性 $h_{i}^{l}$ を引数にとる関数となります。この関数を変えると、グラフの族全体ができあがります。

ChebNetsと通常の空間的グラフ畳み込みニューラルネット

上で定義した通常の空間的グラフ畳み込みニューラルネットは、ChebNetsの単純化です。最初の2つのチェビシェフ関数を使ってChebNetの展開された部分を切り捨てることで、次のようになります

GraphSage

通常の空間的グラフ畳み込みニューラルネットのエッジに対して隣接行列を$\boldsymbol{A}_{ij} = 1$とすると、次のようになります

この方程式では、中心の頂点 $i$ とその近傍に同じテンプレートウェイト $\boldsymbol{W}^{l}$ を与えます。中心点を$\boldsymbol{W}{1}^{l}$とし、one-hot近傍には別のテンプレートノード$\boldsymbol{W}{2}^{l}$を与えることで、これを区別することができます。これにより、GNNの性能はかなり改善されます。このモデルは、近傍が同じ重みを持っているため、本質的にはまだ等方的であると考えられます。

ここで、$\boldsymbol{W}{1}^{l}$と$\boldsymbol{W}{2}^{l}$ は$d \times d$次元です。そして、$h_{i}^{l}$と$h_{j}^{l}$は$d \times 1$次元です。

この方程式では、$\boldsymbol{W}{2}^{l} h{j}^{l}$や$h_{j}^{l}$の長期短期記憶の平均ではなく、その和や最大値をとる操作を行っています

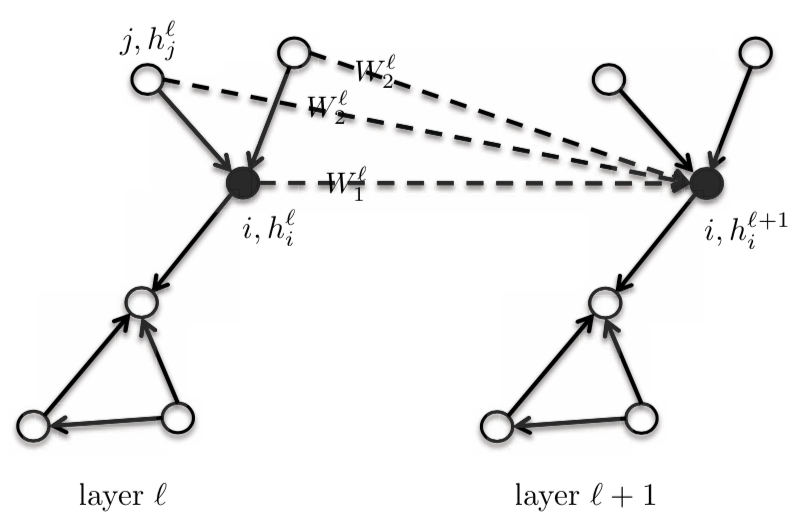
図4: GraphSage

Graph Isomorphism Network (GIN)

Graph Isomorphism Networkは、同型ではないグラフを区別できるアーキテクチャです。同型性とは、グラフ間の等価性を表す尺度です。下の図では、2つのグラフが互いに同型であると考えられています。同型なグラフは同じように扱われ、同型でないグラフは異なるように扱われます。

GINは等方的なグラフ畳み込みニューラルネットです。

ここで、$\texttt{BN}$はバッチ正規化を表しています。

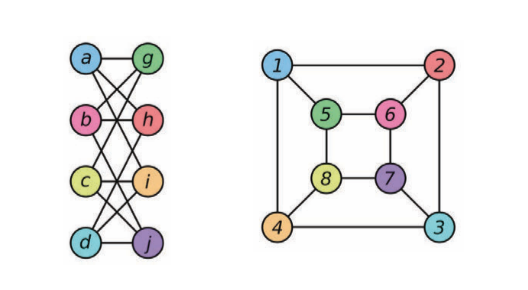
図5: 二つの同型グラフの例

等方的でないグラフ畳み込みニューラルネット

標準的な畳み込みニューラルネットは、異方性フィルター、すなわち、特定の方向を好むフィルターを生成する能力を持っています。これは、方向の構造が上下左右に基づいているからです。しかし、上述のグラフ畳み込みニューラルネットは方向の概念を持たないため、等方性フィルタしか生成できません。異方性は、エッジの特徴を利用して自然に導入することができます。例えば、分子は一重結合、二重結合、三重結合を持つことができます。グラフ的には、異なる近傍ごとに異なる重み付けを導入します。

MoNet

MoNetは、混合ガウスモデル（GMM）のパラメータを学習するためにグラフの次数を使用します。

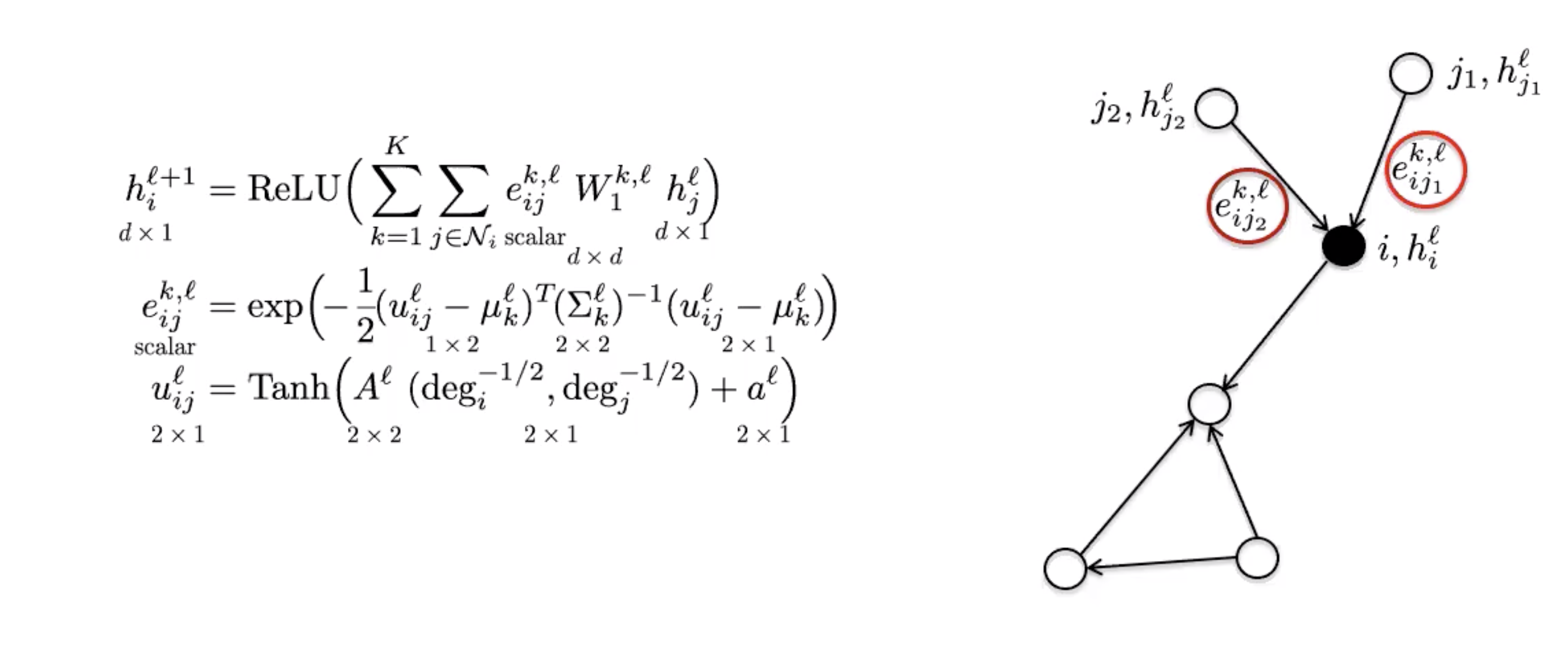
図6: MoNet

Graph Attention Network (GAT)

GATはattention機構を使用することで、近傍を集約する関数に異方性を導入します。

図7: GAT

Gated Graph ConvNet

これは単純なエッジのゲーティング機構を使用しており、GATで使用されているスパースなattention機構のように、よりソフトなattention機構と見ることができます。

図8: Gated Graph ConvNet

Graph Transformer

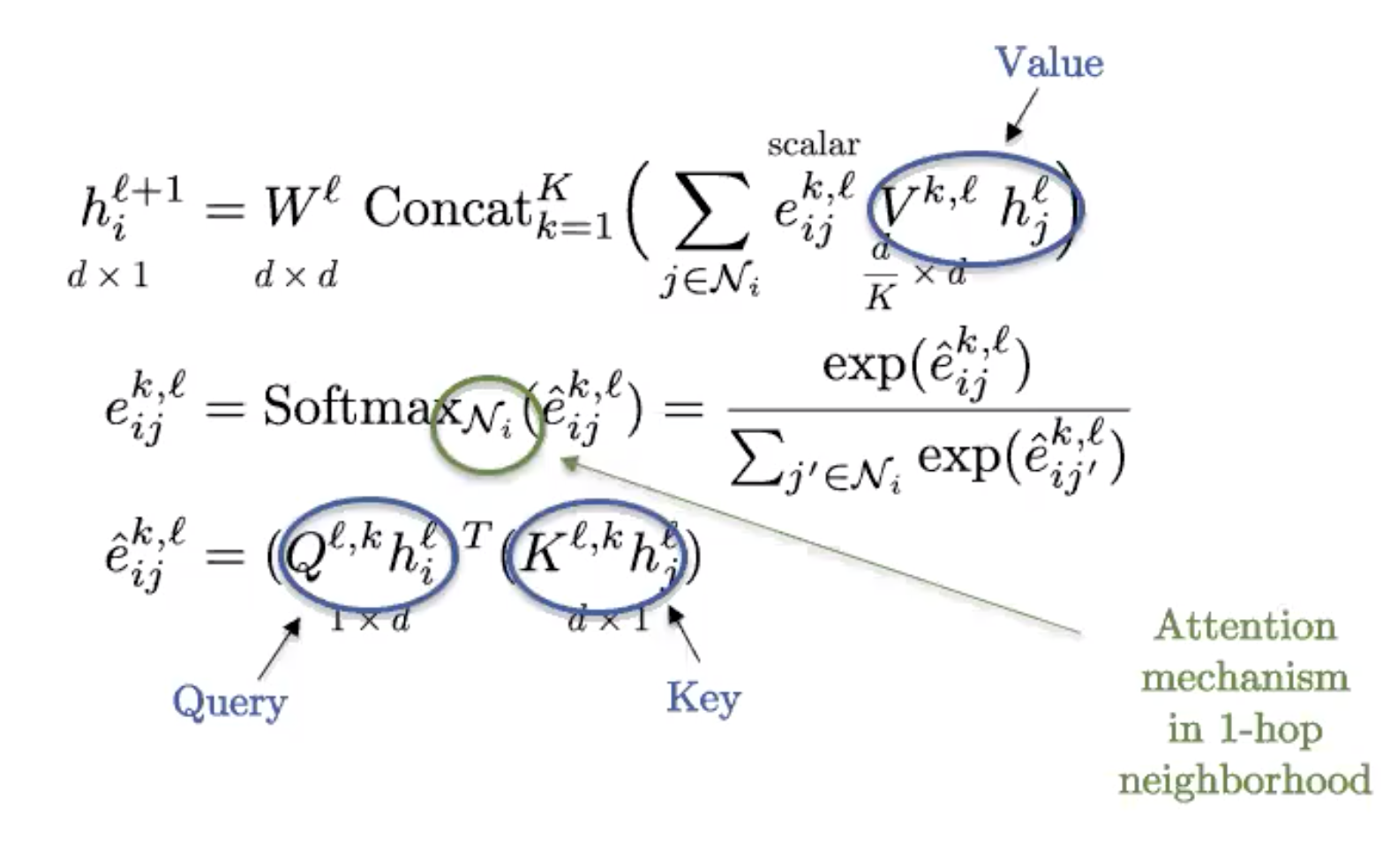
図9: Graph Transformer

これはNLPでよく使われる標準的なtransformerのグラフ版です。グラフが全結合している（2つのノードがすべて1つの辺を共有している）場合、標準的なtransformerと同じになります。

グラフは、スパース性によってその構造が決まるので、全結合しているグラフの持つ構造は些細なものであり、本質的には単なる集合と変わりません。Transformerは、集合ニューラルネットワークとして見ることができ、実際には、現在のところ、特徴の集合を分析するのに最適な技術です。

GNNのベンチマーク

ベンチマークは、どのような分野でも進歩に欠かせないものです。最近リリースされたベンチマークBenchmarking Graph Neural Networksでは、グラフ分類、グラフ回帰、ノード分類、エッジ分類という4つの基本的なグラフ問題に使用できる6つの中規模データセットが提案されています。これらのデータセットは中規模ではありますが、様々なGNNの傾向を統計的に分離するには十分な大きさです。

グラフ回帰の例として、分子の溶解度を予測したいとします。

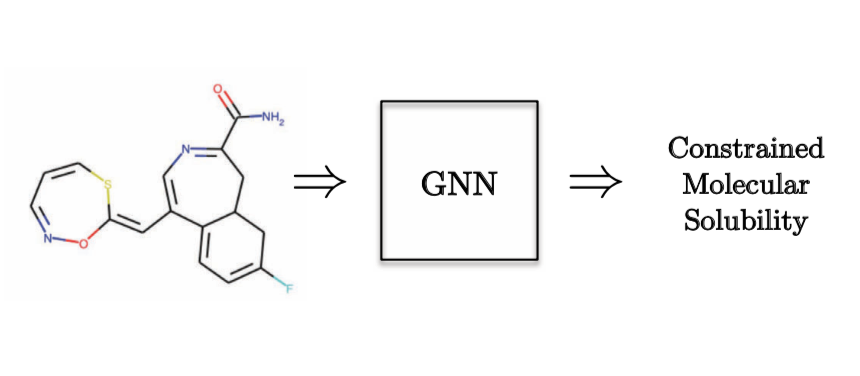
図10: グラフ回帰タスク：量子化学

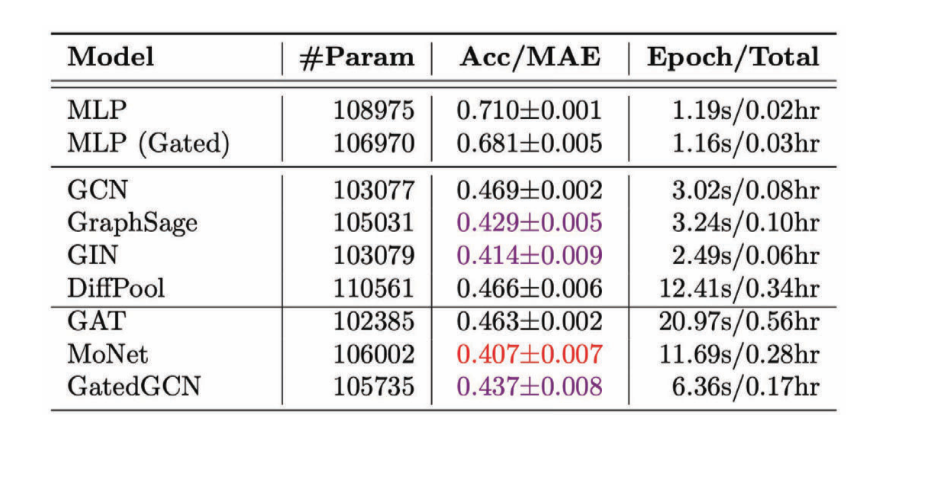
図11: 回帰タスクに対する様々なGCNの性能

ほとんどの場合、異方的なGCNの方が等方的なGCNよりも性能が良いことがわかります。

グラフ分類タスクとしては、画像のスーパーノードがあり、その画像を分類することを目的としたコンピュータビジョンの問題が選ばれました．

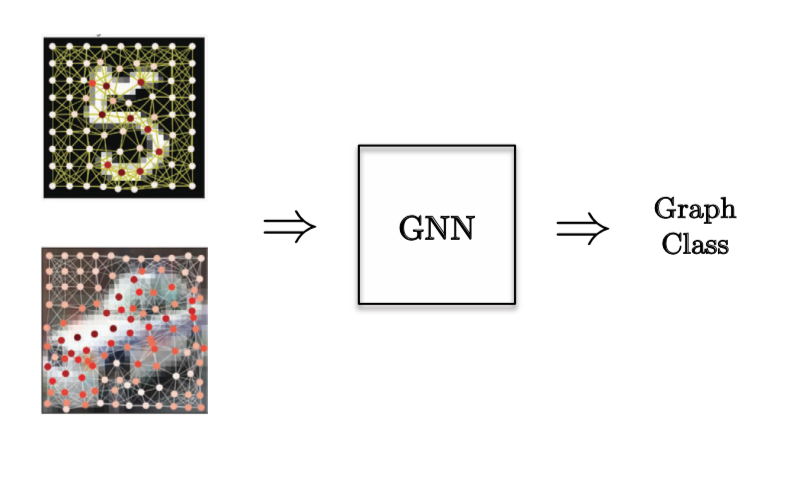
図12: グラフ分類タスク

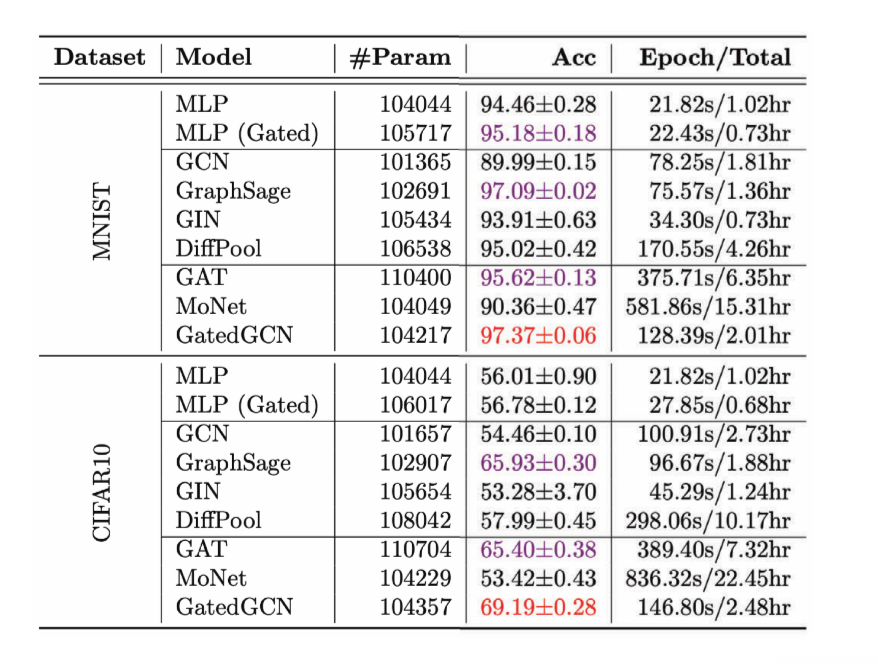
図13: 様々なGCNの、グラフ分類タスクに対する性能

エッジの分類タスクとしては、巡回セールスマン問題(TSP)の組合せ最適化問題について考えました。ここでは、特定のエッジが最適解に属しているかどうかを知りたい場合、そのエッジが最適解に属していればクラス1、そうでなければクラス0になります。 ここでは、明示的なエッジ特徴が必要であり、これに適したモデルはGated GCNだけです。

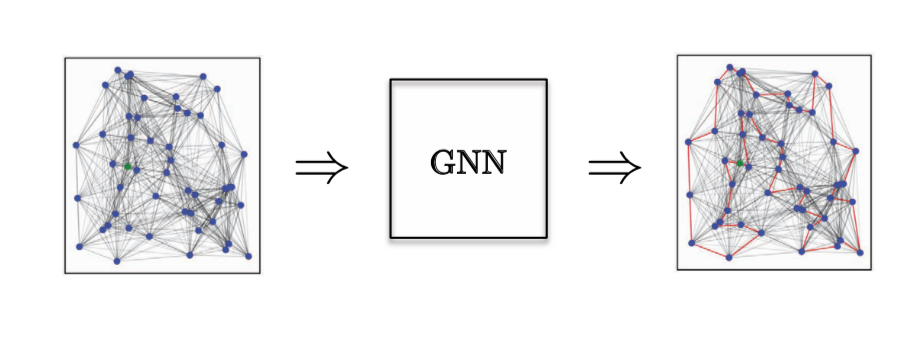
図14: エッジ分類タスク

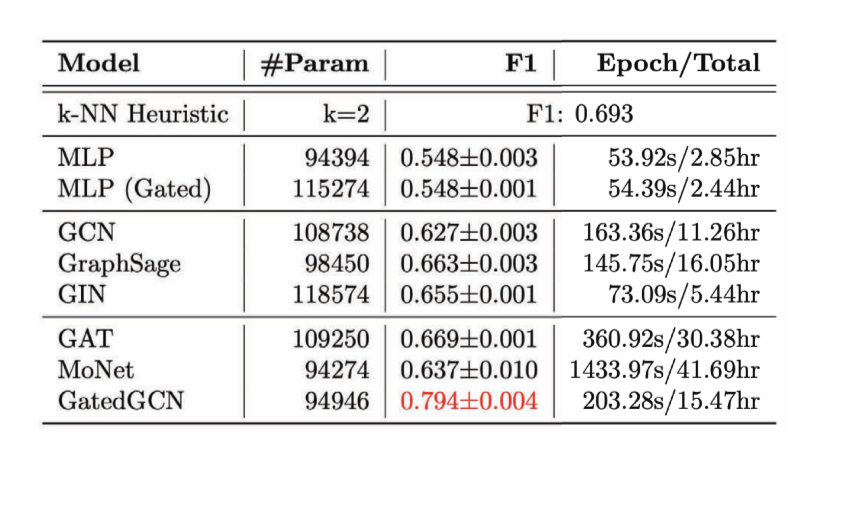
図15: エッジ分類タスクに対する、様々なGCNの性能

GCNは、教師あり学習モデルに限定されるものではなく、自己教師あり学習タスクにも利用できます。Yann LeCun博士によると、ほとんどすべての自己教師あり学習タスクは、何らかのグラフ構造を利用しているといいます。テキストで自己教師あり学習タスクを行う場合、単語の列を取り、不足している単語や新しい文を予測することを学習します。ここにはグラフ構造があり、ある単語が他の単語から何回離れて出現するかを表しています。テキストは線形グラフになり、選択された近傍はTransformerを訓練するために使用されます。対照学習の場合、似ている2つのサンプルと似ていない2つのサンプルがある場合、これは本質的には類似性グラフであり、2つのサンプルが似ているときはリンクされ、リンクされていないときには似ていないとみなされます。

結論

GCNはCNNをグラフ上のデータに一般化します。そのためには畳み込み演算子をグラフ上のデータを扱うように再設計する必要がありました。これをテンプレートマッチングについて行うことで空間的GCNが、スペクトル畳み込みに対して行うことでスペクトルGCNが生まれました。

スパースなグラフとGPUでの実装に対しては（GPUでの実装はスパースな行列の乗算に対しては最適化されていませんが）計算量が線形オーダーです。応用例は以下のように豊富です。

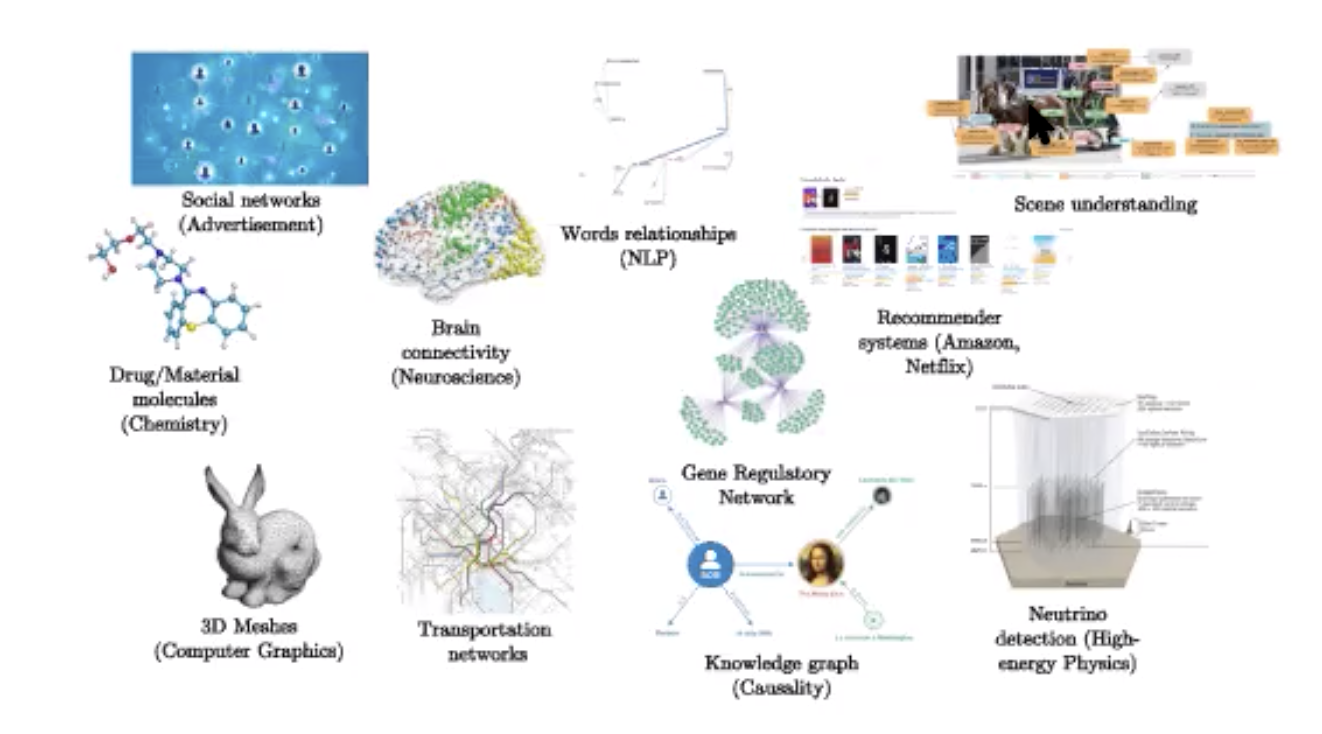
図16: 応用例