Graph Convolution Networks I

🎙️ Xavier Bresson

伝統的な畳み込みニューラルネット

畳み込みニューラルネットは、高次元の学習問題を解決するための強力なアーキテクチャです。

次元の呪いとは何か？

1024×1024ピクセルの画像を考えてみましょう。この画像は1,000,000次元の空間の点として見ることができます。1次元あたり10個のサンプルを使うと、${10}^{1,000,000}$の画像が生成されますが、これは非常に大きい値になります。畳み込みニューラルネットは，例に挙げたような高次元の画像データを最適な表現で抽出するために非常に強力です。

• dim(image) = 1024 x 1024 = ${10}^{6}$
• N = 10 サンプル・次元 –> ${10}^{1,000,000}$ 点 <!–

Fig. 1: ConvNets extract representation of high-dimensional image data.

–>

図1: 畳み込みニューラルネットは高次元な画像のデータの表現を抽出します。

畳み込みニューラルネットに関する主な前提条件：

1. データ（画像、ビデオ、音声）の構成的性質

データは、以下のようなパターンで構成されます：

• 局所性：ニューラルネットワークのニューロンは、隣接する層にしか接続されておらず、ネットワーク内のすべての層に接続されているわけではありません。これを局所的受容野の仮定と呼びます。
• 定常性：画像領域全体で共有されている類似したパターンがいくつかあります。例えば、図2の中央の画像にある黄色のベッドシートです。
• 階層性：低レベルの特徴を組み合わせて、中レベルの特徴を形成します。その後、これらの中レベルの特徴が組み合わされて、徐々に高レベルの特徴が形成されていきます。例えば、視覚的な表現はこのような階層性を持っています。

図2: データは構成的です。

2. 畳み込みニューラルネットによる構成的な構造の活用

畳み込みニューラルネットは構成的な特徴を抽出して、分類器やレコメンダーなどに供給します。

図3: 畳み込みニューラルネットは構成的な構造を活用します。

グラフ領域

データ領域

• 画像、物体、ビデオは2次元、3次元、2+1次元ユークリッド領域（グリッド）上にあります。各ピクセルは赤、緑、青の値のベクトルで表されます。

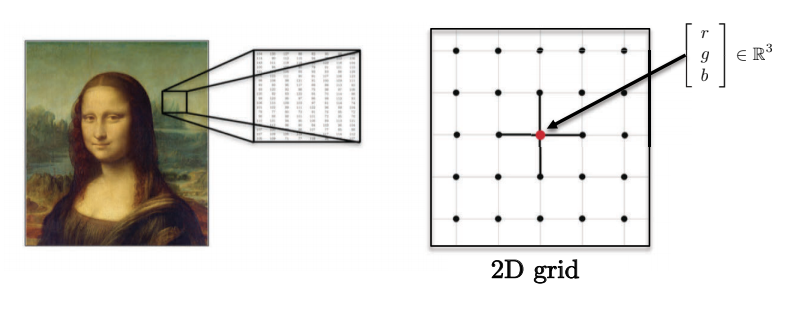
図4: 画像は多次元です。

• 文、単語、音声は1次元ユークリッド空間にあります。例えば、各文字は整数で表すことができます。

  
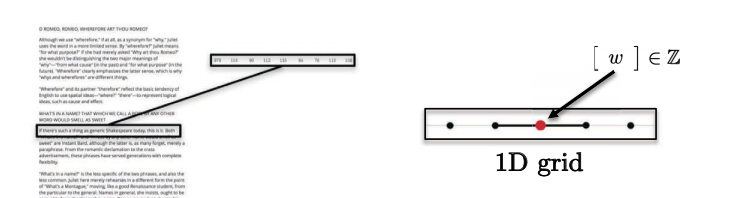
  図5: 系列データは一次元です。

• これらのドメインは強力な規則的な空間構造を持っているため、畳み込みニューラルネットのすべての操作は高速でwell-definedです。

  
  図6: 発話データは1次元のグリッドデータです。

グラフ領域

グラフ領域を考える動機を与えるような例

ソーシャルネットワークを考えてみましょう。ソーシャルネットワークは、2人のユーザ間のペア間の接続がグリッドを形成しないため、グラフ表現で表現するのが最も適しています。グラフのノードはユーザを表し、2つのノード間の辺は2つのノード（ユーザ）間のつながりを表します。各ユーザは、メッセージ、画像、動画などを含む三次元の特徴行列を持っています。

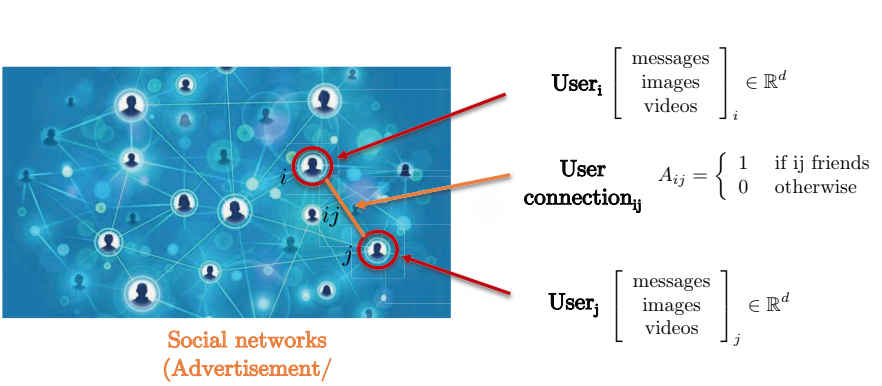
図7: ソーシャルネットワークのグラフ表現。

神経遺伝病を予測するための脳の構造と機能の関係は、グラフを考えるべき動機を与える例です。以下に見られるように、脳はいくつかの関心領域（ROI）で構成されています。これらのROIは、局所的にしか周囲の関心領域に接続されていません。隣接行列は、異なる関心領域間の接続の強さの度合いを表しています。

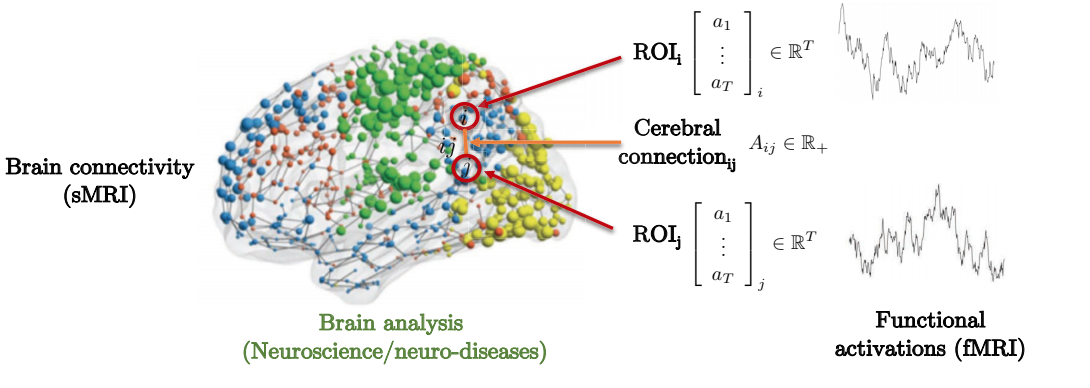
図8: 脳のなかの結合のグラフ表現。

量子化学はまた、グラフで表現できるデータの興味深い例を提供しています。各原子はグラフのノードで表され、辺を使って結合を介して他の原子と接続されています。これらの分子/原子のそれぞれは、関連する電荷、結合タイプなどの異なる特徴を持っています。

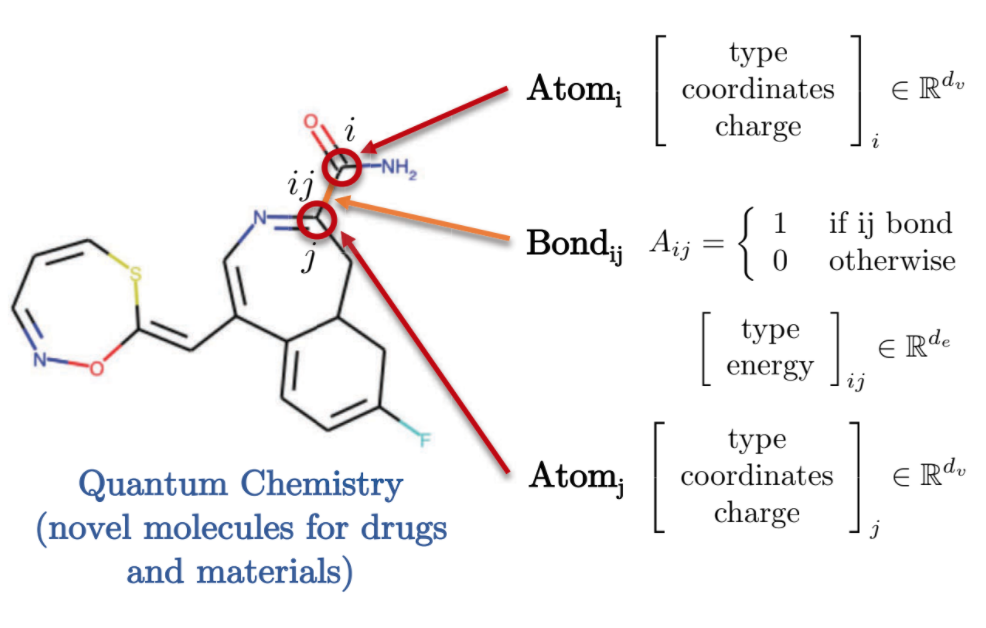
Fig. 9: 量子化学のグラフ表現。

グラフの定義と特徴

• グラフ G は次のように定義されます：
  • 頂点 V
  • 辺 E
  • 隣接行列

• グラフの特徴量：
  • ノードの特徴量：$h_{i}$, $h_{j}$ (原子型)
  • 辺の特徴量：$e_{ij}$ (ボンドタイプ)
  • グラフの特徴量： g (分子エネルギー)

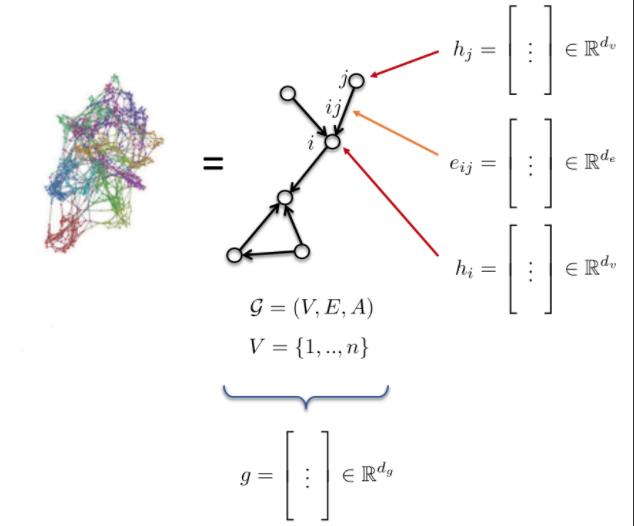
図10: グラフ。

通常の畳み込みニューラルネットの畳み込み

畳み込み

畳み込みを抽象的に定義すると

\(h^{\ell+l} = w^\ell * h^\ell,\) となります。ここで、$h^{\ell+1}$は、$n_1\times n_2\times d$次元で、 $w^\ell$は、$3\times 3\times d$次元で、 $h^\ell$は、$n_1\times n_2\times d$次元です。 例えば、$n_1$と$n_2$は、それぞれ画像の$x$方向と$y$方向の画素数、$d$は各画素の次元数(例えば、色のついた画像の場合は3)です。 つまり、$h^{\ell+1}$は、$(\ell+1)$番目の 隠れ層の特徴表現に畳み込み $w^\ell$を適用して得られた、$(\ell+1)$層目の隠れ層の特徴表現です。 通常、カーネルは、局所的な受信野を表現するために小さくなっています。この場合は、$3 \times 3$や、$5 \times 5$などです。 $h^{\ell+1}$層目の次元が$h^{\ell}$層目の次元と一致するように、パディングを用いていることに注意してください。

例えば、この画像では、カーネルを使うことで線を認識しているのかもしれません。

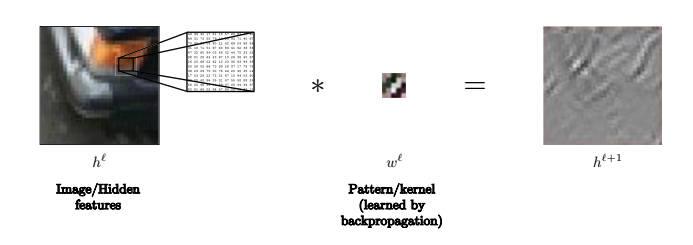
図11: 線の認識のためにカーネルが使われているかもしれない。

畳み込みはどのように定義されているのでしょうか？

より正確には、畳み込みは以下のように定義されています。

\[h_i^{\ell_1} = w^\ell * h_i^\ell\] \[= \sum_{j\in\Omega}\langle w_j^\ell, h_{i-j}^\ell\rangle\] \[= \sum_{j\in\mathcal{N}_i} \langle w_j^\ell, h_{ij}^\ell\rangle\] \[=\sum_{j\in\mathcal{N}_i} \langle \Bigg[w_j^\ell\Bigg], \Bigg[h_{ij}\Bigg]\rangle\]

上記では、畳み込みを テンプレートマッチングとして定義しています。 通常は $h_{i-j}$ の代わりに $h_{i+j}$ を使います。なぜなら前者は実際には相関で、テンプレートマッチング以上のものだからです。

しかし、1行目を使っても2行目を使っても、カーネルが反転しているだけなので、学習には影響しません。

3行目では、$h_{i+j}^\ell$を$h_{ij}^\ell$と書くだけです。

カーネルは非常に小さいので、２行目のように画像全体$\Omega$で合計するのではなく、３行目のように、セル$i$の近傍$\mathcal{N}_i$で合計します。

これにより、畳み込みの計算量は $O(n)$ となります。ここで $n$ は入力画像のピクセル数です。

畳み込みは、$n$の各画素に対して、$d$次元のベクトルの内積を$3 \times 3$の格子上で足し合わせます。

よって、計算量は$n\cdot 3\cdot 3\cdot d$、つまり$O(n)$です。さらに、GPUを用いて$n$の各画素で並列計算が可能です。

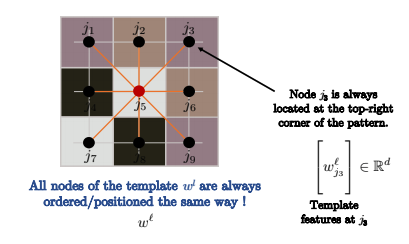
図12: ノードは同じように並んでいる

コンピュータビジョンの標準的な画像に対する畳み込みのように、畳み込みをかけているグラフがグリッドである場合、ノードは上の画像のように順序付けられます。 したがって、 $j_3$ は常にそのパターンの右上にあります。

ですから、下の画像のすべてのノード $i$ に対して、 $i$ と $i’$ のように、カーネルのノードの順序は常に同じになります。 例えば、以下に示すように、パターンの右上隅にある $j_3$ と画像パッチの右上隅にある $j_3$ を常に比較します (ピクセル $i$ に対して畳み込むもの)。 数学的に言えば

\[\langle\Bigg[w_{j_3}^\ell\Bigg], \Bigg[h_{ij_3}^\ell \Bigg]\rangle\]

と

\[\langle\Bigg[w_{j_3}^\ell\Bigg], \Bigg[h_{i'j_3}^\ell \Bigg]\rangle\]

は、常にテンプレートと画像パッチの間の右上隅にあります。

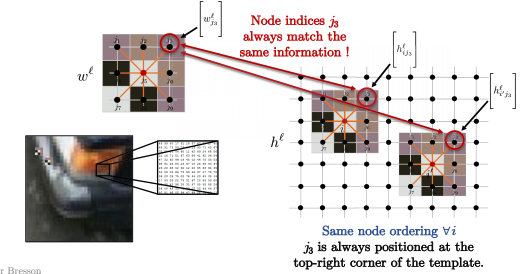
図13: 画像パッチがテンプレートと合う。

テンプレートマッチングをグラフに拡張することはできるでしょうか？

いくつかの問題があります。

1. まず、グラフでは、ノードには順序がありません。

そのため、下の画像のテンプレートでは、ノード $j_3$ には特定の位置はなく、（任意の）インデックスがあるだけです。 だから、下のグラフのノード$i$と$i’$にマッチしようとしても、$j_3$が両方の畳み込みで同じノードにマッチしているかどうかはわかりません。 これは、グラフには右上隅と言うものがないからです。 上下左右という概念がないのです。 このように、テンプレートマッチングには意味がないので、上記のように、テンプレートマッチングの定義をそのまま使うことはできません。

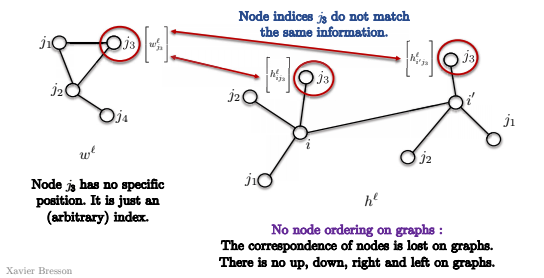
図14: グラフではノードに順序がない。

1. 2つ目の問題は、近傍のサイズが異なる場合があるということです。

例えば、下に示すテンプレート $w^\ell$には4つのノードがありますが、ノード $i$ の近傍には7つのノードがあります。 この２つを比較するにはどうすればよいのでしょうか？

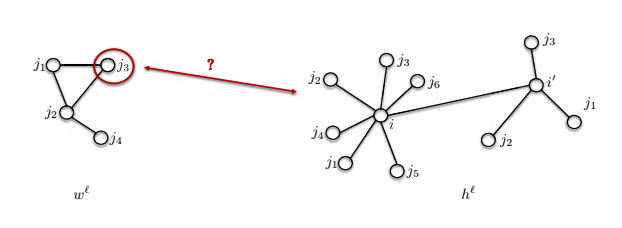
図15: グラフの中での異なる近傍の大きさ。

グラフ畳み込み

ここでは、畳み込み定理を用いて、グラフの畳み込みを定義します。

畳み込み定理は、2つの関数の畳み込みのフーリエ変換は、それらのフーリエ変換の各要素ごとの積であるといっています。

\[\mathcal{F}(w*h) = \mathcal{F}(w) \odot \mathcal{F}(h) \implies w * h = \mathcal{F}^{-1}(\mathcal{F}(w)\odot\mathcal{F}(h))\]

一般にフーリエ変換は$O(n^2)$の計算量ですが、ドメインがグリッドであれば、FFTで$O(n\log n)$の計算量にすることができます。

畳み込み定理をグラフに拡張できるか？

これは二つの疑問を投げかけています。

1. グラフのフーリエ変換はどうやって定義するのか？
2. コンパクトなカーネル（テンプレートマッチングのように）のための高速なスペクトル畳み込みを $O(n)$ 時間で計算するにはどうすればよいか？

\[w *_{\mathcal{G}} h \stackrel{?}{=} \mathcal{F}^{-1}_{\mathcal{G}}(\mathcal{F}_{\mathcal{G}}(w)\odot\mathcal{F}_{\mathcal{G}}(h))\]

グラフニューラルネットワークに対して、これらの2つのデザインを使用します。 テンプレートマッチングは空間的グラフ畳み込みニューラルネットに、畳み込み定理はスペクトル畳み込みニューラルネットに使用されます。

スペクトルグラフ畳み込みニューラルネット

スペクトル畳み込みを行うにはどうすれば良いのでしょうか？

ステップ 1 : グラフラプラシアン

スペクトルグラフ理論の中心的な演算子です。

以下を定義します

\[\begin{aligned} \mathcal{G}=(V, E, A) & \rightarrow \underset{n \times n}{\Delta}=\mathrm{I}-D^{-1 / 2} A D^{-1 / 2} \\ & \quad \text { ただし } \underset{n \times n} D=\operatorname{diag}\left(\sum_{j \neq i} A_{i j}\right) \end{aligned}\]

行列 $A$ は隣接行列であり、$\Delta$ はラプラシアンであり、これは単位行列から行列 $D$ で正規化された隣接行列を引いたものに等しいことに注意してください。これは正規化ラプラシアンと呼ばれ、この文脈では通常ラプラシアンと呼ばれています。

ラプラシアンは、グラフの滑らかさの測定値、言い換えれば、局所的な値 $h_i$ とその近傍 $h_j$ たちの平均値との間の差と解釈されます。下式の$d_i$はノード$i$の滑らかさであり、$\mathcal{N}_{i}$はノード$i$の近傍全ての滑らかさです。

\[(\Delta h)_{i}=h_{i}-\frac{1}{d_{i}} \sum_{j \in \mathcal{N}_{i}} A_{i j} h_{j}\]

上の式は、ノード$i$上の関数$h$にラプラシアンを適用するもので、$h_i$の値から隣接ノード$h_j$の平均値を差し引いたものです。基本的に、信号が非常に滑らかであればラプラシアンの値は小さく、その逆もまた然りです。

ステップ２：フーリエ関数

グラフラプラシアンの固有分解は以下のようになります。

\[\underset{n \times n}{\Delta}=\Phi^{T} \Lambda \Phi\]

ラプラシアンは、$\Phi ^ T$, $\Lambda$, $\Phi$の３つの行列に分解されます。

$\Phi$ は、以下のように定義されていて、それぞれの大きさが $n \times 1$ である列ベクトル、つまりラップ固有ベクトルを含んでいます。そして、これらはフーリエ関数と呼ばれており、正規直交基底を成します。

\[\begin{array}{l}\underset{n \times n}{\Delta}\Phi=\left[\phi_{1}, \ldots, \phi_{n}\right]=\text { and } \Phi^{T} \Phi=\mathrm{I},\left\langle\phi_{k}, \phi_{k^{\prime}}\right\rangle=\delta_{k k^{\prime}} \\\end{array}\]

$\Lambda$ はラプラシアンの固有値を持つ対角行列で、対角線上には $\lambda_1$ から $\lambda_n$ までの値があります。これらの値は、正規化された場合では、典型的には $0$ から $2$ の範囲になります。これらの値は、グラフスペクトルとも呼ばれています。下の式を見てください。

\[\begin{array}{c} \underset{n \times n}\Lambda=\operatorname{diag}\left(\lambda_{1}, \ldots, \lambda_{n}\right) \text { and } 0 \leq \lambda_{1} \leq \ldots \leq \lambda_{n}=\lambda_{\max } \leq 2\end{array}\]

以下に示すのは、固有値分解を確認する例です。ラプラシアン行列$\Lambda$に固有ベクトル$\phi_k$を掛け、結果のシェイプを$n \times 1$とし、結果を$\lambda_k \phi_k$とします。

\[\begin{array}{ll} \underset{n \times 1}{\Delta \phi_{k}}=\lambda_{k} \phi_{k}, & k=1, \ldots, n \\ & \end{array}\]

下の画像は、1次元ユークリッドラプラシアンの固有ベクトルを可視化したものです。

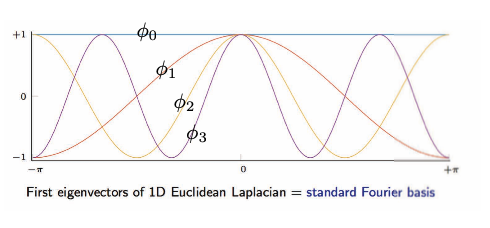
図16: グリッド・ユークリッド領域：一次元ユークリッドラプラシアンの固有ベクトル。

グラフの領域で、左から順に、１番目、２番目、３番目、…のフーリエ関数です。例えば、$\phi_1$では、正（赤）と負（青）の振動があり、$\phi_2$, $\phi_3$でも同じです。これらの振動は、コミュニティやハブなどのグラフの幾何学的な形状に関係するなど、グラフのトポロジーに依存しており、グラフのクラスタリングに役立ちます。以下をみてください。

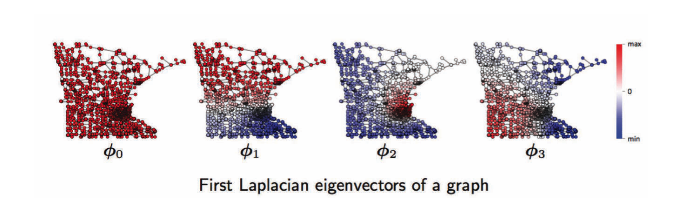
図17: グラフ領域：グラフのフーリエ関数。

ステップ３ : フーリエ変換

\[\begin{aligned} \underset{n \times 1} h &=\sum_{k=1}^{n} \underbrace{\left\langle\phi_{k}, h\right\rangle}_{\mathcal{F}(h)_{k}=\hat{h}_{k}=\phi_{k}^{T} h}\underset{n \times 1}{\phi_{k}} \\ &=\sum_{k=1}^{n} \hat{h}_{k} \phi_{k} \\ &=\underbrace{\Phi \hat{h}}_{ \mathcal{F}^{-1}(\hat{h}) } \end{aligned}\]

フーリエ級数：フーリエ関数による関数 $h$ の分解

関数$h$を取り、各フーリエ関数$\phi_k$に射影し、結果としてスケーリング定数である$k$のフーリエ級数の係数を得て、関数$\phi_k$を掛け合わせます。

フーリエ変換は、基本的には、フーリエ関数に関数 $h$ を射影する操作で、その結果がフーリエ級数の係数となります。

フーリエ変換／フーリエ級数の係数

\[\begin{aligned} \underset{n \times 1}{\mathcal{F}(h)} &=\Phi^{T} h \\ &=\hat{h} \end{aligned}\]

逆フーリエ変換

\[\begin{aligned} \underset{n \times 1}{\mathcal{F}^{-1}(\hat{h})} &=\Phi \hat{h} \\ &=\Phi \Phi^{T} h=h \quad \text { as } \mathcal{F}^{-1} \circ \mathcal{F}=\Phi \Phi^{T}=\mathrm{I} \end{aligned}\]

フーリエ変換は、行列 $\Phi^{T}$ にベクトル $h$ をかける線形演算です。

ステップ４： 畳み込み定理

2つの関数の畳み込みのフーリエ変換は、それらのフーリエ変換の要素毎の積です。

\[\begin{aligned} \underset{n \times 1} {w * h} &=\underbrace{\mathcal{F}^{-1}}_{\Phi}(\underbrace{\mathcal{F}(w)}_{\Phi^{T} w=\hat{w}} \odot \underbrace{\mathcal{F}(h)}_{\Phi^{T} h}) \\ &=\underset{n \times n}{\Phi}\left( \underset{n \times 1}{\hat{w}}\odot \underset{n \times 1}{\Phi^{T} h}\right) \\ &=\Phi\left(\underset{n \times n}{\hat{w}(\Lambda)} \underset{n \times 1}{\Phi^{T} h}\right) \\ &=\Phi \hat{w}(\Lambda) \Phi^{T} h \\ &=\hat{w}(\underbrace{\Phi \Lambda \Phi^{T}}_{\Delta}) h \\ &=\underset{n \times n}{\hat{w}(\Delta)} \underset{n \times1}h \\ & \end{aligned}\]

上の例は、$w$と$h$の畳み込みで、どちらもシェイプが$n \times 1$のものですが、$w$のフーリエ変換と$h$のフーリエ変換の間の要素毎の積の逆数に等しくなります。上の式から、$\hat{w}(\Delta)$と$h$の行列積にも等しいことがわかります。

グラフ$h$と$w$上の2つの関数の畳み込みは、$w$のスペクトル関数を取ってラプラシアンに当てはめて$h$とかけることであり、これがスペクトル畳み込みの定義です。しかし、グラフのノード数$n$ に対して計算量は $\mathrm{O}\left(n^{2}\right)$ です。

限界

平行移動されると関数の形状も変化する可能性がありますが、グラフ領域に対するスペクトル畳み込みは並行移動不変ではないので、グリッド/ユークリッド領域では変化しません。

おすすめの参考書

Spectral graph theory, Fan Chung, (harmonic analysis, graph theory, combinatorial problems, optimization)

---

📝 Bilal Munawar, Alexander Bienstock, Can Cui, Shaoling Chen
Shiro Takagi
27 Apr 2020