Attention and the Transformer

Attention

Transformerのアーキテクチャの話をする前に、attentionの概念を紹介します。attentionには主に2つのタイプがあります：self attention と cross attentionで、これらのカテゴリ内では、ハードなattention と ソフトなattentionがあります。

後述しますが、Transformerはattentionモジュールで構成されています。これはシーケンスではなく、集合間の写像です。

Self Attention (I)

$t$個の入力$\boldsymbol{x}$のなす集合を考えましょう。

ただし各$\boldsymbol{x}_i$は$n$次元のベクトルです。その集合は$t$個の要素を持っているので、各要素は$\mathbb{R}^n$に属しており、その集合を行列として表現することができます$\boldsymbol{X}\in\mathbb{R}^{n \times t}$。

Self-attentionでは、隠れ表現 $h$ は入力の線形結合です。

上述した行列表現を用いて、隠れ層を行列積の形で書くことができます。

ただし$\boldsymbol{a} \in \mathbb{R}^t$は要素が$\alpha_i$の列ベクトルです。

これは、これまで見てきた隠れた表現とは異なることに注意してください。

ベクトル $\vect{a}$ に課す制約に応じて、ハードattentionとソフトattentionが得られます。

ハード Attention

ハードattentionでは、$\alpha$に次のような制約を課します：$\Vert\vect{a}\Vert_0 = 1$。これは、$\vect{a}$がone-hotベクトルであることを意味しています。したがって、入力の線形結合の係数の1つ以外はすべてゼロに等しく、隠れ表現は、要素$\alpha_i=1$に対応する入力$\boldsymbol{x}_i$に帰着されます。

ソフト Attention

ソフトattentionでは、 $\Vert\vect{a}\Vert_1 = 1$ とします。隠れ表現は、係数の和が1になるように入力を線形結合したものです。

Self Attention (II)

$\alpha_i$はどこから来るのでしょうか。

ベクトル$\vect{a} \in \mathbb{R}^t$ は次のようにして得られます：

ここで、$\beta$は、$\text{soft(arg)max}(\cdot)$の逆温度パラメータを表します。$\boldsymbol{X}^{\top}\in\mathbb{R}^{t \times n}$ は、集合$\lbrace\boldsymbol{x}i \rbrace{i=1}^t$の転置行列表現であり、$\boldsymbol{x}$ は、集合の中の一般的な $\boldsymbol{x}i$ を表しています。$X^{\top}$の$j$番目の行は、要素$\boldsymbol{x}_j\in\mathbb{R}^n$に対応しています。なので、$\boldsymbol{X}^{\top}\boldsymbol{x}$の$j$番目の行は、$\boldsymbol{x}_j$と$\lbrace \boldsymbol{x}_i \rbrace{i=1}^t$の中の各$\boldsymbol{x}_i$とのスカラー積となります。

ベクトル$\vect{a}$の構成要素は、「スコア」とも呼ばれます。なぜなら、二つのベクトルのスカラー積は、二つのベクトルがどれだけ似ているかを教えてくれるからです。したがって、$\vect{a}$の要素は、全体の集合がある特定の$\boldsymbol{x}_i$にどれくらい類似しているかについての情報を与えます。

角括弧は任意の引数です。なお、$\arg\max(\cdot)$を使うと、$\alpha$のone-hotベクトルを得てしまうことに注意してください。一方、$\text{soft(arg)max}(\cdot)$を使うと、ソフトattentionになります。いずれの場合も、結果として得られるベクトルの成分の和は１となります。

このようにして$\vect{a}$を生成すると、$\boldsymbol{x}_i$ごとに1つの集合が得られます。さらに、各$\vect{a}_i \in \mathbb{R}^t$を積み上げて、行列$\boldsymbol{A} \in \mathbb{R}^{t \times t}$を得ることができます。

それぞれの隠れ状態は、入力$\boldsymbol{X}$とベクトル$\vect{a}$の線形結合なので、$t$の隠れ状態の集合が得られ、これを行列$\boldsymbol{H}\in \mathbb{R}^{n \times t}$として積み上げることができます。

キーバリューストア

キーバリューストアは、保存 (ストア)、検索 (クエリ)、連想配列 (辞書 / ハッシュテーブル) の管理のために設計されたパラダイムです。

例えば、ラザニアを作るためのレシピを見つけたいとします。レシピブックを持っていて、「ラザニア」と検索すると、これがクエリになります。このクエリは、データセット内のすべての可能性のあるキーに対してチェックされます。クエリが各タイトルとどの程度一致しているかをチェックして、クエリとすべてのキーとの間で最も一致する最大のスコアを見つけます。もし出力がargmax関数であれば、最も高いスコアを持つ単一のレシピを取得します。ソフトなargmax関数を使えば、確率分布を得ることができます。これによって、クエリにマッチするレシピの中から、最も類似した内容から類似してないものへと順番に検索することができます。

基本的には、クエリは質問です。1つのクエリが与えられると、このクエリをすべてのキーに対してチェックして、一致するすべてのコンテンツを検索します。

クエリ、キー、バリュー

それぞれのベクトル$\vect{q}, \vect{k}, \vect{v}$ は、簡単に言えば、特定の入力$\vect{x}$の回転と見ることができます。ここで、$\vect{q}$は、$\vect{W_q}$で回転させただけの$\vect{x}$であり、$\vect{k}$は、$\vect{W_k}$で回転させただけの$\vect{x}$であり、$\vect{v}$についても同様です。学習可能なパラメータを導入するのは今回が初めてであることに注意してください。また、attentionは完全に方向性にのみ基づいているので、非線形性も含めていません。

全ての可能なキーと比較するためには、$\vect{q}$ と $\vect{k}$ は同じ次元でなければなりません。例えば、$\vect{q}, \vect{k} \in \mathbb{R}^{d’}$。

しかし、$\vect{v}$ は任意の次元である可能性があります。ラザニアのレシピの例を続けるならば、クエリは次元をキー、すなわち、検索している異なるレシピのタイトルとして持つ必要があります。検索された対応するレシピの次元、$\vect{v}$は、任意の長さにすることができます。だから、$\vect{v} \in \mathbb{R}^{d’’}$です。

ここでは簡単のために、すべてが $d$ 次元であると仮定します。例えば

これで、$\vect{x}$の集合、つまりクエリの集合、キーの集合、バリューの集合ができました。$t$本のベクトルを積み重ねたので、これらの集合を、それぞれ $t$ 列を持つ行列として積み重ねることができます。このとき、各ベクトルの高さは $d$ です。

一つのクエリ$\vect{q}$ を全てのキー$\vect{K}$からなる行列と比較します。

すると隠れ層は、$\vect{a}$に入っている係数によって重み付られた$\vect{V}$の列の線形結合になります。

$t$のクエリを持っていますので、それに対応する$t$本の$\vect{a}$重み、したがって$t \times t$次元の行列$\vect{A}$を持っていることになります。

したがって、行列表記では次のようになります。

余談ですが、通常は$\beta$を次のように設定します。

これは、次元$d$の選択の違いによって決まる温度を一定に保つために行われるので、次元$d$の平方根で割っています(ベクトル $\vect{1} \in \R^d$ の長さは何か考えてみてください)。

実装する上では、全ての$\vect{W}$を一つの$\vect{W}$にスタックしてから$\vect{q}、\vect{k}、\vect{v}$を計算することで、計算の高速化を行えます。

また、「ヘッド」という概念もあります。上では、ヘッドが一つの例を見ましたが、複数のヘッドを持つこともできます。例えば、$h$個のヘッドがあるとすると、$h$個の $\vect{q}$、 $h$個の $\vect{k}$及び $h$個の $\vect{v}$があり、最終的には、$\mathbb{R}^{3hd}$のベクトルになります。

しかし、元の次元$\R^d$を得るために、$\vect{W_h} \in \mathbb{R}^{d \times hd}$ を使用することでmulti-headの値を変換することができます。これは、キーバリューストアを実装するための一つの方法に過ぎません。

Transformer

Attentionの知識を拡張して、Transformerの基本的な構成要素を解釈します。特に、基本的なTransformerの順伝播を見ることで、標準的なエンコーダ／デコーダパラダイムでattentionがどのように使用されているのかをみて、RNNのようなシークエンシャルなアーキテクチャと比較します。

エンコーダ・デコーダアーキテクチャ

この用語には親しまなければなりません。これはオートエンコーダーのデモで最もよく示されており、ここまでの理解が前提となっています。要約すると、入力はエンコーダとデコーダを通して供給され、データにある種のボトルネックを課して、最も重要な情報だけを強制的に通過させます。この情報はエンコーダブロックの出力に格納され、関連性のない様々なタスクに使用されます。

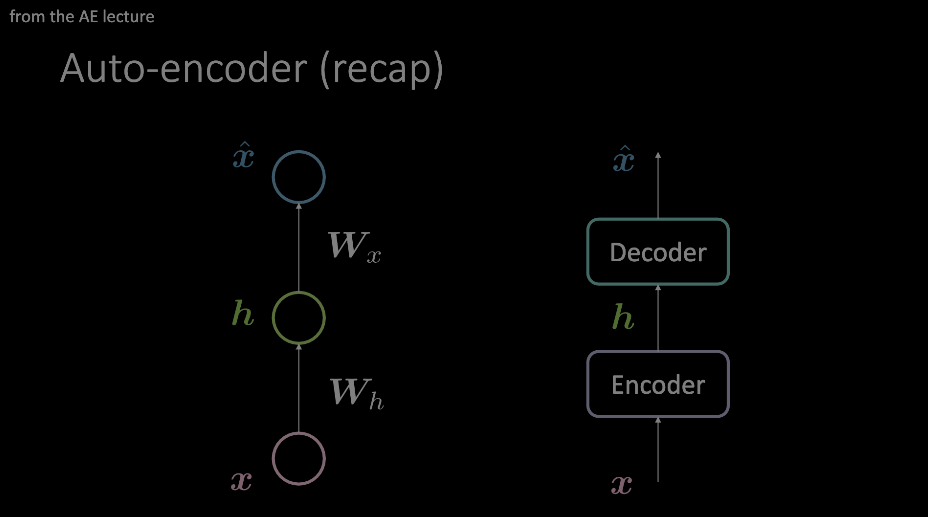
図1: オートエンコーダーの2つの例の図。左のモデルは、2つのアフィン変換＋活性化関数でオートエンコーダーを設計する方法を示しており、右の図は、この単一の「層」を任意の演算モジュールに置き換えています。

私たちの「attention」は、右のモデルに示されているように、オートエンコーダーのレイアウトに引き寄せられていますが、ここで、Transformerの文脈で、内部を見てみましょう。

エンコーダーモジュール

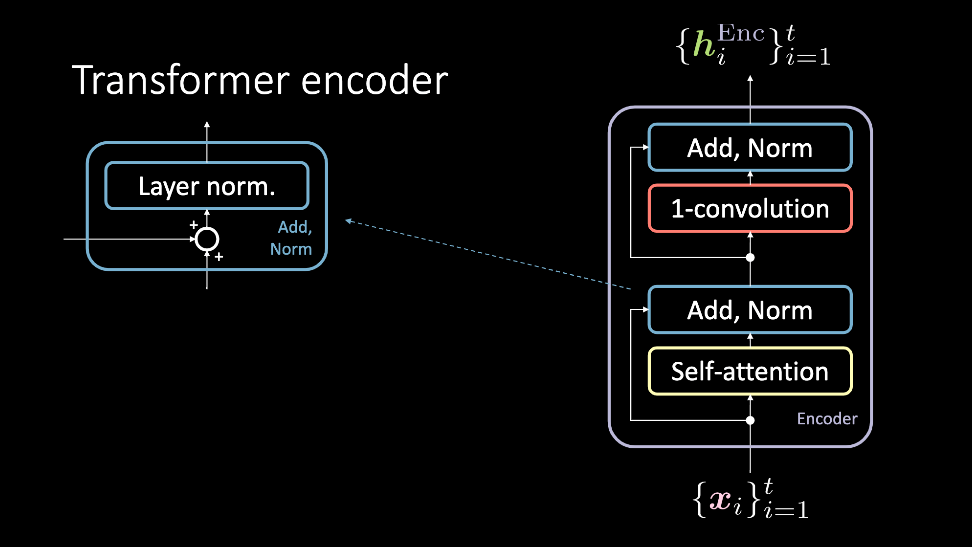
図2: transfomerのエンコーダは、入力集合である $\vect{x}$ の入力を受け、隠れ表現の集合である $\vect{h}^\text{Enc}$ を出力します。

エンコーダモジュールへの一連の入力は、同時にself attentionブロックを通過して Add, Norm ブロックに到達するために順次処理されます。この時点で、それらは再び 1次元畳み込み と Add, Norm ブロックを同時に通過し、結果として隠れ表現の集合として出力されます。そして、この隠れ表現の集合は、任意の数のエンコーダモジュール（つまり、より多くの層）を介して送られるか、デコーダに送られます。ここでは、これらのブロックについて詳しく説明します。

Self-attention

Self-attentionモデルは、通常のattentionモデルです。クエリ、キー、バリューは逐次入力の同じ項目から生成されます。系列データをモデル化しようとするタスクでは、この入力の前にpositional encodingが追加されます。このブロックの出力は、attentionで重み付られた値です。Self-attentionブロックは、$1, \cdots , t$からの入力を受け入れ、$1, \cdots, t$のattentionで重み付られた値を出力し、それが残りのエンコーダーに入力されます。

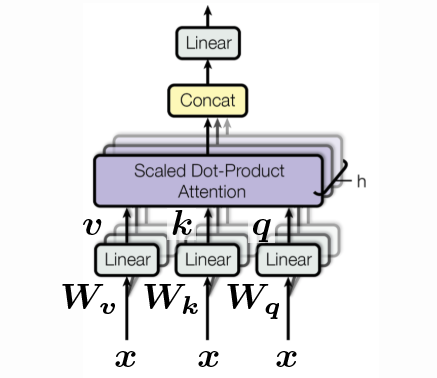
Figure 3: Self-attentionブロック。 入力系列は、3次元に沿った集合として示され、連結されています。

Add, Norm

Add normブロックは２つの構成要素を持っています。residual connectionであるaddブロックと、layer normalizationからなるnormブロックです。

一次元畳み込み

このステップに続いて、1次元畳み込み（別名、位置情報フィードフォワードネットワーク）が適用されます。このブロックは全結合層で構成されています。このブロックでは、どのような値を設定するかによって、出力される $\vect{h}^\text{Enc}$ の次元を調整することができます。

デコーダーモジュール

Transformer のデコーダは、エンコーダと同様の手順に従います。しかし、考慮しなければならない追加のサブブロックが1つあります。さらに、このモジュールへの入力が異なります。

図4: デコーダーのより親切な説明

Cross-attention

Cross attentionは、self-attentionブロックで使用されるクエリ、キー、バリューの設定に従います。 しかし、入力は少し複雑です。デコーダへの入力は、データ点 $\vect{y}i$ であり、これは、self-attentionブロックとadd normブロックを通過し、最終的にcross attentionブロックで終了します。これはcross-attentionへのクエリとして機能します。そこでは、キーバリューのペアは$\vect{h}^\text{Enc}$の出力です。そしてこの出力は過去のすべての$\vect{x}_1, \cdots, \vect{x}{t}$を使って計算されます。

まとめ

$\vect{x}1$から$\vect{x}{t}$の集合がエンコーダを介して送られてきます。Self-attentionといくつかのブロックを使って、出力の表現 $\lbrace\vect{h}^\text{Enc}\rbrace_{i=1}^t$ を得て、それをデコーダに送ります。これにself-attentionをかけた後、cross-attentionをかけます。このブロックでは、クエリは、対象言語におけるシンボルの表現に対応し、キーとバリューは、ソース言語の文（$\vect{x}1$ to $\vect{x}{t}$）のものです。直感的には、cross-attentionは、入力文のどの値が、$\vect{y}t$を構築するのに最も関連性があり、したがって、最も高いattention係数に値するかを見つけます。このcross-attentionの出力は、別の１次元畳み込みサブブロックを介して与えられ、 $\vect{h}^\text{Dec}$ が得られます。指定された対象言語については、ここから、$\lbrace\vect{h}^\text{Dec}\rbrace{i=1}^t$ をいくつかの対象データと比較することで、どのように訓練が起こるのかを簡単に見ることができます。

単語言語モデル

Transformerの最も重要なモジュールを説明する前に、説明せずに残していたいくつかの重要な事実がありますが、Transformerがどのように言語タスクで最先端の結果を達成することができるかを理解するために、今すぐにそれらを議論する必要があります。

Positional encoding

Attention機構を利用することで並列処理が可能になり、モデルの学習時間を大幅に短縮することができますが、逐次的な情報は失われてしまいます。positional encoding機能を用いることで、この文脈を捉えることが可能となります。

意味表現

トランスフォーマーの訓練を通して、多くの隠れ表現が生成されます。PyTorch の単語モデルの例で使用されているものと同様の埋め込み空間を作成するために、cross-attentionの出力は $x_i$ という単語の意味表現を提供します。これによってこのデータセット上でのさらなる実験が可能となります。

コードの概要

ここからは、上で説明したtransformerのブロックを、はるかにわかりやすい、コードという形で見ていきましょう!

最初のモジュールでは、multi-head attentionブロックを見ていきます。このブロックに入力されたクエリー、キー、バリューに応じて、self-attentionにもcross-attentionにも使用できます。

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads, p, d_input=None):
        super().__init__()
        self.num_heads = num_heads
        self.d_model = d_model
        if d_input is None:
            d_xq = d_xk = d_xv = d_model
        else:
            d_xq, d_xk, d_xv = d_input
        # Embedding dimension of model is a multiple of number of heads
        assert d_model % self.num_heads == 0
        self.d_k = d_model // self.num_heads
        # These are still of dimension d_model. To split into number of heads
        self.W_q = nn.Linear(d_xq, d_model, bias=False)
        self.W_k = nn.Linear(d_xk, d_model, bias=False)
        self.W_v = nn.Linear(d_xv, d_model, bias=False)
        # Outputs of all sub-layers need to be of dimension d_model
        self.W_h = nn.Linear(d_model, d_model)

Multi-head attentionクラスの初期化では、d_input が与えられた場合はcross-attentionとなります。それ以外の場合はself-attentionとなります。クエリ、キー、バリューの設定は入力 d_model の線形変換として構築されます。

def scaled_dot_product_attention(self, Q, K, V):
    batch_size = Q.size(0)
    k_length = K.size(-2)

    # Scaling by d_k so that the soft(arg)max doesnt saturate
    Q = Q / np.sqrt(self.d_k)  # (bs, n_heads, q_length, dim_per_head)
    scores = torch.matmul(Q, K.transpose(2,3))  # (bs, n_heads, q_length, k_length)

    A = nn_Softargmax(dim=-1)(scores)  # (bs, n_heads, q_length, k_length)

    # Get the weighted average of the values
    H = torch.matmul(A, V)  # (bs, n_heads, q_length, dim_per_head)

    return H, A

Attentionベクトルでスケーリングされた後の値のpositional enncodingに対応する隠れ層を返します。シーケンス中のどの値がattentionによってマスクされたかを見るために A も返されます。

def split_heads(self, x, batch_size):
    return x.view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)

最後の次元を (heads × depth) に分割します。(batch_size × num_heads × seq_length × d_k) の形にするために転置した後に出力を返します。

def group_heads(self, x, batch_size):
    return x.transpose(1, 2).contiguous().
        view(batch_size, -1, self.num_heads * self.d_k)

Attention headを組み合わせて、バッチサイズとシーケンスの長さに合った正しいシェイプにします。

def forward(self, X_q, X_k, X_v):
    batch_size, seq_length, dim = X_q.size()
    # After transforming, split into num_heads
    Q = self.split_heads(self.W_q(X_q), batch_size)
    K = self.split_heads(self.W_k(X_k), batch_size)
    V = self.split_heads(self.W_v(X_v), batch_size)
    # Calculate the attention weights for each of the heads
    H_cat, A = self.scaled_dot_product_attention(Q, K, V)
    # Put all the heads back together by concat
    H_cat = self.group_heads(H_cat, batch_size)  # (bs, q_length, dim)
    # Final linear layer
    H = self.W_h(H_cat)  # (bs, q_length, dim)
    return H, A

Multi-head attentionの順伝播についてです。

入力が q, k, v に分割され、その時点で、これらの値は、スケーリングされたドット積attention機構を介して入力され、連結され、最終的な線形層へ入力されます。Attentionブロックの最後の出力は、見つかったattentionと、残りのブロックに渡される隠れ表現です。

Transformer/エンコーダーの次のブロックはAdd,Normですが、これはPyTorchにすでに組み込まれている関数です。このように、これは非常にシンプルな実装であり、独自のクラスを必要としません。次は1次元畳み込みブロックです。詳細は前のセクションを参照してください。

これで、すべてのメインクラスがビルドされました（またはビルドしてもらった）ので、次にエンコーダモジュールに移ります。

class EncoderLayer(nn.Module):
    def __init__(self, d_model, num_heads, conv_hidden_dim, p=0.1):
        self.mha = MultiHeadAttention(d_model, num_heads, p)
        self.layernorm1 = nn.LayerNorm(normalized_shape=d_model, eps=1e-6)
        self.layernorm2 = nn.LayerNorm(normalized_shape=d_model, eps=1e-6)

    def forward(self, x):
        attn_output, _ = self.mha(x, x, x)
        out1 = self.layernorm1(x + attn_output)
        cnn_output = self.cnn(out1)
        out2 = self.layernorm2(out1 + cnn_output)
        return out2

最も強力なTransformerでは、任意の数のこれらのエンコーダが互いに積み重ねられています。

Self-attentionはそれ自体では再帰や畳み込みを持たないことを思い出してください。位置に敏感になるように、我々はpositional encodingを提供します。これらは次のように計算されます。

あまりスペースを取らないように、細かい詳細については、ここで使用されている完全なコードについては https://github.com/Atcold/pytorch-Deep-Learning/blob/master/15-transformer.ipynb を参照してください。

Positional encodingと同様に、N個のスタックされたエンコーダ層を持つエンコーダ全体は、以下のように書き出されます

class Encoder(nn.Module):
    def __init__(self, num_layers, d_model, num_heads, ff_hidden_dim,
            input_vocab_size, maximum_position_encoding, p=0.1):
        self.embedding = Embeddings(d_model, input_vocab_size,
                                    maximum_position_encoding, p)
        self.enc_layers = nn.ModuleList()
        for _ in range(num_layers):
            self.enc_layers.append(EncoderLayer(d_model, num_heads,
                                                ff_hidden_dim, p))
    def forward(self, x):
        x = self.embedding(x) # Transform to (batch_size, input_seq_length, d_model)
        for i in range(self.num_layers):
            x = self.enc_layers[i](x)
        return x  # (batch_size, input_seq_len, d_model)

使用例

エンコーダだけを使ってもできるタスクはたくさんあります。付属のノートブックでは、エンコーダがどのように感情分析に使用できるかを見ています。

imdbのレビューデータセットを使って、エンコーダーからテキスト系列の潜在表現を出力し、このエンコーディング過程をバイナリークロスエントロピーで訓練して、映画のレビューが肯定的か否定的かに対応させます。

ここでも詳細の説明は省略して、ノートを参照していただきたいのですが、ここではTransoformerで使われている最も重要なアーキテクチャコンポーネントを紹介します。

class TransformerClassifier(nn.Module):
    def forward(self, x):
        x = Encoder()(x)
        x = nn.Linear(d_model, num_answers)(x)
        return torch.max(x, dim=1)

model = TransformerClassifier(num_layers=1, d_model=32, num_heads=2,
                         conv_hidden_dim=128, input_vocab_size=50002, num_answers=2)

これはモデルが典型的な方法で訓練されるところです。