Prediction and Policy learning Under Uncertainty (PPUU)
🎙️ Alfredo Canziani導入と問題設定
モデルフリー強化学習で運転の仕方を学びたいとしましょう。RLでは、モデルにミスをさせてそこから学習させることでモデルを訓練します。しかし、これは最善の方法ではありません。
そこで、もっと「人間的」な方法で車の運転を学ぶ方法を考えてみましょう。車線変更の例を考えてみましょう。車が時速100km 、つまり大体30m/sの速度で動いていると仮定すると、30m先を見た場合、大体1s先を見ていることになります。
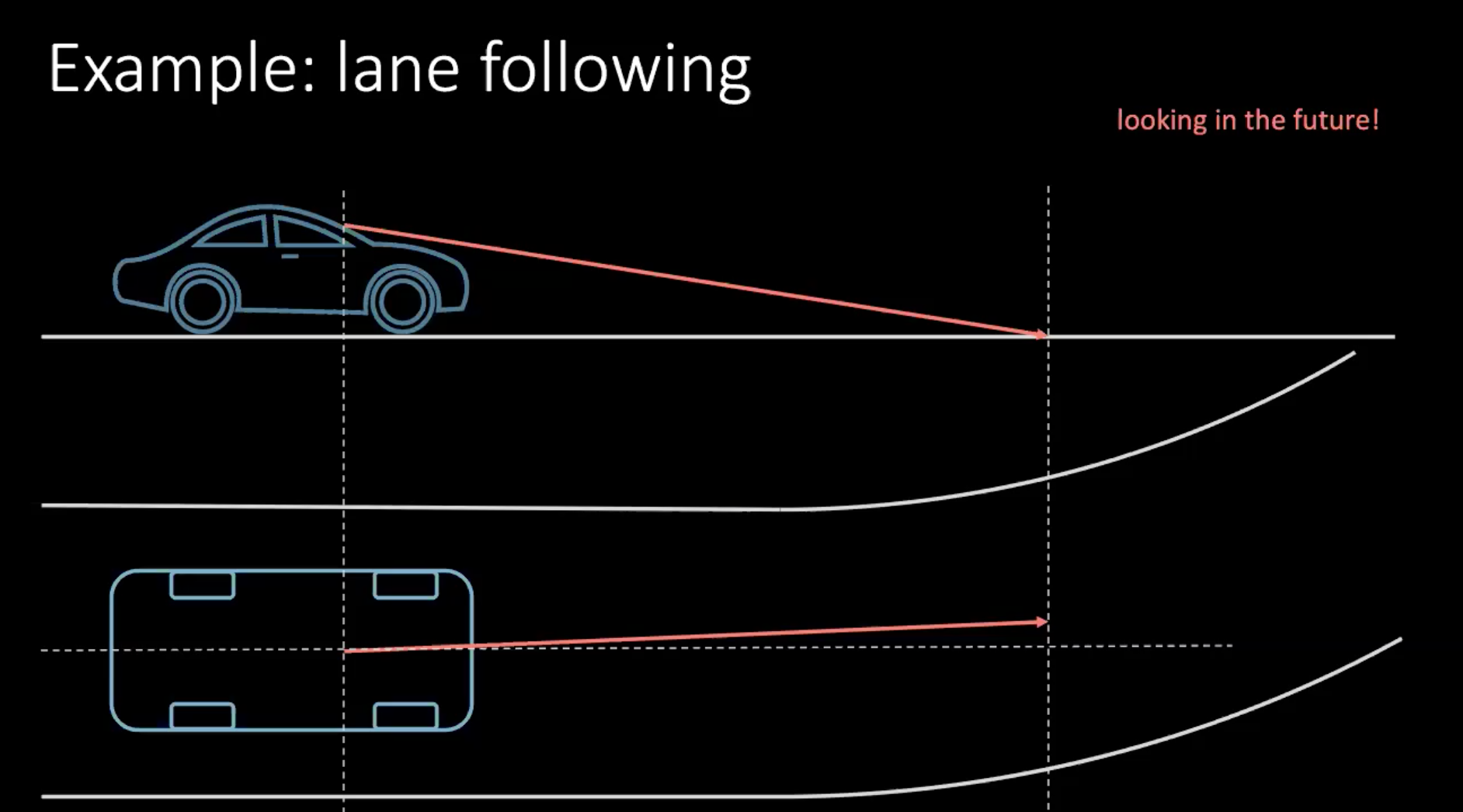
図1: 少し先を予測して運転をする
カーブを切る時には、近い将来のことを考えて判断する必要があります。数メートル先で曲がるためには、今すぐに行動を起こす、ここではハンドルを切る、ことになります。決断をするかどうかは、自分の運転だけでなく、交通の中の周囲の車にも左右されます。私たちの周りの誰もが決定論的ではないので、すべての可能性を考慮に入れることは非常に困難です。
このシナリオで何が起こっているかを分解してみましょう。我々は、入力$s_t$(位置、速度、文脈画像)を受け取り、アクション$a_t$(操舵制御、加速、制動)を生成するエージェント(ここでは頭脳で表現)を持っています。 環境は私たちを新しい状態に連れて行き、コスト$c_t$を返します。
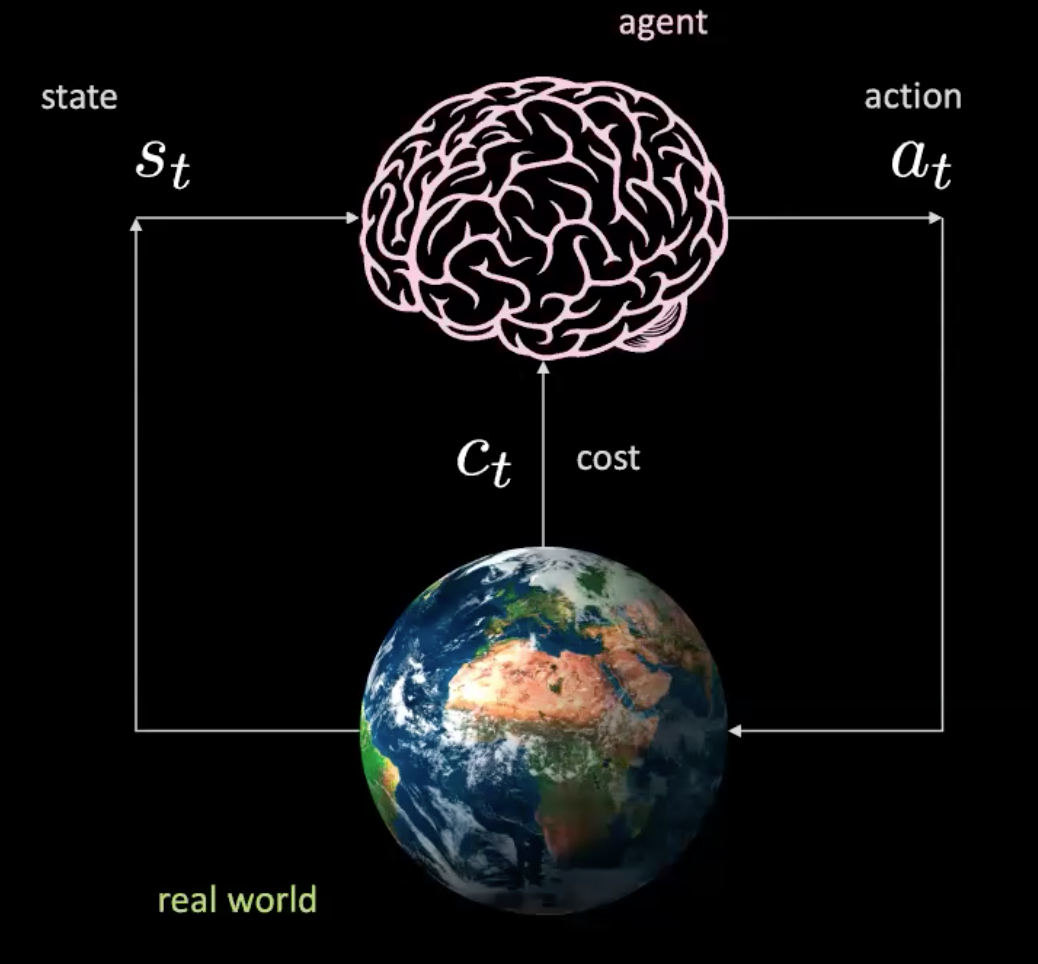
図2: 実世界でのエージェントのイラスト
これは、特定の状態の下で行動を取ると、世界が次の状態と次の結果を与えてくれる単純なネットワークのようなものです。これはモデルフリーで、すべての行動が現実世界と相互作用するからです。しかし、実際に現実世界と対話せずにエージェントを訓練することはできるのでしょうか?
はい、できます。「世界モデルを学習する」のセクションでそれを見てみましょう。
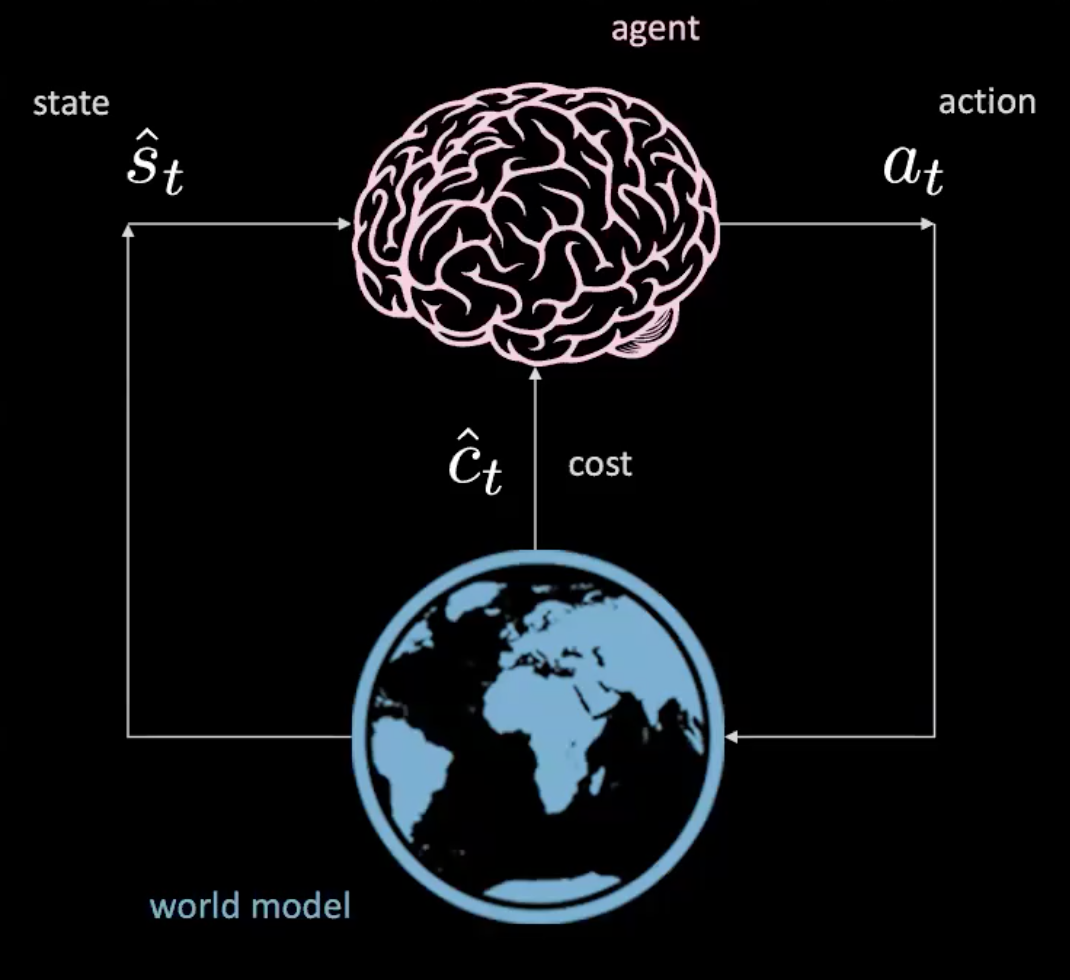
図3: 実世界でのエージェントのイラスト
データセット
世界モデルの学習方法を説明する前に、我々が持っているデータセットを調べてみましょう。高速道路に面した30階建ての建物の上に7台のカメラを設置します。カメラを調整してトップダウンビューを取得し、各車両のバウンディングボックスを抽出します。ある時間$t$で、位置を表す$p_t$を求め、速度を表す$v_t$、車両周辺の現在の交通状態を表す$i_t$を求めます。
運転のキネマティクスがわかっているので、これらを逆算して、運転者が何をしているのかを知ることができます。例えば、車が直線的な一様運動をしている場合、加速度はゼロ(何もしていないことを意味する)であることがわかります。
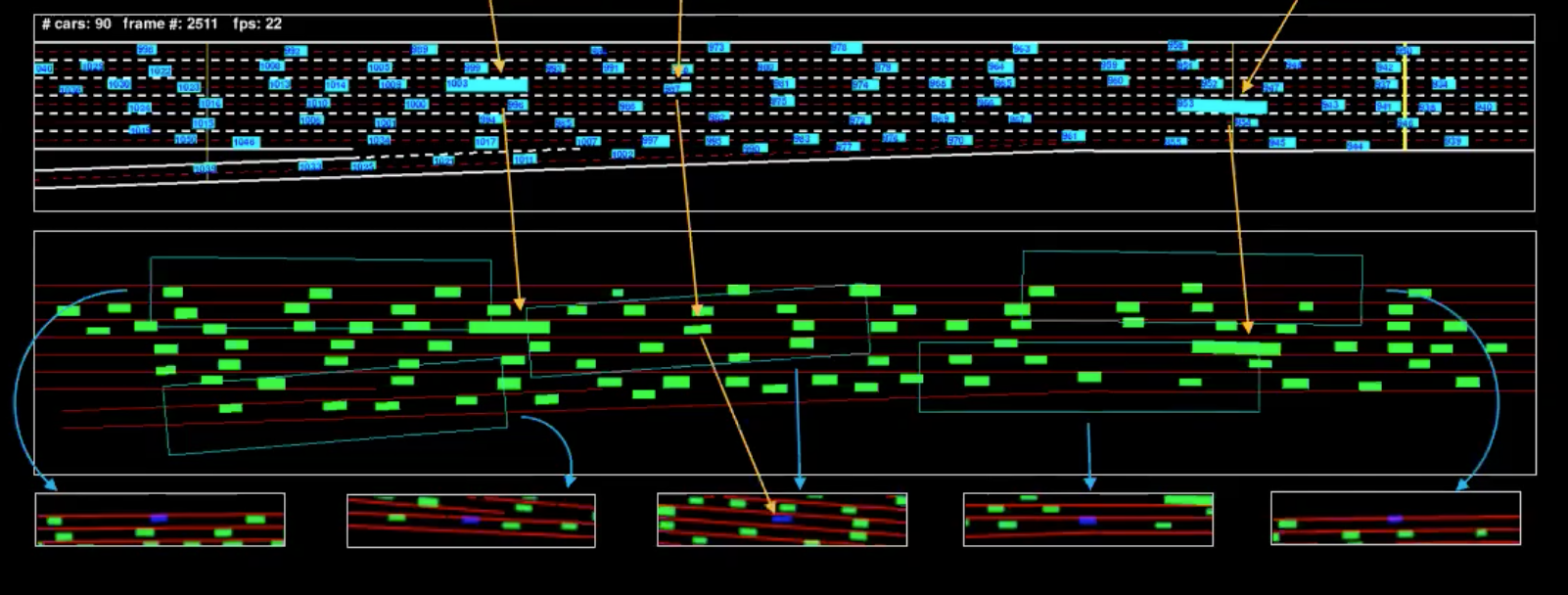
図4: 単一フレームの機械による表現
青色のイラストはフィードで、緑色のイラストは我々が機械表現と呼ぶものです。これをよりよく理解するために、いくつかの車両を分離しました(図中のマーク)。下の図は、これらの車両の視野のバウンディングボックスです。
コスト
ここでは2種類のコストがあります:車線コストと近接コストです。車線コストは車線内の状態を示し、近接コストは他の車との距離を示します。
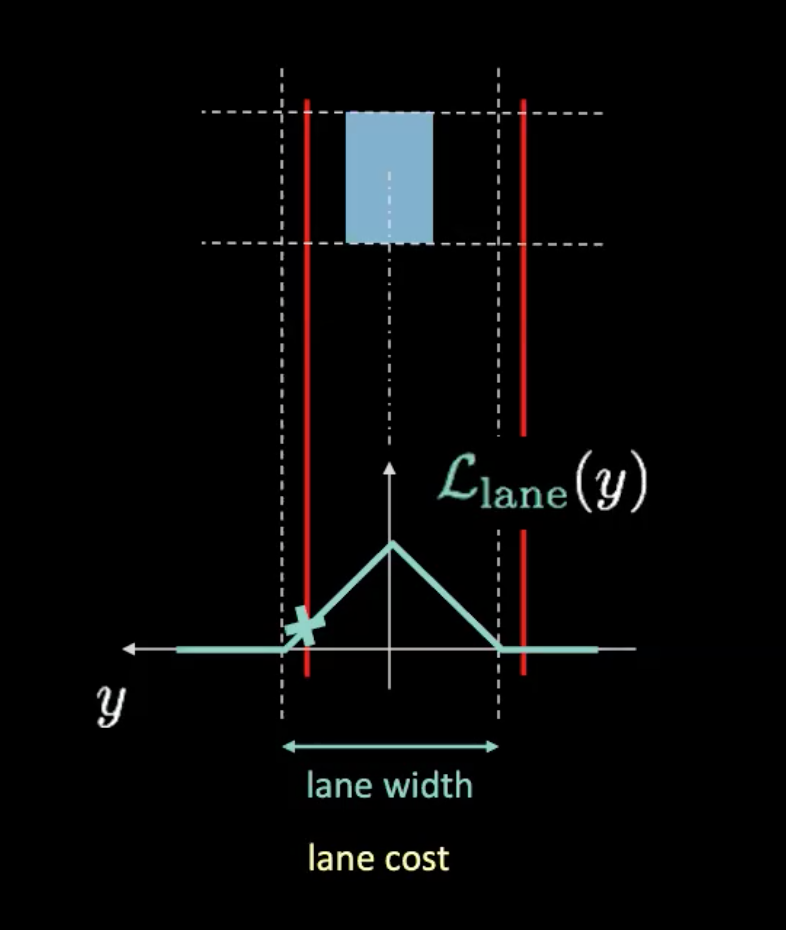
図5: 車線コスト
上の図では、点線は実際の車線を表し、赤線は現在の車の位置から車線のコストを計算するのに役立ちます。 赤線は車の移動に合わせて移動します。赤い線と潜在的なカーブの交点の高さ(シアン色)がコストを示しています。車が車線の中心にいる場合は、赤線の両方が実際の車線と重なり、コストはゼロになります。一方、車が中心から離れると、赤線も移動し、コストはゼロではありません。 <!–
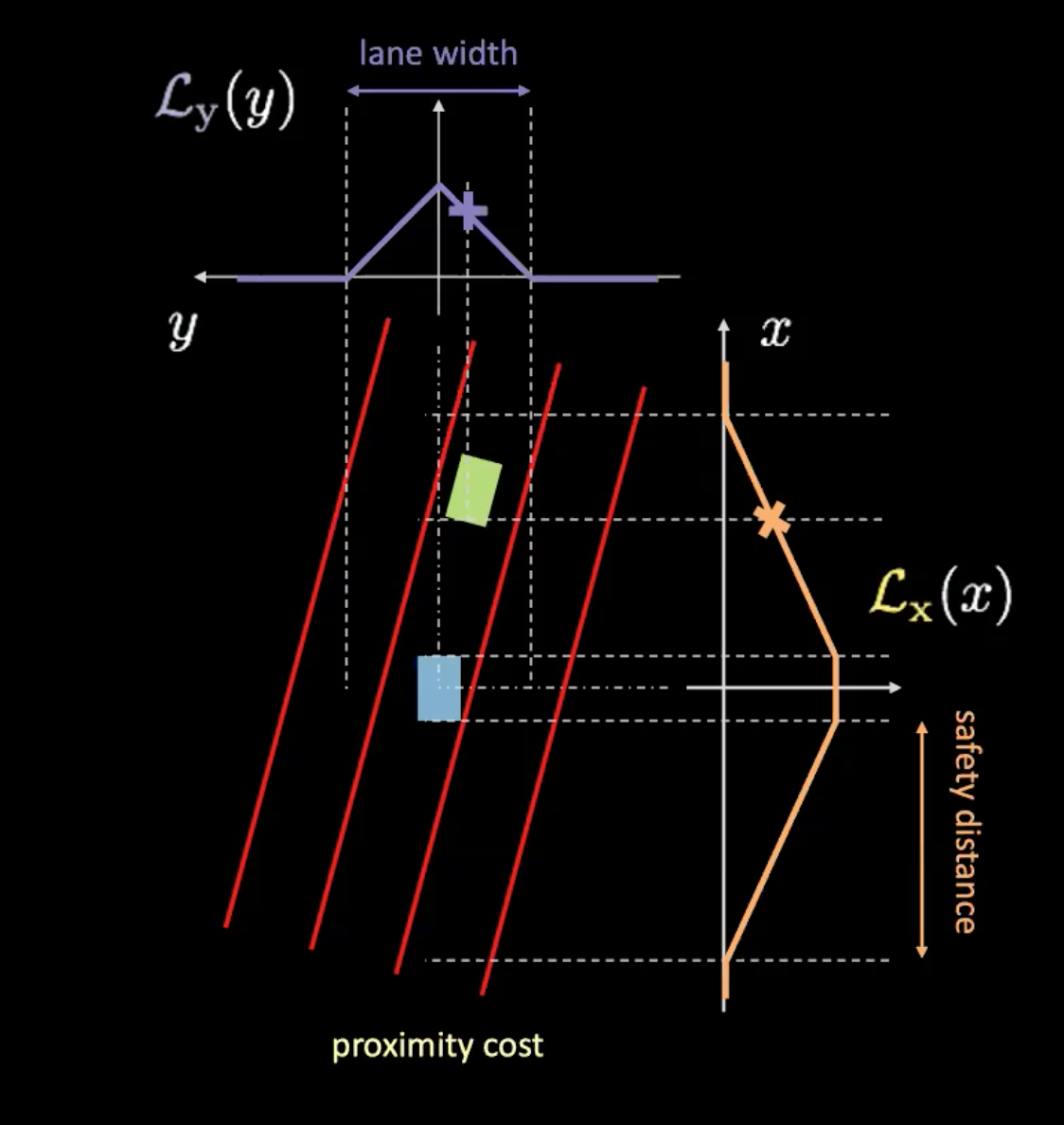
Figure 6: Proximity cost
–>

図6: 近接コスト
近接コストには2つの要素があります($\mathcal{L}_x$と$\mathcal{L}_y$)。この2つの成分は、車線コストと同様に、車の速度に依存します。図6のオレンジ色の曲線が安全距離を示しています。車の速度が速くなると、オレンジ色のカーブが広がります。つまり、車の速度が速くなればなるほど、前方と後方に目を向ける必要が出てくるということです。オレンジ色のカーブと車の交差するところの高さが $\mathcal{L}_x$ を決定します。
これら2つの成分の積が 近接コストを与えてくれます。
世界モデルを学習する
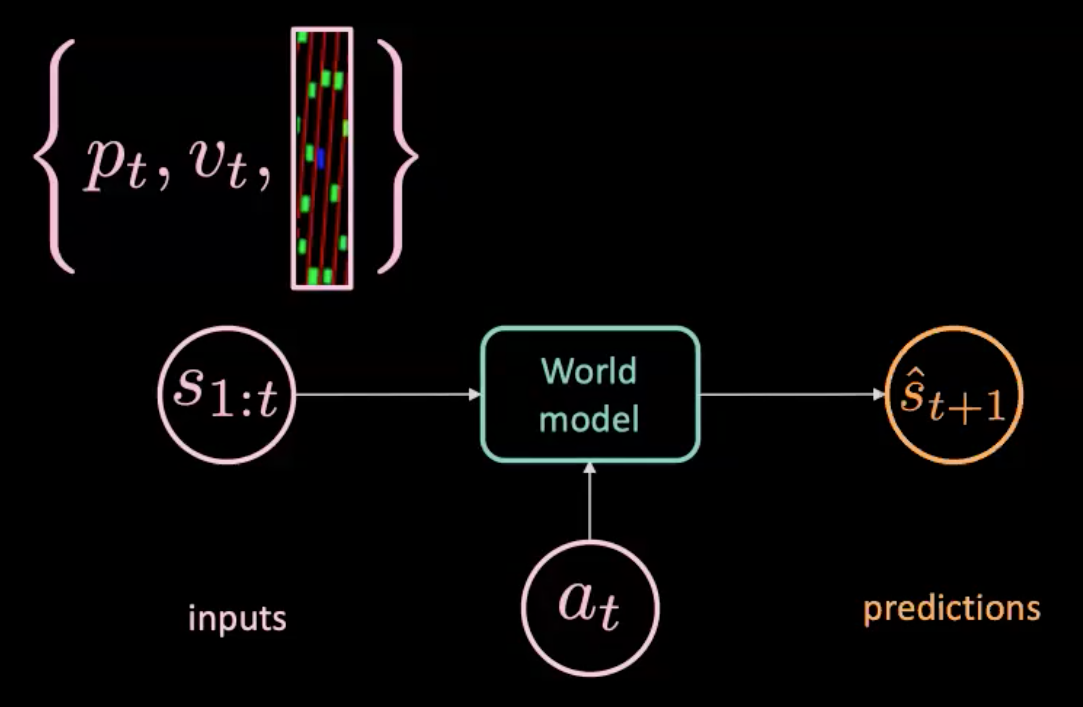
図7: 世界モデルのイラスト
世界モデルは、アクション$a_t$(操縦、ブレーキ、加速)と$s_{1:t}$(各状態をその時の位置、速度、文脈画像で表現した状態の列)を与えられ、次の状態$\hat s_{t+1}$を予測します。 一方、実世界を通して実際に何が起こったかを知ることができます($s_{t+1}$)。予測値($\hat s_{t+1}$)と目標値($s_{t+1}$)の間のMSE(平均二乗誤差)を最適化してモデルを学習します。
決定論的な予測器-デコーダ
世界モデルを学習する方法の一つは、以下に説明する予測器-デコーダモデルを使用することです。
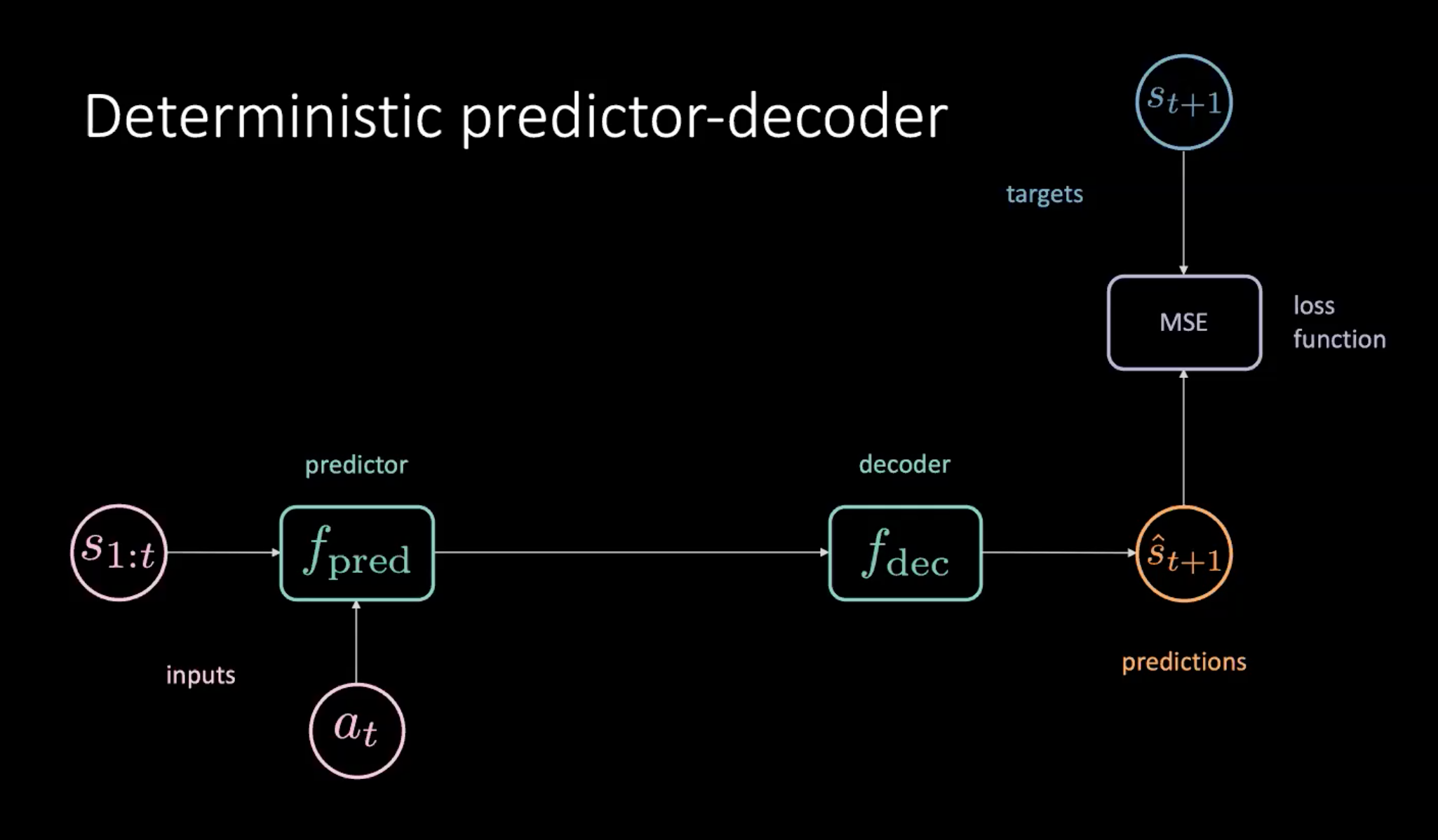
図8: 世界モデルを学習するための決定論的な予測器-デコーダ 図8に示されているように、状態($s_{1:t}$)と行動($a_t$)のシーケンスが予測器モジュールに提供されています。予測器は、デコーダに渡す将来の潜在表現を出力します。デコーダは、将来の潜在表現をデコードし、予測値($\hat s_{t+1}$)を出力します。そして、予測 $\hat s_{t+1}$ とターゲット $s_{t+1}$ の間のMSEを最小化することでモデルを学習します。

図9: 実際の未来と決定論的な未来
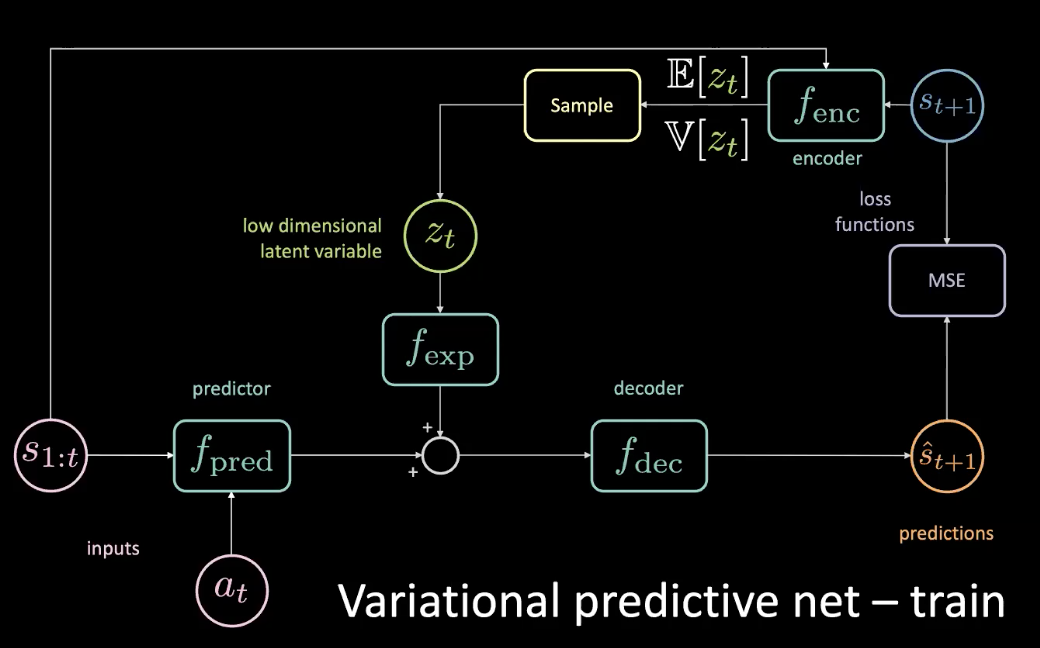
図10: 変分予測ネットワーク:訓練
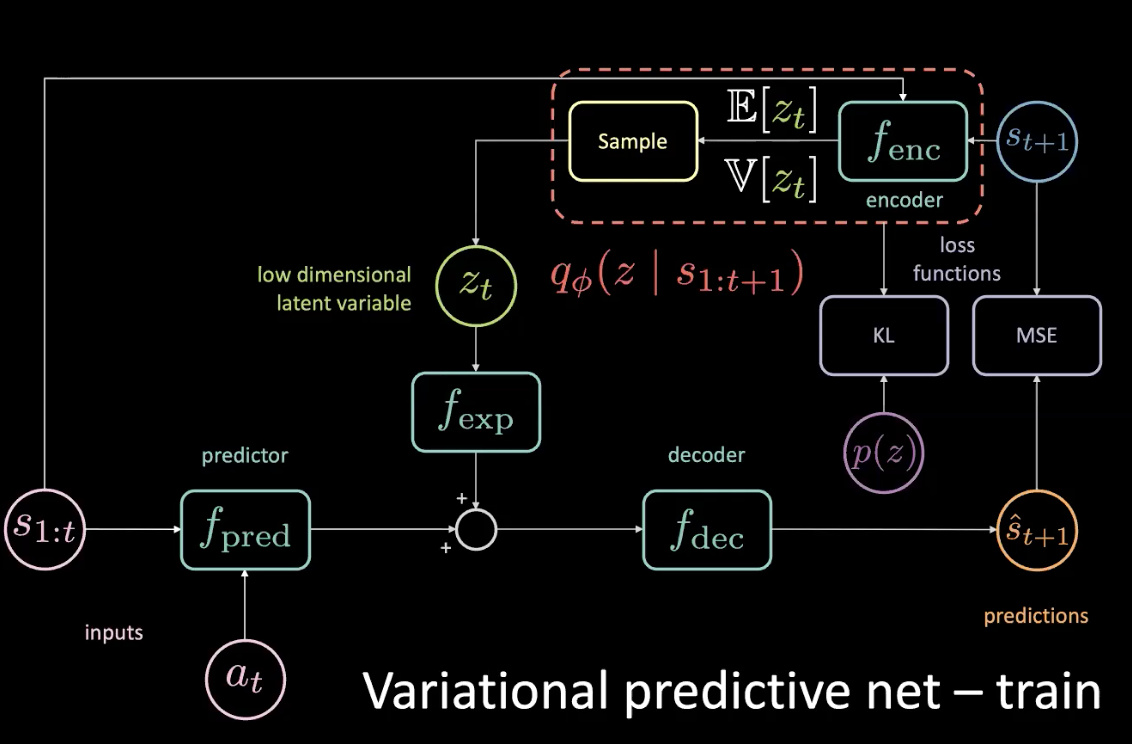
図11: 変分予測ネットワーク:訓練(事前分布つき)
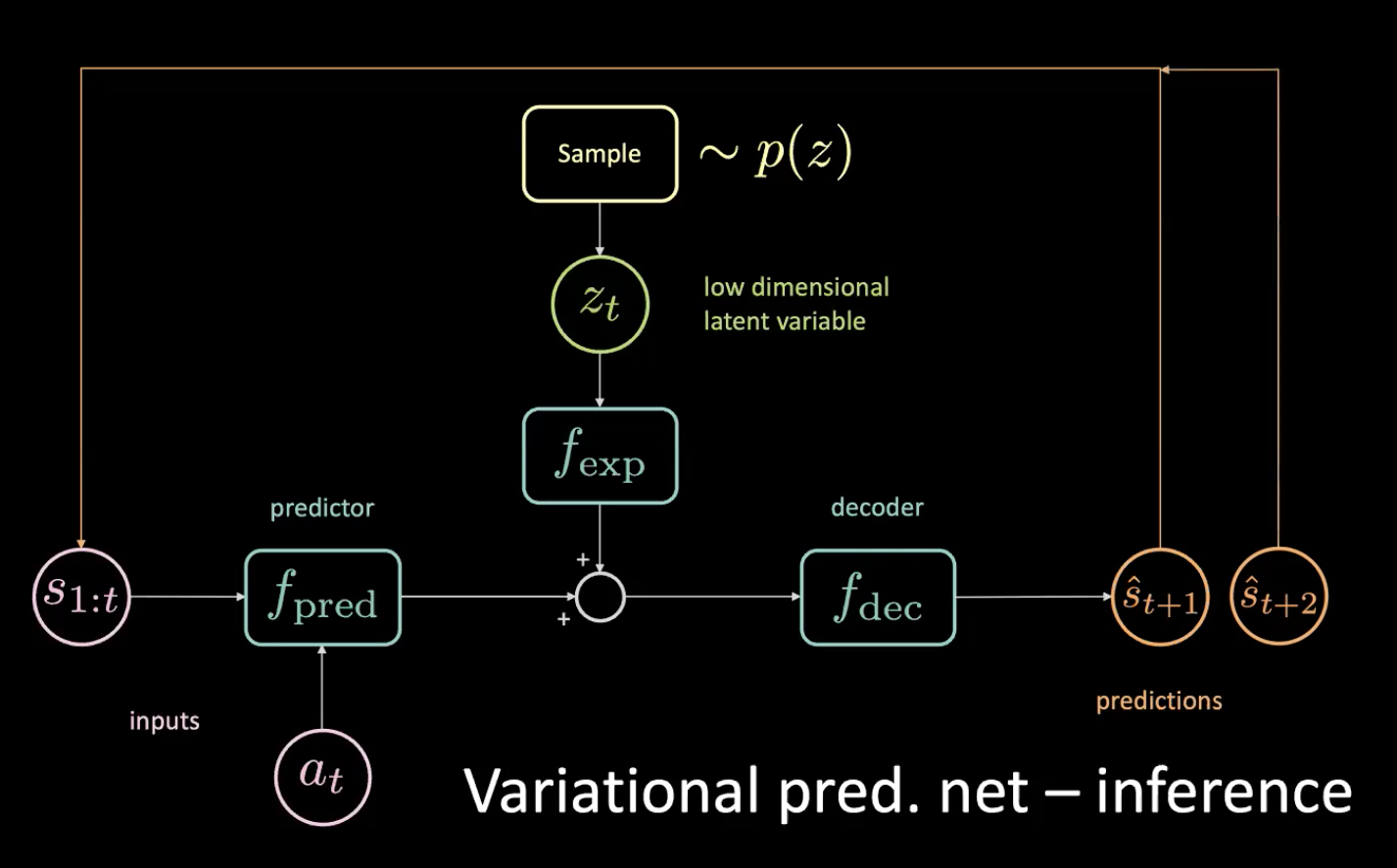
図12: 変分予測ネットワーク:推論
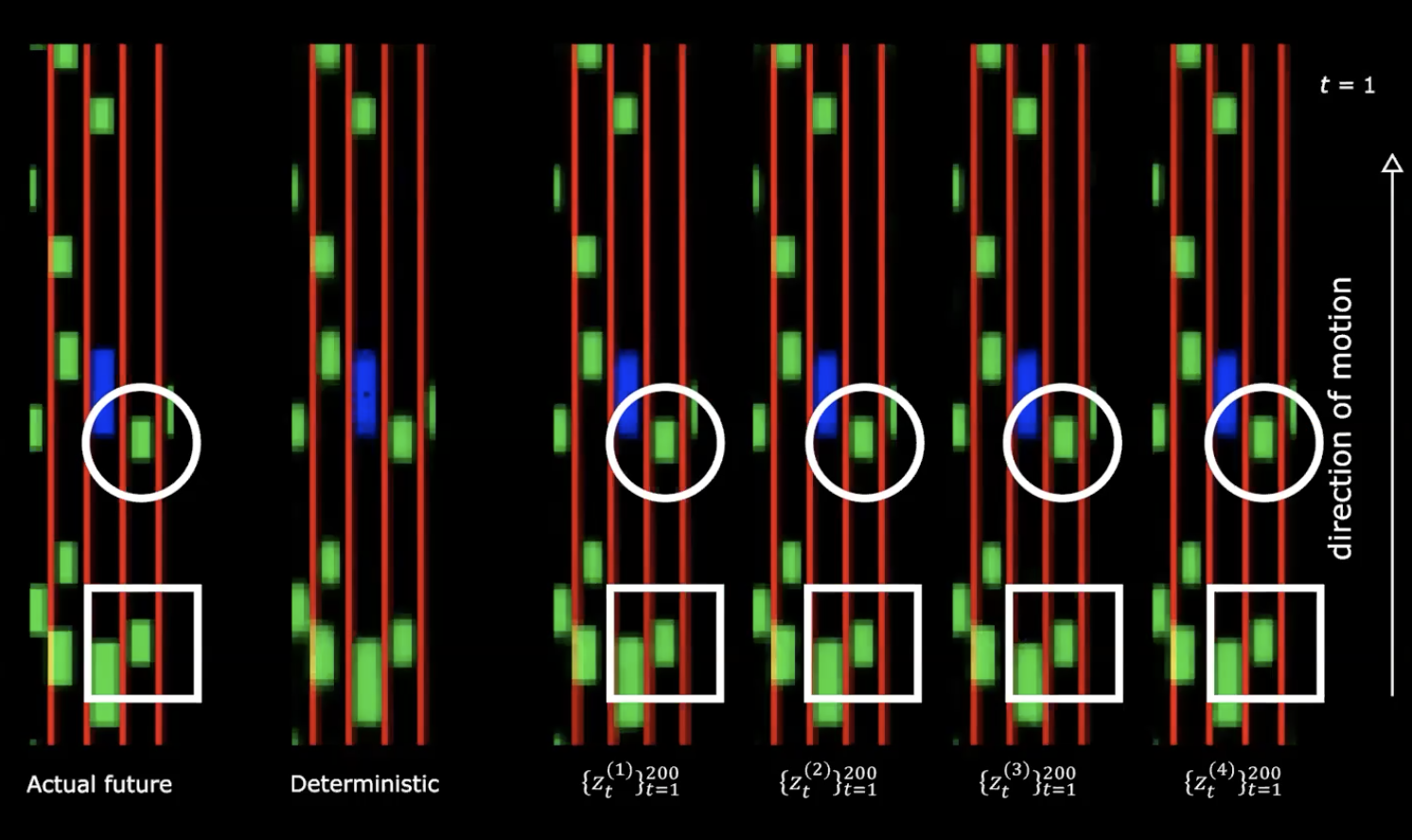
図13: 実際の未来 vs 決定論的な場合
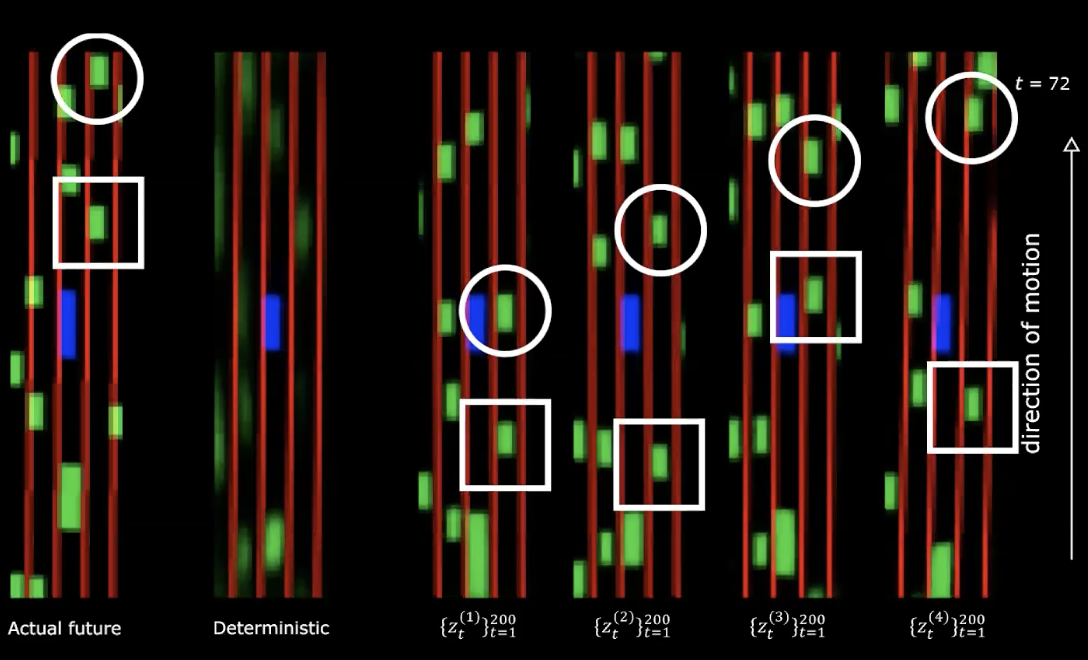
図14: 実際の未来 vs 決定論的な場合:動いた後
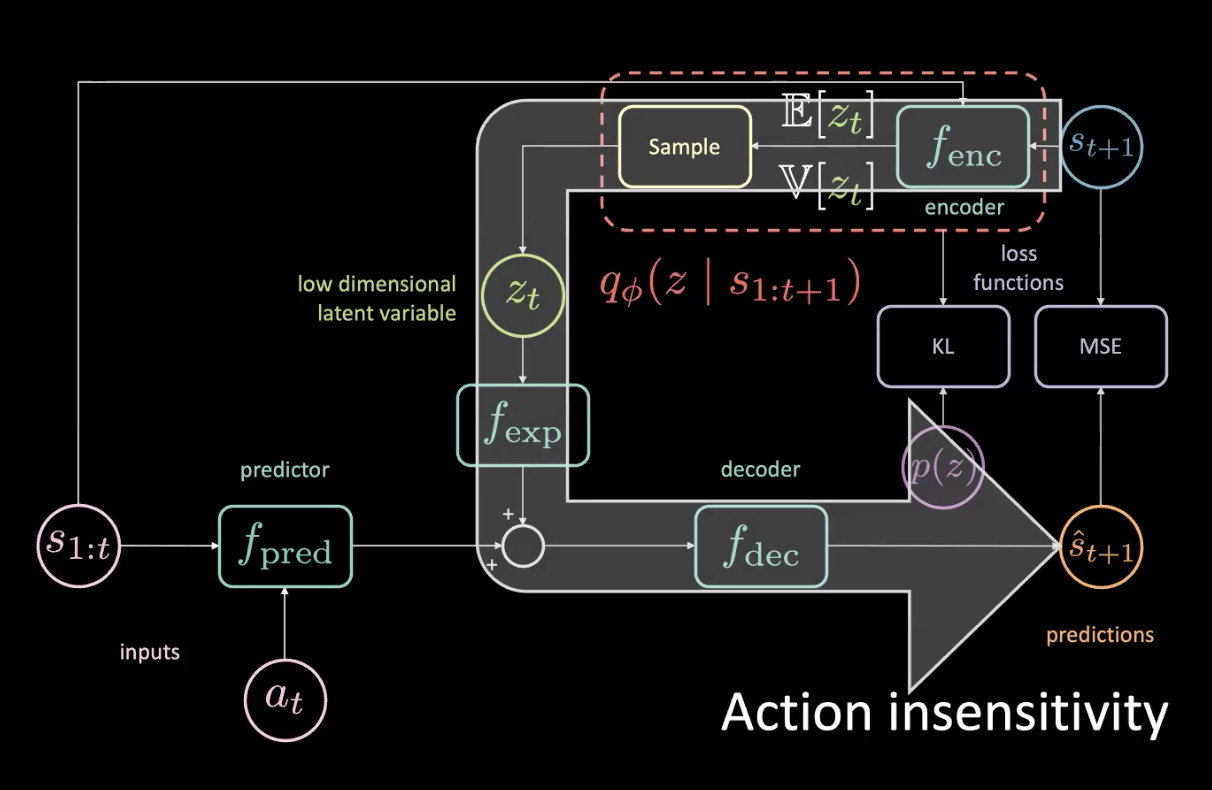
図15: 問題:行動に対する感度の低さ

図16: 問題:行動に対する感度の低さ
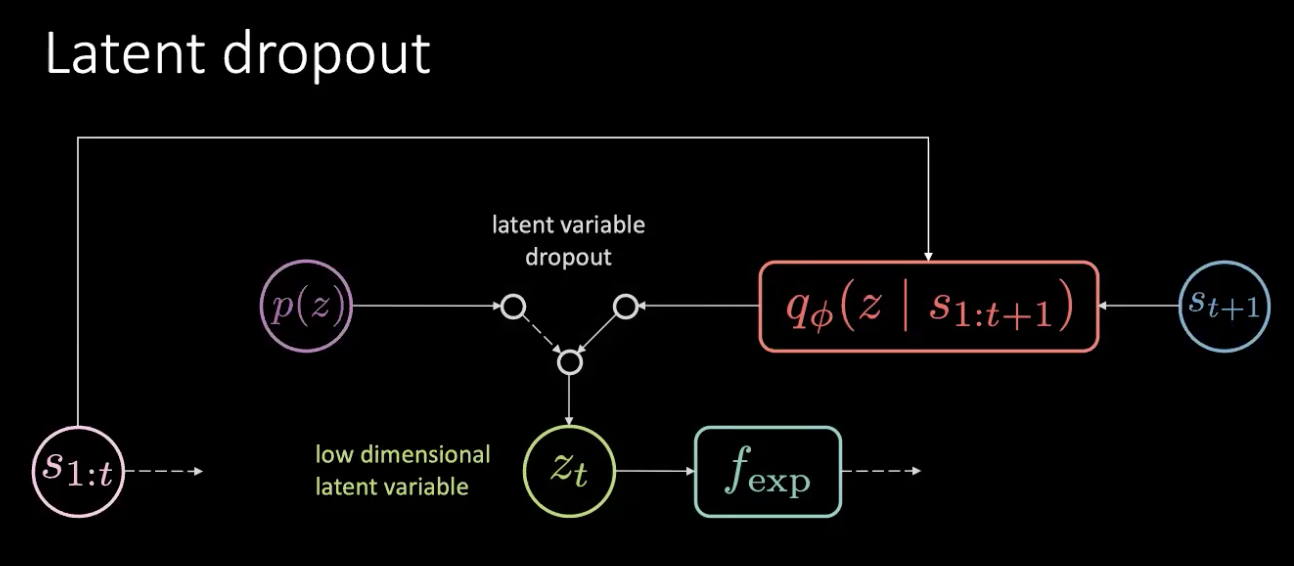
図17: 解決策:潜在変数のドロップアウト

図18: 潜在変数のドロップアウトによる性能
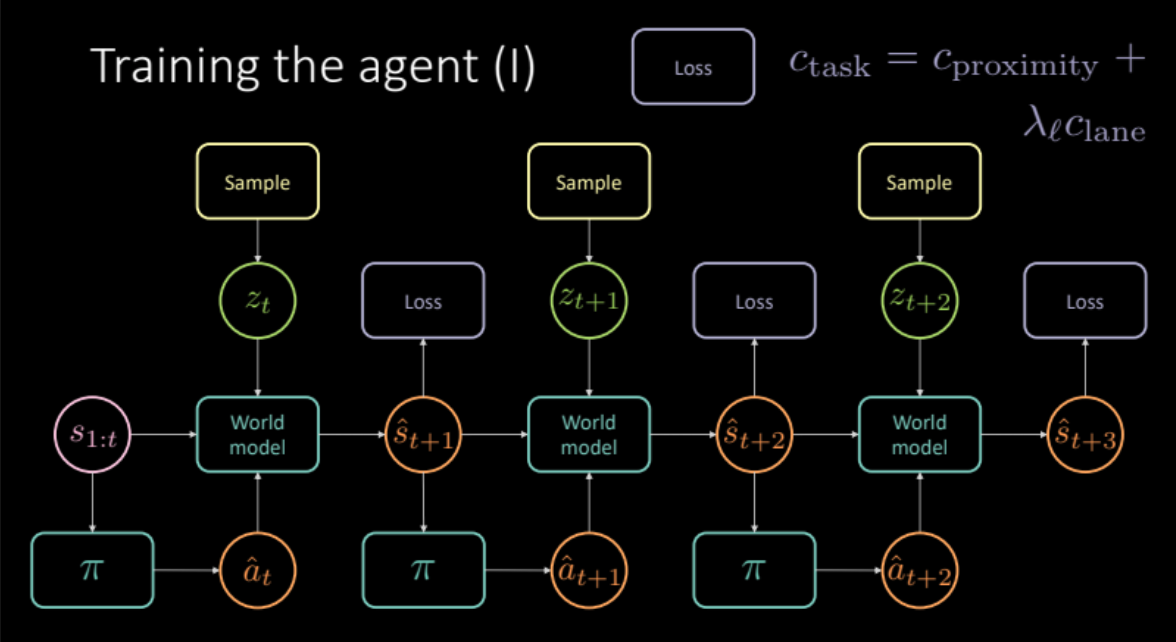
図19: タスク固有のモデルアーキテクチャ

図20: 学習された方策:エージェントはぶつかりあったり、道から離れていきます。
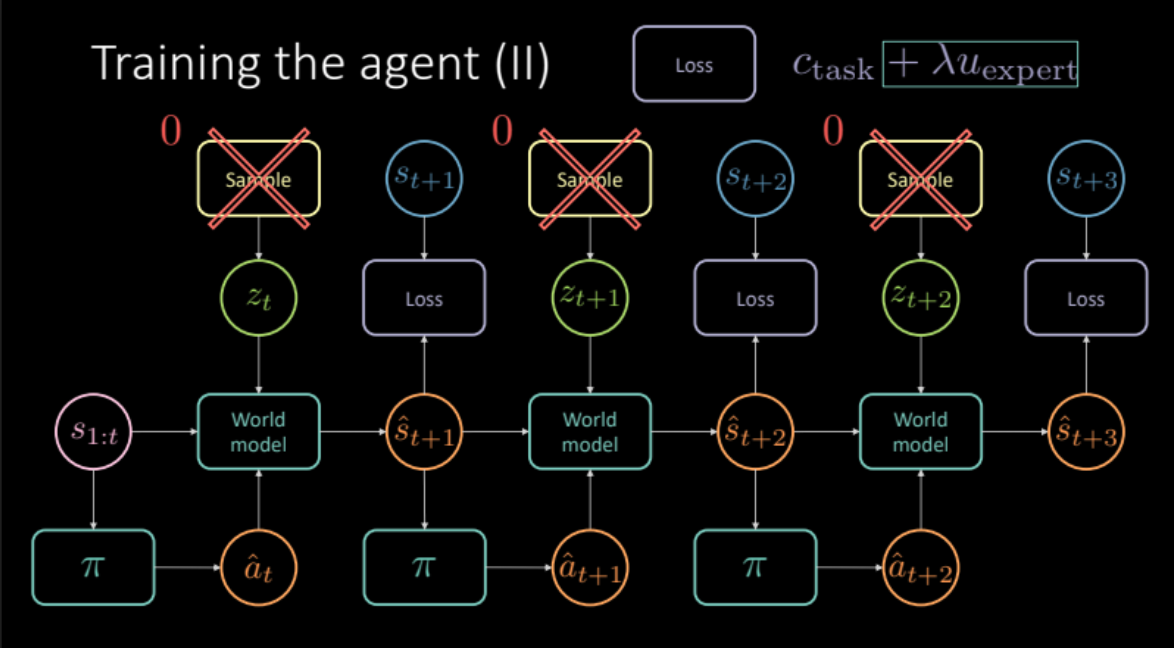
図21: エキスパートによる正則化に基づくモデルアーキテクチャ

図22: エキスパートを真似することで学習された方策
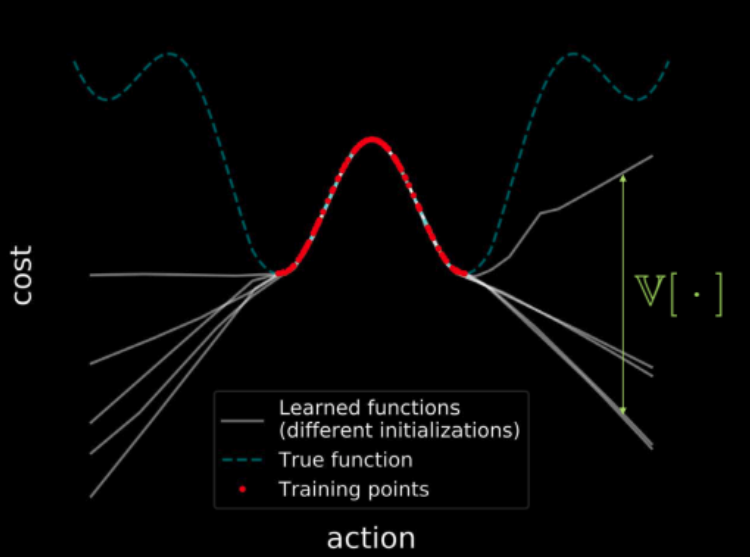
図23: 全入力空間にわたるコストの可視化
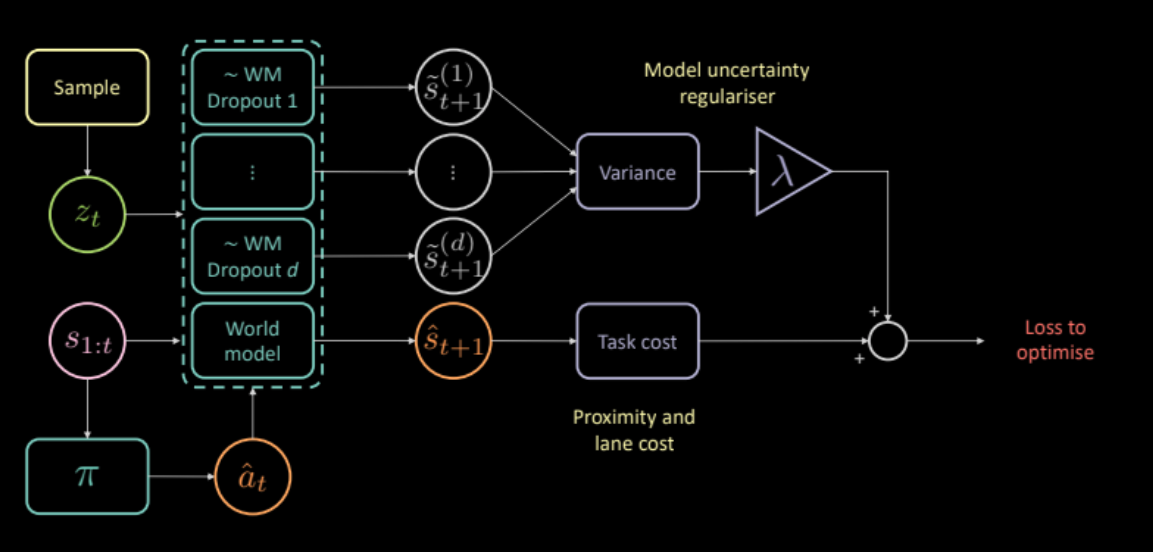
図24: 不確実性に対する正則化を加えたモデルアーキテクチャ

図25: 不確実性の正則化に基づいて学習された方策

図26: 不確実性の正則化つきモデルの性能
📝 Anuj Menta, Dipika Rajesh, Vikas Patidar, Mohith Damarapati
Shiro Takagi
14 April 2020