Loss Functions (cont.) and Loss Functions for Energy Based Models

Binary Cross Entropy (BCE) Loss - nn.BCELoss()

この損失は、2つのクラスしかない場合のためのクロスエントロピーの特殊なケースであり、より単純な関数として表現できます。これは、例えばオートエンコーダーの再構成誤差を測定するために使われます。この式は、$x$ と $y$ が確率であると仮定しているので、厳密には0と1の間にあります。

Kullback-Leibler Divergence Loss - nn.KLDivLoss()

これは、ターゲットがワンホット分布(i.e. $y$がカテゴリ)の場合の単純な損失関数です。ここでも、$x$ と $y$ が確率であると仮定しています。これは、softmaxやlog-softmaxとマージされないという欠点があり、数値的な安定性に問題が生じるかもしれません。

BCE Loss with Logits - nn.BCEWithLogitsLoss()

このバージョンのバイナリクロスエントロピー損失は、softmaxを通過していないスコアを入力に取るため、$x$が0から1の間であると仮定していません。 そして、その範囲内であることを確認するためにシグモイドに渡されます。損失関数は、このように組み合わせると数値的に安定する可能性が高くなります。

Margin Ranking Loss - nn.MarginRankingLoss()

マージン損失は損失の重要なカテゴリーです。2つの入力がある場合、この損失関数は、片方の入力がもう片方の入力よりも少なくともあるマージンの分大きくなるようにしたいということを表しています。この場合、$y$は二値変数 $y \in { -1, 1}$です。2つの入力が2つのカテゴリのスコアだとします。正しいカテゴリのスコアを、正しくないカテゴリのスコアよりも、少なくともいくつかのマージンで大きくしたいとします。 ヒンジ損失のように、$y*(x_1-x_2)$がマージンよりも大きければ、コストは0になります。 それよりも小さければ、コストは直線的に増加します。これを分類に使う場合、$x_1$ は正解のスコア、$x_2$ はミニバッチの中で最もスコアの高い不正解のスコアとなります。エネルギーベースモデル(後述)で使用する場合、この損失関数は正解 $x_1$ を押し下げ、不正解 $x_2$ を押し上げます。

Triplet Margin Loss - nn.TripletMarginLoss()

この損失は、サンプル間の相対的な類似度を測定するために用いられます。例えば、同じカテゴリの2つの画像をCNNに通し、2つのベクトルを得たとします。この2つのベクトル間の距離をできるだけ小さくしたいとします。異なるカテゴリを持つ2つの画像をCNNに通すと、それらのベクトル間の距離は可能な限り大きくなります。この損失関数は、最初の距離を0に、2番目の距離をあるマージンよりも大きくしようとします。 しかし、重要なのは、良いペアの間の距離が悪いペアの間の距離よりも小さいということだけです。

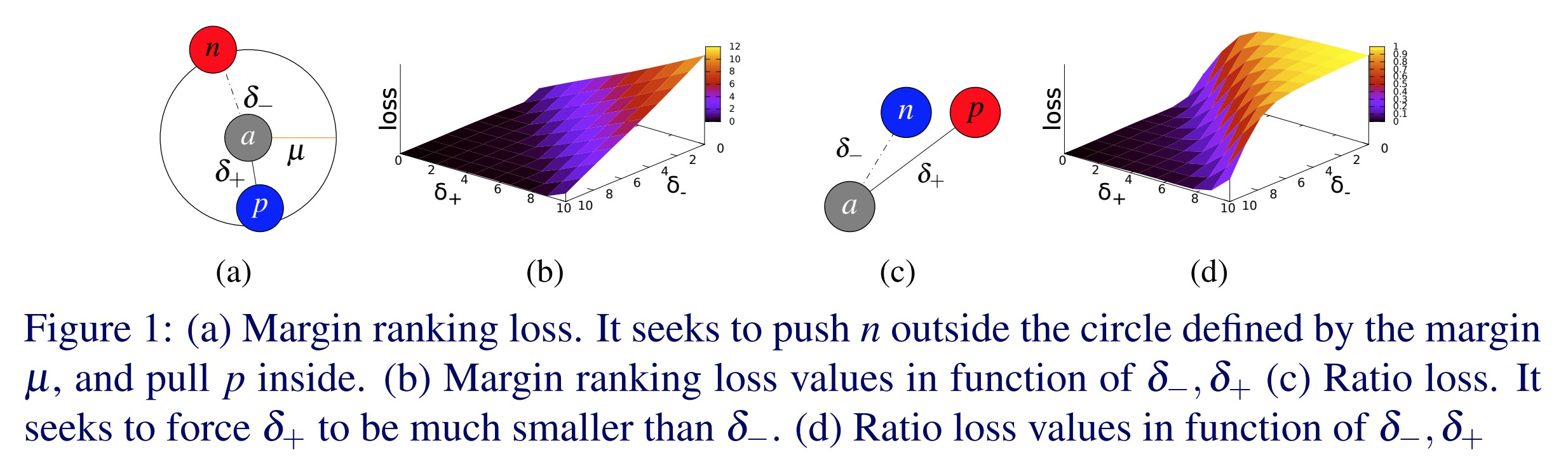
図1: Triplet Margin Loss

これは元々、Googleの画像検索システムの訓練に使われていたものです。当時は、Googleにクエリを入力すると、そのクエリをベクトルにエンコードしていました。そして、そのベクトルを、事前にインデックス化された画像のベクトルの束と比較します。そのようにして、Googleはあなたが投げたクエリベクトルに最も近い画像を検索していました。

Soft Margin Loss - nn.SoftMarginLoss()

入力テンソル$x$とターゲットテンソル$y$（1または-1を含む）の間の2クラス分類ロジスティック損失を最適化する基準を作成します。

• これは、マージン損失のソフトマックス版です。正の値の束と負の値の束があり、ソフトマックスを通過させたいとします。この関数は、正しい$x[i]$の$\text{exp}(-y[i]*x[i])$を、他のものよりも小さくしようとします。
• この損失関数は、$y[i]*x[i]$の正の値をより近くに引き寄せ、負の値をより遠くに引き離そうとしますが、ハードマージンとは対照的に、連続的で指数関数的に減衰する効果を持った損失が得られます。

Multi-Class Hinge Loss - nn.MultiLabelMarginLoss()

このマージンベースの損失は、異なる入力が様々なターゲットを持つことを可能にします。この場合、高いスコアを出したいカテゴリがいくつかあり、すべてのカテゴリのヒンジ損失を合計します。EBMの場合、この損失関数は、希望するカテゴリを押し下げ、希望しないカテゴリを押し上げます。

Hinge Embedding Loss - nn.HingeEmbeddingLoss()

これは2つの入力が似ているか似ていないかを測定するヒンジ埋め込み損失で、半教師あり学習に使用されます。似ているものをまとめて、似ていないものを押しのけます。変数$y$は、スコアのペアがある方向に進む必要があるかどうかを示します。ヒンジ損失を使うと、$y$が1であればスコアは正となり、$y$が-1であればあるマージン$\Delta$が得られます。

Cosine Embedding Loss - nn.CosineEmbeddingLoss()

この損失は、コサイン距離を用いて2つの入力が似ているか似ていないかを測定するために用いられ、非線形埋め込み学習や半教師あり学習などに用いられます。

• 別の言い方をすれば、１から2つのベクトル間の角度のコサインを引いた値が、基本的には正規化されたユークリッド距離となります。
• これを用いる利点は、2つのベクトルの距離をできるだけ大きくしたいときに、ベクトルを非常に長くすることで、ネットワークがこれを達成することが非常に簡単にできてしまうという事実に起因しています。もちろんこれは最適ではありません。ベクトルを大きくするのではなく、ベクトルを正しい方向に回転させたいので、ベクトルを正規化し、正規化されたユークリッド距離を計算します。
• 正の場合、この損失は可能な限りベクトルを揃えようとします。負のペアでは、コサインを特定のマージンよりも小さくしようとします。ここでのマージンは小さな正の値である必要があります。
• 高次元空間では、球の赤道付近に多くの領域があります。正規化後、すべての点は球上で正規化されます。意味的に似ているサンプルが近くにあることが望ましいです。似ていないサンプルは直交していなければなりません。反対の極には1つの点しかないので、それらが互いに反対になって欲しくはありません。むしろ、赤道上には非常に大きなスペースがあるので、この面積を利用できるように、マージンを小さな正の値にしたいのです。

Connectionist Temporal Classification (CTC) Loss - nn.CTCLoss()

連続な（分割されていない）時系列とターゲット系列の間の損失を計算します。

• CTC損失は，入力からターゲットへの可能性のあるアラインメントの確率を合計し、各入力ノードに対して微分可能な損失値を生成します。
• 入力からターゲットへのアラインメントは、多対一であると仮定され、ターゲット系列の長さが入力の長さ以下になるように制限されます。
• 出力がカテゴリのスコアに対応するベクトルの系列である場合に便利です。

図2: 音声認識のためのCTC損失

応用例：音声認識システム

• 目標：10ミリ秒ごとにどの単語が発音されているかを予測します。
• 各単語は音の系列で表されます。
• 人の話すスピードに応じて、異なる長さの音が同じ単語にマッピングされることがあります。
• 入力音列から出力音列への最適なマッピングを見つけます。このための良い方法は、動的プログラミングを使用して、最小コストのパスを見つけることです。

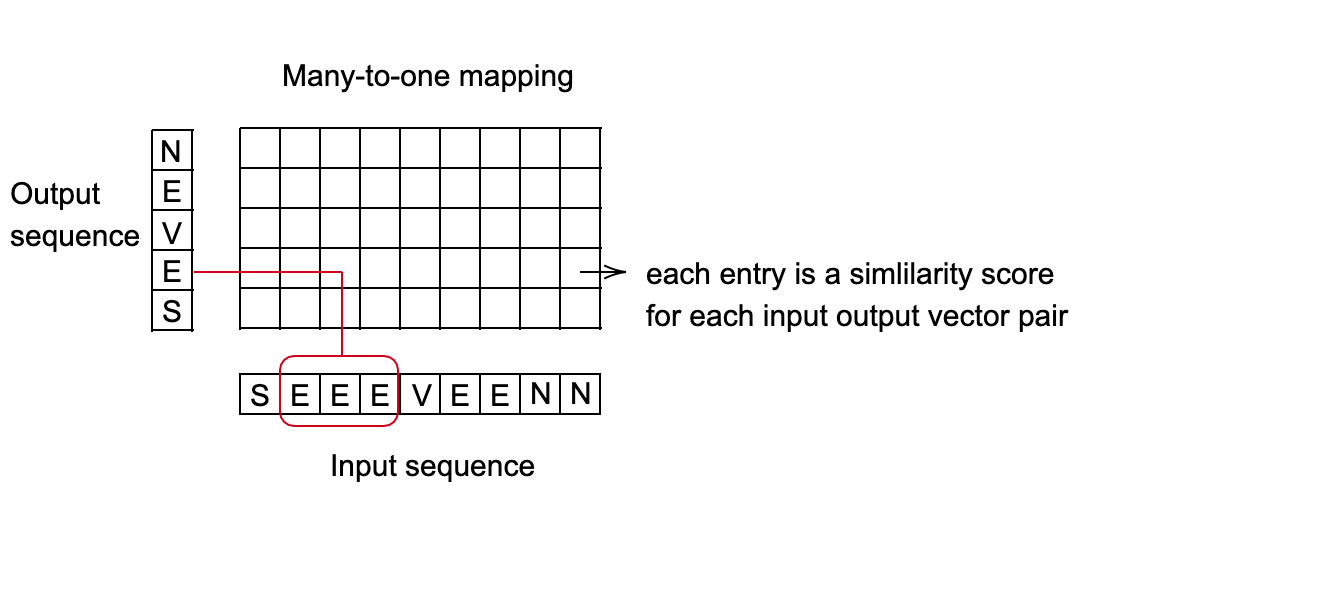
図3: 多対一マッピングのセットアップ

エネルギーベースモデル (Part IV) - 損失関数

アークテクチャと損失汎関数

エネルギー関数の族: $\mathcal{E} = {E(W,Y, X) : W \in \mathcal{W}}$.

訓練集合: $S = {(X^i, Y^i): i = 1 \cdots P}$

損失汎関数: $\mathcal{L} (E, S)$

• 汎関数とは、他の関数の関数を意味します。この場合は、汎関数 $\mathcal{L} (E, S)$は、エネルギー関数$E$の関数です。
• $E$ は $W$ でパラメトライズされているので、汎関数を $W$ の損失関数に変えることができます: $\mathcal{L} (W, S)$
• 訓練集合でエネルギー関数の質を測定します。
• サンプルの並べ替えと反復に対して不変です。

訓練: $W^* = \min_{W\in \mathcal{W}} \mathcal{L}(W, S)$.

損失汎関数の形式：

• $L(Y^i, E(W, \mathcal{Y}, X^i))$ はサンプルごとの損失
• $Y^i$ は理想の答えで、 カテゴリーか画像全体など
• $E(W, \mathcal{Y}, X^i)$ は与えられた $X_i$ に対して $Y$ の変化に対するエネルギー関数
• $R(W)$ は正則化項

良い損失関数の設計

正解のエネルギーを押し下げる。

不正解のエネルギーを押し上げる。特に正解よりも小さい場合。

損失関数の例

Energy Loss

この損失関数は、単に正解のエネルギーを押し下げます。ネットワークが正しく設計されていない場合、正解のエネルギーを小さくしようとするだけで他の場所でエネルギーを押し上げないので、それはほとんど平坦なエネルギー関数になるかもしれません。したがって、システムが崩壊する可能性があります。

Negative Log-Likelihood Loss

この損失関数は正解のエネルギーを押し下げ、確率に比例して全ての答えのエネルギーを押し上げます。これは、$\beta \rightarrow \infty$のとき、パーセプトロンの損失に帰着されます。構造化された出力を用いた識別訓練のために多くのコミュニティで長い間使われてきました。

確率モデルとは、以下を満たすEBMのことです

• エネルギーが、Y(予測される変数)の上で積分できる。
• 損失関数が負の対数尤度

Perceptron Loss

\(L_{perceptron}(Y^i,E(W,\mathcal Y, X^*))=E(W,Y^i,X^i)-\min_{Y\in \mathcal Y} E(W,Y,X^i)\) <!– Very similar to the perceptron loss from 60+ years ago, and it’s always positive because the minimum is also taken over $Y^i$, so $E(W,Y^i,X^i)-\min_{Y\in\mathcal Y} E(W,Y,X^i)\geq E(W,Y^i,X^i)-E(W,Y^i,X^i)=0$. The same computation shows that it give exactly zero only when $Y^i$ is the correct answer.

This loss makes the energy of the correct answer small, and at the same time, makes the energy for all other answers as large as possible. However, this loss does not prevent the function from giving the same value to every incorrect answer $Y^i$, so in this sense, it is a bad loss function for non-linear systems. To improve this loss, we define the most offending incorrect answer. –>

60年以上前のパーセプトロンの損失と非常によく似ていて、最小値も $Y^i$ の上に取られるので、それは常に正です：$E(W,Y^i,X^i)-\min_{Y\in\mathcal Y} E(W,Y,X^i)\geq E(W,Y^i,X^i)-E(W,Y^i,X^i)=0$。同じ計算をすると、$Y^i$が正解のときだけ正確に0を与えることがわかります。

この損失は、正解のエネルギーを小さくすると同時に、他のすべての答えのエネルギーをできるだけ大きくします。しかし、この損失は、すべての不正解 $y^i$ に対して同じ値を与えることを妨げるものではないので、この意味では、非線形系にとっては悪い損失関数と言えます。この損失を改善するために、最も問題となる不正解という概念を定義します。

Generalized Margin Loss

最も問題となる不正解：離散的な場合

$y$ を離散変数とします。すると、ある訓練サンプル $(X^i,Y^i)$ に対して、最も問題となる不正解 $\bar Y^i$ は、不正解となる可能性のあるすべての答えの中で、最も低いエネルギーを持つ答えです。すなわち、

最も問題となる不正解：連続的な場合

$y$を連続変数とします。すると、ある訓練サンプル$(X^i,Y^i)$に対して、最も問題となる不正解 $\bar Y^i$は、正解から少なくとも$\epsilon$離れているすべての答えの中で、最も低いエネルギーを持っている答えです。つまり

離散的なケースでは、最も問題となる不正解は、正解ではないエネルギーが最も小さいものです。連続の場合、 $Y$ が $Y^i$ に極端に近い場合のエネルギーは、 $E(W,Y^i,X^i)$ に近いはずです。さらに、$Y^i$と等しくない$Y$の$\text{argmin}$は0になります。 その結果、ある距離$\epsilon$に対して、$Y^i$から少なくとも$\epsilon$だけ離れた$Y$を「不正解」とすることにします。そのため、最適化は $Y^i$ から少なくとも$\epsilon$離れた $Y$についてだけ行われます。

もし、最も問題となる不正解のエネルギーが正解のエネルギーよりも高いことを、エネルギー関数が保証できるならば、このエネルギー関数はうまく機能するはずです。

Generalized Margin Loss Functionsの例

ヒンジ損失

\(L_{\text{hinge}}(W,Y^i,X^i)=( m + E(W,Y^i,X^i) - E(W,\bar Y^i,X^i) )^+\) ここで、$\bar Y^i$は、最も問題のある不正解です。この損失は、正解と最も問題のある不正解の差が少なくとも$m$であることを要請します。

図4: ヒンジ損失

Ｑ：どのようにして $m$ を選ぶのですか？

A: 任意ですが、最後の層の重みに影響します。

Log Loss

これは、「ソフト」ヒンジ損失と考えることができます。正解と最も問題のある不正解の差をヒンジで構成するのではなく、ソフトヒンジで構成するようになっています。この損失は「無限のマージン」を強制しようとしますが、傾きが指数関数的に減衰するため、それは起こりません。

図5: 対数損失

Square-Square Loss

この損失は、ヒンジの二乗とエネルギーの二乗を組み合わせたものです。この組み合わされたものは、エネルギーを最小化しようとしますが、最も問題のある不正解に対しては、少なくとも$m$のマージンを強制します。これは、Siamese netで使用される損失に非常に似ています。

Other Losses

全体をまとめたものです。良い損失関数と悪い損失関数をまとめてみました。

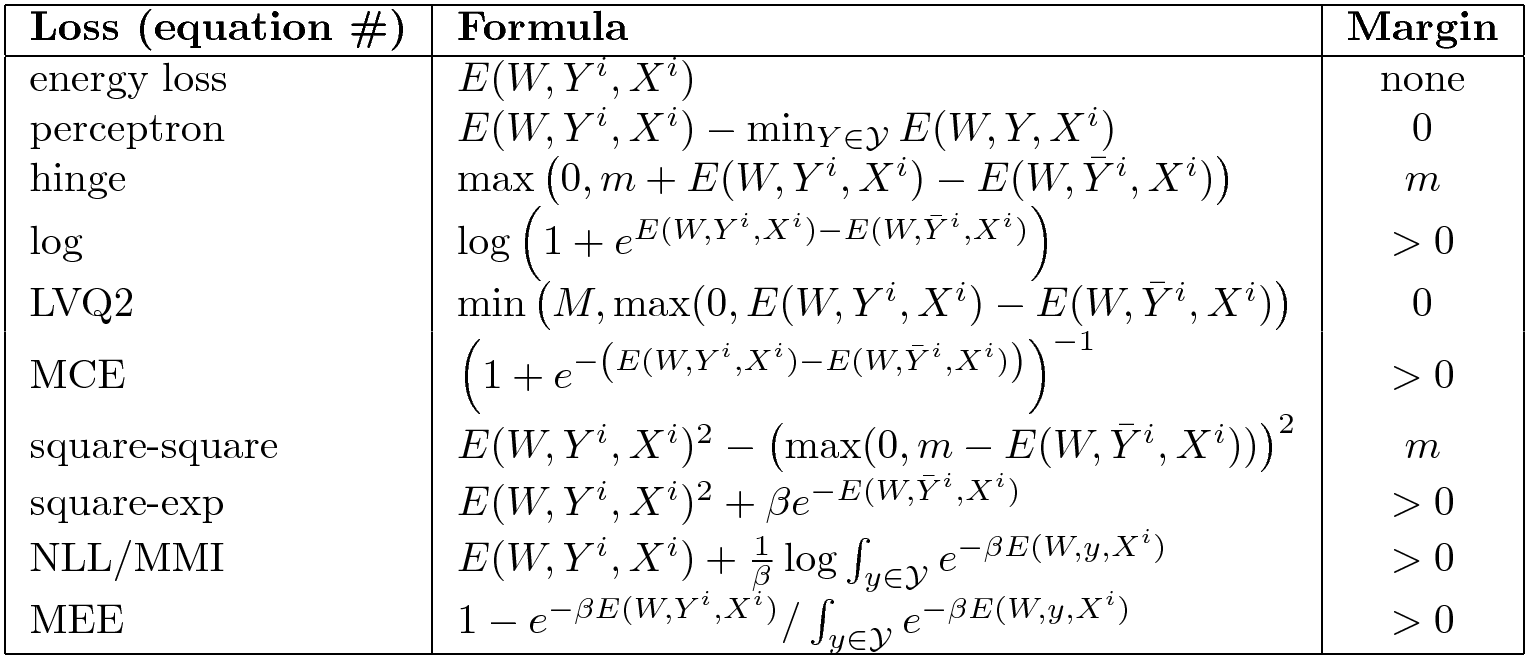
図6: EBM損失関数の選択

右辺は、エネルギー関数がマージンを強制するかどうかを示しています。昔ながらのエネルギー損失は、どこも押し上げないので、マージンがありません。エネルギー損失はすべての問題に適用できるわけではありません。パーセプトロン損失はエネルギーの線形なパラメトリゼーションの部分がある場合には有効ですが、一般的には有効ではありません。ヒンジ損失のように有限のマージンを持つものもあれば、ソフトヒンジのように無限のマージンを持つものもあります。

Q: 連続の場合に最も問題となる不正解 $\bar Y_i$ はどのようにして見つかるのでしょうか？

A: 近すぎるとニューラルネットで定義された関数が動きづらいので、パラメータがあまり動かないかもしれないため、$Y^i$から十分に離れた点を押し上げたいと考えます。しかし、一般的には、これは難しい問題であり、対照的なサンプルを選択する方法が解決しようとする問題です。これには一つの正しい方法はありません。

ここでは、 $y$ が離散的であると仮定しますが、もし連続的であれば、和は積分に置き換えられます。ここで、 $E(W, Y^i,X^i)-E(W,y,X^i)$は、正解と他の答えで評価された$E$の差です。$C(Y^i,y)$はマージンで、一般的には$y^i$と$y$の間の距離の尺度です。モチベーションは、不正解サンプル $y$ で押し上げたい量は、 $y$ と正解サンプル $y_i$ の間の距離に依存しているはずだということです。これは、最適化するのがより困難な損失になる可能性があります。