Activation and loss functions (part 1)

🎙️ Yann LeCun

活性化関数

本日の講義では、重要な活性化関数とそのPyTorchでの実装を見ていきます。これらの活性化関数は、特定の問題に対してより良い働きをすると主張する様々な論文から提案されているものです。

ReLU - nn.ReLU()

\[\text{ReLU}(x) = (x)^{+} = \max(0,x)\]
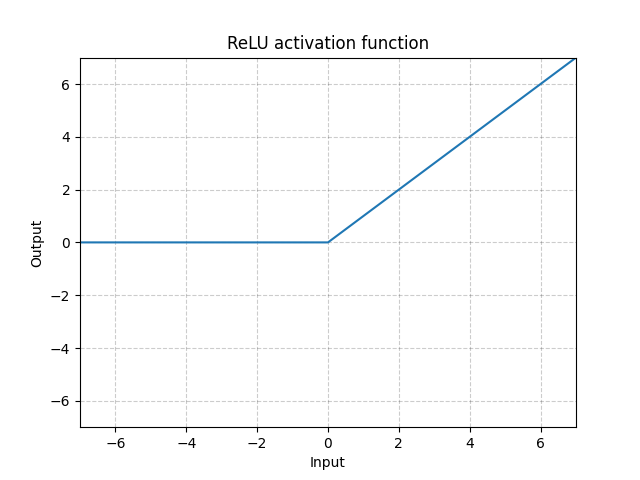
図1: ReLU

RReLU - nn.RReLU()

ReLUには様々亜種があります。Random ReLU (RReLU) は以下のように定義されます。

\[\text{RReLU}(x) = \begin{cases} x, & \text{if $x \geq 0$}\\ ax, & \text{otherwise} \end{cases}\]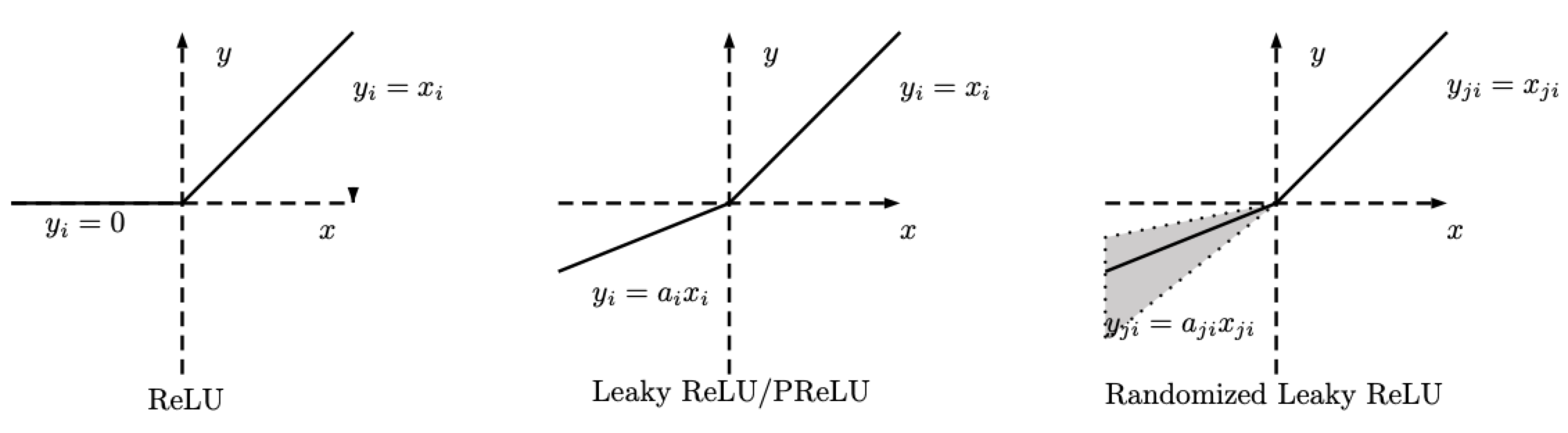
図2: ReLU, Leaky ReLU/PReLU, RReLU

RReLUでは、$a$は、学習中にサンプリングを所定の範囲に保つランダム変数であること、そしてテスト中は固定されたままにされることに注意してください。PReLUでは、$a$も学習されます。Leaky ReLUでは、$a$は固定されています。

LeakyReLU - nn.LeakyReLU()

\[\text{LeakyReLU}(x) = \begin{cases} x, & \text{if $x \geq 0$}\\ a_\text{negative slope}x, & \text{otherwise} \end{cases}\]
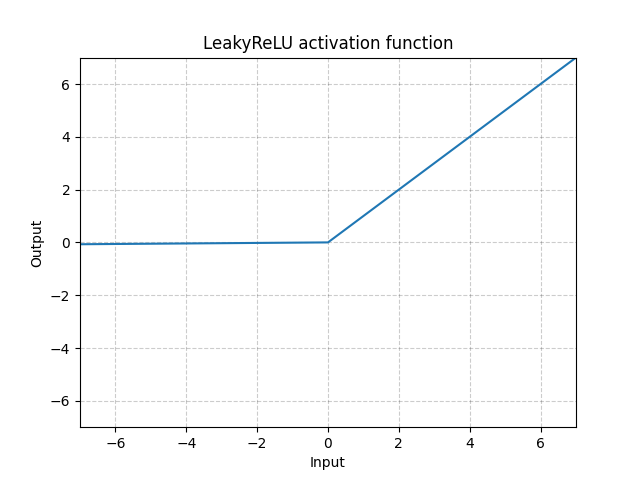
図3: LeakyReLU

ここで、$a$は固定パラメータです。この方程式の一番下の部分は、ReLUニューロンが不活性化することでどのような入力に対しても0しか出力しなくなる問題である、ReLUの死滅の問題を防ぎます。負の傾きを使用することで、ネットワークが勾配を伝搬できるようになり、有用なものを学習することができます。

LeakyReLUは、通常のReLUでは勾配を伝播することがほとんど不可能な狭いニューラルネットに必要です。LeakyReLUを使えば、すべてがゼロになってしまっている領域にいても、ネットワークは勾配を保持することができます。

PReLU - nn.PReLU()

\[\text{PReLU}(x) = \begin{cases} x, & \text{if $x \geq 0$}\\ ax, & \text{otherwise} \end{cases}\]

ここで $a$ は学習可能なパラメータです。

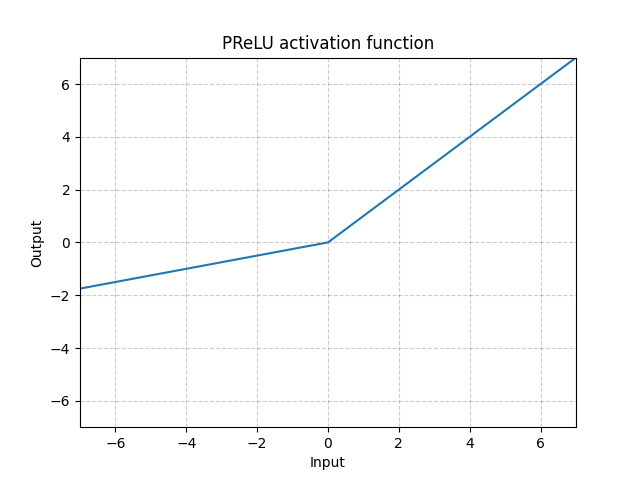
図4: ReLU

上記の活性化関数（すなわち、ReLU、LeakyReLU、PReLU）は、スケール不変です。

Softplus - Softplus()

\[\text{Softplus}(x) = \frac{1}{\beta} * \log(1 + \exp(\beta * x))\]
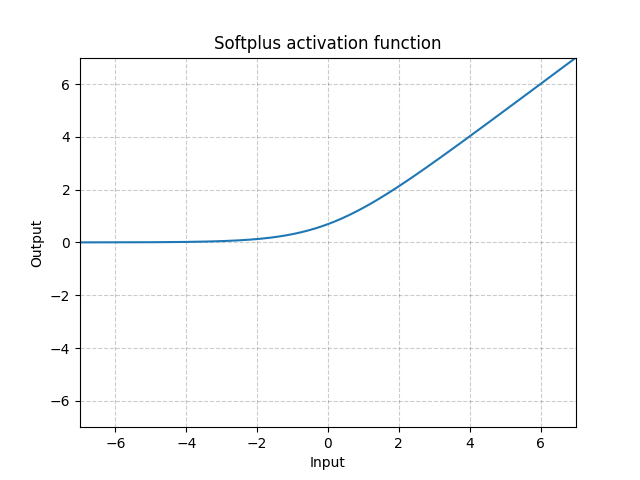
図5: Softplus

SoftplusはReLU関数の滑らかな近似であって、出力が常に正であるように制約を加えるために使うことができます。

この関数は、$\beta$がどんどん大きくなっていくと、ReLUに近づいていきます。

ELU - nn.ELU()

\[\text{ELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x) - 1)\]
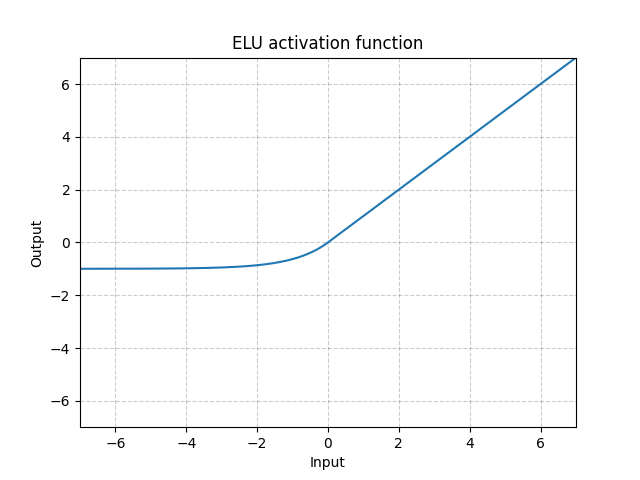
図6: ELU

ReLUとは異なり、0より小さな値を出力できるので、平均出力をゼロにすることを可能になります。したがって、モデルはより速く収束するかもしれません。そして、そのバリエーション(CELU, SELU)は、単にパラメトリゼーションが異なるだけです。

CELU - nn.CELU()

\[\text{CELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x/\alpha) - 1)\]
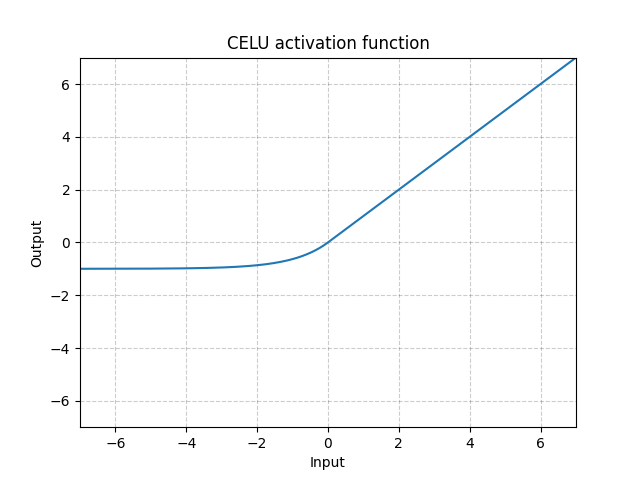
図7: CELU

SELU - nn.SELU()

\[\text{SELU}(x) = \text{scale} * (\max(0, x) + \min(0, \alpha * (\exp(x) - 1))\]
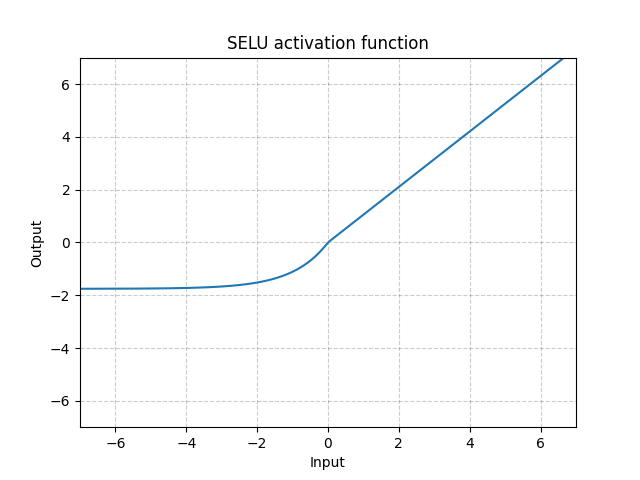
図8: SELU

GELU - nn.GELU()

\[\text{GELU(x)} = x * \Phi(x)\]

ただし$\Phi(x)$ はガウス分布の累積分布関数です。

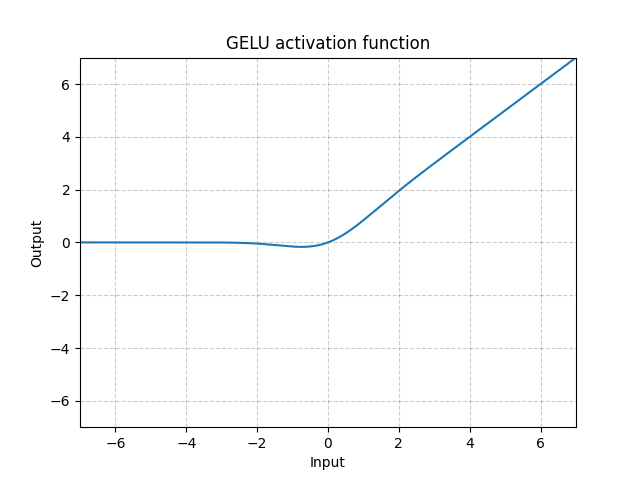
図9: GELU

ReLU6 - nn.ReLU6()

\[\text{ReLU6}(x) = \min(\max(0,x),6)\]
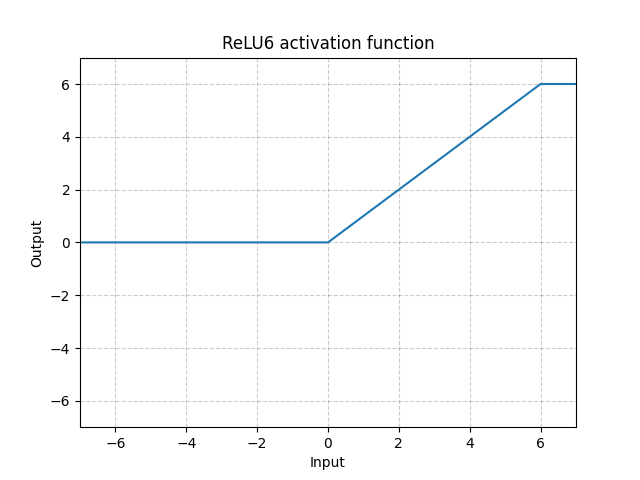
図10: ReLU6

これはReLUが6で飽和していることを示していますが、6を飽和とする理由は特にありませんので、以下のSigmoid関数を利用することで、より良い結果が得られます。

Sigmoid - nn.Sigmoid()

\[\text{Sigmoid}(x) = \sigma(x) = \frac{1}{1 + \exp(-x)}\]
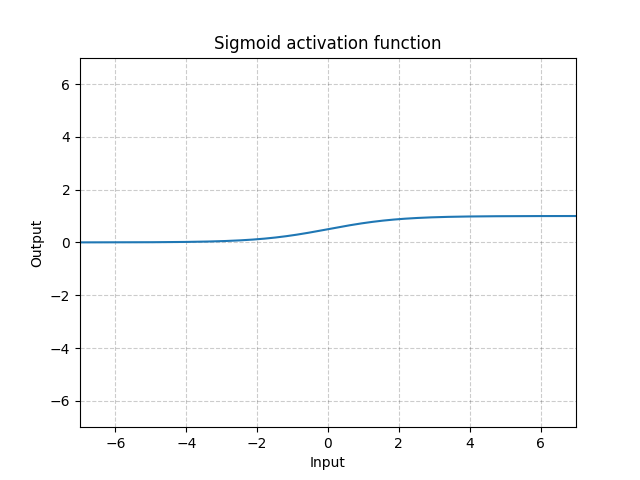
図11: Sigmoid

シグモイドを何層にも重ねると、学習効率が悪くなることがあり、慎重な初期化が必要になります。これは、入力が非常に大きかったり小さかったりすると、シグモイド関数の勾配が0に近くなるからで、この場合、パラメータを更新するための勾配が流れません。これは勾配の飽和として知られています。したがって、ディープニューラルネットワークでは、単一のキンク関数（ReLUなど）が好ましいです。

Tanh - nn.Tanh()

\[\text{Tanh}(x) = \tanh(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)}\]
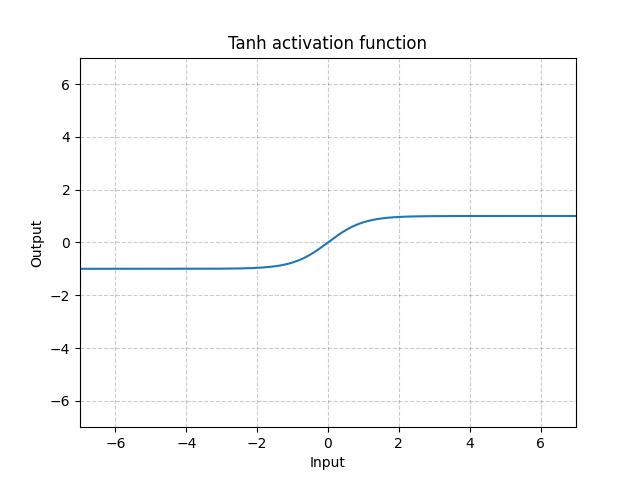
図12: Tanh

Tanhは、-1から1までの範囲で、中心化されていることを除いて、Sigmoidと基本的に同じです。 関数の出力は、ほぼ平均ゼロです。したがって、モデルはより速く収束します。 各入力変数の平均がゼロに近い場合、収束は通常より速くなることに注意してください。例えば、バッチ正規化は同様の理由で学習を高速化します。

Softsign - nn.Softsign()

\[\text{SoftSign}(x) = \frac{x}{1 + |x|}\]
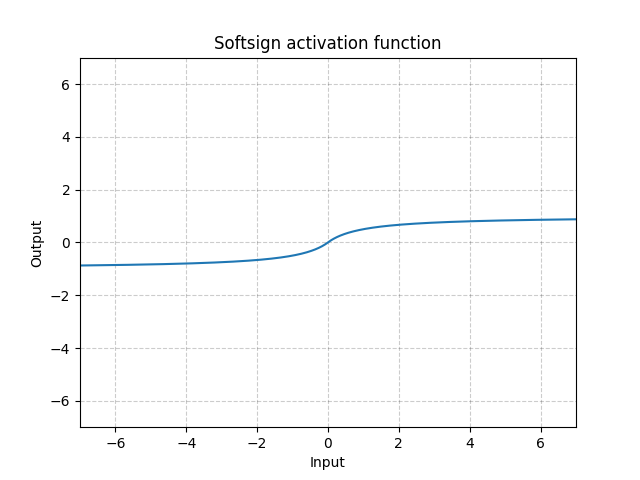
図13: Softsign

これはSigmoid関数に似ていますが、漸近点への到達が遅く、勾配消失問題を緩和します(ある程度)。

Hardtanh - nn.Hardtanh()

\[\text{HardTanh}(x) = \begin{cases} 1, & \text{if $x > 1$}\\ -1, & \text{if $x < -1$}\\ x, & \text{otherwise} \end{cases}\]

線形の範囲である [-1, 1] は min_val と max_valで調節できます。

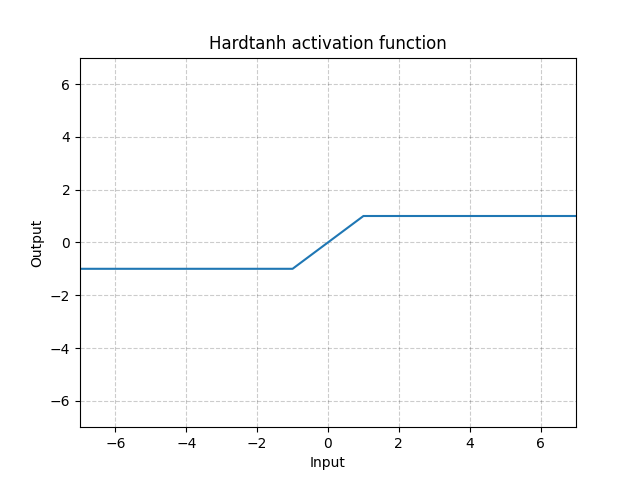
図14: Hardtanh

重みが小さな値の範囲に収まっている時に、驚くほどうまくいきます。

Threshold - nn.Threshold()

\[y = \begin{cases} x, & \text{if $x > \text{threshold}$}\\ v, & \text{otherwise} \end{cases}\]

勾配を逆伝播できないので、ほとんど用いられません。 そしてこれは、60年代、70年代にバイナリーニューロンを使っていた時代に誤差逆伝播法を使うことを妨げていた理由でもあります。

Tanhshrink - nn.Tanhshrink()

\[\text{Tanhshrink}(x) = x - \tanh(x)\]
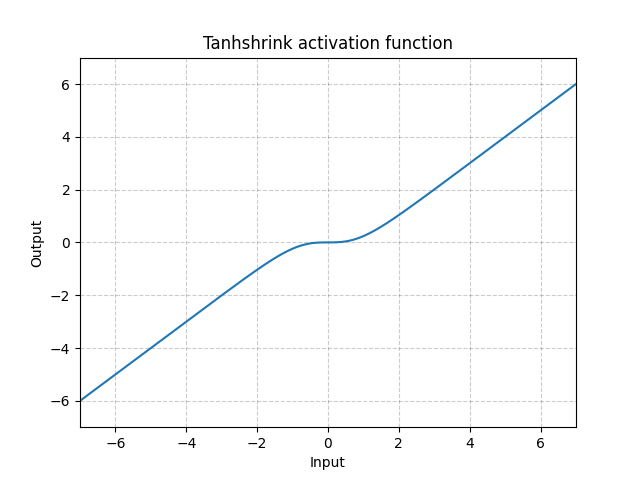
図15: Tanhshrink

潜在変数の値を計算するためのスパース符号化以外では、ほとんど使用されません。

Softshrink - nn.Softshrink()

\[\text{SoftShrinkage}(x) = \begin{cases} x - \lambda, & \text{if $x > \lambda$}\\ x + \lambda, & \text{if $x < -\lambda$}\\ 0, & \text{otherwise} \end{cases}\]
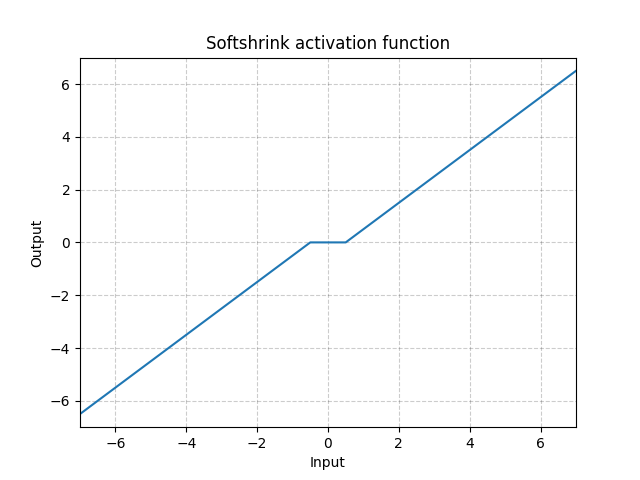
図16: Softshrink

基本的に変数を0に向かって一定数だけ収縮させ、変数が0に近い場合は0にします。 これは、$\ell_1$基準の勾配のステップと考えることができます。またこれは、反復的収縮-閾値調整アルゴリズム(ISTA)のステップの一つでもあります。しかし、標準的なニューラルネットワークでは活性化関数としてはあまり使われていません。

Hardshrink - nn.Hardshrink()

\[\text{HardShrinkage}(x) = \begin{cases} x, & \text{if $x > \lambda$}\\ x, & \text{if $x < -\lambda$}\\ 0, & \text{otherwise} \end{cases}\]
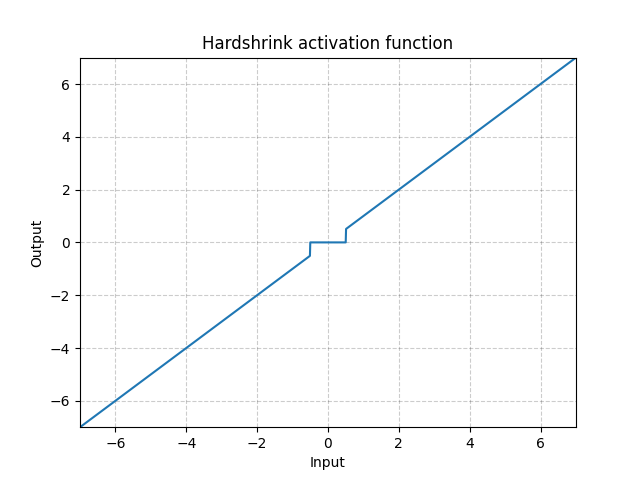
図17: Hardshrink

スパース符号化以外では、ほとんど使用されません。

LogSigmoid - nn.LogSigmoid()

\[\text{LogSigmoid}(x) = \log\left(\frac{1}{1 + \exp(-x)}\right)\]
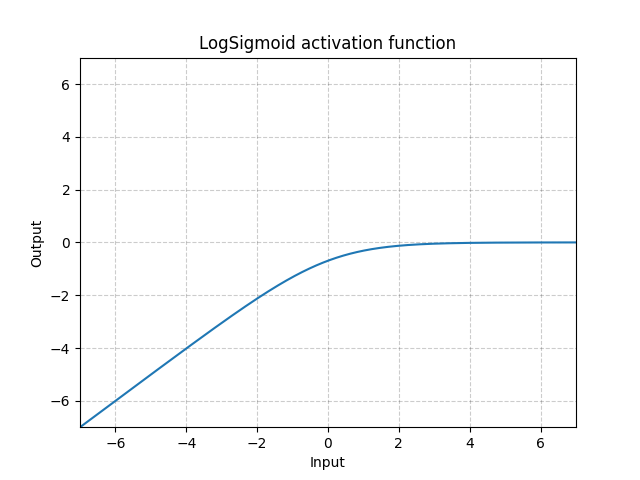
図18: LogSigmoid

ほとんどの場合損失関数で用いられますが、活性化関数としては一般的ではありません。

Softmin - nn.Softmin()

\[\text{Softmin}(x_i) = \frac{\exp(-x_i)}{\sum_j \exp(-x_j)}\]

数を確率分布に変えてくれます。

Soft(arg)max - nn.Softmax()

\[\text{Softmax}(x_i) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}\]

LogSoft(arg)max - nn.LogSoftmax()

\[\text{LogSoftmax}(x_i) = \log\left(\frac{\exp(x_i)}{\sum_j \exp(x_j)}\right)\]

損失関数ではほとんど使われていますが、活性化関数として使うのは一般的ではありません。

Q&A activation functions

nn.PReLU() related questions

• なぜ、すべてのチャンネルで同じ値の $a$ が必要なのでしょうか?

  チャンネルによって 異なる$a$ の値を持たせることもできます。各ユニットのパラメータとして $a$ を使用することができます。それを特徴マップとして共有することもできます。

• $a$は学習するんですか？ $a$を学習することのメリットはなんなのでしょうか？

  $a$は学習するか、固定するかのどちらかです。 固定する理由は、非線形性が負の領域にあっても、非線形性がゼロではない勾配を与えるようにするためです。 学習可能な$a$にすることで、非線形性を線形写像か完全に修正可能かのどちらかに変えることができるようになります。これは、エッジの極に関係なくエッジ検出器を実装するようないくつかの応用に有用かもしれません。

• 非線形性はどのくらい複雑にするのが望ましいのですか？

  理論的には、非線形関数全体を非常に複雑な方法でパラメトライズすることができます。例えば、spring parameterやチェビシェフ多項式などです。パラメトリゼーションは学習過程の一部になるかもしれません。

• パラメトライズすることは、ユニットを増やすよりも何かメリットはありますか？

  それは実際あなたが何をしたいかに依存します。例えば、低次元空間で回帰を行う場合、パラメトライゼーションは役立つかもしれません。しかし、あなたのタスクが画像認識のように高次元空間で行うものである場合は、ただ単に「ある」非線形性が必要なだけであって、単調な非線形性の方がうまくいくでしょう。 要するに、好きな関数をパラメトライズすることはできますが、大きな利点はありません。

Kinkに関する質問

• 一つのkinkと二つのkink

  ダブルキンクは、その中にスケールが組み込まれています。これは、入力層が2倍（または信号の振幅が2倍）になると、出力が全く異なるものになることを意味します。信号は非線形性が高くなりますので、出力は全く異なる挙動になります。一方、キンクが1つだけの関数を持っている場合、入力を2倍にすると、出力も2倍になります。

• キンクを持つ非線形活性化と平滑な非線形活性化の違いについてです。なぜ、あるいはいつ、どちらか一方が好ましくなりますか？

  それはスケール等価性の問題です。キンクが鋭い場合は、入力に2を掛けて、出力に2を掛けます。例えば、滑らかな遷移がある場合、入力を100倍にすると、滑らかな部分が100倍に縮小されているので、出力は鋭いキンクがあるように見えます。入力を100で割ると、キンクは非常に滑らかな凸関数になります。このように、入力のスケールを変えることで、活性化ユニットの振る舞いを変えることができます。

  時々、これが問題になることがあります。例えば、2つ続きの層がある多層ニューラルネットを訓練する場合です。一方の層の重みが他方の層の重みに対してどのくらい大きいかをうまく制御できません。スケールを気にする非線形関数を使っている場合、あなたのネットワークは、最初の層で使用できる重み行列の大きさを選択することができません。なぜなら、スケールの変化が挙動を大きく変えてしまうからです。

  この問題を解決する一つの方法は、各層の重みに厳密にスケールを設定することです。これによってバッチ正規化のように層の重みを正規化することができます。そうすれば、ユニットに入る分散は常に一定になります。スケールを固定すると、2つのキンク関数で非線形性のどの部分を使用するかを選択する手段を持ちません。この「固定」された部分があまりにも「線形」になってしまうと問題になる可能性があります。例えば、シグモイドはゼロ付近でほぼ線形になり、そのためバッチ正規化の出力（0に近い）は「非線形に」活性化することができないかもしれません。

  なぜディープネットワークが単一のキンク関数でよりよく機能するのかは、完全には明らかではありません。これは、スケール等価性に起因すると思われます。

soft(arg)max関数の温度係数

• 温度係数はいつ、なぜ使うのでしょうか？

  ある程度、温度は入ってくる重みと重複しています。softmaxに重み付けされた和が入ってくる場合、パラメータ$\beta$は重みの大きさと重複しています。

  温度は、出力の分布がどれだけ鋭くなるかを制御します。もし $\beta$ がとても大きいと、ゼロか１に近づきます。小さくなると、滑らかになります。$\beta$の極限が０になると、平均値のようになります。もし $\beta$ が無限大になると、argmax関数のように振る舞います。これはもはやsoftmaxではありません。したがって、softmaxの前にある種の正規化があるならば、このパラメータを調整することで、どれだけargmaxに近づくかをコントロールすることができます。 時には、小さな$\beta$から始めることができます。そうすれば、うまく勾配降下法を行うことができます。もしattention機構においてはっきりと決定をしたい場合には、温度をあげます。そうすることで、判断を鋭くすることができます。このトリックは、アニーリングと呼ばれています。self-attention機構のようなmixture of expertsシステムでは有効です。

損失関数

PyTorchには多くの損失関数も実装されています。ここではそのうちのいくつかを見ていきましょう。

nn.MSELoss()

この関数は、入力$x$とターゲット$y$の各要素間の平均二乗誤差(L2ノルムの二乗)を与えます。これはL2損失とも呼ばれます。

サンプル数が $n$ のミニバッチを使用している場合、バッチ内の各サンプルに対して $n$ の損失があります。損失関数には、この損失をベクトルとして保持させるか、あるいは次元を削減するようにして保持させることができます。

次元が削減されていない場合（つまり、reduction='none'を設定している場合）、損失は

\[l(x,y) = L = \{l_1, \dots, l_N\}^\top, l_n = (x_n - y_n)^2\]

となります。ここで、$n$はバッチサイズ、$x$と$y$は、それぞれ合計n個の要素を持つ任意のシェイプのテンソルです。

次元削減オプションは以下の通りです（デフォルト値は reduction='mean' であることに注意してください）。

\[l(x,y) = \begin{cases}\text{mean}(L), \quad &\text{if reduction='mean'}\\ \text{sum}(L), \quad &\text{if reduction='sum'} \end{cases}\]

和はすべての要素を対象とし、$n$で割ります。

$n$による割り算は、 reduction = 'sum'を設定すれば回避できます。

nn.L1Loss()

これは、入力 $x$ とターゲット $y$ (または実際の出力と希望する出力) の各要素間の平均絶対誤差 (MAE) を測定します。

次元削減されていない場合 (つまり、reduction='none'を設定している場合)、損失は次のようになります。

\[l(x,y) = L = \{l_1, \dots, l_N\}^\top, l_n = \vert x_n - y_n\vert\]

ここで、 $N$ はバッチサイズ、$x$ と $y$ はそれぞれ n 個の要素を持つ任意の形状のテンソルです。

また、nn.MSELoss() と同様に 'mean' と 'sum' の reduction オプションを持ちます。 <!– Use Case: L1 loss is more robust against outliers and noise compared to L2 loss. In L2 the errors of those outlier/noisy points are squared, so the cost function gets very sensitive to outliers.

Problem: The L1 loss is not differentiable at the bottom (0). We need to be careful when handling its gradients (namely Softshrink). This motivates the following SmoothL1Loss. –>

使用例： L1損失は、L2損失に比べて、外れ値やノイズに対してよりロバストです。L2では、外れ値やノイズのある点の誤差が2乗されるため、コスト関数は外れ値に対して非常に敏感になります。

問題点:　L1損失は底辺（0）のところでは微分できません。したがって、勾配を扱う際には注意が必要です（すなわち、Softshrink）。これが次のSmoothL1Lossを考える動機となっています。

nn.SmoothL1Loss()

この関数は、要素間の絶対誤差が１以下の場合はＬ２損失、それ以外の場合はＬ1損失を使用します。

\(\text{loss}(x, y) = \frac{1}{n} \sum_i z_i\) ここで、 $z_i$ は次式で与えられます。

\[z_i = \begin{cases}0.5(x_i-y_i)^2, \quad &\text{if } |x_i - y_i| < 1\\ |x_i - y_i| - 0.5, \quad &\text{otherwise} \end{cases}\]

また、reductionのオプションもあります。

これは、Ross Girshick (Fast R-CNN)によって宣伝されています。 Smooth L1 Lossは、Huber LossやElastic Networkとしても知られています。

使用例:　MSELossよりも外れ値の影響を受けにくく、底辺が滑らかです。コンピュータビジョンなどでは、外れ値からの保護のためによく使われています。

問題点:　この関数はスケール（上の関数では$0.5$）を持っています。

コンピュータビジョンのためのL1とL2の比較

多くの異なる $y$ がある場合の予測を行う際には

• MSE (L2損失) を用いた場合、すべての $y$ の平均値が得られ、CVではぼやけた画像が得られることを意味します。
• L1損失を利用する場合、L1距離を最小化する値 $y$ は、ぼやけていない中程度の値ですが、中程度は多次元で定義するのが難しいことに注意してください。

L1を使うと、予測のための画像がよりシャープになります。

nn.NLLLoss()

これはCクラスの分類問題を学習するときに使われる負の対数尤度損失です。

数学的には、NLLLossの入力は(対数)尤度でなければなりませんが、PyTorchはそれを強制しません。そのため、望ましい成分を可能な限り大きくすることが効果的です。

次元削減されていない（つまり :attr:reduction が 'none' に設定されている）損失は次のように記述できます。

\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - w_{y_n} x_{n,y_n}, \quad w_{c} = \text{weight}[c] \cdot \mathbb{1}\{c \not= \text{ignore\_index}\}\]

ただし$N$はバッチサイズです。

もし reduction が 'none' でないばあい　(デフォルトでは 'mean' です)　には、

\[\ell(x, y) = \begin{cases} \sum_{n=1}^N \frac{1}{\sum_{n=1}^N w_{y_n}} l_n, & \text{if reduction} = \text{'mean';}\\ \sum_{n=1}^N l_n, & \text{if reduction} = \text{'sum'.} \end{cases}\]

この損失関数にはオプション引数の weight があり、各クラスに重みを割り当てる1次元テンソルとして渡すことができます。これは、不均衡な訓練データを扱う場合に便利です。

重みと不均衡クラス:

カテゴリー/クラスごとにデータの出現頻度が異なる場合は、重みベクトルが便利です。例えば、一般的なインフルエンザの頻度は肺がんよりもはるかに高いです。サンプル数が少ないカテゴリについては、単純に重みを増やすことができます。

しかし、確率的勾配をうまく利用するためには、重みを設定するよりも、訓練における出現頻度を均等化した方がよいでしょう．

学習中のクラスを均等化するには、各クラスのサンプルを別のバッファに入れます。そして、それぞれのバッファから同じ数のサンプルを選んでミニバッチを生成します。小さい方のバッファが使用するサンプルを使い切ったら、小さい方のバッファを最初から繰り返し、大きい方のクラスのサンプルがすべて使用されるまで繰り返します。このようにしてバッファのデータを用いることで、すべてのカテゴリで同じ頻度を得ることができます。大多数のクラスのすべてのサンプルを使用しないという安易な方法で出現頻度を均等化してはいけません。使わないデータを出さないようにしましょう！

上記の方法の明らかな問題は、NNモデルが実際のサンプルの相対的な出現頻度を知らないことです。これを解決するために、実際のクラスの出現頻度で最後に数回エポックを実行することで、システムを微調整します。

このスキームの直観を得るために、医学部の例に戻ってみましょう：学生は頻繁に起こる病気と同じくらい多くの時間を稀な病気に費やします（稀な病気の方が複雑な病気であることが多いので、もっと多くの時間を費やすかもしれません）。彼らは、それらのすべての特徴に適応することを学び、それを修正して、どれが稀な病気かを知ることを学びます。

nn.CrossEntropyLoss()

この関数は nn.LogSoftmax と nn.NLLLoss を一つのクラスにまとめた物です。この2つを組み合わせることで、正しいクラスのスコアをできるだけ大きくすることができます。

ここで2つの関数を統合した理由は、勾配計算の数値的安定性を高めるためです。softmax以降の値が1や0に近づくと、その対数が0に近づくか、$-\infty$になることがあります。0に近い log の傾きは $\infty$ に近いので、バックプロパゲーションの途中で数値計算上の問題が発生してしまいます。2つの関数を組み合わせると、勾配が飽和するので、最後にはそれなりの数値が得られます。

入力は各クラスの正規化されていないスコアであることが想定されています。

損失は次のように記述することができます。

\[\text{loss}(x, c) = -\log\left(\frac{\exp(x[c])}{\sum_j \exp(x[j])}\right) = -x[c] + \log\left(\sum_j \exp(x[j])\right)\]

あるいは weight という引数が指定された場合には、

\[\text{loss}(x, c) = w[c] \left(-x[c] + \log\left(\sum_j\exp(x[j])\right)\right)\]

となります。この損失は各ミニバッチについての平均をとったものになっています。

クロスエントロピー損失の物理的な解釈は、2つの分布間のダイバージェンスを測るKullback-Leiblerダイバージェンス(KLダイバージェンス)に関連しています。ここでは、(準)分布はxベクトル(予測値)と目標分布(間違ったクラスに0、正しいクラスに1を持つワンホットベクトル)で表されます。

数学的には、

\[H(p,q) = H(p) + \mathcal{D}_{KL} (p \mid\mid q)\]

ただし\(H(p,q) = - \sum_i p(x_i) \log (q(x_i))\) は(二つの分布の間の)クロスエントロピーで、 \(H(p) = - \sum_i p(x_i) \log (p(x_i))\)はエントロピーで、\(\mathcal{D}_{KL} (p \mid\mid q) = \sum_i p(x_i) \log \frac{p(x_i)}{q(x_i)}\) は KLダイバージェンスです。

nn.AdaptiveLogSoftmaxWithLoss()

これは大規模なクラス数（例えば数百万クラス）に対して効率的なソフトマックスの近似計算を行います。計算速度を向上させるためのトリックを実装しています。

手法の詳細は、Edouard Grave, Armand Joulin, Moustapha Cissé, David Grangier, Hervé JégouによるEfficient softmax approximation for GPUsに記載されています。

---

📝 Haochen Wang, Eunkyung An, Ying Jin, Ningyuan Huang
Shiro Takagi
13 April 2020