The Truck Backer-Upper

セットアップ

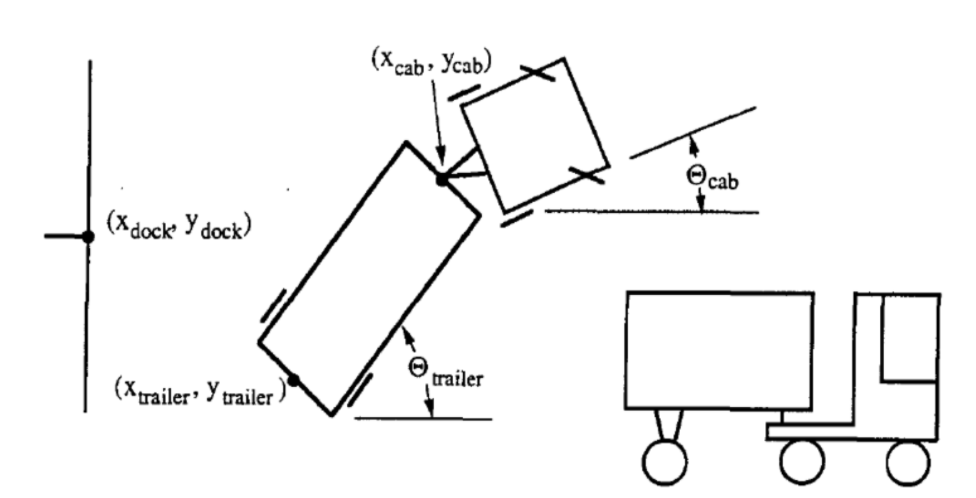
このタスクの目的は、任意の初期位置から積荷を積み下ろしする場所へトラックをバックさせる際のハンドルを制御するような、自己学習する制御システムを作ることです。

図１に示されているように、バックしかできない ことに注意してください。

|| |

トラックの状態は6つのパラメータで表現されます:

<!– - $\tcab$: Angle of the truck

• $\xcab, \ycab$: The cartesian of the yoke (or front of the trailer).
• $\ttrailer$: Angle of the trailer
• $\xtrailer, \ytrailer$: The cartesian of the (back of the) trailer. –>
• $\tcab$: トラックの角度
• $\xcab, \ycab$: トレーラーの正面の座標
• $\ttrailer$: トレーラーの角度
• $\xtrailer, \ytrailer$: トレーラーの後ろ側の座標

制御システムの目的は、各時刻$k$ごとにトラックがある固定した小さな距離をバックした後に、適切な角度$\phi$を選択することです。成否は2つの基準に依存します。

1. トレーラーの後部が、壁の積み込みドックと平行であること。例えば、 $\ttrailer = 0$。
2. トレーラーの後部　($\xtrailer, \ytrailer$) が、上記で示されているような点($x_{dock}, y_{dock}$) にできるだけ近いこと。

より多くのパラメータと可視化

| |

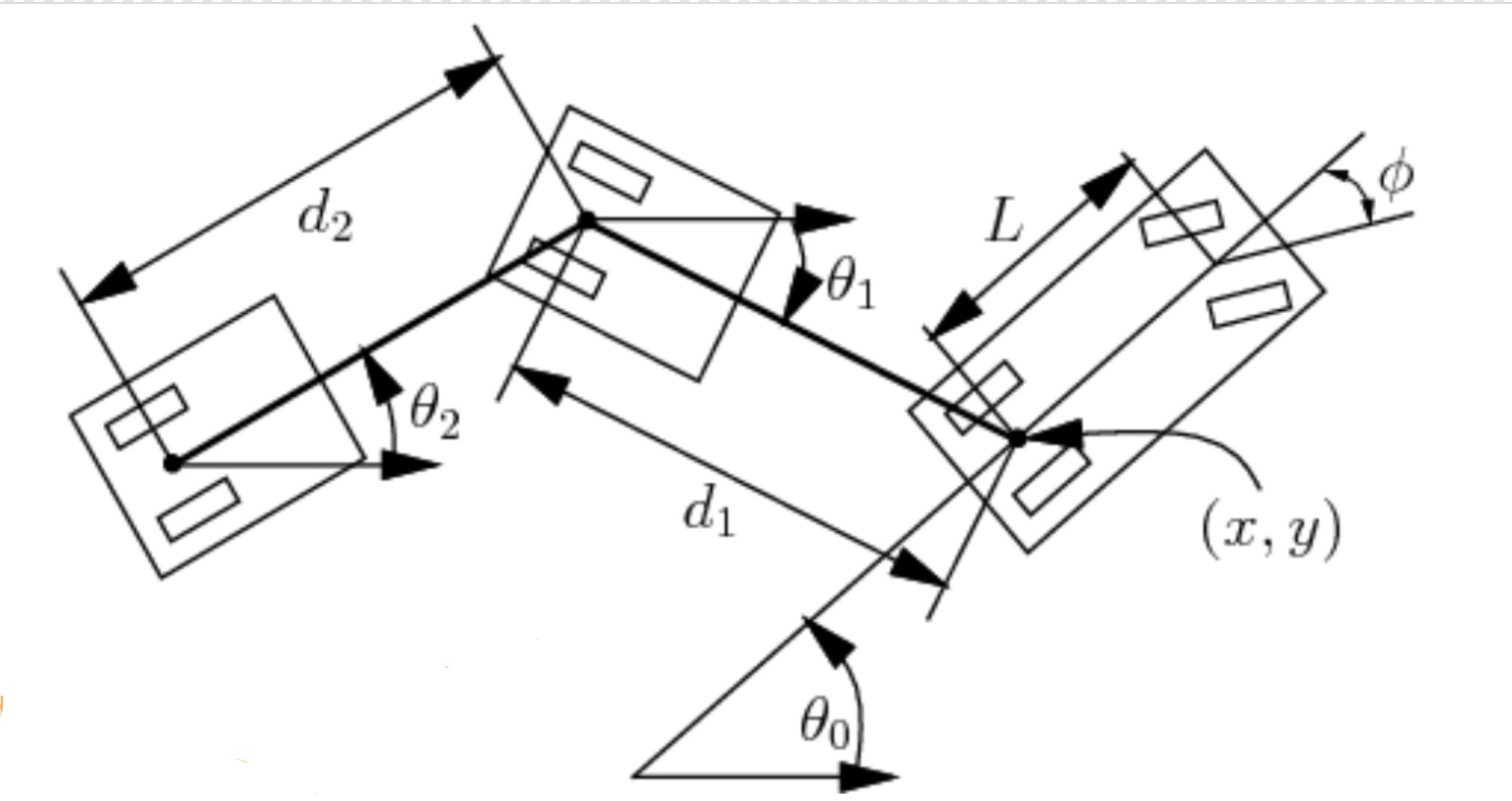
ここでは、図2に示したようなあといくつかのパラメータについて考えてみます。 車の長さ$L$、車とトレーラーの距離$d_1$、トレーラーの長さ$d_2$などが与えられると、角度や位置の変化を計算することができます：

ここで、$s$は符号付き速度を、$\phi$はハンドルの負の舵角を表しています。 これで、$\xcab$, $\ycab$, $\theta_0$, $\theta_1$ の４つのパラメータだけで状態を表現できるようになりました。 これは、長さのパラメータがわかっていて、$\xtrailer, \ytrailer$が$\xcab, \ycab, d_1, \theta_1$で決まるからです。

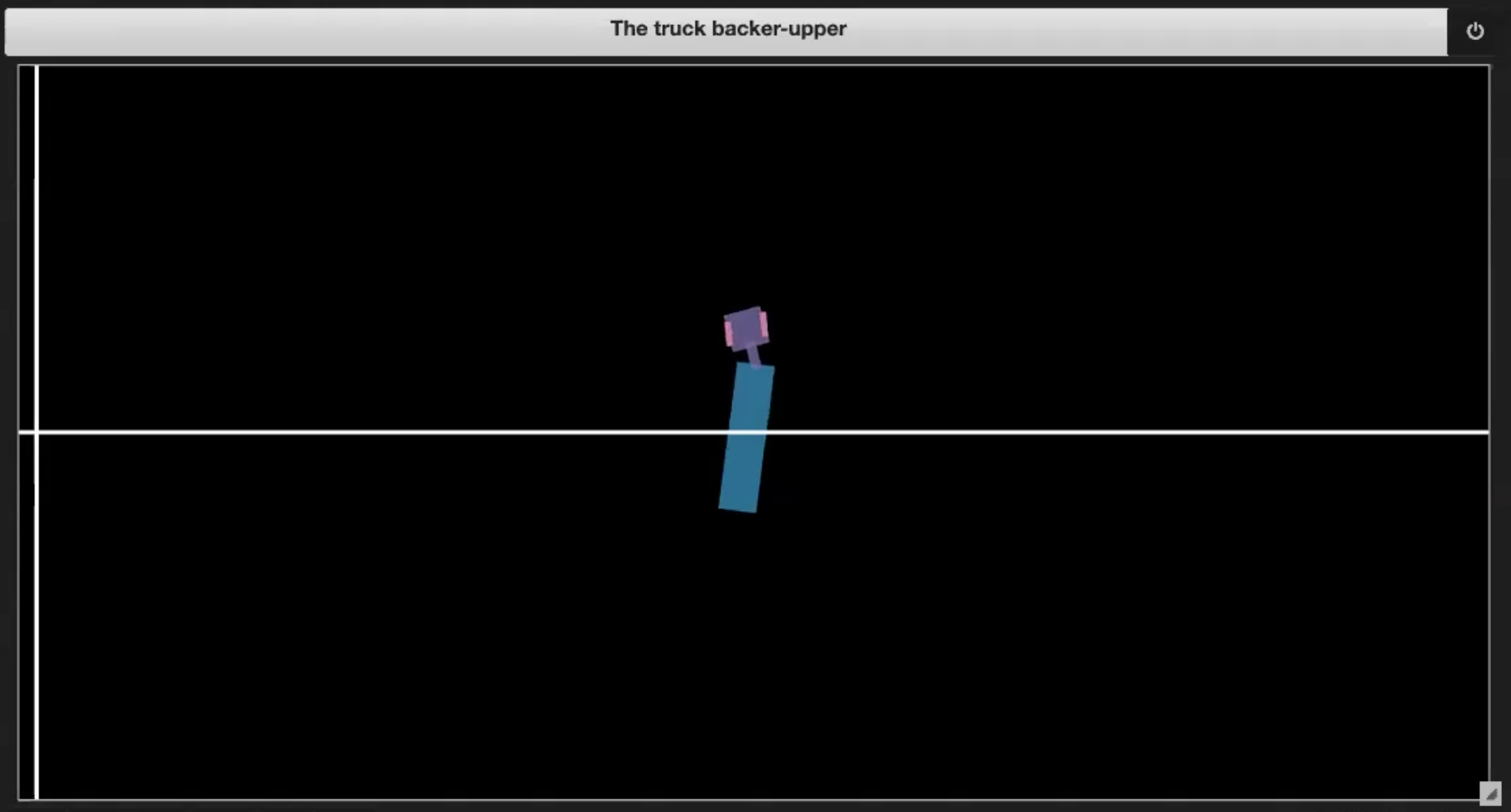
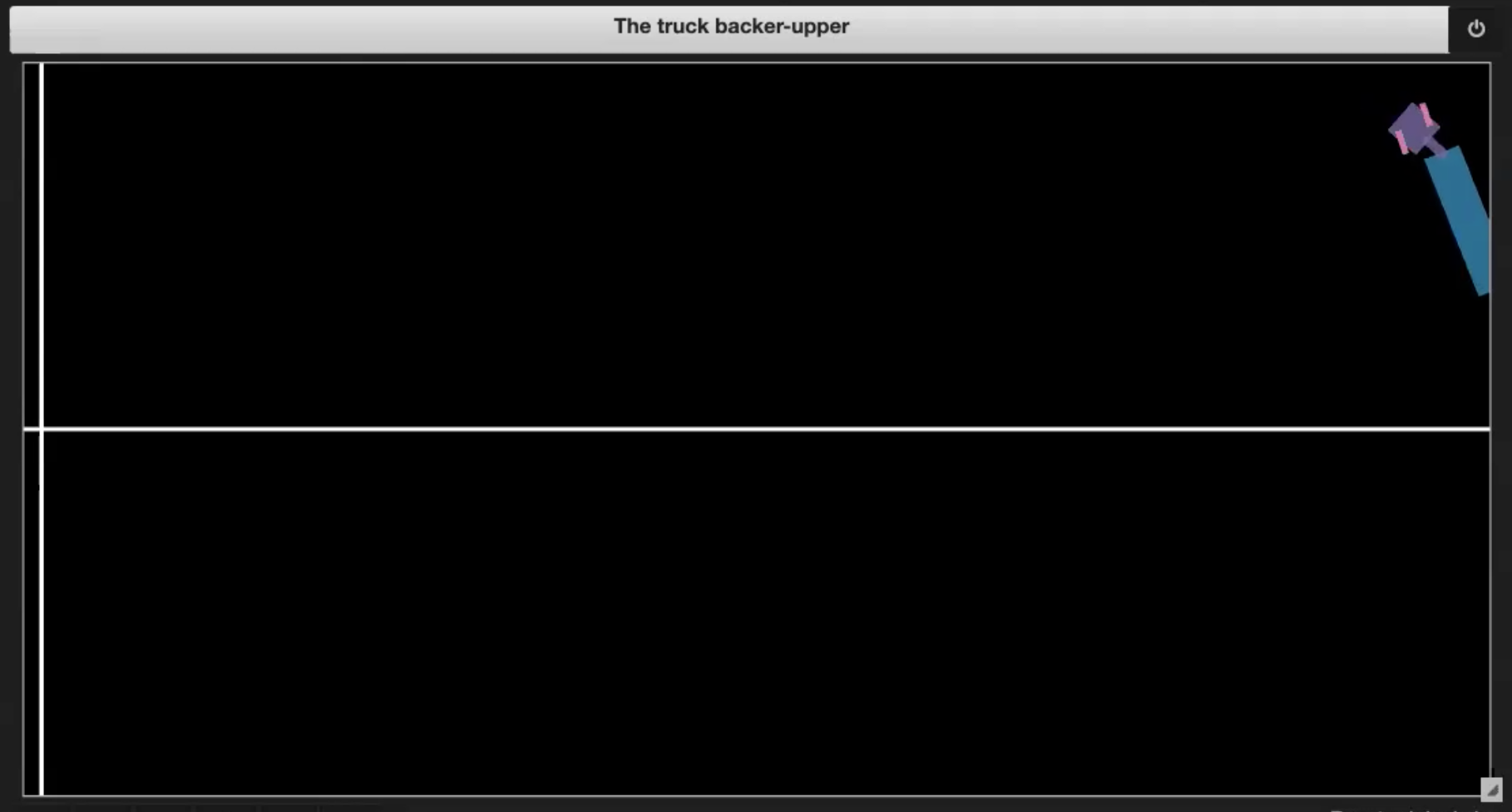
Deep LearningリポジトリのJupyter Notebook から、 いくつかの環境の例を図３(1-4)に示します:

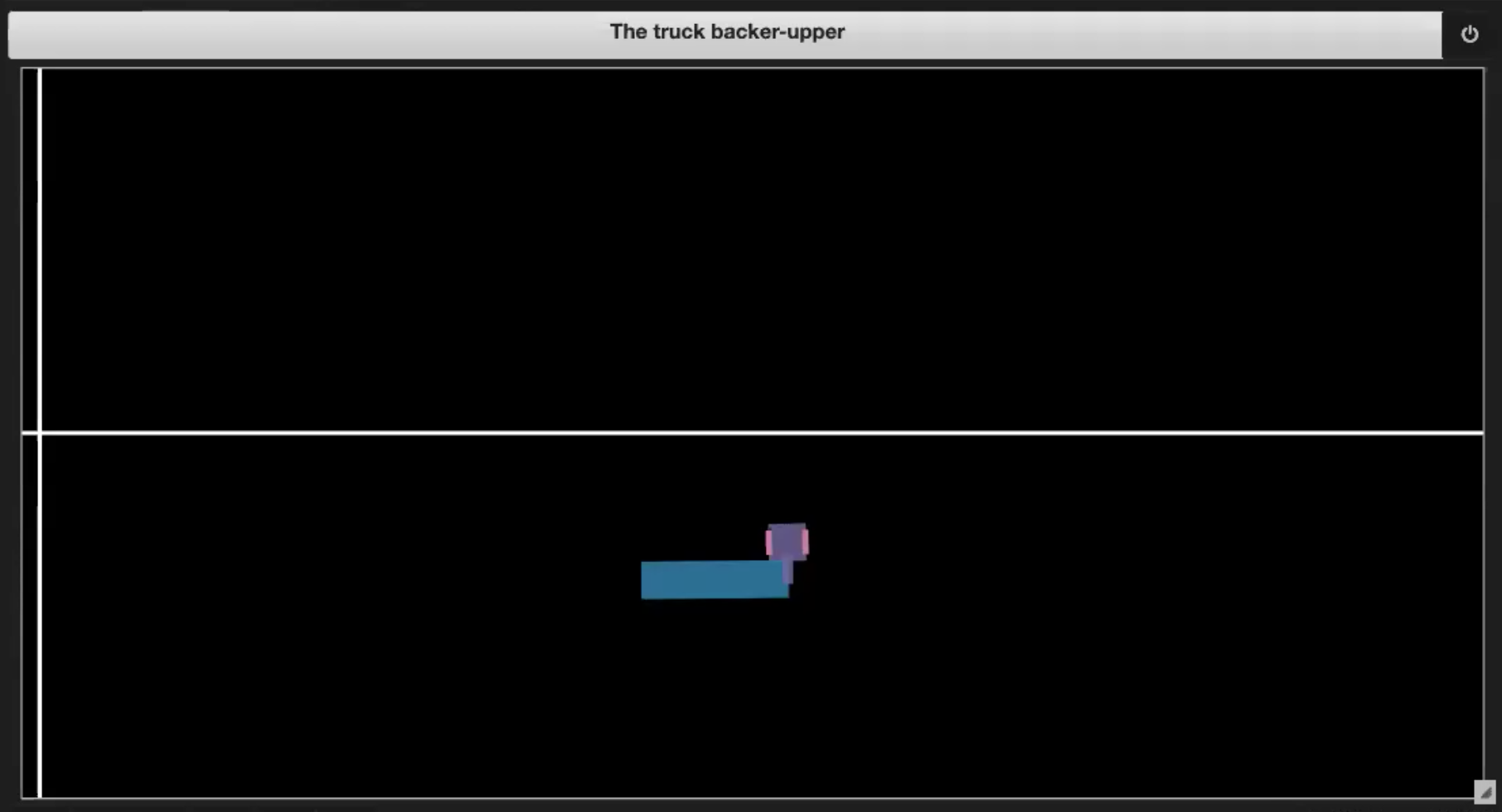| || | 図3.1: 環境のプロットのサンプル | 図3.2: 自分自身に突っ込んでいる　(ジャックナイフ) | | ||

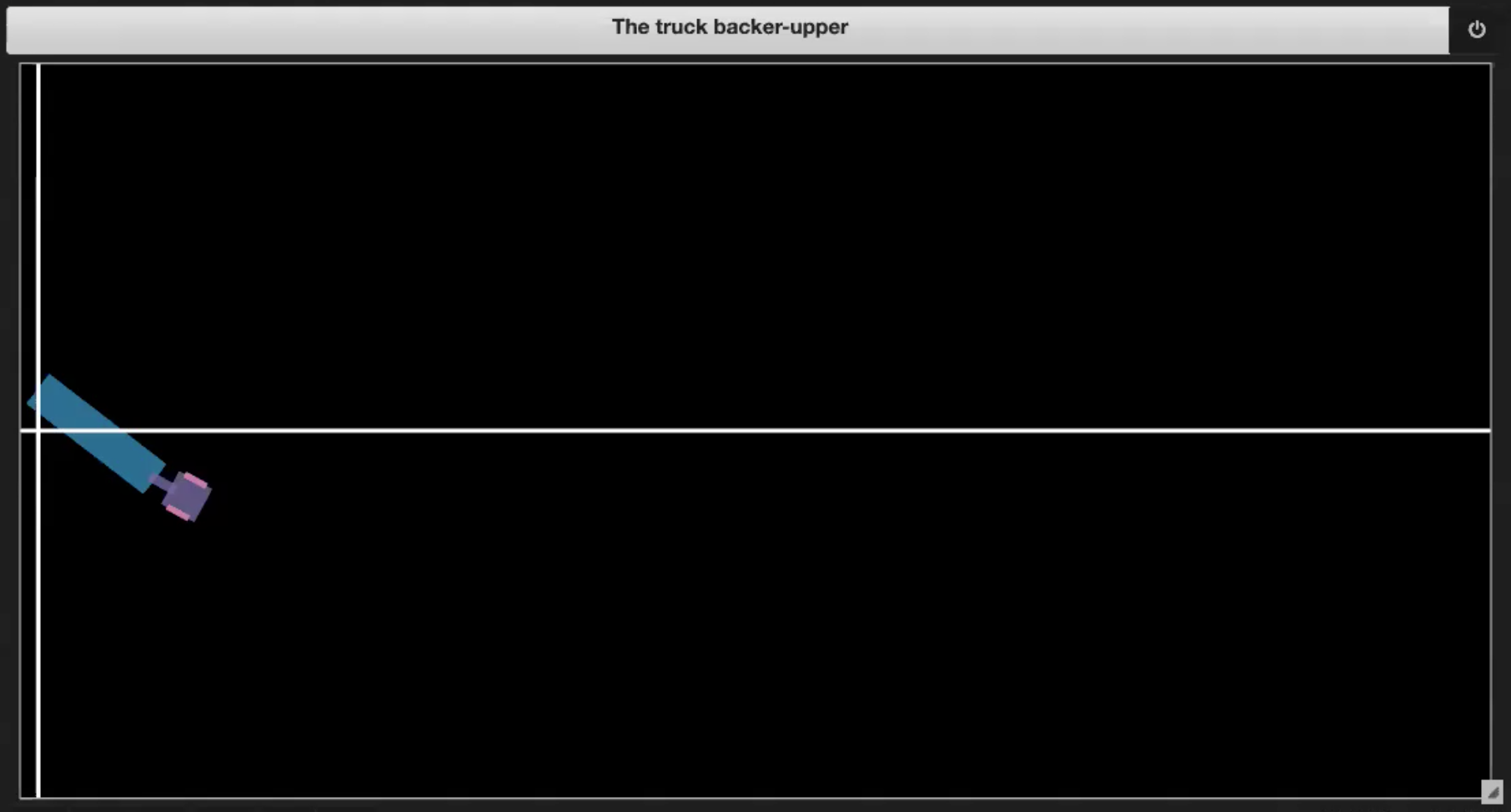
| 図3.3: 境界線の外に出る |図3.4: ドックに到着する|

各時刻$k$で、$-\frac{\pi}{4}$から$\frac{\pi}{4}$までのハンドル操作の信号が入力され、トラックはそれに対応した角度で後退します。

トラックの運転が終了する状況はいくつかあります。

• トラックが自分自身に突っ込んだ場合（図 3.2 のようなジャックナイフ）。
• トラックが境界線の外に出た場合（図 3.3 に示す）。
• トラックがドックに到達した場合（図 3.4 に示す）。

訓練

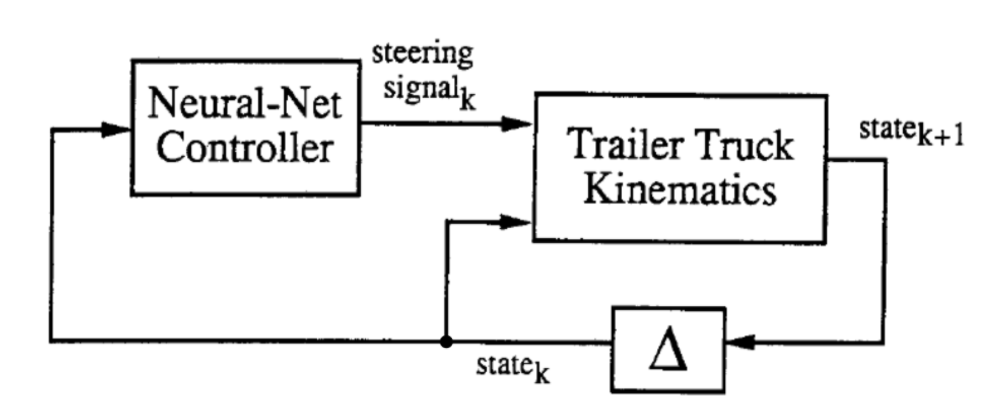
訓練は2段階で行われます。(1)トラックやトレーラーの運動のエミュレータとなるニューラルネットワークの訓練と、(2)トラックを制御するための制御システムとなるニューラルネットワークの訓練である。

| | |

上で示されているように、概念図に描かれている2つのブロックは訓練される予定の2つのネットワークです。各時間ステップ$k$では、「Trailer Truck Kinematics」、つまり今までエミュレータと呼んでいたものが、6次元の状態ベクトルと制御システムから生成されたハンドル操作信号を入力され、時間$k + 1$で新たな6次元の状態を生成します。

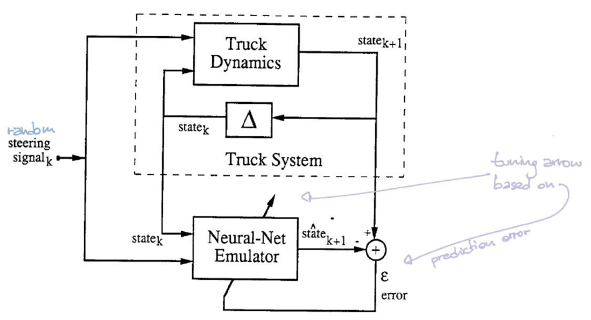
エミュレータ

エミュレータは、現在の位置($\tcab^t$,$\xcab^t, \ycab^t$, $\ttrailer^t$, $\xtrailer^t$, $\ytrailer^t$)と操舵方向 $\phi^t$ を入力として受け取り、次の時間テップの状態を出力します。これは、線形の隠れ層とReLU活性化関数と線形出力層から構成されます。損失関数としてMSE損失を用い、確率的勾配降下法を用いてエミュレータを学習します。

|| |

この設定では、現在地とハンドルの角度が与えられていれば、次のステップの位置をシミュレーターが教えてくれます。したがって、シミュレータをエミュレートするニューラルネットは必要ありません。しかし、より複雑なシステムでは、システムの背後にある方程式にアクセスできないかもしれません。例えば、良い計算可能なこの宇宙の法則を私たちは知りません。ハンドル操作の信号とそれに対応するパスを記録したデータを観測できるだけかもしれません。この場合、この複雑なシステムの動きをエミュレートするためにニューラルネットを訓練したいと考えています。

Class truckに、エミュレータを訓練するために考慮しなければならない重要な2つの関数があります。

1つ目は、計算後のトラックの出力状態を与えるstepという関数です。

def step(self, ϕ=0, dt=1):

    # Check for illegal conditions
    if self.is_jackknifed():
        print('The truck is jackknifed!')
        return

    if self.is_offscreen():
        print('The car or trailer is off screen')
        return

    self.ϕ = ϕ
    x, y, W, L, d, s, θ0, θ1, ϕ = self._get_atributes()

    # Perform state update
    self.x += s * cos(θ0) * dt
    self.y += s * sin(θ0) * dt
    self.θ0 += s / L * tan(ϕ) * dt
    self.θ1 += s / d * sin(θ0 - θ1) * dt

2つ目は、トラックの現在の位置を返すstateという関数です。

def state(self):
        return (self.x, self.y, self.θ0, *self._traler_xy(), self.θ1)

まず二つのリストを生成します。ランダムに生成されたハンドルの角度φとトラックからの初期状態を付け加えた入力リストを生成します。そして、truck.step(ϕ) で計算可能なトラックの出力状態を追加した出力リストを生成します。

これでエミュレーターを訓練できるようになりました。

cnt = 0
for i in torch.randperm(len(train_inputs)):
    ϕ_state = train_inputs[i]
    next_state_prediction = emulator(ϕ_state)

    next_state = train_outputs[i]
    loss = criterion(next_state_prediction, next_state)

    optimiser_e.zero_grad()
    loss.backward()
    optimiser_e.step()

    if cnt == 0 or (cnt + 1) % 1000 == 0:
        print(f'{cnt + 1:4d} / {len(train_inputs)}, {loss.item():.10f}')
    cnt += 1

torch.randperm(len(train_inputs)) は、 $0$ から入力の長さから $1$ を引いた範囲内のインデックスのランダムな並べ替えを与えていることに注意してください。インデックスの並べ替えの後、毎回 φ_state が入力リストからインデックス i で選択されます。線形出力層を持つエミュレータ関数を通して φ_state を入力すると、 next_state_prediction が得られます。エミュレータは以下のように定義されたニューラルネットワークであることに注意してください。

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

ここでは MSE 損失を使用して真の次の状態と次の状態の予測の間の誤差を計算します。ただし、真の次の状態は入力リストからのϕ_state のインデックスに対応するインデックス i を持つ出力リストから来ています。

制御システム

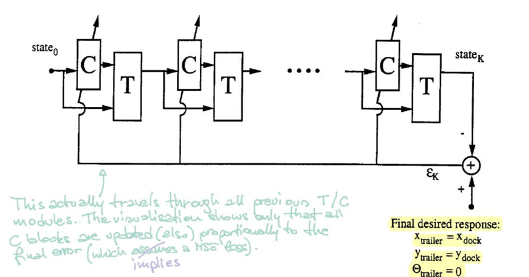
図 5 を参照してください。ブロック$\matr{C}$は制御システムを表しています。現在の状態を入力として受けて、ハンドルの角度を出力します。そして、ブロック$\matr{T}$(エミュレータ)は、状態とハンドルの角度の両方を入力として受けて、次の状態を生成します。

<!–	Fig. 5: State Transition flow diagram	–>
図5: 状態遷移図

制御システムの学習では、ランダムな初期状態から開始し、トレーラがドックと平行になるまで、$\matr{C}$と$\matr{T}$の手順を繰り返します。誤差はトレーラの位置とドックの位置を比較して計算します。 その後、誤差逆伝播を用いて勾配を求め、SGDによって制御システムのパラメータを更新します。

モデルの構造の詳細

これは($m\matr{C}$, $\matr{T}$)の処理の詳細を表したグラフです。まず、状態(6次元ベクトル)が入力され、それに学習可能な重み行列をかけて25個の隠れユニットを得ます。そして、それを別の学習可能な重み行列に通し、出力を得ます。同様に、状態と角度$\phi$ (7次元ベクトル)を2層に分けて入力し、次のステップの状態を生成します。

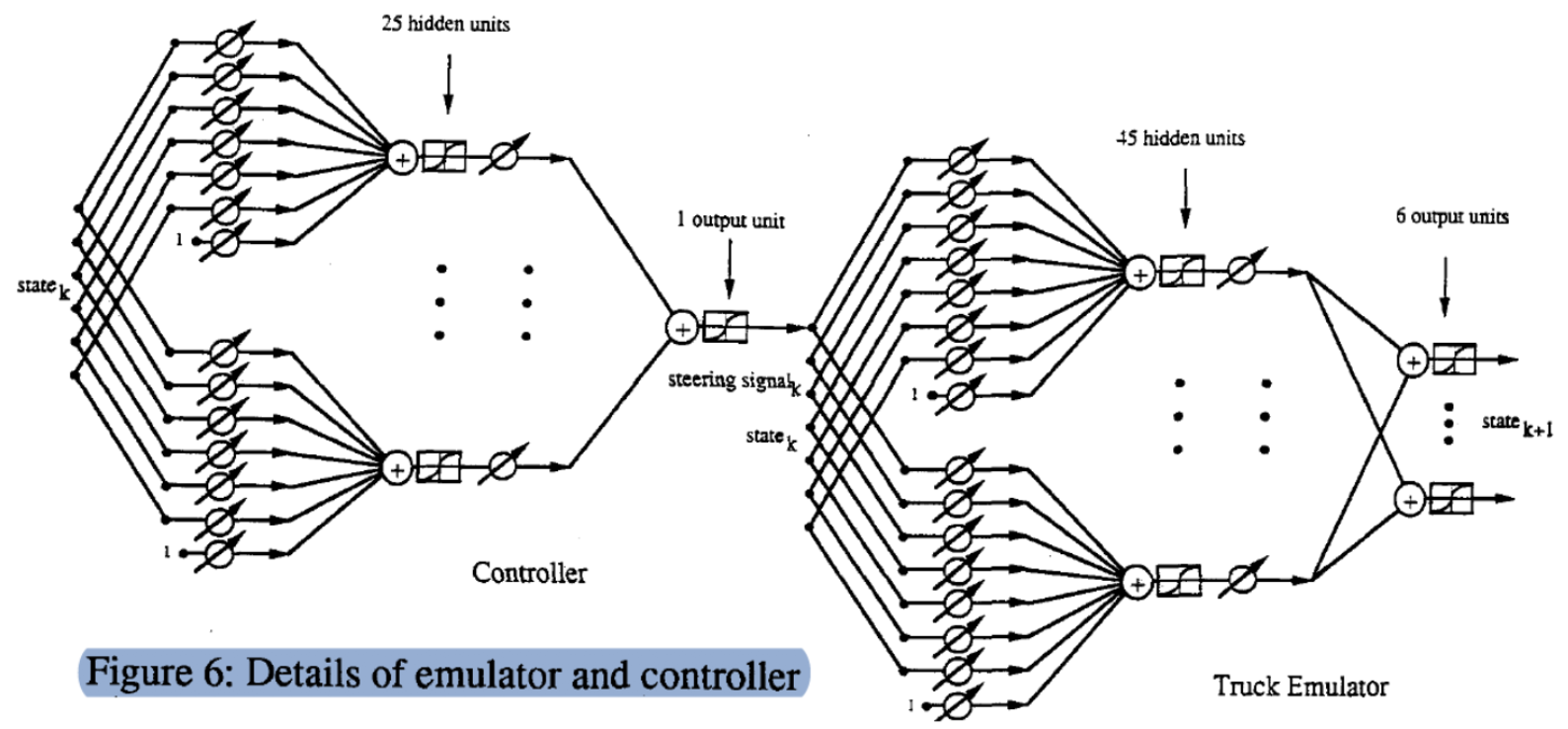
これをより明確に見るために、エミュレータの正確な実装を示します。

state_size = 6
steering_size = 1
hidden_units_e = 45

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

optimiser_e = SGD(emulator.parameters(), lr=0.005)
criterion = nn.MSELoss()

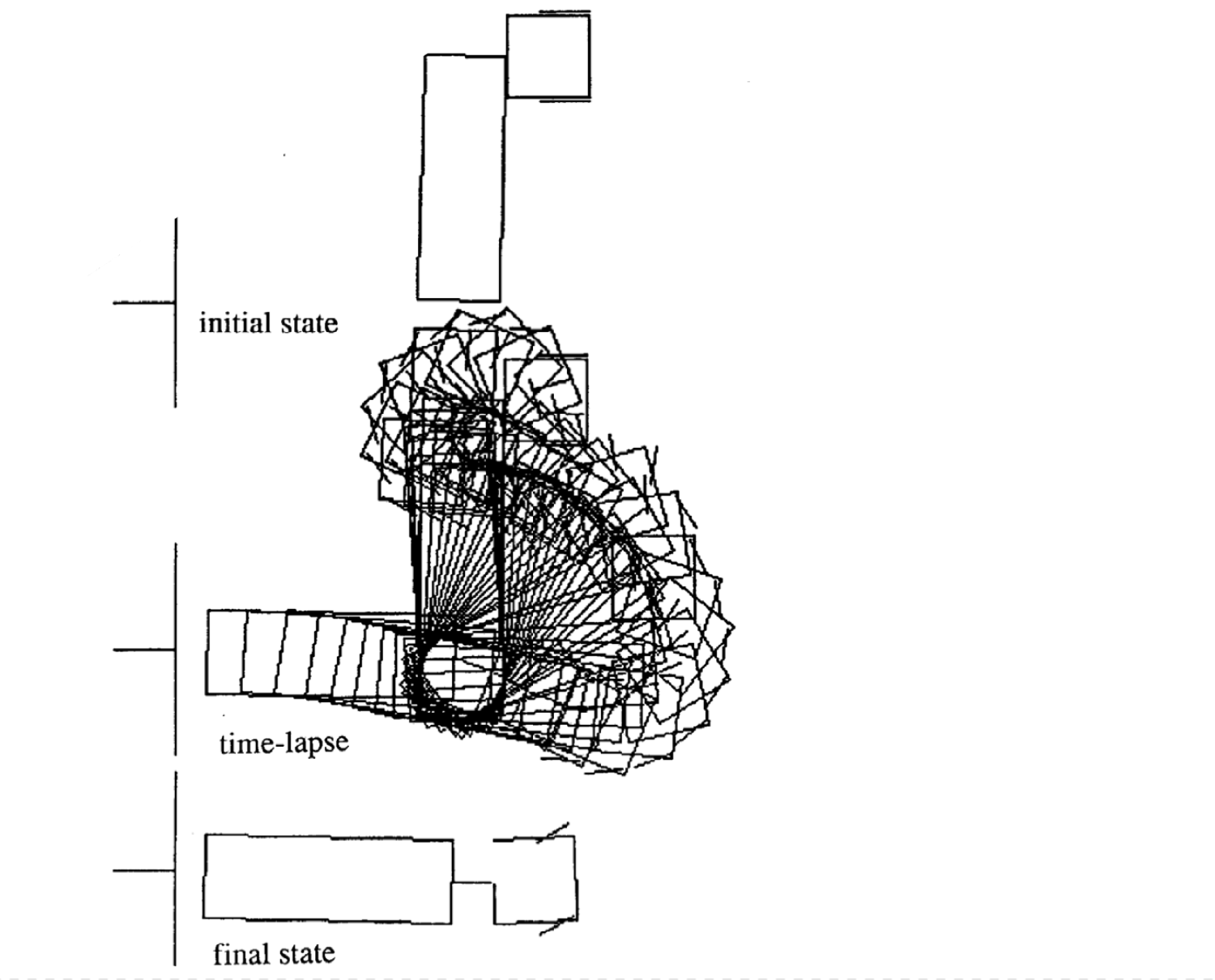
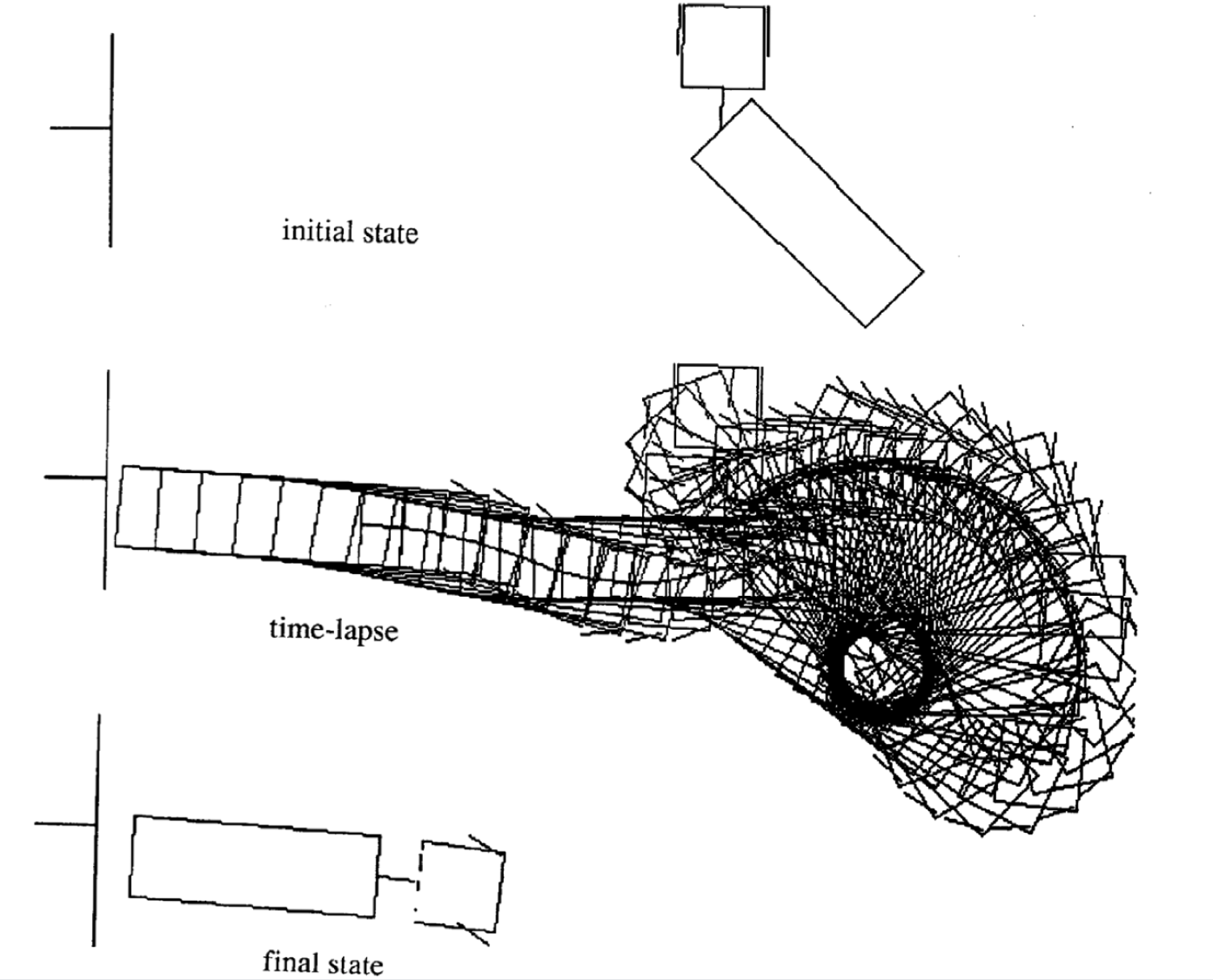
動きの例

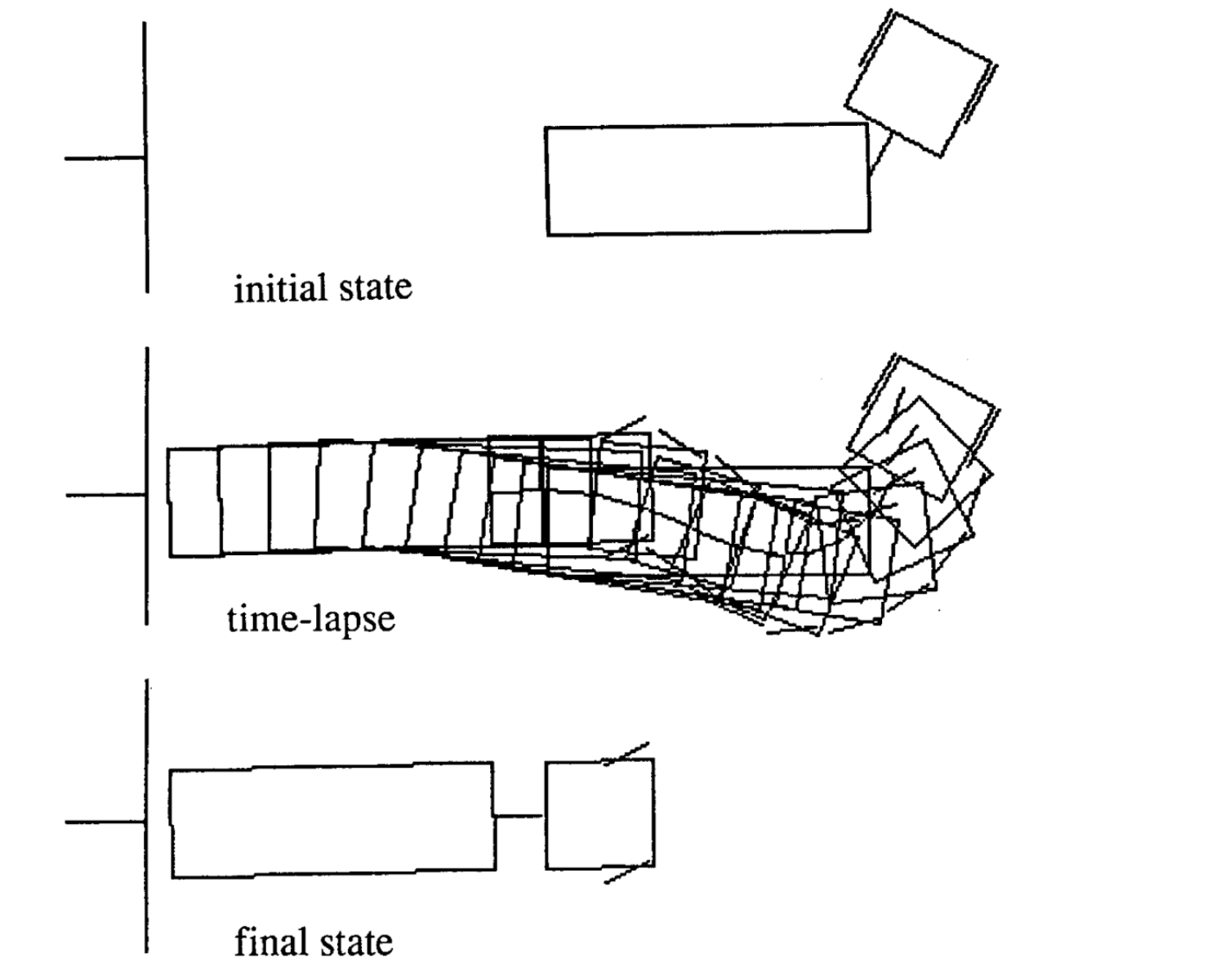
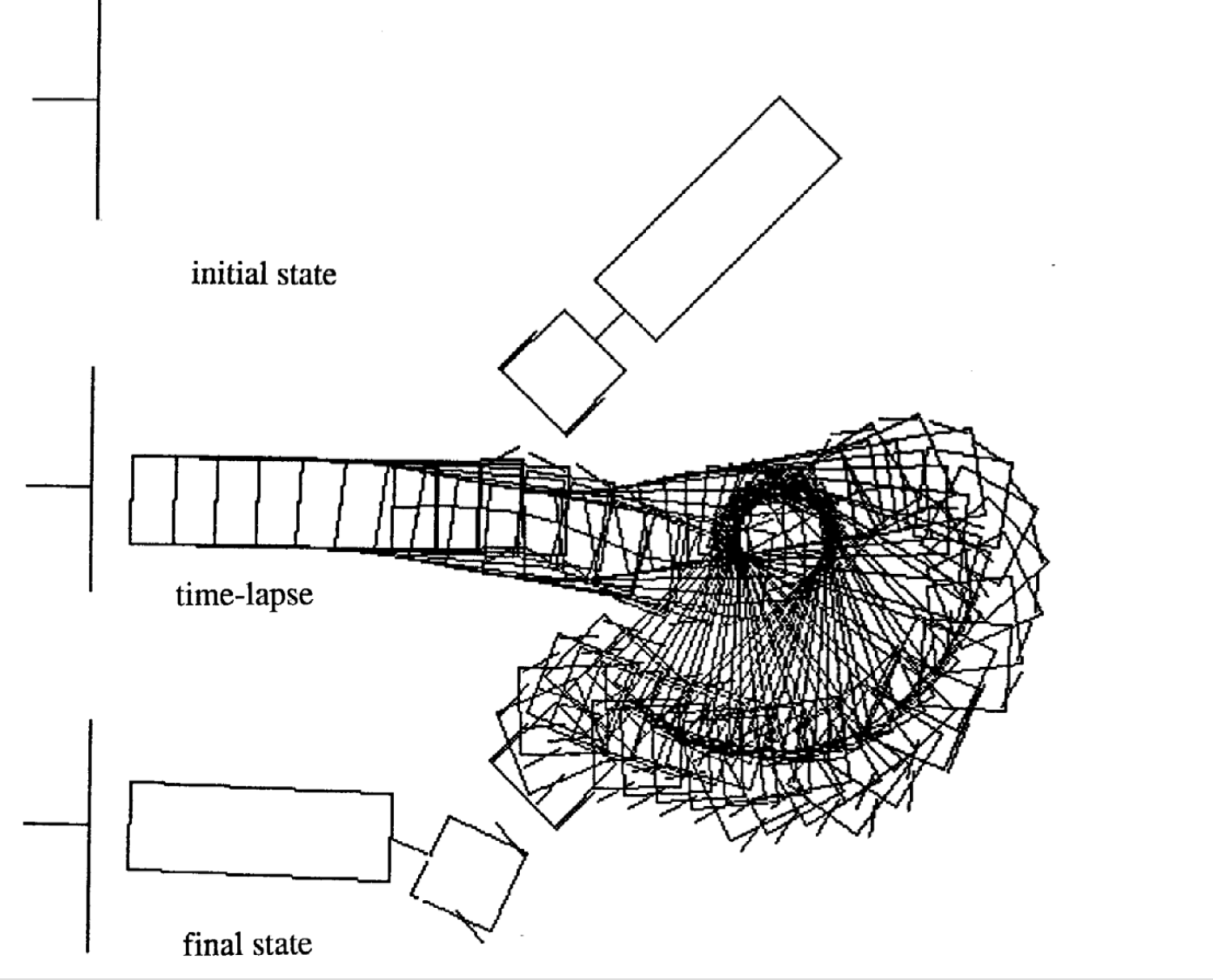
次の4つは異なる初期状態から始めた時の例です。各エピソードの時間ステップがばらついていることに注意してください。

<!–	Fig. 7: Examples of movement for four different initial states	–>
図7: 4つの異なる初期状態から始めた時の例

追加の情報源:

動かせる完全なデモは次のサイトで見ることができます：https://tifu.github.io/truck_backer_upper/。

次のリンクにあるコードもチェックしてみてください：https://github.com/Tifu/truck_backer_upper。